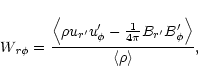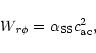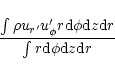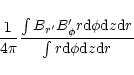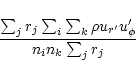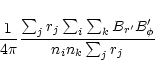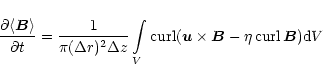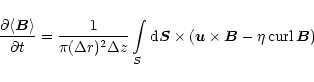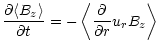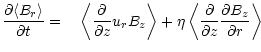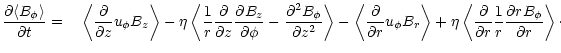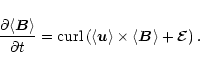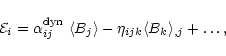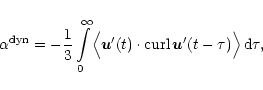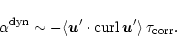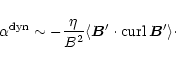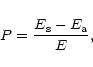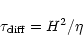A&A 374, 1035-1048 (2001)
DOI: 10.1051/0004-6361:20010797
Global accretion disk simulations of magneto-rotational instability
R. Arlt - G. Rüdiger
Astrophysikalisches Institut Potsdam, An der Sternwarte 16,
14482 Potsdam, Germany
Received 14 December 2000 / Accepted 30 May 2001
Abstract
We perform global three-dimensional simulations
of accretion disks integrating
the compressible, non-viscous, but diffusive MHD equations.
The disk is supposed to be isothermal. We make use of the
ZEUS-3D code integrating the MHD equations and added magnetic
diffusivity.
We measure the efficiency of the angular-momentum transport.
Various model simulations delivered transport parameters of
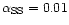 to 0.05 which are consistent with
several local numerical investigations. Two of the models
reach a highly turbulent state at which
to 0.05 which are consistent with
several local numerical investigations. Two of the models
reach a highly turbulent state at which
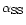 is
of the order of 0.1. After a certain stage of saturating of the
turbulence, Reynolds stress is found to be negative (inward transport)
in many of the models, whereas Maxwell stresses dominate and deliver a
positive (outward) total transport. Several of the models
yield strongly fluctuating Reynolds stresses,
while Maxwell stresses are smooth and always transport outwards.
Dynamo action is found in the accretion disk simulations.
A positive dynamo-
is
of the order of 0.1. After a certain stage of saturating of the
turbulence, Reynolds stress is found to be negative (inward transport)
in many of the models, whereas Maxwell stresses dominate and deliver a
positive (outward) total transport. Several of the models
yield strongly fluctuating Reynolds stresses,
while Maxwell stresses are smooth and always transport outwards.
Dynamo action is found in the accretion disk simulations.
A positive dynamo-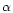 is indicated in the northern
hemisphere of the most prominent run, coming along with
negative kinetic and current
helicities (all having the opposite sign on the southern
side). The dipolar structure of the magnetic field is
maintained throughout the simulations, although indication
for a decay of antisymmetry is found. The simulations covered
relatively thick disks, and results of thin-disk dynamo
models showing quadrupolar fields may not be compatible with
the results presented here.
is indicated in the northern
hemisphere of the most prominent run, coming along with
negative kinetic and current
helicities (all having the opposite sign on the southern
side). The dipolar structure of the magnetic field is
maintained throughout the simulations, although indication
for a decay of antisymmetry is found. The simulations covered
relatively thick disks, and results of thin-disk dynamo
models showing quadrupolar fields may not be compatible with
the results presented here.
Key words: accretion disks - instabilities - magnetic fields
- MHD - turbulence
Accretion processes in astrophysical disks lead to enormous
luminosity and huge changes in disk structure during astronomically
short times. Efficient transport mechanisms are necessary to
achieve such short time-scales. Anisotropic turbulence appears
to be a major physical condition to provide astrophysical disks
with strong transport. As these disks generally exhibit increasing
specific angular momentum towards larger radii and thus fulfill the
stability criterion of Rayleigh, they do not give rise to an instability
leading to turbulence by themselves.
Searches for instabilities in disks with rotation profiles
similar to a Keplerian one unveiled several ways to turbulence
being more or less favorable with respect to their
prerequisites for the disk configuration. Gravitational instability
needs the disk to be either cool or massive. Nonlinear and
nonaxisymmetric perturbations require a severe additional perturber
near the disk; conditions for instability in a purely hydrodynamical
disk were derived by Dubrulle (1993). Hydrodynamic instability
essentially comes down to violating the Rayleigh criterion saying
that a rotation profile with an increasing specific angular momentum with
radius is hydrodynamically stable, that is for
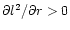 .
Since the typical length of
perturbations caused be external forces is supposed to be very
large, the required amplitude of the perturbations has to
be considerable, too, in order to violate the Rayleigh criterion
locally. If the length scale of the perturbation is comparable
to the radius, a strong alteration of the Keplerian velocity of
several per cent is needed. Convection was shown to deliver
either negligible transport (Stone & Balbus 1996) or inward
angular momentum transport (Kley et al. 1993).
.
Since the typical length of
perturbations caused be external forces is supposed to be very
large, the required amplitude of the perturbations has to
be considerable, too, in order to violate the Rayleigh criterion
locally. If the length scale of the perturbation is comparable
to the radius, a strong alteration of the Keplerian velocity of
several per cent is needed. Convection was shown to deliver
either negligible transport (Stone & Balbus 1996) or inward
angular momentum transport (Kley et al. 1993).
The requirements
for the magnetic shear-flow instability (Balbus & Hawley 1991)
do match astrophysical conditions in accretion disks in many
configurations. All it needs is a radially decreasing
angular velocity and a weak magnetic field threading the
rotating object. It can even be shown that the temperature
range applicable to the magnetic shear-flow
concept is very broad; even very small ionization fractions are sufficient
to magnetize a disk in many cases (Balbus & Hawley 1998).
First numerical approaches to the magnetic shear-flow instability
tackled the local problem; the linear analysis as described
by Balbus & Hawley (1991) were immediately followed by 2D simulations (Hawley & Balbus 1991) of a small box-shaped
domain which was cut out of the disk. These computations
confirmed the relation between magnetic-field strength and
wavenumber derived from the linear analysis earlier, they
showed that the maximum growth rate of any wavenumber is
independent from the field strength and that the system is capable of
transporting angular momentum. Because of being restricted
to axisymmetric problems, they could not provide self-sustained
turbulence which needs dynamo-action, and the slow decay of the
turbulence is an indirect effect of the Cowling theorem.
Improved computations dealt with
a three-dimensional even though local configuration, and particular
care was taken for the radial boundary conditions which are
not simply periodic, but account for the shear due to differential
rotation (Hawley et al. 1995). These comprehensive computations
indeed resulted in magnetically sustained turbulence whose anisotropy
causes efficient outward angular momentum transport. This work
was followed up by stratified models (Stone et al. 1996) covering
more than 50 orbital periods of the box cut-out. As the computational
domain covered 2 density scale heights, this work was a first
step towards global simulations, followed up by similar approaches
such as Ziegler & Rüdiger (2000a,b).
Linear studies of global configurations of disks threaded by
magnetic fields in various directions were carried out. Curry & Pudritz
(1995) investigated the stability for vertical and azimuthal
fields threading the disk. They found in detail that the actual
initial field geometry does not strongly depend on field topology
as was suggested by the numerical simulations of Hawley & Balbus (1991).
Rüdiger et al. (1999) particularly addressed the angular
momentum transport in their linear study. The first nonlinear global
approach by numerical simulations with full azimuthal coverage was
presented by Armitage (1998) who omitted the density stratification
for the sake of a large radial extent of the disk.
A global approach with stratification was then
presented by Hawley (2000) following the evolution of a thick torus
under the influence of an external magnetic field threading parts
of the computational domain. The magnetic shear-flow instability
was found to set in quickly causing enough turbulent viscosity
to soon form a Keplerian velocity profile. All the above mentioned
numerical studies integrate the ideal MHD equations omitting
magnetic diffusivity. Local simulations including diffusivity were
performed by Fleming et al. (2000) which proved the onset of instability
even for low conductivity.
The full understanding of accretion disks implies self-excited
dynamo action as well as angular momentum transport. Can positive
angular momentum transport be coupled with a suitable kinetic
helicity providing the expected dynamo action according to the
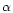 -effect principle? As the kinetic helicity in stratified,
rotating disks is expected to be negative, a wrong sign (positive)
would follow for the dynamo-
-effect principle? As the kinetic helicity in stratified,
rotating disks is expected to be negative, a wrong sign (positive)
would follow for the dynamo-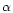 -effect according to the
conventional
-effect according to the
conventional 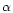 -theories. We present global three-dimensional
diffusive simulations and study the angular momentum transport
as well as dynamo action and the sign of
-theories. We present global three-dimensional
diffusive simulations and study the angular momentum transport
as well as dynamo action and the sign of
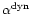 as a
consequence of the correlation with the flow.
as a
consequence of the correlation with the flow.
The computations presented here make use of the ZEUS-3D
code developed for astrophysical problems of magnetohydrodynamics
(see the key papers Stone & Norman 1992a,b, Stone et al. 1992 for
numerical; Clarke et al. 1994 for technical details). We use cylindrical
coordinates and computational domains covering various annuli with a
a vertical extension of z=-1 to +1
and the full azimuthal range of 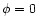 to
to 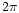 .
See
Table 1 for a list of models presented in this Paper.
The notation
.
See
Table 1 for a list of models presented in this Paper.
The notation 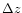 ,
,
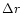 ,
and
,
and
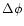 will
refer to the extensions of the computational domain in the
vertical, radial and azimuthal directions, respectively.
In this approach, we assume an isothermal disk to save computation
time on the energy equation. The remaining system for
integration is
will
refer to the extensions of the computational domain in the
vertical, radial and azimuthal directions, respectively.
In this approach, we assume an isothermal disk to save computation
time on the energy equation. The remaining system for
integration is
where 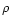 ,
,
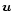 ,
and
,
and 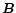 are the density, velocity,
and magnetic field resp.; p is the pressure relating to the density
by
are the density, velocity,
and magnetic field resp.; p is the pressure relating to the density
by
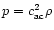 in our model, with the constant sound speed
in our model, with the constant sound speed
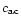 ,
,
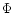 is the gravitational potential (solely from a
central mass M),
is the gravitational potential (solely from a
central mass M), 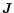 is the current density,
and
is the current density,
and 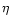 is the magnetic diffusivity which is not an original
ingredient to the ZEUS code. It is constant in time and space.
The computations of the electromotive force in the routines
emfs, mocemfs, and hsmoc of ZEUS-3D are extended with the
appropriate
is the magnetic diffusivity which is not an original
ingredient to the ZEUS code. It is constant in time and space.
The computations of the electromotive force in the routines
emfs, mocemfs, and hsmoc of ZEUS-3D are extended with the
appropriate
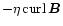 components. We chose
components. We chose
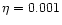 to 0.01.
The additional time-step criterion resulting from the diffusivity
is roughly 0.1 for the finest grid used here. It is therefore
irrelevant for the determination of the time-step which is typically
10-4 or, in the case of strong fluctuations of velocity
and magnetic field, one or two orders of magnitude lower. In
physical units, this diffusivity is large and in fact accounting
for a subgrid turbulent diffusivity which cannot be resolved.
Yet it is small enough to provide numerically sensible magnetic Reynolds
numbers of 103-104, the natural Reynolds numbers being
orders of magnitudes higher though.
to 0.01.
The additional time-step criterion resulting from the diffusivity
is roughly 0.1 for the finest grid used here. It is therefore
irrelevant for the determination of the time-step which is typically
10-4 or, in the case of strong fluctuations of velocity
and magnetic field, one or two orders of magnitude lower. In
physical units, this diffusivity is large and in fact accounting
for a subgrid turbulent diffusivity which cannot be resolved.
Yet it is small enough to provide numerically sensible magnetic Reynolds
numbers of 103-104, the natural Reynolds numbers being
orders of magnitudes higher though.
The gravitational potential is spherically symmetric, whence
the z-component of the gravitation is retained within the disk.
We therefore obtain a density stratification unlike the computations
by Armitage (1998) who omits the z-component of the gravitation
and applies periodic boundary conditions for the upper and lower
boundaries. His approach allows much larger radial extents of
the computational domain as the numerical restrictions from
large density contrasts do not emerge.
The sound speed is always
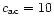 which is
roughly 7% of the average Keplerian velocity
in the simulated ring. The initial density distribution is
Gaussian with r-dependent density scale-height H, thus
which is
roughly 7% of the average Keplerian velocity
in the simulated ring. The initial density distribution is
Gaussian with r-dependent density scale-height H, thus
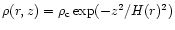 with a density in the equatorial
plane of
with a density in the equatorial
plane of
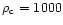 .
The equilibrium hydrodynamic model
settles such that the z-extent of the domain covers 3Hat r=4 and 1.5H at r=6.
.
The equilibrium hydrodynamic model
settles such that the z-extent of the domain covers 3Hat r=4 and 1.5H at r=6.
The magnetic field threads the disk vertically with a mere
z-component. We tried a homogeneous initial field
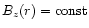 for the z-boundaries as well as a field
for the z-boundaries as well as a field
![\begin{displaymath}%
B_z(r,t=0) = b_0 r^{-1} \sin [2\pi (r-r_{\rm i})/(r_{\rm o}-r_{\rm i})]
\end{displaymath}](/articles/aa/full/2001/30/aah2593/img38.gif) |
(4) |
- where 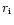 and
and 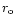 are the inner and outer boundary
radii resp. - which has zero total magnetic flux through the
are the inner and outer boundary
radii resp. - which has zero total magnetic flux through the
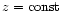 surfaces. The choice of the initial field will have implications
for the topology of the field later on. As the magnetic flux through
the surfaces is kept constant, the first approach will always
preserve a non-zero average magnetic field through the vertical
boundaries, whereas the field penetrating the top and the bottom
of the computational domain can completely vanish in the second
choice of initial fields. The results presented here were obtained
with the second approach of vanishing average initial field Bz.
The parameter b0 was chosen between 50 and 100 giving an amplitude of the
initial magnetic field of
surfaces. The choice of the initial field will have implications
for the topology of the field later on. As the magnetic flux through
the surfaces is kept constant, the first approach will always
preserve a non-zero average magnetic field through the vertical
boundaries, whereas the field penetrating the top and the bottom
of the computational domain can completely vanish in the second
choice of initial fields. The results presented here were obtained
with the second approach of vanishing average initial field Bz.
The parameter b0 was chosen between 50 and 100 giving an amplitude of the
initial magnetic field of
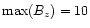 to 20 corresponding to
maximum Alfvén speeds at the upper and lower boundaries of
to 20 corresponding to
maximum Alfvén speeds at the upper and lower boundaries of
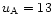 to 26 or
to 26 or
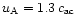 to
to
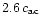 .
The Alfvén velocity in the equatorial plane is subthermal
with
.
The Alfvén velocity in the equatorial plane is subthermal
with
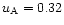 to 0.63 or
to 0.63 or
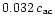 to
to
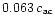 .
.
The initial velocity field is a merely Keplerian motion
following
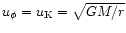 ,
where G is the gravitational
constant and M is the central mass which is 105 in our computational
units. Times are henceforth measured in orbital periods which convert
by
,
where G is the gravitational
constant and M is the central mass which is 105 in our computational
units. Times are henceforth measured in orbital periods which convert
by
 as given in Table 1 from the arbitrary units
of the code.
as given in Table 1 from the arbitrary units
of the code.
The number of cells in each coordinate direction was typically
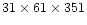 for the z-, r-, and
for the z-, r-, and 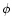 -directions.
The aspect ratio of the grid cells is not unity. Finest resolution
is achieved in radial direction, lowest in azimuthal direction:
-directions.
The aspect ratio of the grid cells is not unity. Finest resolution
is achieved in radial direction, lowest in azimuthal direction:
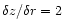 ,
,
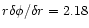 for the most
often used inner radius r=4 and
for the most
often used inner radius r=4 and
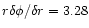 for
r=6 (Models II, III, V, VI, and VII), where
for
r=6 (Models II, III, V, VI, and VII), where 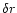 refers to
the mesh width in radial direction and so on. Tests with up to 621 cells
in
refers to
the mesh width in radial direction and so on. Tests with up to 621 cells
in 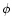 -direction have been carried out, but the increased
computation time does not allow reasonable periods to be covered
by the simulation.
-direction have been carried out, but the increased
computation time does not allow reasonable periods to be covered
by the simulation.
The fastest growing mode of the magneto-rotational instability has
a wavelength of
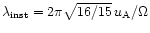 .
With the angular velocity of
.
With the angular velocity of
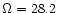 for r=5 which
is the middle of most of the radial ranges used,
we obtain wavelengths between 0.4 and 0.9 with the above
given Alfvén velocities of the initial field strength.
These wavelengths are upper limits as they refer to the
sites of maximum field and minimum density which need not
coincide necessarily. Yet, they are well resolved by the
computation domain covering z-ranges of 2.0 and two
different r-intervals of 1.0 and 2.0.
for r=5 which
is the middle of most of the radial ranges used,
we obtain wavelengths between 0.4 and 0.9 with the above
given Alfvén velocities of the initial field strength.
These wavelengths are upper limits as they refer to the
sites of maximum field and minimum density which need not
coincide necessarily. Yet, they are well resolved by the
computation domain covering z-ranges of 2.0 and two
different r-intervals of 1.0 and 2.0.
The integration of the magnetic fields was done with the
evolution of the electromotive forces by the
Constraint Transport scheme (CT, Evans & Hawley 1988)
which preserves a divergence-free configuration.
The advection scheme of velocity and density involves
the second-order van-Leer interpolation.
Two terms adding a source of viscosity to the hydrodynamic
equations extend the above Navier-Stokes equation as indicated
by dots in Eq. (2). The
von Neumann-Richtmyer artificial viscosity depends on the
square of velocity gradients and acts only on decreasing velocity
in the direction of propagation, i.e. compression. The strength
of this term is denoted by
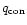 in the implementation
of the ZEUS-3D code. The second
term depends linearly on the velocity gradient and acts on both
compression and expansion; the strength is represented by
in the implementation
of the ZEUS-3D code. The second
term depends linearly on the velocity gradient and acts on both
compression and expansion; the strength is represented by
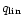 .
Tests with a stable Keplerian flow found the
choice of
.
Tests with a stable Keplerian flow found the
choice of
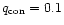 and
and
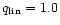 to be suitable.
These values were used throughout all the runs described here.
The Courant number determining the "safety'' of a certain maximum
allowed time step derived from the velocities, magnetic fields, and
the artificial viscosities, is set to 0.5.
to be suitable.
These values were used throughout all the runs described here.
The Courant number determining the "safety'' of a certain maximum
allowed time step derived from the velocities, magnetic fields, and
the artificial viscosities, is set to 0.5.
Occasionally, pockets of extremely low density may emerge
coupled with extraordinarily high speeds exceeding the
Keplerian velocity. We suppress the existence of such
pockets by a mass replenishment as soon as the density
of a certain cell drops below 10-4 the central density.
The actual mass being thus added to the total disk mass
is found to be negligible. The mass replenishment thus
acts like a lower limit for the time step.
The vertical boundary condition on the
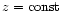 -faces
of our computational domain are closed for the flow, i.e.
uz=0. The boundary condition is stress-free in the sense
of
-faces
of our computational domain are closed for the flow, i.e.
uz=0. The boundary condition is stress-free in the sense
of
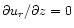 and
and
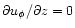 .
The magnetic field has to fulfill the "opposite'' boundary
condition as it is only allowed to cross the boundary
perpendicularly, which is actually implemented affecting the
electromotive force
.
The magnetic field has to fulfill the "opposite'' boundary
condition as it is only allowed to cross the boundary
perpendicularly, which is actually implemented affecting the
electromotive force
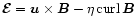 such that
such that
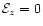 ,
,
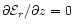 ,
and
,
and
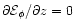 .
.
Computations were carried out with two choices of radial
boundary conditions regarding the velocity.
The first does not allow flow through the
top, bottom and outer radial boundaries. The inner boundary was chosen
to be "outflow'', that is, the physical arrays are constantly extrapolated
into the ghost zones of the computational domain. The only exception is
an inflow, in our case a ur > 0 at the inner boundary. This velocity
component is reset to zero then. All radial velocities ur<0 are
copied to the ghost zones beyond the computational domain. The same
holds for the density and the magnetic-field components. We will
henceforth refer to these models as Model Ia (only inner boundary
has "outflow'') and Ib (inner and outer radial and lower and upper
vertical boundaries have "outflow'').
Since the outflow condition is likely to empty the disk on the viscous
time-scale, the second choice tries to account for the accreted matter
and feeds the disk at the outer radial boundary. We sum up the mass
loss rate at the inner boundary
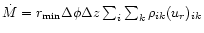 for
the total mass loss. The indices i and k run along the
vertical and azimuthal directions, respectively.
for
the total mass loss. The indices i and k run along the
vertical and azimuthal directions, respectively.
A constant, small inflow velocity
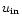 is assumed for the outer boundary. Accordingly, the density at the
outer boundary is determined to account for the mass flux at the
inner boundary. Since we use the average influx, its z-dependence
(nor even the
is assumed for the outer boundary. Accordingly, the density at the
outer boundary is determined to account for the mass flux at the
inner boundary. Since we use the average influx, its z-dependence
(nor even the 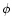 -dependence) is not used for a z- (nor even
-dependence) is not used for a z- (nor even 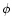 -)
dependent inflow from far radii. The boudary conditions for the outer
radial face are thus
-)
dependent inflow from far radii. The boudary conditions for the outer
radial face are thus
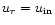 and
and
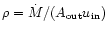 where
where
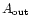 is the
surface of the outer boundary. The magnetic-field conditions are Br=0,
is the
surface of the outer boundary. The magnetic-field conditions are Br=0,
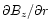 ,
and
,
and
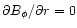 .
Note that this is not consistent with the actual inflow of matter,
but the
.
Note that this is not consistent with the actual inflow of matter,
but the
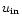 is extremely small, less than
is extremely small, less than
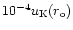 for the slow-inflow models and less than
for the slow-inflow models and less than
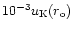 for the fast-infall models (see third column
of Table 1). Upon expanding
for the fast-infall models (see third column
of Table 1). Upon expanding
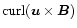 we find
we find
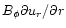 to be the relevant
term generating a contribution to Bz. The field in the last
three zones in Fig. 2 is an effect of this.
to be the relevant
term generating a contribution to Bz. The field in the last
three zones in Fig. 2 is an effect of this.
We tested inflow conditions with homogeneous and Gaussian
and density distribution. It was supposed that an average
influx of mass will establish according to the current viscosity
(either numerical or turbulent) in the disk. These models are referred
to as Model II-VIII in the following.
The azimuthal velocity, 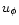 ,
is extrapolated into the radial boundary
zones by a power law r-1.5 based on the last zone of the
computational domain. The velocities are thus not Keplerian,
they just follow the same radial power law.
Since we cover the full azimuthal range in
,
is extrapolated into the radial boundary
zones by a power law r-1.5 based on the last zone of the
computational domain. The velocities are thus not Keplerian,
they just follow the same radial power law.
Since we cover the full azimuthal range in  ,
the
boundaries at the
,
the
boundaries at the
 surfaces are periodic, naturally.
surfaces are periodic, naturally.
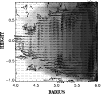 |
Figure 1:
Vertical cut through the disk of Model II after
6.3 orbital revolutions, excluding the high-velocity coronal
component of the disk. The shading represents the azimuthal component,
the arrows are the velocity vectors projected onto the (r,z)-plane. |
| Open with DEXTER |
 |
Figure 2:
Vertical cut through the disk of Model II after
6.3 orbital revolutions with an azimuthal-component shading and poloidal
magnetic-field vectors. |
| Open with DEXTER |
Typical vertical slices from a run of Model II are shown in
Figs. 1 and 2. The central mass is located on the
left side, outside the computational domain. The shadings
represent the azimuthal components of the magnetic and velocity
fields, while the arrows are the (r,z)-projections of the
actual vectors. Shaded areas near the equatorial plane of the disk
show the typical Keplerian velocity profile. However, at high
altitudes above the equator, a strong super-rotation emerges
coupled with relatively high infall velocities. (These high
radial velocities have been cut in Fig. 1 to better
show the velocities in the disk.)
The computational
domain thus covers part of the corona of the disk where the
density falls below 10-3 times the equatorial density.
The infall velocity in the corona is of the same order of magnitude
as the Keplerian velocity, whereas the non-orbital velocities
within the disk are much smaller. The actual flow in the disk
as shown in Fig. 1 is limited
by
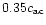 .
.
After saturation of the turbulence, the temporal behavior
of
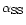 changes. The fairly smooth function turns into
an oscillatory behavior. The typical feature of this moment
is the zero-crossing of the Reynolds stress which is essentially
negative all through the saturation parts of the simulations.
It is expected that the infall of matter at the outer radial
boundary tends to perform relaxation motions, in particular
for Models II-IV where matter falls in homogeneously. The
exclusion of the outermost six cell planes from the computation
of the spatially average
changes. The fairly smooth function turns into
an oscillatory behavior. The typical feature of this moment
is the zero-crossing of the Reynolds stress which is essentially
negative all through the saturation parts of the simulations.
It is expected that the infall of matter at the outer radial
boundary tends to perform relaxation motions, in particular
for Models II-IV where matter falls in homogeneously. The
exclusion of the outermost six cell planes from the computation
of the spatially average
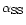 does not alter
the result (the actual relaxation motions are observed only
in the outermost three cell planes). Relaxation motions will
consist mainly of uz components which do not affect radial
angular-momentum transport directly.
does not alter
the result (the actual relaxation motions are observed only
in the outermost three cell planes). Relaxation motions will
consist mainly of uz components which do not affect radial
angular-momentum transport directly.
A problem connected with the homogeneous feeding of the disk
from the outer boundary is the appearance of a "density front''.
This is the reason why the density at the outer boundary is
highest which may look odd in the context of an accretion disk.
This incoming density enhancement can be partly leveled
by the presumed infall velocity at the outer boundary.
According to the standard model of a turbulent disk as essentially
worked out by Shakura & Sunyaev (1973), the 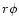 -element of the
stress tensor of velocity and magnetic-field fluctuations,
-element of the
stress tensor of velocity and magnetic-field fluctuations,
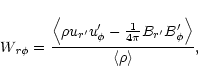 |
(5) |
scales like the speed of sound such as
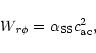 |
(6) |
parameterized by an unknown
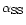 which is smaller than unity
in the case of subsonic turbulence. We normalize the stress by the average
density in the computational domain; other authors used the density
averaged in the equatorial plane leading to lower limits for
which is smaller than unity
in the case of subsonic turbulence. We normalize the stress by the average
density in the computational domain; other authors used the density
averaged in the equatorial plane leading to lower limits for
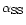 .
This stress measures the angular
momentum transport in the disk; positive values mean outward transport.
We average this quantity over the entire computational domain according to
.
This stress measures the angular
momentum transport in the disk; positive values mean outward transport.
We average this quantity over the entire computational domain according to
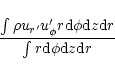 |
(7) |
for the velocity and
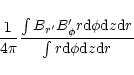 |
(8) |
for the magnetic field fluctuations. As the azimuthal velocity contains
a large supersonic axisymmetric mode - the Keplerian flow - we adopt
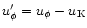 for the azimuthal velocity fluctuations
and
for the azimuthal velocity fluctuations
and
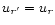 for the other component. The
averaging is in fact carried out on a discrete computational mesh by
for the other component. The
averaging is in fact carried out on a discrete computational mesh by
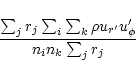 |
(9) |
for the velocity part and
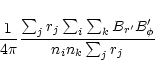 |
(10) |
for the magnetic part.
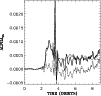 |
Figure 3:
Angular momentum transport by Reynolds (dashed) and Maxwell
(dotted) stresses as derived from a run of Model Ia, that is with
outflow boundary condition at the inner radial face and a closed
boundary for flow and magnetic fields at the outer radial face.
The total transport (thick solid line) is positive
and of the order of 0.0005. |
| Open with DEXTER |
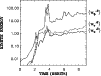 |
Figure 4:
Energy in individual velocity components of Model Ia. |
| Open with DEXTER |
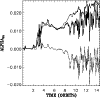 |
Figure 5:
Angular momentum transport by Reynolds (dashed) and Maxwell
(dotted) stresses as derived from a run of Model II.
The total transport (thick solid line) is positive
and of the order of 0.01. |
| Open with DEXTER |
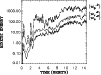 |
Figure 6:
Energy in individual velocity components of Model II. |
| Open with DEXTER |
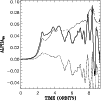 |
Figure 7:
Angular momentum transport by Reynolds (dashed) and Maxwell
(dotted) stresses as derived from a run of Model III. The homogeneous
inflow velocity is ten times higher in this simulation that in
Fig. 5. |
| Open with DEXTER |
The time series of the outflow model Ia is shown in
Fig. 3. Model Ia in particular shows a
short-lived occurrence of strong angular-momentum transport;
a similar but less pronounced behavior is found in Model Ib.
This period is the only time in both Models Ia and Ib when
Reynolds stresses dominate the Maxwell stresses. A similarity
to the transient channel solution as described by Hawley et al. (1995) is likely, although that was found for uniform initial Bz.
Time series for long runs of Models II and Model III are shown in
Figs. 5 and 7.
Generally, the accretion model shows stronger angular momentum
transport than the the simpler inner-outflow Model Ia.
Models Ia and Ib run out of matter after about 8 orbital revolutions
with enabled magnetic fields, and the
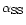 values are no longer meaningful.
values are no longer meaningful.
A striking feature of the accretion Models II and III is the
change of sign in the Reynolds stress after about 4-6 orbits.
We find that, in a long run, the outward angular momentum transport
is a sole consequence of the magnetic stresses. Additionally,
the Reynolds part shows strong amplitude variations unlike the
Maxwell stress.
Figures 4 and 6 show the respective temporal
evolution of the fluctuative kinetic energies. For the z- and
r-components, the zero mode is subtracted such as
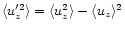 ;
the azimuthal fluctuative energy is found by
;
the azimuthal fluctuative energy is found by
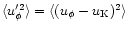 .
All three models show a clear energy "sorting'' of the z-, r-, and
.
All three models show a clear energy "sorting'' of the z-, r-, and
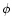 -components in this order.
-components in this order.
A particularly long run was performed with a computational domain
only half as large as Models II and III and is denoted by IV. The
initial and boundary conditions are like in Model II. The
long-term behavior is not too similar to that of Model II with
very strong oscillations of Reynolds versus Maxwell stresses.
A behavior comparable with Model II may be spotted during the
first 8 orbital periods. After that time, the energy sorting
of the radial and vertical components is given up.
All models from Ia to IV appear to be not fully saturated with
respect to the ever-growing kinetic energies.
We should note that a homogeneous infall might be suitable for
a realistic disk in the sense that the infalling matter does not
"know'' the structure of the disk. Nevertheless, numerical
problems may occur when the incoming homogeneous "matter front''
meets the near-Gaussian density structure. Models V and VI
apply an inflow with pre-defined Gaussian infall profile over
z. The respective
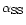 -profiles are shown in
Figs. 8 and 10, the
first having an infall velocity of
-profiles are shown in
Figs. 8 and 10, the
first having an infall velocity of
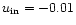 ,
the second
,
the second
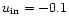 .
The initial behavior is similar to the respective
Models II and III including the change of sign of the Reynolds stress
after a couple of orbits. After as many as 10 orbital periods,
the disk turns into a significantly different regime with
enhanced outward transport in both models.
.
The initial behavior is similar to the respective
Models II and III including the change of sign of the Reynolds stress
after a couple of orbits. After as many as 10 orbital periods,
the disk turns into a significantly different regime with
enhanced outward transport in both models.
The respective kinetic energies are given in Figs. 9
and 11. In contrast to the above studied models,
energies do not develop in an ever-growing way, but appear to fluctuate
about an average. The only exception is the regime change near
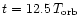 (Model V) and
(Model V) and
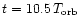 (Model VI)
when the average (essentially of
(Model VI)
when the average (essentially of
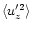 )
changes, but
the stationary appearance remains.
)
changes, but
the stationary appearance remains.
 |
Figure 8:
Angular momentum transport by Reynolds (dashed) and Maxwell
(dotted) stresses as derived from a run of Model V. Density is
not falling in homogeneously, but with a predefined Gaussian vertical
distribution; the (homogeneous) inflow velocity is
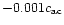 . . |
| Open with DEXTER |
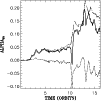 |
Figure 10:
Angular momentum transport by Reynolds (dashed) and Maxwell
(dotted) stresses as derived from a run of Model VI. The inflow
velocity is ten times higher than in model V,
Fig. 8. |
| Open with DEXTER |
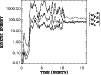 |
Figure 11:
Energy in individual velocity components of Model VI. |
| Open with DEXTER |
The distribution of
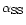 versus time and the z-direction
is shown in Fig. 12 for Models V. Outward angular momentum
transport is marked with white areas, inward transport by dark areas.
Strong transport is observed at large distances from the equator
shortly after the onset of the instability. Regions of outward
transport migrate towards the equator. This is particularly marked
in the Model V plot for which we found a development into a
strong-transport regime (cf. Fig. 8).
Positive angular momentum transport is not restricted to high
altitudes anymore.
versus time and the z-direction
is shown in Fig. 12 for Models V. Outward angular momentum
transport is marked with white areas, inward transport by dark areas.
Strong transport is observed at large distances from the equator
shortly after the onset of the instability. Regions of outward
transport migrate towards the equator. This is particularly marked
in the Model V plot for which we found a development into a
strong-transport regime (cf. Fig. 8).
Positive angular momentum transport is not restricted to high
altitudes anymore.
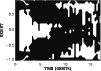 |
Figure 12:
Distribution of the total stress
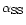 versus time and vertical coordinate for Model V.
Light areas represent inward transport, dark areas outward transport.
versus time and vertical coordinate for Model V.
Light areas represent inward transport, dark areas outward transport. |
| Open with DEXTER |
 |
Figure 13:
Variability of the accretion rate of Model II
in an arbitrary scale. |
| Open with DEXTER |
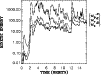
The temporal development of the accretion rate measured
at the inner radial boundary is given in Fig. 13.
As we were free to choose a central disk density, the computation
of the accretion rate in physical units will not provide much
information, whence the arbitrary units in Fig. 13.
Choosing the rough dimensions of an inner protostellar system
of 100 AU radius for scaling the mass flux through our models,
one would obtain an accretion rate of about
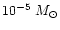 /yr
for Model II shown in the figure.
/yr
for Model II shown in the figure.
The application of accreting boundary conditions allows
relatively long durations of the simulations at constant
total mass. Yet, the influence of the inconsistent outer
radial boundary becomes important after approximately
15 orbital periods. The major part of the mass concentrates
near the outer boundary, while the rest of the disk appears
to run empty with strong inward radial velocities of
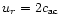 to
to
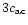 .
At this point, our
adjustment of the inflow density to sustain the total mass
does not match the actual process going on, and a strong
pile-up of density at the inlow boundary will be observed.
The disruption is particularly sudden for Models V, VI, and VII
which are specific in that they have a higher magnetic diffusivity
than the other models.
.
At this point, our
adjustment of the inflow density to sustain the total mass
does not match the actual process going on, and a strong
pile-up of density at the inlow boundary will be observed.
The disruption is particularly sudden for Models V, VI, and VII
which are specific in that they have a higher magnetic diffusivity
than the other models.
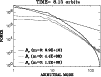 |
Figure 14:
Azimuthal Fourier decomposition of the magnetic-field components
after 8.15 orbital periods in Model V. The dotted
line shows a Kolmogorov power law with exponent -5/3. |
| Open with DEXTER |
Power spectra resulting from Fourier transforms of the magnetic field
of Model V over the the azimuthal and radial directions are shown
in Figs. 14 and 15,
respectively. The azimuthal decomposition of the velocity field
is shown in Fig. 16. The individual
azimuthal spectra for all points in the (z,r)-plane were
averaged, as were the points of the (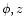 )-plane for the
radial spectra. In the azimuthal spectra, we observe
slight maxima in power at k=5 and k=8, followed by a strong, roughly
power-law decline between
)-plane for the
radial spectra. In the azimuthal spectra, we observe
slight maxima in power at k=5 and k=8, followed by a strong, roughly
power-law decline between 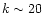 and
and 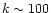 .
The magnetic
spectrum is steeper than the kinetic one. The underlying power-laws
would be
.
The magnetic
spectrum is steeper than the kinetic one. The underlying power-laws
would be
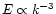 to
to
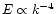 which is significantly
steeper than a Kolmogorov spectrum, and is similar to what Armitage
(1998) found for a global simulation in the far-k range. The Kolmogorov
spectrum of isotropic turbulence would exhibit a wavenumber
exponent of -5/3; here we face MHD turbulence which implies an
effect of Alfvén waves impeding the transfer of energy towards
smaller scales. The energy spectrum of isotropic MHD turbulence
is
which is significantly
steeper than a Kolmogorov spectrum, and is similar to what Armitage
(1998) found for a global simulation in the far-k range. The Kolmogorov
spectrum of isotropic turbulence would exhibit a wavenumber
exponent of -5/3; here we face MHD turbulence which implies an
effect of Alfvén waves impeding the transfer of energy towards
smaller scales. The energy spectrum of isotropic MHD turbulence
is
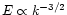 .
Contrasting with the azimuthal decomposition, the radial spectrum
matches the Kolmogorov spectrum over the entire range
of modes as can be seen in Fig. 15.
.
Contrasting with the azimuthal decomposition, the radial spectrum
matches the Kolmogorov spectrum over the entire range
of modes as can be seen in Fig. 15.
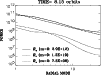 |
Figure 15:
Radial Fourier decomposition of the magnetic-field
components after 8.15 orbital periods in Model V. |
| Open with DEXTER |
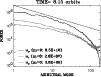 |
Figure 16:
Azimuthal Fourier decomposition of the velocity
components after 8.15 orbital periods in Model V. |
| Open with DEXTER |
Among stratified local simulations, we find a number of very similar results
as regards the magnitude of
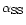 ,
such as in
Stone et al. (1996) who obtained 0.01,
Hawley et al. (1996) where an average of 0.016 was found, with typical
values of 0.01. The largest box used delivered 0.02, the smallest, 0.003.
Upon studying the dependence of the turbulence on the rotation law
,
such as in
Stone et al. (1996) who obtained 0.01,
Hawley et al. (1996) where an average of 0.016 was found, with typical
values of 0.01. The largest box used delivered 0.02, the smallest, 0.003.
Upon studying the dependence of the turbulence on the rotation law
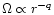 ,
Hawley et al. (1999) found 10-2 for q=1.5.
A most recent local-box simulation by Ziegler & Rüdiger (2000b)
covering 288 orbital periods
resulted in a space-time average of 0.015, where the Reynolds part
was
,
Hawley et al. (1999) found 10-2 for q=1.5.
A most recent local-box simulation by Ziegler & Rüdiger (2000b)
covering 288 orbital periods
resulted in a space-time average of 0.015, where the Reynolds part
was
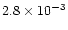 and the Maxwell part was
and the Maxwell part was
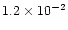 .
The stress was normalized with the averaged equatorial-plane
pressure and thus provides a lower limit for
.
The stress was normalized with the averaged equatorial-plane
pressure and thus provides a lower limit for
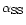 .
The early stratified-box simulations by Brandenburg et al. (1995)
provided
.
The early stratified-box simulations by Brandenburg et al. (1995)
provided
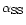 an order of magnitude lower between 0.001
and 0.005. All the models agree upon the dominance of Maxwell
stresses over Reynolds stresses.
an order of magnitude lower between 0.001
and 0.005. All the models agree upon the dominance of Maxwell
stresses over Reynolds stresses.
It is most interesting to note that other global simulations such as
performed by Armitage (1998) or Hawley (2000) result in an order
of magnitude higher values of 0.2 to 0.3. Contrasting with this,
the global spherical, but unstratified simulation by Drecker (2000)
gives again an
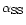 which is an order of magnitude
lower than shown here, i.e. 10-3. Those simulations alone
included a physical viscosity. The simulations of Hawley (2000)
- and with somewhat different objectives, those of Machida et al. (2000)
- had open boundaries in radial and vertical directions. This
fact limits the run-time of the models which are prone to running
out of matter.
which is an order of magnitude
lower than shown here, i.e. 10-3. Those simulations alone
included a physical viscosity. The simulations of Hawley (2000)
- and with somewhat different objectives, those of Machida et al. (2000)
- had open boundaries in radial and vertical directions. This
fact limits the run-time of the models which are prone to running
out of matter.
The amplification of the total magnetic energy by a factor of roughly
103 from the initial magnetic-field perturbation to the
state of strong angular-momentum transport indicates considerable
dynamo action in the disk. In the following we will investigate
the characteristics of magnetic-field generation in our simulations.
The local-box simulations by Hawley et al. (1996) impose severe
constraints on the growth of an average magnetic field because
of the periodicity of the boundary conditions. A non-zero term
of the average magnetic-field growth is due to the shear and requires
the presence of an average radial component, in the local nomenclature
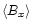 .
We follow their derivation of the averages
by replacing the volume curl integral by a vector-product surface
integral of (3). The average
.
We follow their derivation of the averages
by replacing the volume curl integral by a vector-product surface
integral of (3). The average
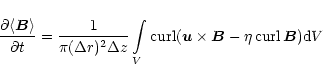 |
(11) |
is equivalent to
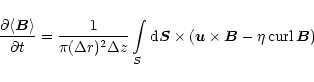 |
(12) |
and delivers average components as
These considerations show that slight initial fluctuations in
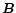 are able to create non-zero average magnetic fields
at any time, even if their
are able to create non-zero average magnetic fields
at any time, even if their
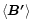 vanishes,
as a consequence of shear and radial accretion through
vanishes,
as a consequence of shear and radial accretion through
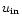 .
In particular, the non-constant vertical profile of the orbital
velocity produces a
.
In particular, the non-constant vertical profile of the orbital
velocity produces a 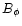 from the initial perturbation Bz.
Fluctuations in the accretion flow generate Br and Bz.
The actual radial differential rotation then quickly produces
from the initial perturbation Bz.
Fluctuations in the accretion flow generate Br and Bz.
The actual radial differential rotation then quickly produces
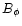 from even very small Br, and toroidal fields are prone
to dominate the disk fields.
from even very small Br, and toroidal fields are prone
to dominate the disk fields.
Kinematic dynamos have been extensively examined in numerous
previous publications concerning various types of geometries.
A widely used mean-field approach circumnavigates the difficulties
with resolving the small scales in a model. We address the applicability
of the mean-field theory to accretion disk dynamos by extracting
characteristic quantities from the simulations.
The mean-field dynamo applies the likely amplification
of a magnetic field through a fluctuative electromotive
force parallel to the actual large-scale magnetic field. This
effect is generally expressed by the term "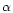 -effect'' and
can be thoroughly studied in e.g. Krause & Rädler (1981).
In a model splitting large and small scales, the induction
equation extends beyond the large-scale electromotive force
such as
-effect'' and
can be thoroughly studied in e.g. Krause & Rädler (1981).
In a model splitting large and small scales, the induction
equation extends beyond the large-scale electromotive force
such as
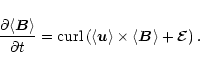 |
(16) |
The 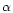 -effect is part of the development of the small-scale
electromotive force as
-effect is part of the development of the small-scale
electromotive force as
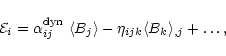 |
(17) |
where
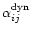 and
and
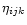 are tensors in general. If
written in components, the induction equation shows that the essential
component of the
are tensors in general. If
written in components, the induction equation shows that the essential
component of the
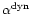 tensor is the
tensor is the
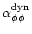 component
which converts azimuthal fields into radial and vertical fields,
whereas the differential rotation converts radial and vertical
fields back into the toroidal component by the large-scale part
component
which converts azimuthal fields into radial and vertical fields,
whereas the differential rotation converts radial and vertical
fields back into the toroidal component by the large-scale part
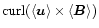 of
Eq. (16). This approximation is usually referred to
as an
of
Eq. (16). This approximation is usually referred to
as an
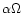 -dynamo.
-dynamo.
Second-order correlation approximation leads to a relation
of
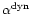 with the helicity of the flow,
with the helicity of the flow,
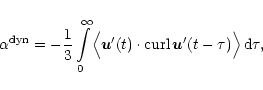 |
(18) |
which is, when approximated by a typical time-scale
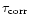 ,
,
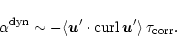 |
(19) |
The same principle is applicable to the current helicity
(Keinigs 1983) giving
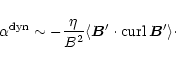 |
(20) |
Among other issues, the evolution of these quantities for
the helicity will be subject of the following sections.
Special attention is pid to the symmetry of the magnetic fields
of the solutions. In general, the preference of a certain symmetry
is a tool to check the consistency with mean-field dynamo models.
Additionally, dipolar (antisymmetric) fields are supposed to
support the launch of winds forming jets from the disk better
than quadrupolar (symmetric) fields, with the latter rather providing
closed field lines within the disk. The mean-field disk dynamo
of Rekowski et al. (2000) produced dipolar magnetic fields
for negative
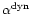 in the northern hemisphere.
in the northern hemisphere.
A number of mean-field dynamo models in one to three dimensions
delivered varying symmetry of the solutions with a major influence
of the boundary conditions - vacuum versus perfectly conducting.
Three-dimensional investigations of stability by Meinel et al. (1990)
and Elstner et al. (1992) found quadrupolar solutions for the
condition of low-conductivity surroundings of the disk, whereas
perfectly conducting boundaries delivered dipolar solutions.
A local model with periodic boundaries will thus not be able
to answer the question of the final symmetry of the solutions.
An ideal global model would comprise the entire investigated object
and is less depending on the surroundings (which will be vacuum
in very good approximation).
The parity of a the toroidal magnetic field is measured by
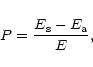 |
(21) |
where 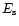 and
and 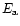 are the symmetric and antisymmetric
energy parts resp., and E is the total energy of in toroidal
field component.
Figures 17 and 18 show
the temporal development of parity of the toroidal magnetic
fields in the Models II and V along with a repeated plot
of
are the symmetric and antisymmetric
energy parts resp., and E is the total energy of in toroidal
field component.
Figures 17 and 18 show
the temporal development of parity of the toroidal magnetic
fields in the Models II and V along with a repeated plot
of
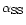 .
.
We should emphasize that the initial perturbation of the magnetic
field had dipolar symmetry. Since the total flux through the
vertical surfaces, however, vanishes, field configurations
with either symmetry may arise from the evolution of the model.
The dipolar initial perturbation may not have been fully
re-organized as the diffusive time-scale
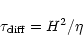 |
(22) |
is 1600 rotation periods for the low-diffusivity model II and 160 revolutions for the high-diffusivity model V. The latter
covered
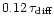 .
An additional experiment
used a completely mixed initial magnetic-field perturbation
according to a distribution which has zero parity in Bz, and the toroidal component immediately
emerging from the slight vertical shear has zero parity, too. Again, the
magnetic flux through the vertical surfaces is zero. Such initial
conditions have been applied to Models II and V. The runs lasted
roughly 10 revolution resulting in parity variations with a slight
tendency towards quadrupolar (symmetric) solution (P from +0.1
to +0.2).
.
An additional experiment
used a completely mixed initial magnetic-field perturbation
according to a distribution which has zero parity in Bz, and the toroidal component immediately
emerging from the slight vertical shear has zero parity, too. Again, the
magnetic flux through the vertical surfaces is zero. Such initial
conditions have been applied to Models II and V. The runs lasted
roughly 10 revolution resulting in parity variations with a slight
tendency towards quadrupolar (symmetric) solution (P from +0.1
to +0.2).
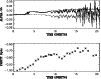 |
Figure 17:
Total
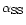 and parity
for Model II with
and parity
for Model II with
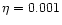 .
A parity of -1 denotes fully antisymmetric.
(dipolar) solutions. .
A parity of -1 denotes fully antisymmetric.
(dipolar) solutions. |
| Open with DEXTER |
Average kinetic helicities were computed based on a layer
slightly below one density scale-height in both hemispheres.
The average is taken in  - and r-direction. There is
a considerable scatter in the time series of the helicity,
but temporal averages are all negative on the northern
side for all models. The only exception is the northern
part of Model II with a near-zero value. Negative sign
also holds for the two test models with mixed-parity initial
perturbation. Average current helicities are also
negative on the northern side (and positive on the southern one)
throughout almost all
models. The only exceptions are the mixed-parity models
which show a current helicity with opposite sign compared
with the kinetic helicity in both hemispheres.
- and r-direction. There is
a considerable scatter in the time series of the helicity,
but temporal averages are all negative on the northern
side for all models. The only exception is the northern
part of Model II with a near-zero value. Negative sign
also holds for the two test models with mixed-parity initial
perturbation. Average current helicities are also
negative on the northern side (and positive on the southern one)
throughout almost all
models. The only exceptions are the mixed-parity models
which show a current helicity with opposite sign compared
with the kinetic helicity in both hemispheres.
Since the angular momentum transport is dominated by
magnetic stresses, we also ask about the energy in
the flow fluctuations and the magnetic field. The temporal evolutions
of these two quantities in Figs. 19 and 20 show a clear difference between
the Models II and V. Kinetic-energy dominance holds for
Model II, whereas magnetic dominance is found for Model V.
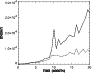 |
Figure 19:
Temporal evolution of kinetic (solid line) and
magnetic (dashed line) energies of Model II with
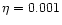 .
The energy is measured as a radial and azimuthal total in a
horizontal layer at z=+0.39 which is - measured in density
scale-heights H - near 1.2H at the inner radial
boundary and near 0.6H at the outer boundary, due to the
variable disk height along radius. .
The energy is measured as a radial and azimuthal total in a
horizontal layer at z=+0.39 which is - measured in density
scale-heights H - near 1.2H at the inner radial
boundary and near 0.6H at the outer boundary, due to the
variable disk height along radius. |
| Open with DEXTER |
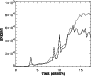 |
Figure 20:
Temporal evolution of kinetic (solid line) and
magnetic (dashed line) energies of Model V with 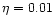 .
The energy is measured as a radial and azimuthal total in a
horizontal layer at z=+0.39. .
The energy is measured as a radial and azimuthal total in a
horizontal layer at z=+0.39. |
| Open with DEXTER |
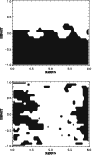 |
Figure 21:
Time-average toroidal magnetic field (TOP)
and the toroidal electromotive force (BOTTOM) shown in spatial distribution. |
| Open with DEXTER |
In order to evaluate the applicability of the
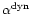 approach,
we compute the average toroidal field
approach,
we compute the average toroidal field
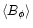 and compare it with the actual average electromotive force
and compare it with the actual average electromotive force
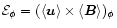 derived directly from the simulated vector fields. A correlation
between the two quantities may justify the
derived directly from the simulated vector fields. A correlation
between the two quantities may justify the 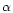 -effect for
dynamo generation of magnetic fields. As a meaningful
-effect for
dynamo generation of magnetic fields. As a meaningful
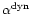 must change its sign at the equator, we plot the correlation
for both hemispheres of the disk separately; the result is given
in Fig. 22. As the temporal fluctuations are strong,
we plot the time-averages of
must change its sign at the equator, we plot the correlation
for both hemispheres of the disk separately; the result is given
in Fig. 22. As the temporal fluctuations are strong,
we plot the time-averages of 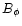 and
and
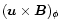 in Fig. 21
only with their resulting sign. The quantities are also averaged
in azimuthal direction and plotted in the (r,z)-plane. White areas
denote a negative sign; the dominance of negative averaged electromotive
forces indicates a positive
in Fig. 21
only with their resulting sign. The quantities are also averaged
in azimuthal direction and plotted in the (r,z)-plane. White areas
denote a negative sign; the dominance of negative averaged electromotive
forces indicates a positive
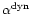 in the northern
hemisphere in accordance with Fig. 22.
in the northern
hemisphere in accordance with Fig. 22.
The classical understanding of the Coriolis force giving
preference to left-handed helicity on the northern hemisphere
(whence positive
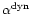 )
appears not applicable for
the correlation plots of Models II and III. The fluctuations
were strong, and no meaningful sign of
)
appears not applicable for
the correlation plots of Models II and III. The fluctuations
were strong, and no meaningful sign of
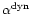 can be derived. However, Models Ia, V, and VI show a mostly
negative averaged EMF for both hemispheres, while
can be derived. However, Models Ia, V, and VI show a mostly
negative averaged EMF for both hemispheres, while
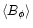 changes its sign. An indication for positive
changes its sign. An indication for positive
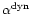 is thus found from these simulations.
is thus found from these simulations.
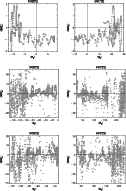 |
Figure 22:
Correlation of the average electromotive force versus
the mean 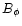 ,
averaged for the northern and southern hemisphere
separately. The quantities were derived, from top to bottom, from the runs
of Models Ia, V, and VI. The sign of the correlation gives an
indication for the sign of the dynamo ,
averaged for the northern and southern hemisphere
separately. The quantities were derived, from top to bottom, from the runs
of Models Ia, V, and VI. The sign of the correlation gives an
indication for the sign of the dynamo 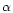 -effect. -effect. |
| Open with DEXTER |
In fact, Models V and VI are those which show saturated kinetic energies.
The other significant difference to the indefinite Models II and III is
the 10 times higher diffusivity, 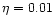 .
Notwithstanding, an indication for a negative
.
Notwithstanding, an indication for a negative
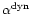 was already found in simulations of a local box cut out of the
disk by Brandenburg et al. (1995). The same sign is found by
Ziegler & Rüdiger (2000b) from long runs of local simulations,
although a clear influence of resistivity on the evolution
was found there. Lowest magnetic Reynolds numbers are
was already found in simulations of a local box cut out of the
disk by Brandenburg et al. (1995). The same sign is found by
Ziegler & Rüdiger (2000b) from long runs of local simulations,
although a clear influence of resistivity on the evolution
was found there. Lowest magnetic Reynolds numbers are
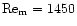 for Model V in this Paper, calculated
with the velocity difference between inner and outer radial
boundary, just as Ziegler & Rüdiger did for the local box.
for Model V in this Paper, calculated
with the velocity difference between inner and outer radial
boundary, just as Ziegler & Rüdiger did for the local box.
These considerations are somewhat limited, since a straight-forward
regression line in Fig. 22 will have a
significant offset from the origin of the graph; a vanishing
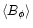 does apparently not coincide with a
vanishing
does apparently not coincide with a
vanishing
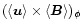 .
The effect of the other field components is considered small though;
while the average hemispherical
.
The effect of the other field components is considered small though;
while the average hemispherical
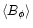 are of the
order of 100, the
are of the
order of 100, the
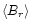 is of order 10 and
is of order 10 and
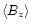 of order unity. A considerable contribution
is suspected from the current density through the
of order unity. A considerable contribution
is suspected from the current density through the
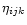 -term
in Eq. (17), and it appears to be quite natural that
an offset in the correlation graphs in Fig. 22
is found. For this reason, we did not plot such regression
lines in the figure.
-term
in Eq. (17), and it appears to be quite natural that
an offset in the correlation graphs in Fig. 22
is found. For this reason, we did not plot such regression
lines in the figure.
Additionally, the sole consideration of the induction
equation in the "classical'' dynamo theory leads to the omission
of the Lorentz force, which is not only essential for the onset
of the magneto-rotational instability but for the maintenance
of the turbulence and the transport of angular momentum as well.
It is thus obvious that the neglect of the back-reaction of
magnetic fields on the flow need not lead to representative
models of Keplerian disks.
Three-dimensional global simulations have shown, that the
magnetic shear-flow instability is a fast mechanism to
generate a turbulent flow in a Keplerian disk. We presented
models with a computational domain covering the full azimuthal
range, accounting for accretion of matter. The Shakura-Sunyaev
parameter
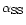 increases rapidly during the
first revolutions after switching on the magnetic field and
reaches 10-2-10-1 at this stage of the computations,
though it appears not yet fully saturated in several of the models.
Maxwell stresses exceed Reynolds stresses almost entirely. The
latter undergo strong fluctuations and are partly negative.
increases rapidly during the
first revolutions after switching on the magnetic field and
reaches 10-2-10-1 at this stage of the computations,
though it appears not yet fully saturated in several of the models.
Maxwell stresses exceed Reynolds stresses almost entirely. The
latter undergo strong fluctuations and are partly negative.
Indications for a dynamo action in the disk are found, the
corresponding dynamo-
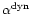 tending to be positive north
of the equatorial plane and negative south of the equatorial
plane. The generated magnetic fields may maintain the turbulence
even if the external field ceases. The strong excitation of
low-order azimuthal modes in the magnetic field is another
promising fact for dynamo action with respect to the
Cowling theorem.
tending to be positive north
of the equatorial plane and negative south of the equatorial
plane. The generated magnetic fields may maintain the turbulence
even if the external field ceases. The strong excitation of
low-order azimuthal modes in the magnetic field is another
promising fact for dynamo action with respect to the
Cowling theorem.
For various reasons, a representative example for an accretion disk
dynamo is provided by Model V (and nearly as well by the similar
Model VI with higher inflow velocity). The time series is sufficiently
long covering more than 18 revolution periods. The angular momentum
transport reaches a saturated level of high efficiency during the
last four orbital periods. The magnetic diffusivity is roughly
two orders of magnitude higher than the numerical diffusivity.
The striking dominance of one sign of the averaged EMF in
Fig. 21 indicates a physically evolved, relevant
state of the system.
The results connected with the outcomes of mean-field dynamo theory
include the following facts: (i) A negative average toroidal
magnetic field is found for the northern hemisphere, a positive on
the southern one. The averaged EMF is negative in both hemisphere
indicating a positive
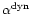 -effect on the
northern side (negative on the southern side). (ii) The correlation
plot of average toroidal field and EMF gives the same picture.
(iii) Negative kinetic and current helicities on the
northern hemisphere (positive on the southern one) are also
consistent with a positive
-effect on the
northern side (negative on the southern side). (ii) The correlation
plot of average toroidal field and EMF gives the same picture.
(iii) Negative kinetic and current helicities on the
northern hemisphere (positive on the southern one) are also
consistent with a positive
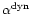 .
(iv) The dipolar structure of the solution contrasts with the
results from mean-field dynamo models of disks which yield
quadrupolar solutions for positive
.
(iv) The dipolar structure of the solution contrasts with the
results from mean-field dynamo models of disks which yield
quadrupolar solutions for positive
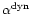 .
We have
to add though that the disks of our Paper are not thin.
Mean-field simulations by Covas et al. (1999) show a transition from
quadrupolar to dipolar fields when the opening angle of the disk
is enlarged, rather representing a torus than a disk.
.
We have
to add though that the disks of our Paper are not thin.
Mean-field simulations by Covas et al. (1999) show a transition from
quadrupolar to dipolar fields when the opening angle of the disk
is enlarged, rather representing a torus than a disk.
The extension of the run-times of such simulations exceeding
the order of diffusion times promises further results about
dynamo action in accretion disks. The connection with mean-field
concepts are most interesting as well as the implications
for jet-launch models.
Acknowledgements
The invaluable help by D. Elstner, Potsdam, in adapting the ZEUS-3D
code for our purposes is greatly acknowledged.
We are grateful to the John v.
Neumann-Institut for Computing at the
Forschungszentrum Jülich, Germany, for the opportunity to use
the Cray T90 computer.
R.A. thanks for the kind support by the Deutsche Forschungsgemeinschaft.
-
Armitage, P. J. 1998, ApJ, 501, L189
In the text
NASA ADS
-
Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214
In the text
NASA ADS
-
Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1
In the text
NASA ADS
-
Balbus, S. A., Hawley, J. F., & Stone, J. M. 1996, ApJ, 467, 76
NASA ADS
-
Brandenburg, A., Nordlund Å., Stein, R. F., & Torkelsson, U.
1995, ApJ, 446, 741
In the text
NASA ADS
-
Clarke, D. A., Norman, M. L., & Fiedler, R. A. 1994, ZEUS-3D
User Manual, Univ. of Illinois
In the text
-
Covas, E., Tavakol, R., Tworkowski, A., et al. 1999, A&A, 345, 669
In the text
NASA ADS
-
Curry, C., & Pudritz, R. E. 1995, ApJ, 453, 697
In the text
NASA ADS
-
Drecker, A., Rüdiger, G., & Hollerbach, R. 2000, MNRAS, 317, 45
In the text
NASA ADS
-
Dubrulle, B. 1993, Icarus, 106, 59
In the text
NASA ADS
-
Elstner, D., Meinel, R., & Beck, R. 1992, A&AS, 94, 587
In the text
NASA ADS
-
Evans, C., & Hawley, J. F. 1988, ApJ, 33, 659
In the text
-
Fleming, T. P., Stone, J. M., & Hawley, J. F. 2000, ApJ, 530, 464
In the text
NASA ADS
-
Hawley, J. F. 2000, ApJ, 528, 462
In the text
NASA ADS
-
Hawley, J. F., & Balbus, S. A. 1991, ApJ, 376, 223
In the text
NASA ADS
-
Hawley, J. F., Balbus, S. A., & Winters, W. F. 1999, ApJ, 518, 394
In the text
NASA ADS
-
Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742
In the text
NASA ADS
-
Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 464, 690
In the text
NASA ADS
-
Keinigs, R. K. 1983, Phys. Fluids, 26, 2558
NASA ADS
-
Kley, W., Papaloizou, J. C. B., & Lin, D. N. C. 1993, ApJ, 416, 679
In the text
NASA ADS
-
Krause, F., & Rädler, K.-H. 1981. Mean-field magneto-hydrodynamics
and dynamo theory (Pergamon)
In the text
-
Machida, M., Hayashi, M. R., & Matsumoto, R. 2000, ApJ, 532, L67
In the text
NASA ADS
-
Meinel, R., Elstner, D., & Rüdiger, G. 1990, A&A, 236, L33
In the text
NASA ADS
-
Rekowski, M. v., Rüdiger, G., & Elstner, D. 2000, A&A, 353, 813
In the text
NASA ADS
-
Rüdiger, G., Primavera, L., Arlt, R., & Elstner, D. 1999,
MNRAS, 308, 887
In the text
NASA ADS
-
Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337
In the text
NASA ADS
-
Stone, J. M., & Balbus, S. A. 1996, ApJ, 464, 346
In the text
In the text
-
Stone, J. M., & Norman M. L. 1992a, ApJS, 80, 753
In the text
NASA ADS
-
Stone, J. M., & Norman, M. L. 1992b, ApJS, 80, 791
NASA ADS
-
Stone, J. M., Mihalas, D., & Norman, M. L. 1992, ApJS, 80, 819
In the text
NASA ADS
-
Stone, J. M., Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 463, 656
NASA ADS
-
Strom, S. E. 1994, Rev. Mex. Astron. Astrofís, 29, 23
NASA ADS
-
Ziegler, U., & Rüdiger, G. 2000a, A&A, 356, 1141
In the text
NASA ADS
-
Ziegler, U., & Rüdiger, G. 2000b, A&A, in press
In the text
Copyright ESO 2001
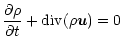
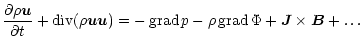
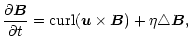
![\begin{displaymath}%
B_z(r,t=0) = b_0 r^{-1} \sin [2\pi (r-r_{\rm i})/(r_{\rm o}-r_{\rm i})]
\end{displaymath}](/articles/aa/full/2001/30/aah2593/img38.gif)