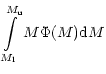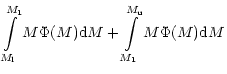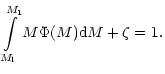A&A 374, 936-956 (2001)
DOI: 10.1051/0004-6361:20010801
Sources of carbon and the evolution
of the abundance
of CNO elements
Y. C. Liang - G. Zhao
-
J. R. Shi
Beijing Astronomical Observatory,
Chinese Academy of Sciences, Beijing 100012, PR China
National Astronomical Observatories,
Chinese Academy of Sciences, Beijing 100012, PR China
Received 29 March 2000 / Accepted 30 May 2001
Abstract
Using the standard infall model of Galactic chemical evolution, we explore the origin of carbon
and calculate the abundance evolution of CNO elements for 8 different models of
stellar nucleosynthesis yields. The results show that, in the early stage of the Galaxy, massive stars are the main producer of carbon, and that as our Galaxy evolves to the late stage,
the longer lived intermediate- and low-mass stars play an increasingly important role, while
at the same time, metal-rich Wolf-Rayet stars eject a significant amount of carbon into the ISM by radiative-driven stellar winds. However, from the present published nucleosynthesis yields we cannot distinguish whether the main source of carbon in the late Galactic stage is just
the massive stars (
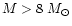 )
alone, or just the intermediate-, low-mass stars and
)
alone, or just the intermediate-, low-mass stars and
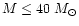 massive stars that do not go through the Wolf-Rayet stage. The 12C
massive stars that do not go through the Wolf-Rayet stage. The 12C
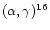 O reaction rate is very important in the stellar nucleosynthesis calculations: a lower rate will give a higher yield of carbon. The contribution to nitrogen is dominated by intermediate- and low-mass stars, and the secondary source of massive stars cannot explain the observed [N/Fe] in metal-poor stars. Most of oxygen is produced by massive stars.
The fact that a higher O abundance in metal-poor stars is derived from the O I 7771-7775 Å triplet than from the forbidden [O I] line at 6300 Å poses a problem.
O reaction rate is very important in the stellar nucleosynthesis calculations: a lower rate will give a higher yield of carbon. The contribution to nitrogen is dominated by intermediate- and low-mass stars, and the secondary source of massive stars cannot explain the observed [N/Fe] in metal-poor stars. Most of oxygen is produced by massive stars.
The fact that a higher O abundance in metal-poor stars is derived from the O I 7771-7775 Å triplet than from the forbidden [O I] line at 6300 Å poses a problem.
Key words: nuclear reactions, nucleosynthesis, abundances -
stars: AGB -
stars: supernova -
stars: Wolf-Rayet -
Galaxy: abundance -
Galaxy: evolution
The abundance trends of the CNO elements are crucial to study
the Galactic chemical evolution (hereafter GCE).
These elements play important roles in the stellar interior as sources of opacity and energy production through the CNO cycle, and thus affect the star's lifetime, its position in the HR diagram, and its heavy-element yields. Carbon is especially
important because it is the first element that is synthesized out of the primordial elements (H,
He, Li).
The main site of carbon synthesis has been a subject of argument for many years.
Burbidge et al. (1957) suggested that carbon is provided by mass loss from
red giants and supergiants. Iben & Truran (1978) concluded from thermally
pulsing models that intermediate-mass and high-mass stars contribute carbon in roughly equal amounts. More recent theoretical and observational studies include the following.
Timmes et al. (1995) used the carbon yields of type II supernova
(hereafter SNII) explosion from Woosley & Weaver (1995) (hereafter WW)
and the yields of intermediate-, low-mass stars (hereafter ILMS)
from Renzini & Voli (1981) (hereafter RV) to calculate the abundance evolution of carbon.
They concluded that the ILMS contribute a significant amount of carbon to the interstellar medium (hereafter ISM). Chiappini et al. (1997) obtained similar results with their two-infall model. Oberhummer et al. (2000) reviewed the ILMS as the major producer of carbon.
Kobulnicky & Skillman (1998) measured
the C/O and N/O ratios of three metal-poor
galaxies with similar metallicities using HST ultraviolet
and ground-based optical spectroscopy.
Their results implied that the mechanisms of C and N production are coupled,
and most of both C and N in galaxies originates in
low- to intermediate-mass stars.
Prantzos et al. (1994)
suggested that if the duration of the halo phase is as long as
 1-2 Gyr, then massive stars with wind-driven mass loss could be the main
carbon source during the whole galactic evolution. Gustafsson et al. (1999) adopted an analytical GCE model to calculate and compare the carbon abundance evolution
in the Galactic disk (-1.6< [Fe/H] <+0.2) and some irregular galaxies. They suggested that
carbon enrichment is caused mainly by superwinds from metal-rich, massive stars.
Karlsson et al. (1999) reported similar results. However, Gustafsson & Ryde
(2000) wrote that the source of carbon is still not clear. Henry et al. (2000)
analyzed the behavior of the N/O and C/O abundance ratios as functions of metallicity
in the Galactic and extragalactic H II regions. Their results showed that C and N originate from separate production sites and are decoupled from one another; and
they suggested that massive stars (
1-2 Gyr, then massive stars with wind-driven mass loss could be the main
carbon source during the whole galactic evolution. Gustafsson et al. (1999) adopted an analytical GCE model to calculate and compare the carbon abundance evolution
in the Galactic disk (-1.6< [Fe/H] <+0.2) and some irregular galaxies. They suggested that
carbon enrichment is caused mainly by superwinds from metal-rich, massive stars.
Karlsson et al. (1999) reported similar results. However, Gustafsson & Ryde
(2000) wrote that the source of carbon is still not clear. Henry et al. (2000)
analyzed the behavior of the N/O and C/O abundance ratios as functions of metallicity
in the Galactic and extragalactic H II regions. Their results showed that C and N originate from separate production sites and are decoupled from one another; and
they suggested that massive stars (
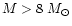 )
dominate the production of carbon, while intermediate-mass stars between 4 and 8
)
dominate the production of carbon, while intermediate-mass stars between 4 and 8 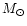 dominate the nitrogen production.
Carigi (2000) adopted different sets of yields to calculate the C/O vs. Galactic
age relation, and suggested massive stars to be the main contributor of carbon.
dominate the nitrogen production.
Carigi (2000) adopted different sets of yields to calculate the C/O vs. Galactic
age relation, and suggested massive stars to be the main contributor of carbon.
From calculated abundance gradients, Hou et al. (2000) argued that carbon comes from stellar winds of massive stars and ILMS. Goswami & Prantzos (2000) using their new GCE model, concluded that the yields in WW are not enough to explain the observed carbon abundance,
and that some other sources, Wolf-Rayet (hereafter W-R) stars or
ILMS, are needed to explain the observed [C/Fe] vs. [Fe/H] curve.
Garnett et al. (1999) measured the gas-phase abundance ratio C/O
in six H II regions in the spiral galaxies M101 and NGC2403, based on
ultraviolet spectroscopy from the HST.
These authors suggested that stellar winds in massive stars
have an important effect on carbon and oxygen, and
their analysis showed that
the source of carbon depended on the assumed UV reddening function. When a flatter
UV reddening (RV=5) was used, the data were consistent with the model
that used the yields of massive stars from WW,
while with a steeper value (RV=3) the data
became more consistent with the model that used the yields
of Maeder (1992) (hereafter M92).
In summary, it is still not clear whether carbon comes from
the SNII explosions of massive stars, from stellar winds of
W-R stars or from ILMS.
In this paper we try to address this question from
two aspects: (1) by using GCE model calculations with different sets of nucleosynthesis yields;
(2) by using the observations of the large sample of dwarfs in our Galaxy as one of the main observational constraints.
For the first aspect,
GCE modelling is an excellent tool to
study the evolution of elements of the whole Galaxy and other galaxies.
The main parameters for setting up such a model
include the form of the infall, the star formation rate (SFR), the initial mass function (IMF) and the nucleosynthesis yields.
The exponential form of infall
(or Gaussian infall form: Chang et al. 1999 and Prantzos & Silk 1998) has been found to be able to
solve the G-dwarfs problem very well.
The SFR and IMF can
be determined from the observed present-day mass function (PDMF)
(Pagel 1997).
The most uncertain factor of GCE model
is the nucleosynthesis yields, which largely decide the evolutionary trends of the elements.
Different research groups have calculated the yields of
stellar nucleosynthesis,
but the results are rather different due to the use of different
input parameters. And different yields will result in
different evolution trends.
We set up a simple GCE model, like the one of Timmes et al. (1995), which
fits some important observations.
We choose the following different nucleosynthesis yields published recently
in our calculations:
for the RV yields of intermediate- and low-mass single stars,
van den Hoek & Groenewegen (1997) (hereafter VG),
Marigo et al. (1996) (hereafter MBC1),
Marigo et al. (1998) (hereafter MBC2) (hereafter, MBC represents
for combined MBC1 and MBC2) and Marigo
(2001) (hereafter M2K);
for the WW yields of massive single stars, Nomoto et al. (1997a) (hereafter N97), M92 and
Portinari et al. (1998) (hereafter PCB);
for the yields of binaries through SNIa explosion,
Nomoto et al. (1997b).
Then we compared and analyzed
the different evolutionary behavior of the CNO elements, particularly C, calculated on the basis of these
different sets of yields.
In the early stage of our Galaxy, massive stars are the main producers of carbon.
As our Galaxy evolves to a
late stage, ILMS play an increasingly important role
in the enrichment of the ISM due to their longer lifetimes.
At the same time,
the high metallicity W-R stars eject significant amounts of carbon into the ISM
by radiative-driven stellar wind (the metallicity influences the
opacities in the outer layers of massive stars, hence their mass loss rate through winds).
Which is the main producer of carbon in the late stage of our
Galaxy? We find an attempt to answer in the following way.
We divide the massive stars
into two mass ranges,
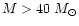 and
and
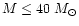 .
And assume that the former does, and the latter does not, go
through the W-R stage.
We then compare the contributions by the W-R stars and ILMS
to carbon in the late Galactic stage.
.
And assume that the former does, and the latter does not, go
through the W-R stage.
We then compare the contributions by the W-R stars and ILMS
to carbon in the late Galactic stage.
In the second part of our work,
we pay particular attention to the observations of field dwarfs
in our Galaxy. Their atmospheres are assumed to
represent perfect records of the chemical compositions of the ISM at the time of their formation,
and we have available
the abundances for a large sample of
field dwarfs in the solar neighborhood.
In addition,
the metallicity distribution of G dwarfs is
very important, because the G dwarfs have lifetimes as long as the Galaxy, their metallicity distribution
reflects the evolution of our Galaxy.
The age-metallicity relation is significant, too,
for reflecting the Galactic evolution.
This paper is organized as follows.
In Sect. 2,
we analyze the observational data.
The GCE model and the relevant
parameters are presented in Sect. 3.
Different nucleosynthesis yields are analyzed in Sect. 4.
Results of the analysis are given in Sects. 5-7.
The main conclusions are summarized in Sect. 8.
Observations of dwarf stars in the general field are very important
to the evolution of chemical abundance
as their atmospheres are thought to represent perfect
records of the chemical compositions of the ISM at the time they
formed.
Carbon abundance can be calculated from
the CH lines in the blue and ultraviolet (UV), the infrared
CO emission, and a few
red and near-infrared C I lines and [C I] forbidden lines.
The [C I] line of low excitation potential being not so
tightly dependent on NLTE considerations,
the values derived from it are less
dependent on the adopted stellar effective temperature than those from the
high-excitation C I lines and CH lines.
However, the small equivalent width (EW) of the [C I] line
makes the measurement difficult.
And the [C I] line at  8727 Å is supposed to be
blended with a weak Fe I line.
Both the [C I] and C I lines become unmeasurably weak in metal-poor
stars ([Fe/H] <-1).
8727 Å is supposed to be
blended with a weak Fe I line.
Both the [C I] and C I lines become unmeasurably weak in metal-poor
stars ([Fe/H] <-1).
The CH line in the UV can be used to obtain the C abundance of halo and disk stars.
Laird (1985) published an extensive study of the C abundances of 116 field dwarfs,
10 faint field giants and 3 Hyades dwarfs
in the range -2.45< [Fe/H] <+0.5. They suggested that the [C/Fe]
were solar
in the whole [Fe/H] range of the samples. Tomkin et al. (1986)
analyzed the spectra
of 32 halo dwarfs, and derived [C/Fe]
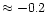 ,
independent of metallicity for stars
with [Fe/H] >-2. And their data showed a rise of C abundance in more metal-poor stars:
[C/Fe]
,
independent of metallicity for stars
with [Fe/H] >-2. And their data showed a rise of C abundance in more metal-poor stars:
[C/Fe]
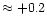 at [Fe/H]
at [Fe/H]
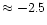 .
Carbon et al. (1987) derived
the C abundances of 83 halo dwarfs, which showed that [C/Fe] is constant over the range
of -2.5< [Fe/H]
.
Carbon et al. (1987) derived
the C abundances of 83 halo dwarfs, which showed that [C/Fe] is constant over the range
of -2.5< [Fe/H]
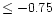 ,
and they found
an upturn at the very low metallicity value.
Wheeler et al. (1989) reviewed these observed trends of
[C/Fe] vs. [Fe/H].
,
and they found
an upturn at the very low metallicity value.
Wheeler et al. (1989) reviewed these observed trends of
[C/Fe] vs. [Fe/H].
Tomkin et al. (1992) derived the C abundances of halo and disk stars
using the C I  9100 Å line.
Their results showed that the C abundances are +0.2 higher than
those derived from the CH lines.
Andersson & Edvardsson (1994) (using [C I] 8727 Å),
Tomkin et al. (1995) (using C I 7100 Å) and
Gustafsson et al. (1999) (using [C I] 8727 Å) obtained the C abundances for large samples
of disk dwarfs
(comprising 85, 105 and 80 stars respectively, with some in common).
Their results showed that
[C/Fe] decreased with
increasing [Fe/H] in the Galactic disk region.
Using CH and C2 lines, Carretta et al. (2000) analyzed a sample of 19 stars,
and reanalyzed the stars of Tomkin et al. (1992) and
Edvardsson et al. (1993). Their results showed that [C/Fe]
is roughly solar in the whole metallicity range of [Fe/H] >-2.5.
9100 Å line.
Their results showed that the C abundances are +0.2 higher than
those derived from the CH lines.
Andersson & Edvardsson (1994) (using [C I] 8727 Å),
Tomkin et al. (1995) (using C I 7100 Å) and
Gustafsson et al. (1999) (using [C I] 8727 Å) obtained the C abundances for large samples
of disk dwarfs
(comprising 85, 105 and 80 stars respectively, with some in common).
Their results showed that
[C/Fe] decreased with
increasing [Fe/H] in the Galactic disk region.
Using CH and C2 lines, Carretta et al. (2000) analyzed a sample of 19 stars,
and reanalyzed the stars of Tomkin et al. (1992) and
Edvardsson et al. (1993). Their results showed that [C/Fe]
is roughly solar in the whole metallicity range of [Fe/H] >-2.5.
Considering the large scatter, we choose to take all the above-mentioned
observations of C abundance
as observational constraints on our GCE calculations.
Oxygen is the third most abundant element in the universe, and it
is very important for the study of GCE.
In general, oxygen is produced by massive stars through
SNII explosions, like other  elements.
Thus, the observations of oxygen, especially in metal-poor region,
give a measure of the contribution by massive stars.
Some parameters required in
GCE calculations can be
determined by the observed [O/Fe] in the stars
(Prantzos et al. 1994).
elements.
Thus, the observations of oxygen, especially in metal-poor region,
give a measure of the contribution by massive stars.
Some parameters required in
GCE calculations can be
determined by the observed [O/Fe] in the stars
(Prantzos et al. 1994).
The oxygen abundance of stars can be derived from the
O I 
 7771-7775 Å triplet,
the [O I]
7771-7775 Å triplet,
the [O I]  6300 Å forbidden line and OH lines
in the UV region.
In main-sequence, metal-poor stars, the [O I] lines are extremely weak
and are difficult to use for this purpose.
Nonetheless, sensitive detectors, high-resolution, and long
exposures have enabled several teams (Spite & Spite 1991;
Nissen & Edvardsson 1992)
to measure the EWs of some dwarfs with [Fe/H]
6300 Å forbidden line and OH lines
in the UV region.
In main-sequence, metal-poor stars, the [O I] lines are extremely weak
and are difficult to use for this purpose.
Nonetheless, sensitive detectors, high-resolution, and long
exposures have enabled several teams (Spite & Spite 1991;
Nissen & Edvardsson 1992)
to measure the EWs of some dwarfs with [Fe/H] 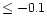 .
However,
the [O I] line
becomes too weak to measure at [Fe/H]
.
However,
the [O I] line
becomes too weak to measure at [Fe/H] 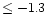 ,
and to provide useful
information on the trend of [O/Fe] vs. [Fe/H].
Thus, for the metal-poor stars,
the O I triplet lines are the preferred choice in dwarfs because
they are of measurable strength for a wide range of stellar temperatures and
they lie in a fairly clear portion of the stellar spectrum.
Molecular OH lines in the near-ultraviolet at
,
and to provide useful
information on the trend of [O/Fe] vs. [Fe/H].
Thus, for the metal-poor stars,
the O I triplet lines are the preferred choice in dwarfs because
they are of measurable strength for a wide range of stellar temperatures and
they lie in a fairly clear portion of the stellar spectrum.
Molecular OH lines in the near-ultraviolet at 
 3060-3200 Å,
are observed in both giants and dwarfs with
3060-3200 Å,
are observed in both giants and dwarfs with
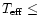 6500 K
(OH lines are destroyed at higher temperatures), and
can be used to derive the O abundance.
6500 K
(OH lines are destroyed at higher temperatures), and
can be used to derive the O abundance.
An interesting result is that
there is a systematic difference of about 0.5 dex between
the O abundances
derived from the permitted and forbidden lines.
The [O I] 6300 line provides about 0.4-0.5 dex of
the lower [O/Fe] values in metal-poor stars
(e.g. Spite & Spite 1991; Spiesman & Wallerstein 1991;
Fulbright & Kraft 1999; Nissen et al. 2000
for dwarfs;
Barbuy 1988; Barbuy & Erdelyi-Mendes 1989;
Sneden et al. 1991 for giants).
The O I triplet and OH lines, on the other hand, produce the higher [O/Fe] values, reaching +1.0 at
[Fe/H]
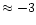 (Abia & Rebolo 1989; King 1994;
Nissen et al. 1994; Israelian et al. 1998;
Boesgaard et al. 1999; Mishenina et al. 2000).
Perhaps the higher O abundance obtained from the O I triplet
was caused by some NLTE effect (Mishenina et al. 2000 and references therein).
Kiselman (1991)
has performed a NLTE analysis of O I
(Abia & Rebolo 1989; King 1994;
Nissen et al. 1994; Israelian et al. 1998;
Boesgaard et al. 1999; Mishenina et al. 2000).
Perhaps the higher O abundance obtained from the O I triplet
was caused by some NLTE effect (Mishenina et al. 2000 and references therein).
Kiselman (1991)
has performed a NLTE analysis of O I  7774 Å and found significant
NLTE corrections, up to 0.4 dex.
However, Takeda (1994) found the NLTE effects to be small
in metal-poor stars.
Another source of discrepancy may be the fact that the O/Fe ratio is very sensitive to
7774 Å and found significant
NLTE corrections, up to 0.4 dex.
However, Takeda (1994) found the NLTE effects to be small
in metal-poor stars.
Another source of discrepancy may be the fact that the O/Fe ratio is very sensitive to
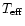 (Nissen & Edvardsson 1992).
King (1993) determined a reduction in the temperature of subgiants of
150-200 K, and obtained similar O abundances from the
(Nissen & Edvardsson 1992).
King (1993) determined a reduction in the temperature of subgiants of
150-200 K, and obtained similar O abundances from the  7774 Å and
7774 Å and
 6300 Å lines.
King & Boesgaard (1995) obtained the O abundances from both the
[O I]
6300 Å lines.
King & Boesgaard (1995) obtained the O abundances from both the
[O I]  6300 Å and O I
6300 Å and O I  7774 Å lines
for a sample of metal-rich F and G dwarfs.
They found that for
7774 Å lines
for a sample of metal-rich F and G dwarfs.
They found that for
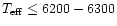 K, no systematic
difference exists in the abundances determined from
the
K, no systematic
difference exists in the abundances determined from
the 
 6300 and 7774 Å lines.
For
6300 and 7774 Å lines.
For
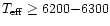 K,
however, the
K,
however, the  7774 Å abundance is substantially higher
than the
7774 Å abundance is substantially higher
than the  6300 Å abundance.
6300 Å abundance.
Thus, many papers have demonstrated that there is a
systematic difference between the values of
O abundance derived from the forbidden and permitted lines.
Possible reasons are as follows. The excitation potential of the O I triplet is very
high (9.15 eV), the line is formed deep down in the atmosphere, and the abundance
determination has a large error;
the near-UV
OH lines at 3060-3200 Å are sensitive to the gas pressure
and electron density in the model atmosphere.
In contrast, the [O I] line
is roughly half as sensitive as the OH and O I lines,
and is insensitive to changes in the ratio of
 -element to iron.
Also, the OH lines are very crowded in the UV region,
which makes their measurement difficult.
-element to iron.
Also, the OH lines are very crowded in the UV region,
which makes their measurement difficult.
Nissen et al. (2000) obtained the O abundances of 13 dwarfs and subgiants using
data from the ESO VLT. They suggested that
the [O/Fe] is nearly constant at 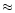 +0.4 for [Fe/H] below
+0.4 for [Fe/H] below 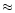 -1.0.
Maciel (2000) suggested that [O/Fe] is not higher than
+0.4 according to the radial O/H abundance gradients in
H II regions, hot stars and PNe, and [Fe/H]
gradients from open cluster stars.
-1.0.
Maciel (2000) suggested that [O/Fe] is not higher than
+0.4 according to the radial O/H abundance gradients in
H II regions, hot stars and PNe, and [Fe/H]
gradients from open cluster stars.
From the foregoing discussion and considering the
similar behavior
between O and 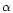 elements ([
elements ([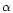 /Fe] is about +0.4 in
metal-poor stars, see Zhao & Magain 1990 and Fuhrmann 1998),
we use the lower O abundances derived from the [O I] line as
observational constraints
on our GCE calculations.
And we will specially discuss the higher abundances in metal-poor stars
obtained from the O I triplet and OH lines in Sect. 8.
Because the observed O abundances of
metal-poor dwarfs are not enough to reflect the abundance evolution,
we have supplemented our data with
some metal-poor giants.
/Fe] is about +0.4 in
metal-poor stars, see Zhao & Magain 1990 and Fuhrmann 1998),
we use the lower O abundances derived from the [O I] line as
observational constraints
on our GCE calculations.
And we will specially discuss the higher abundances in metal-poor stars
obtained from the O I triplet and OH lines in Sect. 8.
Because the observed O abundances of
metal-poor dwarfs are not enough to reflect the abundance evolution,
we have supplemented our data with
some metal-poor giants.
The N I line can be used in the abundance determination of nitrogen, but this can only be done for
reasonably metal-rich stars.
Clegg et al. (1981) obtained the N abundances of 20 disk stars
(-0.9< [Fe/H] <+0.4)
using the N I line, and suggested that [N/Fe]
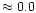 .
For halo stars, some results have been derived
from NH lines in the UV region. Tomkin & Lambert (1984),
Laird (1985) and Carbon et al. (1987) obtained
similar results, [N/Fe]
.
For halo stars, some results have been derived
from NH lines in the UV region. Tomkin & Lambert (1984),
Laird (1985) and Carbon et al. (1987) obtained
similar results, [N/Fe]
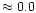 ,
irrespective of metallicity in the range -2< [Fe/H] <+0.3.
Indeed, there are still some difficulties
in deriving reliable N abundance from the NH bands at
,
irrespective of metallicity in the range -2< [Fe/H] <+0.3.
Indeed, there are still some difficulties
in deriving reliable N abundance from the NH bands at

 3360 and 3370 Å.
The difficulties are (a) uncertainties in the continuous opacities at
these wavelengths, (b) severe atomic-line contamination of the NH
features, (c) uncertainty in the dissociation energy of this molecule.
(d) the crowdedness of the lines in the UV region.
Also, it is very difficult to derive the N abundance from the CN bands
at
3360 and 3370 Å.
The difficulties are (a) uncertainties in the continuous opacities at
these wavelengths, (b) severe atomic-line contamination of the NH
features, (c) uncertainty in the dissociation energy of this molecule.
(d) the crowdedness of the lines in the UV region.
Also, it is very difficult to derive the N abundance from the CN bands
at 
 4200 or 3800 Å. Possible reasons are that
the dissociation energy of CN is not known to better than a
factor of 2, and that the determination of N abundance from CN depends on a
prior determination of reliable C abundance from other features,
and that the CN bands are extremely weak in very metal-poor stars.
A detailed discussions
can be found in Wheeler et al. (1989).
4200 or 3800 Å. Possible reasons are that
the dissociation energy of CN is not known to better than a
factor of 2, and that the determination of N abundance from CN depends on a
prior determination of reliable C abundance from other features,
and that the CN bands are extremely weak in very metal-poor stars.
A detailed discussions
can be found in Wheeler et al. (1989).
Table 1 summarises the sources of the observations of carbon, nitrogen and oxygen.
Most of the objects are dwarfs and subgiants;
a few metal-poor giants provide additional O abundance data
derived from the [O I]  6300 Å forbidden
line.
6300 Å forbidden
line.
Table 1:
Observational data from different references and the line sources.
References |
C |
N |
O |
[Fe/H] |
Numbers of stars |
| |
line, wavelength (Å) |
line, wavelength (Å) |
line, wavelength (Å) |
|
|
| 1 |
C I, [C I], CH |
N I 8683 |
O I 6158, [O I] 6300 |
[
-0.90,+0.40] |
20 |
| 2 |
[C I] 8727 |
|
|
[
-1.00,+0.25] |
85 |
| 3 |
[C I] 8727 |
|
|
[
-1.06,+0.26] |
80 |
| 4 |
C I 7100 |
|
|
[
-0.80,+0.20] |
105 |
| 5 |
C I 9100 |
|
O I 7770 triplet |
[
-3.00,-0.80] |
34 |
| 6 |
CH 4300 |
NH 3360 |
|
[
-2.45,+0.50] |
116 |
| 7 |
CH 4300 |
|
|
[
-2.60,-0.70] |
32 |
| 8 |
CH 4300 |
NH 3360 |
|
[
-3.20,-1.50] |
83 |
| 9 |
CH C2 |
CN |
O I, [O I] |
[
-2.61,+0.12] |
19 (some giants) |
| 10 |
|
NH 3360 |
|
[
-2.30,-0.30] |
14 |
| 11 |
|
|
[O I] 6300 |
[
-1.60,+0.30] |
7 |
| 12 |
|
|
[O I] 6300 |
-1.74,-1.43 |
2 |
| 13 |
|
|
[O I] 6300 |
[
-0.80,+0.30] |
23 |
| 14 |
|
|
[O I] 6300 |
-2.84,-2.31 |
2 |
| 15 |
|
|
[O I] 6300 |
[
-1.80,-0.70] |
13 |
| 16 |
|
|
O I 7770 triplet |
[
-1.03,+0.26] |
86 |
| 17 |
|
|
O I 7770 triplet |
[
-1.00,+0.10] |
90 |
| 18 |
|
|
O I 7770 triplet |
-1.84,-2.08 |
2 |
| 19 |
|
|
O I 7770 triplet |
[
-2.50,-0.50] |
14 (some giants) |
| 20 |
|
|
O I 7770 triplet |
[
-2.72,-0.47] |
14 |
| 21 |
|
|
O I 7770 triplet |
-3.00 |
1 |
| 22 |
|
|
O I 7770 triplet |
[
-3.50,-0.20] |
30 |
| 23 |
|
|
OH |
[
-3.00,-0.30] |
24 |
| 24 |
|
|
OH |
[
-3.02,-0.50] |
24 |
| 25 |
|
|
OH 3138-3155 |
[
-3.20,-1.80] |
9 |
| 26 |
|
|
OH , CO |
-1.22 |
1 |
| 27 |
|
|
[O I] 6300 |
[
-1.20,-0.10] |
24 (some giants) |
| 28 |
|
|
[O I] 6300 |
[
-3.00,-1.10] |
20 (giants) |
| 29 |
|
|
[O I] 6300 |
[
-2.35,+0.37] |
18 (giants) |
| 30 |
|
|
[O I] 6300 |
[
-2.88,-1.80] |
10 (giants) |
1. Clegg et al. (1981); 2. Andersson & Edvardsson (1994);
3. Gustafsson et al. (1999); 4. Tomkin et al. (1995);
5. Tomkin et al. (1992); 6. Laird (1985);
7. Tomkin et al. (1986); 8. Carbon et al. (1987);
9. Carretta et al. (2000); 10. Tomkin & Lambert (1984);
11. Spite & Spite (1991);
12. Spiesman & Wallerstein (1991); 13. Nissen & Edvardsson (1992);
14. Fulbright & Kraft (1999); 15. Nissen et al. (2000);
16. Edvardsson et al. (1993); 17. Chen et al. (2000);
18. Beveridge & Sneden (1994);
19. Mishenina et al. (2000); 20. Boesgaard & King (1993);
21. King (1994; 22. Abia & Rebolo (1989);
23. Israelian et al. 1998; 24. Boesgaard et al. (1999);
25. Nissen et al. (1994); 26. Balachandran & Carney (1996);
27. Barbuy & Erdelyi-Mendes (1989); 28. Barbuy (1988);
29. Gratton & Ortolani (1986); 30. Sneden et al. (1991).
The age-metallicity relation for the solar neighborhood
is one of the important observational constraints; it shows
the [Fe/H]-represented
metallicity as a function of the star's age. The observational data and
scatter are taken from Carlberg et al. (1985),
Meusinger et al. (1991) and
Edvardsson et al. (1993) (their Tables 14 and 15).
Another important observational constraint is the
metallicity distribution of long-lived G-type stars.
Because these stars have long main-sequence lifetimes of about 15 Gyr,
comparable to the estimated age of the Galaxy, they
represent a sample of stars which have not been removed by stellar
evolution. The observational metallicity
distribution of G dwarfs is taken from Chang et al. (1999).
The solar abundances of CNO elements are
taken from Grevesse & Sauval (1998).
A general, standard infall GCE model, namely,
a multizone model for GCE without mass exchange among the zones is adopted in our present study.
The rate of change of the surface mass density of isotope i in every zone in the
gas at a given Galactocentric radius r and time t is
where the first term describes the disappearance of isotope i due to new star
formation, the second term describes the enrichment due to stellar wind mass
loss of low mass single stars, the third term represents the rate of enrichment
due to binary systems that undergo SNIa explosions. The free parameter 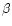 is
the amplitude factor of type Ia supernova (hereafter SNIa) explosion and
is
the amplitude factor of type Ia supernova (hereafter SNIa) explosion and
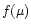 is the binary distribution
function. The fourth term represents the enrichment due to single
stars or binary systems that do not undergo type Ia events in the mass interval
is the binary distribution
function. The fourth term represents the enrichment due to single
stars or binary systems that do not undergo type Ia events in the mass interval
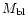 to
to
 .
The fifth term represents the enrichment rate due to
massive stars that become SNII explosions with masses between
.
The fifth term represents the enrichment rate due to
massive stars that become SNII explosions with masses between
 to
to 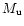 .
The last term represents the infall of the primordial material.
Xi(r,t) is the
elemental yield from nucleosynthesis (see Sect. 4). More details have been given by
Matteucci & François (1989) and Timmes et al. (1995).
.
The last term represents the infall of the primordial material.
Xi(r,t) is the
elemental yield from nucleosynthesis (see Sect. 4). More details have been given by
Matteucci & François (1989) and Timmes et al. (1995).
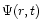 (SFR):
Analytical prescriptions for the SFR can be
obtained from the observations. Schmidt (1959) suggested that the SFR is
related to the
surface mass density of interstellar gas
(SFR):
Analytical prescriptions for the SFR can be
obtained from the observations. Schmidt (1959) suggested that the SFR is
related to the
surface mass density of interstellar gas
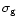 .
Subsequent studies showed
that the SFR
depends not only on the surface mass density of gas but also on the total surface
mass density of the ISM (Talbot & Arnett 1975; Dopita & Ryder 1994;
Timmes et al. 1995; Chiappini et al. 1997; Dwek 1998).
.
Subsequent studies showed
that the SFR
depends not only on the surface mass density of gas but also on the total surface
mass density of the ISM (Talbot & Arnett 1975; Dopita & Ryder 1994;
Timmes et al. 1995; Chiappini et al. 1997; Dwek 1998).
We adopt a similar formula to that of Timmes et al. (1995):
![\begin{displaymath}\Psi(r,t)=\nu \sigma_{\rm tot}(r,t)\left [\frac {\sigma_{\rm ...
...m tot}(r,t)}
\right ]^{n} M_{\odot}\,{\rm pc^{-2}\,Gyr^{-1}},
\end{displaymath}](/articles/aa/full/2001/30/aah2126/img41.gif) |
(2) |
where n is in the range 1-2 (Timmes et al. 1995),
which we fix at 1.5 throughout our calculation,
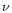 is the efficiency factor in unit Gyr-1,
which can be adjusted around the value 1.0.
is the efficiency factor in unit Gyr-1,
which can be adjusted around the value 1.0.
 (IMF):
For the solar neighborhood, the IMF is given in a series of papers.
The first formula was applied by
Salpeter (1955), who suggested the single power-law form:
(IMF):
For the solar neighborhood, the IMF is given in a series of papers.
The first formula was applied by
Salpeter (1955), who suggested the single power-law form:
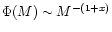 (x=1.35),
normalized to 1 over a given mass range.
Then
Scalo (1986) suggested that the power law should become steeper
for
(x=1.35),
normalized to 1 over a given mass range.
Then
Scalo (1986) suggested that the power law should become steeper
for
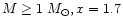 .
Following them, more authors suggested that
IMF should flatten at the low mass end, for example Kroupa et al. (1993).
Dwek (1998) analyzed these results,
and gave a similar formula as Kroupa et al. (1993) (for three mass ranges).
An important issue
for the IMF is it being "top-heavy'', meaning that
the formation frequency of massive stars in the early Galactic stage
was higher than at the present.
Recently, the question of a changing IMF as our Galaxy evolves has been examined.
Chiappini et al. (2000) found that
the metallicity distribution of G dwarfs is well explained by a constant IMF, rather than by
a changing one.
Martinelli & Matteucci (2000)
found that, with a changing IMF, even though
the metallicity distribution of G dwarfs could be reproduced, other important observations of [O/Fe] would then not fit so well.
.
Following them, more authors suggested that
IMF should flatten at the low mass end, for example Kroupa et al. (1993).
Dwek (1998) analyzed these results,
and gave a similar formula as Kroupa et al. (1993) (for three mass ranges).
An important issue
for the IMF is it being "top-heavy'', meaning that
the formation frequency of massive stars in the early Galactic stage
was higher than at the present.
Recently, the question of a changing IMF as our Galaxy evolves has been examined.
Chiappini et al. (2000) found that
the metallicity distribution of G dwarfs is well explained by a constant IMF, rather than by
a changing one.
Martinelli & Matteucci (2000)
found that, with a changing IMF, even though
the metallicity distribution of G dwarfs could be reproduced, other important observations of [O/Fe] would then not fit so well.
In our calculation, we adopt the formula of Dwek (1998):
where C1, C2 and C3, the normalized coefficients, are determined from the normalization
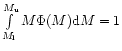 ,
with
,
with
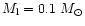 and
and
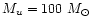 .
In fact, the bulk of chemical enrichment is caused by the stars
with
.
In fact, the bulk of chemical enrichment is caused by the stars
with
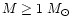 .
Thus,
it is meaningful to fix the fraction
.
Thus,
it is meaningful to fix the fraction  of the total stellar mass distributed in
stars above
of the total stellar mass distributed in
stars above
 (M1), which is equivalent to fixing
(M1), which is equivalent to fixing  ,
namely,
,
namely,
Pagel (1997) explained this method in detail.
In our calculations
for different sets of yields, we adjust  so that the results give a good fit to
the observations, especially the metallicity distribution of G dwarfs.
so that the results give a good fit to
the observations, especially the metallicity distribution of G dwarfs.
 Infall: The infall rate is generally taken to follow an exponent law
(Matteucci & François 1989; Timmes et al. 1995)
or Gaussian form (Prantzos & Silk 1998; Chang et al. 1999).
We adopt the specific form
of Timmes et al. (1995),
but with
Infall: The infall rate is generally taken to follow an exponent law
(Matteucci & François 1989; Timmes et al. 1995)
or Gaussian form (Prantzos & Silk 1998; Chang et al. 1999).
We adopt the specific form
of Timmes et al. (1995),
but with
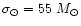 pc-2 (Sackett 1997).
pc-2 (Sackett 1997).
 Main-sequence lifetimes
Main-sequence lifetimes
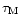 :
The main-sequence lifetimes of stars are
taken from Schaller et al. (1992), which
have been used generally
in GCE calculations,
such as Timmes et al. (1995) and Prantzos & Silk (1998).
:
The main-sequence lifetimes of stars are
taken from Schaller et al. (1992), which
have been used generally
in GCE calculations,
such as Timmes et al. (1995) and Prantzos & Silk (1998).
The stars are divided into binary and single stars.
We only consider SNIa explosion for the binary stars,
and divide the single stars into
two groups: intermediate-, low-mass stars (
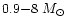 ,
or
,
or
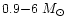 in case of strong overshooting)
and massive stars (
in case of strong overshooting)
and massive stars (
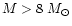 ,
or
,
or
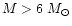 in case of strong overshooting).
in case of strong overshooting).
The first detailed nucleosynthesis calculation for ILMS was made
by RV (M=
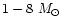 ,
Z= 0.004, 0.02). Recently,
VG extended the calculation to
M=
,
Z= 0.004, 0.02). Recently,
VG extended the calculation to
M=
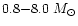 and Z= 0.001, 0.004, 0.008, 0.02, 0.04.
Forestini & Charbonnel (1997) calculated the evolution
of stars with M= 3, 4, 5, 6, 7
and Z= 0.001, 0.004, 0.008, 0.02, 0.04.
Forestini & Charbonnel (1997) calculated the evolution
of stars with M= 3, 4, 5, 6, 7
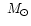 and Z= 0.005, 0.02.
MBC calculated the evolution
of stars with
and Z= 0.005, 0.02.
MBC calculated the evolution
of stars with
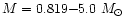 and
Z=0.008, 0.02
for the case of strong overshooting,
which means that the stars evolve rapidly so that the upper mass limit of
ILMS is changed from the standard value of 8
and
Z=0.008, 0.02
for the case of strong overshooting,
which means that the stars evolve rapidly so that the upper mass limit of
ILMS is changed from the standard value of 8 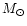 to 6
to 6 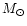 .
M2K gave a new set of stellar
yields (for
.
M2K gave a new set of stellar
yields (for
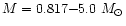 and Z= 0.004, 0.008, 0.02)
based on the results of an updated evolution calculation.
and Z= 0.004, 0.008, 0.02)
based on the results of an updated evolution calculation.
In our calculations, we choose the results of RV
(their
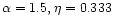 case),
VG, MBC and M2K as the yields
of ILMS for their wide mass ranges and metallicity-dependent results.
RV only gave results of
case),
VG, MBC and M2K as the yields
of ILMS for their wide mass ranges and metallicity-dependent results.
RV only gave results of
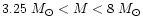 for the case of
for the case of
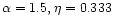 .
In fact, the hot-bottom burning (HBB) process
is not important for low
mass stars, but is very significant for
intermediate mass stars above
.
In fact, the hot-bottom burning (HBB) process
is not important for low
mass stars, but is very significant for
intermediate mass stars above
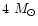 .
So we choose the results with
.
So we choose the results with
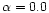 for the lower mass stars.
M2K calculated three sets of yields with
for the lower mass stars.
M2K calculated three sets of yields with
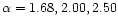 for stars with
for stars with
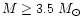 .
.
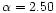 is too high to
fit the observations (M2K), so we only consider the results for
is too high to
fit the observations (M2K), so we only consider the results for
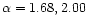 .
.
Type Ia SN explosions are assumed to occur in close binary systems
(Whelan & Iben 1973). In this model, the explosion is caused by
a carbon-deflagration of the material
accreting on the degenerate white dwarf (Nomoto et al. 1997b),
and the ejecta is dominated by the 56Fe isotope.
In this paper, the nucleosynthesis yields of SNIa explosions are taken
from the classical W7-model of Nomoto et al. (1997b), in which 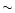
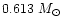 of Fe is produced.
of Fe is produced.
A star in the mass range of 8-10
 (or 6-8
(or 6-8
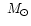 in the case of strong overshooting) generally develops a degenerate O-Ne-Mg
core after C-burning and eventually explodes as an electron capture supernova,
leaving a neutron star of
in the case of strong overshooting) generally develops a degenerate O-Ne-Mg
core after C-burning and eventually explodes as an electron capture supernova,
leaving a neutron star of
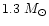 as a remnant and expelling a very small quantity of heavy elements.
as a remnant and expelling a very small quantity of heavy elements.
A star with a higher initial mass will end its life with an Fe-core
collapse type II SN explosion.
Some authors, including WW, N97, M92 and PCB,
calculated the stellar nucleosynthesis yields
for such stars either with or without mass loss through wind.
The results differ because of different choices of the
parameters.
We have carefully compared their parameters and results in
Liang & Zhao (2001).
Some of the parameters adopted by them are listed in Table 2, including
the stellar mass, metallicity, and 12C
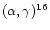 O reaction rate.
O reaction rate.
Limongi et al. (2000) calculated the presupernova nucleosynthesis
of massive stars with
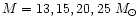 and Z=0.02,
and the explosive nucleosynthesis of stars with
Z=10-3, 0.
They did not give the yields of stars with
and Z=0.02,
and the explosive nucleosynthesis of stars with
Z=10-3, 0.
They did not give the yields of stars with
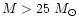 ,
which
are very important for tracing the chemical evolution. And
they did not give the explosive nucleosynthesis of stars with Z=0.02.
So we did not use their results in our calculation of the abundance evolution of CNO elements in the present paper.
,
which
are very important for tracing the chemical evolution. And
they did not give the explosive nucleosynthesis of stars with Z=0.02.
So we did not use their results in our calculation of the abundance evolution of CNO elements in the present paper.
WW calculated, for a large mass range, the metallicity-dependent yields of SNII explosion, and the results
have been widely used in GCE models (e.g.
Timmes et al. 1995; Chiappini et al. 1997)
Timmes et al. (1995) suggested that the results of
abundance evolution would be better
if the Fe yields of WW is reduced by a factor of 2.
Samland (1998) suggested that the actual Fe yield of SNII
explosion should be
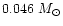 ,
approximately a factor of 2 less than the WW value.
Carigi (1994)
used 0.075
,
approximately a factor of 2 less than the WW value.
Carigi (1994)
used 0.075 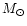 as the Fe yields of SNII explosion in their GCE model.
Chieffi et al. (1998)
calculated the nucleosynthesis of SNII explosion for a
as the Fe yields of SNII explosion in their GCE model.
Chieffi et al. (1998)
calculated the nucleosynthesis of SNII explosion for a
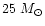 star,
and got an
Fe yield of about
0.075
star,
and got an
Fe yield of about
0.075
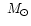 .
SN 1987A, for an initial main sequence mass of 20
.
SN 1987A, for an initial main sequence mass of 20
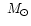 ,
ejected 0.075
,
ejected 0.075
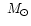 of Fe, while
for the same initial mass, WW got 0.151
of Fe, while
for the same initial mass, WW got 0.151
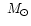 ,
again twice as large.
Because of these findings
we reduced the results of WW by a factor of 2 in our calculations.
,
again twice as large.
Because of these findings
we reduced the results of WW by a factor of 2 in our calculations.
N97 extended the calculations of Thielemann et al. (1996) to include
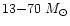 ,
solar metallicity stars.
We should note that
N97 used the evolution of the He core instead that of the entire star.
They used a relation
,
solar metallicity stars.
We should note that
N97 used the evolution of the He core instead that of the entire star.
They used a relation
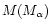 to transfer the result for a helium core of mass
to transfer the result for a helium core of mass
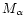 to that of a star of initial mass M (Sugimoto & Nomoto 1980).
This can be understood since
the total ejecta of star must be the sum of the contributions of both
the He-core and the envelope of mass
to that of a star of initial mass M (Sugimoto & Nomoto 1980).
This can be understood since
the total ejecta of star must be the sum of the contributions of both
the He-core and the envelope of mass
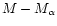 .
(Thomas et al. 1998).
.
(Thomas et al. 1998).
Both M92 and PCB considered radiative-driven stellar wind in their
calculations, which was
important for massive stars, especially the W-R stars.
The synthesized elements of C, N and O, in particular, C, can be ejected
into the ISM in stellar wind.
How to choose the yields of W-R stars?
Massey et al. (1995) studied the massive stars both in the
general field and associations
of the Magellanic Clouds.
Their data showed that stars with initial masses
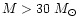 evolved
through the W-R phase in the Large Magellanic Cloud (LMC); while the statistics of
the Small Magellanic Cloud (SMC)
are consistent with a somewhat higher mass limit of
possibly
evolved
through the W-R phase in the Large Magellanic Cloud (LMC); while the statistics of
the Small Magellanic Cloud (SMC)
are consistent with a somewhat higher mass limit of
possibly
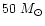 .
Conti (1995) suggested that the W-R stars are highly evolved,
luminous, hot, and (mostly)
He-burning descendants of the most massive stars in the solar neighborhood, with masses
.
Conti (1995) suggested that the W-R stars are highly evolved,
luminous, hot, and (mostly)
He-burning descendants of the most massive stars in the solar neighborhood, with masses
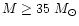 .
In the present paper, we follow
the suggestions of Maeder & Conti (1994) and the references therein and assume that the stars
with
.
In the present paper, we follow
the suggestions of Maeder & Conti (1994) and the references therein and assume that the stars
with
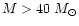 will evolve through the W-R stage.
So we divide the massive stars into two mass ranges,
will evolve through the W-R stage.
So we divide the massive stars into two mass ranges,
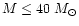 and
and
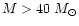 ,
in our discussion
on the source of carbon.
For the upper mass limit of massive stars, we choose
,
in our discussion
on the source of carbon.
For the upper mass limit of massive stars, we choose
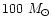 ,
following the suggestion of Leitherer (1995), and the usual practice with the upper mass limit of IMF used in many GCE models
(e.g. PCB, Prantzos & Silk 1998)
,
following the suggestion of Leitherer (1995), and the usual practice with the upper mass limit of IMF used in many GCE models
(e.g. PCB, Prantzos & Silk 1998)
M92 did not give Fe yields. When we use the M92 set of yields,
we choose the following values: 0.15
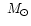 for stars with initial main sequence mass
for stars with initial main sequence mass
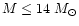 ,
0.075
,
0.075
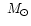 for
for
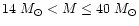 ,
and 0.15
,
and 0.15
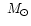 for
for
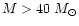 .
These choices are based on the following considerations.
In the case of SN 1987A (20
.
These choices are based on the following considerations.
In the case of SN 1987A (20
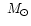 during
the main-sequence stage), the light curve, powered by the decay of 56Ni
and 56Co, gives a determination of the produced 56Fe of
0.075
during
the main-sequence stage), the light curve, powered by the decay of 56Ni
and 56Co, gives a determination of the produced 56Fe of
0.075
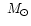 ,
and for SN 1993J (main-sequence mass 14
,
and for SN 1993J (main-sequence mass 14
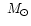 ),
one of 0.15
),
one of 0.15
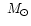 .
(Thielemann et al. 1996). Carigi (1994)
adopted 0.075
.
(Thielemann et al. 1996). Carigi (1994)
adopted 0.075
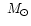 of Fe
for a SNII explosion and 0.15
of Fe
for a SNII explosion and 0.15
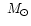 for a SNIb explosion. Since SNIb takes place in W-R stars, and
since we assume that the stars with
for a SNIb explosion. Since SNIb takes place in W-R stars, and
since we assume that the stars with
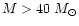 will undergo the W-R stage,
so we use the value 0.15
will undergo the W-R stage,
so we use the value 0.15
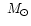 in such cases.
in such cases.
M92 only gave the yield of N ejected in
wind, and not the final value. Thus the N yields used in
our calculations
are lower limits.
We set up a standard infall model of GCE
to map out
the abundance evolution of carbon, nitrogen and oxygen in the solar
neighborhood.
We choose the general formulae of SFR and IMF, and slightly adjust
them by changing 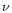 and
and 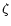 respectively.
The 8 sets of nucleosynthesis yield,
described in Sect. 4 are then used to set up 8 specific models.
For each model,
we try to fit the observational age-metallicity relation, the
metallicity distribution of G dwarfs and the [O/Fe] vs. [Fe/H] relation.
The calculated results will then be discussed:
the [C/Fe] vs. [Fe/H] relation, in this section.
the [N/Fe] vs. [Fe/H] and [O/Fe] vs. [Fe/H] relations
in Sects. 6 and 7, respectively.
respectively.
The 8 sets of nucleosynthesis yield,
described in Sect. 4 are then used to set up 8 specific models.
For each model,
we try to fit the observational age-metallicity relation, the
metallicity distribution of G dwarfs and the [O/Fe] vs. [Fe/H] relation.
The calculated results will then be discussed:
the [C/Fe] vs. [Fe/H] relation, in this section.
the [N/Fe] vs. [Fe/H] and [O/Fe] vs. [Fe/H] relations
in Sects. 6 and 7, respectively.
In this model labelled (VG+WW), we use the yields of VG for ILMS,
and WW for massive stars (see Sect. 4).
The calculated age-metallicity relation, metallicity distribution of G dwarfs and [O/Fe] vs. [Fe/H]
relation can all fit the observations well (Figs. 1a,c,d).
The predicted abundance evolution of carbon is given in Fig. 1b; this
shows that [C/Fe] vs. [Fe/H]
is approximately constant in time. The predicted trend agrees with the observations, including
even
the increasing positive [C/Fe] below [Fe/H] <-1.5.
The reason of positive [C/Fe] may be that for the massive stars,
the C yields are high and the Fe yields are
relative low.
In medium metal-poor region, [Fe/H] >-1.0,
[C/Fe] slightly increases, showing the important
C contribution from ILMS.
Up to the late evolutionary stage of the Galaxy,
the ratio of SNIa rate to SNII rate increases, therefore the [C/Fe] value
decreases with increasing [Fe/H] in the range of [Fe/H] >-0.5.
The results show that the combined contribution of carbon
by VG and WW can
explain the observed [C/Fe] vs. [Fe/H] relation.
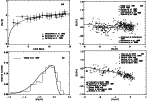 |
Figure 1:
Results using the nucleosynthesis yields of VG for ILMS and
WW for massive stars (the solid lines) (model VG+WW).
a) The age-metallicity relation in the solar neighborhood;
b) The [C/Fe] vs. [Fe/H] relation;
c) The metallicity distribution of G dwarfs in the solar neighborhood;
d) The [O/Fe] vs. [Fe/H] relation.
The corresponding observations are shown in the figures. |
| Open with DEXTER |
Using the yields of N97 for massive stars and those of VG for ILMS (model VG+N97),
our GCE results can fit the observational
age-metallicity relation,
metallicity distribution of G dwarfs and [O/Fe] values (Figs. 2a,c,d).
But the predicted C abundance is too low to fit
the observations (Fig. 2b).
Compared to WW,
the lower C yields calculated by N97 may be mainly caused by
the choice of a higher rate of
12C
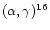 O reaction. Also,
the authors of N97 themselves have compared
the different nucleosynthesis results based on two different
12C
O reaction. Also,
the authors of N97 themselves have compared
the different nucleosynthesis results based on two different
12C
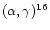 O reaction rates from
Caughlan et al. (1985) (hereafter CFHZ)
and Caughlan & Fowler (1988) (hereafter CF) respectively.
CFHZ gave a higher reaction rate than CF:
O reaction rates from
Caughlan et al. (1985) (hereafter CFHZ)
and Caughlan & Fowler (1988) (hereafter CF) respectively.
CFHZ gave a higher reaction rate than CF:
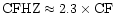 ;
and WW adopted
;
and WW adopted
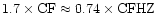 in their calculation, which is lower than in N97.
So when [O/Fe] can be matched, [C/Fe] is lower than the observations.
These results underline the importance of the 12C
in their calculation, which is lower than in N97.
So when [O/Fe] can be matched, [C/Fe] is lower than the observations.
These results underline the importance of the 12C
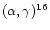 O reaction rate
to elemental nucleosynthesis.
O reaction rate
to elemental nucleosynthesis.
Certainly, besides the 12C
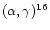 O reaction rate,
convective mechanism and explosion energy can affect the
nucleosynthesis yields (N97).
O reaction rate,
convective mechanism and explosion energy can affect the
nucleosynthesis yields (N97).
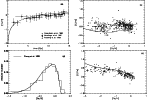 |
Figure 2:
Same as Fig. 1, but with the nucleosynthesis yields of VG for ILMS
and N97 for massive stars (model VG+N97). |
| Open with DEXTER |
The results predicted by model VG+M92 can fit the observed age-metallicity
relation,
metallicity distribution of G dwarfs and [O/Fe] vs. [Fe/H] (Figs. 3a,c,d).
There is a strong increase in the calculated [C/Fe] for [Fe/H] >-1.2 (Fig. 3b).
What is the main contributor?
ILMS? Stellar winds of W-R stars? Or a combined contribution of the two?
Let us try to identify the main source.
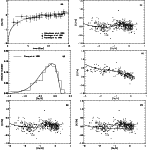 |
Figure 3:
a- d) are same as in Fig. 1,
but with the nucleosynthesis yields of VG for ILMS and M92 for massive stars (model VG+M92).
e) The calculated [C/Fe] vs. [Fe/H] only considering
the C yields of massive stars of M92;
f) The calculated [C/Fe] vs. [Fe/H] considering C yields of VG for ILMS and
C yields of only
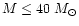 stars from M92 for massive stars.
stars from M92 for massive stars. |
| Open with DEXTER |
Figure 3e gives the result for only the yields of massive stars of M92.
It shows the predicted [C/Fe] increases with metallicity
in metal-rich region.
The calculated [C/Fe] using the yields of ILMS (VG) and only massive stars with
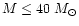 (M92) is
presented in Fig. 3f: here, the calculated [C/Fe]
is slightly lower than the observations in metal-rich region.
The difference between Figs. 3e and 3f
shows that the contribution to carbon
from stellar wind of high metallicity W-R stars calculated by
M92 is greater than the contribution from ILMS given by VG.
The
(M92) is
presented in Fig. 3f: here, the calculated [C/Fe]
is slightly lower than the observations in metal-rich region.
The difference between Figs. 3e and 3f
shows that the contribution to carbon
from stellar wind of high metallicity W-R stars calculated by
M92 is greater than the contribution from ILMS given by VG.
The
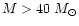 massive stars with higher metallicity, the W-R stars,
can eject significant amounts of carbon, which
causes the [C/Fe] value to increase with increasing
metallicity in the range of [Fe/H] >-1.0 in Fig. 3e.
massive stars with higher metallicity, the W-R stars,
can eject significant amounts of carbon, which
causes the [C/Fe] value to increase with increasing
metallicity in the range of [Fe/H] >-1.0 in Fig. 3e.
Using results of RV as the yields of ILMS and WW for massive stars (model RV+WW),
we calculated the corresponding age-metallicity relation, metallicity distribution
of G dwarfs, [O/Fe] vs. [Fe/H] and [C/Fe] vs. [Fe/H] (Figs. 4a-d).
When these three
results match the observations, [C/Fe] first increases slightly and then decreases,
and is slightly higher than
the prediction of model VG+WW in metal-rich region.
These results show that the RV calculation gives more carbon than does VG
due to the use of different parameter values
(see M2K, Liang & Zhao 2001 for details).
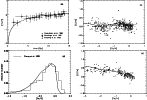 |
Figure 4:
Same as Fig. 1, but with the nucleosynthesis yields of RV for ILMS
and WW for massive stars (model RV+WW). |
| Open with DEXTER |
Figures 5a,c,d show that the calculated results using model RV+N97
can fit the observations,
i.e., the age-metallicity relation, the metallicity distribution of G dwarfs
and the [O/Fe] vs. [Fe/H] relation.
The calculated [C/Fe] vs. [Fe/H] then shows that
more carbon is given by RV than VG, and this
increases the predicted [C/Fe] in metal-rich region (Fig. 5b).
Because N97 gives low carbon yields for the reason of adopting a low
12C
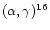 O
reaction rate,
[C/Fe] falls below the observations in the whole metallicity range (Fig. 5b).
O
reaction rate,
[C/Fe] falls below the observations in the whole metallicity range (Fig. 5b).
 |
Figure 5:
Same as Fig. 1, but with the nucleosynthesis yields of RV for ILMS
and N97 for massive stars (model RV+N97). |
| Open with DEXTER |
Figures 6a-d display the results based on the yields of RV for ILMS
and of M92 for massive stars (model RV+M92).
Figs. 6a,c,d show the calculations can fit the corresponding observations, while Fig. 6b shows that
[C/Fe] increases with metallicity in metal-rich region (Fig. 6b).
There are no apparent difference here between this model and
the model VG+M92 (Fig. 3b);
this can be
understood because the C contribution
from W-R stars given by M92 is
higher than that from ILMS given by RV or VG.
Figure 6e shows the [C/Fe] vs. [Fe/H] relation based only on the
yields of massive stars
from M92; with no contribution from ILMS,
this is still higher than the observations in metal-rich region.
Figure 6f exhibits the predicted [C/Fe] using the yields of RV for ILMS and those of M92
for massive stars with
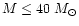 ;
it
fits the observations, and shows a slightly higher [C/Fe]
than is given by model VG+M92 in metal-rich region (Fig. 3b).
This result shows that RV gives higher C yields
than does VG with a different choice of the parameters.
;
it
fits the observations, and shows a slightly higher [C/Fe]
than is given by model VG+M92 in metal-rich region (Fig. 3b).
This result shows that RV gives higher C yields
than does VG with a different choice of the parameters.
 |
Figure 6:
Same as Fig. 3, but with nucleosynthesis yields of RV for ILMS
and M92 for massive stars (model RV+M92). |
| Open with DEXTER |
It is proper to combine the yields of MBC and PCB
together since they used
the same parameters (Padova group).
They adopted a larger
convective overshooting, so that stars with
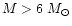 rather than
the standard >8
rather than
the standard >8 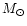 would end their lives through SNII explosions.
Both the age-metallicity relation and metallicity distribution of G dwarfs
can fit the observations well (Figs. 7a,c).
The O abundance is slightly lower than the observations (Fig. 7d), which may be caused by
the lower 12C
would end their lives through SNII explosions.
Both the age-metallicity relation and metallicity distribution of G dwarfs
can fit the observations well (Figs. 7a,c).
The O abundance is slightly lower than the observations (Fig. 7d), which may be caused by
the lower 12C
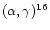 O reaction rate (CF) used by the
Padova group.
The predicted [C/Fe] vs. [Fe/H] relation is given in Fig. 7b, which
shows a strong increase of [C/Fe] with increasing metallicity
from [Fe/H]
O reaction rate (CF) used by the
Padova group.
The predicted [C/Fe] vs. [Fe/H] relation is given in Fig. 7b, which
shows a strong increase of [C/Fe] with increasing metallicity
from [Fe/H]
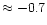 on.
on.
Figure 7e displays the [C/Fe] based only on the contribution of carbon from massive stars; it
shows that W-R stars with a high metallicity (
Z=0.008, 0.02) can
eject significant amounts of carbon into the ISM, much more than the lower metallicity stars.
Thus, [C/Fe] increases steeply starting from [Fe/H]
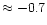 .
The subsequent decrease from [Fe/H]
.
The subsequent decrease from [Fe/H]
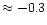 on is
the result of Fe contribution from SNIa explosions.
on is
the result of Fe contribution from SNIa explosions.
Figure 7f shows the case of only ILMS and the
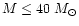 part of massive stars; there is basic
fit to the observations.
Comparing Figs. 7b, 7e and 7f, we find the main effect of the C yields from metal-rich W-R stars
is the obvious increase of [C/Fe] in metal-rich region shown
in Fig. 7b; - an increase to above the
observations.
part of massive stars; there is basic
fit to the observations.
Comparing Figs. 7b, 7e and 7f, we find the main effect of the C yields from metal-rich W-R stars
is the obvious increase of [C/Fe] in metal-rich region shown
in Fig. 7b; - an increase to above the
observations.
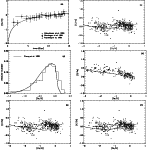 |
Figure 7:
Same as Fig. 3, but with nucleosynthesis yields of MBC for ILMS
and PCB for massive stars (model MBC+PCB). |
| Open with DEXTER |
We use the nucleosynthesis yields of M2K
in our GCE calculations because this new set of yields
include the results of
ILMS with the low metallicity value Z=0.004,
which may contain significant information on the ILMS
during the early Galactic stage.
We combine M2K and PCB in our
model M2K+PCB.
The calculated age-metallicity relation, metallicity distribution of
G dwarfs and [O/Fe] vs. [Fe/H] relation again match the observations, and are similar
to the results of model MBC+PCB, and so are not shown here.
The predicted evolution of [C/Fe] with metallicity is given
in Fig. 8a, which shows
a strong increase
with increasing metallicity
from [Fe/H]
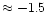 on. In order to understand
this increase, we re-calculate the [C/Fe] vs. [Fe/H] relation using only
the contribution of massive stars (Fig. 8c),
and only the yields of ILMS and
on. In order to understand
this increase, we re-calculate the [C/Fe] vs. [Fe/H] relation using only
the contribution of massive stars (Fig. 8c),
and only the yields of ILMS and
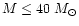 massive stars (Fig. 8d)
respectively.
Comparing Figs. 8c and 7e, and
Figs. 8d and 7f, we guess that maybe it is the ILMS with Z=0.004 that produce a significant
amount of carbon,
which lead to the strong increase of [C/Fe]
displayed in Fig. 8a.
Figure 8e confirms our guess, in which the solid line represents
the calculated [C/Fe] vs. [Fe/H] relation using only the yields of
Z=0.008, 0.02
(the same metallicities as in MBC)
of M2K for ILMS and PBC for massive stars,
and the dashed line represents
the results of model MBC+PCB (the same line as in Fig. 7b).
massive stars (Fig. 8d)
respectively.
Comparing Figs. 8c and 7e, and
Figs. 8d and 7f, we guess that maybe it is the ILMS with Z=0.004 that produce a significant
amount of carbon,
which lead to the strong increase of [C/Fe]
displayed in Fig. 8a.
Figure 8e confirms our guess, in which the solid line represents
the calculated [C/Fe] vs. [Fe/H] relation using only the yields of
Z=0.008, 0.02
(the same metallicities as in MBC)
of M2K for ILMS and PBC for massive stars,
and the dashed line represents
the results of model MBC+PCB (the same line as in Fig. 7b).
The solid and dashed lines in Fig. 8f
represent the corresponding results for nitrogen.
Figs. 8e, f show that
the nitrogen yields of M2K with
Z=0.008, 0.02 are very similar to
the corresponding results of MBC,
though M2K gave more carbon and nitrogen according to the updated parameters,
resulting in the slightly higher [C/Fe] and [N/Fe] values in metal-rich region.
Figure 8b illustrates the [N/Fe] vs. [Fe/H] relation using the yields of M2K for ILMS; the relation
is higher than that shown in Fig. 8f.
These results show
that ILMS with low metallicity Z=0.004 contribute
very important amounts of C and N to the ISM (also see Fig. 1 of M2K).
The lower metallicity ILMS have higher C and N abundances
because for them the HBB process is more efficient,
and mass loss is less so.
The lower mass loss rates correspond to longer TP-AGB lifetimes,
hence a greater number of the third dredge-up events and a longer duration of the HBB process.
The up-to-date nucleosynthesis calculations (VG) only go as low as
Z=0.001.
Calculations of ILMS of even lower metallicities are needed;
these may revise the
trends of elemental abundance evolution, and provide different hints
to the early GCE history.
Though the nucleosynthesis results with
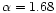 and 2.00 given by M2K
are different (more nitrogen is produced by intermediate mass stars with
and 2.00 given by M2K
are different (more nitrogen is produced by intermediate mass stars with
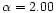 than with
than with
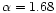 ),
we find
no obvious differences between these two sets of results.
So we only give the GCE results based on the yields with
),
we find
no obvious differences between these two sets of results.
So we only give the GCE results based on the yields with
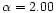 in this paper.
in this paper.
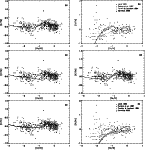 |
Figure 8:
a) The calculated [C/Fe] vs. [Fe/H] using nucleosynthesis yields of M2K
for ILMS and PCB for massive stars (model M2K+PCB);
b) Same as a) but for nitrogen;
c) The calculated [C/Fe] vs. [Fe/H] considering only yields of massive stars from
PCB without ILMS;
d) The calculated [C/Fe] vs. [Fe/H] considering yields of M2K for ILMS and only
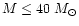 massive stars from PCB;
e) The solid line represents the [C/Fe] vs. [Fe/H] relation
considering the yields of PCB for massive stars and M2K
only with Z=0.008 and Z=0.02 metallicities for ILMS,
and the dashed line represents the same result as in Fig. 7b;
f) Same as e) but for nitrogen.
massive stars from PCB;
e) The solid line represents the [C/Fe] vs. [Fe/H] relation
considering the yields of PCB for massive stars and M2K
only with Z=0.008 and Z=0.02 metallicities for ILMS,
and the dashed line represents the same result as in Fig. 7b;
f) Same as e) but for nitrogen. |
| Open with DEXTER |
In summary, we give and analyze the calculated abundance evolution of carbon
using 8 recently published sets of nucleosynthesis yields.
The parameters of the 8 models are listed in Table 3.
Here are some of the obvious implications of the parameters. The higher the 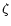 value,
the more contribution comes from massive stars, and then the predicted O abundance will be
higher,
especially in low metallicity region. A higher
value,
the more contribution comes from massive stars, and then the predicted O abundance will be
higher,
especially in low metallicity region. A higher 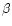 value means
a higher SNIa rate, hence a greater amount of Fe element from SNIa explosion.
A higher
value means
a higher SNIa rate, hence a greater amount of Fe element from SNIa explosion.
A higher 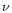 value
represents a higher SFR, more stars form,
leading to an increase in the O abundance and [Fe/H],
and the effect is more obvious in metal-poor region.
At the same time, a higher
value
represents a higher SFR, more stars form,
leading to an increase in the O abundance and [Fe/H],
and the effect is more obvious in metal-poor region.
At the same time, a higher 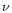 will lead to a higher peak in the metallicity distribution of G dwarfs.
will lead to a higher peak in the metallicity distribution of G dwarfs.
The 12C
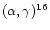 O reaction rate is very important to
stellar nucleosynthesis. It determines the C and O abundances,
hence the abundances of the heavier elements.
Generally, in nucleosynthesis calculations, the
12C
O reaction rate is very important to
stellar nucleosynthesis. It determines the C and O abundances,
hence the abundances of the heavier elements.
Generally, in nucleosynthesis calculations, the
12C
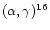 O reaction rates given by CFHZ and CF are
widely used. CFHZ gives higher values than does CF:
O reaction rates given by CFHZ and CF are
widely used. CFHZ gives higher values than does CF:
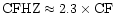 .
And the higher reaction rate
leads to a lower C abundance. N97 exhibited this result in their Fig. 7.
They suggested that the actual reaction rate was between CFHZ and CF.
WW adopted 1.7
.
And the higher reaction rate
leads to a lower C abundance. N97 exhibited this result in their Fig. 7.
They suggested that the actual reaction rate was between CFHZ and CF.
WW adopted 1.7 CF (
CF (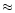
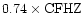 )
to be the actual reaction rate
in their nucleosynthesis calculations. They gave higher C yields
than did N97.
)
to be the actual reaction rate
in their nucleosynthesis calculations. They gave higher C yields
than did N97.
For the higher massive stars, stellar wind mass loss strongly affects the C yields,
so the effect caused by the 12C
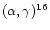 O reaction rate
is obscured. The lower reaction rate of CF has led to
the lower O yields of PCB.
O reaction rate
is obscured. The lower reaction rate of CF has led to
the lower O yields of PCB.
Leitherer (1995) suggested that the most massive stars known in the universe
have masses around 100 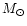 and lifetimes of a few Myrs. They are rare:
in the solar neighborhood only about one such massive star is counted
per 105 to 106 solar-type stars.
There are three key phases during the evolution of a massive
star: O star, luminous blue variable star and Wolf-Rayet star.
The mass loss of a massive star can be calculated from UV wind lines,
H
and lifetimes of a few Myrs. They are rare:
in the solar neighborhood only about one such massive star is counted
per 105 to 106 solar-type stars.
There are three key phases during the evolution of a massive
star: O star, luminous blue variable star and Wolf-Rayet star.
The mass loss of a massive star can be calculated from UV wind lines,
H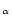 or radio fluxes.
The UV P Cygni profile, ubiquitous in O-type stars,
provides a direct indication of stellar wind;
H
or radio fluxes.
The UV P Cygni profile, ubiquitous in O-type stars,
provides a direct indication of stellar wind;
H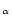 has been recognized as the prime source of mass-loss
in early-type stars;
and winds in hot stars can be readily
observed at IR-mm-radio wavelengths via the free-free "thermal" excess
caused by the stellar wind. The mass loss rate scales as
Z0.5 for O stars and early B stars, as Z0.8 for mid-B supergiants,
and as Z1.7 for A supergiants (Kudritzki & Puls 2000; Crowther
2000a).
has been recognized as the prime source of mass-loss
in early-type stars;
and winds in hot stars can be readily
observed at IR-mm-radio wavelengths via the free-free "thermal" excess
caused by the stellar wind. The mass loss rate scales as
Z0.5 for O stars and early B stars, as Z0.8 for mid-B supergiants,
and as Z1.7 for A supergiants (Kudritzki & Puls 2000; Crowther
2000a).
W-R stars are easily detectable due to their
intrinsic brightness and the profound effects on the interstellar environment.
They eject a large amount of material into the ISM via
the radiative-driven stellar wind.
The nucleosynthesis calculations show that
the ejected carbon by massive stars
are very important to the enrichment of the ISM.
In general, the mass loss rate of massive stars adopted
in the stellar evolution calculations are
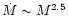 and
and
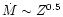 (M92; PCB).
However, according to recent reviews, our knowledge of the mass loss of massive stars is not
very clear.
(M92; PCB).
However, according to recent reviews, our knowledge of the mass loss of massive stars is not
very clear.
Meynet & Maeder (2000) calculated the evolution of stars with rotation, and suggested
that rotation can increase mass loss, also can bring significant surface He-and N-enhancements; the enhancements are the greater for the higher the mass and the rotation.
In his review, Crowther (2000a) found that the
recent mass-loss rates for Galactic W-R stars indicated a
downward revision of 2-4 relative to previous calibrations
(e.g. Langer 1989:
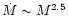 )
due to clumping
(e.g. Schmutz 1997).
Indeed, metallicity affects the yields of carbon.
When mass loss gets very efficient, 12C will increase because He-burning
products can be revealed on the surface. If mass loss is extreme, anyway,
12C and 16O yields may even decrease because most of the mass is rapidly lost
in the wind in the form of 4He.
But at present, the question of a Z-dependent mass loss in W-R stars remains open.
Crowther (2000a) suggested that
there is a clear distinction among spectral
subtypes in galaxies with different metallicities, which is qualitatively
explained by evolutionary and spectroscopic models (Crowther 2000b).
WN stars in LMC show negligible spectroscopic difference from their Galactic
counterparts. And the situation is less clear for the SMC, since most W-R stars
are complicated by binarity (Crowther 2000a).
)
due to clumping
(e.g. Schmutz 1997).
Indeed, metallicity affects the yields of carbon.
When mass loss gets very efficient, 12C will increase because He-burning
products can be revealed on the surface. If mass loss is extreme, anyway,
12C and 16O yields may even decrease because most of the mass is rapidly lost
in the wind in the form of 4He.
But at present, the question of a Z-dependent mass loss in W-R stars remains open.
Crowther (2000a) suggested that
there is a clear distinction among spectral
subtypes in galaxies with different metallicities, which is qualitatively
explained by evolutionary and spectroscopic models (Crowther 2000b).
WN stars in LMC show negligible spectroscopic difference from their Galactic
counterparts. And the situation is less clear for the SMC, since most W-R stars
are complicated by binarity (Crowther 2000a).
Comparing our calculated results using different nucleosynthesis yields
(Sects. 5.1-5.8),
considering the uncertainty of stellar wind mass loss
of massive stars (see Sect. 5.10),
and assuming that the actual
12C
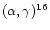 O reaction rate to be between the values of CFHZ and CF,
we choose to use
the results of model VG+WW
in an analysis of the contributions of carbon by stars of different masses.
O reaction rate to be between the values of CFHZ and CF,
we choose to use
the results of model VG+WW
in an analysis of the contributions of carbon by stars of different masses.
Here, the reason of choosing VG rather than RV for ILMS is
because of suggestions that the yields of RV are not successful
in predicting the observed C/O and N/O ratios in stars and planetary nebulae,
or in reproducing the carbon stars of relatively low luminosities
in the Magellanic Clouds (Gustafsson et al. 1999).
Figure 9 shows the fraction of carbon contributed by massive stars
based on the WW yields for
massive stars and the VG yields for ILMS, as a function of the
Galactic age.
In the early Galactic stage, almost all the carbon is produced by massive stars.
As the age advances, ILMS contribute more and more,
and an overtake the massive stars
from about 1.65 Gyr on.
At the present epoch, many low mass stars have also evolved and ejected matter into the ISM, and the relative contribution by the ILMS is further increased.
 |
Figure 9:
The relative contribution of massive stars
to carbon production at different Galactic ages using the results of WW
for nucleosynthesis yields of
massive stars and VG for ILMS. |
| Open with DEXTER |
The element nitrogen includes a primary and a secondary component.
If nitrogen production depends on the initial CNO abundance,
the [N/Fe] would be dependent on [Fe/H], and this part of nitrogen is
secondary;
however, if nitrogen production is chiefly
primary, then [N/Fe] would be independent of the value of [Fe/H].
Laird (1985) and Carbon et al. (1987)
found the observed [N/Fe] to be
constant over the entire metallicity range, although
the precise level is uncertain.
So, it seems that the observations require a
primary nitrogen source from massive stars.
However, if the observed constant nitrogen in low
metallicity region is correct, then the present yields by massive stars cannot
supply the needed primary nitrogen source (Timmes et al. 1995;
Chiappini et al. 1997).
Our results, based on the recently published nucleosynthesis yields
of massive stars, also point to an absence of a primary nitrogen source.
Figures 10a-c show the calculated results of [N/Fe] vs. [Fe/H]
using our GCE models VG+WW, VG+N97 and VG+M92 respectively.
Those models with the RV yields of ILMS give similar trends
to these with the VG yields;
so we do not show them here. The [N/Fe] values of
model MBC+PCB and M2K+PCB will be given
in Sect. 5.8.
In these figures, the solid lines represent the results with
the N yields of
both ILMS and massive stars,
and the dashed lines represent the results with only the contribution from massive stars.
These results show that ILMS are the dominant donor of nitrogen,
while
massive stars have provided only a small part to the ISM
during the whole Galactic age up to the present.
However, in the range of -3< [Fe/H] <-2, [N/Fe] increases steeply
(solid lines in Figs. 10a, c),
due to
intermediate mass stars as source of secondary nitrogen.
As metallicity increases up to [Fe/H]  -1.0,
[N/Fe] increases gradually, - typical behaviour of
secondary nitrogen.
As [Fe/H] increases further,
[N/Fe] approaches the solar value, which shows that the primary
nitrogen from LIMS plays
an important role in the production of nitrogen since that time.
-1.0,
[N/Fe] increases gradually, - typical behaviour of
secondary nitrogen.
As [Fe/H] increases further,
[N/Fe] approaches the solar value, which shows that the primary
nitrogen from LIMS plays
an important role in the production of nitrogen since that time.
From another aspect, comparison between the results shown in Figs. 10a and 10c
confirms further that the ILMS are the main source of nitrogen.
These two figures are based the models VG+WW and VG+M92 which use different N yields
from massive stars, yet the results are very similar, so we infer that
it is the N yields of ILMS that provide the bulk of nitrogen to the ISM.
In addition,
we should note that M92 gives only the N yields of stellar wind
and does not include contribution from
SNII explosions, so the dashed line is higher
in Fig. 10a than in Fig. 10c.
Again, the predicted N abundance evolution by the models MBC+PCB and M2K+PCB
also support the statement that ILMS are the dominant N contributor (see Figs. 8b, f).
The model VG+N97 predicts high [N/Fe] in early Galactic stage, though
not as high as the solar abundance. A possible reason is that N97 only gives the
yields of solar metallicity massive stars,
which eject more nitrogen than do low metallicity stars.
With increasing metallicity,
Fe from SNIa explosions
plays an increasingly more important role in the enrichment of the ISM,
and this leads to a [N/Fe] decrease with the Galactic evolution
(dashed line in Fig. 10b).
In general, the relative weight of the secondary and primary components on the
theoretical yield of
14N of ILMS depends on the interplay between the secondary enrichment
caused by the first and second
dredge-up episodes, and the primary contribution given by the CNO-cycle during the
envelope burning.
13C and 14N are regarded as secondary elements in the sense
that they are formed from 12C and 16O originally present in the star
at the time of its formation. Typical in this sense is the secondary production
of 13C and 14N during the first dredge-up,
and the secondary production of 14N during the second dredge-up. However,
when the third dredge-up process operates in conjunction with the HBB process,
primary 13C and 14N
are produced. Meanwhile the primary 12C, dredged up after each He-shell flash is
later converted in part into primary 13C and 14N by the burning at
the base of the convective envelope during the interpulse phase.
Is it sure that the observed [N/Fe] is near 0.0
in metal-poor region?
Carbon et al. (1987) found two stars with high N abundances,
HD74000 with [N/Fe]  +0.9, HD25329 with [N/Fe]
+0.9, HD25329 with [N/Fe]  +0.45.
Laird (1985)
obtained high N abundances
for four stars, HD74000 with [N/Fe]
+0.45.
Laird (1985)
obtained high N abundances
for four stars, HD74000 with [N/Fe]  +1.15 and [Fe/H] =-2.02,
HD97916 with [N/Fe]
+1.15 and [Fe/H] =-2.02,
HD97916 with [N/Fe]  +0.75 and [Fe/H] =-1.30,
HD160617 with [N/Fe]
+0.75 and [Fe/H] =-1.30,
HD160617 with [N/Fe] 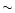 +1.65 and [Fe/H] =-1.99,
HD166913 with [N/Fe]
+1.65 and [Fe/H] =-1.99,
HD166913 with [N/Fe] 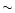 +0.70 and [Fe/H] =-1.80.
The possible reasons for
the very high N abundance given by the authors are: (1) internal mixing;
(2) mass transfer in a binary system;
(3) primordial N enhancement.
Beveridge & Sneden (1994) reanalyzed
the chemical abundances of two N-rich dwarf stars, namely HD 74000 and HD 25329.
Their results showed that all the very heavy elements synthesized through neutron-capture s-process
were enhanced in these two stars.
It is likely that the
enrichment of N and the very heavy elements originated in material dredged up from the
helium burning shell of former AGB stars.
Also, Carbon et al. (1987) pointed out that,
omitting the N-rich objects, the observed [N/Fe] vs. [Fe/H] plot showed a negative
correlation with [Fe/H].
In this sense, our results can basically fit the observations.
More explorations of metal-poor N-rich objects are needed.
+0.70 and [Fe/H] =-1.80.
The possible reasons for
the very high N abundance given by the authors are: (1) internal mixing;
(2) mass transfer in a binary system;
(3) primordial N enhancement.
Beveridge & Sneden (1994) reanalyzed
the chemical abundances of two N-rich dwarf stars, namely HD 74000 and HD 25329.
Their results showed that all the very heavy elements synthesized through neutron-capture s-process
were enhanced in these two stars.
It is likely that the
enrichment of N and the very heavy elements originated in material dredged up from the
helium burning shell of former AGB stars.
Also, Carbon et al. (1987) pointed out that,
omitting the N-rich objects, the observed [N/Fe] vs. [Fe/H] plot showed a negative
correlation with [Fe/H].
In this sense, our results can basically fit the observations.
More explorations of metal-poor N-rich objects are needed.
We now
follow Sect. 5.11 and calculate the contribution by massive stars
to nitrogen using the model VG+WW.
Figure 10d shows
the fractional contribution as a function of
the Galactic age.
We note that, except at the extreme early stage before the intermediate mass stars
began to evolve,
the relative contribution from massive stars
is very low in the early stage,
and that it gradually increases with
the evolution of the Galaxy, then slightly decreases in the late stage.
This trend means that the yield of nitrogen varies strongly with the metallicity.
However, the proportion of nitrogen contributed by massive stars is generally very low,
even the peak is less than 20%.
WW calculated a very low N yield for stars with zero metallicity,
on the order of
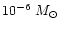 .
The N yields of ILMS with low metallicities
are higher than WW, for example, the newly formed and ejected nitrogen
from 8
.
The N yields of ILMS with low metallicities
are higher than WW, for example, the newly formed and ejected nitrogen
from 8  stars with Z=0.001 is about
stars with Z=0.001 is about
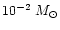 ,
thus, the intermediate mass stars
have been making important contributions since they began to evolve
and eject materials into the ISM.
With increase of metallicity, the N yield of massive stars also increases,
as is shown by rising part of the curve
of Fig. 10d.
The eventual decrease in the curve
at the late stage is probably caused by the higher N yield from the ILMS with higher metallicities.
,
thus, the intermediate mass stars
have been making important contributions since they began to evolve
and eject materials into the ISM.
With increase of metallicity, the N yield of massive stars also increases,
as is shown by rising part of the curve
of Fig. 10d.
The eventual decrease in the curve
at the late stage is probably caused by the higher N yield from the ILMS with higher metallicities.
 |
Figure 10:
a) The calculated [N/Fe] vs. [Fe/H] relation using nucleosynthesis
yields of VG for ILMS and WW for massive stars. The solid line represents
the result with both the contributions of
ILMS and massive stars, and the dashed line represents
the result with only massive stars.
b) Same as a) but with the yields of N97 for massive stars.
c) Same as a) but with the yields of M92 for massive stars.
d) The relative contribution of massive stars to nitrogen production
with the Galactic
ages predicted by using the yields of VG for ILMS and WW for massive stars. |
| Open with DEXTER |
The source of oxygen is generally clear, namely, it is
produced mainly in
short-lived, massive stars and ejected through SNII explosions.
As our Galaxy evolves, more and more Fe is produced through long lifetime SNIa explosions,
and the ratio [O/Fe] decreases.
This trend is shown in all of our calculated results given in Sect. 5.
Conti et al. (1967) presented the first data indicating
the existence of an oxygen overabundance in metal-poor stars.
Many authors continued to explore the evolution of [O/Fe],
and confirmed the overabundance of oxygen in metal-poor stars (see Sect. 2).
Edvardsson
et al. (1993) and Chen et al. (2000) separately obtained
the oxygen abundances of a large
sample of disk stars, both showed that [O/Fe]
decreases
with increasing metallicity in Galactic disk stars.
For halo stars, however, available observations exhibit an apparent contradiction,
namely,
the [O/Fe] values of metal-poor giants derived from the [O I] forbidden
line (+0.4)
are lower
than those of dwarfs from the O I triplet at  7770 Å and OH lines
(+1.0) (see Fig. 11).
And using the
7770 Å and OH lines
(+1.0) (see Fig. 11).
And using the  6300 Å forbidden line, similar abundance values to the giants
have been obtained for some metal-poor dwarfs,
though the line
is very weak in these stars (Nissen et al. 2000).
6300 Å forbidden line, similar abundance values to the giants
have been obtained for some metal-poor dwarfs,
though the line
is very weak in these stars (Nissen et al. 2000).
The difference can be understood from two aspects.
In the first aspect, we believe that oxygen has a similar behavior to other
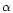 elements (Mg, Si, S, Ca), that is,
we believe that the lower [O/Fe] in metal-poor region
is true, and the relatively higher ratio derived from the O I triplet or OH line is wrong.
The reasons are as follows.
The O I
triplet has a very high excitation feature (9.15 eV) and is quite sensitive to the
temperature structure of the adopted model atmosphere, and NLTE effects
cause the higher O abundance derived from it.
And the OH lines in the UV are
very sensitive to the temperature structure of the stellar atmosphere and/or
to NLTE effects too.
According to this argument,
there should be no obvious change in the O abundance
as the dwarfs evolve to the giants.
elements (Mg, Si, S, Ca), that is,
we believe that the lower [O/Fe] in metal-poor region
is true, and the relatively higher ratio derived from the O I triplet or OH line is wrong.
The reasons are as follows.
The O I
triplet has a very high excitation feature (9.15 eV) and is quite sensitive to the
temperature structure of the adopted model atmosphere, and NLTE effects
cause the higher O abundance derived from it.
And the OH lines in the UV are
very sensitive to the temperature structure of the stellar atmosphere and/or
to NLTE effects too.
According to this argument,
there should be no obvious change in the O abundance
as the dwarfs evolve to the giants.
On the other hand, if we believe that the higher [O/Fe] derived
from the O I triplet and OH line reflects the true O abundance,
then we have to reconsider the abundance evolution
of oxygen, hence the GCE result.
Maybe the top-heavy IMF is true, which favours the formation of
massive stars in the early Galactic stage,
hence a high O abundance.
This assumption would imply a corresponding high [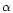 /Fe] in metal-poor dwarfs, which is not found in
present available data.
Could the difference between [O/Fe] and [
/Fe] in metal-poor dwarfs, which is not found in
present available data.
Could the difference between [O/Fe] and [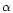 /Fe]
mean that their behaviors are not similar?
Perhaps NLTE effects can revise the present [
/Fe]
mean that their behaviors are not similar?
Perhaps NLTE effects can revise the present [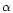 /Fe] value.
Recently, Zhao & Gehren (2000) reported that NLTE
effects can increase the [Mg/Fe] abundance, and the corrections are larger
for the lower metallicities of the metal-poor stars.
Thus, maybe NLTE corrections can also
increase the abundances of other
/Fe] value.
Recently, Zhao & Gehren (2000) reported that NLTE
effects can increase the [Mg/Fe] abundance, and the corrections are larger
for the lower metallicities of the metal-poor stars.
Thus, maybe NLTE corrections can also
increase the abundances of other 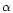 elements at the early Galactic stage.
elements at the early Galactic stage.
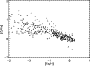 |
Figure 11:
The observed [O/Fe] vs. [Fe/H] data.
Oxygen abundances derived from [O I] 6300 Å forbidden line
are indicated by triangles, from O I triplet by pluses,
and from OH lines in UV region by diamonds. |
| Open with DEXTER |
Goswami & Prantzos (2000) pointed out three reasons for the higher [O/Fe]
value
in low metallicity region: (1) The Fe produced by SNIa explosions
entered the galactic
scene as early as [Fe/H] 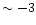 ,
instead of [Fe/H]
,
instead of [Fe/H] 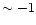 in the "standard"
scenario; (2) the O yields from massive stars are, for some reasons, metallicity dependent;
(3) there is the possibility of
the yields of Fe and all elements heavier than oxygen being metallicity-dependent.
in the "standard"
scenario; (2) the O yields from massive stars are, for some reasons, metallicity dependent;
(3) there is the possibility of
the yields of Fe and all elements heavier than oxygen being metallicity-dependent.
Using the standard GCE model, we have attempted an exploration of
the questions of the sources of carbon
and the abundance evolution of CNO elements.
Because the yield of stellar nucleosynthesis is a very important parameter
of the GCE model, and different yields give different evolutionary
behaviors of the elements, we chose the recently published different
nucleosynthesis yields:
the yields given by RV, VG, MBC and M2K for intermediate-, low-mass single stars; the results of the classical W7 model of
Nomoto et al. (1997b) for binary stars through SNIa explosions; the
yields given by WW, N97, M92 and PCB for massive single stars.
Then we set up 8 specific models for the combinations, VG+WW, VG+N97, VG+M92, RV+WW, RV+N97, RV+M92,
MBC+PCB and M2K+PCB.
Our results show that, after fitting the predicted age-metallicity relation,
metallicity distribution of G dwarfs and [O/Fe] vs. [Fe/H] relation
to the observations, very different [C/Fe] vs. [Fe/H] relations
are given by the different models with different yield combinations.
The 12C
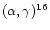 O reaction rate is very important to
stellar nucleosynthesis calculations. Hence, it affects the results of the GCE calculations.
A higher rate of this reaction
will produce less carbon, and a lower rate, more.
A suitable choice is between the values given by CFHZ and CF.
O reaction rate is very important to
stellar nucleosynthesis calculations. Hence, it affects the results of the GCE calculations.
A higher rate of this reaction
will produce less carbon, and a lower rate, more.
A suitable choice is between the values given by CFHZ and CF.
Generally speaking, in the early stage
of our Galaxy, massive stars are the main contributor of carbon.
As our Galaxy evolves to the
late stage, the long lifetime ILMS begins to play an important role
in the enrichment of the ISM.
At the same time,
the high metallicity W-R stars eject significant amounts of
carbon into the ISM
by radiative-driven stellar wind; the metallicity influences the outer
opacities and therefore the mass loss rate by stellar winds in massive stars.
However, on the present published nucleosynthesis yields,
our results still cannot distinguish the source of carbon in metal-rich Galactic stage. It may be that
just the massive stars (
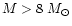 )
are sufficient to account for the observed [C/Fe] values (see Figs. 3e, 6e); or it may be just the ILMS and
)
are sufficient to account for the observed [C/Fe] values (see Figs. 3e, 6e); or it may be just the ILMS and
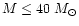 massive stars without the W-R stars
are enough to explain the observed carbon in metal-rich stars
(see Figs. 1b, 6f, 7f).
massive stars without the W-R stars
are enough to explain the observed carbon in metal-rich stars
(see Figs. 1b, 6f, 7f).
However, we can at least distinguish the different contributions of
ILMS and massive stars to carbon from our calculations.
Having comparing the GCE results shown in Sects. 5.1-5.8,
and considered the undetermined characters of stellar wind mass loss
of massive stars,
and assuming the actual
12C
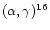 O reaction rate to be between CFHZ and CF, we calculated
the respective contributions to carbon from massive stars and ILMS in the model WW+VG.
Figure 9 shows that,
in the early stage, almost all carbon is produced by massive stars;
with increase of the Galactic age, the contribution from ILMS becomes more and more and eventually exceeds that of the massive stars.
The latter contribution is increased when the contribution from W-R stars is included.
O reaction rate to be between CFHZ and CF, we calculated
the respective contributions to carbon from massive stars and ILMS in the model WW+VG.
Figure 9 shows that,
in the early stage, almost all carbon is produced by massive stars;
with increase of the Galactic age, the contribution from ILMS becomes more and more and eventually exceeds that of the massive stars.
The latter contribution is increased when the contribution from W-R stars is included.
Henry et al. (2000) gave an excellent analysis on the source of C and N.
But they only gave
detailed results for the yields of VG for ILMS and M92
for massive stars. And they increased the yields of M92 in their calculations
(see their Table 3), which increased the contribution of carbon
from massive stars.
Carigi (2000) compared different set of yield, and suggested that massive stars
with stellar wind are the main source of carbon.
Compared to their work, we use the abundances of a large sample of dwarf stars as
one of the most important observational constraints
rather than just the stellar age. The reason is that
few halo stars have determined
ages, while the results reported by Edvardsson et al. (1993), Gustafsson
et al. (1999) and Chen et al. (2000)
are only for disk stars,
so the element abundance in the early stage of the Galaxy cannot be tested by observations.
In addition, we divided the massive stars into two ranges,
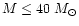 and
and
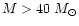 ,
so that we can compare the carbon contributions
given by W-R stars and ILMS more clearly.
And we use the new set of nucleosynthesis yields of
M2K, which contain important information
on low metallicity ILMS.
,
so that we can compare the carbon contributions
given by W-R stars and ILMS more clearly.
And we use the new set of nucleosynthesis yields of
M2K, which contain important information
on low metallicity ILMS.
Our results confirm that most of nitrogen is produced by ILMS, especially
by intermediate mass stars. And the present yields given by massive stars
cannot supply the needed primary N source.
Massive stars produce the main part of oxygen in the universe.
But the observed O abundances derived from different atomic
lines lead to
obvious differences in the [O/Fe] determination in metal-poor stars.
Maybe we should check the procedure and many corresponding
parameters to obtain abundance of oxygen.
Also, perhaps this difference
hints at some new information on Galactic chemical evolution, especially,
it is necessary to understand the evolution of our Galaxy in the early stage
carefully.
Acknowledgements
We thank Dr. B. Edvardsson for very valuable suggestions
on the original manuscript.
We thank Dr. T. Kiang and Dr. P. Podsiadlowski for spending much time and energy
to help us to improve the English expression.
Thank Dr. L. C. Deng
for the interesting discussions about massive stars,
and thank Zhang Yanxia and Fan Yingjie for their friendly help.
This research work is supported by the National Natural Science Foundation of
China under grant No. 19725312
and NKBRSF G1999075406.
- Abia, C., & Rebolo, R. 1989,
ApJ, 347, 186
In the text
NASA ADS
- Andersson, H., & Edvardsson, B. 1994,
A&A, 290, 590
In the text
NASA ADS
- Balachandran, S. C., & Carney, B. W. 1996,
AJ, 111, 946
In the text
NASA ADS
- Barbuy, B. 1988,
A&A, 191, 121
In the text
NASA ADS
- Barbuy, B., & Erdelyi-Mendes, M. 1989,
A&A, 214, 239
In the text
NASA ADS
- Beveridge, C. R., & Sneden, C. 1994,
AJ, 108, 285
In the text
NASA ADS
- Boesgaard, A. M., & King, J. R. 1993,
AJ, 106, 2309
In the text
NASA ADS
- Boesgaard, A. M., King, J. R., Deliyannis, C. P., & Vogt, S. S. 1999,
AJ, 117, 492
In the text
NASA ADS
- Burbidge, E. M., Burbidge, G. R., Fowler, W. A., & Hoyle, F. 1957,
Rev. Mod. Phys., 29, 547
In the text
- Carbon, D. F., Barbuy, B., Kraft, R. P., Friel, E. D., & Suntzeff, N. B. 1987, PASP, 99, 335
In the text
NASA ADS
- Carigi, L. 1994,
ApJ, 424, 181
In the text
NASA ADS
- Carigi, L. 2000,
Rev. Mex. Astron. Astrofis. 36
[astro-ph/0005042]
In the text
- Carlberg, R. G., Dawson, P. C., Hsu, T., & VandenBerg, D. A. 1985,
ApJ, 294, 674
In the text
NASA ADS
- Carretta, E., Gratton, R. G., & Sneden, C. 2000,
A&A, 356, 238
In the text
NASA ADS
- Caughlan, G. R., Fowler, W. A., Harris, M. J., & Zimmerman, B. A. 1985,
At. Data Nucl. Data Tables, 32, 197 (CFHZ)
In the text
NASA ADS
- Caughlan, G. R., & Fowler, W. A. 1988,
At. Data Nucl. Data Tables, 40, 283 (CF)
In the text
NASA ADS
- Chang, R. X., Hou, J. L., Shu, C. G., & Fu, C. Q. 1999,
A&A, 350, 38
In the text
NASA ADS
- Chen, Y. Q., Nissen, P. E., Zhao, G., Zhang, H. W., & Benoni, T. 2000,
A&AS, 141, 491
In the text
NASA ADS
- Chiappini, C., Matteucci, F., & Gratton, R. 1997,
ApJ, 477, 765
In the text
NASA ADS
- Chiappini, C., Matteucci, F., & Padoan, P. 2000,
ApJ, 528, 711
In the text
NASA ADS
- Chieffi, A., Limongi, M., & Straniero, O. 1998,
ApJ, 502, 737
In the text
NASA ADS
- Clegg, R. E. S., Lambert, D. L., & Tomkin, J. 1981,
ApJ, 250, 262
In the text
NASA ADS
- Conti, P. E. 1995, in The 11th IAP Astrophysics Meeting,
Proc. The Interplay Between Massive Star Formation, the ISM and
Galaxy Evolution, ed. D. Kunth, B. Guiderdoni, M. Heydari-Malayeri, T. X. Thuan (Paris: Éditions Frontières), 37
In the text
- Conti, P. S., Greenstein, J. L., Spinard, H., Wallerstein, G., & Vardya, M. S. 1967, ApJ, 148, 105
In the text
NASA ADS
- Crowther, P. A., 2000a, in
Proc. The Influence of Binaries on Stellar Population Studies,
ed. D. Vanbeveren (Kluwer) [astro-ph/0010581]
In the text
- Crowther, P. A. 2000b,
A&A, 356, 191
In the text
NASA ADS
- Dopita, M. A., & Ryder, S. D. 1994,
ApJ, 430, 163
In the text
NASA ADS
- Dwek, E. 1998,
ApJ, 501, 643
In the text
NASA ADS
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993,
A&A, 275, 101
In the text
NASA ADS
- Forestini, M., & Charbonnel, C. 1997,
A&AS, 123, 241
In the text
NASA ADS
- Fuhrmann, K. 1998,
A&A, 338, 161
In the text
NASA ADS
- Fulbright, J. P., & Kraft, R. P. 1999,
ApJ, 118, 527
In the text
- Garnett, D. R., Shields, G. A., Peimbert, M., et al. 1999, ApJ, 513, 168
In the text
NASA ADS
- Grevesse, N., & Sauval, A. J. 1998,
Space Sci. Rev., 85, 161
In the text
NASA ADS
- Goswami, A., & Prantzos, N. 2000,
A&A, 359, 151
In the text
- Gratton, R. G., & Ortolani, S. 1986,
A&A, 169, 201
In the text
NASA ADS
- Gustafsson, B., Karlsson, T., Olsson, E., Edvardsson, B., & Ryde, N. 1999,
A&A, 342, 426
In the text
NASA ADS
- Gustafsson, B., & Ryde, N. 2000, in
IAU Symp. 177, The carbon Star Phenomenon, ed. R. F. Wing (Kluwer, Dordrecht), 481
In the text
- Henry, R. B. C., Edmunds, M. G., & Köppen, J. 2000,
ApJ, 541, 660
In the text
NASA ADS
- Hou, J. L., Prantzos, N., & Boissier, S. 2000,
A&A, 362, 921
In the text
NASA ADS
- Iben, I. Jr., & Truran, J. W. 1978,
ApJ, 220, 980
In the text
NASA ADS
- Israelian, G., García López, R. J., & Rebolo, R. 1998,
ApJ, 507, 805
In the text
NASA ADS
- Karlsson, T., Edvardsson, B., Gustafsson, B., Olsson, E., & Ryde, N. 1999, Ap&SS, 265, 261
In the text
NASA ADS
- King, J. R. 1993,
AJ, 106, 1206
In the text
NASA ADS
- King, J. R. 1994,
ApJ, 436, 331
In the text
NASA ADS
- King, J. R., & Boesgaard, A. M. 1995,
AJ, 109, 383
In the text
NASA ADS
- Kiselman, D. 1991,
A&A, 245, L9
In the text
NASA ADS
- Kobulnicky, H. A., & Skillman, E. D. 1998,
ApJ, 497, 601
In the text
NASA ADS
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993,
MNRAS, 262, 545
In the text
NASA ADS
- Kudritzki, R-.P., & Puls, J. 2000,
ARA&A, 38, 613
In the text
NASA ADS
- Laird, J. B. 1985,
ApJ, 289, 556
In the text
NASA ADS
- Leitherer, C. 1995, in
Proc. The 11th IAP Astrophysics Meeting,
The Interplay Between Massive Star Formation, the ISM and
Galaxy Evolution, ed.
D. Kunth, B. Guiderdoni, M. Heydari-Malayeri, T. X. Thuan (Paris: Éditions Frontières), 27
In the text
- Langer, N. 1989,
A&A ,220, 135
In the text
NASA ADS
- Liang, Y. C., & Zhao, G. 2001,
Progress in Natural Science, in press
In the text
- Limongi, M., Straniero, O., & Chieffi, A. 2000,
ApJS, 129, 625
In the text
NASA ADS
- Maciel, W. J. 2000,
Rev. Mex. Astron. Astrofis. SC
[astro/ph-0012179]
In the text
- Maeder, A. 1992,
A&A, 264, 105 (M92)
In the text
NASA ADS
- Maeder, A., & Conti, P. E. 1994,
ARA&A, 32, 227
In the text
NASA ADS
- Marigo, P. 2001,
A&A, 370, 194 (M2K)
In the text
NASA ADS
- Marigo, P., Bressan, A., & Chiosi, C. 1996,
A&A, 313, 545 (MBC1)
In the text
NASA ADS
- Marigo, P., Bressan, A., & Chiosi, C. 1998,
A&A, 331, 564 (MBC2)
In the text
NASA ADS
- Martinelli, A., & Matteucci, F. 2000,
A&A, 353, 269
In the text
NASA ADS
- Massey, P., Lang, C. C., DeGioia-Eastwood, K., & Garmany, C. D. 1995,
ApJ, 438, 188
In the text
NASA ADS
- Matteucci, F., & François, P. 1989,
MNRAS, 239, 885
In the text
NASA ADS
- Meusinger, H., Reimann, H.-G., & Stecklum, B. 1991,
A&A, 245, 57
In the text
NASA ADS
- Meynet, G., & Maeder, A. 2000,
A&A, 361, 101
In the text
NASA ADS
- Mishenina, T. V., Korotin, S. A., Klochkova, V. G., & Panchuk, V. E. 2000,
A&A, 353, 978
In the text
NASA ADS
- Nissen, P. E., & Edvardsson, B. 1992,
A&A, 261, 255
In the text
NASA ADS
- Nissen, P. E., Gustafsson, B., Edvardsson, B., & Gilmore, G. 1994,
A&A, 285, 440
In the text
NASA ADS
- Nissen, P. E., Primas, F., & Asplund, M. 2000,
24th meeting of the IAU, Joint Discussion 8,
Oxygen Abundances in Old Stars and Implications
to Nucleosynthesis and Cosmology
( Manchester, UK)
In the text
- Nomoto, K., Hashimoto, M., Tsujimoto, T., et al. 1997a,
Nucl. Phys., A616, 79c (N97)
In the text
- Nomoto, K., Iwamoto, K., Nakasato, N., et al. 1997b,
Nucl. Phys., A621, 467c
In the text
- Oberhummer, H., Csótó, A., & Schlattl, H. 2000,
Science, 289, 88
In the text
NASA ADS
- Pagel, B. E. J. 1997,
Nucleosynthesis and Chemical Evolution of Galaxies
(Cambridge University Press), 206
In the text
- Portinari, L., Chiosi, C., & Bressan, A. 1998,
A&A, 334, 505 (PCB)
In the text
NASA ADS
- Prantzos, N., & Silk, J. 1998,
ApJ, 507, 229
In the text
NASA ADS
- Prantzos, N., Vangioni-Flam, E., & Chauveau, S. 1994,
A&A, 285, 132
In the text
NASA ADS
- Renzini, A., & Voli, M. 1981,
A&A, 94, 175 (RV)
In the text
NASA ADS
- Sackett, P. D. 1997,
ApJ, 483, 103
In the text
NASA ADS
- Salpeter, E. E. 1955,
ApJ, 121, 161
In the text
NASA ADS
- Samland, M. 1998,
ApJ, 496, 155
In the text
NASA ADS
- Scalo, J. M. 1986,
Fund. Cosmic Phys., 11, 1
In the text
NASA ADS
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992,
A&AS, 96, 269
In the text
NASA ADS
- Schmidt, M. 1959,
ApJ, 129, 243
In the text
NASA ADS
- Schmutz, W. 1997,
A&A, 321, 268
In the text
NASA ADS
- Spiesman, W. J., & Wallerstein, G. 1991,
AJ, 102, 1790
In the text
NASA ADS
- Spite, M., & Spite, F. 1991,
A&A, 252, 689
In the text
NASA ADS
- Sneden, C., Kraft, R. P., Prosser, C. F., & Langer, G. E. 1991,
AJ, 102, 2001
In the text
NASA ADS
- Sugimoto, D., & Nomoto, K. 1980,
Space Sci. Rev., 25, 155
In the text
NASA ADS
- Takeda, Y. 1994,
PASJ, 46, 53
In the text
NASA ADS
- Talbot, Jr. R. J., & Arnett, W. D. 1975,
A&A, 197, 551
In the text
- Thielemann, F.-K., Nomoto, K., & Hashimoto, M. 1996,
ApJ, 460, 408
In the text
NASA ADS
- Thomas, D., Greggio, L., & Bender, R. 1998,
MNRAS, 296, 119
In the text
NASA ADS
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995,
ApJS, 98, 617
In the text
NASA ADS
- Tomkin, J., Lemke, M., Lambert, D. L., & Sneden, C. 1992,
AJ, 104, 1568
In the text
NASA ADS
- Tomkin, J., & Lambert, D. L. 1984,
ApJ, 279, 220
In the text
NASA ADS
- Tomkin, J., Sneden, C., & Lambert, D. L. 1986,
ApJ, 302, 415
In the text
NASA ADS
- Tomkin, J., Woolf, V. M., Lambert, D. L., & Lemke, M. 1995,
AJ, 109, 2204
In the text
NASA ADS
- Van den Hoek, L. B., & Groenewegen, M. A. T. 1997,
A&AS, 123, 305 (VG)
In the text
NASA ADS
- Wheeler, J. C., Sneden, C., & Truran, Jr. J. W. 1989,
ARA&A, 27, 279
In the text
NASA ADS
- Whelan, J., & Iben, I. Jr. 1973,
ApJ, 186, 1007
In the text
NASA ADS
- Woosley, S. E., & Weaver, T. A. 1995,
ApJS, 101, 181 (WW)
In the text
NASA ADS
- Zhao, G., & Gehren, T. 2000,
A&A, 362, 1077
In the text
NASA ADS
- Zhao, G., & Magain, P. 1990,
A&A, 238, 242
In the text
NASA ADS
Copyright ESO 2001
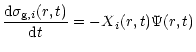
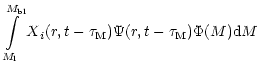
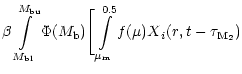
![$\displaystyle \Psi (r,t-\tau _{{\rm M}_2}){\rm d}{\mu} \Bigg ] {\rm d}{M_{\rm b}}$](/articles/aa/full/2001/30/aah2126/img29.gif)
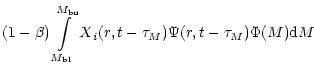
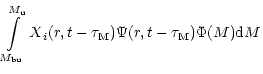
![$\displaystyle \left [\frac {{\rm d} \sigma{_i}(r,t)}{{\rm d}t}\right ]_{\rm inf} ,$](/articles/aa/full/2001/30/aah2126/img32.gif)
![\begin{displaymath}\Psi(r,t)=\nu \sigma_{\rm tot}(r,t)\left [\frac {\sigma_{\rm ...
...m tot}(r,t)}
\right ]^{n} M_{\odot}\,{\rm pc^{-2}\,Gyr^{-1}},
\end{displaymath}](/articles/aa/full/2001/30/aah2126/img41.gif)
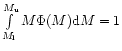 ,
with
,
with