A&A 374, L21-L24 (2001)
DOI: 10.1051/0004-6361:20010872
The size of penumbral fine structure
P. Sütterlin
Sterrenkundig Instituut Utrecht, Postbus 80000, 3507
TA Utrecht, The Netherlands
Received 21 May 2001 / Accepted 19 June 2001
Abstract
I present power spectra of penumbral and granular intensity
variations from a speckle-restored G-band image sequence of sunspot
NOAA 9407 taken on April 1, 2001 with the Dutch Open Telescope on La
Palma. I compare spatial power spectra of the sunspot penumbra with
spatial power spectra from granulation with and without filigree.
Relative to the granular power distribution, the penumbral power
spectrum is enhanced over a wide range in spatial frequency peaking at
0
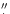 35. For smaller scales, the penumbral power distribution
closely resembles that of the granular intensity variations. In
contrast, the power spectrum of granulation with filigree exhibits
increased power down to the resolution limit of 0
35. For smaller scales, the penumbral power distribution
closely resembles that of the granular intensity variations. In
contrast, the power spectrum of granulation with filigree exhibits
increased power down to the resolution limit of 0
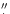 22, indicating
the presence of unresolved magnetic elements.
22, indicating
the presence of unresolved magnetic elements.
Key words: Sun: magnetic fields - sunspots
Sunspot penumbrae remain a source of many open questions in solar
physics (e.g. Thomas & Weiss 1992). While it is generally
accepted that the structuring of a penumbra into more or less radially
directed dark and bright filaments is dominated by magnetic fields,
the composition of the penumbral filaments remains controversial. Do
they form a flat layer on top of the granulation, or do they
constitute a thick structure extending down in the sun? How large are
the individual elements? While the former question requires
theoretical modeling (see e.g. Jahn 1997), the latter
issue can benefit from high angular resolution observations. I address
the second question here.
The typical size of a penumbral filament is
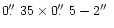 (Sobotka 1997), but there are
measurements that go down to 0
(Sobotka 1997), but there are
measurements that go down to 0
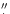 11 (Stachnik et al. 1983).
The numerical model of Schlichenmaier et al. (1998) uses flux tubes of
50km diameter. A model of Sánchez Almeida (1998) postulates that
the whole penumbra consists of tiny fibrils as small as
1-10km. Although the fibrils would be too narrow to be observed
individually (being much smaller than the photon mean free path), such
a micro-structured magnetic atmosphere (MISMA) allows Sánchez to
explain the broadband circular polarization characteristics of
penumbrae (but see Martínez Pillet 2000 and the comments in
Sánchez Almeida 2001 and Martínez Pillet 2001).
11 (Stachnik et al. 1983).
The numerical model of Schlichenmaier et al. (1998) uses flux tubes of
50km diameter. A model of Sánchez Almeida (1998) postulates that
the whole penumbra consists of tiny fibrils as small as
1-10km. Although the fibrils would be too narrow to be observed
individually (being much smaller than the photon mean free path), such
a micro-structured magnetic atmosphere (MISMA) allows Sánchez to
explain the broadband circular polarization characteristics of
penumbrae (but see Martínez Pillet 2000 and the comments in
Sánchez Almeida 2001 and Martínez Pillet 2001).
Sánchez Almeida & Bonet (1998) analyzed spatial power spectra of penumbral
intensity variations and claim that these follow closely the combined
modulation transfer function (MTF) of the telescope and atmosphere,
implying a basically flat power spectrum of the intrinsic intensity
variations. This conclusion is somewhat ambiguous because the MTF for
the atmospheric disturbances could not be measured from the data but
was extrapolated from other sources and became uncertain below 0
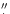 4. However, the authors point out that this ambiguity may be
removed by methods such as speckle image reconstruction that deliver
the MTF down to the resolution limit of the telescope. The Dutch Open
Telescope (DOT) at the Observatorio del Roque de Los Muchachos on La
Palma (Hammerschlag & Bettonvil 1998) represents a new solar telescope
which indeed employs speckle reconstruction as its standard observing
technique. Under standard seeing conditions the speckle image
processing delivers the theoretical resolution limit of 0
4. However, the authors point out that this ambiguity may be
removed by methods such as speckle image reconstruction that deliver
the MTF down to the resolution limit of the telescope. The Dutch Open
Telescope (DOT) at the Observatorio del Roque de Los Muchachos on La
Palma (Hammerschlag & Bettonvil 1998) represents a new solar telescope
which indeed employs speckle reconstruction as its standard observing
technique. Under standard seeing conditions the speckle image
processing delivers the theoretical resolution limit of 0
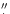 2 at
4300Å (aperture 45cm). In this analysis I use DOT speckle
observations of a sunspot penumbra to test whether the spatial fine
structure is resolved at this limit.
2 at
4300Å (aperture 45cm). In this analysis I use DOT speckle
observations of a sunspot penumbra to test whether the spatial fine
structure is resolved at this limit.
A one-hour time sequence of G-band images (4305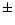 5Å) of
sunspot NOAA 9407 (radius
5Å) of
sunspot NOAA 9407 (radius 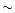 19
19
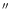 )
was obtained on April 1, 2001 with the DOT using the new CCD camera (10 bit, 1296
)
was obtained on April 1, 2001 with the DOT using the new CCD camera (10 bit, 1296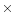 1030 px, see Rutten et al. 2000). The data were taken in bursts
of 100 images at a rate of 6fps to permit the speckle reconstruction
described below. In total, 120 such bursts were collected at a cadence
of 30s during 9:00-10:00UT. The seeing conditions were quite
good, with Fried parameter
r0=7-10 cm. The image scale in
the secondary focus of the DOT was set to 0
1030 px, see Rutten et al. 2000). The data were taken in bursts
of 100 images at a rate of 6fps to permit the speckle reconstruction
described below. In total, 120 such bursts were collected at a cadence
of 30s during 9:00-10:00UT. The seeing conditions were quite
good, with Fried parameter
r0=7-10 cm. The image scale in
the secondary focus of the DOT was set to 0
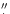 071 per pixel to
allow sampling up to the resolution limit (0
071 per pixel to
allow sampling up to the resolution limit (0
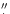 2) also along
diagonals.
2) also along
diagonals.
 |
Figure 1:
Example of a speckle-reconstructed image of
NOAA 9407. The position of the spot was N11E21 (
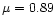 ), the arrow marks the direction towards disk
center. The inset in the lower right is an enlargement of the granular
area containing filigree that is marked in the main image. The dash
measures 1 arcsec. ), the arrow marks the direction towards disk
center. The inset in the lower right is an enlargement of the granular
area containing filigree that is marked in the main image. The dash
measures 1 arcsec. |
| Open with DEXTER |
The first step in the data reduction was speckle reconstruction
through treating the individual bursts with the speckle masking
algorithm (Weigelt & Wirnitzer 1983; von der Lühe 1984). This method
requires a burst of many frames that show the same object with varying
atmospheric distortion in order to sample the seeing. The frames of
one such burst are combined using a model for the atmospheric
influence (Korff 1973) and a statistical approach for
summing the Fourier phases in a bispectrum (Lohmann et al. 1983)
into a single image that is free of atmospheric influence and is also
corrected for the theoretical modulation transfer function (MTF) of
the telescope, based on the actual aperture including all
secondary-focus obstructions but without optical aberrations. The
restriction is that the frames in each burst have to be collected
before the object changes. For the solar photosphere this implies that
the burst must be completed within the time span in which a solar
disturbance crosses a telescope resolution element. Permitting
horizontal velocities of a few km/s, the size of the pixel size, which
corresponds to 50km on the sun, limits the burst duration to about
15 s. At 6fps frame rate this allows bursts of 100 frames. At
reasonable seeing conditions (Fried parameter
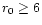 cm)
this number suffices to obtain reconstructions close to the
diffraction limit. At yet better seeing (
cm)
this number suffices to obtain reconstructions close to the
diffraction limit. At yet better seeing (
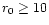 cm) the
reconstruction is complete, revealing structures down to the
resolution limit of the optic. The reconstruction also quantifies the
value of the Fried parameter r0 during each burst.
cm) the
reconstruction is complete, revealing structures down to the
resolution limit of the optic. The reconstruction also quantifies the
value of the Fried parameter r0 during each burst.
Burst-mode image acquisition and subsequent speckle reconstruction
have been selected to be the standard observing mode of the
DOT. Speckle-restored movies of this (and other) time sequences are
available on the DOT website![[*]](/icons/foot_motif.gif) .
.
I selected the image with the highest Fried parameter r0 in
the sequence for further investigation. It is shown in
Fig. 1 and it had r0=10 cm. The inset at the
lower right shows a magnification of an area containing filigree to
demonstrate that the reconstruction reveals fine structure down to the
telescope's diffraction limit.
Close inspection of the data showed that an electronic interference in
the read-out system of the CCD camera introduced spurious high
frequency variations in the data. This signal is constrained to wave
numbers higher than approximately 39
Mm-1.
Therefore a low-pass filter with that cut-off was applied to the data,
slightly reducing the actual resolution limit to 0
 22.
22.
The sun being spherical produces clinching of solar surface images
along the radial direction by a factor
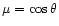 ,
while
the orthogonal direction remains unaffected (neglecting curvature and
approximating solar polar coordinates by Cartesian ones). For the
position of the spot (N11E21) this correction factor is
,
while
the orthogonal direction remains unaffected (neglecting curvature and
approximating solar polar coordinates by Cartesian ones). For the
position of the spot (N11E21) this correction factor is 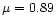 .
The angle between north and the direction towards disk center is
156
.
The angle between north and the direction towards disk center is
156 .
I computed the corresponding transformation matrix
and regridded the image using cubic interpolation. The resulting rhomb
was then clipped back to a rectangle, slightly reducing the
field. Figure 2 shows the destretched spot. The pixel size
of 0
.
I computed the corresponding transformation matrix
and regridded the image using cubic interpolation. The resulting rhomb
was then clipped back to a rectangle, slightly reducing the
field. Figure 2 shows the destretched spot. The pixel size
of 0
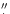 07 now covers the same geometrical size on the solar surface
in both directions, i.e. 51.5 km.
07 now covers the same geometrical size on the solar surface
in both directions, i.e. 51.5 km.
 |
Figure 2:
Sunspot image after correction for
geometrical distortion. The superimposed curves indicate the
positions of the slices. |
| Open with DEXTER |
Penumbral filaments are radially oriented. In order to obtain
information on their cross-sections one has to examine intensity
variations along circular paths around the spot. Unfortunately, the
spot is not circular and possesses some areas where the penumbra is
irregular. I therefore used only partial circle paths and chose to use
slices of constant length, so that the opening angle of the sector
decreases with increasing radius. The positions of the selected slices
are shown in Fig. 2. The intensity along each arc was
interpolated from the image using a constant step width corresponding
to 1 pixel, again using cubic interpolation. I used seven slices in
the penumbra to evaluate spatial power spectra. Seven more arc-shaped
slices are located in the relatively quiet sunspot moat for comparison
with standard granulation behavior. Straight cuts that sample more
active granulation were taken in a region that contains filigree (at
the upper right of the spot).
An apodisation window was applied for the computation of the power
spectra to remove the influence of non-periodic boundary conditions. I
used a simple cosine falloff over the outer 10% of each segment. The
data sampling is fine enough to fully cover the resolution of the
telescope, so that there are no aliasing effects.
Polynomic interpolation of data before computing a power spectrum
tends to produce spurious signals. This can be seen in
Fig. 3: beyond the cut-off frequency of the telescope
the power spectrum of the granulation with filigree, which was not
interpolated on circular paths, drops down, while for the interpolated
ones it stays at approximately 10-8. This artificial signal
is however much smaller than the measured values and therefore does
not influence the results.
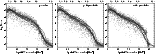 |
Figure 3:
Power spectra of the selected slices
through penumbra (left), quiet (middle), and active granulation
(right). Dots: power spectra per slice; diamonds: average. The thick
curve is a fit to the average values, the dashed curves show the power
distribution of the other two categories. |
| Open with DEXTER |
Figure 3 shows the power spectra along the selected
slices, split between the three types of area. There are no
distinctive differences between the different paths in each area type,
so all power values are plotted with the same symbol. The diamonds are
the averages over the different slices, with the solid curve a
smoothed fit. Each plot also repeats the fits from the other two
panels to facilitate comparisons.
None of the three power spectra show evidence of constancy with
frequency but they all exhibit a steady decline out to the resolution
limit (0
 22) without apparent flattening. The shape and slope of
the power spectrum of granulation without filigree match the result of
previous investigations that also used image reconstruction
(von der Lühe & Dunn 1987; Wilken et al. 1997; Sánchez Cuberes et al. 2000).
22) without apparent flattening. The shape and slope of
the power spectrum of granulation without filigree match the result of
previous investigations that also used image reconstruction
(von der Lühe & Dunn 1987; Wilken et al. 1997; Sánchez Cuberes et al. 2000).
Compared to the power spectrum of the quiet granulation, the penumbral
power spectrum shows a region of enhanced power in the range between
13 and 32
Mm-1 with a broad maximum at 25
Mm-1, corresponding to a structure size of
0
 35. This value coincides with the width given by
Sobotka (1997) as the typical size of penumbral
filaments. For higher wavenumbers (
35. This value coincides with the width given by
Sobotka (1997) as the typical size of penumbral
filaments. For higher wavenumbers (
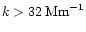 )
the
power spectra of the penumbral filaments and the quiet granulation are
identical.
)
the
power spectra of the penumbral filaments and the quiet granulation are
identical.
One might argue that the steady decline is due to incomplete
restoration or imperfections in the numerical treatment. However, the
active granulation containing filigree deviates from this behavior and
exhibits clearly increased power up to 38
Mm-1 where
the low pass filter sets in. This proves that the reconstruction
indeed does uncover structures out to the resolution limit, if they
are present. Assuming that this excess of power continues towards
higher wave-numbers one can infer that the size of the filigree is
below the resolution limit. This suggestion is strengthened by
inspecting single bright points in the inset in Fig. 1:
these are circular and closely resemble the Airy function of the
telescope for point objects.
Our speckle-restored high-resolution data do not agree with the notion
of intrinsically flat spatial power spectra. The penumbral enhancement
of spatial power over 0
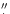 3-0
3-0
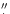 6 over granular power behavior
supports the earlier result that penumbral filaments have preferred
widths of about 250 km. Contrary to Sánchez Almeida & Bonet (1998) who used
a broad band continuum filter, these data were taken in the G-band and
might therefore sample the atmosphere in a somewhat different
height. The resulting power spectra may differ slightly between
continuum and G-band, but it is unlikely that they do so in basic
properties.
6 over granular power behavior
supports the earlier result that penumbral filaments have preferred
widths of about 250 km. Contrary to Sánchez Almeida & Bonet (1998) who used
a broad band continuum filter, these data were taken in the G-band and
might therefore sample the atmosphere in a somewhat different
height. The resulting power spectra may differ slightly between
continuum and G-band, but it is unlikely that they do so in basic
properties.
It should also be pointed out that inspection of the power spectra
presented by Sánchez Almeida & Bonet (1998) also shows an indication of
enhanced power around 0
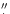 35, however the authors attribute that to
the MTF that is very uncertain below 0
35, however the authors attribute that to
the MTF that is very uncertain below 0
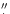 4. The results presented
here do not suffer from this uncertainty, as the speckle
reconstruction delivers the true MTF of telescope and atmosphere down
to the resolution limit of 0
4. The results presented
here do not suffer from this uncertainty, as the speckle
reconstruction delivers the true MTF of telescope and atmosphere down
to the resolution limit of 0
 22.
22.
This result does neither confirm nor disprove the MISMA concept of
Sánchez Almeida (1998), but the question that arises is why, if the
basic structures in the penumbra have MISMA widths of a few km only
each, they build conglomerates preferentially at 200-500km cross-cut
scales.
Acknowledgements
This research is funded by the European Solar Magnetometry Network
(ESMN) under EC-TMR contract ERBFMRXCT98019. The DOT project is funded
by Utrecht University, the Netherlands Graduate School for Astronomy
NOVA and the Netherlands Organization for Scientific Research NWO. The
new DOT data acquisition system was built by the Instrumentele Groep
Fysica IGF at Utrecht. R. H. Hammerschlag and F. C. M. Bettonvil
assisted in the observing. I acknowledge helpful comments from
R. J. Rutten and the referee.
-
Hammerschlag, R. H., & Bettonvil, F. C. M. 1998,
New Astron. Rev., 42, 485
In the text
NASA ADS
-
Jahn, K. 1997,
in 1st Advances in Solar Physics Euroconference,
Advances in Physics of Sunspots, ASP Conf. Ser., 118, 122
In the text
-
Korff, D. 1973,
J. Opt. Soc. Am., 63, 971
In the text
-
Lohmann, A. W., Weigelt, G., & Wirnitzer, B. 1983,
Appl. Opt., 22, 4028
In the text
NASA ADS
-
Martínez Pillet, V. 2000,
A&A, 361, 734
In the text
NASA ADS
-
Martínez Pillet, V. 2001,
A&A, 369, 644
In the text
NASA ADS
-
Rutten, R. J., Hammerschlag, R. H., Bettonvil, F. M., & Sütterlin, P.
2000,
in AAS/Solar Physics Division Meeting,
vol. 32, 02107
In the text
-
Sánchez Almeida, J. 2001,
A&A, 369, 643
In the text
NASA ADS
-
Sánchez Almeida, J. 1998,
ApJ, 497, 967
In the text
NASA ADS
-
Sánchez Almeida, J., & Bonet, J. A. 1998,
ApJ, 505, 1010
In the text
NASA ADS
-
Sánchez Cuberes, M., Bonet, J. A., Vázquez, M., & Wittmann, A. D.
2000, ApJ, 538, 940
In the text
NASA ADS
-
Schlichenmaier, R., Jahn, K., & Schmidt, H. U. 1998,
A&A, 337, 897
In the text
NASA ADS
-
Sobotka, M. 1997,
in 1st Advances in Solar Physics Euroconference,
Advances in Physics of Sunspots, ASP Conf. Ser., 118, 155
In the text
-
Stachnik, R. V., Nisenson, P., & Noyes, R. W. 1983,
ApJ, 271, L37
In the text
NASA ADS
-
Thomas, J. H., & Weiss, N. O. (ed.) 1992,
Sunspots: Theory and observations, Proceedings of the NATO Advanced
Research Workshop on the Theory of Sunspots, Cambridge, United Kingdom, Sept.
22-27, 1991
In the text
-
von der Lühe, O. 1984,
J. Opt. Soc. Am. A, 1, 510
In the text
-
von der Lühe, O., & Dunn, R. B. 1987,
A&A, 177, 265
In the text
NASA ADS
-
Weigelt, G., & Wirnitzer, B. 1983,
Optics Lett., 8, 389
In the text
NASA ADS
-
Wilken, V., de Boer, C. R., Denker, C., & Kneer, F. 1997,
A&A, 325, 819
In the text
NASA ADS
Copyright ESO 2001


