1 - CRAAG - Observatoire d'Alger, BP 63, Bouzaréah, Alger, Algeria
2 - Université de Nice-Sophia Antipolis, UMR n
3 - Observatoire de la Côte d'Azur, Département CERGA, Avenue Copernic, 06130 Grasse, France
A&A 374, 1100-1107 (2001)
DOI: 10.1051/0004-6361:20010780
R. Moussaoui1 - A. Irbah 1 - E. Fossat 2 - J. Borgnino 2 - F. Laclare 3 - C. Delmas 3 - F. X. Schmider 2
1 - CRAAG - Observatoire d'Alger, BP 63, Bouzaréah, Alger, Algeria
2 - Université de Nice-Sophia Antipolis, UMR n![]() 6525 Astrophysique, Parc
Valrose, 06108 Nice Cedex 2, France
6525 Astrophysique, Parc
Valrose, 06108 Nice Cedex 2, France
3 - Observatoire de la Côte d'Azur, Département
CERGA, Avenue Copernic, 06130 Grasse, France
Received 31 January 2000 / Accepted 3 May 2001
Abstract
Solar diameter measurements performed with the Calern Observatory astrolabe (O.C.A -
France) during more than two solar cycles show temporal variations. Due to the weather, seasonal
effects and instrumental characteristics, recorded solar data are non uniformly sampled and present
temporal gaps. Thus, to analyze these data, diameter measurements averaged over one or more months
have generally been considered. This limits the accessible harmonic terms to a low frequency range.
To determine short-term periodicities from the observed variations, all daily solar data need to be
considered and also corrected from the zenithal distance. In the present work, we use two methods
to analyze solar diameter measurements recorded at Calern Observatory astrolabe during the
observation period 1975-1996. They are based on least square fits and deconvolution of the
observation window function. Results deduced from the analysis confirm harmonic terms already found
by other authors but also reveal new higher frequencies.
Key words: Sun: fundamental parameters - Sun: oscillations - methods: data analysis
In a previous paper, Laclare et al. (1996) presented solar diameter measurements performed with the Calern Observatory astrolabe (Observatoire de la Côte d'Azur - France). Two other papers were published after that discussing the obtained mean value of the solar diameter and its observed variations (Laclare et al. 1999a, 1999b). Monthly values of the apparent solar diameter were reported in these papers and some discussions developed around the recorded data and solar phenomena. This solar observation program began in 1975 when the first diameter measurements were performed. Since then, data have been recorded every clear day at various zenithal distances except for short time periods when the instrument was not operated. The long and homogeneous time series of visual observations allowed us to investigate temporal variations of the Sun's radius. The results published by Laclare et al. (1996) were in good agreement with those found by other authors who had analyzed the same solar diameter measurements but on a different time scale (Gavryusev et al. 1994; Delache et al. 1985). The detailed analysis of these data sets is however complicated by the non uniform data sampling due to the weather, seasonal effects and instrumental characteristics. In addition, a linear decrease of solar diameter measurements as a function of the zenithal distance was reported by Laclare et al. (1996) and Irbah et al. (1994). Although not being completely understood, this effect must be taken into account and empirically corrected for reducing the level of noise in the long term time series. In all the previous spectral studies, monthly diameter measurements were used without correcting the data for the zenithal distance effect. Specific methods were also developed because of the non uniform data sampling and the presence of temporal gaps responsible for perturbations in the harmonic analysis (Vigouroux & Delache 1993; Gavryusev et al. 1991). In fact, this precludes making an efficient use of the standard FFT routines and thus, requires specific considerations of the data peculiarities in order to optimize the spectral analysis.
The aim of this paper is to present a new spectral analysis of solar diameter measurements recorded from 1975 to 1996 at the Calern Observatory astrolabe. All daily recorded data are taken into account rather than monthly diameter means. They are also corrected for the zenithal distance effect. After a brief presentation of solar data, the analysis methods are presented. Two methods have been developed in order to address the data sampling peculiarities. An artificial signal with amplitude and noise properties similar to the solar data ones is first built. It is then used to develop and test the analysis methods. These are then applied to the real solar diameter variations observed with the solar astrolabe. The results obtained by this spectral analysis are finally presented and discussed.
The observations consist of the solar diameter measurements performed at the Calern Observatory astrolabe during approximately two solar cycles (1975-1996). The principle of the measurement and the instrumentation have already been described in several papers (Laclare et al. 1996, 1980; Laclare & Merlin 1991). The time series corresponds to a set of more than 5700 values obtained by visual and CCD observations. During the complete period of observations, data have been recorded at different zenithal distances. In this study, only visual observations will be considered since they have been regularly performed by the same observer during all the 21 years. In fact, CCD observations exist only since 1988, so that they cover a shorter time period. However, previous studies have shown a good agreement between visual and CCD observations (Laclare et al. 1996; Irbah et al. 1994). Thus, the merging of the two data sets will be possible in further studies with a good level of confidence. All visual observations of the solar diameter performed since 1975 with Calern Observatory astrolabe are presented in Fig. 1. In previous studies, a linear decrease of solar diameter measurements with the zenithal distance was observed (Laclare et al. 1996; Irbah et al. 1994). Thus, we correct the data for this effect by reducing all diameter measurements to the zenith (secZ =1). The zenithal distance effect has been taken into account in the data shown in Fig. 1 as the one used all during this work.
![\begin{figure}
\par\includegraphics[height=6.5cm,width=8.2cm,clip]{MS9612f1.eps}
\end{figure}](/articles/aa/full/2001/30/aa9612/Timg3.gif) |
Figure 1: Solar diameter measurements performed with the Calern Observatory astrolabe during the period 1975-1996. |
| Open with DEXTER | |
The data are not filtered and a solar cycle type of oscillation is clearly visible. This encourages us to develop spectral analysis in order to estimate all harmonic component terms in the data variation. We can also observe in the figure that data are non uniformly sampled and present some seasonal gaps which are principally present during the winter. In fact, during this observation period, the Calern Observatory astrolabe could only observe at large zenithal distance, so that the data are then too scattered. To analyze all solar data rather than monthly mean values, the non uniform data sampling, temporal gaps and non uniform noise require use of appropriate methods. In this spectral analysis, two methods that take into account these data peculiarities have been developed and are applied to the complete data sets. They are now described in the next section.
The major problem in spectral analysis of non uniformly sampled or gapped time series is the presence of more or less regular sidelobes in the power spectrum depending on the more or less regular distribution of gaps in the time domain. This makes frequency detection very difficult. Many methods have been developed to analyze non uniformly sampled signals. We will focus our study on two methods. The first and probably simplest one consists of least square fitting harmonic functions in the frequency range of interest with a chosen frequency sampling (Belmonte et al. 1991; Ponman 1981). A power spectrum is then obtained through a periodogram. The other method consists of deconvolving the signal from the observation temporal window by a mean daily uniform sampling and standard FFT routines.
To develop and test the two methods, a synthetic signal
![]() with the same temporal data
sampling as the diameter measurements is used. It is the sum of four sine-functions with arbitrary
amplitudes, frequencies and phases. They are chosen, however, to have amplitude and frequency of
the same order as that which we expect to find in the real data. To include some other effects (due
to Earth atmosphere, observer and instrument biaises), a normally distributed noise Ba is added
to the synthetic signal. The final signal is then defined by :
with the same temporal data
sampling as the diameter measurements is used. It is the sum of four sine-functions with arbitrary
amplitudes, frequencies and phases. They are chosen, however, to have amplitude and frequency of
the same order as that which we expect to find in the real data. To include some other effects (due
to Earth atmosphere, observer and instrument biaises), a normally distributed noise Ba is added
to the synthetic signal. The final signal is then defined by :
| (1) |
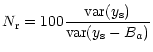 |
(2) |
![\begin{figure}
\par\includegraphics[height=5.2cm,width=8.3cm,clip]{MS9612f2a.eps...
...3mm}
\includegraphics[height=5.2cm,width=8.2cm,clip]{MS9612f2b.eps}
\end{figure}](/articles/aa/full/2001/30/aa9612/Timg10.gif) |
Figure 2: The synthetic signal. a) Without noise. b) With 85% of additional noise (see text). Note the different vertical scales of the plots. |
| Open with DEXTER | |
The least square fit analysis consists of adjusting the harmonic functions inside selected
frequency ranges to the signal. Let
xt,(t=t0,tn) be the data set representing the temporal
signal x(t) sampled over n+1 points. All the data are then fitted by a sine-function with a
frequency ![]() ,
an amplitude R and a phase
,
an amplitude R and a phase ![]() ,
so the residual E has a minimum value
for a given set of the 3 parameters
,
so the residual E has a minimum value
for a given set of the 3 parameters
![]() :
:
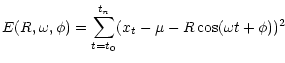 |
(3) |
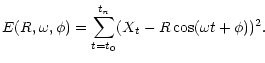 |
(4) |
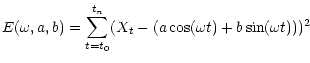 |
(5) |
This method consists of deconvolving the time series from the observation temporal window. This
implies use of a uniform sampling time to permit the use of the FFT routines. The observed signal
S(t) can be written as the product of the true signal X(t) and the window function P(t):
| (6) |
| (7) |
It is assumed that this relation of convolution remains almost true on the power spectrum. It is
not true, but this approximation becomes better and better with statistical independence between
signal and window on one hand, and an infinite time of integration on the other hand (Fossat 1992).
Both conditions are reasonably well satisfied. This approximation can be written:
| (8) |
| (9) |
 |
(10) |
In order to test the ability of the analysis methods to extract an harmonic signal with a small amplitude, the above synthetic signal with 85% additional noise (Fig. 2) has been included in the complete process.
The level of noise present in the signal and the spreading of each peak in the complicated sidelobe
structure do not allow us to find all harmonic term components with a first analysis. An iterative
procedure is then used to extract all periodicities. At each iteration, we consider only the most
important peak in the periodogram which is higher than a given threshold. This is taken to be equal
to ![]() where
where ![]() denotes the standard deviation calculated over all the signals obtained
at the given iteration. Thus, the first iteration gives access to the largest peak of the
periodogram. To find the second peak, we suppress from the data the contribution of the first
periodicity. Its sidelobe structure is also suppressed, so that the visibility of fainter harmonics
is improved. After that, the next iteration gives access to the largest peak which corresponds to
the second periodicity in the signal. We repeat the iterative procedure until all periodicities
larger than the given threshold have been detected.
denotes the standard deviation calculated over all the signals obtained
at the given iteration. Thus, the first iteration gives access to the largest peak of the
periodogram. To find the second peak, we suppress from the data the contribution of the first
periodicity. Its sidelobe structure is also suppressed, so that the visibility of fainter harmonics
is improved. After that, the next iteration gives access to the largest peak which corresponds to
the second periodicity in the signal. We repeat the iterative procedure until all periodicities
larger than the given threshold have been detected.
![\begin{figure}
\par\includegraphics[height=9.4cm,width=7.9cm,clip]{MS9612f3.eps}
\end{figure}](/articles/aa/full/2001/30/aa9612/Timg35.gif) |
Figure 3: Periodogram of the noisy synthetic signal. From the top of the figure, we have. a) First. b) Second. c) Third. d) Fourth. e) Fifth iteration. |
| Open with DEXTER | |
This method was applied to the noisy synthetic signal shown in Fig. 2 and allowed the detection
of all periodic components as well as their respective amplitudes (Fig. 3). Table 1 presents the
obtained results where we can see that frequencies are better determined than the amplitudes. The
precision of this last parameter is however acceptable since the noise amplitude in the signal is
equal to 85%. In Table 1, the error on the extracted harmonic terms is defined as:
 |
(11) |
| Simulated | Obtained | ||
| values | values | ||
| Amplitude | 0.3000 | 0.32 | 7 |
| (
|
0.2500 | 0.25 | 2 |
| 0.2000 | 0.22 | 8 | |
| 0.1500 | 0.14 | 5 | |
| angular velocity | 0.0123 | 0.01226 | 0.30 |
| (
|
0.2000 | 0.20003 | 0.01 |
| 0.0085 | 0.00853 | 0.40 | |
| 0.0368 | 0.03678 | 0.05 |
The method of the deconvolution of the temporal observation window has been tested on the same
noisy synthetic signal. It is first uniformly daily sampled by adding zeros when there is no data.
The FFT routine is then used to compute the power spectrum of the synthetic signal (Fig. 4a).
Figure 4b shows the power spectrum deconvolved from the observation temporal window and Fig. 4c
the same one but with an ideal signal uniformly sampled and without gaps and noise. Figure 4b shows
that the main effect of the deconvolution is enhancement of the harmonic peaks, due to the recovery
of the power that was spread in the sidelobes. In some cases, these sidelobes are visibly
decreased. As for the least square method, we observe a better estimation of frequencies than
amplitudes (see Sect. 3.3.1). Due to the window deconvolution effects, the amplitudes are
substantially different in the deconvolved and the original spectrum (Fig. 4). Indeed, the part of
the input period energy is spread on the sidelobes due to the deconvolution. This energy returns to
the true periods when the deconvolution method is applied. Consequently, the relative strength of
the input periods is increased by a factor of about 2 but not totally recovered, as shown in Fig. 4. All simulated periodicities are, however, found when we use a ![]() threshold for the detection (see Table 2).
threshold for the detection (see Table 2).
![\begin{figure}
\par\includegraphics[height=9.9cm,width=8.8cm,clip]{MS9612f4.eps}
\end{figure}](/articles/aa/full/2001/30/aa9612/Timg42.gif) |
Figure 4: a) Power spectrum of the synthetic signal. b) The deconvolved one. c) The same signal but uniformly sampled and without gaps and noise. The dotted lines represent the given threshold. |
| Open with DEXTER | |
| Simulated | Obtained | ||
| values | values | ||
| Amplitude | 0.3000 | 0.27 | 11 |
| (
|
0.2500 | 0.10 | 58 |
| 0.2000 | 0.23 | 14 | |
| 0.1500 | 0.14 | 9 | |
| angular velocity | 0.0123 | 0.0123 | 0.23 |
| (
|
0.2000 | 0.1992 | 0.40 |
| 0.0085 | 0.0085 | 0.30 | |
| 0.0368 | 0.0368 | 0.04 |
Despite an important noise level (85%), the two methods have proved able to analyze the simulated
signal and detect all frequency components using a ![]() threshold. The amplitudes are,
however, not precisely determined by the two methods because of positive or negative interferences
between noise and signal. Thus, some frequencies could remain undetected with the chosen threshold
if the noise rate is greater than 85%.
threshold. The amplitudes are,
however, not precisely determined by the two methods because of positive or negative interferences
between noise and signal. Thus, some frequencies could remain undetected with the chosen threshold
if the noise rate is greater than 85%.
The two methods have been applied to the astrolabe data obtained from 1975 to 1996 at Calern Observatory. Each diameter measurement has been corrected for the zenithal distance effect, being reduced to the zenith (secZ=1). In each case, all daily measurements have been used.
Data are analyzed using the least square fit method following the same iterative procedure
described in Sect. 3.3.1. Results obtained after five iterations are presented in Table 3.
This analysis allows us to detect frequencies that have amplitudes higher than the chosen threshold
(![]() for each iteration). At the end of the iterative procedure, the smallest threshold value
was equal to 0.037''. If we decrease it again, we find other harmonic components
but they may be artifacts due to the observation window or noise. The choice of the detection
threshold is then fundamental and we attempt to detect the periodicities in the data with this
given criterion. The final results obtained with the least square fit method are summarized in
Table 3.
for each iteration). At the end of the iterative procedure, the smallest threshold value
was equal to 0.037''. If we decrease it again, we find other harmonic components
but they may be artifacts due to the observation window or noise. The choice of the detection
threshold is then fundamental and we attempt to detect the periodicities in the data with this
given criterion. The final results obtained with the least square fit method are summarized in
Table 3.
| Iterations | Detected periodicity (day) |
| First | 3823 |
| Second | 348 |
| Third | 946 |
| Fourth | 1863 |
| Fifth | 121.9 |
All daily measurements have been used to satisfy as well as possible the deconvolution requirements (see Sect. 3.2). Each daily value is the average of all diameter measurements recorded on the same day. They are reported on a fixed date, giving then an approximation of the data sample diameter. The deconvolution method is applied to the data using the observation window function shown in Fig. 5.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{MS9612f5.eps}
\par\end{figure}](/articles/aa/full/2001/30/aa9612/Timg43.gif) |
Figure 5: The observation temporal window function. |
| Open with DEXTER | |
We remind the reader that it is a uniformly sampled daily function over the whole observation time
period equal to zero if there is no data on that day and to the number of diameter measurements if
there is. The power spectrum obtained without and with the deconvolution method is represented in
Fig. 6. The frequency range is divided into two juxtaposed and differently scaled domains in
order to better display the result of the deconvolution method. The still imperfect validity of the
assumptions made for using the deconvolution method is manifested by the occurrence of negative
values in the resulting power spectrum. These non physical values show the level of confidence of
the method. As for the simulated signal analysis, the window convolution is reduced then improving
the definition of the frequency range. The obtained results confirm the periodicities already found
with the least square method but also reveal a few more in the high frequency range (see Table 4).
These periodicities, which were at the noise level in the least square method, are detected here
using the ![]() threshold equal to 0.027''. The deconvolution of the window
function reduces the mean background level by a factor equal to about 2. These results were
obtained from the data set composed with all visual observations of diameter measurements recorded
from 1975 to 1996. In order to observe if the detected periods were always present during all the
observation period, we split the data set into two parts (1975-1986 and 1986-1996) and analyze them separately. The spectral analysis of the two subsets lead to the power spectra shown in Fig. 7.
We can notice that the power spectrum obtained from the first subset (1975-1986) is more noisy than
the second one (1986-1996). This is due to the fact that during the first half observation period,
data are more scattered and present more temporal gaps than the second one (see Fig. 1). All low
frequencies are detected in the first subset (Fig. 7a) but the high frequencies, like the 27 day
period for example, are not. However, we cannot conclude at the moment that these
short-periodicities did not exist during the period 1975-1986 because of the higher noise level. On
the other hand, all periodicities appear in the power spectrum obtained from the second subset
(Fig. 7b).
threshold equal to 0.027''. The deconvolution of the window
function reduces the mean background level by a factor equal to about 2. These results were
obtained from the data set composed with all visual observations of diameter measurements recorded
from 1975 to 1996. In order to observe if the detected periods were always present during all the
observation period, we split the data set into two parts (1975-1986 and 1986-1996) and analyze them separately. The spectral analysis of the two subsets lead to the power spectra shown in Fig. 7.
We can notice that the power spectrum obtained from the first subset (1975-1986) is more noisy than
the second one (1986-1996). This is due to the fact that during the first half observation period,
data are more scattered and present more temporal gaps than the second one (see Fig. 1). All low
frequencies are detected in the first subset (Fig. 7a) but the high frequencies, like the 27 day
period for example, are not. However, we cannot conclude at the moment that these
short-periodicities did not exist during the period 1975-1986 because of the higher noise level. On
the other hand, all periodicities appear in the power spectrum obtained from the second subset
(Fig. 7b).
![\begin{figure}
\par\includegraphics[height=8.4cm,width=8.8cm,clip]{MS9612f6.eps}
\end{figure}](/articles/aa/full/2001/30/aa9612/Timg44.gif) |
Figure 6:
a) Power spectrum without deconvolution. b) With deconvolution of the
observation window. The dotted lines represent the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[height=8.5cm,width=8.8cm,clip]{MS9612f7.eps}
\end{figure}](/articles/aa/full/2001/30/aa9612/Timg45.gif) |
Figure 7: The power spectrum obtained from the two data sets. a) Period 1975-1986. b) Period 1986-1996. (see text). |
| Open with DEXTER | |
| Least square method | Deconvolution method | Gavryusev et al.' results | ||||
| Periodicity | Amplitude | Fraction of the | Periodicity | Amplitude | Fraction of the | Periodicity |
| (day) | (
|
mean radius | (day) | (
|
mean radius | (day) |
| (10-3) | (10-3) | |||||
| 3823 | 0.10 | 0.11 | 4096 | 0.09 | 0.10 | 4098 |
| 1863 | 0.07 | 0.06 | 2048 | 0.04 | 0.04 | 1848 |
| 946 | 0.06 | 0.06 | 910 | 0.05 | 0.05 | 915 |
| - | - | - | - | - | - | 612 |
| - | - | - | - | - | - | 468 |
| - | - | - | - | - | - | 402 |
| 348 | 0.05 | 0.05 | 357 | 0.04 | 0.04 | 345 |
| - | - | - | - | - | - | 312 |
| - | - | - | - | - | - | 285 |
| - | - | - | 264.3 | 0.04 | 0.05 | - |
| - | - | - | - | - | - | 249 |
| 121.9 | 0.04 | 0.04 | 122.3 | 0.03 | 0.03 | - |
| - | - | - | 52.1 | 0.03 | 0.03 | - |
| - | - | - | 27.7 | 0.03 | 0.03 | - |
Two spectral methods were developed and used to analyze the solar diameter measurements recorded at
the solar astrolabe during the period of 1975 to 1996. All daily rather than monthly data were
analyzed after being corrected from the zenithal distance effect. This allows us to explore the
high frequency range of the solar data power spectrum. Table 4 summarizes the results obtained from
the two spectral analysis. In each case, a ![]() threshold was adopted in order to detect
periodicities in the data. In the table we can see the period, the amplitude and the fraction of
this amplitude compared to the average radius which is the same for both cases. The low frequencies
obtained by the two methods are in good agreement with those already reported by others (Gavryusev
et al. 1994; Delache et al. 1985). They differ, however, from Gavryusev et al.'s results in the middle and high frequency ranges (see Table 4). Their non-detection of our 3 highest
frequencies is due to the filtering applied to the solar data since monthly and smoothed diameter
values were analyzed. In addition, they used data covering only one solar cycle (1978-1991) in
their study. Our deconvolution method reveals new higher frequencies previously undetected, such as
the 27 day period. The short-periodicities are not detected with the deconvolution method applied
to the data obtained from the first half of the observation period (1975-1986). Since during this
period data are more scattered and present more temporal gaps, the requirements of the
deconvolution method are not satisfied. Thus, we are not able to conclude that they did not exist
during this observation period. They were found, however, with the second half observation period
(1986-1996). The least square fit method also did not reveal the same short-periodicities at the
threshold was adopted in order to detect
periodicities in the data. In the table we can see the period, the amplitude and the fraction of
this amplitude compared to the average radius which is the same for both cases. The low frequencies
obtained by the two methods are in good agreement with those already reported by others (Gavryusev
et al. 1994; Delache et al. 1985). They differ, however, from Gavryusev et al.'s results in the middle and high frequency ranges (see Table 4). Their non-detection of our 3 highest
frequencies is due to the filtering applied to the solar data since monthly and smoothed diameter
values were analyzed. In addition, they used data covering only one solar cycle (1978-1991) in
their study. Our deconvolution method reveals new higher frequencies previously undetected, such as
the 27 day period. The short-periodicities are not detected with the deconvolution method applied
to the data obtained from the first half of the observation period (1975-1986). Since during this
period data are more scattered and present more temporal gaps, the requirements of the
deconvolution method are not satisfied. Thus, we are not able to conclude that they did not exist
during this observation period. They were found, however, with the second half observation period
(1986-1996). The least square fit method also did not reveal the same short-periodicities at the
![]() detection threshold. This is probably due to the temporal gaps in solar data which did
not allow us to detect the short periodicities with the fixed
detection threshold. This is probably due to the temporal gaps in solar data which did
not allow us to detect the short periodicities with the fixed ![]() threshold, since each peak
is partly spread out by the convolution. The deconvolution method leads however, to systematically
higher periods. This is due to the power spectrum sampling that is obtained by the Fourier
Transform and its sampling is related to the analyzed signal length (Fig. 6).
threshold, since each peak
is partly spread out by the convolution. The deconvolution method leads however, to systematically
higher periods. This is due to the power spectrum sampling that is obtained by the Fourier
Transform and its sampling is related to the analyzed signal length (Fig. 6).
The 11-year and 27-day periodicities in the diameter measurements are related to things already known about the Sun : its magnetic activity cycle and its rotation rate. For this reason there is little doubt that they could be misinterpretation of artifact effects. Now, the other peaks are not related to well known periodicities but in some instances (2.5 years, 4 months), they are also found in other types of data (Javaraiah & Komm 1999; Djurovic & Pâquet 1995) and in any case, they show up in the deconvolution as well as the 27-day, so that they must be regarded as probably significant. The fact that the 27-day peak is so sharp is extremely interesting because it then defines precisely one period, while the solar surface exhibits the well known differential rotation with latitude and the astrolabe diameter measurements scan a rather broad range of latitudes. How these measurements are able to precisely select this unique period of rotation is now something to be investigated, as well as how the solar rotation can be visible in diameter measurements.
Visual observations of the solar diameter performed at the Calern Observatory astrolabe during approximately two solar cycles show variations at various time scales. Since the beginning of the solar experiment in 1975 till now, data were recorded every day except when the weather was bad or in case of seasonal effects relative to the instrument characteristics. These discontinuities induce peculiarities in the solar data set that is non uniformly sampled and they present some temporal gaps. Thus, special spectral analysis methods were required in order to disentangle the harmonic terms of the observed variations from the windows convolution artifacts. For this purpose, we have developed two methods which take into account the data peculiarities. The first one is a least square fit method based on adjusting harmonic functions to the data inside frequency ranges, followed by an iterative process of selection of the highest detected amplitudes. The second one is the spectrum deconvolution of the temporal window function. A synthetic signal with characteristics similar to the solar time series has been used in order to validate the two methods. Contrary to all previous analyses, daily data have been taken into account rather than monthly values. In addition, they have been corrected for the zenithal distance effect by reducing them to the zenith. The two methods have been applied to the 21 year data set and permitted to extract new harmonic components in the observed variations. The low frequencies obtained from the two spectral methods are in good agreement with those previously published by other authors who have analyzed the same data. They also present some similarity to the periodicities deduced from the Sun's differential rotation studies, such as that of 2.5 years. Since daily solar diameter measurements were used, the methods were able to determine shorter periodicities from the observed variations. Thus, the deconvolution method of the temporal window observation reveals also high frequencies in solar diameter variations, such as the 4 month and 27 day periods. The last one is also presumably linked to the solar rotational period. The least square fit method did not convincingly show the same results in the high frequency range, since it is not free of the sidelobes induced by the non uniform data sampling. This work then reveals harmonic term components in the observed variations of the solar diameter measurements directly related to the Sun's rotation which need to be further investigated.
Acknowledgements
This work has been performed with support of the Algerian Research National Program (PNR) and the French Foreign affair Ministry in the framework of scientific cooperation between France and Algeria (contract 00 MDU 501)