A&A 374, 839-860 (2001)
DOI: 10.1051/0004-6361:20010793
P. R. Williams 1,2 - A. H. Nelson 3
1 - Department of Physics and Astronomy, Cardiff University,
PO Box 913, Cardiff, CF2 3YB, UK
2 -
Astronomical Institute, Tohoku University,
Aoba, Sendai, 980-8578, Japan
3 -
Department of Physics and Astronomy, Cardiff University,
PO Box 913, Cardiff, CF2 3YB, UK
Received 12 November 1999 / Accepted 2 May 2001
Abstract
A simulation is described in which the numerical galaxy formed
compares favourably in every measurable respect with contemporary bright
spiral galaxies, including the formation of a distinct stellar bulge
and large scale spiral arm shocks in the gas component. This is
achieved in spite of the fact that only idealized proto-galactic
initial conditions were used, and only simple phenomenological
prescriptions for the physics of the interstellar medium (ISM) and star
formation were implemented. In light of the emphasis in recent
literature on the importance of the link between galaxy formation and
models of the universe on cosmological scales, on the details of the
physics of the ISM and star formation, and on apparent problems therein,
the implications of this result are discussed.
Key words: galaxies: spiral, formation, evolution, kinematics and dynamics,
fundamental parameters -
methods: N-body simulations
During the past decade our observational knowledge of the evolution of galaxies to high redshift has considerably improved (Bunker & van Breugel 1999). On larger scales recent observations of the cosmic microwave background have given a greater confidence in the validity of the standard cosmological models (de Bernardis et al. 2000). However extensions of these cosmological models to galactic scales suggest that there are possibly serious discrepancies between the characteristics of galaxies predicted by galaxy formation in such cosmological contexts and those observed. Specifically, these theories predict too many dwarf galaxies in comparison to the numbers of satellite galaxies in the Local Group (Klypin et al. 1999; Moore et al. 1999a); the largest of disk galaxies are predicted to have too little angular momentum and thus are more centrally condensed than those observed (Navarro & Benz 1991; Navarro & White 1993; Navarro et al. 1995); and the predicted inner mass profiles of halos appear to be far steeper than those inferred from the rotation curves of dwarf and low surface brightness galaxies (Flores & Primack 1994; Burkert 1995; de Blok & McGaugh 1997; Hernandez & Gilmore 1998; Moore et al. 1999b). Recent studies have highlighted potentially very important numerical issues related to these problems, particularly concerning the implementation of interstellar processes which occur on length scales much smaller than those presently resolvable in simulations; and how such galacto-microscopic physics may be consistently and effectively implemented in such galaxy formation simulations (Yepes et al. 1997; Sommer-Larsen et al. 1999; Hultman & Pharasyn 1999; Springel 2000). In addition, many possible physical and astrophysical solutions have also been suggested, for example, modifications to the dark matter physics (Sommer-Larsen & Dolgov 1999; Spergel & Steinhardt 2000; White & Croft 2000; Firmani et al. 2000; Yoshida et al. 2000; Burkert 2000; Hannestad & Scherrer 2000; Riotto & Tkachev 2000); modifications to the manner in which the primordial power spectrum evolves (Kaminokowski & Liddle 2000); and work emphasizing the importance of supernovae feedback and other interstellar physics to the gross structure of galaxies (Navarro et al. 1996; Navarro & Steinmetz 1997; Weil et al. 1998; Gelato & Sommer-Larsen 1999; Bullock et al. 2000).
In order to assess the importance of these recent developments, it is useful to view the current state of galaxy formation theory in the broader context of the development of galaxy formation theory to date. Gravitational collapse of dense proto-galactic clouds is now the standard paradigm for galaxy formation, and constituted the basis of the early galaxy formation scenarios of von Weizsäcker (1951) and Hoyle (1953). Using data on dwarf stars, Eggen et al. (1962) showed that the present structure of the Galaxy is consistent with such a collapse hypothesis, in that the oldest stars generally have high angular momentum. The observed rotation curves of disk galaxies are also in keeping with the collapse hypothesis, in that if proto-galaxies initially gain their angular momentum through tidal torques, and angular momentum transport during collapse is not significant, galaxies have typically collapsed by a factor of 5-10 (Mestel 1963; Fall & Efstathiou 1980). Also, exponential surface density profiles, a defining characteristic of observed stellar disks, are a natural consequence of such a scenario (Gunn 1982). Lynden-Bell (1967) demonstrated that if such a proto-galactic collapse is predominantly dissipationless, perhaps relevant to the formation of spheroidals, the proto-galaxy may reach equilibrium on a timescale much shorter than that expected from the star-star relaxation time, via violent relaxation.
To build on these early ideas, it was necessary to relax any restrictive assumptions imposed on the model physics or on the geometry of the evolving protogalaxy, and hence to use computer simulation. Early examples of such simulations can be found in, for example, van Albada (1982), Larson (1969,1974,1975,1976), Gott & Thuan (1976), Lake & Carlberg (1988,1988), Katz & Gunn (1991), and Katz (1992), and the last two decades have seen a number of key developments which have allowed galaxy formation research to accelerate along this path. Firstly there has been a huge increase in the processing power of computers, and secondly efficient numerical techniques applicable to the galaxy formation problem have been developed, principally Treecode gravity (Barnes & Hut 1986; Hernquist & Katz 1989) and Smoothed Particle Hydrodynamics (Lucy 1977; Gingold & Monaghan 1977; Hernquist & Katz 1989; Monaghan 1992).
A proto-galaxy can be defined as a region of the universe that encloses the gas which will eventually constitute a galaxy just prior to this gas forming significant amounts of stars. Thus in order to construct a computer model of a protogalaxy and its evolution, one must specify:
The direction of recent simulation work has been to try to further our understanding of galaxy formation by coupling galaxy formation to cosmological models of the large scale structure of the universe (Navarro & White 1993,1994; Steinmetz & Müller 1994,1995; Navarro & Steinmetz 1997; Weil et al. 1998); and by increasing the sophistication of the prescription of dissipational physics (Yepes et al. 1997; Navarro & Steinmetz 1997; Weil et al. 1998; Hultman & Pharasyn 1999; Springel 2000). While it is natural for galaxy formation to develop in such directions, it must be recognized that the observational constraints on these issues are not strong. While significant advances have been made in probing galaxies to higher and higher redshifts, and in characterizing the gas content of the Universe as a function of redshift, we are still without direct observational evidence of a galaxy formation event. The life-cycle of galaxies cannot yet be observed in a statistical manner, as has been done for stars. Thus observational data cannot yet directly impose strong constraints on points (1) or (2).
However there are a number of things that can be inferred from observations of contemporary galaxies. Firstly, galaxies are found to have characteristic length and mass scales (Rees & Ostriker 1977), while there are no such scales associated with gravitation. Furthermore, the fact that galaxies have gaseous and stellar disks indicates that significant levels of star formation cannot have occurred prior to or during their collapse. Thus it is strongly suggested that dissipational physics played an important role in the formation of galaxies.
This in turn implies that a cosmological power spectrum of density fluctuations (based on gravity alone) which is able to successfully reproduce the large scale structure of the Universe, is not necessarily relevant to galaxy formation on smaller scales. Such a power spectrum, when extrapolated to sub-protogalactic scales, lacks the effects of gas physics, which may play a dominant role in determining the noise spectrum on these scales during the epoch of galaxy formation.
Thus, while the long term aim of galaxy formation theory must be to develop an integrated picture of galaxy formation in a cosmological context, it is at present still productive to investigate galaxy formation neglecting cosmological considerations. This will allow us to investigate the mechanisms of self-gravitating gaseous collapse which may be relevant to galaxy formation, and to ascertain to what extent comparison of the final result with contemporary galaxies can put constraints on (1) and (2). Following this line of reasoning, and given our present limited understanding of the interstellar medium, we investigate here the extent to which the simplest choices of initial conditions and physics for a protogalaxy, when evolved into the fully non-linear regime, can reproduce the properties of contemporary galaxies. It turns out that the such simulations reproduce these properties remarkably well.
The initial conditions were a uniform density sphere of ![]() gas and
gas and ![]() collisionless dark matter by mass, in solid body rotation, and with a
radial velocity directly proportional to radius. The particles were
initially laid down on a uniform grid. This matter
configuration is defined by four parameters: the total
mass M, the initial radius
collisionless dark matter by mass, in solid body rotation, and with a
radial velocity directly proportional to radius. The particles were
initially laid down on a uniform grid. This matter
configuration is defined by four parameters: the total
mass M, the initial radius ![]() ,
the initial angular velocity
,
the initial angular velocity
![]() ,
and a radial velocity scaling constant
,
and a radial velocity scaling constant ![]() .
The values used in this simulation were
.
The values used in this simulation were
![]()
![]() ,
,
![]() kpc,
kpc,
![]() Gyr-1, and
Gyr-1, and
![]() kms-1Mpc-1. This is equivalent to a total angular momentum
kms-1Mpc-1. This is equivalent to a total angular momentum
![]() kgm2s-1, a total energy of
kgm2s-1, a total energy of
![]() J, and thus a spin parameter of
J, and thus a spin parameter of
![]() (Peebles 1969).
(Peebles 1969).
For the purposes of modeling galaxy formation at the spatial resolution
presently possible in galaxy formation simulations, a model of the ISM
which describes the bulk behaviour of interstellar gas on scales of
several tens of parsecs and larger is required. In order to construct
such a macroscopic model it is reasonable to first consider the state of
interstellar gas in the solar neighbourhood and in external spiral
galaxies. The dominant gas component in the local ISM is found to be
thermodynamically cold, less than 102 K; dense, greater than 10 cm-3; and magnetized to a dynamically significant level. It is this
cloud phase which dominates the bulk motions of gas in
galaxies (Binney & Merrifield 1998). Both the velocity
dispersion of small clouds in the Solar neighbourhood (Stark & Brand
1989) and the velocity dispersion which characterizes the bulk
motions of gas in spiral galaxies is found to be of order 10 kms-1
(Spitzer 1978). Thus a model of the ISM in which gas is in the
form of an ensemble of small clouds which themselves behave as a
collisional fluid was adopted. Analogous to an ideal gas, the gas of
small clouds is characterized by a bulk velocity dispersion ![]() ,
and a mass
density
,
and a mass
density ![]() ,
which together provide a source of pressure
,
which together provide a source of pressure
![]() .
In this simulation
.
In this simulation
![]() kms-1 was used, based on the
measured velocity dispersion of clouds in the local ISM (Stark & Brand
1989). Such a simple model for the ISM was first suggested by Cowie
(1980), and this model may be considered
as a first order approximation to a detailed description of the
multi-phase ISM (McKee & Ostriker 1977).
The Cowie model has in effect been used extensively in simulations of
galaxy dynamics and galaxy mergers (Theis & Hensler 1993;
Mihos & Hernquist 1994; Englmaier & Gerhard 1997).
kms-1 was used, based on the
measured velocity dispersion of clouds in the local ISM (Stark & Brand
1989). Such a simple model for the ISM was first suggested by Cowie
(1980), and this model may be considered
as a first order approximation to a detailed description of the
multi-phase ISM (McKee & Ostriker 1977).
The Cowie model has in effect been used extensively in simulations of
galaxy dynamics and galaxy mergers (Theis & Hensler 1993;
Mihos & Hernquist 1994; Englmaier & Gerhard 1997).
The star formation rate density
![]() was determined by a Schmidt law (Schmidt 1959)
was determined by a Schmidt law (Schmidt 1959)
![]() ,
where
,
where
![]() is the
total gas density. From observations of the global star formation rate
density in spiral galaxies, a Schmidt law index
is the
total gas density. From observations of the global star formation rate
density in spiral galaxies, a Schmidt law index
![]() has
been deduced and was used here (Buat 1992; Kennicutt
1997). A wide range of simple theoretical models of star formation in
spiral galaxies also produce a similar value (Wyse 1986; Larson
1988, 1992; Kennicutt 1989, 1997; Wyse & Silk
1989; Elmegreen 1994; Sleath &
Alexander 1995). The constant
has
been deduced and was used here (Buat 1992; Kennicutt
1997). A wide range of simple theoretical models of star formation in
spiral galaxies also produce a similar value (Wyse 1986; Larson
1988, 1992; Kennicutt 1989, 1997; Wyse & Silk
1989; Elmegreen 1994; Sleath &
Alexander 1995). The constant ![]() was chosen such that for
a typical present day ISM gas density
was chosen such that for
a typical present day ISM gas density
![]()
![]() pc-3 (Binney & Tremaine 1987), and for a
total galaxian gas mass of
pc-3 (Binney & Tremaine 1987), and for a
total galaxian gas mass of
![]()
![]() (Hodge 1994), the implied global star
formation rate
(Hodge 1994), the implied global star
formation rate
![]()
![]() yr-1,
comparable to the measured present day star formation rates in
intermediate to late type spiral galaxies (Kennicutt 1989). Based
on these assumptions, the value
yr-1,
comparable to the measured present day star formation rates in
intermediate to late type spiral galaxies (Kennicutt 1989). Based
on these assumptions, the value
![]()
![]() pc3/2Gyr-1 was used.
pc3/2Gyr-1 was used.
The numerical code was based on the Treecode-SPH algorithm described by Hernquist & Katz (1989), modified to run on a distributed parallel computer, and to include an algorithm to model star formation. Full details of all the numerical methods and algorithms used, including tests and validations, are to be found in Williams (1998).
The gravitational softening length ![]() was kept constant in space
and time with a value
was kept constant in space
and time with a value
![]() pc. Gravitational accelerations
were evaluated to quadrupole order, using a cell opening angle of
pc. Gravitational accelerations
were evaluated to quadrupole order, using a cell opening angle of
![]() .
The modified cell tolerance criteria given by
Barnes (1994) was used to avoid errors in the calculation of
gravitational accelerations such as those reported by Salmon &
Warren (1994).
.
The modified cell tolerance criteria given by
Barnes (1994) was used to avoid errors in the calculation of
gravitational accelerations such as those reported by Salmon &
Warren (1994).
The kernel radius of each SPH particle ![]() was allowed to vary such
that at all times between 30 and 50 neighbours were contained within
was allowed to vary such
that at all times between 30 and 50 neighbours were contained within
![]() .
Kernel radii were evolved as described by Hernquist & Katz
(1989). However, occasionally this approach did not
predict a kernel radius containing the required number
of neighbours. In these cases,
.
Kernel radii were evolved as described by Hernquist & Katz
(1989). However, occasionally this approach did not
predict a kernel radius containing the required number
of neighbours. In these cases, ![]() was iteratively updated and the
tree data structure was re-examined until the required number of
neighbours within
was iteratively updated and the
tree data structure was re-examined until the required number of
neighbours within
![]() was achieved. This process was found to incur
little additional computational cost. The artificial viscosity
prescription of Gingold & Monaghan (1983) was used, with
viscosity parameters
was achieved. This process was found to incur
little additional computational cost. The artificial viscosity
prescription of Gingold & Monaghan (1983) was used, with
viscosity parameters
![]() .
.
As the simulation evolved, each SPH particle converted its gas mass into
stellar mass at a rate controlled by a Schmidt law, and kept track of
the amount of mass in gas and stars. Globally, when a small amount
![]() of the total gas mass had been converted into stellar mass,
this stellar mass was re-distributed amongst
of the total gas mass had been converted into stellar mass,
this stellar mass was re-distributed amongst ![]() new
collisionless star particles of mass
new
collisionless star particles of mass
![]() .
In
this simulation
.
In
this simulation
![]()
![]() ,
i.e. one
thousandth of the initial gas mass, and
,
i.e. one
thousandth of the initial gas mass, and
![]() .
The positions
of these
.
The positions
of these ![]() new star particles were chosen such that the
recent star formation history and spatial
distribution of newly formed stellar mass was statistically represented.
Numerical tests indicate that this algorithm gives consistent results
over a range of values for
new star particles were chosen such that the
recent star formation history and spatial
distribution of newly formed stellar mass was statistically represented.
Numerical tests indicate that this algorithm gives consistent results
over a range of values for ![]() and
and ![]() (Williams 1998).
(Williams 1998).
A second order individual particle timestep integration scheme was used
to improve efficiency, as described by Hernquist & Katz
(1989). Each particle was assigned an individual timestep which
is a power of two division of the largest allowed timestep, and a second
order time-centred leapfrog integration scheme was used. Collisionless
particles were assigned a timestep using the criteria given by Katz
(1991), while the timestep for SPH particles was calculated
using the minimum of this timestep and the SPH Courant condition given by
Hernquist & Katz (1989). A Courant number of
![]() was used for all particles.
was used for all particles.
A simple method of parallelization was implemented in which the most computationally expensive parts of the Treecode-SPH algorithm, the evaluation of gravitational accelerations, the searching for SPH neighbours, and the calculation of SPH summations, were parallelized. All processors held all particle data in memory. Each processor was assigned an equal fraction of each particle species for the duration of the simulation, and calculated their gravitational accelerations, found their SPH neighbours, and calculated their SPH summations when required.
The numbers of gas and dark matter particles used were 33552 and 33401
respectively. Conversion of all gas mass to stellar
mass would have resulted in the formation of 64000 star particles.
Particle data was output every
![]() yr, and the
simulation was evolved for a total of
yr, and the
simulation was evolved for a total of
![]() yr. Typically
13 timestep levels were used, equivalent to a range in timesteps of
8192. This increased to 32768 (15 timestep levels) during the most
dynamically active periods of evolution, although, the distribution of
particles amongst the timestep levels was found to have a long tail to
small timesteps: at any given time, no more than
yr. Typically
13 timestep levels were used, equivalent to a range in timesteps of
8192. This increased to 32768 (15 timestep levels) during the most
dynamically active periods of evolution, although, the distribution of
particles amongst the timestep levels was found to have a long tail to
small timesteps: at any given time, no more than ![]() of particles had
timesteps smaller than that of the 10th smallest timestep level. Thus the
individual particle timestep integration scheme made significant savings
in computational cost in comparison to a single timestep algorithm.
The simulation took 15 days using 32 processors (roughly 1.3 CPU years)
on the Cray T3E at the Edinburgh Parallel Computing Centre, as part of
the Virgo Consortium's time allocation (Jenkins et al. 1998). This
is equivalent to roughly
of particles had
timesteps smaller than that of the 10th smallest timestep level. Thus the
individual particle timestep integration scheme made significant savings
in computational cost in comparison to a single timestep algorithm.
The simulation took 15 days using 32 processors (roughly 1.3 CPU years)
on the Cray T3E at the Edinburgh Parallel Computing Centre, as part of
the Virgo Consortium's time allocation (Jenkins et al. 1998). This
is equivalent to roughly
![]() timestep iterations.
timestep iterations.
Figures 1 to 6 show an evolutionary sequence of
the gas, stellar, and dark matter. Each page refers to one
instant in the simulation, and is labelled with the time from the
beginning of the simulation
![]() .
All lengths are shown in
kiloparsecs, although the range in spatial scale viewed generally
varies from frame to frame. Particle plots are an effective way
of illustrating the detailed structural features and the general
evolution of a simulation such as that discussed here. However, when
the dynamical range in density and the number of particles is large,
such plots can be misleading to the eye in regions of extremum
density. In low density regions the small number of particles can
give the impression of empty holes, while these particles are really
points in a tenuous continuum fluid. In high density regions particles can
appear as a uniform solid mass, the actual density structure
being completely saturated to the eye. Also, it is difficult to
convey the very dynamical nature of simulations using only static
images. With these limitations in mind, we encourage readers to supplement
their reading of this paper by viewing the series of animations
to be found at
http://www.astro.cf.ac.uk/pub/Alistair.Nelson/indexgf.html.
.
All lengths are shown in
kiloparsecs, although the range in spatial scale viewed generally
varies from frame to frame. Particle plots are an effective way
of illustrating the detailed structural features and the general
evolution of a simulation such as that discussed here. However, when
the dynamical range in density and the number of particles is large,
such plots can be misleading to the eye in regions of extremum
density. In low density regions the small number of particles can
give the impression of empty holes, while these particles are really
points in a tenuous continuum fluid. In high density regions particles can
appear as a uniform solid mass, the actual density structure
being completely saturated to the eye. Also, it is difficult to
convey the very dynamical nature of simulations using only static
images. With these limitations in mind, we encourage readers to supplement
their reading of this paper by viewing the series of animations
to be found at
http://www.astro.cf.ac.uk/pub/Alistair.Nelson/indexgf.html.
Figures 7 and 8 show the final gas, stellar, and dark matter surface density profiles, and the final rotation curve of the numerical galaxy formed. The evolution of the global properties, and the structural parameters of the numerical galaxy versus time and redshift are shown in Figs. 9 to 13.
The formation and evolution of this numerical galaxy was found to fall naturally into five broad phases in which specific physical mechanisms and processes were found to dominate the evolution of the numerical galaxy. Each of the following sections is labelled with a rough estimate of the epoch to which the description applies, although it should be remembered that there are no distinct temporal boundaries between the phases.
![\begin{figure}
\par\includegraphics[width=\widthone]{MS09391f01.ps}\includegraph...
...hone]{MS09391f05.ps}\includegraphics[width=\widthone]{MS09391f06.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg101.gif) |
Figure 1:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\widthone]{MS09391f07.ps}\includegraph...
...hone]{MS09391f11.ps}\includegraphics[width=\widthone]{MS09391f12.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg102.gif) |
Figure 2:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\widthone]{MS09391f13.ps}\includegraph...
...hone]{MS09391f17.ps}\includegraphics[width=\widthone]{MS09391f18.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg103.gif) |
Figure 3:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\widthone]{MS09391f19.ps}\includegraph...
...hone]{MS09391f23.ps}\includegraphics[width=\widthone]{MS09391f24.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg104.gif) |
Figure 4:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\widthone]{MS09391f25.ps}\includegraph...
...hone]{MS09391f29.ps}\includegraphics[width=\widthone]{MS09391f30.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg105.gif) |
Figure 5:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\widthone]{MS09391f31.ps}\includegraph...
...widthone]{MS09391f33.ps}\includegraphics[width=7.5cm]{MS09391f34.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg106.gif) |
Figure 6:
The gas and stellar mass components, top and bottom
respectively, at
|
| Open with DEXTER | |
As the radial expansion was halted by gravity, the outer shell of
mass reached maximum radius (roughly 300 kpc), see Fig. 1, although mass at smaller radii was still expanding.
At this time, the dark matter particles still retained their initial
grid structure to a high degree of accuracy, while the gas particles
had to a greater extent dispersed from the initial lattice. This was due
to the stochastic nature of errors in quantities evaluated using SPH, and the
propagation of these errors in time. Note that the errors
in the individual particle positions have a negligible effect on the
bulk distribution of matter. The low initial gas density resulted in a
low initial star formation rate of 0.04 ![]() yr-1, which
decreased smoothly to 0.02
yr-1, which
decreased smoothly to 0.02 ![]() yr-1 as the sphere of matter
expanded and the gas density decreased. Only
yr-1 as the sphere of matter
expanded and the gas density decreased. Only
![]() of gas was converted to stellar matter during this phase.
of gas was converted to stellar matter during this phase.
Successively inner shells of matter achieved zero radial
velocity and began to fall in at an increasingly faster rate,
see Figs. 2 and 3. As the collapse progressed, the
mass distributions became flattened in the x-z plane due to
rotation. In the central regions of the swiftly deepening potential
well, increasingly more dark matter collapsed past gas which was
initially at the same radius. The highest densities
encountered at the point of maximum collapse were of order
200 ![]() pc-3, although only roughly
pc-3, although only roughly
![]()
![]() (
(![]() )
of gas achieved such values.
)
of gas achieved such values.
By
![]() Gyr, Fig. 3, the gas
distribution had begun to flatten to a disk-like structure, and
viscously dissipate energy. As a consequence, layers of gas in the
x-y plane had begun to collide and shock in the equatorial plane.
Because of inhomogeneity on scales of less than of order 1 kpc in
the distribution of gas particles on either side of
the equatorial plane of the proto-galactic cloud, the gas was
unable to viscously dissipate all kinetic energy in the direction
perpendicular to the proto-galactic disk and shock to a perfectly
thin disk. Thus, the gas clumps impacting on the plane of the
proto-galactic disk exhibited damped oscillations about this plane.
This is most clearly seen in the central regions of the numerical
proto-galaxy, where the impact velocity onto the x-y plane
was largest, see Fig. 3. Although this behaviour was short
lived, the high density gas maintained a sufficiently large amplitude
of oscillation about the x-y plane for a sufficient length of time
to form stars in a roughly spherical distribution at the centre during
the proceeding evolution, see Fig. 14. Thus it is suggested
that galactic bulges may form in this fashion.
Gyr, Fig. 3, the gas
distribution had begun to flatten to a disk-like structure, and
viscously dissipate energy. As a consequence, layers of gas in the
x-y plane had begun to collide and shock in the equatorial plane.
Because of inhomogeneity on scales of less than of order 1 kpc in
the distribution of gas particles on either side of
the equatorial plane of the proto-galactic cloud, the gas was
unable to viscously dissipate all kinetic energy in the direction
perpendicular to the proto-galactic disk and shock to a perfectly
thin disk. Thus, the gas clumps impacting on the plane of the
proto-galactic disk exhibited damped oscillations about this plane.
This is most clearly seen in the central regions of the numerical
proto-galaxy, where the impact velocity onto the x-y plane
was largest, see Fig. 3. Although this behaviour was short
lived, the high density gas maintained a sufficiently large amplitude
of oscillation about the x-y plane for a sufficient length of time
to form stars in a roughly spherical distribution at the centre during
the proceeding evolution, see Fig. 14. Thus it is suggested
that galactic bulges may form in this fashion.
![\begin{figure}
\mbox{
\includegraphics[width=7.6cm]{MS09391f35.ps}\includegraphics[width=7.6cm]{MS09391f36.ps} }
\par\end{figure}](/articles/aa/full/2001/30/aa9391/Timg113.gif) |
Figure 7:
The stellar surface density and gas stellar surface density
profiles, taken at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm]{MS09391f37.ps}\hspace*{1.5mm}
\includegraphics[width=6.9cm]{MS09391f38.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg115.gif) |
Figure 8:
The dark matter surface density profile and rotation curve,
taken at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm]{MS09391f39.ps}\hspace*{7mm}
\includegraphics[width=7cm]{MS09391f40.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg116.gif) |
Figure 9:
The global star formation rate SFR and the gas mass fraction
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm]{MS09391f41.ps}\hspace*{8.5mm}
\includegraphics[width=6.9cm]{MS09391f42.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg117.gif) |
Figure 10:
Total specific angular momentum |j| and total angular
momentum |J|, versus time
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm]{MS09391f43.ps}\hspace*{8.5mm}
\includegraphics[width=7.8cm]{MS09391f44.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg118.gif) |
Figure 11:
Gas disk and gas pseudo-bulge scale lengths
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.9cm]{MS09391f45.ps}\hspace*{8.5mm}
\includegraphics[width=7.6cm]{MS09391f46.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg122.gif) |
Figure 12:
Stellar disk and stellar bulge scale lengths
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=\widthone]{MS09391f47.ps}\includegraph...
...hone]{MS09391f49.ps}\includegraphics[width=\widthone]{MS09391f50.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg123.gif) |
Figure 13:
The dark matter volume density profile, taken at
|
| Open with DEXTER | |
During this phase the star formation rate increased sharply from
0.02 ![]() yr-1 to 4.3
yr-1 to 4.3 ![]() yr-1, and
roughly
yr-1, and
roughly
![]()
![]() of gas was converted into stars
over a timescale of 3.2 Gyr. For the duration of most of the collapse,
the star formation remained roughly evenly distributed throughout the
proto-galactic cloud. However by
of gas was converted into stars
over a timescale of 3.2 Gyr. For the duration of most of the collapse,
the star formation remained roughly evenly distributed throughout the
proto-galactic cloud. However by
![]() Gyr, Fig. 3, star formation had begun to become more concentrated
within discrete peaks in the gas density distribution.
Gyr, Fig. 3, star formation had begun to become more concentrated
within discrete peaks in the gas density distribution.
The approximately spherical re-expansion of the dark matter component allowed the re-expansion of the gas disc in the horizontal direction due to conservation of angular momentum, see Figs. 3 and 4. During this phase the gas component fragmented into distinct high density objects, which subsequently formed individual stellar components.
The central region of smooth dark matter density grew as
successive shells of mass fell onto the central halo. This process was
complete once all dark matter had passed through the central regions,
and had either become part of the smooth featureless central halo (via violent
relaxation), or continued to expand outwards in radius, see Fig. 3. The low density outer regions
of the dark matter distribution, which contained roughly ![]() of the
dark matter, had not undergone full violent relaxation,
so that remnants of the initial configuration were still visible.
Subsequent to this re-expansion, the parameters describing the dark
matter surface density profile exhibited a damped oscillatory behaviour,
which can be interpreted physically as a damped radial pulsation in the
dark matter halo. Only two periods of oscillation were observed before
the dark matter halo settled to an equilibrium configuration over the region in
which the luminous galaxy components would eventually form and evolve,
see Fig. 13.
of the
dark matter, had not undergone full violent relaxation,
so that remnants of the initial configuration were still visible.
Subsequent to this re-expansion, the parameters describing the dark
matter surface density profile exhibited a damped oscillatory behaviour,
which can be interpreted physically as a damped radial pulsation in the
dark matter halo. Only two periods of oscillation were observed before
the dark matter halo settled to an equilibrium configuration over the region in
which the luminous galaxy components would eventually form and evolve,
see Fig. 13.
The re-expansion of the dark matter allowed the gas mass which had
experienced high densities at maximum collapse to also re-expand. This
gas, having radiatively dissipated away most
of its energy in motion perpendicular to the proto-galactic disk, could
only centrifugally re-expand in the horizontal plane. This outwardly
moving ring of mass collided and shocked into the infalling gas, and began
to fragment. Radial growth of the overall gas disk continued due to infall
from the gaseous halo. The disk height was found to be roughly 1 kpc,
but slowly became thinner as viscous forces damped out oscillations
perpendicular to the proto-disk. The gas mass at this time, just
after
![]() Gyr, Fig. 3, was found to reside in three different environments: dense clumps, a highly inhomogeneous and geometrically complex inter-clump
medium, and a smooth distribution of infalling gas from the low density
gaseous halo. The formation of the dense clumps occurred through
localized gravitational collapse within the proto-galactic
disk. Gas mass in the centres of these clumps had a density of
typically
Gyr, Fig. 3, was found to reside in three different environments: dense clumps, a highly inhomogeneous and geometrically complex inter-clump
medium, and a smooth distribution of infalling gas from the low density
gaseous halo. The formation of the dense clumps occurred through
localized gravitational collapse within the proto-galactic
disk. Gas mass in the centres of these clumps had a density of
typically
![]()
![]() pc-3, implying a Jeans length
pc-3, implying a Jeans length
![]() of
of
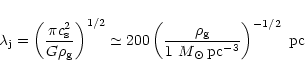 |
(1) |
Due to the highly clumpy nature of the gas during this phase, the geometric centre, as defined by the position of the largest central clump, was often significantly offset from the centre of mass, which resulted in large fluctuations in the fitting parameters describing the overall surface density of the proto-disk, see Figs. 11 and 12. The disk surface density profiles were affected to a lesser extent than the bulge profiles, since the outer regions were less sensitive to the choice of geometric centre, and the outer radial bins were azimuthally averaged over a larger area. Note that both the stellar and gas disk surface density profiles had begun to evolve in a stable fashion by the end of this phase (with the exception of the glitch between 7 and 7.2 Gyr, which will be discussed in more detail in the following section).
By
![]() Gyr, Figs. 4, 6 main sub-galaxies had
formed, with masses in the range
Gyr, Figs. 4, 6 main sub-galaxies had
formed, with masses in the range
![]() to
to
![]()
![]() ,
and major axes from 2 to 3.25 kpc.
Peak gas densities in these evolved sub-galaxies were found to be of order
10 to 100
,
and major axes from 2 to 3.25 kpc.
Peak gas densities in these evolved sub-galaxies were found to be of order
10 to 100 ![]() pc-3, a factor of roughly 103 higher
than the surrounding material, and a factor of roughly 108 higher
than the extended gaseous halo. These values compare to a total gas
density of 0.042
pc-3, a factor of roughly 103 higher
than the surrounding material, and a factor of roughly 108 higher
than the extended gaseous halo. These values compare to a total gas
density of 0.042 ![]() pc-3 in The Galaxy at the Solar
radius (Binney & Tremaine 1987). The tidal torques induced
through the non-circular orbits of the sub-galaxies caused their
peak density to periodically fluctuate. The fraction of the
total mass of each of the sub-galaxies in gaseous form
varied from 0.18 to 0.78, the heaviest generally having the lowest
gas mass fractions, the highest mean densities, and the highest star
formation rates. The sub-galaxies were found to be supported by a
combination of rotation and velocity dispersion. Their orbits were frequently
found to be inclined to the plane of the proto-disk, but typically
at inclination angles less than
pc-3 in The Galaxy at the Solar
radius (Binney & Tremaine 1987). The tidal torques induced
through the non-circular orbits of the sub-galaxies caused their
peak density to periodically fluctuate. The fraction of the
total mass of each of the sub-galaxies in gaseous form
varied from 0.18 to 0.78, the heaviest generally having the lowest
gas mass fractions, the highest mean densities, and the highest star
formation rates. The sub-galaxies were found to be supported by a
combination of rotation and velocity dispersion. Their orbits were frequently
found to be inclined to the plane of the proto-disk, but typically
at inclination angles less than
![]() ,
see Fig. 4. The linear sizes and masses of these sub-galaxies are
similar to those inferred from the clumps of luminosity
observed (sometimes with apparently linear distributions) in some
of the Hubble Deep Field galaxies (Williams et al. 1996; van den
Bergh et al. 1996; Abraham et al. 1994; Mobasher et al. 1996; Clements & Couch 1996); and a distribution of
clumpy star formation, roughly confined to a disk would appear as a
chain-like structure if the disk were viewed edge-on.
,
see Fig. 4. The linear sizes and masses of these sub-galaxies are
similar to those inferred from the clumps of luminosity
observed (sometimes with apparently linear distributions) in some
of the Hubble Deep Field galaxies (Williams et al. 1996; van den
Bergh et al. 1996; Abraham et al. 1994; Mobasher et al. 1996; Clements & Couch 1996); and a distribution of
clumpy star formation, roughly confined to a disk would appear as a
chain-like structure if the disk were viewed edge-on.
![\begin{figure}
\par\includegraphics[width=7.25cm]{MS09391f51.ps}\par\includegraphics[width=7.25cm]{MS09391f52.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg133.gif) |
Figure 14:
The central sub-galaxy, taken at
|
| Open with DEXTER | |
During this phase the global star formation rate fell to roughly 27 ![]() yr-1 after reaching a peak of 35
yr-1 after reaching a peak of 35 ![]() yr-1during the formation of the sub-galaxies. Roughly
yr-1during the formation of the sub-galaxies. Roughly ![]() of the initial
gas mass,
of the initial
gas mass,
![]()
![]() ,
was converted to stellar
material over a timescale of
,
was converted to stellar
material over a timescale of
![]() yr. During this phase
the ratio of gas mass inside of the sub-galaxies to that outside was
roughly 0.2, while the ratio of typical gas densities inside to that
outside was 103. Therefore, the star formation
rate densities inside the sub-galaxies were typically a factor
of
(103)1.5=104.5 higher than those outside: during this
epoch star formation activity was concentrated in the sub-galaxies.
yr. During this phase
the ratio of gas mass inside of the sub-galaxies to that outside was
roughly 0.2, while the ratio of typical gas densities inside to that
outside was 103. Therefore, the star formation
rate densities inside the sub-galaxies were typically a factor
of
(103)1.5=104.5 higher than those outside: during this
epoch star formation activity was concentrated in the sub-galaxies.
![\begin{figure}
\par\includegraphics[width=7.3cm]{MS09391f53.ps}\par\includegraphics[width=7.3cm]{MS09391f54.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg135.gif) |
Figure 15:
The highest density sub-galaxy, taken at
|
| Open with DEXTER | |
By
![]() Gyr disruption of the sub-galaxies by tidal
torques, the progressive circularization of gas and star particle
orbits, and the removal of inhomogeneity in the gas and stellar density
distributions had begun. This was the most dynamically active epoch in the
numerical galaxy's evolution. The tidal disruption of the sub-galaxies
resulted in shocks and linear features in the gas, as well as arcs of
stellar mass around the central sub-galaxy, see Figs. 4
and 5. This stellar mass was formed in the sub-galaxies
before their disruption, and was not associated with the high density
gas found in the shocked regions formed.
Gyr disruption of the sub-galaxies by tidal
torques, the progressive circularization of gas and star particle
orbits, and the removal of inhomogeneity in the gas and stellar density
distributions had begun. This was the most dynamically active epoch in the
numerical galaxy's evolution. The tidal disruption of the sub-galaxies
resulted in shocks and linear features in the gas, as well as arcs of
stellar mass around the central sub-galaxy, see Figs. 4
and 5. This stellar mass was formed in the sub-galaxies
before their disruption, and was not associated with the high density
gas found in the shocked regions formed.
The evolution during this phase was dominated by the merging of
the two most massive and most bound sub-galaxies. Firstly there is the
proto-bulge type object at the centre of the galaxy, see Fig. 14. This sub-galaxy's morphology was that of a miniature
disk galaxy, consisting of a thin gas disk, a thicker stellar disk and
stellar spherical bulge, and contained some of the oldest
stellar mass in the numerical galaxy formed in the early post-collapse
phase. At
![]() Gyr this sub-galaxy had a total mass of
Gyr this sub-galaxy had a total mass of
![]()
![]() ,
a gas fraction of 0.18, and a central
peak gas density of roughly 500
,
a gas fraction of 0.18, and a central
peak gas density of roughly 500 ![]() pc-3. This
object was the least bound of the two sub-galaxies in question,
due to its comparatively large size. The second sub-galaxy, see
Fig. 15, condensed out of the low density gas at
large radii in the proto-disk (see Fig. 4,
pc-3. This
object was the least bound of the two sub-galaxies in question,
due to its comparatively large size. The second sub-galaxy, see
Fig. 15, condensed out of the low density gas at
large radii in the proto-disk (see Fig. 4,
![]() ,
the core/ring gas object), and thus
spent a long time away from disruptive torques early in its evolution,
which allowed the sub-galaxy to become sufficiently bound to evolve
its own stellar component. Subsequent tidal interactions induced the
gas in the sub-galaxy's central regions to very high densities, at
times greater than 103
,
the core/ring gas object), and thus
spent a long time away from disruptive torques early in its evolution,
which allowed the sub-galaxy to become sufficiently bound to evolve
its own stellar component. Subsequent tidal interactions induced the
gas in the sub-galaxy's central regions to very high densities, at
times greater than 103 ![]() pc-3, and correspondingly
high star formation rates. This sub-galaxy was dwarf irregular in
morphology, and obtained a gas ring by disrupting a smaller mass
sub-galaxy while orbiting the central sub-galaxy. During this
encounter, the sub-galaxy underwent significant gas infall into its
central regions, and became very compact. The sub-galaxy's total mass
and gas mass fraction were
pc-3, and correspondingly
high star formation rates. This sub-galaxy was dwarf irregular in
morphology, and obtained a gas ring by disrupting a smaller mass
sub-galaxy while orbiting the central sub-galaxy. During this
encounter, the sub-galaxy underwent significant gas infall into its
central regions, and became very compact. The sub-galaxy's total mass
and gas mass fraction were
![]()
![]() and 0.32
respectively. The eventual merger of this
with the proto-bulge type object resulted in the
destruction of the latter, see the animation to be found at
http://www.astro.cf.ac.uk/pub/Alistair.Nelson/indexgf.html. This event induced
high star formation rates in the central
regions, and spread the stellar component of the central
sub-galaxy into a thick disk structure. The interaction induced
strong shocks and spiral arms in the gas and stellar matter, however the
nucleus of the second sub-galaxy was sufficiently bound to remain intact
during the interaction, and inherited the position of numerical galaxy centre.
Peak gas densities increased by roughly an order of magnitude during
this interaction.
and 0.32
respectively. The eventual merger of this
with the proto-bulge type object resulted in the
destruction of the latter, see the animation to be found at
http://www.astro.cf.ac.uk/pub/Alistair.Nelson/indexgf.html. This event induced
high star formation rates in the central
regions, and spread the stellar component of the central
sub-galaxy into a thick disk structure. The interaction induced
strong shocks and spiral arms in the gas and stellar matter, however the
nucleus of the second sub-galaxy was sufficiently bound to remain intact
during the interaction, and inherited the position of numerical galaxy centre.
Peak gas densities increased by roughly an order of magnitude during
this interaction.
The parameters describing the stellar disk and gas disk evolved
steadily during this phase: scale lengths showing only a slight decrease,
see Figs. 11 and 12. In the gas disk, this reflects
the growth of the disk through infall, and the decrease in the ratio
between the inner and outer disk surface density. As a consequence, star
formation activity was weighted less towards the inner disk regions as the
disk grew, and thus the scale length of the stellar disk increased.
The gas disk central surface density remained roughly constant after
this time. This can be interpreted as a balance between star formation,
which tends to flatten the gas profile, and therefore lowers the central
surface density; and infall of gas onto the disk, which increases the
gas density of the disk. The stellar central surface density
increased during this phase, reflecting the vigorous star formation activity
present in the numerical galaxy disk during this epoch. The parameters
describing the stellar bulge and central gas
regions were highly variable during this phase, since during the merger
of the two largest sub-galaxies these fitting functions used were not
appropriate descriptors of the bulge mass distribution, which accounts for the
glitches at ![]() Gyr in Figs. 11 and 12.
Gyr in Figs. 11 and 12.
The global star formation rate decreased from 27 ![]() yr-1 to 6
yr-1 to 6 ![]() yr-1 over a period of
yr-1 over a period of
![]() yr. This decrease was generally smooth, but
punctuated with small peaks, associated with the tidally induced
star formation activity in the sub-galaxies. This was especially true
during the merger of the two largest sub-galaxies. During this
phase,
yr. This decrease was generally smooth, but
punctuated with small peaks, associated with the tidally induced
star formation activity in the sub-galaxies. This was especially true
during the merger of the two largest sub-galaxies. During this
phase,
![]()
![]() of gas mass was converted
into stellar mass, a similar amount to that converted during the
previous phase, but over a duration of time twice as long.
of gas mass was converted
into stellar mass, a similar amount to that converted during the
previous phase, but over a duration of time twice as long.
By this time, the numerical galaxy had stabilized: any further
variations in morphology or structural parameters were small, and occurred
on long timescales, see Figs. 5 and 6.
The remaining three sub-galaxies orbited on almost circular trajectories
with shallow angles to the plane of the gas disk, thus they were long
lived and difficult to disrupt by tidal interactions. Close tidal
interactions between the central mass concentration and
the remaining sub-galaxies were found to induce periodic and
long-lived spiral structure in the central regions. During the later
stages of this phase, one sub-galaxy survived for 3 orbits of period
roughly 220 Myr, before interacting with another sub-galaxy. This
resulted in the first sub-galaxy being slung-shot out into an
eccentric orbit. The second sub-galaxy adopted an orbit similar to
that of the first, and induced further periodic shocks in
the inner gas disk. This continued for a further 3 orbits of
similar period, i.e. a gravitational exchange event took place,
see Fig. 5 where the two sub-galaxies are at
![]() and
and
![]() ,
and then Fig. 6 where they are at
,
and then Fig. 6 where they are at
![]() and
and
![]() respectively.
respectively.
Shocks were found to be associated with the spiral structure prevalent
during this phase, and were also observed in an adjoining arm between
the sub-galaxy and the central stellar concentration. See Fig. 16, where the change in the direction of the gas flow
post-shock and the induced spiral structure can be clearly seen. The
density contrast between the pre-shock and post-shock gas was found to
be roughly 6. When the simulation was terminated at t
![]() Gyr, Fig. 6, the gas disk had become smoother, although
long-lived spiral structure in the central regions was still present.
Only
Gyr, Fig. 6, the gas disk had become smoother, although
long-lived spiral structure in the central regions was still present.
Only
![]()
![]() of gas remained to fall onto the
disk, and the gas disk had thinned substantially to a height of less
than 200 pc (compare Figs. 4 and 5).
of gas remained to fall onto the
disk, and the gas disk had thinned substantially to a height of less
than 200 pc (compare Figs. 4 and 5).
![\begin{figure}
\par\includegraphics[width=7.7cm]{MS09391f55.ps}\end{figure}](/articles/aa/full/2001/30/aa9391/Timg148.gif) |
Figure 16:
A plot of gas particles with associated velocity vectors,
taken at
|
| Open with DEXTER | |
The parameters describing the gas disk and bulge evolved steadily: the gas disk had a roughly constant central surface density and scale length, while the central regions of the gas profile had a decreasing central surface density and an increasing scale length, see Figs. 11 and 12. This can be interpreted as the central peak in gas surface density simultaneously flattening and decreasing in surface density due to star formation activity preferentially in the central regions. During this phase the parameters describing the stellar disk and bulge evolved systematically with an additional oscillatory behaviour, see Fig. 12. The systematic evolution involved slowly increasing central surface densities and decreasing scale lengths; while the oscillatory behaviour in the central surface densities, more prevalent in the disk parameters, was anti-correlated with those in the scale lengths. Such an evolution can be interpreted physically as a radial pulsation, with a period of roughly 200 Myr, similar to the rotational period in the numerical galaxy disk. The pulsations in the bulge and disk components were only roughly in phase, and were generally more regular in the disk region. It is notable that this behaviour began just after the merger of the two largest sub-galaxies.
The global star formation rate was found to decrease from 6 ![]() yr-1 to 3
yr-1 to 3 ![]() yr-1 over a period of
1 Gyr. During this phase
yr-1 over a period of
1 Gyr. During this phase
![]()
![]() of
gas mass was converted into stellar mass, resulting in a final stellar
mass of
of
gas mass was converted into stellar mass, resulting in a final stellar
mass of
![]()
![]() (46016 star particles were
formed in total), and a total gas fraction of 0.28. As the high star
formation rates within the sub-galaxies decreased
the peak in gas density at their centres, the star formation activity
became much less concentrated within the sub-galaxies and was found
to be more homogeneously spread through the galaxy disk.
(46016 star particles were
formed in total), and a total gas fraction of 0.28. As the high star
formation rates within the sub-galaxies decreased
the peak in gas density at their centres, the star formation activity
became much less concentrated within the sub-galaxies and was found
to be more homogeneously spread through the galaxy disk.
The numerical galaxy's final parameters are summarized in Tables 1 and 2, and the final surface density profiles and rotation curve are shown in Figs. 7 and 8. The tabulated statistics indicate that the numerical galaxy is similar in gas fraction (Roberts & Haynes 1994), star formation rate (Kennicutt 1997), disk size (Roberts & Haynes 1994), bulge size (de Jong 1996a, 1996b), bulge-to-disk ratio (Simien & de Vaucouleurs 1986; de Jong 1996a, 1996b), rotation curve (Casertano & van Gorkom 1991; Persic & Salucci 1995), gas surface density profile (Young & Scoville 1991), and stellar surface density profile (de Jong & van der Kruit 1994) to bright spiral galaxies in the local Universe such as The Galaxy and M 31. Based on this quantitative comparison, the Hubble type of this numerical galaxy may be estimated as Sbc.
| Global Numerical Galaxy Properties | |
| SFR / |
3 |
| 0.28 | |
|
|
5.9 |
|
|
0.8 |
|
|
1.0 |
|
|
0.1 |
| Numerical Galaxy Parameters | |
| Bulge: | |
| 2.3 | |
|
|
0.045 |
|
|
0.3 |
|
|
0.8 |
|
|
56 |
|
|
11 |
|
|
17 |
|
|
0.6 |
|
|
8 |
| Disk: | |
| 10 | |
|
|
0.6 |
|
|
3.8 |
|
|
13 |
|
|
67 |
|
|
100 |
|
|
22 |
|
|
26 |
|
|
0.3 |
| Dark Matter Halo: | |
|
|
0.1 |
|
|
5.2 |
| 18 | |
| 230 |
In summary, the main conclusions of this paper are:
On length scales below the gravitational softening length ![]() and the SPH kernel radius h, the physics of gravity and hydrodynamics
respectively are not resolved. In this simulation all
gravitational features discussed are much larger than
and the SPH kernel radius h, the physics of gravity and hydrodynamics
respectively are not resolved. In this simulation all
gravitational features discussed are much larger than
![]() pc:
proto-galactic clumps (one to several kpc), the stellar bulge (3 kpc),
sub-galaxies (1 to 3 kpc), disks (20 kpc in radius, although the
vertical structure is unresolved), warps (10 kpc), tidal bridges (a few
to several kpc), and spiral arms (20 kpc in length, 1 kpc in thickness).
One feature on a scale less than
pc:
proto-galactic clumps (one to several kpc), the stellar bulge (3 kpc),
sub-galaxies (1 to 3 kpc), disks (20 kpc in radius, although the
vertical structure is unresolved), warps (10 kpc), tidal bridges (a few
to several kpc), and spiral arms (20 kpc in length, 1 kpc in thickness).
One feature on a scale less than ![]() which has been resolved to
the limit of h is the shock front on the inner edge of the spiral
arms. However this a hydrodynamic discontinuity associated with the
transonic flows induced by the non-axisymmetric potential, and in which
gravity does not play a direct role. The shock discontinuity occurs over
a scale less than 100 pc, comparable to the value of h in the
postshock region.
which has been resolved to
the limit of h is the shock front on the inner edge of the spiral
arms. However this a hydrodynamic discontinuity associated with the
transonic flows induced by the non-axisymmetric potential, and in which
gravity does not play a direct role. The shock discontinuity occurs over
a scale less than 100 pc, comparable to the value of h in the
postshock region.
![\begin{figure}
\par\includegraphics[width=8.9cm]{ms09391f56.ps}\\ [2mm]
\includegraphics[width=9cm]{ms09391f57.ps}\vspace{-4mm}
\end{figure}](/articles/aa/full/2001/30/aa9391/Timg157.gif) |
Figure 17: A comparison of the star formation rate and stellar density profiles in the re-run simulations. The re-runs with: low amplitude Poisson noise (same resolution), no initial noise but with one quarter, and one eighth of the number of particles are shown in red, blue and green respectively. The simulation discussed in detail in this paper is shown in black. Due to the high computational cost incurred, the Poisson-noise rerun had to be terminated at 8 Gyr, and thus the stellar surface density profiles shown here were taken at this time. Note that during the epochs in which star formation activity was concentrated within the sub-galaxies, roughly from 6.2 to 6.7 Gyr, there is a significant discrepancy in the lowest resolution simulation. However, these differences have little baring on the equilibrium stellar surface density profiles shown. Before the range of timescales shown, the star formation rates were found to be identical. |
| Open with DEXTER | |
Because h was allowed to evolve freely such that between 30 and 50 neighbours were contained within 2h, a small number of particles at
the centres of the sub-galaxies (less than ![]() )
had very small values
of h. Typical values within the central 200 pc of the highest density
sub-galaxies were of order 60 pc, while the smallest values encountered
were roughly 5 pc. On these sub-
)
had very small values
of h. Typical values within the central 200 pc of the highest density
sub-galaxies were of order 60 pc, while the smallest values encountered
were roughly 5 pc. On these sub-![]() scales gravity is not modeled
accurately, and furthermore, since such scales are of similar order to the
sizes of cold clouds in the ISM, a continuum approximation begins to be
inappropriate. Clearly in these regions the physics of self-gravitational
hydrodynamics is not modeled accurately, but all the structures
relevant to the comparison of these results with observations are of
much larger scale, and are accurately modeled. To support this
assertion a number of re-runs of this simulation
were carried out. In these it was arranged that a typical value of h would
not be smaller than roughly 175 pc by decreasing the total number of
particles from 130000, to 32000 in the first re-run, and to 16000 in
the second re-run. These simulations can be viewed at
http://www.astro.cf.ac.uk/pub/Alistair.Nelson/indexgf.html,
and Fig. 17 shows a comparison of the star formation rates and
final surface density profiles. As a result the
SPH resolution within the central 200 pc of the sub-galaxies was
degraded to typically 150 and 200 pc, with a minimum of 30 and 70 pc
respectively. While the details of the fragmentation process
differ between the simulations, their gross evolution is very similar,
and the resultant numerical galaxies were found to have similar properties and
structural parameters. Differences in star formation rates are most
apparent during the phase in which star formation in the sub-galaxies
dominates the global star formation rate. However the conclusions of
this paper are not dependent on the internal structure of these
sub-galaxies or their detailed star formation rates, which will both
be sensitive to the detailed physics of a multiphase ISM and the
mechanisms of star formation. In light of the
considerable uncertainties with these issues at present, it is
sufficient that these sub-galaxies are recognized as sites of early
star formation, formed as a consequence of the physics of
self-gravitating gas. Thus for the purposes of the analysis
discussed in this paper, such limitations have no effect on the
conclusions presented here.
scales gravity is not modeled
accurately, and furthermore, since such scales are of similar order to the
sizes of cold clouds in the ISM, a continuum approximation begins to be
inappropriate. Clearly in these regions the physics of self-gravitational
hydrodynamics is not modeled accurately, but all the structures
relevant to the comparison of these results with observations are of
much larger scale, and are accurately modeled. To support this
assertion a number of re-runs of this simulation
were carried out. In these it was arranged that a typical value of h would
not be smaller than roughly 175 pc by decreasing the total number of
particles from 130000, to 32000 in the first re-run, and to 16000 in
the second re-run. These simulations can be viewed at
http://www.astro.cf.ac.uk/pub/Alistair.Nelson/indexgf.html,
and Fig. 17 shows a comparison of the star formation rates and
final surface density profiles. As a result the
SPH resolution within the central 200 pc of the sub-galaxies was
degraded to typically 150 and 200 pc, with a minimum of 30 and 70 pc
respectively. While the details of the fragmentation process
differ between the simulations, their gross evolution is very similar,
and the resultant numerical galaxies were found to have similar properties and
structural parameters. Differences in star formation rates are most
apparent during the phase in which star formation in the sub-galaxies
dominates the global star formation rate. However the conclusions of
this paper are not dependent on the internal structure of these
sub-galaxies or their detailed star formation rates, which will both
be sensitive to the detailed physics of a multiphase ISM and the
mechanisms of star formation. In light of the
considerable uncertainties with these issues at present, it is
sufficient that these sub-galaxies are recognized as sites of early
star formation, formed as a consequence of the physics of
self-gravitating gas. Thus for the purposes of the analysis
discussed in this paper, such limitations have no effect on the
conclusions presented here.
Previous authors have commonly constrained h to be greater than
![]() .
However there are a number of reasons why this may not be
the most appropriate procedure, and may result in unwanted consequences.
The particles with
.
However there are a number of reasons why this may not be
the most appropriate procedure, and may result in unwanted consequences.
The particles with
![]() discussed above were also found to have
the smallest timesteps in the simulation, and these timesteps were not
determined by the h dependent hydrodynamic Courant condition (see
Hernquist & Katz 1989, Eq. (2.37)), but rather the timestep
condition determined from accelerations and velocities (see
Katz 1991, Eq. (1)). Thus if h were increased to
discussed above were also found to have
the smallest timesteps in the simulation, and these timesteps were not
determined by the h dependent hydrodynamic Courant condition (see
Hernquist & Katz 1989, Eq. (2.37)), but rather the timestep
condition determined from accelerations and velocities (see
Katz 1991, Eq. (1)). Thus if h were increased to
![]() for all particles which would have
for all particles which would have
![]() in our high
resolution simulation, keeping the same total number of particles, a
large increase in the number of neighbours per SPH summation would
result, and thus a large increase in computational cost.
In the case of this simulation the required CPU time would have
increased from 1.3 to 10 CPU years, while the accuracy and resolution of
the hydrodynamical features would have been degraded.
The purpose of softening gravity is to allow particles to pass each
other on scales less than
in our high
resolution simulation, keeping the same total number of particles, a
large increase in the number of neighbours per SPH summation would
result, and thus a large increase in computational cost.
In the case of this simulation the required CPU time would have
increased from 1.3 to 10 CPU years, while the accuracy and resolution of
the hydrodynamical features would have been degraded.
The purpose of softening gravity is to allow particles to pass each
other on scales less than ![]() without unrealistic two body
effects (Hockney & Eastwood 1989); while SPH kernel radii hare chosen to ensure that a sufficient number of neighbours are included
in summations that stochastic fluctuations are suppressed, and
quantities are evaluated to sufficient accuracy (Monaghan 1992).
Thus the purpose behind h and
without unrealistic two body
effects (Hockney & Eastwood 1989); while SPH kernel radii hare chosen to ensure that a sufficient number of neighbours are included
in summations that stochastic fluctuations are suppressed, and
quantities are evaluated to sufficient accuracy (Monaghan 1992).
Thus the purpose behind h and ![]() are distinctly
different; and independent of whether or not an
are distinctly
different; and independent of whether or not an
![]() condition
is implemented, gravity will be inaccurately modeled on scales less than
condition
is implemented, gravity will be inaccurately modeled on scales less than
![]() .
On these grounds there would appear to be no strong physical
argument for also limiting h to greater than
.
On these grounds there would appear to be no strong physical
argument for also limiting h to greater than ![]() .
.
Furthermore, galaxy-forming simulations in which a
![]() constraint was imposed have revealed that such a constraint can also
affect the large scale characteristics of the resultant numerical
galaxies. When excessively large values of h are used in the central
regions of a numerical galaxy, SPH summations sample over a large range of
velocities. As a result, shear viscosity becomes effective in
transporting angular momentum radially outwards and gas mass inwards,
and the numerical galaxy becomes unphysically centrally concentrated. It
was also found that such a constraint on h results in inaccuracies in
all quantities calculated using SPH summations. For example, densities
and pressure forces were found to be as much as 100 times smaller when
h was constrained. As demonstrated in the simulations discussed here,
such problems can be avoided by a) not imposing such a criteria on h,
and b) using a sufficiently high number of particles.
constraint was imposed have revealed that such a constraint can also
affect the large scale characteristics of the resultant numerical
galaxies. When excessively large values of h are used in the central
regions of a numerical galaxy, SPH summations sample over a large range of
velocities. As a result, shear viscosity becomes effective in
transporting angular momentum radially outwards and gas mass inwards,
and the numerical galaxy becomes unphysically centrally concentrated. It
was also found that such a constraint on h results in inaccuracies in
all quantities calculated using SPH summations. For example, densities
and pressure forces were found to be as much as 100 times smaller when
h was constrained. As demonstrated in the simulations discussed here,
such problems can be avoided by a) not imposing such a criteria on h,
and b) using a sufficiently high number of particles.
No initial distribution of noise was used in the simulation discussed
here, however it is more appropriate to consider this simulation as
having a minimal amplitude of initial noise. The noisy distribution of
particles which evolved in this simulation, see Fig. 1, is an
artificial artefact of numerical inaccuracies in the SPH and Treecode
method, propagated in time. Such small random velocities play the same
role as a Poisson spectrum of noise with low amplitude. Note that all
numerical methods are subject to such truncation errors, although the
effects of such errors are usually hidden by the initial non-regular
particle distribution. A number of re-runs were carried out to gauge the
importance of the spectrum of noise on the conclusions of this
paper. The simulation was repeated with each particle displaced from
its grid position a small amount in each Cartesian direction, chosen
randomly from a Gaussian with zero mean and standard deviation one tenth
of the grid separation. The resultant numerical galaxy was found to
evolve in a similar fashion to that discussed here, and the equilibrium
structural parameters were found to differ by no more than ![]() .
See
Fig. 17 and the animations
http://www.astro.cf.ac.uk/pub/Alistair.Nelson/indexgf.html.
Thus these re-run simulations show that the conclusions of this paper
are not sensitive to the initial distribution of artificial noise,
provided it does not have an amplitude as large as that deduced from
applying a CDM power spectrum on this scale (see below).
.
See
Fig. 17 and the animations
http://www.astro.cf.ac.uk/pub/Alistair.Nelson/indexgf.html.
Thus these re-run simulations show that the conclusions of this paper
are not sensitive to the initial distribution of artificial noise,
provided it does not have an amplitude as large as that deduced from
applying a CDM power spectrum on this scale (see below).
It is not straightforward to compare quantitively this simulation with those published previously, since there are many differences in the implementation of the physics of the ISM and star formation, and the initial configuration of small scale noise in the particle distribution. However, even with these differences, the general evolution and star formation history of this simulation is very similar to those presented by, for example, Katz & Gunn (1991), Katz (1992), and Steinmetz & Müller (1994, 1995), which could also have been well described by the five phase paradigm of galaxy formation. There are three main differences in evolution between these simulations and the evolution of that analysed here. Firstly, the simulations of Katz (1992) and Steinmetz & Müller (1994, 1995) formed significant sub-structure in both the gas and dark matter particle distributions during the expansion and collapse of the proto-galaxy (phase I and II), which resulted in a higher star formation rate than in the simulation analysed here. Secondly, this sub-structure resulted in sub-galaxies with associated dark matter halos, and sub-galaxies which have orbits out of the plane of the forming disk galaxy. However, Katz (1992) reports that such sub-galaxies lose their dark matter halos in the ensuing global collapse. Therefore these evolved sub-galaxies can be considered as essentially the same class of object as the sub-galaxies formed in the simulation analysed here, although their formation mechanism is slightly different. It is notable that the sizes and masses of these sub-galaxies are similar to those found in the minor dwarf satellites of The Local Group (Hodge 1994). Thirdly, this increase in the level of inhomogeneity in comparison to the simulation discussed here results in a more asymmetric potential well. Therefore the galaxy disks are commonly found to form with their angular momentum vectors significantly displaced in direction from the angular momentum vector of their dark matter halo, and have significant warps. In contrast, the low level of inhomogeneity in this simulation produced a galaxy whose dark matter halo and galaxy disk angular momentum vectors were almost aligned: the numerical galaxy disk in this simulation is oriented, to within a few degrees, perpendicular to the initial axes of rotation, although weak warps are observable in the gas disk, see Fig. 5.
Unlike previous simulations, the numerical galaxy discussed here was not found to be deficient in angular momentum, did not have an overabundance of dwarf companions, and did not have a rotation curve inconsistent with observations. All three of these results are due to the minimal level of initial inhomogeneity used. While angular momentum was transferred from the gas to the dark matter component during collapse, see Fig. 10, this effect was not catastrophic. This may indicate that (in addition to ensuring that h is not too large, to avoid artificial angular momentum transfer) decreasing the amplitude of noise on sub-galactic, or even possibly sub-cluster, scales (in comparison to the accepted amplitudes inferred for CDM power-spectrum) is necessary to avoid a high degree of fragmentation and transfer of angular momentum early in a proto-galactic collapse. As was suggested in the introduction, the origins of such a modification to the CDM power spectrum may lie in the importance of the dissipational physics of the pre-galactic gas on these scales; physical processes missing from the CDM power spectrum. Galaxies are intrinsically dissipational objects: it is natural to suppose that the initial conditions from which they formed also had a strongly dissipational element to their makeup.
A number of studies have focused on the importance of the detailed chain of thermodynamic processes at play in a multiphase ISM (Yepes et al. 1997; Hultman & Pharasyn 1999), and the role of energy feedback from stars (Navarro & White 1993; Springel 2000). The isothermal model used here does not try to explicitly model these processes, but implicitly assumes that when averaged over length scales of order h and larger, dissipative losses in the ISM are balanced by energy input from stars and supernovae and compressional heating. Thus this model is most appropriately considered as a zeroth order approximation to these more sophisticated prescriptions. While undoubtedly the detailed balance of energy exchange in the ISM does play a role in determining galaxy structure, length scales associated with such processes are of the order of 1 kpc and less, and the gross structural components of a galaxy have characteristic length scales of a few to 20 kpc. Thus it is tenable that the formation of these components is well modeled by the isothermal assumption, and the results of this paper confirm this.
Finally, the mechanism of bulge formation suggested by the evolution and
formation of the stellar bulge component in this simulation
provides a natural, robust manner in which such components may form. The
oscillation of cells of gas about the plane of the forming galaxy disk
may be expected to occur to some extent irrespective of the specific
details of the ISM at that time. Theories forwarded to date on
the origin of the bulge component in spiral galaxies fall into three
broad classes: hypotheses which question the differences between bulge
components and other galaxian features such as spiral arms and bars
(Kormendy 1993; Wyse et al. 1997); bulge formation by the
merger of stellar and gaseous material with an existing galaxy disk
(Tremaine et al. 1975; Kauffmann 1996); and bulge growth by secular
evolution of a galaxy disk (Hasan & Norman 1990; Courteau et al. 1996; Noguchi 2000). In contrast to these bulge
formation scenarios, the mechanism proposed here is an intrinsic part of
the process of forming a galaxy, and is a natural result of the core
gravitational and dissipational physics. During the merger of the
sub-galaxies (phase IV), it was found that the bulge did grow in a
secular fashion similar to that suggested by Noguchi
(2000). However this was not the principal
mechanism by which the bulge component formed. At the end of the
simulation, only ![]() of the stellar mass within 3 kpc
of the centre of the numerical galaxy had actually fallen in from
outside of this radius; the rest had formed in situ.
of the stellar mass within 3 kpc
of the centre of the numerical galaxy had actually fallen in from
outside of this radius; the rest had formed in situ.
Acknowledgements
The authors would like to thank Profs. C. Frenk, P. Hut, and M. Noguchi for supporting the publication of this paper, and Prof. C. Frenk for helpful suggestions on its revision. PRW thanks the Particle Physics and Astronomy Research Council of the UK for the award of a studentship, and The Royal Society and the Japanese Society for the Promotion of Science for the award of a Research Fellowship.