at 1.2
A&A 374, 871-877 (2001)
DOI: 10.1051/0004-6361:20010777
D. Reimers 1 - R. Baade 1 - H.-J. Hagen1 - S. Lopez2
1 - Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112, 21029 Hamburg, Germany
2 - Departamento de Astronomia, Universidad de Chile, Casilla 36-D, Santiago, Chile
Received 7 March 2001 / Accepted 25 May 2001
Abstract
STIS Echelle observations at a resolution of
![]() and UVES/VLT spectroscopy at a resolution of
and UVES/VLT spectroscopy at a resolution of
![]() of the luminous QSO HE 0515-4414 (
of the luminous QSO HE 0515-4414 (
![]() ,
B = 15.0) reveal four intervening O VI absorption
systems in the redshift range
,
B = 15.0) reveal four intervening O VI absorption
systems in the redshift range
![]() (1.38503, 1.41601, 1.60175, 1.67359). In addition, two associated
systems at
z = 1.69707 and
z = 1.73585 are present. Noteworthy
is an absorber at z = 1.385 with
(1.38503, 1.41601, 1.60175, 1.67359). In addition, two associated
systems at
z = 1.69707 and
z = 1.73585 are present. Noteworthy
is an absorber at z = 1.385 with
![]() and strong O VI (N(O VI)/N(H I)
and strong O VI (N(O VI)/N(H I)
![]() 1) and C IV doublets, while a nearby much
stronger Ly
1) and C IV doublets, while a nearby much
stronger Ly ![]() absorber (log
absorber (log
![]() ,
,
![]() )
does not reveal any heavy element
absorption. For the first time, high resolution observations allow one
to measure radial velocities of H I, C IV and
O VI simultaneously in several absorption systems (1.385,
1.674, 1.697) with the result that significant velocity
differences (up to
)
does not reveal any heavy element
absorption. For the first time, high resolution observations allow one
to measure radial velocities of H I, C IV and
O VI simultaneously in several absorption systems (1.385,
1.674, 1.697) with the result that significant velocity
differences (up to
![]() ,
are observed between
H I and O VI, while smaller differences (up to
,
are observed between
H I and O VI, while smaller differences (up to
![]() )
are seen between C IV and
O VI. We tentatively conclude that H I, O VI,
and C IV are not formed in the same volumes and that
therefore conclusions on ionization mechanisms are not possible
from the observed column density ratios O VI/H I or
O VI/C IV. The number density of O VI
absorbers with
)
are seen between C IV and
O VI. We tentatively conclude that H I, O VI,
and C IV are not formed in the same volumes and that
therefore conclusions on ionization mechanisms are not possible
from the observed column density ratios O VI/H I or
O VI/C IV. The number density of O VI
absorbers with
![]() mÅ is
mÅ is
![]() ,
roughly a factor of 5 less than that found by
Tripp et al. (2000) at low redshift. However, this number is
uncertain and further lines of sight will be probed in the next
HST cycle. An estimate of the cosmological mass-density of the
O VI-phase yields
,
roughly a factor of 5 less than that found by
Tripp et al. (2000) at low redshift. However, this number is
uncertain and further lines of sight will be probed in the next
HST cycle. An estimate of the cosmological mass-density of the
O VI-phase yields
![]() for
for
![]() and an assumed
ionization fraction O VI/O = 0.2. It should be noted that
this result is subject to large systematic errors. This
corresponds to an increase by roughly a factor of 15 between
and an assumed
ionization fraction O VI/O = 0.2. It should be noted that
this result is subject to large systematic errors. This
corresponds to an increase by roughly a factor of 15 between
![]() (this work) and the value found by Tripp et al. (2000) at
(this work) and the value found by Tripp et al. (2000) at
![]() ,
if the same oxygen abundance
,
if the same oxygen abundance
![]() is assumed. Agreement with the simulations by Davé
et al. (2001) can be obtained, if the oxygen abundance increases
by a factor of
is assumed. Agreement with the simulations by Davé
et al. (2001) can be obtained, if the oxygen abundance increases
by a factor of ![]() 3 over the same redshift interval.
3 over the same redshift interval.
Key words: cosmology: observations - intergalactic medium -
quasars: absorption lines -
quasars: individual: HE 0515-4414
Recent observations of intervening O VI absorbers in
HST-STIS Echelle spectra of bright, low redshift QSOs have
provided strong evidence that in the local universe a considerable
fraction of baryonic matter might be "hidden'' in a warm (![]()
![]() K)
intergalactic medium (Savage et al. 1998; Tripp et al. 2000;
Tripp & Savage 2000). This observation is in
accordance with models of hierarchical structure formation by Cen
& Ostriker (1999) and Davé et al. (2001) which predict that a
considerable fraction of all baryons reside in a warm-hot phase of
the intergalactic medium (WHIM) shock-heated to temperatures of
K)
intergalactic medium (Savage et al. 1998; Tripp et al. 2000;
Tripp & Savage 2000). This observation is in
accordance with models of hierarchical structure formation by Cen
& Ostriker (1999) and Davé et al. (2001) which predict that a
considerable fraction of all baryons reside in a warm-hot phase of
the intergalactic medium (WHIM) shock-heated to temperatures of
![]() K. The same models predict that the fraction of
baryons residing in this WHIM increases strongly with decreasing
redshift from less than 5% at z = 3 to 30-40% at z =
0. Can this prediction be verified or disproved by observations,
or can observations even impose constraints on the models? This
appears difficult for various reasons. First of all, the WHIM is
difficult to detect (cf. Davé et al. 2001), both as diffuse
X-ray emission of the hotter parts or in absorption through the
O VI doublet. In addition, the temperature distribution of
the WHIM varies with redshift so that a complete census would
require the detection of all components as a function of redshift.
The warm O VI component has the additional complication
that both the oxygen abundance and the ionization process cannot
be determined from O VI observations alone. While at low
redshift (z < 0.3) collisional ionization is the most probable
process since the ionizing extragalactic UV background is diluted,
O VI can be produced easily by photoionization at redshifts
K. The same models predict that the fraction of
baryons residing in this WHIM increases strongly with decreasing
redshift from less than 5% at z = 3 to 30-40% at z =
0. Can this prediction be verified or disproved by observations,
or can observations even impose constraints on the models? This
appears difficult for various reasons. First of all, the WHIM is
difficult to detect (cf. Davé et al. 2001), both as diffuse
X-ray emission of the hotter parts or in absorption through the
O VI doublet. In addition, the temperature distribution of
the WHIM varies with redshift so that a complete census would
require the detection of all components as a function of redshift.
The warm O VI component has the additional complication
that both the oxygen abundance and the ionization process cannot
be determined from O VI observations alone. While at low
redshift (z < 0.3) collisional ionization is the most probable
process since the ionizing extragalactic UV background is diluted,
O VI can be produced easily by photoionization at redshifts
![]() and has been observed to be ubiquitous in the low-density
IGM (Schaye et al. 2000). On the other hand O VI is not
expected to be produced by photoionization for
and has been observed to be ubiquitous in the low-density
IGM (Schaye et al. 2000). On the other hand O VI is not
expected to be produced by photoionization for ![]() since
the reionization of He II is incomplete (Reimers et al.
1997; Heap et al. 2000) and the IGM therefore opaque to photons
with energies above 4 Rydberg. The intermediate redshift
range remains which for z < 1.9 requires high-resolution UV-spectroscopy
of a bright, high-redshift QSO. In this paper, we present combined
high-resolution HST/STIS observations of O VI absorption
supplemented by ESO-VLT/UVES spectroscopy of the accompanying
H I and C IV lines in the brightest known
intermediate redshift QSO HE 0515-4414 (
since
the reionization of He II is incomplete (Reimers et al.
1997; Heap et al. 2000) and the IGM therefore opaque to photons
with energies above 4 Rydberg. The intermediate redshift
range remains which for z < 1.9 requires high-resolution UV-spectroscopy
of a bright, high-redshift QSO. In this paper, we present combined
high-resolution HST/STIS observations of O VI absorption
supplemented by ESO-VLT/UVES spectroscopy of the accompanying
H I and C IV lines in the brightest known
intermediate redshift QSO HE 0515-4414 (
![]() ,
B =
15.0) discovered by the Hamburg/ESO Survey (Reimers et al.
1998). The data have been taken mainly with the aim of studing the
evolution of the Ly
,
B =
15.0) discovered by the Hamburg/ESO Survey (Reimers et al.
1998). The data have been taken mainly with the aim of studing the
evolution of the Ly ![]() forest and its metal content in the
range z = 1 to 1.7. In this first paper we concentrate on the
intervening O VI absorption.
forest and its metal content in the
range z = 1 to 1.7. In this first paper we concentrate on the
intervening O VI absorption.
HE 0515-4414 was observed with STIS for 31500 s on three occasions
between January 31 and February 2, 2000 with the medium resolution
NUV echelle mode (E230M) and a
![]() aperture which
provides a resolution of
aperture which
provides a resolution of ![]() 30000 (
30000 (
![]() ). We used the HST pipeline data with an additional
correction for inter-order background correction (Rosa, private
communication). The spectrum covers the range between 2279Å and
). We used the HST pipeline data with an additional
correction for inter-order background correction (Rosa, private
communication). The spectrum covers the range between 2279Å and ![]() 3080Å. The coverage at the red end guarantees
overlap with the UVES spectra which extend shortwards to
3080Å. The coverage at the red end guarantees
overlap with the UVES spectra which extend shortwards to ![]() 3050Å.
3050Å.
The spectra were extracted using an algorithm that attempts to reduce
the statistical noise to a minimum. After bias-subtracting and
flat-fielding of the individual CCD frames, the seeing profiles were
fitted with a Gaussian in two steps. In a first step the three
parameters of the Gaussian - width, amplitude, and offset from the
previously defined orders - were unconstrained; in the second step
only the amplitudes were allowed to vary, with width and offset held
fixed at values found by a
![]() -clipping fit along the
dispersion direction to the values obtained in the first step. Flux
values were assigned with a variance according to the Poisson
statistics and the read-out noise, while cosmic-ray shots were
assigned with infinite variances. Thus, the extraction procedure
recovers the total count number even at wavelengths where the spatial
profile is partially modified by cosmic-ray hits.
-clipping fit along the
dispersion direction to the values obtained in the first step. Flux
values were assigned with a variance according to the Poisson
statistics and the read-out noise, while cosmic-ray shots were
assigned with infinite variances. Thus, the extraction procedure
recovers the total count number even at wavelengths where the spatial
profile is partially modified by cosmic-ray hits.
The extracted spectra were wavelength calibrated using as reference Th-Ar spectra taken after each science exposure. All wavelength solutions typically were accurate to better than 1/10 pixel. The wavelength values were converted to vacuum heliocentric values and each spectrum of a given instrumental configuration was binned onto a common linear wavelength scale (of typically 0.04 Å per pixel). Finally, the reduced spectra were added, weighting by the inverse of the flux variances.
Our analysis was carried out using a multiple line fit procedure to
determine the parameters
![]() (line center wavelength),
N (column density), and b (line broadening velocity)
for each absorption component. We have written a FORTRAN program based on the
Levenberg-Marquardt algorithm to solve this nonlinear regression problem
(see, e.g., Bevington & Robinson 1992). We have included additional
parameters describing the local continuum curvature by a low order
Legendre polynomial. A free floating continuum is a prerequisite for an adequate
profile decomposition in the case of complex line ensembles.
(line center wavelength),
N (column density), and b (line broadening velocity)
for each absorption component. We have written a FORTRAN program based on the
Levenberg-Marquardt algorithm to solve this nonlinear regression problem
(see, e.g., Bevington & Robinson 1992). We have included additional
parameters describing the local continuum curvature by a low order
Legendre polynomial. A free floating continuum is a prerequisite for an adequate
profile decomposition in the case of complex line ensembles.
To improve the numerical efficiency we have to provide adequate initial parameters.
In some cases the success of the fitting depends on good starting parameters, since
the algorithm tends to converge to the nearest, not necessarily global,
minimum of the chi-square merit function. A first approximation can be found neglecting the
instrumental profile and
converting the flux profile into apparent optical depths using the relation
![\begin{displaymath}\tau_{\rm a}(\lambda) = \ln [F_{\rm c}(\lambda)/F_{\rm obs}(\lambda)]\,,
\end{displaymath}](/articles/aa/full/2001/30/aa1253/img28.gif) |
(1) |
Having obtained first-guess parameters we proceed with Doppler
profile fitting using artificial test lines with z=0 and f=1,
where f is the oscillator strength. It can be shown that most
Voigt profiles are well represented by the purely velocity
broadened Doppler core. The size of the fit region depends on the
complexity and extent of the absorption line ensembles. Indeed,
the number of free parameters should be less than 100 to preserve
the numerical efficiency. One specific characteristic of our
technique is the simultaneous continuum normalization which can
reconstruct the true continuum level even in cases, where the
background is hidden by numerous lines. The multi component
profile is the convolution of the intrinsic spectrum and the
instrumental spread function
![]() :
:
![\begin{displaymath}F(\lambda) = P(\Delta\lambda) \otimes \left\{ F_{\rm c}(\lamb...
...rod_i
\exp[-\tau_i(\lambda,\lambda_{\rm c},N,b)] \right\}\cdot
\end{displaymath}](/articles/aa/full/2001/30/aa1253/img34.gif) |
(2) |
After line identification the parameters of the test lines can be transformed to the actual redshift and
oscillator strength. However, the contribution of unknown profile components can still be considered
using the test line results. A final Voigt profile fit with all identified components includes the
simultaneous multiplet treatment, keeping the redshift, column density, and line width the same
during the chi-square minimization.
The upper limit of the column densities of non-detected lines is estimated assuming a ![]() significance level for the equivalent width.
significance level for the equivalent width.
We searched for O VI lines associated with known Ly ![]() and Ly
and Ly ![]() absorbers. Therefore, as a starting point, we tried to identify
all Ly
absorbers. Therefore, as a starting point, we tried to identify
all Ly ![]() lines. Line identification and the analysis of the
Ly
lines. Line identification and the analysis of the
Ly ![]() forest will be presented in some detail in a later
paper. At the resolution of
forest will be presented in some detail in a later
paper. At the resolution of ![]() 30000 (STIS) and
30000 (STIS) and ![]() 50000 (UVES),
narrow metal lines can usually be distinguished
easily from hydrogen lines. In all Ly
50000 (UVES),
narrow metal lines can usually be distinguished
easily from hydrogen lines. In all Ly ![]() absorption systems
with column densities log
absorption systems
with column densities log
![]() 13.5 we searched for metal
lines, in particular for O VI, C IV, N V,
Si IV, C III, N III. In a first step, all
lines within
13.5 we searched for metal
lines, in particular for O VI, C IV, N V,
Si IV, C III, N III. In a first step, all
lines within
![]() were considered to be
plausibly associated with the Ly
were considered to be
plausibly associated with the Ly ![]() /Ly
/Ly ![]() systems.
Within this selection criterium we have found 6 systems with
probable O VI absorption, listed in Table 1. Due to the
moderate S/N ratio of the STIS spectra (between 10 and 20 per
resolution element) the detection limit of O VI is
estimated to lie between
systems.
Within this selection criterium we have found 6 systems with
probable O VI absorption, listed in Table 1. Due to the
moderate S/N ratio of the STIS spectra (between 10 and 20 per
resolution element) the detection limit of O VI is
estimated to lie between
![]() at the lower limit of the
z range and
at the lower limit of the
z range and
![]() near the quasar.
near the quasar.
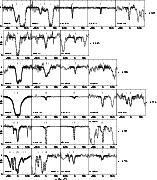 |
Figure 1: Selected absorption line profiles of systems with O VI detection. The normalized flux is plotted vs. rest-frame velocity of the hydrogen main component. Long tick marks indicate the position of the primary lines, while short tick marks indicate additional absorption components. It should be noted that some profile ensembles contain lines which do not belong to the same absorption system. The dotted curves represent our fit models. |
| Open with DEXTER | |
With the present STIS spectra of HE 0515-4414 the redshift range
![]() has been covered for the first time at
sufficiently high resolution to undertake a sensitive search for
O VI absorbers. We have detected 6 O VI systems. Two
of them (z = 1.697, 1.736) are either associated with the QSO or
in the proximity zone of the extremely luminous QSO. The system z
= 1.416 is marginal, since only the 1031Å line is detected.
Including the latter, we have 4 detections in the range z = 1.21to 1.67 which yield a number density of O VI absorbers with
has been covered for the first time at
sufficiently high resolution to undertake a sensitive search for
O VI absorbers. We have detected 6 O VI systems. Two
of them (z = 1.697, 1.736) are either associated with the QSO or
in the proximity zone of the extremely luminous QSO. The system z
= 1.416 is marginal, since only the 1031Å line is detected.
Including the latter, we have 4 detections in the range z = 1.21to 1.67 which yield a number density of O VI absorbers with
![]() 25mÅ of
25mÅ of
![]() .
Compared with the findings by Tripp et al. (2000) of
.
Compared with the findings by Tripp et al. (2000) of
![]() at
at
![]() ,
the number density at
,
the number density at
![]() is roughly a factor of 5 lower. Tripp et al.
(2000) compared their finding of a high number density of
weak O VI absorbers (
is roughly a factor of 5 lower. Tripp et al.
(2000) compared their finding of a high number density of
weak O VI absorbers (
![]() 30 mÅ) in
H 1821+643 and PG 0953+415 with other classes of absorbers and
found that the weak O VI number density is more comparable
to that of the low z weak Ly
30 mÅ) in
H 1821+643 and PG 0953+415 with other classes of absorbers and
found that the weak O VI number density is more comparable
to that of the low z weak Ly ![]() absorbers - which have
absorbers - which have
![]() for
for
![]() 50mÅ - than to other types of metal absorbers like Mg II. In
HE 0515-4414 we have at least 42 Ly
50mÅ - than to other types of metal absorbers like Mg II. In
HE 0515-4414 we have at least 42 Ly ![]() systems (the exact
number being unknown due to the line blending problem) with
systems (the exact
number being unknown due to the line blending problem) with
![]() 50mÅ in the range
50mÅ in the range
![]() which yields roughly
which yields roughly
![]()
![]() . Among these, roughly half of them are strong,
saturated Ly
. Among these, roughly half of them are strong,
saturated Ly ![]() lines with a detected Ly
lines with a detected Ly ![]() line.
Again, while our STIS spectrum of HE 0515-4414 confirms the number
density of Ly
line.
Again, while our STIS spectrum of HE 0515-4414 confirms the number
density of Ly ![]() absorbers found previously (see Weymann et al.
1998), the number of O VI absorbers with
absorbers found previously (see Weymann et al.
1998), the number of O VI absorbers with
![]() mÅ is lower than the number of Ly
mÅ is lower than the number of Ly ![]() absorbers
with
absorbers
with
![]() mÅ by a factor of 10. It is
noteworthy that, except the z = 1.674 system, O VI is
detected in lower column density Ly
mÅ by a factor of 10. It is
noteworthy that, except the z = 1.674 system, O VI is
detected in lower column density Ly ![]() absorbers (log
absorbers (log
![]() ). Following the calculations by Tripp et al.
(2000) and earlier work by Storrie-Lombardi et al. (1996) and
Burles & Tytler (1996), the mean cosmological mass-density of
O VI absorbers can be written in units of the critical
density
). Following the calculations by Tripp et al.
(2000) and earlier work by Storrie-Lombardi et al. (1996) and
Burles & Tytler (1996), the mean cosmological mass-density of
O VI absorbers can be written in units of the critical
density
![]() as
as
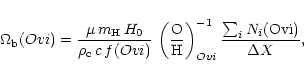 |
(3) |
Over the redshift interval z = 1.21 to z = 1.67 we have
![]() for
q0 = 1/2.
for
q0 = 1/2.
![]() is
is
![]() (Table 1).
Assuming
(Table 1).
Assuming
![]() ,
following Tripp et al. (2000)
and Tripp & Savage (2000), which is close to the maximum for both
collisional ionization and photoionization, we obtain a lower
limit
,
following Tripp et al. (2000)
and Tripp & Savage (2000), which is close to the maximum for both
collisional ionization and photoionization, we obtain a lower
limit
![]() (O VI)
(O VI)
![]()
![]() .
The only reliably
measured heavy element abundances at
.
The only reliably
measured heavy element abundances at
![]() are from
DLAs. Typically the metal abundance (e.g. from Zn) is 1/10 solar
(Pettini et al. 1999; Vladilo et al. 2000). There is, however,
no guarantee that these abundances apply also to the O VI
absorbers among the low column density systems. Assuming 1/10
solar for the oxygen abundance, we have
are from
DLAs. Typically the metal abundance (e.g. from Zn) is 1/10 solar
(Pettini et al. 1999; Vladilo et al. 2000). There is, however,
no guarantee that these abundances apply also to the O VI
absorbers among the low column density systems. Assuming 1/10
solar for the oxygen abundance, we have
![]() .
With the same
assumptions Tripp et al. (2000) derived a value
.
With the same
assumptions Tripp et al. (2000) derived a value
![]() .
Using a somewhat different formalism for
the derivation of
.
Using a somewhat different formalism for
the derivation of
![]() ,
namely Eq. (6) from
Tripp & Savage (2000), we get with the same assumptions
,
namely Eq. (6) from
Tripp & Savage (2000), we get with the same assumptions
![]() (O VI)
(O VI)
![]() .
Both from the number counts of the O VI
systems and the estimate of the mean O VI density the
unavoidable conclusion seems to be that at
.
Both from the number counts of the O VI
systems and the estimate of the mean O VI density the
unavoidable conclusion seems to be that at
![]() ,
the
baryon content of the O VI phase contains a factor of
,
the
baryon content of the O VI phase contains a factor of ![]() less material than at
less material than at
![]() .
.
Our results on O VI absorbing clouds in HE 0515-4414 can be summarized as follows:
Our finding, that the O VI phase at
![]() contains a factor of
contains a factor of ![]() less material than at z = 0.21,
provided the O VI/O ratio and the oxygen abundance are
similar, appears to be inconsistent with the simulations of Davé
et al. (2001) who predict an increase of the mass-fraction of
baryons in the warm-hot phase of the IGM by at most a factor of 4
between z = 1.5 and 0.2. An increase in the mean oxygen
abundance in the low density IGM by a factor of
less material than at z = 0.21,
provided the O VI/O ratio and the oxygen abundance are
similar, appears to be inconsistent with the simulations of Davé
et al. (2001) who predict an increase of the mass-fraction of
baryons in the warm-hot phase of the IGM by at most a factor of 4
between z = 1.5 and 0.2. An increase in the mean oxygen
abundance in the low density IGM by a factor of ![]() 3 over the
same redshift range would restore consistency with the theoretical
predictions. However, at present we do not see a possibility to
test this hypothesis. Furthermore, as long as we do not understand
the ionization to O VI quantitatively, the fractional
ionization O VI/O might vary between z = 1.5 and 0.2.
Finally, our result is still debatable due to small number
statistics. More lines of sight, both at low and intermediate
redshift, have to be probed.
3 over the
same redshift range would restore consistency with the theoretical
predictions. However, at present we do not see a possibility to
test this hypothesis. Furthermore, as long as we do not understand
the ionization to O VI quantitatively, the fractional
ionization O VI/O might vary between z = 1.5 and 0.2.
Finally, our result is still debatable due to small number
statistics. More lines of sight, both at low and intermediate
redshift, have to be probed.
Acknowledgements
This work has been supported by the Verbundforschung of the BMBF/DLR under Grant No. 50 OR 99111. S.L. acknowledges financial support by FONDECYT grant Nand by the Deutsche Zentralstelle für Arbeitsvermittlung.