A&A 374, 1150-1160 (2001)
DOI: 10.1051/0004-6361:20010736
Pseudo-Schwarzschild description of transonic spherical accretion
onto compact objects
Tapas K. Das
1 -
A. Sarkar 2
1 - Inter University
Centre For Astronomy And Astrophysics, Post Bag 4 Ganeshkhind, Pune 411 007,
India
2 -
National Centre For Radio Astrophysics, TIFR, Post Bag 3 Ganeshkhind, Pune 411 007, India
Received 6 March 2001/ Accepted 9 May 2001
Abstract
A number of "modified'' Newtonian potentials of various forms
are available in the literature
which accurately approximate some general relativistic effects important
for studying accretion discs around a Schwarzschild black hole.
Such potentials may be called "pseudo-Schwarzschild'' potentials because they nicely
mimic the space-time around a non-rotating/slowly
rotating compact object.
In this paper, we examine the validity of the
application of some of these potentials to study the spherically symmetric,
transonic, hydrodynamic accretion onto a Schwarzschild black hole.
By comparing the values of various dynamical and thermodynamic accretion parameters
obtained for flows using these potentials with full general relativistic
calculations, we have shown that though the potentials
discussed in this paper were originally proposed to mimic the
relativistic effects manifested in disc accretion,
it is quite reasonable to use most of the
potentials in studying various dynamical as well as thermodynamic
quantities
for spherical accretion to compromise between the ease of
handling of a Newtonian description of gravity and the realistic situations
described by complicated general relativistic calculations. Also we have shown that
depending on the chosen regions of parameter space
spanned by specific energy  and adiabatic index
and adiabatic index
 of the flow, one potential may have more
importance than another and we could identify which
potential is the best approximation for full general relativistic
flow in Scwarzschild space-time for particular
values of
of the flow, one potential may have more
importance than another and we could identify which
potential is the best approximation for full general relativistic
flow in Scwarzschild space-time for particular
values of  and
and  .
.
Key words: accretion, accretion discs - black hole physics - hydrodynamics
Stationary, spherically symmetric and transonic hydrodynamic accretion of
adiabatic fluid on to a gravitating astrophysical object at rest was
studied in a seminal paper by Bondi (1952) using purely Newtonian Potential
and by including the pressure effect of the accreting material. Later,
Michel (1972) discussed fully general relativistic polytropic accretion on
to a Schwarzschild black hole by formulating the governing equations for steady
spherical flow of a perfect fluid in the Schwarzschild metric. Following
Michel's relativistic generalization of Bondi's treatment,
Begelman (1978) discussed some aspects of the critical (sonic) points of the flow
for such
an accretion. Using an unrelaxed mono-energetic particle distribution and
assuming the fact that the relaxation time of such a particle distribution
is very long compared to the typical flow time scale or dynamical time
scale of steady accretion on to black holes, Blumenthal & Mathews (1976)
developed a model where the connection between the nonrelativistic to the
relativistic regime of the spherically accreting material could be
established. Taking the fully ionized one-temperature (
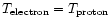 )
hydrogen
gas (governed by an exact relativistic equation of state) to be the
fundamental constituent of the accreting material, Brinkmann (1980) treated
spherically symmetric stationary accretion in Schwarzschild space time and
showed that the temperature of accreting material at the Schwarzschild radius
is one order of magnitude smaller than the flow temperature
obtained by using
a simple polytropic equation of state.
Recently, Malec (1999) provided the solution for general
relativistic spherical accretion with and without back reaction and showed
that relativistic effects enhance mass accretion when back reaction is
neglected.
)
hydrogen
gas (governed by an exact relativistic equation of state) to be the
fundamental constituent of the accreting material, Brinkmann (1980) treated
spherically symmetric stationary accretion in Schwarzschild space time and
showed that the temperature of accreting material at the Schwarzschild radius
is one order of magnitude smaller than the flow temperature
obtained by using
a simple polytropic equation of state.
Recently, Malec (1999) provided the solution for general
relativistic spherical accretion with and without back reaction and showed
that relativistic effects enhance mass accretion when back reaction is
neglected.
Meanwhile, the theory of the
accretion disc found prior importance because of the
fact that disc accretion describes more realistic astrophysical situations
found in nature. The beginning of modern accretion disc physics is
traditionally attributed to the two classical articles by Shakura & Sunyaev
(1973) and Novikov & Thorne (1973). While Shakura & Sunyaev (1973) calculated
the disk structure and related phenomena using purely Newtonian potential, Novikov
& Thorne provided a fully general relativistic description of accretion
discs around black holes; later on, some aspects of which were modified by
Riffert & Herold (1995). However, rigorous investigation of transonic disc
structure was found to be extremely complicated in full general relativistic
space time (Chakrabarti 1996 and references therein). At the same time it was
understood that as relativistic effects play an important role in the
regions close to the accreting black hole (where most of the
gravitational potential energy is released), purely Newtonian gravitational
potential (in the form
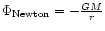 )
cannot be a realistic choice to describe
transonic black hole accretion in general. To compromise between the ease of
handling of a
Newtonian description of gravity and the realistic situations
described by complicated general relativistic calculations, a series of
"modified'' Newtonian potentials have been introduced
to describe the general relativistic effects that are
most important for accretion disk structure around Schwarzschild and Kerr
black holes (see Artemova et al. 1996 for further discussion).
Introduction of such potentials allows one to investigate the
complicated physical processes taking place in disc accretion in a
semi-Newtonian framework by avoiding pure general relativistic calculations
that
most of the features of spacetime around a compact object are retained and
some crucial properties of the analogous relativistic
solutions of disc structure could be reproduced with high accuracy.
Hence, those potentials might be designated as "pseudo-Kerr'' or "pseudo-Schwarzschild'' potentials, depending on whether they are used to mimic the
space time around a rapidly rotating or non rotating/slowly rotating
(Kerr parameter
)
cannot be a realistic choice to describe
transonic black hole accretion in general. To compromise between the ease of
handling of a
Newtonian description of gravity and the realistic situations
described by complicated general relativistic calculations, a series of
"modified'' Newtonian potentials have been introduced
to describe the general relativistic effects that are
most important for accretion disk structure around Schwarzschild and Kerr
black holes (see Artemova et al. 1996 for further discussion).
Introduction of such potentials allows one to investigate the
complicated physical processes taking place in disc accretion in a
semi-Newtonian framework by avoiding pure general relativistic calculations
that
most of the features of spacetime around a compact object are retained and
some crucial properties of the analogous relativistic
solutions of disc structure could be reproduced with high accuracy.
Hence, those potentials might be designated as "pseudo-Kerr'' or "pseudo-Schwarzschild'' potentials, depending on whether they are used to mimic the
space time around a rapidly rotating or non rotating/slowly rotating
(Kerr parameter 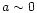 )
black
hole respectively.
)
black
hole respectively.
It is important to note that although a number of such
"pseudo'' potentials are available in the
literature to study various aspects of
disc accretion, no such potentials are available which had been solely
derived to describe spherically symmetric accretion on to a Schwarzschild
(or Kerr) black hole. In this paper, we will concentrate on some of the
"pseudo-Schwarzschild'' disc potentials (potentials introduced to study
accretion discs
around a Schwarzschild black hole) to investigate whether those potentials could
be used to study Spherical accretion, and if
so, how "good'' the choice would be for various such potentials.
Also, we would like to check which potential among those would be the "best-fit'' to
approximate the full general relativistic description of
transonic, spherically symmetric accretion on to a Schwarzschild black
hole. In doing so, we
solve the equations of motion of spherically accreting fluid in full
Schwarzschild space-time as well as for
motion under various "pseudo''-potentials,
to study the variation of different
dynamical and thermodynamic quantities (like Mach number of the flow, flow
temperature etc.) with radial distance measured from the accreting black hole for
the full
general relativistic spherical flow (hereafter FGRSF)
as well as for accretion using
various "pseudo- Schwarzschild'' potentials. We then compare the results
obtained using such potentials with the solutions of exact relativistic
problems in a Schwarzschild metric. The plan of the paper is as follows:
In next section, we will describe four "pseudo-Schwarzschild'' disc potentials
available in the literature and some of their basic features. In Sect. 3,
we will provide the basic equations governing spherically symmetric
accretion in full relativistic as well as in various
"pseudo''-relativistic spacetimes. In Sect. 4 we
will discuss how to solve those equations to find various
dynamical quantities which are to be mutually compared and
we present our results. Finally in Sect. 5 we conclude by discussing
the suitability of various "pseudo'' potentials
in approximating the results obtained from
exact relativistic
calculations. For the rest of this paper, we will use the terms "modified-Newtonian potential'' and "pseudo (Schwarzschild) potentials''
synonymously.
From now, we will define the Schwarzschild radius 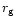 as
as
(where
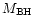 is the mass of the black hole, Gis universal gravitational
constant and c is velocity of light in vacuum) so that the marginally bound
circular orbit
is the mass of the black hole, Gis universal gravitational
constant and c is velocity of light in vacuum) so that the marginally bound
circular orbit 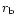 and the last stable circular orbit
and the last stable circular orbit 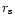 take the values
take the values
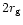 and
and
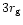 respectively for a typical Schwarzschild black hole. Also,
total
mechanical energy per unit mass on
respectively for a typical Schwarzschild black hole. Also,
total
mechanical energy per unit mass on 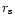 (sometimes called
"efficiency'' e) may be computed as -0.057 for this
case. Also, we will use a simplified geometric unit throughout this paper where
radial distance r is be scaled in units of
(sometimes called
"efficiency'' e) may be computed as -0.057 for this
case. Also, we will use a simplified geometric unit throughout this paper where
radial distance r is be scaled in units of 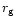 ,
radial dynamical
velocity
u and polytropic sound speed a of
the flow is scaled in units of c (the
velocity
of light in vacuum), mass m is scaled in units of
,
radial dynamical
velocity
u and polytropic sound speed a of
the flow is scaled in units of c (the
velocity
of light in vacuum), mass m is scaled in units of
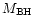 and all
and all
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1237f1.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg36.gif) |
Figure 1:
Newtonian potential
 and other
pseudo-potentials
and other
pseudo-potentials 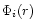 's (i=1, 2, 3, 4) are plotted as a function of
the logarithmic radial distance from the accreting black hole. Except 's (i=1, 2, 3, 4) are plotted as a function of
the logarithmic radial distance from the accreting black hole. Except 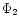 ,
all
other pseudo-potentials have a singularity at one Schwarzschild radius ,
all
other pseudo-potentials have a singularity at one Schwarzschild radius
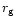 .
For .
For
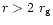 ,
while the relative stiffness factor ,
while the relative stiffness factor 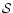 is maximum
for
is maximum
for 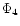 ,
it is minimum for ,
it is minimum for 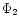 ,
see text for details. ,
see text for details. |
| Open with DEXTER |
other derived quantities would be scaled
accordingly. Also, for simplicity, we will use G=c=M=1.
Below we would like to
briefly describe four
different "pseudo-Schwarzschild'' potentials (expressed in
the system of units discussed above) and to provide the "free fall''
acceleration obtained using such potentials in compact form.
Paczynski & Wiita (1980) introduced a "pseudo-Schwarzschild''
potential of the form
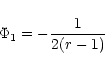 |
(1a) |
which accurately reproduces the positions of 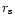 and
and 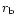 and gives the value
of efficiency to be -0.0625. Also the Keplerian distribution of angular
momentum obtained using this potential is exactly same as
that obtained in pure
Schwarzschild geometry. Although this potential (as well as the other
"pseudo'' potentials available in the literature) does not
satisfy the boundary condition exactly on the horizon, however,
close to the
horizon, accretion flows are supposed to be highly supersonic and the
dynamical infall time scale becomes too small to allow significant radiation
from infalling fluid. Even if there are significant amounts
of radiation, it
does not contribute too much to the overall radiation coming out from the
disc, due to the fact that radiation emitted from the
very close viscinity of the
black hole is highly redshifted. Thus, errors in calculation
close to the horizon may
have very little impact on the emitted disc spectrum and for all practical
purposes, the
Paczynski & Wiita (1980)
potential is considered to be the best approximation of
pure Schwarzschild spacetime while treating the disc accretion
(Artemova 1996). It is worth mentioning here that this potential
was first introduced to study a thick accretion disc with super Eddington
Luminosity. Also,
it is interesting to note that although it had been thought of
in
terms of disc accretion, it is spherically symmetric (with a scale shift of
and gives the value
of efficiency to be -0.0625. Also the Keplerian distribution of angular
momentum obtained using this potential is exactly same as
that obtained in pure
Schwarzschild geometry. Although this potential (as well as the other
"pseudo'' potentials available in the literature) does not
satisfy the boundary condition exactly on the horizon, however,
close to the
horizon, accretion flows are supposed to be highly supersonic and the
dynamical infall time scale becomes too small to allow significant radiation
from infalling fluid. Even if there are significant amounts
of radiation, it
does not contribute too much to the overall radiation coming out from the
disc, due to the fact that radiation emitted from the
very close viscinity of the
black hole is highly redshifted. Thus, errors in calculation
close to the horizon may
have very little impact on the emitted disc spectrum and for all practical
purposes, the
Paczynski & Wiita (1980)
potential is considered to be the best approximation of
pure Schwarzschild spacetime while treating the disc accretion
(Artemova 1996). It is worth mentioning here that this potential
was first introduced to study a thick accretion disc with super Eddington
Luminosity. Also,
it is interesting to note that although it had been thought of
in
terms of disc accretion, it is spherically symmetric (with a scale shift of
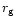 ). So in principle, it can definitely be used to study spherical
accretion also on to a Schwarzschild black hole.
). So in principle, it can definitely be used to study spherical
accretion also on to a Schwarzschild black hole.
To analyse the normal modes of accoustic oscillations within a
thin accretion
disc around a compact object (slowly rotating black hole or weakly
magnetized neutron star), Nowak & Wagoner (1991) approximated some of the
dominant relativistic effects of the accreting
black hole (slowly rotating or
nonrotating) via a modified Newtonian potential of the form
![\begin{displaymath}\Phi_{2}=-\frac{1}{2r}\left[1-\frac{3}{2r}+12{\left(\frac{1}{2r}\right)}^{\!\!2}\right]
\end{displaymath}](/articles/aa/full/2001/30/aa1237/img38.gif) |
(1b) |
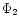 has correct form of
has correct form of 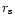 as in the Schwarzschild case
but is unable to
reproduce the value of
as in the Schwarzschild case
but is unable to
reproduce the value of 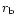 .
This potential has the correct general relativistic value of the
angular velocity (as measured at infinity) at
.
This potential has the correct general relativistic value of the
angular velocity (as measured at infinity) at 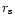 .
Also it reproduces the
radial epicyclic frequency
.
Also it reproduces the
radial epicyclic frequency 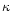 (for
(for
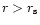 )
close to its value obtained
from general relativistic calculations. However, this potential gives the
value of efficiency as -0.064 which is larger than that produced by
)
close to its value obtained
from general relativistic calculations. However, this potential gives the
value of efficiency as -0.064 which is larger than that produced by
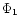 ,
hence the disc spectrum computed using
,
hence the disc spectrum computed using 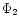 would be more
luminous compared to a disc structure studied using
would be more
luminous compared to a disc structure studied using 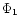 .
.
Remembering that the free-fall acceleration plays a very crucial
role in Newtonian gravity, Artemova et al. (1996) proposed two different
"pseudo'' potentials to study disc accretion around a non-rotating black hole.
The first potential proposed by them produces exactly the
same value of the free-fall
acceleration of a test particle at a given value of r as is obtained
for a test particle at rest with respect to the Schwarzschild reference
frame, and is given by
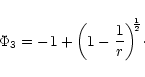 |
(1c) |
The second one gives the value of the free fall acceleration that is equal
to the value of the covariant component of the three dimensional free-fall
acceleration vector of a test particle that is at rest in the Schwarzschild
reference frame and is given by
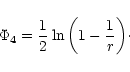 |
(1d) |
Efficiencies produced by 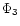 and
and 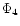 are -0.081 and -0.078
respectively. The magnitude of efficiency produced by
are -0.081 and -0.078
respectively. The magnitude of efficiency produced by 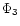 being
maximum, calculation of disc structure using
being
maximum, calculation of disc structure using 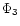 will give the maximum
amount of energy dissipation and the corresponding spectrum would be the
most luminous one. However, as both
will give the maximum
amount of energy dissipation and the corresponding spectrum would be the
most luminous one. However, as both 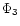 and
and
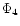 stems from the
consideration of free fall acceleration and calculates the dependence of
free fall accleration on radial distance in the Schwarzschild metric
(which
describes a spherically symmetric gravitational field in vacuum), it
appears to be
quite justified to use those potentials to study spherically symmetric
accretion.
stems from the
consideration of free fall acceleration and calculates the dependence of
free fall accleration on radial distance in the Schwarzschild metric
(which
describes a spherically symmetric gravitational field in vacuum), it
appears to be
quite justified to use those potentials to study spherically symmetric
accretion.
From now we will refer to
all these four potentials as  in
general where
in
general where
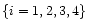 would correspond to
would correspond to 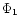 (Eq. (1a)),
(Eq. (1a)), 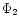 (Eq. (1b)),
(Eq. (1b)), 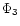 (Eq. (1c)) and
(Eq. (1c)) and 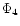 (Eq. (1d))
respectively.
In Fig. 1, we plot various
(Eq. (1d))
respectively.
In Fig. 1, we plot various  's as a function of the radial distance
measured from the accreting black hole in units of
's as a function of the radial distance
measured from the accreting black hole in units of 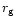 .
Also in the same plot,
purely Newtonian potential
.
Also in the same plot,
purely Newtonian potential
 is plotted.
If we now define a quantity
is plotted.
If we now define a quantity
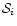 to be the "relative stiffness''
of a potential
to be the "relative stiffness''
of a potential  as:
as:
(that is,
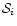 is a measure of the numerical value of any ith
potential at a radial distance r), we find that for
is a measure of the numerical value of any ith
potential at a radial distance r), we find that for
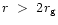 :
:
which indicates that while 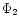 is a "flatter'' potential compared to the
pure Newtonian potential
is a "flatter'' potential compared to the
pure Newtonian potential
 ,
all other "pseudo'' potentials are
"steeper'' to
,
all other "pseudo'' potentials are
"steeper'' to
 for
for
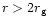 .
.
One can write the modulus of free fall
acceleration obtained from all "pseudo'' potentials except for 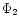 in a compact form as
in a compact form as
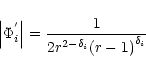 |
(2a) |
where
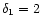 ,
,
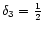 and
and
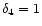 .
.
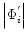 denotes the absolute value of the
space derivative of
denotes the absolute value of the
space derivative of  ,
i.e.,
,
i.e.,
whereas acceleration produced by 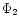 can be computed as,
can be computed as,
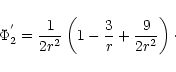 |
(2b) |
In the next section,we would like to describe how one can investigate
transonic spherical accretion using these potentials. Also, we will discuss
how to calculate various dynamical quantities for full general relativistic
bondi flow in a Schwarzschild metric. One standard method to investigate
classical transonic bondi flow is to formulate the basic conservation
equations, i.e., conservation of baryon number (obtained by integrating
continuity
equation) and conservation of specific energy (obtained by
integrating Euler's equation
using a specific equation of state for accreting matter) and then to
simultaneously solve these conservation equations to get
critical (sonic) quantities as functions of various accretion parameters
(like specific energy  ,
adiabatic index
,
adiabatic index  or accretion rate
or accretion rate
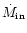 in the flow)
and also to calculate the values of various dynamical and
thermodynamic quantities (like Mach number M, of the
flow, flow temperature, T, etc.) as functions of various accretion
parameters (like
in the flow)
and also to calculate the values of various dynamical and
thermodynamic quantities (like Mach number M, of the
flow, flow temperature, T, etc.) as functions of various accretion
parameters (like
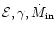 etc.) or radial distance (measured from the central
accretor in the unit of Schwarzschild radius
etc.) or radial distance (measured from the central
accretor in the unit of Schwarzschild radius 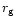 ).
Also a common practice is
to study the variation of
Mach number M (ratio of the local dynamical velocity
uto the local sound velocity a;
).
Also a common practice is
to study the variation of
Mach number M (ratio of the local dynamical velocity
uto the local sound velocity a;
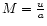 )
with radial distance r (measured in units of
)
with radial distance r (measured in units of 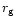 )
to
investigate the "transonicity'' of the
flow for a fixed set of input parameters.
We will
perform the above mentioned calculations for accretion in pure Schwarzschild
spacetime as well as for accretion in "pseudo-Schwarzschild'' space time
using
)
to
investigate the "transonicity'' of the
flow for a fixed set of input parameters.
We will
perform the above mentioned calculations for accretion in pure Schwarzschild
spacetime as well as for accretion in "pseudo-Schwarzschild'' space time
using  's and compare the results obtained for various
's and compare the results obtained for various
 's with exact
relativistic calculations.
As accretion onto a
black hole is necessarily transonic to satisfy
the inner boundary condition at the event horizon, unlike Bondi's
(1952) original work,
here we will concentrate only on transonic solutions, i.e., we will deal with accretion
(wind) which is subsonic (supersonic) far away from the black hole and
approaches (moves away from)
the hole supersonically (subsonically)
after crossing a sonic point (the location of which can be
determined as a function of
's with exact
relativistic calculations.
As accretion onto a
black hole is necessarily transonic to satisfy
the inner boundary condition at the event horizon, unlike Bondi's
(1952) original work,
here we will concentrate only on transonic solutions, i.e., we will deal with accretion
(wind) which is subsonic (supersonic) far away from the black hole and
approaches (moves away from)
the hole supersonically (subsonically)
after crossing a sonic point (the location of which can be
determined as a function of  and
and  ,
see Sect. 3) on its way
towards (away from) the accretor.
,
see Sect. 3) on its way
towards (away from) the accretor.
For a schwarzschild metric of the form
the energy momentum tensor
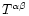 for a perfect fluid
can be written as (Shapiro & Teukolsky 1983)
for a perfect fluid
can be written as (Shapiro & Teukolsky 1983)
where
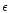 and p are proper energy density and pressure of the
fluid (evaluated in the local inertial rest frame of the fluid)
respectively and
and p are proper energy density and pressure of the
fluid (evaluated in the local inertial rest frame of the fluid)
respectively and
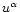 is the four velocity commonly known as
is the four velocity commonly known as
Equations of motion which are to be solved for our purpose are,
1) Conservation of mass flux or baryon number conservation:
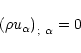 |
(3a) |
and
2) Conservation of momentum or energy flux (the
general relativistic Euler
equation obtained by taking the four divergence of
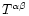 ):
):
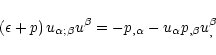 |
(3b) |
where the semicolons denote the covariant derivatives.
Following Michel (1972), one can rewrite Eqs. (3a) and (3b) for
spherical accretion as
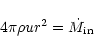 |
(4a) |
and
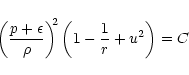 |
(4b) |
as two fundamental conservation equations for time
independant hydrodynamical flow of matter on to a
Schwarzschild black hole without back-reaction of the
flow on to the metric itself.
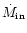 is the mass
accretion rate and C is a constant
(related to the total enthalpy influx)
to be evaluated
for a specific equation of state.
is the mass
accretion rate and C is a constant
(related to the total enthalpy influx)
to be evaluated
for a specific equation of state.
For a polytropic equation of state i.e.,
and defining
 ,
where
,
where
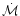 is a measure of the
entropy of the flow (n is a polytropic constant of the flow defined as
is a measure of the
entropy of the flow (n is a polytropic constant of the flow defined as
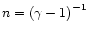 )
and is another
conserved quantity of the flow, one can rewrite
conservation Eqs. (4a) and (4b) as (see Chakrabarti 1996 and
references therein):
)
and is another
conserved quantity of the flow, one can rewrite
conservation Eqs. (4a) and (4b) as (see Chakrabarti 1996 and
references therein):
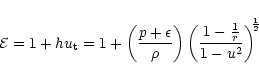 |
(5a) |
and
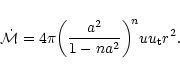 |
(5b) |
Where
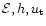 and a are the conserved specific energy
of the flow excluding its rest mass,
specific enthalpy, specific binding
energy and local adiabatic sound speed
respectively. Equation (5b) may be considered as the outcome of
the conservation
of mass and entropy along the flow line.
The expression for a can be written as (Weinberg 1972; Frank et al.
1992):
and a are the conserved specific energy
of the flow excluding its rest mass,
specific enthalpy, specific binding
energy and local adiabatic sound speed
respectively. Equation (5b) may be considered as the outcome of
the conservation
of mass and entropy along the flow line.
The expression for a can be written as (Weinberg 1972; Frank et al.
1992):
 |
(6) |
Where T is the flow temperature, 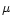 is the mean molecular weight and
is the mean molecular weight and
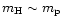 is the mass of the hydrogen atom.
is the mass of the hydrogen atom.
One can now easily derive the expression for the velocity
gradient
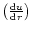 (by differentiating Eqs. (5a) and (5b))
as
(by differentiating Eqs. (5a) and (5b))
as
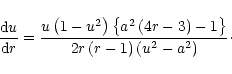 |
(7a) |
Since the flow is assumed to be smooth everywhere, if
the denominator of Eq. (7a) vanishes at any radial distance
r, the numerator must also vanish there to maintain the
continuity of the flow. One therefore arrives at the so
called "sonic point (alternately, the "critical point''![[*]](/icons/foot_motif.gif) ) conditions'' by simultaneously making
the numerator and denominator of Eq. (7a) equal zero.
The sonic point conditions then can be expressed as follows
) conditions'' by simultaneously making
the numerator and denominator of Eq. (7a) equal zero.
The sonic point conditions then can be expressed as follows
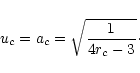 |
(7b) |
For a specific value of  and
and  ,
location of the sonic point
,
location of the sonic point
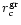 can be obtained by solving the following equation
algebraically
can be obtained by solving the following equation
algebraically
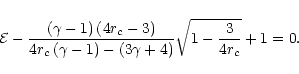 |
(7c) |
The spherical surface of radius r=rc can be defined as the
"accoustic horizon'' because for
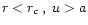 and any
accoustic disturbances created in this region are
advected towards the black hole. Thus no accoustic
disturbances created within this radius can cross the
accoustic horizon and escape to the region r > rc.
and any
accoustic disturbances created in this region are
advected towards the black hole. Thus no accoustic
disturbances created within this radius can cross the
accoustic horizon and escape to the region r > rc.
To
determine the behaviour of the solution near the sonic
point, one needs to evaluate the value of
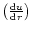 at that
point (we denote it by
at that
point (we denote it by
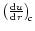 )
by applying L'Hospitals' rule to Eq. (7a). It is
easy to show that
)
by applying L'Hospitals' rule to Eq. (7a). It is
easy to show that
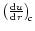 can be obtained by solving the
following quadratic equations algebraically:
can be obtained by solving the
following quadratic equations algebraically:
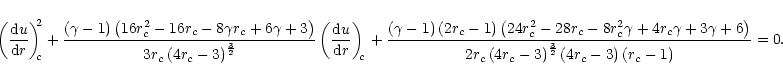 |
(7d) |
It is now quite straightforward to simultaneously
solve Eqs. (5a) and (5b) to
get the integral curves of the flow for a fixed value
of  and
and  .
Detailed methodology for this purpose will
be discussed
in Sect. 4.
.
Detailed methodology for this purpose will
be discussed
in Sect. 4.
For any "pseudo-Schwarzschild'' potential  ,
the
equation of motion for spherically accreting material
onto the accretor
is given by
,
the
equation of motion for spherically accreting material
onto the accretor
is given by
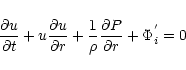 |
(8a) |
where symbols have their
usual meaning.
The first term of Eq. (8a) is the Eulerian time derivative of the
dynamical velocity at a given r, the second term
is the "advective'' term, the third term
is the
momentum deposition due to pressure gradient and the
final term is due to the gravitational acceleration
for a particular ith potential  .
The continuity
equation can be written as
.
The continuity
equation can be written as
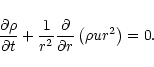 |
(8b) |
For a polytropic equation of state, the steady state
solution (apart from a geometric factor of  )
of Eqs. (8a) and (8b) is
)
of Eqs. (8a) and (8b) is
1) Conservation of specific energy  of the flow:
of the flow:
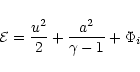 |
(9a) |
and
2) Conservation of Baryon number (or accretion rate
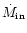 ):
):
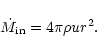 |
(9b) |
Using
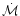 as defined earlier
(
as defined earlier
(
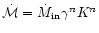 ),
Eq. (9b) can be rewritten as
),
Eq. (9b) can be rewritten as
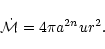 |
(9c) |
It is now quite straightforward to derive the space
gradient of dynamical velocity
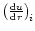 for flow in any particular ith potential
for flow in any particular ith potential  as
as
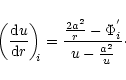 |
(10a) |
Using either Eq. (2a) or (2b), one can substitute the
value of any specific ith
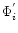 in Eq. (10a) to get the
value of
in Eq. (10a) to get the
value of
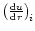 for motion under particular ith
pseudo-Schwarzschild potential. One can also calculate
the sonic point quantities (as described in Sect. 3.1)
as
for motion under particular ith
pseudo-Schwarzschild potential. One can also calculate
the sonic point quantities (as described in Sect. 3.1)
as
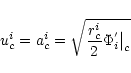 |
(10b) |
where superscript i denotes the specific
value of sonic quantities for a particular ith
potential  ,
and
,
and
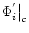 is the
value of
is the
value of
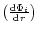 evaluated at the corresponding sonic point
ric. The value of sonic point ric for any ith potential
evaluated at the corresponding sonic point
ric. The value of sonic point ric for any ith potential
 can be obtained
by algebraically solving the following equation
can be obtained
by algebraically solving the following equation
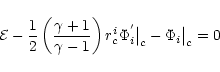 |
(10c) |
where
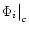 is the value of ith potential at the
corresponding sonic point ric.
Similarly, the value of
is the value of ith potential at the
corresponding sonic point ric.
Similarly, the value of
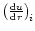 for any
for any  at its
corresponding sonic point ric can be obtained by
solving the following quadratic equation:
at its
corresponding sonic point ric can be obtained by
solving the following quadratic equation:
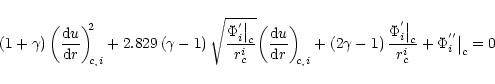 |
(10d) |
where
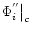 is the value of
is the value of
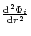 at the corresponding
critical point ric.
at the corresponding
critical point ric.
One can simultaneously solve Eqs. (9a) and (9b)
(alternatively, Eqs. (9a) and (9c))
for any specific  for a
fixed value of
for a
fixed value of  and
and  to obtain various dynamical and thermodynamic flow quantities.
We discuss the detailed
methodology in Sect. 4.
to obtain various dynamical and thermodynamic flow quantities.
We discuss the detailed
methodology in Sect. 4.
![\begin{figure}
\def \floatcounterend{}
\par\includegraphics[width=15cm,height=13.5cm,clip]{MS1237f2.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg106.gif) |
Figure 2:
(a,b,c,d).
The deviation
(
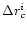 )
of the value of sonic points
ric's obtained for flows using various )
of the value of sonic points
ric's obtained for flows using various  's from 's from
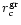 as a function of specific energy as a function of specific energy  and adiabatic
index
and adiabatic
index  of the flow is plotted for flows in of the flow is plotted for flows in 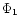 (Fig. 1a),
(Fig. 1a), 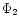 (Fig. 1b), (Fig. 1b), 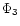 (Fig. 1c) and
(Fig. 1c) and 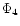 (Fig. 1d). It is observed
that while
(Fig. 1d). It is observed
that while
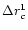 is a minimum for ultra-relativistic (
is a minimum for ultra-relativistic (
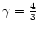 )
flow, )
flow,
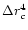 becomes a minimum as the flow approaches
a pure-non-relativistic (
becomes a minimum as the flow approaches
a pure-non-relativistic (
 )
limit, see text for
detail. )
limit, see text for
detail. |
| Open with DEXTER |
Solving Eqs. (7c) and (10c) for a fixed value of  and
and
 ,
the sonic point could be obtained for FGRSF and for flows in various
pseudo-potentials respectively. We denote
,
the sonic point could be obtained for FGRSF and for flows in various
pseudo-potentials respectively. We denote
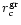 to
be the sonic point for
FGRSF and ric to be the sonic point for flow in ith potential
to
be the sonic point for
FGRSF and ric to be the sonic point for flow in ith potential
 ,
and define
,
and define
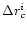 as:
as:
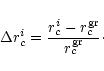 |
(11) |
In Fig. 2, we plot various
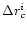 's
(along the z axis) as a function of specific energy
's
(along the z axis) as a function of specific energy
 (along the x axis) and adiabatic index
(along the x axis) and adiabatic index  (along the
y axis) of the flow. The difference in the general profile
of variation of
(along the
y axis) of the flow. The difference in the general profile
of variation of
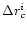 for various
for various  's
with
's
with  and
and  is quite obvious from the figure.
It is observed that when
is quite obvious from the figure.
It is observed that when  is kept fixed at its minimum value
(
is kept fixed at its minimum value
(
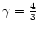 ),
),
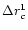 (
(
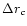 for flows in
for flows in
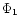 )
is always positive (which means
)
is always positive (which means
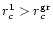 always) and
is at a
minimum for low energy and starts increasing nonlinearly with an
increase of
always) and
is at a
minimum for low energy and starts increasing nonlinearly with an
increase of
 .
At a certain value of
.
At a certain value of  ,
it produces a peak and starts falling,
with further increase of
,
it produces a peak and starts falling,
with further increase of  .
The peak value of
.
The peak value of
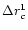 is observed
to be
is observed
to be  0.15. Unlike
0.15. Unlike
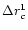 ,
,
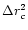 falls very sharply with
falls very sharply with  and shows a "dip'' at
and shows a "dip'' at
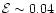 ,
then starts increasing with
,
then starts increasing with  monotonically and nonlinearly,
keeping
monotonically and nonlinearly,
keeping
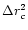 negative for all values
of
negative for all values
of  which indicates that
which indicates that
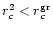 for ultra-relativistic flow (
for ultra-relativistic flow (
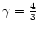 )
)![[*]](/icons/foot_motif.gif) ,
for all values of
,
for all values of  we consider here.
For
we consider here.
For 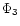 and
and 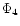 ,
we observe that
,
we observe that
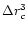 and
and
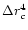 monotonically decreases
with
monotonically decreases
with  and also
and also
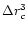 and
and
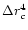 are always negative e.g.,
are always negative e.g.,
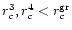 for all
for all
 we consider here. It is observed that
for ultra-relativistic flow,
we consider here. It is observed that
for ultra-relativistic flow,
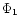 is the best approximation to study transonic
spherically symmetric polytropic accretion to produce the sonic point
closest to the sonic point formed for FGRSF in general, especially
in high energy regime,
i.e., for high value of
is the best approximation to study transonic
spherically symmetric polytropic accretion to produce the sonic point
closest to the sonic point formed for FGRSF in general, especially
in high energy regime,
i.e., for high value of  ,
while
,
while 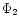 is the worst approximation
for studying the same phenomena for same set of boundary conditions. If we
define a hypothetical quantity
is the worst approximation
for studying the same phenomena for same set of boundary conditions. If we
define a hypothetical quantity
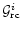 which is a measure of "goodness''
of a particular ith potential
which is a measure of "goodness''
of a particular ith potential  regarding the closest approximation
of
sonic points obtained for
FGRFS, we find that following sequence holds good for
ultra-relativistic flow:
regarding the closest approximation
of
sonic points obtained for
FGRFS, we find that following sequence holds good for
ultra-relativistic flow:
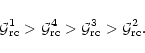 |
(12) |
The situation starts changing as the value of  increases.
The general profile of
increases.
The general profile of
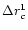 is unchanged but its peak
starts shifting towards the lower
is unchanged but its peak
starts shifting towards the lower  values with increasing
values with increasing
 and the overall deviation starts increasing. For
purely nonrelativistic flow (
and the overall deviation starts increasing. For
purely nonrelativistic flow (
 ),
),
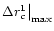 is found to be
quite large. For all
values of
is found to be
quite large. For all
values of  ,
,
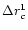 is found to be positive,
which means
that
is found to be positive,
which means
that
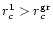 for all values of
for all values of  and
and  .
.
However, the behaviour of
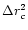 starts changing drastically with
an increase in
starts changing drastically with
an increase in  .
The "dip'' produced by
.
The "dip'' produced by
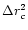 for low values of
for low values of  starts
smearing out with an increase in
starts
smearing out with an increase in
 and
and
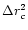 becomes positive with higher
becomes positive with higher  for a fixed value of
for a fixed value of  .
For higher
.
For higher  it has been observed that if we study variation of
it has been observed that if we study variation of
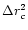 with
with  and
and  ,
,
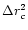 starts with a very high negative value at lower
starts with a very high negative value at lower  with
with
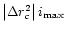 (where
(where
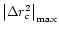 stands for the maximum value
of the modulus of
stands for the maximum value
of the modulus of
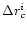 ),
monotonically decreasing with
),
monotonically decreasing with
 ,
reaches zero and becomes positive and increases nonlinearly up to
a maximum value (this time, a "peak'') and then starts falling
again with an increase of
,
reaches zero and becomes positive and increases nonlinearly up to
a maximum value (this time, a "peak'') and then starts falling
again with an increase of  .
So for high values of
.
So for high values of
 ,
smearing out of the "dip'' in
,
smearing out of the "dip'' in
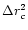 vs.
vs.  curve is
compensated by the appearance of
a "peak'' at some value of
curve is
compensated by the appearance of
a "peak'' at some value of  .
It is also observed that
the peak starts shifting towards the higher value of
.
It is also observed that
the peak starts shifting towards the higher value of  as
as
 is increased. It is also observed that as we go from ultra-relativistic
flow towards purely non-relativistic flow,
a zero appears in
is increased. It is also observed that as we go from ultra-relativistic
flow towards purely non-relativistic flow,
a zero appears in
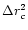 vs.
vs.  curve, which indicates that at least one value of
curve, which indicates that at least one value of  (for a fixed
(for a fixed
 )
is available where r2c would be exactly equal to
)
is available where r2c would be exactly equal to
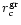 .
.
As  is increased, not much change is observed in the
general profile
of
is increased, not much change is observed in the
general profile
of
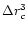 except that
except that
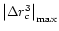 decreases with increase in
decreases with increase in  .
The change in profile of
.
The change in profile of
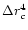 with increasing
with increasing  is much more interesting. It is
observed that with increasing
is much more interesting. It is
observed that with increasing  ,
not only does a zero appear in
,
not only does a zero appear in
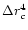 vs.
vs.  (for a fixed value of
(for a fixed value of  )
curve
(which means that for some values of
)
curve
(which means that for some values of  and
and  ,
r4c can be exactly equal to
,
r4c can be exactly equal to
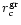 ), but also
the value of
), but also
the value of
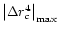 decreases considerably
with an increase
in
decreases considerably
with an increase
in  and
as the flow approaches its purely non-relativistic limit,
we observe that the overall deviation produced by
and
as the flow approaches its purely non-relativistic limit,
we observe that the overall deviation produced by 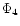 in approximating
in approximating
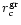 is quite small in general
(percentage deviation produced by
is quite small in general
(percentage deviation produced by
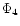 is found to be within the limit of 10
is found to be within the limit of 10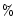 for
purely non-relativistic
flow), which indicates that
use of
for
purely non-relativistic
flow), which indicates that
use of 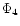 is the
best possible approximation of the Schwarzschild metric for
nonrelativistic flow (flow with high
is the
best possible approximation of the Schwarzschild metric for
nonrelativistic flow (flow with high  value), regarding reproduction
of the sonic point for a flow with fixed
value), regarding reproduction
of the sonic point for a flow with fixed  and
and  .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1237f3.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg127.gif) |
Figure 3:
Variation of Mach number M (plotted along the Y axis)
with radial distance (plotted along X axis in logarithmic scale) for
accretion and wind for a fixed energy (
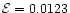 )
and
adiabatic index ( )
and
adiabatic index (
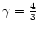 )
of the flow. The solid lines represent
the variation obtained for FGRSF. For same )
of the flow. The solid lines represent
the variation obtained for FGRSF. For same  and
and  ,
sonic
points ric's
obtained for flow in defferent pseudo-potentials and for FGRSF are all different
which is clearly observed from the figure. While the value of ,
sonic
points ric's
obtained for flow in defferent pseudo-potentials and for FGRSF are all different
which is clearly observed from the figure. While the value of
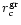 is obtained as is obtained as
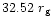 ,
values of r1c, r2c, r3c and r4c are obtained as ,
values of r1c, r2c, r3c and r4c are obtained as
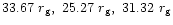 and
and
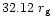 respectively where ric's are the sonic points for various respectively where ric's are the sonic points for various  's. 's. |
| Open with DEXTER |
We have mentioned earlier that study of the integral curves,
i.e., the variation of Mach number of the flow M with radial
distance r(measured from the accreting hole in units of 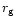 )
is
essential to investigate the "transonicity'' of the flow. Let us first
consider FGRSF. From Eq. (7c), one can obtain the sonic point
)
is
essential to investigate the "transonicity'' of the flow. Let us first
consider FGRSF. From Eq. (7c), one can obtain the sonic point
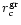 for a fixed value of
for a fixed value of  and
and  .
The value
of
.
The value
of
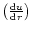 at
at
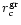 is then calculated using Eq. (7d). One can numerically
solve Eqs. (5a) and (5b) simultaneously to obtain the value of the Mach
number (and other dynamical quantities) as a function of radial distance
for a fixed value of
is then calculated using Eq. (7d). One can numerically
solve Eqs. (5a) and (5b) simultaneously to obtain the value of the Mach
number (and other dynamical quantities) as a function of radial distance
for a fixed value of  and
and  .
It is well known that for
spherically symmetric accretion onto a Schwarzschild black hole, two solutions
are obtained while solving the governing conservation equations, e.g.,
equation for conservation of specific energy and from baryon number
(or specific entropy)
conservation equation. One solution out of these two corresponds to the
accretion process and the other is for the wind. Using Eq. (6),
it is easy to calculate the flow temperature at all points of the flow
(for accretion as well as for the wind branch).
.
It is well known that for
spherically symmetric accretion onto a Schwarzschild black hole, two solutions
are obtained while solving the governing conservation equations, e.g.,
equation for conservation of specific energy and from baryon number
(or specific entropy)
conservation equation. One solution out of these two corresponds to the
accretion process and the other is for the wind. Using Eq. (6),
it is easy to calculate the flow temperature at all points of the flow
(for accretion as well as for the wind branch).
For accretion in pseudo potentials  's, the procedure is exactly the
same. Sonic point ric is obtained by solving Eq. (10c) for the ith
potential
's, the procedure is exactly the
same. Sonic point ric is obtained by solving Eq. (10c) for the ith
potential  for a fixed value of
for a fixed value of  and
and  .
.
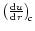 for that particular
potential is then obtained by solving Eq. (10d). Starting from ric,
Eqs. (9a) and (9b) (alternatively, Eqs. (9a) and (9c))
could be simultaneously solved (using Eq. (10a)) to get the variation of
Mach number of the flow (as well as of other dynamical quantities) as a
function of radial distance measured
in units of
for that particular
potential is then obtained by solving Eq. (10d). Starting from ric,
Eqs. (9a) and (9b) (alternatively, Eqs. (9a) and (9c))
could be simultaneously solved (using Eq. (10a)) to get the variation of
Mach number of the flow (as well as of other dynamical quantities) as a
function of radial distance measured
in units of 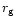 .
The solution
for accretion as well as for wind branch can be obtained to investigate
the "transonicity'' of the flow by plotting Mach number M as a function of
radial distance r. Temperature of the flow Ti (for any ith potential
.
The solution
for accretion as well as for wind branch can be obtained to investigate
the "transonicity'' of the flow by plotting Mach number M as a function of
radial distance r. Temperature of the flow Ti (for any ith potential  )
can easily be obtained by solving Eq. (6) for
ai, pi and
)
can easily be obtained by solving Eq. (6) for
ai, pi and 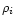 for a fixed value of
for a fixed value of  and
and  .
.
In Fig. 3, we plot the variation of Mach number as a function of the
radial distance
(in logarithmic scale)
for FGRSF as well as for flows in all  's. The
energy of the flow (for FGRSF and for flows in all
's. The
energy of the flow (for FGRSF and for flows in all  's) are kept
constant at a value 0.0123 and value of
's) are kept
constant at a value 0.0123 and value of  is taken to be
is taken to be
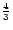 .
.
![\begin{figure}
\def \floatcounterend{}
\par\includegraphics[width=8.8cm,clip]{MS1237f4a.eps}\par\includegraphics[width=8.8cm,clip]{MS1237f4b.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg131.gif) |
Figure 4:
(a,b).
Variation of the absolute value of the slope of
the Mach number M (plotted on the Y axis as
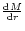 )
of
accretion (Fig. 4a) and wind (Fig. 4b) with radial distance
(plotted along X axis in logarithmic scale) measured from the accretor in units
of )
of
accretion (Fig. 4a) and wind (Fig. 4b) with radial distance
(plotted along X axis in logarithmic scale) measured from the accretor in units
of 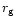 .
All input parameters are same as that of Fig. 3. Solid line
represents FGRSF. The slope in M is found to increase towards the
accretor non-linearly and monotonically for the accretion branch and the space
rate of change of M for .
All input parameters are same as that of Fig. 3. Solid line
represents FGRSF. The slope in M is found to increase towards the
accretor non-linearly and monotonically for the accretion branch and the space
rate of change of M for 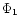 is clearly seen to be steepest while that
of
is clearly seen to be steepest while that
of 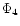 is observed to be the flattest. For wind, the change is not
monotonic; rather it produces a peak at the subsonic branch.
is observed to be the flattest. For wind, the change is not
monotonic; rather it produces a peak at the subsonic branch. |
| Open with DEXTER |
It is observed that sonic points of FGRSF
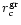 ,
as well as flows in
other potentials ric are all different, which is normally
expected (except for the very special value of
,
as well as flows in
other potentials ric are all different, which is normally
expected (except for the very special value of  for which either the
for which either the
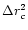 or
or
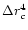 vanishes, see Figs. 2b and 2d).
While the value of
vanishes, see Figs. 2b and 2d).
While the value of
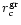 is obtained as
is obtained as
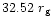 ,
values of r1c, r2c, r3c and r4c
are obtained as
,
values of r1c, r2c, r3c and r4c
are obtained as
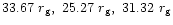 and
and
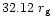 respectively. It is also to be noted that although the general profile
of the integral curves are almost same (except for
flows in
respectively. It is also to be noted that although the general profile
of the integral curves are almost same (except for
flows in 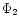 where the
change in curvature is slightly different to that of others, especially
for the supersonic accretion branch), the curves do not overlap in
general.
The amount of deviation (from FGRSF) of integral curves drawn for
various
where the
change in curvature is slightly different to that of others, especially
for the supersonic accretion branch), the curves do not overlap in
general.
The amount of deviation (from FGRSF) of integral curves drawn for
various  's is quite prominent for the supersonic branch
of accretion and the derivation is
observed to be not that significant
(except for flows in
's is quite prominent for the supersonic branch
of accretion and the derivation is
observed to be not that significant
(except for flows in 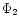 )
for corresponding
subsonic branches of accretion, as well as for the supersonic branch
of winds. The deviation maximises with the decrease of radial distance
from the accretion black hole. This is quite obvious because close to the
accretor,
the general relativistic effects would be much more prominent thus the
deviation would be higher. Also it is interesting to note that for the same
energy
)
for corresponding
subsonic branches of accretion, as well as for the supersonic branch
of winds. The deviation maximises with the decrease of radial distance
from the accretion black hole. This is quite obvious because close to the
accretor,
the general relativistic effects would be much more prominent thus the
deviation would be higher. Also it is interesting to note that for the same
energy  (and even for a fixed sonic point common to both
FGRSF and flows in all
(and even for a fixed sonic point common to both
FGRSF and flows in all  's which may be obtained
by properly tunning
the corresponding
's which may be obtained
by properly tunning
the corresponding  's), the maximum value of the Mach number
's), the maximum value of the Mach number
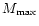 of the flow in different
of the flow in different  's
are very different.
One can observe from the figure that there exists a particular value
of r (for a fixed
's
are very different.
One can observe from the figure that there exists a particular value
of r (for a fixed  and
and  )
where the "crossing-over''
of
)
where the "crossing-over''
of 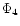 with FGRSF at the supersonic branch of the
accretion is quite distinct, that is, the
Mach number attained
for flows in
with FGRSF at the supersonic branch of the
accretion is quite distinct, that is, the
Mach number attained
for flows in 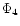 at a particular point is exactly
equal to the Mach number produced by FGRSF. Also, the general profile for
the variation of Mach number of the flow in
at a particular point is exactly
equal to the Mach number produced by FGRSF. Also, the general profile for
the variation of Mach number of the flow in 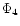 is
extremely close to the profile
obtained in FGRSF almost throughout the flow
except very close (
is
extremely close to the profile
obtained in FGRSF almost throughout the flow
except very close (
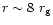 in this case) to the black hole. However, no such mutual crossing over is observed
in between flows in various
in this case) to the black hole. However, no such mutual crossing over is observed
in between flows in various  's.
's.
If
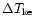 and
and
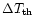 are the relative gain in the kinetic
energy and thermal energy of the flow respectively, it is easy to show
that the change in Mach number
are the relative gain in the kinetic
energy and thermal energy of the flow respectively, it is easy to show
that the change in Mach number 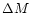 could be approximated as:
could be approximated as:
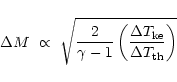 |
(13) |
for spherical accretion in all pseudo potentials discussed here. Also it is
easy to understand that the Mach number profile as well as the
rate of change of Mach number at a particular point should be related to the
form of the potential  used to study the flow (and in general to
the metric used to describe the spacetime). Also
used to study the flow (and in general to
the metric used to describe the spacetime). Also
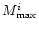 ,
the
maximum value of M which could be attended for
a particular set of
,
the
maximum value of M which could be attended for
a particular set of  and
and  for flows in
any ith potential
for flows in
any ith potential
 (for the range of r shown here),
should be related to the nature of the potential used to describe the
flow. It is observed that
for
(for the range of r shown here),
should be related to the nature of the potential used to describe the
flow. It is observed that
for
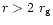 ,
,
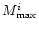 anticorrelates with
anticorrelates with
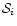 (the "relative stiffness'' of the ith potential) for
i=1, 3, 4 but correlates with
(the "relative stiffness'' of the ith potential) for
i=1, 3, 4 but correlates with
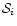 for i=2.
for i=2.
As change in the Mach number is a result of a
mutual tug of war in between
change in dynamical velocity and polytropic sound
speed (alternatively, in between the mechanical and thermal energy
of the flow, see Eq. (13)), it might be interesting
to investigate the variation of the slope of the
Mach number (which might be
considered as the measure
of the degree of
"transonicity'' of the flow) with radial distance r for
two different branches of solutions, namely, accretion and wind. In Figs. 4a and 4b we plot the absolute value of
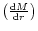 as a function of
as a function of
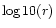 for accretion (Fig. 4a) and wind
(Fig. 4b) for FGRSF as well as for flows in various
for accretion (Fig. 4a) and wind
(Fig. 4b) for FGRSF as well as for flows in various  s. For
accretion we see that
s. For
accretion we see that
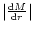 increases nonlinearly and
monotonically as the flow comes closer to the black hole,
which indicates that for all flows, instantaneous changes in kinetic energy of
the flow is always greater than the instantaneous change in thermal
energy, i.e.,
increases nonlinearly and
monotonically as the flow comes closer to the black hole,
which indicates that for all flows, instantaneous changes in kinetic energy of
the flow is always greater than the instantaneous change in thermal
energy, i.e.,
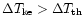 for all values of r,
which is not the case for winds. For winds (see Fig. 4b), change of
for all values of r,
which is not the case for winds. For winds (see Fig. 4b), change of
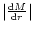 is not monotonic rather it
always shows a peak in the
subsonic branch for FGRSF
as well as for flows in all
is not monotonic rather it
always shows a peak in the
subsonic branch for FGRSF
as well as for flows in all  's. The appearance of the peak
for flows in pseudo potentials is due to the fact that from the close
vicinity of the event horizon up to a certain distance
's. The appearance of the peak
for flows in pseudo potentials is due to the fact that from the close
vicinity of the event horizon up to a certain distance 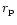 (
(
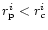 and
and
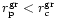 always), the local gain in
kinetic energy at any point is higher than the local thermal energy
gain. So up to
always), the local gain in
kinetic energy at any point is higher than the local thermal energy
gain. So up to
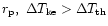 but after
but after
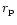 ,
,
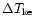 decreases and
decreases and
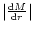 starts falling as the wind approaches to the sonic point.
It is easy to
understand that as
starts falling as the wind approaches to the sonic point.
It is easy to
understand that as  is kept constant throughout the flow (for accretion as well
as for the wind branch), the bulk motion acceleration of the flow is a
continuous process throughout the accretion towards the black hole but
for winds the acceleration process dominates only up to
is kept constant throughout the flow (for accretion as well
as for the wind branch), the bulk motion acceleration of the flow is a
continuous process throughout the accretion towards the black hole but
for winds the acceleration process dominates only up to 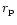 and gets
the major part of the outward acceleration in the region bounded in
and gets
the major part of the outward acceleration in the region bounded in
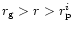 ,
though the exact physical reason behind this is not
clearly understood. However, it should be remembered that the above argument holds
only for flows in pseudo potentials and not for FGRSF; because for
FGRSF, the total energy term can not be decoupled into various counterparts
with individual origin e.g., mechanical energy
,
though the exact physical reason behind this is not
clearly understood. However, it should be remembered that the above argument holds
only for flows in pseudo potentials and not for FGRSF; because for
FGRSF, the total energy term can not be decoupled into various counterparts
with individual origin e.g., mechanical energy
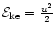 or thermal energy
or thermal energy
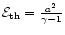 etc.
etc.
It is clear from the figure
that the location of
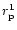 (
(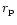 for flows in
for flows in 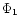 )
is located furthest away from the black hole and
)
is located furthest away from the black hole and
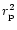 is located
closest to the black hole with the following sequence:
is located
closest to the black hole with the following sequence:
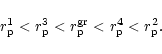 |
(14) |
It is also observed that with increase of  ,
the sequence in Eq. (14)
is maintained but the location of all
,
the sequence in Eq. (14)
is maintained but the location of all 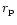 s moves towards the
black hole. Thus, the regions from where the wind (in various
s moves towards the
black hole. Thus, the regions from where the wind (in various  's)
is accelerated, moves closer to the hole as the flow approaches to its
non-relativistic limit.
If we define
's)
is accelerated, moves closer to the hole as the flow approaches to its
non-relativistic limit.
If we define
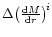 to be:
to be:
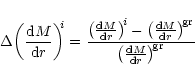 |
(15) |
then one can show
that for a fixed value of  and
and  ,
the
following sequence are maintained for various
,
the
following sequence are maintained for various  s as:
s as:
for accretion where
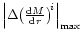 stands for the maximum value of
stands for the maximum value of
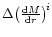 .
Whereas for wind it is observed that:
.
Whereas for wind it is observed that:
Also note that for the accretion branch all
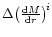 change sign except
change sign except
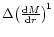 .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1237f5.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg163.gif) |
Figure 5:
Variation of the temperature deviation (
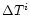 s) of
the accretion flow with radial distance for ultra relativistic
( s) of
the accretion flow with radial distance for ultra relativistic
(
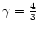 )
flow in various )
flow in various  s. While the difference
in flow temperature in between any Ti
(flow temperature for a particular ith potential s. While the difference
in flow temperature in between any Ti
(flow temperature for a particular ith potential  )
and )
and
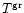 (flow temperature for FGRSF), is plotted along
the Y axis, the distance from the
central
accretor (in logarithmic scale in units of (flow temperature for FGRSF), is plotted along
the Y axis, the distance from the
central
accretor (in logarithmic scale in units of 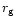 )
is plotted along X axis.
The maximum amount of deviation is obtained close to the accretor,
which is
expected. It is clearly observed from the figure that use of )
is plotted along X axis.
The maximum amount of deviation is obtained close to the accretor,
which is
expected. It is clearly observed from the figure that use of 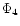 and
(except very close to the black hole)
and
(except very close to the black hole) 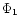 are the
best approximation of the
FGRSF flow temperature. Almost the same sort of deviation
is found for the wind branch (not shown in the figure).
are the
best approximation of the
FGRSF flow temperature. Almost the same sort of deviation
is found for the wind branch (not shown in the figure). |
| Open with DEXTER |
One can easily show that at any point of the flow,
the flow temp Ti for flow in any particular
 s can be re-written as:
s can be re-written as:
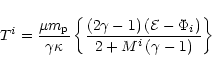 |
(16) |
where Mi is the corresponding Mach number for the ith pseudo potential.
As it has been stated that Mi can be calculated at each point of the flow,
one can compute Ti from knowledge of Mis using Eq. (16). After defining
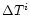 to be:
to be:
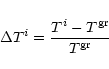 |
(17) |
where
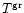 could be computed using Eq. (6), one can plot
could be computed using Eq. (6), one can plot
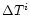 as a function of radial distance (in units of
as a function of radial distance (in units of 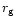 )
to investigate
which
)
to investigate
which  produces the
corresponding Ti closest to
produces the
corresponding Ti closest to
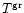 at a
particular radial distance and for a fixed value of the
at a
particular radial distance and for a fixed value of the
 and
and  .
In Fig. 5 we plot
.
In Fig. 5 we plot
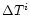 vs.
vs.
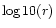 to demonstrate the dependence
of
to demonstrate the dependence
of
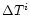 on radial distance. It is clear from the figure that except
for
T1, all other Tis are always higher than
on radial distance. It is clear from the figure that except
for
T1, all other Tis are always higher than
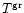 ,
which indicates
that all
,
which indicates
that all  s except
s except 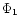 produce hotter flow than
FGRSF in general.
For
produce hotter flow than
FGRSF in general.
For 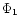 ,
very close to the hole the flow is cooler compared
to FGRSF up to a certain distance,
after which
,
very close to the hole the flow is cooler compared
to FGRSF up to a certain distance,
after which 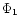 also produces
T1 higher to
also produces
T1 higher to
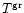 .
The point at which T1 becomes equal to
.
The point at which T1 becomes equal to
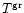 ,
gets
shifted away from the black hole with increasing
,
gets
shifted away from the black hole with increasing  ,
keeping
,
keeping  fixed. Also,
it is observed that
fixed. Also,
it is observed that
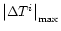 increases with increasing
increases with increasing  .
From Fig. 5 it is clear that
throughout its way from infinity to the event horizon,
.
From Fig. 5 it is clear that
throughout its way from infinity to the event horizon, 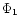 and
and 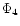 produces very good approximation of FGRSF regarding calculation of
flow temperature. However, after a certain point very close to the
black hole (after the crossing the point where
produces very good approximation of FGRSF regarding calculation of
flow temperature. However, after a certain point very close to the
black hole (after the crossing the point where
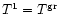 ),
),
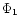 produces a sudden and sharp deviation of the
flow temperature from
FGRSF, physical reason for which is not clearly understood.
More or less the
same sort of profile in the
produces a sudden and sharp deviation of the
flow temperature from
FGRSF, physical reason for which is not clearly understood.
More or less the
same sort of profile in the
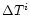 vs.
vs.
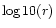 curve is also
observed for wind branch.
curve is also
observed for wind branch.
In this paper we
have solved a set of algebraic and differential equations
governing various dynamical and thermodynamic behaviouars
of Bondi (1954) type accretion in a full Schwarzschild metric
as well as for motion under a number of "pseudo-Schwarzschild''
potentials, to examine the suitability in
application of those
potentials in investigating spherically symmetric
transonic accretion onto a non-rotating black
hole. We have shown that though the potentials
discussed here were originally proposed to mimic the
relativistic effects manifested in the disc accretion,
it is quite reasonable to use most of the
potentials in studying various dynamical as well as thermodynamic
quantities
for spherical accretion. Also, we have shown that
depending on the chosen regions of parameter space
spanned by specific energy  and adiabatic index
and adiabatic index
 of the flow, one potential may be
important than others and we could identify which
potential is the best approximation for FGRSF for what
values of
of the flow, one potential may be
important than others and we could identify which
potential is the best approximation for FGRSF for what
values of  and
and  .
We have restricted ourselves to the
study of simple polytropic flows only.
However, the
validity of using all these
.
We have restricted ourselves to the
study of simple polytropic flows only.
However, the
validity of using all these  s discussed here can easily
be examined for isothermal accretion and wind as well as for flows
with other equations of state. Work in this direction is
reported elsewhere (Sarkar & Das 2001).
s discussed here can easily
be examined for isothermal accretion and wind as well as for flows
with other equations of state. Work in this direction is
reported elsewhere (Sarkar & Das 2001).
It is observed that among all pseudo
potentials, 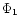 (potential proposed by Paczynski & Wiita
1980) and
(potential proposed by Paczynski & Wiita
1980) and 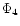 (one of the potentials proposed by
Artemova et al. 1996) are in general the best in the
sense that they provide very reasonable approximation
to the full general relativistic solution. While
(one of the potentials proposed by
Artemova et al. 1996) are in general the best in the
sense that they provide very reasonable approximation
to the full general relativistic solution. While 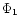 is the best approximation for ultra-relativistic flow,
is the best approximation for ultra-relativistic flow,
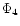 happens to be the best approximation as the flow
tends to be fully non relativistic, i.e,
happens to be the best approximation as the flow
tends to be fully non relativistic, i.e,
 tends to have the
value
tends to have the
value
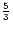 .
Also we see that there are certain cases for
which one or more of the pseudo potentials may give the
exact match with FGRSF for a particular value of
.
Also we see that there are certain cases for
which one or more of the pseudo potentials may give the
exact match with FGRSF for a particular value of  or
or
 (for a fixed r) in finding some dynamical (rc, M etc.) or
thermodynamic (flow temperature T, for example) quantity.
(for a fixed r) in finding some dynamical (rc, M etc.) or
thermodynamic (flow temperature T, for example) quantity.
It is worth mentioning that as long as one is not
interested in astrophysical processes extremely close
(within
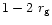 )
to a black hole horizon, one may safely
use the "pseudo'' potentials discussed here to study
spherically symmetric accretion on to a Schwarzschild
black hole with the advantage that use of these
potentials would simplify calculations by allowing one
to use some basic features of flat geometry
(additivity of energy or de-coupling of various
energy components, i.e., thermal (
)
to a black hole horizon, one may safely
use the "pseudo'' potentials discussed here to study
spherically symmetric accretion on to a Schwarzschild
black hole with the advantage that use of these
potentials would simplify calculations by allowing one
to use some basic features of flat geometry
(additivity of energy or de-coupling of various
energy components, i.e., thermal (
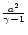 )
Kinetic (
)
Kinetic (
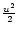 )
or
gravitational (
)
or
gravitational ( )
etc.) which is not possible for
calculations in a purely Schawarzschild metric. Also, one
can study more complex many body problems such as
accretion from an ensemble of companions or overall
effeciency of accretion onto an ensemble of black holes
in a galaxy or for studying numerical hydrodynamic or
magnetohydrodynamic flows
around a black hole etc. as simply as can be done in a
Newtonian framework, but with far better
accuracy. However, one should be careful in using these
potentials to study spherically symmetric accretion
because of the fact that none of the potentials discussed here
are "exact'' in a sense that they are not directly
derivable from the Einstein equations.
These potentials
could only be used to obtain more
accurate correction terms over and above the pure
Newtonian results and any "radically'' new results
obtained using these potentials should be cross-checked
very carefully with the exact general relativistic theory.
)
etc.) which is not possible for
calculations in a purely Schawarzschild metric. Also, one
can study more complex many body problems such as
accretion from an ensemble of companions or overall
effeciency of accretion onto an ensemble of black holes
in a galaxy or for studying numerical hydrodynamic or
magnetohydrodynamic flows
around a black hole etc. as simply as can be done in a
Newtonian framework, but with far better
accuracy. However, one should be careful in using these
potentials to study spherically symmetric accretion
because of the fact that none of the potentials discussed here
are "exact'' in a sense that they are not directly
derivable from the Einstein equations.
These potentials
could only be used to obtain more
accurate correction terms over and above the pure
Newtonian results and any "radically'' new results
obtained using these potentials should be cross-checked
very carefully with the exact general relativistic theory.
Although the theory of disc accretion has priority
over spherical accretion because of the fact that
accretion discs describe more realistic situations
found in nature, it is not unreasonable to
concentrate on spherical accretion because for
certain cases, that may be quite useful and
use of these potentials makes a complicated problem
simpler to
study. For example, for a supermassive black hole
immersed in intergalactic space in such a way that
matter falling on to it has negligible intrinsic
angular momentum, the accretion (at least
close to the hole) is quasi spherical and transonic spherical
accretion might be a good approximation to mimic the
situation. Same sort of approximation is valid when an
accreting black hole is embedded in a number of donor
stars (or star clusters) where the angular momentum of the stars are
randomly oriented in such a way that the vector sum
of the intrinsic angular momentum carried by the
accreting matter as a whole may be quite negligible, so as to
make Bondi-type accretion a good approximation. In fact, a
number of recent works (Coker &
Markoff 2001 and references therein;
Das 1999, 2000, 2001a,b;
Toropin et al. 1999; Kovalenko & Eremin 1998;
Titarchuk et al. 1996, 1997;
Wang & Sutherland 1997; Zampieri et al. 1996;
Yim & Park 1995; Markovic 1995;
Tsuribe et al. 1995; Kazhdan & Murzina 1994;
Fortner 1993) still deal with spherical
accretion to investigate some basic astrophysical
processes the black holes and neutron stars. So we believe that
work presented in this paper is relevant and will be useful
in investigation of
various aspects of accretion and wind around
non-rotating and slowly rotating compact objects.
Acknowledgements
We are grateful to Prof. P. J. Wiita and Prof. I. Novikov for useful
discussions.
- Artemova, I. V., Bjornsson, G., &
Novikov, I. D. 1996, ApJ, 461, 565
In the text
NASA ADS
- Begelman, M. C. 1978, A&A, 70, 583
In the text
NASA ADS
- Blumenthal, G. R., & Mathews, W. G. 1976, ApJ, 203, 714
In the text
NASA ADS
- Bondi, H. 1952, MNRAS, 112, 195
In the text
NASA ADS
- Brinkmann, W. 1980, A&A, 85, 146
In the text
NASA ADS
- Chakrabarti, S. K. 1996, Phys. Reports, 266, No. 5 & 6, 229
In the text
NASA ADS
- Coker, R. F., & Markoff, S. 2001, to appear in the
Proceedings of IAU, 205
In the text
- Das, T. K. 1999, MNRAS, 308, 201
In the text
NASA ADS
- Das, T. K. 2000, MNRAS, 318, 294
In the text
NASA ADS
- Das, T. K. 2001a, submitted to MNRAS
In the text
- Das, T. K. 2001b, A&A, in press
- Frank, J., King, A., & Raine, D. 1992, Accretion Power in
Astrophysics, 2nd edition (Cambridge University Press)
In the text
- Fortner, B. I. 1993, Ph.D. Thesis, Illinois Univ., Urbana-Champaign
In the text
- Kazhdan, Y. M., & Murzina, M. 1994, MNRAS, 270, 351
In the text
NASA ADS
- Kovalenko, I. G., & Eremin, M. A. 1998, MNRAS, 298, 861
In the text
NASA ADS
- Malec, E. 1999, Phys. Rev. D, 60, 104043
In the text
- Markovic, D. 1995, MNRAS, 277, 11
In the text
NASA ADS
- Michel, F. C. 1972, Astrophys. Space Sci., 15, 153
In the text
NASA ADS
- Novikov, I. D., & Thorne, K. 1973, in Black Holes, Les Astres Occlus, ed. B & C. De Witt (New York: Gordon & Breach), 343
In the text
- Nowak, A. M., & Wagoner, R. V. 1991, ApJ, 378, 656
In the text
NASA ADS
- Paczynski, B., & Wiita, P. J. 1980, A&A, 88, 23
In the text
NASA ADS
- Riffert, H., & Herold, H. 1995, ApJ, 450, 508
In the text
NASA ADS
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes,
White Dwarfs and Neutrin stars (John Wiley and Sons Inc)
In the text
- Sarkar, A., & Das, T. K. 2001, IJMPD, in press
In the text
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337
In the text
NASA ADS
- Titarchuk, L., Mastichiadis, A., &
Kylafis, N. D. 1997, ApJ, 487, 834
In the text
NASA ADS
- Titarchuk, L., Mastichiadis, A.,
& Kylafis, N. D. 1996, A&A, 120, 171
In the text
- Toropin, Yu. M., Toropina, O. D., Savelyev, V. V., Romanova, M.
M., Chechetkin, V. M., & Lovelace, R. V. E. 1999, ApJ, 517, 906
In the text
NASA ADS
- Wang, J. C. L., & Sutherland, R. S. 1998, in Accretion Processes in Astrophysical Systems: Some Like it Hot! ed. S. S. Holt, & T. R. Kallman, AIP Conf. Proc., 431, 413
- Tsuribe, T., Umemura, M., & Fukue, J. 1995, Publications of the Astronomical Society of Japan, vol. 47, No. 1, 73
In the text
- Weinberg, S. 1972, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (John Wiley & Sons)
In the text
- Yim, S. Y., & Park, M. 1995,
Publications of the Korean Astronomical Society, 10(1), 79
In the text
NASA ADS
- Zampieri, L., Miller, J. C., & Turolla, R. 1996, MNRAS, 281, 1183
In the text
NASA ADS
Copyright ESO 2001
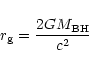
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1237f1.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg36.gif)
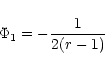
![\begin{displaymath}\Phi_{2}=-\frac{1}{2r}\left[1-\frac{3}{2r}+12{\left(\frac{1}{2r}\right)}^{\!\!2}\right]
\end{displaymath}](/articles/aa/full/2001/30/aa1237/img38.gif)
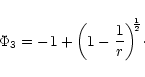
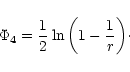
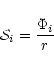
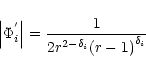
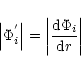
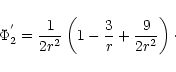
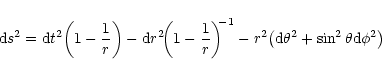
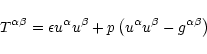
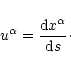
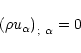
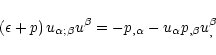
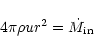
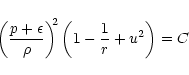
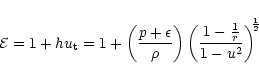
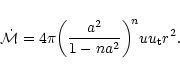

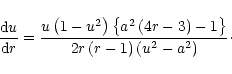
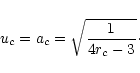
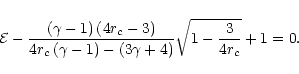
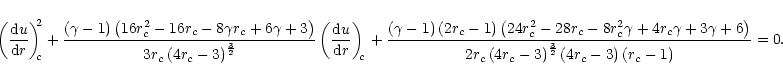
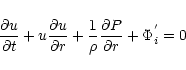
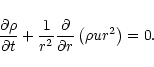
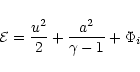
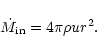
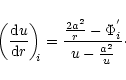
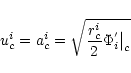
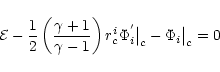
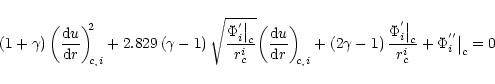
![\begin{figure}
\def \floatcounterend{}
\par\includegraphics[width=15cm,height=13.5cm,clip]{MS1237f2.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg106.gif)
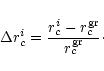
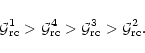
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1237f3.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg127.gif)
![\begin{figure}
\def \floatcounterend{}
\par\includegraphics[width=8.8cm,clip]{MS1237f4a.eps}\par\includegraphics[width=8.8cm,clip]{MS1237f4b.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg131.gif)
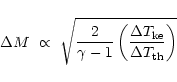
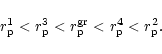
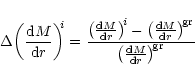
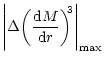
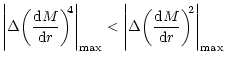
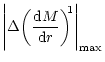
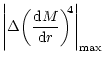
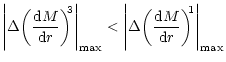
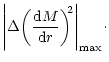
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS1237f5.eps}\end{figure}](/articles/aa/full/2001/30/aa1237/Timg163.gif)