

Up: Cosmic shear statistics and cosmology
Subsections
We summarize the different statistics we shall measure, and
how they depend on cosmological models.
We concentrate on 2-point statistics and variances, since
higher order moments are more difficult to measure, and will be
addressed in a forthcoming paper.
Let us assume a normalised source redshift distribution parameterized as:
![\begin{displaymath}%
n(z_{\rm s})={\beta\over z_0 \ \Gamma\left({1+\alpha\over \...
...pha \exp\left[-\left({z_{\rm s}\over z_0}\right)^\beta\right],
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img51.gif) |
(2) |
with the parameters
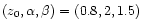 ,
which is consistent
with a limiting magnitude
,
which is consistent
with a limiting magnitude
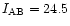 given by Cohen et al. (2000) (it corresponds
to a mean redshift of 1.2). However, in contrast to Cohen et al. (2000) we only have
photometric data (in one color), which prevents us from inferring the accurate
redshift distribution
of our galaxies. The impact of this uncertainty is discussed below. We adopted
a simplified approach consisting in looking at the sensitivity of cosmological
parameter estimation for three realistic redshift distributions. Therefore in
addition to the distribution expressed in Eq. (2) with z0=0.8,
we will consider two
other sets, one is
given by Cohen et al. (2000) (it corresponds
to a mean redshift of 1.2). However, in contrast to Cohen et al. (2000) we only have
photometric data (in one color), which prevents us from inferring the accurate
redshift distribution
of our galaxies. The impact of this uncertainty is discussed below. We adopted
a simplified approach consisting in looking at the sensitivity of cosmological
parameter estimation for three realistic redshift distributions. Therefore in
addition to the distribution expressed in Eq. (2) with z0=0.8,
we will consider two
other sets, one is
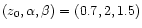 and the other
and the other
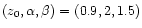 ,
which
,
which
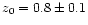 (similar to the
redshift error quoted in Rhodes et al. 2001), corresponding to an uncertainty
in the mean redshift of
(similar to the
redshift error quoted in Rhodes et al. 2001), corresponding to an uncertainty
in the mean redshift of 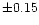 .
The three models are shown in Fig. 2, together with the redshift
distribution used in Wilson et al. (2000) corresponding to a magnitude distribution
.
The three models are shown in Fig. 2, together with the redshift
distribution used in Wilson et al. (2000) corresponding to a magnitude distribution
![$I\simeq [22.5,23.5]$](/articles/aa/full/2001/30/aa1091/img8.gif) ,
slightly brighter than our survey (the thick solid
line).
,
slightly brighter than our survey (the thick solid
line).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ndez.ps} %\end{figure}](/articles/aa/full/2001/30/aa1091/Timg54.gif) |
Figure 2:
The thin solid line shows our redshift distribution
model given by Eq. (2) with
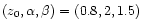 .
Two other models will also be used: one is .
Two other models will also be used: one is
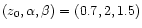 (thin dashed line) and one is (thin dashed line) and one is
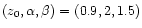 (thin dot-dashed
line). The thick solid line corresponds to the model used in Wilson et al. (2000) for the
(thin dot-dashed
line). The thick solid line corresponds to the model used in Wilson et al. (2000) for the
![$I\simeq [22.5,23.5]$](/articles/aa/full/2001/30/aa1091/img8.gif) galaxies. All the distributions are normalised.
galaxies. All the distributions are normalised. |
We define the power spectrum of the convergence as
(following the notation in Schneider et al. 1998):
where
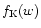 is the comoving angular diameter distance out to a distance w(
is the comoving angular diameter distance out to a distance w(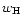 is the horizon distance),
and n(w(z)) is the redshift distribution of the sources given in
Eq. (2).
is the horizon distance),
and n(w(z)) is the redshift distribution of the sources given in
Eq. (2).
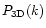 is the non-linear mass power spectrum,
and k is the 2-dimensional wave vector perpendicular to the
line-of-sight.
For a top-hat smoothing window of radius
is the non-linear mass power spectrum,
and k is the 2-dimensional wave vector perpendicular to the
line-of-sight.
For a top-hat smoothing window of radius
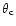 ,
the
variance is:
,
the
variance is:
![\begin{displaymath}%
\langle\gamma^2\rangle={2\over \pi\theta_{\rm c}^2} \int_0^\infty~{{\rm d}k\over k} P_\kappa(k)
[J_1(k\theta_c)]^2,
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img62.gif) |
(4) |
where J1 is the first Bessel function of the first kind.
The aperture mass
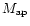 was introduced in Kaiser et al. (1994):
was introduced in Kaiser et al. (1994):
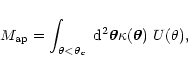 |
(5) |
where
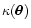 is the convergence field, and
is the convergence field, and 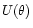 is a
compensated filter
(i.e. with zero mean). Schneider et al. (1998) applied this statistic to the cosmic
shear measurements. They showed that the aperture mass variance is related to
the convergence power spectrum by:
is a
compensated filter
(i.e. with zero mean). Schneider et al. (1998) applied this statistic to the cosmic
shear measurements. They showed that the aperture mass variance is related to
the convergence power spectrum by:
![\begin{displaymath}%
\langle M_{\rm ap}^2\rangle={288\over \pi\theta_c^4} \int_0^\infty~{{\rm d}k\over k^3}
P_\kappa(k) [J_4(k\theta_c)]^2.
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img66.gif) |
(6) |
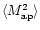 can be calculated directly from the shear
can be calculated directly from the shear
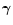 without the need for a mass reconstruction.
without the need for a mass reconstruction.
For each galaxy, we
define the tangential and radial shear components (
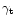 and
and
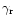 )
with respect to the center of the aperture:
)
with respect to the center of the aperture:
where 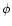 is the position angle between the x-axis and the line connecting
the aperture center to the galaxy.
It is then easy to show that the aperture mass is related to the tangential shear
by:
is the position angle between the x-axis and the line connecting
the aperture center to the galaxy.
It is then easy to show that the aperture mass is related to the tangential shear
by:
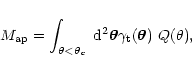 |
(8) |
where the filter 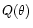 is given from
is given from 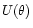 :
:
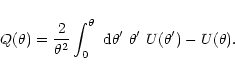 |
(9) |
If
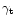 is replaced by
is replaced by
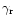 in Eq. (8), then
the lensing signal vanishes, due to the curl-free property
of the shear field (Kaiser et al. 1994)
in Eq. (8), then
the lensing signal vanishes, due to the curl-free property
of the shear field (Kaiser et al. 1994)![[*]](/icons/foot_motif.gif) .
This remarkable property constitutes a test of the lensing origin of the
signal. The change from
.
This remarkable property constitutes a test of the lensing origin of the
signal. The change from
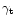 to
to
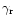 can simply
be accomplished just by rotating the galaxies by 45 degrees
in the aperture (i.e. changing a curl-free field to a pure curl field).
Hereafter we call the
can simply
be accomplished just by rotating the galaxies by 45 degrees
in the aperture (i.e. changing a curl-free field to a pure curl field).
Hereafter we call the
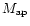 statistic measured with the
45 degree rotated galaxies the R-mode (R for radial mode), and
statistic measured with the
45 degree rotated galaxies the R-mode (R for radial mode), and
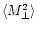 the corresponding variance.
It is interesting to note that the R-mode is not expected to vanish
if the measured signal is due to spin alignments of galaxies
(Crittenden et al. 2000b). Therefore it can be
used to constrain the amount of residual systematics as well as the
degree of the spin alignment of the galaxies leading to their intrinsic alignment.
the corresponding variance.
It is interesting to note that the R-mode is not expected to vanish
if the measured signal is due to spin alignments of galaxies
(Crittenden et al. 2000b). Therefore it can be
used to constrain the amount of residual systematics as well as the
degree of the spin alignment of the galaxies leading to their intrinsic alignment.
From the shear
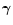 and its projections defined in
Eq. (7) we can also define
various galaxy pairwise correlation functions related to the
convergence power spectrum.
Note that the tangential and radial shear projections in what follows
are performed using the relative location vector of the
pair members, not from an aperture center.
The following correlation functions can be defined (Miralda-Escudé 1991; Kaiser 1992):
and its projections defined in
Eq. (7) we can also define
various galaxy pairwise correlation functions related to the
convergence power spectrum.
Note that the tangential and radial shear projections in what follows
are performed using the relative location vector of the
pair members, not from an aperture center.
The following correlation functions can be defined (Miralda-Escudé 1991; Kaiser 1992):
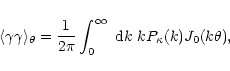 |
(10) |
![\begin{displaymath}%
\langle\gamma_{\rm t}\gamma_{\rm t}\rangle_\theta={1\over 4...
...^\infty~{\rm d} k~
k P_\kappa(k) [J_0(k\theta)+J_4(k\theta)],
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img80.gif) |
(11) |
![\begin{displaymath}%
\langle\gamma_{\rm r}\gamma_{\rm r}\rangle_\theta={1\over 4...
...^\infty~{\rm d} k~
k P_\kappa(k) [J_0(k\theta)-J_4(k\theta)],
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img81.gif) |
(12) |
where 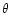 is the pair separation angle. The cross-correlation
is the pair separation angle. The cross-correlation
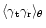 is expected to vanish for
parity reasons (there is no preferred orientation on average).
is expected to vanish for
parity reasons (there is no preferred orientation on average).
It is easy to see that the
Eqs. (4), (6), (10)-(12)
are different
ways to measure the same quantity, that is the convergence power
spectrum
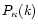 .
Ultimately the goal is to deproject
.
Ultimately the goal is to deproject
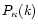 in order to
reconstruct the 3D mass power spectrum from Eq. (3),
but this is beyond the scope of
this paper. Here we restrict our analysis to a joint detection
of these statistics, and show that they are consistent with
the gravitational lensing hypothesis. We will also examine the
constraints on the power spectrum normalization
in order to
reconstruct the 3D mass power spectrum from Eq. (3),
but this is beyond the scope of
this paper. Here we restrict our analysis to a joint detection
of these statistics, and show that they are consistent with
the gravitational lensing hypothesis. We will also examine the
constraints on the power spectrum normalization 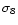 and the
mean density of the universe
and the
mean density of the universe 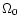 .
.
Let us now define the estimators we used to measure the quantities given in
Eqs. (4), (6), (10)-(12).
The variance of the shear is simply obtained by a cell averaging
of the squared shear
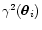 over the cell index i. An
unbiased estimate of the squared shear for the cell i is:
over the cell index i. An
unbiased estimate of the squared shear for the cell i is:
![\begin{displaymath}%
E[\gamma^2(\vec{\theta}_i)]={\displaystyle \sum_{\alpha=1}^...
...vec\theta_l)
\over
\displaystyle \sum_{k\ne l}^{N_i} w_k w_l},
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img86.gif) |
(13) |
where wk is the weight for the galaxy k, and Ni is the number of galaxies
in the cell i. The cell averaging over the survey is then an unbiased
estimate of the shear variance
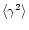 .
However, due to
the presence of masked areas (mentioned in Sect. 4.1),
some cells may have a very
low number of galaxies compared to others. Instead of applying an arbitrary sharp
cut off on the fraction of the apertures filled with masks
(as in previous works) we decided to keep all the cells, and to weight
each of them with the squared sum of the galaxy weights located in the cell.
The cell averaging is now defined as:
.
However, due to
the presence of masked areas (mentioned in Sect. 4.1),
some cells may have a very
low number of galaxies compared to others. Instead of applying an arbitrary sharp
cut off on the fraction of the apertures filled with masks
(as in previous works) we decided to keep all the cells, and to weight
each of them with the squared sum of the galaxy weights located in the cell.
The cell averaging is now defined as:
![\begin{displaymath}%
E[\gamma^2]={\displaystyle \sum_{\rm cells}
\left[E[\gamma^...
...{\rm cells} \left[\left(\sum_{k=1}^{N_i} w_k\right)^2\right]},
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img88.gif) |
(14) |
where i identifies the cell. One potential problem with this
procedure is that
the sum of the weights is related to the number of objects in
the aperture, which is affected by magnification bias, and therefore
correlated with the shear signal measured in the same aperture. Fortunately
the first non-vanishing contribution of this weighting scheme
is a third order effect (of order 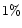 ), and is therefore
negligible
), and is therefore
negligible![[*]](/icons/foot_motif.gif) .
The advantage is that we can use all
cells without wondering about their filling factor, and it
naturaly down-weights the cells which contain a large fraction of
poorly determined galaxy ellipticities. The weighting scheme of
Eq. (14) has been tested against numerical simulation, using
a simulated survey with the same survey geometry as our data: it
gave unbiased measures of the lensing signal applied to the galaxies.
.
The advantage is that we can use all
cells without wondering about their filling factor, and it
naturaly down-weights the cells which contain a large fraction of
poorly determined galaxy ellipticities. The weighting scheme of
Eq. (14) has been tested against numerical simulation, using
a simulated survey with the same survey geometry as our data: it
gave unbiased measures of the lensing signal applied to the galaxies.
The
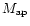 statistic is calculated from a similar
estimator, although the smoothing window is no longer a top-hat but
the Q function defined in Eq. (9). An unbiased estimate of
statistic is calculated from a similar
estimator, although the smoothing window is no longer a top-hat but
the Q function defined in Eq. (9). An unbiased estimate of
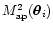 in the cell i is:
in the cell i is:
![\begin{displaymath}%
E[M_{\rm ap}^2(\vec{\theta}_i)]={\displaystyle \sum_{k\ne l...
...ta_k)Q(\theta_l)
\over
\displaystyle \sum_{k\ne l}^N w_k w_l},
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img92.gif) |
(15) |
where
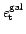 is the tangential galaxy ellipticity, and Q is given
by (see Schneider et al. 1998):
is the tangential galaxy ellipticity, and Q is given
by (see Schneider et al. 1998):
![\begin{displaymath}%
Q(\theta)={6\over \pi}\left({\theta\over \theta_c}\right)^2
\left[1-\left({\theta\over \theta_c}\right)^2\right].
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img94.gif) |
(16) |
The estimation of
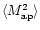 over the survey is then
given by the same expression
as in Eq. (14), with
over the survey is then
given by the same expression
as in Eq. (14), with
![$E[\gamma^2(\vec{\theta}_i)]$](/articles/aa/full/2001/30/aa1091/img95.gif) replaced by
replaced by
![$E[M_{\rm ap}^2(\vec{\theta}_i)]$](/articles/aa/full/2001/30/aa1091/img96.gif) .
We emphasize that the
this filter probes
effective scales
.
We emphasize that the
this filter probes
effective scales
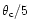 ,
and not
,
and not
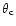 (see Fig. 2 in Schneider et al. 1998). Therefore we have to be careful when comparing the
signal at different scales between different estimators.
(see Fig. 2 in Schneider et al. 1998). Therefore we have to be careful when comparing the
signal at different scales between different estimators.
The shear correlation function
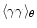 at separation
at separation 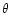 is obtained by identifying all the pairs of galaxies
falling in the separation interval
is obtained by identifying all the pairs of galaxies
falling in the separation interval
![$[\theta-{\rm d}\theta,\theta+{\rm d}\theta]$](/articles/aa/full/2001/30/aa1091/img99.gif) ,
and calculating the pairwise shear correlation:
,
and calculating the pairwise shear correlation:
![\begin{displaymath}%
E[\gamma\gamma;\theta]={\displaystyle \sum_{\alpha=1}^2}{\d...
...ec\theta_l)
\over \displaystyle \sum_{\rm pairs} w_k w_l}\cdot
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img100.gif) |
(17) |
The tangential and radial correlation functions
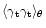 and
and
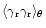 are measured also from Eq. (17) by replacing
are measured also from Eq. (17) by replacing
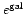 with
with
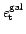 and
and
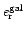 respectively
and dropping the sum over
respectively
and dropping the sum over  .
It is worth noting that the estimators given here are
independent of the angular correlation properties of the
source galaxies.
.
It is worth noting that the estimators given here are
independent of the angular correlation properties of the
source galaxies.


Up: Cosmic shear statistics and cosmology
Copyright ESO 2001
![\begin{displaymath}%
n(z_{\rm s})={\beta\over z_0 \ \Gamma\left({1+\alpha\over \...
...pha \exp\left[-\left({z_{\rm s}\over z_0}\right)^\beta\right],
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img51.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ndez.ps} %\end{figure}](/articles/aa/full/2001/30/aa1091/Timg54.gif)
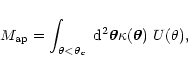
![]() and
and
![]() )
with respect to the center of the aperture:
)
with respect to the center of the aperture:
![]() and its projections defined in
Eq. (7) we can also define
various galaxy pairwise correlation functions related to the
convergence power spectrum.
Note that the tangential and radial shear projections in what follows
are performed using the relative location vector of the
pair members, not from an aperture center.
The following correlation functions can be defined (Miralda-Escudé 1991; Kaiser 1992):
and its projections defined in
Eq. (7) we can also define
various galaxy pairwise correlation functions related to the
convergence power spectrum.
Note that the tangential and radial shear projections in what follows
are performed using the relative location vector of the
pair members, not from an aperture center.
The following correlation functions can be defined (Miralda-Escudé 1991; Kaiser 1992):
![]() is the pair separation angle. The cross-correlation
is the pair separation angle. The cross-correlation
![]() is expected to vanish for
parity reasons (there is no preferred orientation on average).
is expected to vanish for
parity reasons (there is no preferred orientation on average).
![]() .
Ultimately the goal is to deproject
.
Ultimately the goal is to deproject
![]() in order to
reconstruct the 3D mass power spectrum from Eq. (3),
but this is beyond the scope of
this paper. Here we restrict our analysis to a joint detection
of these statistics, and show that they are consistent with
the gravitational lensing hypothesis. We will also examine the
constraints on the power spectrum normalization
in order to
reconstruct the 3D mass power spectrum from Eq. (3),
but this is beyond the scope of
this paper. Here we restrict our analysis to a joint detection
of these statistics, and show that they are consistent with
the gravitational lensing hypothesis. We will also examine the
constraints on the power spectrum normalization ![]() and the
mean density of the universe
and the
mean density of the universe ![]() .
.
![]() over the cell index i. An
unbiased estimate of the squared shear for the cell i is:
over the cell index i. An
unbiased estimate of the squared shear for the cell i is:
![]() statistic is calculated from a similar
estimator, although the smoothing window is no longer a top-hat but
the Q function defined in Eq. (9). An unbiased estimate of
statistic is calculated from a similar
estimator, although the smoothing window is no longer a top-hat but
the Q function defined in Eq. (9). An unbiased estimate of
![]() in the cell i is:
in the cell i is:
![\begin{displaymath}%
Q(\theta)={6\over \pi}\left({\theta\over \theta_c}\right)^2
\left[1-\left({\theta\over \theta_c}\right)^2\right].
\end{displaymath}](/articles/aa/full/2001/30/aa1091/img94.gif)
![]() at separation
at separation ![]() is obtained by identifying all the pairs of galaxies
falling in the separation interval
is obtained by identifying all the pairs of galaxies
falling in the separation interval
![]() ,
and calculating the pairwise shear correlation:
,
and calculating the pairwise shear correlation: