A&A 374, 784-799 (2001)
DOI: 10.1051/0004-6361:20010685
S. Britzen1 - J. Roland2 - J. Laskar3 - K. Kokkotas4 - R. M. Campbell5 - A. Witzel6
1 - Netherlands Foundation for Research in Astronomy, Oude
Hoogeveensedijk 4, 7991 PD Dwingeloo,
The Netherlands
2 - Institut
d'Astrophysique, 98bis boulevard Arago, 75014 Paris, France
3 - Bureau des
Longitudes, 77 avenue Denfert Rochereau, 75014 Paris, France
4 -
Department of Physics, Aristotle University of Thessaloniki, Thessaloniki
54006, Greece
5 - Joint Institute for VLBI in Europe, Oude Hoogeveensedijk
4, 7991 PD Dwingeloo, The Netherlands
6 - MPIfR, Auf dem Hügel 69, 53121
Bonn, Germany
Received 11 July 2000 / Accepted 10 May 2001
Abstract
VLBI monitoring of PKS 0420-014 at 3.6 cm performed during the
period 1989.32-1992.48 reveals superluminal jet components in a strongly
curved jet. We present a binary black hole model capable of simultaneously
explaining the flux-density variations and the motions of jet components on
helical trajectories in active galactic nuclei. From VLBI observations we
derive the characteristics of the parsec-scale jet of PKS 0420-014. Moreover,
we use the optical light curve of the quasar PKS 0420-014 over the time span
1989.67-1993.93 to determine the characteristics of the binary black hole
system. We propose that galactic and extragalactic radio sources with jets are
due to the existence of binary systems. Extragalactic binary systems are the
results of mergers and provide a natural explanation why only a small fraction
of quasars are radio sources and why extragalactic radio sources are
associated with elliptical galaxies. These binary systems will be one of the
primary targets for the Laser Interferometer Space Antenna (LISA).
Key words: black holes physics - gravitational waves - quasars: individual: PKS 04020-014 - radio continuum: galaxies
Extragalactic compact radio sources associated with nuclei of galaxies often
show flux-density variations across the wavelength spectrum on different
timescales. VLBI-component ejection in these sources is often associated with
an optical and/or a ![]() -ray outburst. Typical sources of this kind are
3C 273 and 3C 345 (see Zensus 1997 and references therein). Moreover, VLBI
observations show that jet components of several sources move on helical
trajectories. The radio source 3C 273 shows cycles of quasi-periodic activity
and ejections of VLBI components on helical paths close to the nucleus. It has
been shown by Roland et al. (1994) that the variability of 3C 273 can be
explained by a precessing accretion disk. In the case of the BL Lac Object OJ
287, the optical variability recorded over a time span of one hundred years
can be successfully explained by a binary black hole (BBH) model, e.g.,
Sillanpää et al. (1988) and Lehto & Valtonen (1996). According to
Lehto & Valtonen (1996) the smaller black hole of a binary pair crosses the
accretion disk of the larger black hole during the orbit, and causes the
substructure inside the major outbursts. Vicente et al. (1996) find evidence
from 3.6 cm geodetic VLBI monitoring of OJ 287 for a helical morphology of the
jet and for component ejection during optical outbursts. Their findings are
consistent with the supermassive BBH model proposed to explain the periodic
optical outbursts. Other sources where BBH models in the nuclei have been
discussed are Mrk 501 (Conway & Wrobel 1995) and 1928+738 (Roos et al. 1993).
PKS 0420-014 is known for its pronounced flux-density variability across
several wavelength bands. Wagner et al. (1995) predict jet component ejection
and component motion on a curved path within the framework of the lighthouse
model (Camenzind & Krockenberger 1992) based on the observed optical flaring.
Recently, Britzen et al. (2000a) published the results of nine epochs of VLBI
monitoring of PKS 0420-014 taken over a period of three years (1989.32-1992.48). Wagner et al. (1995) used four of these epochs to demonstrate for
the first time superluminal motion on a curved path in this source. Britzen et al. (2000a) studied the structural evolution of PKS 0420-014 and found
superluminal motion with
-ray outburst. Typical sources of this kind are
3C 273 and 3C 345 (see Zensus 1997 and references therein). Moreover, VLBI
observations show that jet components of several sources move on helical
trajectories. The radio source 3C 273 shows cycles of quasi-periodic activity
and ejections of VLBI components on helical paths close to the nucleus. It has
been shown by Roland et al. (1994) that the variability of 3C 273 can be
explained by a precessing accretion disk. In the case of the BL Lac Object OJ
287, the optical variability recorded over a time span of one hundred years
can be successfully explained by a binary black hole (BBH) model, e.g.,
Sillanpää et al. (1988) and Lehto & Valtonen (1996). According to
Lehto & Valtonen (1996) the smaller black hole of a binary pair crosses the
accretion disk of the larger black hole during the orbit, and causes the
substructure inside the major outbursts. Vicente et al. (1996) find evidence
from 3.6 cm geodetic VLBI monitoring of OJ 287 for a helical morphology of the
jet and for component ejection during optical outbursts. Their findings are
consistent with the supermassive BBH model proposed to explain the periodic
optical outbursts. Other sources where BBH models in the nuclei have been
discussed are Mrk 501 (Conway & Wrobel 1995) and 1928+738 (Roos et al. 1993).
PKS 0420-014 is known for its pronounced flux-density variability across
several wavelength bands. Wagner et al. (1995) predict jet component ejection
and component motion on a curved path within the framework of the lighthouse
model (Camenzind & Krockenberger 1992) based on the observed optical flaring.
Recently, Britzen et al. (2000a) published the results of nine epochs of VLBI
monitoring of PKS 0420-014 taken over a period of three years (1989.32-1992.48). Wagner et al. (1995) used four of these epochs to demonstrate for
the first time superluminal motion on a curved path in this source. Britzen et al. (2000a) studied the structural evolution of PKS 0420-014 and found
superluminal motion with
![]() ranging from 2 to 14 c for
five jet components. In addition they discuss evidence for a correlation
between component ejection and flux-density outbursts.
ranging from 2 to 14 c for
five jet components. In addition they discuss evidence for a correlation
between component ejection and flux-density outbursts.
Helical trajectories and the flaring behavior seen in the optical light curve
(1989-1993) of PKS 0420-014 have been explained in the framework of the
lighthouse model (Camenzind & Krockenberger 1992; Wagner et al.
1995). However, in this scenario the mass of the central object is found to be
very large: i.e., for an orbital radius of the knot of 0.2 light years it is
![]() and for an orbital radius of 0.75 light
years it is
and for an orbital radius of 0.75 light
years it is
![]() (Wagner et al. 1995). The
observational data base necessary to test and restrict theoretical models for
PKS 0420-014 has recently been significantly improved due to a more detailed
analysis of the VLBI epochs (Britzen et al. 2000a). This enables a new attempt
in modelling this source. To explain the origin of the precession of the
accretion disk and the origin of the optical light curve, we propose that
PKS 0420-014 contains a binary system of massive black holes. As we will see,
the BBH model requires significantly fewer massive black holes compared to the
lighthouse model.
(Wagner et al. 1995). The
observational data base necessary to test and restrict theoretical models for
PKS 0420-014 has recently been significantly improved due to a more detailed
analysis of the VLBI epochs (Britzen et al. 2000a). This enables a new attempt
in modelling this source. To explain the origin of the precession of the
accretion disk and the origin of the optical light curve, we propose that
PKS 0420-014 contains a binary system of massive black holes. As we will see,
the BBH model requires significantly fewer massive black holes compared to the
lighthouse model.
We first develop the mathematical formalism of the binary system model and the precession of the accretion disk. We then briefly discuss the overall flux-density variability observed for PKS 0420-014 and the kinematic information deduced from the VLBI observations of the jet components. We apply the BBH model to show that the kinematics of the jet components can be explained by the precession of the accretion disk and that the light curve of the optical outbursts can be explained by the motion of the jet-emitting black hole around the center of gravity of the system. Using VLBI and optical observations, we deduce the characteristics of the binary system. Finally, we discuss the hypothesis that binary systems underlie the existence of compact radio sources, and we investigate the possibility of detecting low frequency gravitational waves from such systems using the LISA experiment.
In this section, we develop the mathematical formalism to
describe a system consisting of two black holes and the influence of this
system on the jet and its emission. We assume that the nuclei of extragalactic
radio sources eject two fluids (the two-fluid model: Sol et al. 1989;
Pelletier & Roland 1989, 1990; Pelletier & Sol 1992). These are:
(i) an e
![]() plasma called the jet. It is mildly relativistic, ejected by the
nucleus at speeds
plasma called the jet. It is mildly relativistic, ejected by the
nucleus at speeds
![]() ;
;
(ii) an e![]() plasma called
the beam. It is relativistically ejected by the nucleus at speeds
plasma called
the beam. It is relativistically ejected by the nucleus at speeds
![]() i.e.,
i.e.,
![]() where
where
![]() is the bulk Lorentz factor.
is the bulk Lorentz factor.
The e
![]() jet carries most of the mass and the kinetic energy ejected by
the nucleus, and is responsible for the formation of kpc-jets, hot spots, and
extended lobes. The relativistic e
jet carries most of the mass and the kinetic energy ejected by
the nucleus, and is responsible for the formation of kpc-jets, hot spots, and
extended lobes. The relativistic e![]() beam moves in a channel through the
mildly relativistic jet and is responsible for the formation of superluminal
sources and their
beam moves in a channel through the
mildly relativistic jet and is responsible for the formation of superluminal
sources and their ![]() -ray emission (Roland et al. 1994). The relativistic
beam can propagate if the magnetic field B is parallel to the flow in the
beam and in the mixing layer between the beam and the jet and if it is greater
than a critical value (Pelletier et al. 1988; Achatz & Schlickeiser 1993).
The magnetic field in the e
-ray emission (Roland et al. 1994). The relativistic
beam can propagate if the magnetic field B is parallel to the flow in the
beam and in the mixing layer between the beam and the jet and if it is greater
than a critical value (Pelletier et al. 1988; Achatz & Schlickeiser 1993).
The magnetic field in the e
![]() jet rapidly becomes toroidal (Pelletier
& Roland 1990). The observational evidence for the two-fluid model has been
discussed by Roland & Hetem (1996) for instance. Recent observational
evidence for relativistic ejection of e
jet rapidly becomes toroidal (Pelletier
& Roland 1990). The observational evidence for the two-fluid model has been
discussed by Roland & Hetem (1996) for instance. Recent observational
evidence for relativistic ejection of e![]() beams comes from the
beams comes from the ![]() -ray observations of MeV sources (Roland & Hermsen 1995; Skibo et al. 1997)
and from VLBI polarization observations (Attridge et al. 1999). The formation
of the X-ray and
-ray observations of MeV sources (Roland & Hermsen 1995; Skibo et al. 1997)
and from VLBI polarization observations (Attridge et al. 1999). The formation
of the X-ray and ![]() -ray spectra, assuming relativistic ejections of
e
-ray spectra, assuming relativistic ejections of
e![]() beams, has been investigated by Marcowith et al. (1995, 1998) in the
case of Centaurus A. The possible existence of VLBI components with two
different speeds has been recently pointed out in the case of the radio
galaxies Centaurus A (Tingay et al. 1998) and M 87 (Biretta et al. 1999). In
addition to observations of one-sided superluminal sources, the existence of
two-sided subluminal VLBI sources has been well established in the case of
Cygnus A (Krichbaum et al. 1998), 3C 338 (Feretti et al. 1993), and Centaurus
A (Tingay et al. 1998).
beams, has been investigated by Marcowith et al. (1995, 1998) in the
case of Centaurus A. The possible existence of VLBI components with two
different speeds has been recently pointed out in the case of the radio
galaxies Centaurus A (Tingay et al. 1998) and M 87 (Biretta et al. 1999). In
addition to observations of one-sided superluminal sources, the existence of
two-sided subluminal VLBI sources has been well established in the case of
Cygnus A (Krichbaum et al. 1998), 3C 338 (Feretti et al. 1993), and Centaurus
A (Tingay et al. 1998).
We assume that the relativistic beam moves along the magnetic field lines,
which are perturbed by the precession of the accretion disk (Roland et al.
1994). We suppose that the accretion disk makes an angle
![]() with
the plane (xOy), such that the perturbed beam is on the surface of a cone
with symmetry axis
with
the plane (xOy), such that the perturbed beam is on the surface of a cone
with symmetry axis
![]() and opening angle
and opening angle
![]() .
Moreover, we suppose that the ejected component moves with a constant speed
characterized by its bulk Lorentz factor
.
Moreover, we suppose that the ejected component moves with a constant speed
characterized by its bulk Lorentz factor
![]() and follows the magnetic
field lines. The perturbation of the magnetic field propagates with a speed
given by the Alfvén speed
and follows the magnetic
field lines. The perturbation of the magnetic field propagates with a speed
given by the Alfvén speed ![]() .
The coordinates of the component moving in
the perturbed beam are given by
.
The coordinates of the component moving in
the perturbed beam are given by
| (4) |
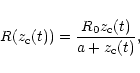
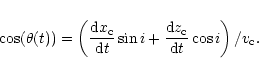
![\begin{eqnarray*}\delta(t)=\frac{1}{\gamma_{\rm c}[1-\beta_{\rm c}\cos(\theta(t))]}\;,
\end{eqnarray*}](/articles/aa/full/2001/30/aa10101/img44.gif)
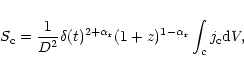
{\rm d}t^{\prime}.
\end{eqnarray*}](/articles/aa/full/2001/30/aa10101/img49.gif)
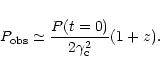
In order to explain the origin of the precession, we propose that the nucleus
is part of a binary system (see Appendix I). In the following, index 1 denotes
the black hole ejecting the VLBI components, index d denotes the
accretion disk and index 2 denotes the second black hole (the correspondence
with indices in Appendix I is 0, 1, 2 respectively). The two black holes orbit
in the plane (xOy), and the origin is centered at the mass center of the
system. The elliptical orbit is given by
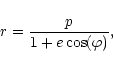
| x1(t)= |
(7) |
| y1(t)= |
(8) |
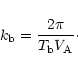
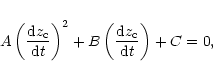
Two sorts of variability have been detected in the source PKS 0420-014. The source is known for its pronounced flux-density variability in several parts of the electromagnetic spectrum (Wagner et al. 1995; Britzen et al. 2000a and references therein). PKS 0420-014 did undergo a simultaneous optical/gamma-ray flaring at the time of a radio outburst, providing an opportunity to investigate the relation between the structural evolution and the flaring activity seen in the radio, optical, and gamma-ray regimes (Wagner et al. 1995; Britzen et al. 2000a).
A detailed description and analysis of five years of optical monitoring within the Hamburg Quasar
Monitoring Program and at the Landessternwarte in Heidelberg is presented in
Wagner et al. (1995). PKS 0420-014 reveals two modes of variability at
optical wavebands (see Fig. 1, this paper). On top of an almost
regular major flaring cycle having a period of ![]() 13 months (peaks in early
1990, 1991, and 1992) in which each flare lasts about one month, variations on
shorter timescales are detected. The EGRET instrument detected gamma-radiation
above 100 MeV during two observation periods in early 1992 (Hartman et al.
1999). The epoch of the strong gamma-ray flaring in 1992 coincided with the
strongest outburst of optical emission observed in 5 yrs of monitoring since
1989 (Wagner et al. 1995).
13 months (peaks in early
1990, 1991, and 1992) in which each flare lasts about one month, variations on
shorter timescales are detected. The EGRET instrument detected gamma-radiation
above 100 MeV during two observation periods in early 1992 (Hartman et al.
1999). The epoch of the strong gamma-ray flaring in 1992 coincided with the
strongest outburst of optical emission observed in 5 yrs of monitoring since
1989 (Wagner et al. 1995).
VLBI monitoring performed at 3.6 cm revealed structural variability in the jet of PKS 0420-014 (Britzen et al. 2000a) possibly correlated with brightness variations in several bands. The BBH model introduced in the previous section is capable of explaining the radio morphology and its changes, as well as the flux-density flaring observed in the optical waveband. In the following section, we apply this model to the quasar PKS 0420-014. A summary of the flux-density variability and a detailed description of the VLBI monitoring can be found in Britzen et al. (2000a); first results of the BBH modelling have already been presented in Britzen et al. (1998b).
Britzen et al. (2000a) present nine VLBI observations of the OVV quasar
PKS 0420-014 performed at
![]() cm between 1989.32 and 1992.48 and
one VLBI observation at 43 GHz. A subsample of four of the nine VLBI
observations have already been presented in Wagner et al. (1995). In these
four epochs the motion of the two brightest jet components with respect to the
core was traced and for the first time superluminal motion as well as motion
on a curved path could be proven for this source. The large number of VLBI
observations available now enables a more detailed analysis of the jet
structure out to core separations of
cm between 1989.32 and 1992.48 and
one VLBI observation at 43 GHz. A subsample of four of the nine VLBI
observations have already been presented in Wagner et al. (1995). In these
four epochs the motion of the two brightest jet components with respect to the
core was traced and for the first time superluminal motion as well as motion
on a curved path could be proven for this source. The large number of VLBI
observations available now enables a more detailed analysis of the jet
structure out to core separations of ![]() 3 mas, and out to
3 mas, and out to ![]() 6 mas with
higher uncertainties in parameter estimates. The jet can be well described by
up to eight distinct jet components. In this analysis, we concentrate on the
five innermost components (A-E), labelled according to their
increasing separation from the core, see Figs. 3-5. A linear regression analysis yields superluminal motion of
value
6 mas with
higher uncertainties in parameter estimates. The jet can be well described by
up to eight distinct jet components. In this analysis, we concentrate on the
five innermost components (A-E), labelled according to their
increasing separation from the core, see Figs. 3-5. A linear regression analysis yields superluminal motion of
value
![]() for component A,
for component A,
![]() (B),
(B),
![]() (C),
(C),
![]() (D), and
(D), and
![]() (E). The components seem
to separate faster in the vicinity of the core; the "older'' jet components,
at larger core separations, move more slowly.
(E). The components seem
to separate faster in the vicinity of the core; the "older'' jet components,
at larger core separations, move more slowly.
In this article, we assume:
The global VLBI observations performed at 43 GHz indicate a similar path for
the jet components, but one in which the bending continues towards the
innermost region and becomes even more pronounced with a
![]() turn
within 0.5 mas of the core. The total bending within the inner 2 mas must be
at least
turn
within 0.5 mas of the core. The total bending within the inner 2 mas must be
at least
![]() .
Britzen et al. (2000a) estimate epochs of
component ejection from the core using the derived component velocities and
trajectories. They discuss possible correlations between epochs of component
ejection and multiwavelength flux-density activity. Although the sampling of
the flux-density data and the large error bars of the calculated component
ejection epochs do not allow a definite correlation of such events, the onset
of ejection of the relativistic particles responsible for the radio emission
of components A and B appears to occur before the ejection of the relativistic
particles responsible for their simultaneous optical/gamma-ray flaring. The
observational data shown in this paper result from elliptical Gaussian
modelfitting and have been discussed in detail in Britzen et al. (2000a). The
uncertainties for each component assumed there are: for the flux S,
.
Britzen et al. (2000a) estimate epochs of
component ejection from the core using the derived component velocities and
trajectories. They discuss possible correlations between epochs of component
ejection and multiwavelength flux-density activity. Although the sampling of
the flux-density data and the large error bars of the calculated component
ejection epochs do not allow a definite correlation of such events, the onset
of ejection of the relativistic particles responsible for the radio emission
of components A and B appears to occur before the ejection of the relativistic
particles responsible for their simultaneous optical/gamma-ray flaring. The
observational data shown in this paper result from elliptical Gaussian
modelfitting and have been discussed in detail in Britzen et al. (2000a). The
uncertainties for each component assumed there are: for the flux S, ![]()
![]() ;
for the distance r from the core,
;
for the distance r from the core,
![]() mas.
mas.
We propose to explain the phenomena seen in PKS 0420-014 in the radio and the
optical regime using only the BBH model. The precession of the accretion disk
and the motion of the black holes around the center of gravity of the BBH
system produce two different perturbations of the magnetic field lines which
confine the e![]() beam. The perturbations of the magnetic field lines
propagate along the beam with a speed given by the Alfvén speed. Within this
model, the VLBI observations can be explained by the precession of the
accretion disk, and the optical light curve by the motion of the black hole
ejecting the radio jets around the center of gravity of the BBH system. The
problem that complicates the modelling of both wavelength regimes is the
different variability timescales and amplitudes of the observed phenomena. The
optical light curve of PKS 0420-014 shows variations with peaks of about 2
magnitudes with a typical time scale of about 1 year. The radio flux-density
of the VLBI component B increases over several years with brightness
variations somewhat smaller than a factor of 10. As the e
beam. The perturbations of the magnetic field lines
propagate along the beam with a speed given by the Alfvén speed. Within this
model, the VLBI observations can be explained by the precession of the
accretion disk, and the optical light curve by the motion of the black hole
ejecting the radio jets around the center of gravity of the BBH system. The
problem that complicates the modelling of both wavelength regimes is the
different variability timescales and amplitudes of the observed phenomena. The
optical light curve of PKS 0420-014 shows variations with peaks of about 2
magnitudes with a typical time scale of about 1 year. The radio flux-density
of the VLBI component B increases over several years with brightness
variations somewhat smaller than a factor of 10. As the e![]() responsible
for the optical light curve and the e
responsible
for the optical light curve and the e![]() responsible for the radio
emission follow the same trajectories, the different behaviors observed in
radio and optical ranges imply that the relativistic e
responsible for the radio
emission follow the same trajectories, the different behaviors observed in
radio and optical ranges imply that the relativistic e![]() responsible for
the optical light curve are emitted during a much shorter time than the
relativistic e
responsible for
the optical light curve are emitted during a much shorter time than the
relativistic e![]() responsible for the radio emission.
responsible for the radio emission.
Hence, one can explain the variability of PKS 0420-014 as arising from a long burst of
relativistic e![]() responsible for the synchrotron radio emission and a
shorter burst of very energetic relativistic e
responsible for the synchrotron radio emission and a
shorter burst of very energetic relativistic e![]() responsible for the
synchrotron optical emission, where the emission of the e
responsible for the
synchrotron optical emission, where the emission of the e![]() responsible
for the synchrotron radio emission precedes the short burst of more energetic
e
responsible
for the synchrotron radio emission precedes the short burst of more energetic
e![]() responsible for the optical synchrotron emission. This behavior is
typical of compact variable sources (Tornikoski et al. 1994). Thus, the
optical emission is modeled as the emission of a point-source component and
the radio emission is modeled as the integrated emission of an elongated
component along the beam. Let us note that the difference between the optical
and the radio light curve cannot be explained by a possible deceleration of
the VLBI component. We aim to obtain one set of parameters that allows us to
fit the optical and VLBI data simultaneously. As indicated previously we
assume the geometry of the system is the same for the different VLBI
components and the bulk Lorentz factors and the duration of the emission of
the e
responsible for the optical synchrotron emission. This behavior is
typical of compact variable sources (Tornikoski et al. 1994). Thus, the
optical emission is modeled as the emission of a point-source component and
the radio emission is modeled as the integrated emission of an elongated
component along the beam. Let us note that the difference between the optical
and the radio light curve cannot be explained by a possible deceleration of
the VLBI component. We aim to obtain one set of parameters that allows us to
fit the optical and VLBI data simultaneously. As indicated previously we
assume the geometry of the system is the same for the different VLBI
components and the bulk Lorentz factors and the duration of the emission of
the e![]() responsible for the synchrotron radio emission of the different
VLBI components are different.
responsible for the synchrotron radio emission of the different
VLBI components are different.
In this section we describe how we derived the model parameters that give the
best representation of the VLBI observations. In particular, the results of
the VLBI monitoring include the flux-density evolution with time (Fig. 2), the linear separation of the components from the core as
functions of time (Figs. 3-5), and the
apparent speed of the components as a function of time (Fig. 6).
We want to determine the geometry of the perturbed magnetic field lines in
which the e![]() plasma (the beam) propagates. The geometry of the system
is characterized by three parameters: the inclination angle i, the opening
angle of the ejection cone
plasma (the beam) propagates. The geometry of the system
is characterized by three parameters: the inclination angle i, the opening
angle of the ejection cone
![]() ,
and the radius of the helical
trajectory
,
and the radius of the helical
trajectory ![]() .
In addition, the model depends on the precession
period
.
In addition, the model depends on the precession
period ![]() ,
the propagation speed of the perturbations along the magnetic
field lines (i.e., the Alfvén speed)
,
the propagation speed of the perturbations along the magnetic
field lines (i.e., the Alfvén speed) ![]() ,
and finally the bulk Lorentz
factor
,
and finally the bulk Lorentz
factor
![]() that characterizes the speed of the ejected component. We
assume a priori that the geometry is the same for the various components. We
then model the results for component B under the assumption that the
bulk Lorentz factors of the various components are different. The observed
brightness and kinematic evolution of jet component B which constrain
our model parameters are:
that characterizes the speed of the ejected component. We
assume a priori that the geometry is the same for the various components. We
then model the results for component B under the assumption that the
bulk Lorentz factors of the various components are different. The observed
brightness and kinematic evolution of jet component B which constrain
our model parameters are:
The beginning of the variability pattern (
![]() )
visible in the
optical light curve (Wagner et al. 1995) is caused by the birth of component
B. As can be seen in Fig. 1, the ejection of component B can
not account for all the variability features and we assume that the ejection
of component A contributes as well to the optical flaring later. We
therefore fit the 1989.67-1993.93 optical light curve as a blend of emissions
of components A and B. Wagner et al. (1995) supposed that an
optical light curve with half the period indicated in Fig. 1 is possible, in
that case the period of the BBH system will be reduced by a factor 2. Assuming
that the nucleus of PKS 0420-014 is a binary system, we then have the
following free parameters: the masses of the two black holes m1 (mass of
the black hole ejecting the radio plasma) and m2 (mass of the second
black hole), the eccentricity of the orbit e, and the rotation period
)
visible in the
optical light curve (Wagner et al. 1995) is caused by the birth of component
B. As can be seen in Fig. 1, the ejection of component B can
not account for all the variability features and we assume that the ejection
of component A contributes as well to the optical flaring later. We
therefore fit the 1989.67-1993.93 optical light curve as a blend of emissions
of components A and B. Wagner et al. (1995) supposed that an
optical light curve with half the period indicated in Fig. 1 is possible, in
that case the period of the BBH system will be reduced by a factor 2. Assuming
that the nucleus of PKS 0420-014 is a binary system, we then have the
following free parameters: the masses of the two black holes m1 (mass of
the black hole ejecting the radio plasma) and m2 (mass of the second
black hole), the eccentricity of the orbit e, and the rotation period
![]() .
The main constraints from the optical light curve are the amplitudes
of the optical peaks and the time separation between the peaks. In Sect. 4.2
we underlined the necessity to investigate 4 different Alfvén speeds;
additionally we investigated the range
.
The main constraints from the optical light curve are the amplitudes
of the optical peaks and the time separation between the peaks. In Sect. 4.2
we underlined the necessity to investigate 4 different Alfvén speeds;
additionally we investigated the range
![]() for the masses of the 2 black holes and
for the masses of the 2 black holes and ![]() for the
orbital eccentricity. Our calculations were done for the 3 possible
inclination angles
for the
orbital eccentricity. Our calculations were done for the 3 possible
inclination angles
![]() and
and ![]() with the bulk
Lorentz factors
with the bulk
Lorentz factors
![]() and
and
![]() for
the VLBI components B and A respectively. A fit of the
optical light curve is possible for the 4 values of the Alfvén speed; however
the variations of the VLBI flux density of component B constrain the
Alfvén speed reliably to
for
the VLBI components B and A respectively. A fit of the
optical light curve is possible for the 4 values of the Alfvén speed; however
the variations of the VLBI flux density of component B constrain the
Alfvén speed reliably to
![]() value. We find that the parameter
combination given in Table 3 allows us to fit the data best. A fit of the
optical light curve is possible for values of the eccentricity
value. We find that the parameter
combination given in Table 3 allows us to fit the data best. A fit of the
optical light curve is possible for values of the eccentricity
![]() ,
and in the following we will adopt the value e=0 for the
eccentricity, remarking that the characteristics of the binary system do not
change significantly for
,
and in the following we will adopt the value e=0 for the
eccentricity, remarking that the characteristics of the binary system do not
change significantly for
![]() .
.
We show the fit of the optical light curve in Fig. 1 obtained for
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10101fig1.eps}\end{figure}](/articles/aa/full/2001/30/aa10101/Timg130.gif) |
Figure 1: Fit of the optical light curve of PKS 0420-014. The optical light curve (Wagner et al. 1995) is shown with dots, superimposed are the emission of component A indicated by the dashed line and the emission of component B indicated by the continuous line. |
| Open with DEXTER | |
We determine the characteristic sizes of the binary system we found. As
the 3 inclination angles are possible, to simplify the discussion and to
determine some mean values for the binary system, we will assume in the
following that the inclination angle is
![]() .
As the mass of the
accretion disk is much smaller than the masses of the two black holes, the
precession period
.
As the mass of the
accretion disk is much smaller than the masses of the two black holes, the
precession period ![]() of the accretion disk is given by (see Appendix I)
of the accretion disk is given by (see Appendix I)![]()
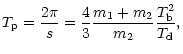 |
(12) |
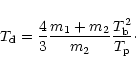 |
(13) |
The amplitude of the motion of the black hole ejecting radio jets is about 30
![]() as in the case of PKS 0420-014.
as in the case of PKS 0420-014.
An important constraint concerning the modelling of the
characteristics of VLBI component-emission comes from the difference between
the flux-density variations observed in the optical and the radio. Indeed,
the optical light curve shows flaring with an amplitude of 2 magnitudes with a
typical time-scale of about 1 year and the radio flux density of the VLBI
component B increases over years with brightness variations somewhat smaller
than a factor of 10. As mentioned previously this important difference can
be explained if the durations of the emission of the e![]() responsible for
the optical synchrotron emission and for the radio emission are different,
namely the relativistic e
responsible for
the optical synchrotron emission and for the radio emission are different,
namely the relativistic e![]() responsible for the optical light curve are
emitted during a much shorter time than the relativistic e
responsible for the optical light curve are
emitted during a much shorter time than the relativistic e![]() responsible
for the radio emission. This difference can be understood if we consider that
the optical emission is due to a point source component and that the radio
emission is due to an extended component whose observed flux is integrated
along the beam. The typical time scale of the duration of the emission of the
relativistic particles for component B is found to be about 25 yrs
of proper time which corresponds to about 1.2 yrs of observed time (see Fig. 7). The VLBI flux-density variations of component B are
shown in Fig. 2 (during the first year, the observed flux-density
is reduced by synchrotron self absorption).
responsible
for the radio emission. This difference can be understood if we consider that
the optical emission is due to a point source component and that the radio
emission is due to an extended component whose observed flux is integrated
along the beam. The typical time scale of the duration of the emission of the
relativistic particles for component B is found to be about 25 yrs
of proper time which corresponds to about 1.2 yrs of observed time (see Fig. 7). The VLBI flux-density variations of component B are
shown in Fig. 2 (during the first year, the observed flux-density
is reduced by synchrotron self absorption).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10101fig2.eps}\end{figure}](/articles/aa/full/2001/30/aa10101/Timg143.gif) |
Figure 2:
The flux-density of component B; VLBI observations are shown with
dots and the calculated flux-density is indicated by the continuous line. The
derived duration of the emission of the relativistic particles responsible for
the radio emission is |
| Open with DEXTER | |
If the typical time scale of the duration of the emission of the relativistic
particles for components A and B is found to be about 25 yrs, for the other components that have smaller bulk Lorentz factors it
would be about 10 yrs (see Table 5). For the case of PKS 0420-014, we
determined the bulk Lorentz factors of components C, D and E
using their mean apparent speeds obtained from VLBI observations. We show the
core separations of components B, C, D and E in Figs. 3-5. A newly ejected VLBI component first looks like a point component and
then becomes elongated along the beam. So we expect to see a trajectory
corresponding to a point source at the beginning and then a mean trajectory
corresponding to an elongated component later. In Figs. 3-5 we plot
the core separations as a function of the time corresponding both to a point
component (dashed line) and to a component having an extended emission
duration as given in Table 5, i.e., about 25 yrs for components A
and B and about 10yrs for the other components (continuous line).
| Component |
|
Duration | Birth | |
| A | 10 |
|
1.22 | 1991.13 |
| B | 8 |
|
3.14 | 1989.21 |
| C | 5.2 |
|
4.54 | 1987.81 |
| D | 3.9 |
|
|
|
| E | 2.5 |
|
|
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10101fig3.eps}\end{figure}](/articles/aa/full/2001/30/aa10101/Timg151.gif) |
Figure 3: Core separation of component B. The dashed line corresponds to a point component and the continuous line corresponds to a component which duration of the relativistic particles is given in Table 5. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10101fig4.eps}\end{figure}](/articles/aa/full/2001/30/aa10101/Timg152.gif) |
Figure 4: Core separation of component C. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10101fig5.eps}\end{figure}](/articles/aa/full/2001/30/aa10101/Timg153.gif) |
Figure 5: Core separations of components D and E. |
| Open with DEXTER | |
The variations of the apparent speeds of the VLBI components A, B and
C are shown in Fig. 6. We mention an important consequence of the
geometry determined previously. If we increase the bulk Lorentz factor to
![]() ,
the maximum apparent speed is limited to
,
the maximum apparent speed is limited to
![]() .
So a change of the bulk Lorentz factor
between 10 and 20 does not change the apparent speed predicted by the
model significantly. Should the apparent speed of a new component increase
towards values of
.
So a change of the bulk Lorentz factor
between 10 and 20 does not change the apparent speed predicted by the
model significantly. Should the apparent speed of a new component increase
towards values of ![]() ,
this could be an indication for a changing geometry
of the source; e.g., the angle
,
this could be an indication for a changing geometry
of the source; e.g., the angle
![]() between the accretion disk and
the plane of the two black holes can become smaller, producing a smaller
opening angle of the ejection cone of the newly ejected components.
between the accretion disk and
the plane of the two black holes can become smaller, producing a smaller
opening angle of the ejection cone of the newly ejected components.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10101fig6.eps} %
\end{figure}](/articles/aa/full/2001/30/aa10101/Timg157.gif) |
Figure 6:
Apparent speeds of the VLBI components A, B and C. The asymtotic
apparent speed corresponding to
|
| Open with DEXTER | |
We determined the birth dates of the components and calculated the ages
corresponding to epoch 1992.35. We list them together with the bulk Lorentz
factors and the duration of the emission of the relativistic particles in
Table 5. We obtained estimates on the age of component A from the age
of component B determined by the VLBI observations of the core
separation and applying the delay of 1.92 yrs between peaks corresponding to
each component, as deduced from the optical light curve (see Fig. 1). The
times given in Table 5 correspond to observed times. The proper times of the
VLBI components A, B, C and D have been plotted in Fig. 7.
From the observed age of the components we can deduce the proper times
corresponding to the beginning of the emission of relativistic particles for
each VLBI component. The proper times corresponding to the beginning of the
emission of the VLBI components are about 20 yrs for component A,
50 yrs for component B, 60 yrs for component C, and 75
yrs for component D. The determination of the proper times of the
VLBI components serves to check the consistency of the bulk Lorentz factors
with the durations of the emission of relativistic particles found for the
components. Indeed, the fit using an arbitrary value of
![]() ,
different from
,
different from
![]() as discussed in Sect. 4.2 yields
bulk Lorentz factors and durations for the different VLBI components that lead
to incompatible proper times for the different components. Let us remark that
for PKS 0420-014, the time delay between the ejection of new VLBI components
is not related a priori to the rotation period of the binary system, which is
about 150 yrs. In the case of component B, the beginning of the
emission of the e
as discussed in Sect. 4.2 yields
bulk Lorentz factors and durations for the different VLBI components that lead
to incompatible proper times for the different components. Let us remark that
for PKS 0420-014, the time delay between the ejection of new VLBI components
is not related a priori to the rotation period of the binary system, which is
about 150 yrs. In the case of component B, the beginning of the
emission of the e![]() responsible for the radio emission is 1989.21 (see
Table 5) and the beginning of the emission of the e
responsible for the radio emission is 1989.21 (see
Table 5) and the beginning of the emission of the e![]() responsible for
the optical emission is about 1989.8. This difference in the observed times
between the ejection of the e
responsible for
the optical emission is about 1989.8. This difference in the observed times
between the ejection of the e![]() responsible for the radio and the
optical emissions corresponds to about 10 years of proper time (see Fig. 7),
and has to be compared to the duration of the emission of the e
responsible for the radio and the
optical emissions corresponds to about 10 years of proper time (see Fig. 7),
and has to be compared to the duration of the emission of the e![]() responsible for the radio emission, which is about 25 yrs of proper time. As
indicated previously, this difference between these two times indicates that
the variability of PKS 0420-014 can be explained by a long burst of
relativistic e
responsible for the radio emission, which is about 25 yrs of proper time. As
indicated previously, this difference between these two times indicates that
the variability of PKS 0420-014 can be explained by a long burst of
relativistic e![]() responsible for the synchrotron radio emission and a
shorter burst of very energetic relativistic e
responsible for the synchrotron radio emission and a
shorter burst of very energetic relativistic e![]() responsible for the
synchrotron optical emission, where the emission of the e
responsible for the
synchrotron optical emission, where the emission of the e![]() responsible
for the synchrotron radio emission precedes the short burst of more energetic
e
responsible
for the synchrotron radio emission precedes the short burst of more energetic
e![]() responsible for the optical synchrotron emission.
responsible for the optical synchrotron emission.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{10101fig7.eps}\end{figure}](/articles/aa/full/2001/30/aa10101/Timg158.gif) |
Figure 7: The proper times of VLBI components A, B, C and D. Crosses indicates the begining of the emission of the relativistic particles for each VLBI component. |
| Open with DEXTER | |
Helical trajectories and the flaring behavior seen in the optical light curve
of PKS 0420-014 have been explained in the framework of the lighthouse model
(Camenzind & Krockenberger 1992; Wagner et al. 1995). However, in this
scenario the mass of the central object is found to be very large, i.e.
![]() .
.
The BBH model we propose requires less massive black holes. Due to the
relativistic speed of the components, the observed time is shortened, so that
the binary period and the precession period can produce effects observable on
time scales ranging from 1 to 10 yrs. The optical light curve can show peaks
separated by about one year (Fig. 1). The observed separation of
the light-curve peaks in time is related to the rotation period of the binary
system, but is not simply the rotation period of the BBH system shortened by
the relativistic speed (one has to take into account the effect of the
propagation speed of the beam perturbations, i.e., the Alfvén speed). However,
the observed delay between the emission of VLBI components and the optical
brightness variations is not necessarily related a priori to the rotation
period of the binary system. Further, the amplitude of the peaks of the
optical light curve depends strongly of the ratio
m1/m2. In the case
of PKS 0420-014, we have
![]() and the amplitude of the
peaks is about 2 magnitudes. However, radio sources containing a binary system
whose mass ratio is
and the amplitude of the
peaks is about 2 magnitudes. However, radio sources containing a binary system
whose mass ratio is
![]() will show helical VLBI trajectories
but optical light curves with peaks of very small amplitude after a new VLBI
component is ejected. To fit the VLBI observations, we assumed that the bulk
Lorentz factors of the various components were different. This is possible if
the environment of the clouds emitting the photons responsible for the Compton
drag changes with time. As indicated previously, within the geometry we
determined the ejected components cannot have apparent speeds larger than
will show helical VLBI trajectories
but optical light curves with peaks of very small amplitude after a new VLBI
component is ejected. To fit the VLBI observations, we assumed that the bulk
Lorentz factors of the various components were different. This is possible if
the environment of the clouds emitting the photons responsible for the Compton
drag changes with time. As indicated previously, within the geometry we
determined the ejected components cannot have apparent speeds larger than
![]() .
If VLBI observations of new components of
PKS 0420-014 show apparent speeds exceeding
.
If VLBI observations of new components of
PKS 0420-014 show apparent speeds exceeding ![]() ,
this can indicate a
change of the geometry, for instance the angle
,
this can indicate a
change of the geometry, for instance the angle
![]() of the
accretion disk with the rotation plane of the binary system could be decreasing.
of the
accretion disk with the rotation plane of the binary system could be decreasing.
An important consequence that we can deduce from the difference between the
optical light curve and the flux-density variations of the ejected VLBI
components is the following. The optical light curve shows peaks of about 2
magnitudes and the radio flux density evolution does not show similar peaks
during the five first years. This can be understood if the relativistic
e![]() responsible for the radio emission are ejected over a much longer
time than those responsible for the optical emission. This points out an
important characteristic of the variability of nuclei of extragalactic radio
sources: the emission of the e
responsible for the radio emission are ejected over a much longer
time than those responsible for the optical emission. This points out an
important characteristic of the variability of nuclei of extragalactic radio
sources: the emission of the e![]() (more precisely: the density and the
energy of the emitted e
(more precisely: the density and the
energy of the emitted e![]() )
is strongly variable with time. As an
important consequence, not all radio sources necessarily show relativistic
ejections of e
)
is strongly variable with time. As an
important consequence, not all radio sources necessarily show relativistic
ejections of e![]() ,
and subluminal radio sources are observable if the
mildly relativistic e
,
and subluminal radio sources are observable if the
mildly relativistic e
![]() jet contains relativistic e- accelerated by
magnetic field reconnection close to the accretion disk. Another important
consequence found from the fit of the optical light curve and the radio data
is that the burst of the most energetic e
jet contains relativistic e- accelerated by
magnetic field reconnection close to the accretion disk. Another important
consequence found from the fit of the optical light curve and the radio data
is that the burst of the most energetic e![]() responsible for the optical
emission occurs after the beginning of the emission of the e
responsible for the optical
emission occurs after the beginning of the emission of the e![]() responsible for the radio emission. VLBI observations of compact radio sources
at mm-wavelengths show either helically curved paths within one milliarcsecond
separation of the core (see e.g., Krichbaum et al. 1993) or jets with small
changes in PA due to intrinsic bends in the first milliarcsecond
(Rantakyrö et al. 1998). These observations can be explained if the
opening angle of the ejection cone, which is equal to the angle between the
accretion disk and the plane of the orbit of the two black holes, is large.
The angle found for PKS 0420-014 is particularly large. Britzen et al.
(2000b) found a tendency for the gamma-bright sources to have slightly higher
curvature of their VLBI trajectories than for the gamma-weak sources.
responsible for the radio emission. VLBI observations of compact radio sources
at mm-wavelengths show either helically curved paths within one milliarcsecond
separation of the core (see e.g., Krichbaum et al. 1993) or jets with small
changes in PA due to intrinsic bends in the first milliarcsecond
(Rantakyrö et al. 1998). These observations can be explained if the
opening angle of the ejection cone, which is equal to the angle between the
accretion disk and the plane of the orbit of the two black holes, is large.
The angle found for PKS 0420-014 is particularly large. Britzen et al.
(2000b) found a tendency for the gamma-bright sources to have slightly higher
curvature of their VLBI trajectories than for the gamma-weak sources.
The observations of PKS 0420-014 and some other compact sources suggest that their nuclei contain a BBH system. More generally, we will assume that extragalactic radio sources are associated with galaxies formed after the merging of galaxies and that the formation of extragalactic radio sources is related to the presence of binary black hole systems in their nuclei. This hypothesis could then explain why
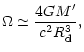 |
(14) |
| (15) |
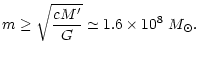 |
(16) |
Galactic radio sources that contain radio jets are especially suited to test the "binary hypothesis'' for the formation of extragalactic radio sources and the two-fluid model of radio sources. Ten galactic radio sources have shown evidence of relativistic jets (Mirabel & Rodríguez 1999). Some like SS 433 (Romney et al. 1987) and GRO J1655-40 (Hjellming & Rupen 1995) show helical jet paths or "wiggles'' on the VLBI scale. Moreover, we can observe:
Let us finish by discussing an important consequence of the fact that all
radio sources with jets might be associated with binary systems. These systems
will emit gravitational waves and may be detectable by the LISA experiment.
Assuming that the two black holes are moving circularly, then the energy
losses of the system due to the emission of gravitational waves are given by
(Landau & Lifshitz 1989)
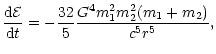 |
(17) |
| (18) |
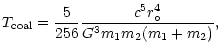 |
(19) |
We can estimate the typical timespan in which this system will be observable
by LISA. If we assume an optimistic lower limit in the bandwidth of LISA of
![]() Hz, then the corresponding period of the system will be
Hz, then the corresponding period of the system will be
![]() s and the separation between the 2 black holes will be
0.00037 pc. The collision of such a system occurs after about 2.6 yrs, so
due to its huge mass the binary system will spend a very short period of its
life in the expected bandwidth. Still during the final phase the signal will
be detectable. Even if the signal of the inspiral phase is outside the
bandwidth of LISA (Larson et al. 1999), the signal from the merging phase will
be detectable. Finally, when the two BHs coalesce, the resulting BH will have
a total mass
s and the separation between the 2 black holes will be
0.00037 pc. The collision of such a system occurs after about 2.6 yrs, so
due to its huge mass the binary system will spend a very short period of its
life in the expected bandwidth. Still during the final phase the signal will
be detectable. Even if the signal of the inspiral phase is outside the
bandwidth of LISA (Larson et al. 1999), the signal from the merging phase will
be detectable. Finally, when the two BHs coalesce, the resulting BH will have
a total mass
![]() and the quasinormal ringing
will be at a frequency of
and the quasinormal ringing
will be at a frequency of
![]() Hz (Kokkotas & Schmidt 1999).
Hz (Kokkotas & Schmidt 1999).
Assuming that the lifetime of a active radio galaxy is about 107 yrs,
there will be about 103 times more galaxies containing a binary black
hole system than active radio galaxies. As the space density of active radio
galaxies is about
![]() (Condon 1996), within a sphere of
104 Mpc (which corresponds to a redshift
(Condon 1996), within a sphere of
104 Mpc (which corresponds to a redshift
![]() ,
assuming
,
assuming
![]() km s-1 Mpc-1 and q0=0.5) we will find about
km s-1 Mpc-1 and q0=0.5) we will find about
![]() galaxies containing a binary system of massive black holes.
Thus, at any moment we can expect to have about one galaxy that contains a
binary system of massive black holes in a phase that should be observable with
LISA. Let us mention an important characteristic of the evolution of
extragalactic radio sources (Roland et al. 1985; Roland & Rhee 1989;
Roland et al. 1990). When the nucleus stops its activity, the evolution of
extended lobes of radio sources associated with clusters of galaxies is
dominated by synchrotron and inverse Compton losses rather than diffusion
losses and then one can observe that the radio spectrum evolves following the
two Kardashev laws (when expansion loses are stopped by the pressure of the
intergalactic medium, an equilibrium between the injection of new material
from the nucleus and radiation losses is reached and a first break happens in
the radio spectrum i.e. the radio spectrum is characterized by the two
spectral indices
galaxies containing a binary system of massive black holes.
Thus, at any moment we can expect to have about one galaxy that contains a
binary system of massive black holes in a phase that should be observable with
LISA. Let us mention an important characteristic of the evolution of
extragalactic radio sources (Roland et al. 1985; Roland & Rhee 1989;
Roland et al. 1990). When the nucleus stops its activity, the evolution of
extended lobes of radio sources associated with clusters of galaxies is
dominated by synchrotron and inverse Compton losses rather than diffusion
losses and then one can observe that the radio spectrum evolves following the
two Kardashev laws (when expansion loses are stopped by the pressure of the
intergalactic medium, an equilibrium between the injection of new material
from the nucleus and radiation losses is reached and a first break happens in
the radio spectrum i.e. the radio spectrum is characterized by the two
spectral indices
![]() and
and
![]() ,
latter
when the nucleus stops to inject new material in the extended lobe a second
break happens in the radio spectrum and the high frequency spectrum is
characterized by the spectral index
,
latter
when the nucleus stops to inject new material in the extended lobe a second
break happens in the radio spectrum and the high frequency spectrum is
characterized by the spectral index
![]() ).
The age of the extended lobes without input of new material from the nucleus
of the galaxy is of order of 108 yrs. These observations exclude a
scenario where the nucleus restarts its activity every 107 yrs. Moreover,
the energy contained in the extended lobes can reach 1061 ergs, i.e.
corresponds to about
).
The age of the extended lobes without input of new material from the nucleus
of the galaxy is of order of 108 yrs. These observations exclude a
scenario where the nucleus restarts its activity every 107 yrs. Moreover,
the energy contained in the extended lobes can reach 1061 ergs, i.e.
corresponds to about
![]() ,
so the nucleus
cannot have a recurrent activity every say 107 yrs and the radio source
cannot have 103 phases of activity.
,
so the nucleus
cannot have a recurrent activity every say 107 yrs and the radio source
cannot have 103 phases of activity.
Although these estimates are quite uncertain, massive BBH systems will be one
of the primary targets for LISA (Larson et al. 1999). Moreover, a simple
estimation shows that such systems, due to their large masses, will be
observable by LISA regardless of their distance. Indeed, the amplitude h of
the gravitational wave on earth is
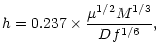 |
(20) |
For massive BBH systems we obtain:
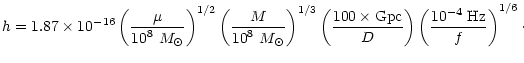 |
(21) |
The structural evolution of the quasar PKS 0420-014 can be modelled by a precession of the accretion disk. We explain the precession of the accretion disk by the presence of a binary system of black holes in the nucleus. We show that the light curve of the optical outburst associated with the birth of a new VLBI component can be explained by the motion of the beam-emitting black hole around the center of gravity of the BBH system. The amplitude of the optical peaks is very sensitive to the ratio of the masses of the binary system.
More generally, we propose that the formation of galactic and extragalactic compact radio sources containing jets can be related to the existence of binary systems. The existence of binary systems due to mergers in extragalactic radio sources can provide a natural explanation to understand why only about 5-10% of the quasars are radio sources and why extragalactic radio sources are associated with elliptical galaxies. The hypothesized existence of binary systems in all radio sources provides possible targets for the research of gravitational waves using the LISA experiment.
Acknowledgements
Part of this work was supported by the European Commission, TMR Programme, Research Network Contract ERBFMRXCT97-0034 CERES.
Let
P0,P1,P2 be three objects of mass
m0,m1,m2, and
![]() ,
where O is at the origin of an
inertial reference frame. Note that this treatment places no assumptions or
specific assignments on the masses 0, 1, 2; In the body of the text, the black
hole that emits the VLBI components corresponds to mass 0, the accretion disk
to mass 1, and the other black hole to mass 2.
,
where O is at the origin of an
inertial reference frame. Note that this treatment places no assumptions or
specific assignments on the masses 0, 1, 2; In the body of the text, the black
hole that emits the VLBI components corresponds to mass 0, the accretion disk
to mass 1, and the other black hole to mass 2.
In the canonical
variables
![]() ,
their motion is described by the Hamiltonian
,
their motion is described by the Hamiltonian
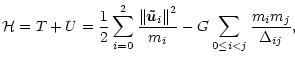 |
(22) |
The Jacobi coordinates are obtained through the linear transformation A:
![$\displaystyle \left[ \begin{array}{c} {\vec r}_0 \\ {\vec r}_1 \\ {\vec r}_2\...
...[
\begin{array}{c}
{\vec u}_0 \\ {\vec u}_1 \\ {\vec u}_2 \end{array}\right],$](/articles/aa/full/2001/30/aa10101/img192.gif) |
(23) |
![$\displaystyle %
\left[ \begin{array}{c} \vec{\tilde r}_0 \\ \vec{\tilde r}_1 \...
...\vec{\tilde u}_0 \\ \vec{\tilde u}_1 \\ \vec{\tilde u}_2 \end{array}\right] .$](/articles/aa/full/2001/30/aa10101/img193.gif) |
(24) |
| (25) |
| (26) |
Using these formulas, we obtain for the kinetic energy
| (28) |
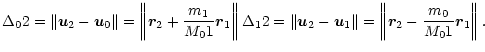 |
(30) |
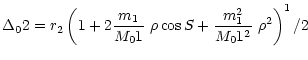 |
(31) | ||
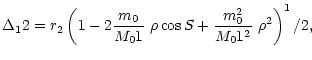 |
| (32) |
![\begin{figure}
\includegraphics[width=8cm,clip]{10101fig8.eps}\end{figure}](/articles/aa/full/2001/30/aa10101/Timg220.gif) |
Figure 8: Jacobi coordinates. |
| Open with DEXTER | |
| |
Figure 9:
Elliptical elements. The longitude of te ascending node, |
| Open with DEXTER | |
The Hamiltonian
![]() corresponds to a disjoint sum of two
Keplerian problems: motion of m1 around m0, and motion of m2around the center of mass of m0 and m1. These two-body problems are
expressed naturally in elliptical variables (ak: semi-major axis, ek: eccentricity, ik: inclination, Mk: mean anomaly,
corresponds to a disjoint sum of two
Keplerian problems: motion of m1 around m0, and motion of m2around the center of mass of m0 and m1. These two-body problems are
expressed naturally in elliptical variables (ak: semi-major axis, ek: eccentricity, ik: inclination, Mk: mean anomaly,
![]() :
argument of perihelion,
:
argument of perihelion,
![]() :
longitude of the node, for k=1,2). In
order to have canonical variables, we can use the Delaunay elliptical
variables, but here we will prefer the rectangular complex variables of
Poincaré defined from the classical elliptical elements as (Laskar 1990;
Laskar & Robutel 1995):
:
longitude of the node, for k=1,2). In
order to have canonical variables, we can use the Delaunay elliptical
variables, but here we will prefer the rectangular complex variables of
Poincaré defined from the classical elliptical elements as (Laskar 1990;
Laskar & Robutel 1995):
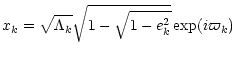 |
|||
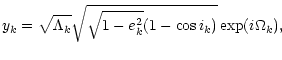 |
(33) |
| (34) |
| (35) |
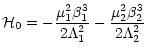 |
(37) |
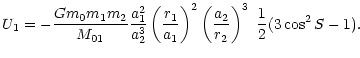 |
(38) |
Now we use the classical expansions of r/a, a/r, and ![]() in
elliptical variables in order to expand
in
elliptical variables in order to expand
![]() in elliptical variables.
We retain only up to second order terms in this expansion, and then only the
secular part of the Hamiltonian, i.e., the terms that do not depend of the
longitudes. This system will thus reflect the long term precession motion of
the orbits, and not the short term oscillations of small amplitude. With
in elliptical variables.
We retain only up to second order terms in this expansion, and then only the
secular part of the Hamiltonian, i.e., the terms that do not depend of the
longitudes. This system will thus reflect the long term precession motion of
the orbits, and not the short term oscillations of small amplitude. With
![]() ,
we obtain
,
we obtain
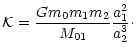 |
(40) |
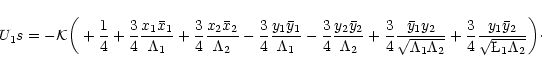 |
(41) |
As the secular Hamiltonian does not depend on the longitudes, from e.g.,
(37), we have immediately
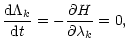 |
(42) |
| (45) |
| (46) |
| (47) |
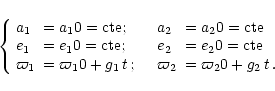 |
(49) |
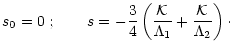 |
(50) |
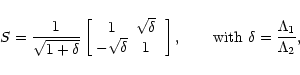 |
(51) |
![\begin{displaymath}%
\left[\begin{array}{c}w_1 \\ w_2\end{array}\right] =S^-1\le...
...ray}\right]\left[\begin{array}{c}y_1 \\ y_2\end{array}\right].
\end{displaymath}](/articles/aa/full/2001/30/aa10101/img266.gif) |
(52) |
![\begin{displaymath}%
\frac{\rm d}{{\rm d}t}\left[
\begin{array}{c}w_1 \\ w_2\end...
...}\right] \left[ \begin{array}{c}w_1 \\ w_2\end{array}\right] ,
\end{displaymath}](/articles/aa/full/2001/30/aa10101/img267.gif) |
(53) |
| (54) |
![\begin{displaymath}%
\left[ \begin{array}{c} y_1 \\ y_2\end{array}\right] =\frac...
...\right] \left[
\begin{array}{c}
w_1 \\ w_2\end{array}\right] .
\end{displaymath}](/articles/aa/full/2001/30/aa10101/img269.gif) |
(55) |
When
![]() ,
we have
,
we have
![]() ,
and the solutions
becomes
,
and the solutions
becomes
![]() ,
which gives
,
which gives
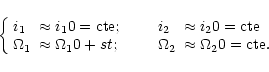 |
(56) |
In the case of the binary system, we can obtain the
![]() equation similar
to Eq. (6) in the following way. Calling
equation similar
to Eq. (6) in the following way. Calling
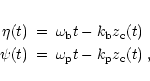
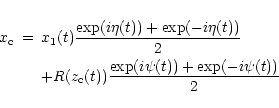
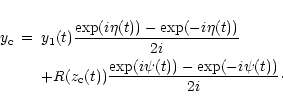
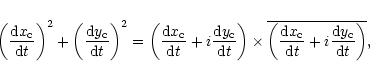
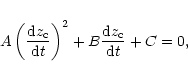
| A | = | 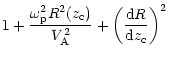 |
|
![$\displaystyle {+}\frac{\omega_{\rm b}^{2}\,x_{1}^{2}(t)}{2V_{\rm A}^{2}}\,[1{-}...
...}\frac
{\,\omega_{\rm b}^{2}\,y_{1}^{2}(t)}{2V_{\rm A}^{2}}[1{+}\cos(2\eta(t))]$](/articles/aa/full/2001/30/aa10101/img282.gif) |
|||
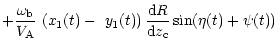 |
|||
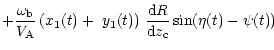 |
|||
| (57) | |||
| B | = | 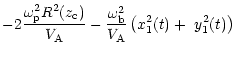 |
|
![$\displaystyle +\frac{\omega_{\rm b}^{2}}{V_{\rm A}}\left[ x_{1}^{2}(t)-\,\,y_{1}^{2}(t)\right]
\cos(2\eta(t))$](/articles/aa/full/2001/30/aa10101/img288.gif) |
|||
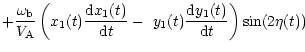 |
|||
![$\displaystyle +\omega_{\rm b}\,\left[ y_{1}(t)-\,\,x_{1}(t)\right] \frac{{\rm d}R}{{\rm d}z_{\rm c}}\sin
(\eta(t)+\psi(t))$](/articles/aa/full/2001/30/aa10101/img290.gif) |
|||
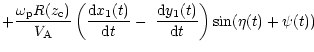 |
|||
![$\displaystyle -\omega_{\rm b}\left[ x_{1}(t)+\,\,y_{1}(t)\right] \frac{{\rm d}R}{{\rm d}z_{\rm c}}\sin
(\eta(t)-\psi(t))$](/articles/aa/full/2001/30/aa10101/img292.gif) |
|||
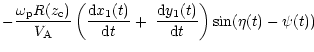 |
|||
![$\displaystyle -2\frac{\omega_{\rm b}\omega_{\rm p}R(z_{\rm c})}{V_{\rm A}}\left[ x_{1}(t)+\,\,y_{1}
(t)\right] \cos(\eta(t)-\psi(t))$](/articles/aa/full/2001/30/aa10101/img294.gif) |
|||
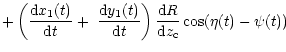 |
|||
![$\displaystyle +2\frac{\omega_{\rm b}\omega_{\rm p}R(z_{\rm c})}{V_{\rm A}}\left[ x_{1}(t)-\,\,y_{1}
(t)\right] \cos(\eta(t)+\psi(t))$](/articles/aa/full/2001/30/aa10101/img296.gif) |
|||
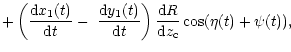 |
(58) | ||
| C | = | 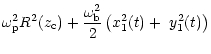 |
|
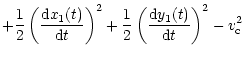 |
|||
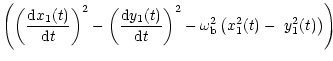 |
|||
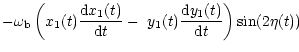 |
|||
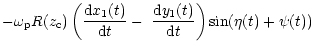 |
|||
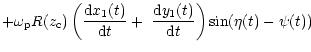 |
|||
| (59) |