A&A 374, 638-645 (2001)
DOI: 10.1051/0004-6361:20010727

A photometric study of the massive binary RY Sct

G. Djurasevic ¹ - M. Zakirov ² - M. Eshankulova ³ - S. Erkapic ¹

1 - Astronomical Observatory, Volgina 7, 11050 Belgrade, Yugoslavia - Astronomical Institute of Uzbek Academy of Sciences, Astronomicheskaya 33, 700052 Tashkent, Uzbekistan and Isaac Newton Institute of Chili, Uzbek branch
2 - Astronomical Institute of Uzbek Academy of Sciences, Astronomicheskaya 33, 700052 Tashkent, Uzbekistan

Received 14 April 2000 / Accepted 17 May 2001

Abstract
The present study deals with the problem of the estimation of the orbital and physical parameters for the EB-type eclipsing binary RY Sct, based on the interpretation of new photometric U B V R observations. The light curves obtained at the Maidanak Observatory during 1979-94 show a slight asymmetry around the secondary minima and a small difference in the height of the successive maxima. The light curves are analysed in the framework of the Roche computer model (Djurasevic 1992a) by applying the inverse-problem method (Djurasevic 1992b) based on Marquardt's (1963) algorithm. The analysis shows that RY Sct system is in an overcontact configuration $(f_{\rm over}\sim 33\%)$ with q=m₂/m₁=3.3 and $i\sim 84\hbox{$.\!\!^\circ$ }3$, generating total-annular eclipses. The basic parameters of the system and of the active region are estimated for all individual U, B, V and R light curves. Our results suggested a mass exchange between the components and mass loss through the outer Lagrangian point L₃. This could be taken as a possible mechanism in the formation of the circumstellar envelope of toroidal form lying in the orbital plane of the system.

Key words: stars: binaries: eclipsing, close - stars: early-type - stars: individual: RY Sct

1 Introduction

The early-type eclipsing binary RY Sct ( ${\rm HD \ 169515=}$ ${\rm BD-12^\circ5045}$) is a peculiar system with an orbital period ${P\sim 11\hbox{$.\!\!^{\rm d}$ }125}$, whose optical spectrum, classified as around B0pe, is characterized by strong [FeIII], [SiIII] emission lines and emission lines of hydrogen, helium, etc. Radio emission (Hughes & Woodsworth 1973), and infrared excess (Geisel 1970) dominated by extremely large stellar silicate excess (Grasdelen et al. 1979) indicated that the massive binary system RY Sct is surrounded by an extensive peculiar circumstellar nebula containing gas and dust. A shallow and asymmetrical emission feature observed at the base of ${\rm H_{\alpha}}$ indicated the presence of material expanding at higher velocities (de Martino et al. 1992). These authors suggested a multiple shell nebula and an asymmetrical mass outflow from the system. In the papers by Gehrz et al. (1995) and Smith et al. (1999) is shown a very complex structure of the ionized circumstellar nebula located at the inner edge of a more extended IR dust torus.

While some authors (e.g. Milano et al. 1981; de Martino et al. 1992) found that RY Sct is in the overcontact phase (with the more-massive cooler star and less-massive hotter one), Cowley & Hutchings (1976), King & Jameson (1979), Giuricin & Mardirossian (1981), Antokhina & Cherepashchuk (1988) and Antokhina & Kumsiashvili (1999) proposed a $\beta$ Lyrae model, where the secondary is hotter (O5) but under-luminous because of an obscuring disc. In the last two papers, the authors used a new value q=m₂/m₁=3.3 of the mass ratio (Skul'skij 1985, 1992). Some of the authors suggest that RY Sct is very probably in a short-lived evolutionary stage of the rapid mass-exchange phase, and is likely to evolve into a Wolf-Rayet ( ${\rm WR+OB}$) binary system.

Because of the high activity of this massive binary, producing the light-curve variation, we need new observations and a new analysis. In order to improve our present knowledge of this early-type massive binary we explore the new UBVR light curves made at Maidanak observatory. The large masses and high luminosities make new estimates of RY Sct's fundamental parameters and the system's evolutionary status of great interest.

2 New observations

The new photoelectric UBVR observations of RY Sct in Johnson's system were obtained by using the telescopes with the apertures of 0.4-m and 0.6-m at Maidanak Observatory (Uzbekistan) during 1979-1994. Our photoelectric observations of RY Sct were carried out using a one-channel photometer with standard UBVR filters. The comparison star used in the differential photometry was ${\rm BD-12^\circ5036}$ (V=9.048, U-B=0.200, B-V=0.287, V-R=0.315) and for a further check ${\rm BD-12^\circ5031}$ ( V=10.068, U-B=-0.36, B-V=0.250, V-R=0.321) was chosen. The magnitudes and colour indices are based on comparisons with photometric standard stars in Selected Areas 110-112, 114 (Moffett & Barness 1979). The total number of observations of the variable star are: 435 in U, 484 in B, 490 in V and 471 in R.

The orbital phases are calculated by using Giatti's (1980) ephemeris formulae

$$\begin{eqnarray*}{\rm Min~I} = 2443342.42 + 11\hbox{$.\!\!^{\rm d}$ }12471\times E. \end{eqnarray*}$$

3 The light-curve analysis and the results

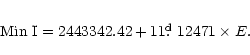
To estimate the parameters of this system, we analysed our new light curves using Djurasevic's (1992a) programme generalised to the case of an overcontact configuration (Djurasevic et al. 1998). The programme is based on the Roche model and on the principles arising from the paper by Wilson & Devinney (1971). The light-curve analysis was made by applying the inverse-problem method (Djurasevic 1992b) based on Marquardt's (1963) algorithm.

According to this method, the stellar size in the model is described by the filling factors for the critical Roche lobes $F_{\rm 1,2}$ of the primary and secondary component, respectively, which tell us to what degree the stars in the system fill their corresponding critical lobes. For synchronous rotation of the components, these factors are expressed as the ratio of the stellar polar radii, $R_{\rm 1,2}$, and the corresponding polar radii of the critical Roche lobes, i.e., $F_{\rm 1,2}=R_{\rm 1,2}/R_{\rm Roche_{1,2}}$. In the case of an overcontact configuration the potential $\Omega_{\rm 1,2}$ characterising the common photosphere, is derived with a filling factor of the critical Roche lobe $F_{\rm 1}>1$ of the primary, while the factor $F_{\rm 2}$ may be excluded from further consideration. The degree of overcontact is defined in the classical way (Lucy & Wilson 1979) as:

$$\begin{eqnarray*}f_{\rm over}[\%]=100\cdot(\Omega_{\rm 1,2}-\Omega_{\rm i})/(\Omega_{\rm o}- \Omega_{\rm i}), \end{eqnarray*}$$

where $\Omega_{\rm 1,2}$, $\Omega_{\rm i}$, and $\Omega_{\rm o}$ are the potentials of the common photosphere and of the inner and outer contact surfaces, respectively. To achieve more reliable estimates of the model parameters in the light curve analysis programme, we applied a quite dense coordinate grid, having $72\times144=$10368 individual elementary cells per star. The intensity and angular distribution of the radiation of individual cells are determined by the stellar effective temperature, limb-darkening, gravity-darkening and by the effect of reflection in the system.

We obtain optimum model parameters through the minimisation of $S=\Sigma{\rm (O{-}C)}^2$, where O-C is the residual between the observed (LCO) and synthetic (LCC) light curves for a given orbital phase. The minimisation of S is done in an iterative cycle of corrections of the model parameters. Some of these parameters can be determined a priori in an independent way while the others are found by solving of the inverse problem.

In previous versions of our programme, there were two different possibilities in the application of the model with respect to the treatment of the radiation law: the simple black-body theory, or the stellar atmosphere models by Carbon & Gingerich (1969) (CG). Our current version of the programme for the light-curve analysis uses the new promising Basel Stellar Library (BaSeL). We have explored the "corrected'' BaSeL model flux distributions, consistent with extant empirical calibrations (Lejeune et al. 1997, 1998), and with a large range of effective temperatures 2000 K $\le T_{\rm eff}\le$ 35000 K, surface gravities, $3\le {\rm log} \ g\le 5$ and metallicity, ${\rm -1\le[Fe/H]\le 1}$, where [Fe/H] is the logarithmic metal abundance. The surface gravities can be derived very accurately from the masses and radii of the close binary (CB) stars by solving the inverse problem of the light-curve analysis, but the temperature determination is related to the assumed metallicity and strongly depends on the photometric calibration.

In the inverse-problem solving, the fluxes are calculated in each iteration for the current values of temperatures and ${\rm log} \ g$ by interpolation in both of these quantites in atmosphere tables, as an input, for a given metallicity of the CB components. The metallicity of the involved CB components can be different. It is because of this that we can use individual, different tables as an input for each star, and in this way choose the best calculations for its particular atmospheric parameters. Compared to Vaz et al. (1995), our two-dimensional flux interpolation in $T_{\rm eff}$ and ${\rm log} \ g$ is based on the application of the bicubic spline interpolation (Press et al. 1992). This proved to be a good choice.

By choosing and fixing the particular input switch, the programme for the light-curve analysis can be simply redirected to the Planck or CG approximation, or to the more realistic BaSeL model atmospheres. A change in the assumed metallicity causes a noticeable change in the predicted stellar effective temperature. The value of the chemical abundance of the components was obtained by checking several different values around solar metallicity. In the case of RY Sct, the best fit of the UBVR light curves was obtained for the metallicity of the components ${\rm [Fe/H]_{hot,cool}=0.1}$. The indices (hot, cool) correspond to the hotter and cooler system's components respectively. Our analysis gives ${\rm log} \ g\ < 3$ (see Table 1) as the final solution for the system. We have a problem here arising from the extrapolation of BaSeL fluxes for the values ${\rm log} \ g\ < 3$ whose impact on the final results is difficult to estimate. Therefore, instead of BaSeL model atmospheres we finally choosed the CG approximation which yields lower disagreement between individual U, B, V and R solutions than the simple black-body approximation.

In the analysis of the light curves we avoided the somewhat questionable practice of forming normal points, and included all observations. The iterating process of optimisation converged very fast to the overcontact configuration with the mass ratio of the components $q=m_{\rm cool}/m_{\rm hot}=3.3$ (Skul'skij 1985, 1992). Because of that, we expected mutual tidal effects to synchronise stellar rotational and orbital periods. Therefore, in the inverse problem we adopted $f_{\rm hot,cool}=\omega_{\rm hot,cool}/\omega_{\rm K}=1.0$ for nonsynchronous rotation coefficients, where $f_{\rm hot,cool}$ is the ratio of the angular rotation rate ( $\omega_{\rm hot,cool}$) to the Keplerian ( $\omega_{\rm K}$) orbital revolution rate. Because the temperature scale of the hotter star is quite inaccurate, and having in mind that the determination of the effective temperature becomes complicated in the case of surrounding material, we used two different hypotheses concerning the temperature of the less-massive (hotter) star: $T_{\rm hot}=28\,000$ K (Hyp. I) and $T_{\rm hot}=30\,000$ K (Hyp. II). These values may be appropriate to a spectral assignment near B0. In previous analyses both these values were used. By considering these hypotheses we tried to estimate to what extent the results of the light-curve analysis are dependent on the adopted temperature value. The gravity-darkening coefficients, following Lucy (1967), and Rafert & Twigg (1980), were set to $\beta_{\rm hot,cool}=0.25$ according to the stars' temperature. This value corresponds to von Zeipel's law for fully radiative envelopes. Consequently, for the component's albedos we adopted the values $A_{\rm hot,cool}=1.0$, corresponding to full reradiation, with the same criterion. The limb-darkening coefficients ( $u_{\rm hot,cool}$) were derived according to stellar effective temperature and surface gravity via the polynomial proposed by Díaz-Cordovés et al. (1995). During the optimisation process, according to the temperature changes, we have an automatic recomputation of the limb-darkening. For the R-filter the limb-darkening was taken from the tables published by Al Naimy (1977). The solutions obtained in the light-curve analysis gave the overcontact configuration, with a high degree of overcontact ( $f_{\rm over} \sim 33\%$ - Hyp. I and $f_{\rm over} \sim 32\%$ - Hyp. II) and with significantly lower temperature of the more-massive (cooler) component ( $T_{\rm cool}\sim$ 24240 K - Hyp. I and $T_{\rm cool}\sim$ 25990 K - Hyp. II). The light-curve analysis show that the less-massive (hotter) component is eclipsed at the primary minimum. For the orbit inclination of the RY Sct we found $i\sim 84\hbox{$.\!\!^\circ$ }3$.

Because of the slight asymmetry around the secondary minima and the small difference in the height of the successive maxima, after achieving the first convergence, one also includes free parameters related to spots into the iterative optimisation process. According to our analysis, the relatively good fitting of the observations was achieved under the assumption of a relatively large hot area on the more-massive (cooler) star, near the neck region between the components ( $A_{\rm S1}=T_{\rm S1}/T_{\rm cool}\sim 1.23$, $\theta_{\rm S1}\sim 49^\circ$ and $\lambda_{\rm S1}\sim 167^\circ$). The obtained overcontact configuration, with the fixed mass ratio of the components $q=m_{\rm cool}/m_{\rm hot}=3.3$, and considerable temperature difference between the components, suggested a significant mass and energy transfer from the hotter less-massive component to the cooler one. These effects can be a physical cause of the hot area in the neck region on the more-massive star. In our programme this active region is approximated by a circular spot, described by the temperature contrast of the spot with respect to the surrounding photosphere ( $A_{\rm S}=T_{\rm S}/T_{\rm cool}$), by the angular dimension (radius) of the spot ( $\theta_{\rm S}$) and by the longitude ( $\lambda_{\rm S}$) and latitude ( $\varphi_{\rm S}$) of the spot centre. The longitude ( $\lambda_{\rm S}$) is measured clockwise (as viewed from the direction of the +Z-axis) from the +X-axis (the line connecting the stars' centres) in the range $0^\circ$-$360^\circ$. The latitude ( $\varphi_{\rm S}$) is measured from $0^\circ$ at the stellar equator (orbital plane) to $+90^\circ$towards the "north'' (+Z) and $-90^\circ$ towards the "south'' (-Z) pole. The assumed physical nature of the hot region allowed an approximation on its location, which also reduced the number of free model parameters: it is in the equatorial zone at the secondary ( $\varphi_{\rm S}=0^\circ$).

The quality of the fit of the observations can be improved by introducing an additional active region on the more-massive (cooler) star. The optimum solutions of the inverse problem (see Table 1) present this additional active region as a hot area in the equatorial zone of the star ( $A_{\rm S2}=T_{\rm S2}/T_{\rm cool}\sim 1.28$, $\theta_{\rm S2}\sim 29^\circ$ and $\lambda_{\rm S1}\sim 323^\circ$). This hot area is located near the external Lagrange point, L₃, and it is very probably that from this region we have the intensive gas outflow, which can be one of the causes giving rise to the circumstellar nebula around the system. We suggest that matter is emanating near the L₃ point which implies that material is flowing from the less-massive primary towards the secondary. After having passed through the neck region the material is accelerated very likely by radiation pressure and lost from the system. By analysing high-resolution spectroscopic observations de Martino et al. (1992) found that three mechanisms could be responsible for the explanation of the nebula around RY Sct: mass loss by stellar wind, mass outflow from the external Lagrange point or a major expulsion phase from the system. The study of Milano et al. (1981) indicates that the system is in a high degree of overcontact (41%) which also could favour mass loss from the external Lagrange point during the mass exchange phase as the main mechanism.

  

Table 1: Results of the analysis of the RY Sct light curves obtained by solving the inverse problem for the Roche model with two active hot areas on the more-massive (cooler) component.

$$\begin{tabular}{@{}lllllllll@{}} {$ \begin{array}{@{}lllllll... ...\\ \noalign{\smallskip } \hline \end{array}$}\end{tabular}$$

Fixed parameters: Hyp. I $T_{\rm hot}=28\,000$ K - temperature of the less-massive (hotter) star,

Hyp. II $T_{\rm hot}=30\,000$ K - temperature of the less-massive (hotter) star, $f_{\rm hot}=f_{\rm cool}=1.00$ - nonsynchronous rotation coefficients of the components,

$q=m_{\rm cool}/m_{\rm hot}=3.3$ - mass ratio of the components,

$\beta_{\rm hot,cool}=0.25$ - gravity-darkening coefficients of the components,

$A_{\rm hot,cool}=1.0$ - albedo coefficients of the components.

$\varphi_{\rm hs}=0^\circ$ - hot spot latitude (equatorial zone of the star),

Carbon & Ggingerich (CG) approximation.

Note: n - number of observations, ${\rm\Sigma (O{-}C)^2}$ - final sum of squares of residuals between observed (LCO) and synthetic (LCC) light curves, ${\rm\sigma}$ - standard deviation of the observation, $A_{\rm S1,2}=T_{\rm S1,2}/T_{\rm cool}$ - spots' temperature coefficient, $\theta_{\rm S1,2}$ and $\lambda_{\rm S1,2}$ - spots' angular dimensions and longitudes (in arc degrees), $F_{\rm hot}$ - filling factor for the critical Roche lobe of the hotter less-massive star, $T_{\rm cool}$ - temperature of the more-massive cooler star, i - orbit inclination (in arc degrees), $u_{\rm hot,cool}$ - limb-darkening coefficients of the components, $\Omega_{\rm hot,cool}$ - dimensionless surface potentials of the primary and secondary, $\Omega_{\rm in}$, $\Omega_{\rm out}$ - the potentials of the inner and outer contact surfaces respectively, $f_{\rm over}[\%]=100\cdot(\Omega_{\rm hot,cool}-\Omega_{\rm in})/(\Omega_{\rm out}-\Omega_{\rm in})$ - degree of overcontact, $L_{\rm h}/L_{\rm s}=L_{\rm hot}/(L_{\rm hot}+L_{\rm cool})$ - luminosity of the hotter star (including spots on the cooler one), $M^{\rm hot,cool}_{\rm bol}$ - absolute bolometric magnitudes of RY Sct components, $\cal M_{\rm hot,cool} {[{\it M}_{\odot}]}$ - stellar masses in solar units, $\cal R_{\rm hot,cool} {[{\it R}_{\odot}]}$ - mean radii of stars in solar units, ${\rm log} \ g_{\rm hot,cool}$ - logarithm (base 10) of the mean surface acceleration (effective gravity) for components and $a_{\rm orb} {[R_{\odot}]}$ - orbital semi-major axis in units of solar radius.

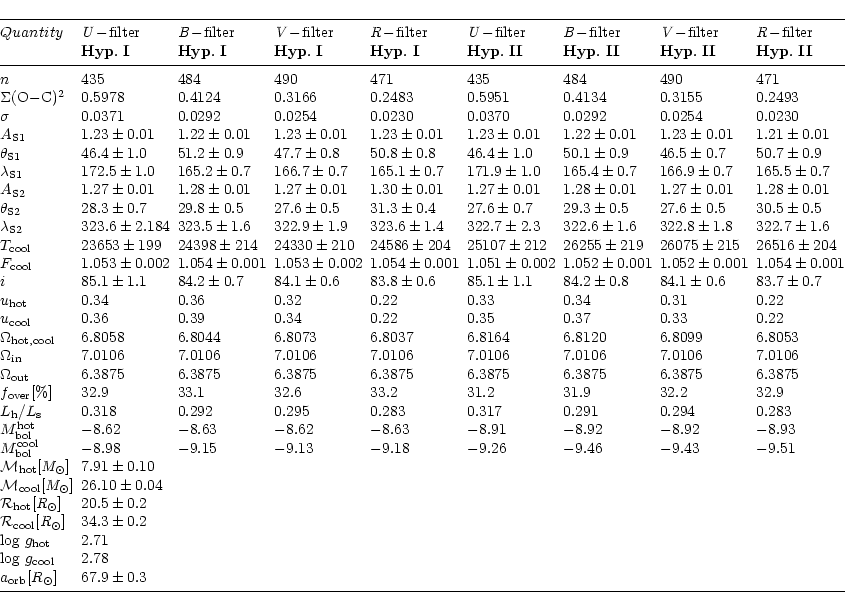
The parameters derived from the light-curve analysis are listed in Table 1. The errors of the parameters' estimates arise from the nonlinear least-squares method, on which the inverse-problem method is based. The first three rows of the table present the number of observations n, the final sum of squares of residuals between observed (LCO) and synthetic (LCC) light curves

$$\begin{eqnarray*}\sum_{i=1}^n ({\rm O}_i-{\rm C}_i)^2, \end{eqnarray*}$$

and the standard deviation of the residuals

$$\begin{eqnarray*}\sigma=\sqrt{\sum_{i=1}^n ({\rm O}_i-{\rm C}_i)^2\over (n-1)}\cdot \end{eqnarray*}$$

In the same table the spot characteristics (spot temperature factor, $A_{\rm S}=T_{\rm S}/T_{\rm cool}$, angular radius, $\theta_{\rm S}$ and longitude, $\lambda_{\rm S}$) are also given. The determination of these parameters is based on a simultaneous fitting of the available light curves in the U, B, V and R photometric bands.

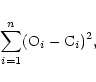
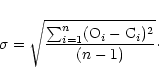
In the analysis of the results listed in Table 1 we can see that the adopted value of the temperature of the less-massive (hotter) star does not have significant influence on the quality of the fit and parameters of the active regions. Of course, the impact of the adopted hypothesis is more significant in the estimate of the temperature of the more-massive (cooler) component. Compared to Hyp. I ( $T_{\rm hot}=28\,000$ K), Hyp. II ( $T_{\rm hot}=30\,000$ K) yielded a temperature of the cooler component higher by about 1750 K. These temperature differences are reflected in the estimates of the absolute bolometric magnitudes of RY Sct components (see Table 1) which are about $0\hbox{$.\!\!^{\rm m}$ }3$ higher within Hyp. II. The noted differences do not significantly change the character of the obtained solutions.

Finally, in Table 1 we present some important absolute parameters. They are derived from the mass ratio of the components $q=m_{\rm cool}/m_{\rm hot}=3.3$ (Skul'skij 1985, 1992). The uncertainties of these parameters may be larger than we estimated. Our estimate of the accuracy in the determination of these parameters is based on the influence of formal errors arising from the nonlinear method of the light-curve analysis, and on the differences between individual U, B, V and R solutions, also. Having in mind the errors of the input parameters of the model, which are treated as fixed in the inverse-problem method, the real errors of the parameters will definitely be larger. But, based on the available data, we cannot give a real estimate of the total accuracy of the system parameters.

If we compare the values of the fundamental parameters of the system to previously published values, we can notice significant differences that are the consequences of the different mass-ratio values applied. For example, Giuricin & Mardirossian (1981) obtained ${\cal M}_{\rm hot}\sim 38~{M_{\odot}}$ and ${\cal M}_{\rm cool}\sim 47~{M_{\odot}}$ as the masses of the components with q=1.25. Our present determination with q=3.3 gives ${\cal M}_{\rm hot}\sim 8~{M_{\odot}}$ and ${\cal M}_{\rm cool}\sim 26~{M_{\odot}}$.

Following from the inverse-problem solutions for individual light curves, Fig. 1 (left) presents the optimum fit of the observed light curves (LCO) by synthetic ones (LCC). The light curves are normalised to the brightness at the orbital phase of 0.25. The final residuals (O-C) between the observed (LCO) and optimum synthetic (LCC) light curves are given, too. The right-hand column on these figures shows the view of RY Sct's Roche models, obtained with the parameters estimated by analysing the corresponding light curves. Thanks to such plots, one sees how a CB system would look like at a certain orbital phase, chosen so that the active hot regions are visible. To save space, here we give only the graphical presentation of the results obtained within (Hyp. I) since the differences in the fitting quality and estimated geometrical parameters of the system within both of the hypotheses are insignificant. Finally, the bottom row of this panel gives the new observed UBVR light curves, drawn together, and the changes of the colour indices U-B, B-V and V-R with orbital phase. These colour indices exhibit some variability with orbital phase around the primary minimum. This effect may be attributed to the temperature differences between the system's components, and partially to the influence of the hot active regions.

Figure 1: Left: observed (LCO) and final synthetic (LCC) light curves of RY Sct with O-C residuals obtained by solving the inverse problem within the framework of the Roche model with two hot areas on the more-massive cooler star; Right: the view of the Roche model for RY Sct at the orbital phase 0.75 with parameters estimated by solving the inverse problem; Bottom row: Left: the observed new UBVR light curves; Right: The changes of the colour indices U-B, B-V and V-R with orbital phase.

Open with DEXTER

4 Possible membership of RY Sct to association Ser OB1

The binary system RY Sct projects itself onto the celestial sphere in the region of the OB association Ser OB1. Zakirov (1985) discussed the possible membership of the binary system RY Sct to this association. He found r = 1.5 kpc as the distance to the young open cluster NGC 6611 geometrically connected with the association. On the H-R diagram the components of RY Sct are in the branch that is occupied by cluster stars. Thus, the author concluded that the binary system is a possible member of this association. Milano et al. (1981) estimated the distance to the binary system at 1.6 kpc which agreed with Zakirov's results.

We have reconsidered the problem of the RY Sct membership of the Ser OB1 association in view of the new data obtained in this paper. The knowledge of the system's brightness at maximum and the relative contributions of the components $L_{\rm hot}$ and $L_{\rm cool}$ to the total brightness (see Table 1) allow us to estimate stellar magnitudes and colour indices of the components. A comparison of the obtained colour indices of the components to their tabelar values for appropriate temperatures (Straizys 1977) gave colour-excesses $E(B-V)_{\rm hot}=1.29$ and $E(B-V)_{\rm cool}=1.25$. On average we have a colour excess of E(B-V)=1.27 for this binary system. Following Straizys's recommendations (1977) we have adopted ${A({\rm V})\sim4\hbox{$.\!\!^{\rm m}$ }22}$ as the interstellar absorption. From Table 1 ( $M^{\rm hot}_{\rm bol}$ and $M^{\rm cool}_{\rm bol}$) and from the bolometric correction (Popper 1980) these data provides us with the absolute stellar magnitudes of the components, $M_{\rm hot(V)}\sim-5\hbox{$.\!\!^{\rm m}$ }79$ (Hyp. I) and $M_{\rm hot(V)}\sim-5\hbox{$.\!\!^{\rm m}$ }96$ (Hyp. II), $M_{\rm cool(V)}\sim-6\hbox{$.\!\!^{\rm m}$ }75$ (Hyp. I) and $M_{\rm hot(V)}\sim-6\hbox{$.\!\!^{\rm m}$ }82$ (Hyp. II). On the basis of the hot and cool components of the system we have a RY Sct distance modulus of 11.83 (Hyp. I) and 11.89 (Hyp. II) and 11.99 (Hyp. I) and 12.00 (Hyp. II). If we average these distance obtained for each of the components, we find m-M=11.93. By comparing the bolometric corrections for the stars in different tables we can see that the differences are in the interval $\pm 0\hbox{$.\!\!^{\rm m}$ }2$. The cosmic dispersion of the absolute stellar magnitudes for OV stars amounts to ${\rm\pm0\hbox{$.\!\!^{\rm m}$ }6}$, (Mdzinarishvili 1985). Having in mind these errors, we can estimate the distance to RY Sct as $m-M=11.9\pm 0.6$. Another approach to distance determination for eclipse systems employs Barnes-Evans (Lacy 1977) relation which connects the visual apparent stellar magnitude, free from absorption, to its radius, parallax and visual surface brightness. The last parameter can be calculated (Lacy 1977) and we can use the existing tables (e.g., Popper 1980). By employing this relation we have distance moduli of 11.85 (Hyp. I) and 11.96 (Hyp. II) for the hot component of RY Sct, and 11.90 (Hyp. I) and 12.06 (Hyp. II) for the cool component. Based on these data the averaged distance is m-M=11.94. In this way the distance modulus for RY Sct, estimated via these two independent methods, amounts to $m-M=11.9\pm 0.6$. The distance to the Ser OB1 association, estimated from Hipparcos data (Dambis et al. 2001) is 11.4. The mean radial velocity of the members of the association amounts to ${\rm -3.0\pm 11.6~km~s^{-1}}$ (Mel'nik & Efremov 1995), and Skul'skij (1992) finds ${\rm 12 \ km \ s^{-1}}$ as the the velocity of the center of masses for RY Sct. The intrinsic motion of RY Sct is as small as it is for other association members (Roser & Bastian 1993). Quite probably this indicates that RY Sct is a member of the Ser OB1 association. The core of this association is a young open cluster NGC 6611 whose age is estimated to be 1.2 million years (Dambis 1999). This is quite likely the age limit of the RY Sct system too.

5 Discussion and conclusions

A summary of our results, given in Table  1, proved that the Roche model with two hot active regions on the more-massive (cooler) component of RY Sct can successfully simulate the observed light curves. Synthetic light curves, obtained by solving the inverse problem, fit the observations very well, and we have quite good agreement between the solutions for individual light curves in different UBVR filters of the photometric system.

All this suggests the suitability of our Roche model with hot areas on the more-massive (cooler) star in simulating the real observations. Without these active regions we have a fit of a much poorer quality.

The results describe RY Sct's system as an overcontact configuration ( $f_{\rm over} \sim 33\%$ - Hyp. I and $f_{\rm over} \sim 32\%$ - Hyp. II) with a significant temperature difference between the components ( $\Delta T=T_{\rm hot}-T_{\rm cool} \sim$ 3770 K - Hyp. I and $\Delta T=T_{\rm hot}-T_{\rm cool} \sim$ 4010 K - Hyp. II). These solutions together with a mass ratio of $q=m_{\rm cool}/m_{\rm hot}=3.3$ suggest a significant mass and energy transfer from the less-massive (hotter) secondary onto the more-massive (cooler) primary. The hot area on the cooler star, near the neck region, can be taken as a consequence of this mass and energy exchange between the components through the connecting neck of the common envelope. Apparently, another hot area (near the external Lagrange point L₃) is the zone of an intensive mass outflow from the system. Without this hot region we have a poorer fit again. This mechanism, together with mass loss through stellar wind, could be responsible for the existing nebula around RY Sct.

Because of the revolution of the system the mass loss through the outer Lagrangian point L₃ may lead to a toroidal geometry of the circumstellar nebula in the equatorial plane of the system. With this hypothesis we expect a thermally emitting circumstellar dust torus, seen edge-on, with the inner surface ionized by the central star. The papers by Gehrz et al. (1995) and Smith et al. (1999) speak in favour of such a model. The last paper, based on the analysis of Hubble space telescope ${\rm H_{\alpha}}$ image of the RY Sct shows a very complex structure of the ionized nebula located at the inner edge of a more extended IR dust torus.

The orbit inclination, estimated at $i\sim 84\hbox{$.\!\!^\circ$ }3$, shows that the system RY Sct generates total-annular eclipses. Using q=3.3 as the mass ratio (Skul'skij 1985, 1992), Antokhina & Kumsiashvili (1999), obtained a similar value of the orbit inclination. Their model of this system with a disk is different from our overcontact model with active regions. However, the estimates of the basic parameters are similar and close to ours since the same mass ratio is applied.

The parameters of RY Sct obtained in this paper suggest as quite possible that this binary system belongs to the association Ser OB1.

Previously the light-curve analysis for this system was performed in the frame of the Roche model with an accretion disc around the more-massive component, also. That model was developed for the W Ser-type of systems (Djurasevic 1992c), and later the model was modified for light-curve analysis of the cataclysmic variables (Djurasevic 1996). Since the fitting quality within that model was of a much poorer quality we think that such a model can be rejected as less probable.

The results obtained in this paper are different from the results in previously published light-curve analyses. Above all this is a consequence of the different models of the system and mass ratio adopted and applied in the light-curve analysis. This makes a direct comparison difficult to perform. A key problem is definitely the mass ratio on which the estimates of the parameters are directly depending. In general, we can say that our results affirm the overcontact model of the system with mass exchange between the components and mass loss through the outer Lagrangian point L₃. This could be a possible mechanism in the formation of a circumstellar envelope of toroidal form lying in the orbital plane of the system.

Acknowledgements

Two of us (G.D. & S.E.) have been partially supported by the Ministry of Sciences and Technology of Serbia through the project "Astrometrical, Astrodynamical and Astrophysical investigations''. The authors thank G. C. Arzumanyatz for his contribution in the observations of the system during 1994.

References

 

• Al Naimy, H. H. 1977, Ap&SS, 53, 181 NASA ADS  
• Antokhina, Eh. A., & Cherepashchuk, A. M. 1988, Pisma v AZh, 14(3), 252 In the text  
• Antokhina Eh. A. and Kumsiashvili M. I., 1999, Pisma v AZh, 25, 711 In the text  
• Carbon, D., & Gingerich, O. 1969, in Theory and Observation of Normal Stellar Atmospheres, ed. O. Gingerich (MIT Press, Cambridge), 377 In the text  
• Cowley, A. P., & Hutchings, J. B. 1976, PASP, 88, 456 In the text NASA ADS  
• Dambis, A. K. 1999, Astron. Lett., 25, 7 In the text NASA ADS  
• Dambis, A. K., Mel'nik, A. M., & Rastorguev, A. C. 2001, Astron. Lett., 27, 68 In the text  
• Díaz-Cordovés, J., Claret, A., & Giménez, A. 1995, A&AS, 110, 329 In the text NASA ADS  
• Djurasevic, G. 1992a, Ap&SS, 196, 241 In the text NASA ADS  
• Djurasevic, G. 1992b, Ap&SS, 197, 17 In the text NASA ADS  
• Djurasevic, G. 1992c, Ap&SS, 196, 267 In the text NASA ADS  
• Djurasevic, G. 1996, Ap&SS, 240, 317 In the text NASA ADS  
• Djurasevic, G., Zakirov, M., Hojaev, A., & Arzumanyants, G. 1998, A&AS, 131, 17 In the text NASA ADS  
• de Martino, D., Vittone, A. A., Rossi, C., & Giovannelli, F. 1992, A&A, 254, 266 NASA ADS  
• Gehrz, R. D., et al. 1995, ApJ, 439, 417 In the text NASA ADS  
• Geisel, S. L. 1970, ApJL, 161, L105 In the text NASA ADS  
• Giatti, F., Mammano, A., Margoni, R., Milano, L., Strazzulla, G., & Vittone, A. 1980, A&AS, 41, 143 In the text NASA ADS  
• Giuricin, G., & Mardirossian, F. 1981 A&A, 101, 138 In the text NASA ADS  
• Grasdelen, G. L., Hackwell, J. A., Gehrz, R. D., & McClain, D. 1979, ApJL, 234, L129 In the text NASA ADS  
• Hughes, V. A., & Woodsworth, A. 1973, Nature Phys. Sci., 242, 116 In the text  
• King, A. R., & Jameson, R. F. 1979, A&A, 71, 326 In the text NASA ADS  
• Lacy, C. H. 1977, ApJ, 213, 458 In the text NASA ADS  
• Lejeune, T., Cuisinier, F., & Buser, R. 1997, A&AS, 125, 229 In the text NASA ADS  
• Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65 In the text NASA ADS  
• Lucy, L. B. 1967, Zs. f. Ap., 65, 89 In the text  
• Lucy, L. B., & Wilson, R. E. 1979, ApJ, 231, 502 In the text NASA ADS  
• Marquardt, D. W. 1963, J. Soc. Ind. Appl. Math. 11(2), 431 In the text  
• Mdzinarishvili, T. G. 1985, Bull. Abast. Obs., 59, 117 In the text  
• Mel'nik, A. M., & Efremov, Yu. N. 1995, Astron. Lett., 21, 10 NASA ADS  
• Milano, L., Vittone, A., Ciatti, F., Mammano, A., Margoni, R., & Strazzulla, G. 1981, A&A, 100, 59 In the text NASA ADS  
• Moffett, T. J., & Barness, III T. G. 1979, AJ, 84, 627 In the text NASA ADS  
• Popper, D. M. 1980, ARA&A, 18, 115 In the text NASA ADS  
• Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in Fortran, The Art of Scientific Computing, Second Edition (Cambridge University Press, New York), 120 In the text  
• Rafert, J. B., & Twigg, L. W. 1980, MNRAS, 139, 78 In the text  
• Roser, S., & Bastian, U. 1993, PPM star catalogue: position and proper motions, Heidelberg, Astron. Rechen. Inst., 3 In the text  
• Skul'skij, M. Yu. 1985, Byull. Abastum. astrofiz. observ., 58, 101 In the text  
• Skul'skij, M. Yu. 1992, Astron. zhurn., 69, 803 In the text  
• Smith, N., Gehrz, R. D., Humphreys, R. M., et al. 1999, AJ, 118, 960 In the text NASA ADS  
• Straizys, V. 1977, Multicolor stellar photometry, Mokslas, Vilnus In the text  
• Vaz, L. P. R., Anderson, J., & Rabello Soares, M. C. A. 1995, A&A, 301, 693 In the text NASA ADS  
• Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 In the text NASA ADS  
• Zakirov, M. M. 1985, Bull. Abastuman Obs., 58, 425 In the text NASA ADS