A&A 374, 740-745 (2001)
DOI: 10.1051/0004-6361:20010493
S. Seitz1 - P. Schneider2
1 -
Universitätssternwarte München, Scheinerstr. 1, 81679 München, Germany
2 -
Institut für Astropysik und Extraterrestische Forschung, Auf dem
Hügel 71, 53121 Bonn, Germany
Received 10 February 1998 / Accepted 30 March 2001
Abstract
A new method for the reconstruction of the projected mass distribution
of clusters of galaxies from the image
distortion of background galaxies is discussed. This method is
essentially equivalent to the one we developed previously, i.e., the
noise-filtering method, but has several practical advantages:
(1) it is much easier to implement; (2) it can be easily applied to
wide-field images, since the constraints on the number of gridpoints
are much weaker than for the previous method, and (3) it can be easily
generalized to more complicated field geometries, such as that of the
Wide Field Planetary Camera 2 (WFPC2) onboard HST. We have tested the
performance of our new inversion method (for which a FORTRAN-77
implementation is available from the authors) using
simulated data, demonstrating that it fares very favourably.
Key words: cosmology: theory - methods: numerical
Here, we shall present a slightly revised version of the noise-filter inversion method, which removes some of the technical drawbacks of the original formulation. In particular, our new method can be applied to arbitrarily-shaped data fields (which is of great interest given the geometry of the WF chips of the WFPC2 on-board HST) and can be used with better resolution than the previous formulation. In addition, the numerical encoding of the new version is substantially easier and requires much less memory. We shall formulate the inversion problem and its solution in Sect. 2, and present some practical issues in Sect. 3. Numerical tests of this method in comparison to other reconstruction methods are presented in Sect. 4, and we summarize in Sect. 5 our findings. One application of our new method has been presented in the mass reconstruction of the cluster MS1358+62 by Hoekstra et al. (1998).
Just before finalizing this manuscript, Lombardi & Bertin (1999)
submitted a paper to the astro-ph preprint
server. Two results of that paper are
particularly relevant for the present discussion: They have shown that
of all (direct) finite-field mass reconstructions, those with
vanishing curl in the kernel ![]() - see Eq. (6) below - have
the smallest rms error; requiring that noise-free data yield an exact
mass reconstruction, they rederived the inversion method of Paper I.
Second, they have independently derived our new inversion method,
Eq. (7) below, from a variational principle.
- see Eq. (6) below - have
the smallest rms error; requiring that noise-free data yield an exact
mass reconstruction, they rederived the inversion method of Paper I.
Second, they have independently derived our new inversion method,
Eq. (7) below, from a variational principle.
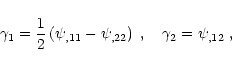 |
(1) |
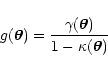 |
(2) |
![\begin{displaymath}K(\vec{\theta}):=\ln \left[{1-\kappa(\vec{\theta})}\right]\;,
\end{displaymath}](/articles/aa/full/2001/29/aah0882/img14.gif) |
(3) |
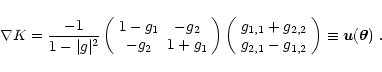 |
(4) |
The right-hand-side of this equation can be considered as an observable, obtained from local averages of image ellipticities and by finite differencing the resulting field g.
Equation (4) can be solved (up to an additive constant) by line
integration, and several schemes for this have been proposed
(Schneider 1995; Kaiser et al. 1995; Bartelmann 1995; Squires &
Kaiser 1996). The reason why different schemes yield different results
can be seen by noting that the vector field ![]() comes from (noisy)
observational estimates, and thus will in general not be a gradient
field. Therefore, the equation
comes from (noisy)
observational estimates, and thus will in general not be a gradient
field. Therefore, the equation
![]() has no solution in
general, since
has no solution in
general, since ![]() has a rotational component due to observational
noise. On the other hand, if
has a rotational component due to observational
noise. On the other hand, if ![]() is a gradient field, then all
line integration schemes are equivalent.
is a gradient field, then all
line integration schemes are equivalent.
In Paper I, we split the vector field into a gradient part and a
rotational part,
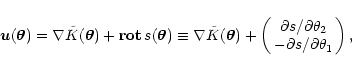 |
(5) |
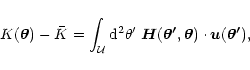 |
(6) |
Whereas the method of Paper I passed all numerical tests, it has a few
features which are unwanted: (1) If the geometry deviates from that of
a circle or a rectangle, the Greens function can no longer be obtained
analytically. However, a numerical determination of the Greens
function is impractical owing to its singularity. For this reason, the
mass reconstruction of the cluster Cl 0939+4713 from WFPC2 data (Seitz
et al. 1996) was carried out by splitting the field into two
rectangles and combine them appropriately in the overlap region. This
is certainly not the optimal method, since each of the two individual
reconstructions made no use of the shear information outside the
respective rectangle. (2) If a quadratic field is covered by an
![]() grid of
grid of
![]() and
and
![]() values, the necessary
memory for storing
values, the necessary
memory for storing ![]() consists of 2 N4 real numbers. Hence, if
one increases N beyond
consists of 2 N4 real numbers. Hence, if
one increases N beyond ![]() ,
the memory requirement quickly
approaches the capacity of commonly used workstations. However, due to
the singularity of the Greens function, one likes to have small grid
spacings to obtain an accurate numerical estimate of the integral (6)
- see Squires & Kaiser (1996) for comments on this point. (3)
Although the solution for
,
the memory requirement quickly
approaches the capacity of commonly used workstations. However, due to
the singularity of the Greens function, one likes to have small grid
spacings to obtain an accurate numerical estimate of the integral (6)
- see Squires & Kaiser (1996) for comments on this point. (3)
Although the solution for ![]() was given explicitly in Paper I, it
is complicated and not easily encoded (though quickly
evaluated). In order for the noise-filtering method to become a
standard and readily available tool, one would like to have an easier
method to solve for K.
was given explicitly in Paper I, it
is complicated and not easily encoded (though quickly
evaluated). In order for the noise-filtering method to become a
standard and readily available tool, one would like to have an easier
method to solve for K.
These three points can be avoided in the following simple manner: Taking the divergence of (5) leads to
| (7a) |
Since
![]() on the boundary,
on the boundary,
![]() is
perpendicular to the normal vector
is
perpendicular to the normal vector ![]() at the boundary of
at the boundary of ![]() ,
so
that
,
so
that
|
|
(7b) |
Hence, K can be obtained as the solution of the Neumann problem
given by (7a,b). There are efficient and quick methods for a
numerical solution of this problem; we have
employed a relaxation method with successive overrelaxation (see Press
et al. 1992, p. 857). Choosing the overrelaxation parameter as in
Eq. (19.5.21) of Press et al. (1992), a stable solution was
found after about 20 N iterations on an ![]() grid in
grid in
![]() .
.
The previously mentioned drawbacks of the method presented in Paper I
are now avoided. The Neumann problem (7) can be solved for any
geometry; for example, for the WF-part of the WFPC2 one merely needs to
formulate the boundary condition (7b) at 6 sides, instead of 4 for a
rectangle. The memory requirement is reduced to a few times N2 real
numbers, so that N can easily be of order a few hundred. In fact,
for N=200, the solution of (7) takes about 2 min on an IBM risc
6000 processor. And finally, the numerical code for solving (7)
shrinks tremendously compared to that needed to evaluate ![]() .
.
In order to obtain a mass reconstruction from galaxy ellipticities, the following three steps are needed:
(1) The galaxy ellipticities are spatially smoothed to obtain an
unbiased estimate of the local reduced shear. If
![]() is the
complex ellipticity of the i-th galaxy at position
is the
complex ellipticity of the i-th galaxy at position
![]() ,
and
,
and
![]() is a smoothing scale, we calculate g at a
position
is a smoothing scale, we calculate g at a
position
![]() as
as
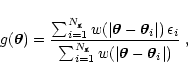 |
(8) |
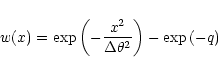 |
(9) |
(2) The vector field ![]() is obtained from g using (4). Finite
differencing is employed, with one-sided second-order differentiation
rules taken at the boundary
is obtained from g using (4). Finite
differencing is employed, with one-sided second-order differentiation
rules taken at the boundary
![]() .
A further differentiation
then yields
.
A further differentiation
then yields
![]() .
.
(3) The Neumann problem (7) is then solved, using the method described
above![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{H0882F1.ps}\end{figure}](/articles/aa/full/2001/29/aah0882/Timg43.gif) |
Figure 1: The power spectra of various mass inversion methods, as explained in the main text. |
| Open with DEXTER | |
Reconstructions for the case with a lens were performed using the following methods: the original Kaiser & Squires (1993) reconstruction, generalized to account for non-linear effects as described in Paper I; a finite-field reconstruction based on line integration (Schneider 1995); the noise-filtering method (NF) as described in Paper I; and the new noise-filtering method as presented here. The reconstructions were analyzed by Fourier-decomposition of their difference from the input mass distribution (or, more precisely, the input field of K). We used several values of the number of gridpoints per dimension. The noise filtering inversion developed here was implented in two versions (NF1, NF2); in the first case, (7a&b) was solved on the same grid as for the other inversion techniques. In the second case, the solution for K was obtained on a grid two times as dense and K was estimated on the sparser grid afterwards.
It turns out that reconstructions with the new technique developed
here (NF1) are always smoother than any of the other methods considered
here. This is because
![]() is used instead of
is used instead of ![]() itself. The operation
itself. The operation
![]() effectively yields a loss of
signal and noise on length scales of two grid points. To obtain
reconstructions with the same resolution we thus double the number of
gridpoints in NF2, calculate
effectively yields a loss of
signal and noise on length scales of two grid points. To obtain
reconstructions with the same resolution we thus double the number of
gridpoints in NF2, calculate ![]() and its divergence and K on the
dense grid. Finally K is calculated on the sparser grid by averaging
over 4 gridpoints. The power spectra of these NF2 reconstructions
are always very similar to the original
NF-reconstruction. Those of the NF1 reconstructions are more similar
to reconstructions on a sparser grid, where the high frequency power
is reduced due to the loss of degrees of freedom. Hence,
the recovery of the signal and the sensitivity to the
noise in the NF2 and NF-method are identical, and therefore the
comparisons with the other methods given in Paper I apply.
To compare our results with those of Squires & Kaiser (1996) we also
consider the case with no shear and surface density in the data
field (i.e. the "noise-only-case'').
This approach investigates the quality of the reconstruction (the
quality of the "no-mass-detection'')
for the case that there is no mass in the field at all, whereas we
have investigated before how good a two-dimensional
mass distribution can be recovered. Given that a method which involves
a lot of smoothing will always fare better in the no-lens case than one
which spatially resolves noise, it is clear that the no-lens
comparison is not the relevant test [the "best'' inversion in that
case is obtained by setting
and its divergence and K on the
dense grid. Finally K is calculated on the sparser grid by averaging
over 4 gridpoints. The power spectra of these NF2 reconstructions
are always very similar to the original
NF-reconstruction. Those of the NF1 reconstructions are more similar
to reconstructions on a sparser grid, where the high frequency power
is reduced due to the loss of degrees of freedom. Hence,
the recovery of the signal and the sensitivity to the
noise in the NF2 and NF-method are identical, and therefore the
comparisons with the other methods given in Paper I apply.
To compare our results with those of Squires & Kaiser (1996) we also
consider the case with no shear and surface density in the data
field (i.e. the "noise-only-case'').
This approach investigates the quality of the reconstruction (the
quality of the "no-mass-detection'')
for the case that there is no mass in the field at all, whereas we
have investigated before how good a two-dimensional
mass distribution can be recovered. Given that a method which involves
a lot of smoothing will always fare better in the no-lens case than one
which spatially resolves noise, it is clear that the no-lens
comparison is not the relevant test [the "best'' inversion in that
case is obtained by setting
![]() in (6)!].
in (6)!].
We found again that the noise properties of NF and NF2 reconstructions are (almost) identical, whereas that of NF1 is different for reasons already discussed. For a dense grid (N=80) all noise filtering methods become more and more equal, and the short wavelength behavior approaches that of KS (solid line). In any case, the KS method is by far the "best'' as long as there is no mass in the field. As we already pointed out in Paper I, this is because more (and exact) information is used, namely that the shear is (set equal to) zero outside the data field. The fact that the noise of the KS inversion in Fig. 6 of Squires & Kaiser (1996) is slightly larger than that of the NF inversion at small wavelengths is due to the fact that in their implementation of the KS algorithm, the shear field was not obtained by smoothing the galaxy ellipticities, but the inversion was performed by straight summation, which leads to shot noise (Seitz & Schneider 1995).
Squires & Kaiser (1996) suspected that the increase of noise of the
finite field inversion comes from the fact that they are more
sensitive to noise at the boundary of the data field. This point is
clarified in Fig. 1. The upper and lower solid curves denote the
power spectra for the NF and KS method on a
![]() grid. The
underlying galaxy distribution and thus shear field for each of the
individual reconstructions is by construction absolutely the same for
the NF and KS-case. We then embed the true data field
grid. The
underlying galaxy distribution and thus shear field for each of the
individual reconstructions is by construction absolutely the same for
the NF and KS-case. We then embed the true data field ![]() in a
two times as large field and distribute additional galaxies with the
same density and ellipticity distribution in the outer region. The
galaxies inside
in a
two times as large field and distribute additional galaxies with the
same density and ellipticity distribution in the outer region. The
galaxies inside ![]() are unchanged. The shear field is calculated in
the large field and KS-reconstructions are obtained in the same
region. We cut out the surface mass density in the original field
are unchanged. The shear field is calculated in
the large field and KS-reconstructions are obtained in the same
region. We cut out the surface mass density in the original field ![]() and calculate the power spectrum of the reconstruction error in the
same way as for the other mass reconstructions within
and calculate the power spectrum of the reconstruction error in the
same way as for the other mass reconstructions within ![]() .
We point
out that in this case the shear field within
.
We point
out that in this case the shear field within ![]() is not the same as
in the above case because now galaxies outside the field contribute to
the estimate of the shear field within
is not the same as
in the above case because now galaxies outside the field contribute to
the estimate of the shear field within ![]() .
This makes the shear
field statistically smoother inside
.
This makes the shear
field statistically smoother inside ![]() .
But as can be seen in
Fig. 1 (long-dashed-dotted curve) the reconstruction error within
.
But as can be seen in
Fig. 1 (long-dashed-dotted curve) the reconstruction error within
![]() is larger than for KS-reconstructions of the small field (solid
line) - because the data outside
is larger than for KS-reconstructions of the small field (solid
line) - because the data outside ![]() are no longer "ideal
assumptions'' (
are no longer "ideal
assumptions'' (
![]() )
but noisy measurements affected by the
intrinsic ellipticity distribution of the galaxies. We then perform
reconstructions on the large field where the shear field is obtained
in the same way as before, but values on gridpoints within
)
but noisy measurements affected by the
intrinsic ellipticity distribution of the galaxies. We then perform
reconstructions on the large field where the shear field is obtained
in the same way as before, but values on gridpoints within ![]() are
substituted by the estimate obtained in the small field only. Thus the
g field and its noise properties within
are
substituted by the estimate obtained in the small field only. Thus the
g field and its noise properties within ![]() are now identical to
that of the KS and NF reconstructions of the small field. At the same
time the transition to the shear field outside
are now identical to
that of the KS and NF reconstructions of the small field. At the same
time the transition to the shear field outside ![]() becomes less
continuous which mimics an artifical increase of noise at the boundary
of
becomes less
continuous which mimics an artifical increase of noise at the boundary
of ![]() .
The power spectrum obtained from KS-reconstructions of that
g-field (dotted curve) is higher than the long-dashed-dotted curve,
as expected.
.
The power spectrum obtained from KS-reconstructions of that
g-field (dotted curve) is higher than the long-dashed-dotted curve,
as expected.
To obtain a KS-reconstruction where almost no information on data
outside ![]() is used, we increase the noise outside
is used, we increase the noise outside ![]() by doubling
the width of the ellipticity distribution for galaxies outside
by doubling
the width of the ellipticity distribution for galaxies outside
![]() .
The shear field is calculated in the large field and the surface
density is KS-reconstructed. The power spectrum of the reconstruction
error within the small field is shown as short-dashed-dotted line -
and it is very similar to the power spectrum of the finite field
NF-reconstruction. One could argue that this large increase is caused
mainly by the fact that by the averaging procedure (8) the increased
noise outside
.
The shear field is calculated in the large field and the surface
density is KS-reconstructed. The power spectrum of the reconstruction
error within the small field is shown as short-dashed-dotted line -
and it is very similar to the power spectrum of the finite field
NF-reconstruction. One could argue that this large increase is caused
mainly by the fact that by the averaging procedure (8) the increased
noise outside ![]() is partly tranferred in
is partly tranferred in ![]() .
To show that this is
not true we again consider the case where the shear field is
calculated in the large region as before, but where the values inside
.
To show that this is
not true we again consider the case where the shear field is
calculated in the large region as before, but where the values inside
![]() are the same as used for the KS- and NF-reconstruction of the
small field
are the same as used for the KS- and NF-reconstruction of the
small field ![]() .
We find that the reconstruction error is then only
marginally decreased (short-dashed curve). But still one could argue
that in this case the possibly non-smooth transition from the
g-field inside
.
We find that the reconstruction error is then only
marginally decreased (short-dashed curve). But still one could argue
that in this case the possibly non-smooth transition from the
g-field inside ![]() to that outside could significantly contribute
to the noise. Therefore we smoothed that transition on the neighboring
gridpoints outside the data field. The corresponding power spectrum
(long-dashed curve) shows that the smootheness of this transition has
only a small effect on the noise properties of the reconstruction
within
to that outside could significantly contribute
to the noise. Therefore we smoothed that transition on the neighboring
gridpoints outside the data field. The corresponding power spectrum
(long-dashed curve) shows that the smootheness of this transition has
only a small effect on the noise properties of the reconstruction
within ![]() .
This comparison demonstrates that the KS-reconstruction
becomes worse the noisier the data outside
.
This comparison demonstrates that the KS-reconstruction
becomes worse the noisier the data outside ![]() are and that the
assumption of
are and that the
assumption of
![]() outside
outside ![]() is responsible for the
high quality of the KS-reconstruction if there is no mass in the
field. Since this is not the case for most fields currently observed,
one is urged to use a method which is exact on finite fields (see
Squires & Kaiser 1996).
is responsible for the
high quality of the KS-reconstruction if there is no mass in the
field. Since this is not the case for most fields currently observed,
one is urged to use a method which is exact on finite fields (see
Squires & Kaiser 1996).
Finally we apply the new noise filtering to the WFPC-2 geometry.
Instead of performing a power-spectrum analysis, we have calculated
the mean-square deviation of the reconstructed density field
![]() (shifted such that the mean value of K over the field
(shifted such that the mean value of K over the field ![]() equals the true one) from the input distribution (see also Fig. 10
in Paper I). We consider again two cases, the "no-lens-case'' and
that of a mass distribution
which was now chosen similar to that in the cluster Cl 0939 (see
Fig. 2)
equals the true one) from the input distribution (see also Fig. 10
in Paper I). We consider again two cases, the "no-lens-case'' and
that of a mass distribution
which was now chosen similar to that in the cluster Cl 0939 (see
Fig. 2)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{H0882F2.ps}\end{figure}](/articles/aa/full/2001/29/aah0882/Timg51.gif) |
Figure 2:
This mass distribution was used when the
rms-error for the NF and NF1 are compared in Fig. 3; it was chosen
to similar to that of the cluster Cl0939. The contours
and surface plot shows
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H0882F3.ps}\end{figure}](/articles/aa/full/2001/29/aah0882/Timg53.gif) |
Figure 3:
The mean rms deviation (defined as |
| Open with DEXTER | |
We have derived a new version of the noise-filtering cluster mass reconstruction algorithm originally proposed in Paper I, which is easier to implement, easier to use on large fields where the required number of gridpoints can quickly exceed the number possible in using the method of Paper I, and which can easily be generalized to more complicated geometries; the particularly relevant case of the WFPC-2 geometry was considered explicitly. From extensive numerical tests we have shown that the noise properties of this version is basically identical to that of the method described in Paper I. In agreement with Fig. 6 of Squires & Kaiser (1996), we conclude that the noise-filtering method is the best known direct finite-field inversion method. The comparison between the maximum probability method (Squires & Kaiser 1996) and the method presented here, carried out on the mosaic of WFPC-2 centered on the cluster MS1358+62 (Hoekstra et al. 1998), yielded no easily visible difference in performance of these two methods.
Acknowledgements
We thank Bill Press for a very fruitful discussion which triggered the work presented here. This work was supported by the "Sonderforschungsbereich 375-95 für Astro-Teilchenphysik'' der Deutschen Forschungsgemeinschaft.