A&A 374, 504-522 (2001)
DOI: 10.1051/0004-6361:20010642

NGC 7654: An interesting cluster to study star formation history[*]

A. K. Pandey1 - Nilakshi1 - K. Ogura2 - Ram Sagar1 - K. Tarusawa3


1 - State Observatory, Manora Peak, Naini Tal, 263 129, India
2 - Kokugakuin University, Higashi, Shibuya-ku, Tokyo 150-8440, Japan
3 - Kiso Observatory, School of Science, University of Tokyo, Mitake-mura, Kiso-gun, Nagano 397-0101, Japan

Received 8 February 2001 / Accepted 27 April 2001

Abstract
CCD $UBVI_{\rm C}$ photometry in a wide field around the open cluster NGC 7654 has been carried out for $\sim$17860 stars, down to $V\sim20$. The reddening across the cluster region is found to be variable with $E(B-V)_{\rm min} = 0.46$ to $E(B-V)_{\rm max}=0.80$. The cluster is situated at a distance of 1380 $\pm$ 70 pc. The colour magnitude diagrams show a large age spread in the ages. Star formation was biased towards relatively higher masses during the early phase of star formation whereas most of the low mass stars of the cluster were formed during the later phase. The star formation seems to have been a gradual process that proceeded sequentially in mass and terminated with the formation of most massive stars. The present data do not support a uniform mass function (MF) for different regions in the cluster. Although for the whole cluster region, the MF in the observed mass range $0.8 \leq M_{\odot} \leq 4.5$, can be represented by a single power law with a slope $\Gamma= -1.40 \pm 0.07$, however it indicates various features when examined carefully. In three subregions of the cluster the slope $\Gamma $, for the mass range $\sim$ $1.5< M_{\odot}<4.0$, comes out to be $-1.07\pm 0.08$ and $-1.28\pm 0.20$ for the inner and intermediate regions and it becomes steeper in the outermost region ( $\Gamma = -2.78 \pm 0.21$). For stars having masses $<\sim$1.5 $M_{\odot}$ the MF, in the inner and intermediate regions, can be represented by a power law having a steeper slope, whereas in the outer region a turnover can be seen in the MF at $M\sim 1.5~M_{\odot}$. The age of NGC 7654 is found to be comparable to its two-body relaxation time-scale; therefore this may also be a reason for the observed mass segregation in the cluster.

Key words: open clusters and associations: general - ISM: dust extiction - stars: formation


1 Introduction

The open star clusters are among the most useful objects in the Galaxy and are being used to analyze the large scale properties of our Galaxy. They are laboratories where we can test the theories of stellar evolution and star formation. Determination of their mass function (MF) provides constraints on the theory of star formation in open clusters (Miller & Scalo 1979). On the other hand studies related to the spatial structure and stability of galactic open clusters help to understand the cluster-formation processes in our Galaxy, since these depend upon physical conditions of the molecular clouds from which star clusters are formed (Pandey et al. 1990).


  \begin{figure} \par\includegraphics[width=13.6cm,clip]{MS1127fig1.ps} \end{figure} Figure 1: V band image of the cluster NGC 7654.
Open with DEXTER

The stability of an open cluster in our Galaxy also depends upon its structure. Kholopov (1969) found that the nucleus and the corona (the extended region of the cluster which generally contains faint stars) are two main regions in open clusters. The nucleus region of clusters contains relatively bright and massive ($\geq$3 $M_{\odot}$) stars and consequently it is a well-studied region of the clusters. However, the coronae of star clusters, which generally contains a large number of faint stars, has not been studied in detail. In fact the spatial distribution of these faint and low-mass stars ($\leq$$1~M_\odot$) defines the actual boundary of the clusters. Consequently coronal regions have very important bearing on studies related to the MF and the structure and evolution of open clusters. Observations of low mass stars ( $M\leq1\,M_\odot$) in the coronae are of critical importance in determining the true shape of the cluster MF (Scalo 1998; Kroupa 2001). A detailed analysis of the structure of coronae of open clusters will help in understanding the effects of external environment like the galactic tidal field and impulsive encounters with interstellar clouds, etc., on dynamical evolution of open star clusters.

Extensive studies of the coronal regions of the open clusters have not so far been carried out mainly because of the non-availability of photometry in a large field around open star clusters. Now with a combination of CCD mounted on Schmidt telescopes, such extensive studies of coronae of star clusters are possible. Keeping above discussions in mind we embarked to carry out extensive studies of the coronal regions of star clusters using the 2K $\times$ 2K CCD mounted on the Kiso Schmidt telescope which gives a $\sim$50 arcminute square field.

The radial density profile for the cluster NGC 7654, derived by Nilakshi et al. (2001) using the digitized sky survey DSS-2, indicates an excess of stars in the coronal region and thus seems an interesting object to study in detail. The open cluster NGC 7654 ( $\alpha_{2000} = {23^{\rm h}} {24.2}^{\rm m} $, $\delta_{2000} = 61\hbox{$^\circ$ }35'$, Trumpler class I2r) is located in the Cassiopeia constellation. The cluster has a dense core with some very bright B stars. Figure 1 shows V band image of the cluster NGC 7654. The interstellar reddening, distance and age of the cluster have been obtained by various authors (Fenkart & Schröder 1985; Viskum et al. 1997 and references therein; Choi et al. 1999). The reported values for the E(B-V) range from 0.49 mag to 0.62 mag, the distance estimates range from 1.21 kpc to 1.51 kpc whereas the derived age has a quite wide range, 25 Myr (Harris 1976) to 158 Myr (Viskum et al. 1997).

Our aim is to study the mass function and stellar evolutionary aspects of the cluster by observing a wide field. The observations, data reduction, and comparison with the previous photometries are given in the next section. The cluster radius, other photometric results and mass function of the cluster are described in the subsequent sections of the paper.

2 Observations and data reduction

The CCD $UBVI_{\rm C}$ observations of the cluster NGC 7654 were carried out using the 105 cm Schmidt telescope of the Kiso Observatory on November 3, 1999. The CCD camera used a SITe 2048 $\times$ 2048 TK2048E chip having a pixel size 24 $\mu$. At the Schmidt focus (f/3.1) each pixel corresponds to $1\hbox{$.\!\!^{\prime\prime}$ }5$and the entire chip covers a field of $\sim$ $50 \times 50$ arcmin2 on sky. In the present work we have used an area of $\sim$ $40 \times 40$ arcmin2. The read-out noise and gain of the CCD are 23.2 e- and 3.4 e-/ADU respectively. Initially there were cumuli in the sky but later on sky condition improved. The FWHM of the star images was $\sim$4 $\hbox{$^{\prime\prime}$ }$. The log of the observations is given in Table 1. A number of bias and dome flat frames were also taken during the observing runs. To standardize the observations on the Kiso Schmidt we generated secondary standards in the field of NGC 7654 by observing Landolt (1992) stars using 104-cm Sampurnanand telescope of the State Observatory, Naini Tal.


 

 
Table 1: Log of observations taken on November 3, 1999.

Filter		 Exposure Number of
  time (s) frames

U		 60 1
U 180 10
B 20 10
B 60 3
V 10 10
V 60 2
I 10 6
I 60 3


The data analysis was carried out at the State Observatory, Naini Tal. Cleaning of the frames was done using the ESO MIDAS software package and different clean frames of same exposure time and filters were co-added. The photometric measurements of the stars were performed using the DAOPHOT II profile fitting software. The stellar images were well sampled and a variable PSF was applied. When brighter stars are saturated on deep-exposure frames, their magnitudes have been taken from short-exposure frames. Most of the stars brighter than V = 10.5 could not be measured because they were saturated even on the shortest exposure frames. Profile-fitting photometry gives the error in the magnitude determination, the goodness of the fit parameter, $\chi $, which is a measure of the average rms deviation to the PSF fit normalized to the expected errors. It also gives a shape parameter, Sharpness, which measures how well the PSF fits the object. The image parameters and errors provided by DAOPHOT were used to reject poor measurements. The error, parameter $\chi $ and sharpness for the measurements used in the analysis are shown in Fig. 2. The photometric data along with the position of the stars measured in the cluster are given in the Table 2, which is available in electronic form only. The format of Table 2 is shown below.


 

 
Table 2: $UBVI_{\rm C}$ photometric data of the stars in the field of NGC 7654. X, Y are the pixel coordinates shown in Fig. 1. $\sigma _U, \sigma _B, \sigma _V,$ and $\sigma _I$ are the errors in the $U,B,V,I_{\rm C}$ bands respectively. $\chi _V$ and SV are the image parameter $\chi $ and Sharpness in V band respectively. Radius is with respect to the center X=855, Y=755.

No.

 X Y V B-V V-I U-B $\sigma _I$ $\sigma_V$ $\sigma_B$ $\sigma_U$ $\chi _V$ SV Radius
                          ( $\hbox{$^{\prime\prime}$ }$ )

1		 859.52 749.70 16.184 0.933 1.255 0.282 0.026 0.012 0.018 0.022 0.690 -0.085 6.970
2 846.39 756.64 18.772 1.313 1.638 * 0.030 0.080 0.050 * 0.470 -0.067 8.767
3 863.96 754.34 19.519 1.313 1.662 * 0.067 0.157 0.117 * 0.460 0.098 8.980
4 851.90 764.30 18.554 1.210 1.582 0.072 0.042 0.067 0.047 0.149 0.500 0.056 9.800
5 860.27 765.22 18.210 0.860 1.304 0.463 0.049 0.048 0.027 0.232 0.490 0.148 11.496
6 847.41 763.80 20.555 1.215 2.479 -1.301 0.095 0.416 0.235 0.190 0.440 -0.023 11.623
7 847.84 743.90 17.958 1.061 1.553 0.469 0.029 0.050 0.024 0.183 0.660 0.096 13.206
8 869.02 754.93 19.319 1.324 1.690 -0.629 0.051 0.139 0.072 0.175 0.510 -0.449 14.017
9 841.48 749.38 19.647 1.082 1.890 * 0.059 0.180 0.098 * 0.470 0.107 14.643
10 840.13 756.36 17.957 1.037 1.508 0.495 0.029 0.044 0.044 0.166 0.570 0.107 14.936
11 867.65 746.25 20.326 0.883 2.348 * 0.068 0.409 0.126 * 0.590 0.704 15.383
12 860.70 772.02 18.883 1.051 1.882 * 0.053 0.097 0.058 * 0.400 -0.098 17.947
13 837.64 743.65 18.416 0.861 1.313 0.464 0.056 0.072 0.034 0.245 0.650 -0.027 20.739
14 866.71 773.21 14.327 0.584 0.761 0.366 0.021 0.008 0.021 0.006 1.400 -0.104 21.645
15 854.99 777.48 12.870 0.460 0.636 -0.020 0.022 0.007 0.016 0.007 1.510 -0.073 22.480
16 877.86 760.22 19.111 0.980 1.660 0.382 0.051 0.095 0.055 0.380 0.390 -0.099 23.454
17 848.52 777.56 17.818 0.648 1.560 0.223 0.070 0.058 0.053 0.109 0.390 -0.101 23.468
18 830.84 756.63 17.689 1.057 1.196 0.831 0.040 0.033 0.031 0.189 0.540 -0.059 24.220



 

 
Table 3: Comparison of the present CCD photometry with the available photometries in the literature. The difference $\Delta $ (literature - present data) is in magnitude. Mean and $\sigma $ are based on N stars in a V magnitude bin.


V range		 $\Delta V $ $\Delta (B-V)$ $\Delta (U-B)$ $\Delta (V-I) $
  ${\rm Mean}\pm \sigma$ N ${\rm Mean}\pm \sigma$ N ${\rm Mean}\pm \sigma$ N ${\rm Mean}\pm \sigma$ N


Hoag et al. (1961):

                
10.0-11.0 - $0.105\pm0.017$ 3 $0.029\pm0.023$ 3 $0.052\pm0.031$ 3    
11.0-12.0 - $0.080\pm0.021$ 4 $-0.004\pm0.050$ 4 $0.077\pm0.033$ 4    
12.0-13.0 - $0.061\pm0.000$ 1 $-0.052\pm0.000$ 1 $0.029\pm0.000$ 1    
13.0-14.0 - $0.018\pm0.054$ 7 $0.014\pm0.050$ 7 $0.011\pm0.034$ 7    
14.0-15.0 - $0.178\pm0.123$ 4 $0.088\pm0.096$ 4 $0.007\pm0.068$ 4    
Choi et al. (1999):                
10.0-11.0 $ 0.029\pm0.027$ 2 $-0.019\pm0.002$ 2        
11.0-12.0 $-0.037\pm0.031$ 9 $0.017\pm0.040$ 9 $0.043\pm0.044$ 8    
12.0-13.0 $ 0.038\pm0.038$ 20 $0.028\pm0.046$ 20 $0.033\pm0.033$ 20    
13.0-14.0 $-0.047\pm0.040$ 29 $0.019\pm0.038$ 29 $0.018\pm0.035$ 29    
14.0-15.0 $-0.043\pm0.046$ 52 $0.022\pm0.058$ 52 $0.023\pm0.059$ 50    
15.0-16.0 $-0.049\pm0.050$ 25 $0.072\pm0.079$ 25 $0.052\pm0.098$ 25    
16.0-17.0 $-0.083\pm0.056$ 55 $0.118\pm0.088$ 55 $0.090\pm0.179$ 54    
17.0-18.0 $-0.082\pm0.106$ 45 $0.110\pm0.169$ 45 $0.040\pm0.230$ 37    
Stetson (2000):                
10.0-11.0 $0.166\pm0.013$ 2 $-0.165\pm0.007$ 2     $0.204\pm0.060$ 2
11.0-12.0 $0.127\pm0.060$ 8 $-0.173\pm0.039$ 8     $0.209\pm0.033$ 8
12.0-13.0 $0.135\pm0.027$ 10 $-0.135\pm0.032$ 10     $0.184\pm0.022$ 10
13.0-14.0 $0.136\pm0.018$ 15 $-0.124\pm0.033$ 15     $0.163\pm0.042$ 15
14.0-15.0 $0.131\pm0.037$ 17 $-0.109\pm0.053$ 17     $0.153\pm0.039$ 17
15.0-16.0 $0.140\pm0.033$ 10 $-0.060\pm0.086$ 10     $0.157\pm0.046$ 10
16.0-17.0 $0.104\pm0.061$ 20 $-0.007\pm0.058$ 20     $0.136\pm0.061$ 20
17.0-18.0 $0.165\pm0.080$ 33 $-0.024\pm0.166$ 33     $0.097\pm0.182$ 33



  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS1127fig2.ps} \end{figure} Figure 2: The DAOPHOT error and image parameters $\chi $ and Sharpness in V band as a function of magnitude for the measurements used in the analysis.
Open with DEXTER

2.1 Comparison with the previous photometries


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{MS1127fig3.ps} \end{figure} Figure 3: Comparison of the present CCD photometry with the photoelectric photometry by Hoag et al. (filled circles) and with the CCD photometries by Choi et al. (open circles) and Stetson (crosses).
Open with DEXTER

A comparison of the present CCD photometry with the available photoelectric (Hoag et al. 1961) and CCD photometry (Choi et al. 1999; Stetson 2000) has been carried out. The difference $\Delta $ (literature - present data) as a function of V magnitude is shown in Fig. 3 and statistical results are given in Table 3. The comparison with the photometry of Hoag et al. (1961) indicates that the colours obtained in the present work are in fair agreement with theirs whereas the Vmagnitude obtained by us are fainter by $\sim$0.07 mag. A comparison with the CCD photometry of Choi et al. (1999) and Stetson (2000) indicates that:

1.
The V magnitudes obtained by us are systematically fainter by $\sim$0.05  mag and brighter by $\sim$0.14 mag than those reported by Choi et al. (1999) and Stetson (2000) respectively;

2.
The (B-V) colours of brighter stars ($V\leq $ 15) obtained in the present work are in agreement with those given by Choi et al. (1999) whereas (B-V) colours of stars fainter than V=15 show a blueward trend in $\Delta (B-V)$ with increasing V magnitude. The (B-V) colours (for stars brighter than $V\leq $ 15.0) reported by Stetson (2000) are bluer by $\sim$0.13 mag because of difference in the V magnitude as mentioned above. The (B-V) colours for stars fainter than $V\sim15.0$ show a blueward trend in $\Delta (B-V)$ with increasing V magnitude;


 

 
Table 4: Completeness factor (CF) of photometric data in different radial (r) regions. The $N_{\rm f}$, $N_{\rm a}$, $N_{\rm r}$ are number of frames generated, numbers of stars added and number of stars recovered, respectively.


Range in mag

 $N_{\rm f}$ $r<180\hbox{$^{\prime\prime}$ }$ 180 $\hbox{$^{\prime\prime}$ }\leq r< 400\hbox{$^{\prime\prime}$ }$ 400 $\hbox{$^{\prime\prime}$ }\leq r\leq 700\hbox{$^{\prime\prime}$ }$ $r>700\hbox{$^{\prime\prime}$ }$
    $N_{\rm a}$ $N_{\rm r}$ CF $N_{\rm a}$ $N_{\rm r}$ CF $N_{\rm a}$ $N_{\rm r}$ CF $N_{\rm a}$ $N_{\rm r}$ CF
V band:                          
12.50-13.50 1 7 7 1.00 33 33 1.00 58 58 1.00 293 293 1.00
13.50-14.50 3 16 16 1.00 100 98 0.98 226 224 0.99 1005 994 0.99
14.50-15.50 5 35 30 0.86 165 160 0.97 472 464 0.98 1798 1759 0.98
15.50-16.50 7 72 66 0.92 258 236 0.91 692 670 0.97 2840 2716 0.96
16.50-17.50 9 94 79 0.84 408 341 0.84 1061 952 0.90 4203 3821 0.91
17.50-18.50 11 163 82 0.50 605 319 0.53 1546 914 0.59 6166 3735 0.61
18.50-19.50 13 309 52 0.17 928 151 0.16 2572 452 0.18 10274 1744 0.17
B band:                          
12.50-13.50 1 1 1 1.00 4 4 1.00 1 1 1.00 33 33 1.00
13.50-14.50 3 11 11 1.00 36 36 1.00 79 79 1.00 371 369 0.99
14.50-15.50 5 15 14 0.93 105 102 0.97 258 253 0.98 1085 1066 0.98
15.50-16.50 7 39 34 0.87 179 172 0.96 474 459 0.97 1888 1834 0.97
16.50-17.50 9 74 61 0.82 271 236 0.87 744 705 0.95 3019 2803 0.93
17.50-18.50 11 102 72 0.71 412 315 0.76 1093 940 0.86 4362 3789 0.87
18.50-19.50 13 172 60 0.35 649 255 0.39 1644 749 0.46 6590 2954 0.45


3.
The (U-B) colours of brighter stars ($V\leq $ 16.0) obtained by us are systematically bluer by $\sim$0.03 mag in comparison to those given by Choi et al. (1999). The $\Delta $ increases for V> 16.0 mag without having any trend as observed in case of (B-V) colour;

4.
The (V-I) colours reported by Stetson (2000) are redder by $\sim$0.16 mag in comparison to those obtained by us.

2.2 Completeness of the photometric data

It is very important to check the completeness of data and to make necessary corrections in the sample to take into account incompleteness that may occur because of various reasons e.g., crowding of the stars. The correction is necessary if we want to analyze the luminosity function(LF)/ mass function (MF) of the stars in the cluster. To determine the completeness factor we used ADDSTAR routine of DAOPHOT II. This method has been used by various authors (cf. Sagar & Griffiths 1998). Briefly, the method consists of randomly adding artificial stars of known magnitudes and positions into the original frame. The frames are re-reduced using the same procedure used for the original frame. The ratio of number of stars recovered to those added in each magnitude interval gives the completeness factor, CF, as a function of magnitude.

The luminosity function (LF), defined as the distribution of stars per unit magnitude range, can in principal be obtained from frame in one wavelength band only. However, we know that the cluster region is contaminated by the field stars and with only a single passband we cannot decide whether the star is really a member of the cluster. Two passbands, such as B and V, are required to identify the cluster members. We used the V, (B-V)CMD to determine the membership and to construct the LF of the cluster. Detailed procedure will be discussed in Sect. 6.1. Although the use of two colours gives a realistic LF of the cluster, it further complicates the estimation of completeness of the data. Mateo (1988), with an assumption that the star counts in two bands are independent, adopted a completeness factor as a product of the CF values obtained for two different bands, whereas, Sagar & Richtler (1991) adopted the minimum value of the completeness factors of the pair to correct the star counts. They argued that the two frames are not independent.

To test the ability of these techniques Banks (1994) and Banks et al. (1995) performed numerical simulations and concluded that the method of Mateo (1988) increasingly overestimates the incompleteness correction as the magnitude increases. The method suggested by Sagar & Richtler estimates an actual LF except when the value of CF fell below 50 percent, which Stetson (1991) defines as the limiting magnitude of a CCD frame. We used the procedure given by Sagar & Griffiths (1998) to correct the data incompleteness in the following manner.

We added artificial stars to both B and V images in such a way that they have similar geometrical locations but differ in B brightness according to mean (B-V)colours of the MS stars. The luminosity distribution of artificial stars has been chosen in such a way that more stars are inserted into the fainter magnitudes bins. In total about 15 percent stars are added so that the crowding characteristics of the original frame does not change significantly. The details of the distribution of the added stars are given in Table 4. The stars recovered in both B and V bands have been used to determine the data completeness factor CF, for the four radial regions as a function of brightness, and the value thus obtained are also given in Table 4. As expected the incompleteness of the data increases with increasing magnitudes and increasing stellar crowding. The minimum value of the CF of the pair thus obtained is used to correct the data for the incompleteness.

3 Radial stellar surface density

As the area of the CCD observation is quite large, it can be used to study the radial extent and structure of the cluster. The center of the cluster is derived iteratively by calculating average X and Y positions of stars within 300 pixels from an eye estimated center, until they converged to a constant value. An error of a few pixels is expected in locating the cluster center. The (X,Y) pixel coordinates of the cluster center are found to be (855, 755), which corresponds to $\alpha_{2000}= 23^{\rm h} 24^{\rm m} 33^{\rm s}$, $\delta_{2000}= +61^{\circ} 34\hbox{$^\prime$ }10\hbox{$^{\prime\prime}$ }$.

To determine the radial surface density we divided the cluster into a number of concentric circles. Projected radial stellar density in each concentric circle was obtained by dividing the number of stars in each annulus by its area. Densities thus obtained are plotted for different magnitude levels in the left panel of Fig. 4.


  \begin{figure} \par\includegraphics[width=17cm,clip]{MS1127fig4.ps} \end{figure} Figure 4: The radial variation of the projected stellar density for different magnitude levels. Dashed lines show the density of field stars.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=14.3cm,width=7.65cm,clip]{MS1127fig5.ps} \end{figure} Figure 5: The (U-B)/(B-V) diagram for the stars in three subregions of the cluster. The continuous and dashed curves in the upper panel represent the main-sequence (MS) for Z=0.008 and 0.02 respectively shifted along the slope of the reddening of 0.72. The MS for Z=0.008 is also fitted for minimum and maximum value of the reddening in the three subregions of the cluster (for detail see text).
Open with DEXTER

The density distribution shown in the left panel of Fig. 4 may be affected by the presence of field stars. To see their effect on the cluster structure, we carried out the following analysis. It is difficult to separate field stars from the cluster, only on the basis of the photometry. However, the contribution of the field stars can be reduced if we select a sample of stars near a well defined main-sequence (MS) in the colour-magnitude diagram. To select such a sample we defined blue and red envelope of the MS (cf. Sect. 7) and the radial density distribution of the MS sample is also shown in the right panel of Fig. 4. Both the samples show an almost same radial distribution of the density. However the radial distribution for stars V< 20 indicate an excess of density at $r\sim 300\hbox{$^{\prime\prime}$ }$. The density excess disappears in the radial distribution of samples having stars $V\leq $17.0. The radial distribution of stars having $V\leq $ 17.0 indicates that the extent of the cluster is about 700 arcsec with a core radius, defined as the radius at which the surface density drops to half of its central value, of about 225 arcsec. To study various parameters, e.g., interstellar extinction, IMF etc., in detail we divided the cluster into three subregions as the inner region ( $r<180\hbox{$^{\prime\prime}$ }$), the intermediate region (180 $\hbox{$^{\prime\prime}$ }\leq r< 400\hbox{$^{\prime\prime}$ }$) and the outer region (400 $\hbox{$^{\prime\prime}$ }\leq r\leq 700\hbox{$^{\prime\prime}$ }$). The stars located in the region having $r>700\hbox{$^{\prime\prime}$ }$ have been used to estimate the field star contamination in the cluster region.

4 Interstellar extinction

The cluster NGC 7654 is located in an interam-region (cf. Fenkart & Schröder 1985) and suffers from a strong interstellar absorption. Danford & Thomas (1981) have found that the cluster has non-uniform reddenings with an excess for stars in the southern half. The interstellar extinction E(B-V) in the cluster region can be estimated using the (U-B)/(B-V) colour-colour diagram. The colour-colour diagram for the three subregions of the cluster are shown in Fig. 5. Here as well as in Sect. 5 we used E(B-V) values of only those stars which have $ V_{\rm error} \leq 0.02 $. Since the inner region of the cluster is less contaminated by field stars, a comparison of the observed MS in the inner region with the intrinsic MS will be least affected by field star contamination. In Fig. 5 an unreddened MS for Z=0.02 and 0.008 by Bertelli et al. (1994) is shifted along a line having a slope E(U-B)/E(B-V)= 0.72. We find that both the curves indicate a mean reddening of $E(B-V)\sim$ 0.56 for the cluster, however the MS for Z=0.008 show a better fit in the range 0.8 $\leq B-V \leq$1.1 as compared to the MS for the solar metallicity. Therefore in the ensuing section we use the stellar model of Bertelli et al. (1994) for Z = 0.008.

The spatial distribution of interstellar matter within the cluster can also be studied with the help of (U-B/B-V) colour-colour diagram. Figure 5 indicates a variable reddening in the cluster region. Reddening E(B-V) varies in the inner region from 0.46 to 0.64 mag, whereas in the two other regions the reddening varies from 0.54 to 0.80 mag. Thus the differential reddening $\Delta E(B-V)= E(B-V)_{\rm max}-E(B-V)_{\rm min}$ varies from 0.18 mag in the inner region to 0.26 mag in the outer region.

The extinction for individual stars having spectral type earlier than A0 has been derived using the Q-method (Johnson & Morgan 1953). The distribution of the reddening E(B-V) in various radius bins is shown in Fig. 6, which indicates that maxima of the distribution shifts from 0.53 mag in the central region to 0.68 mag in the outer region of the cluster. The mean reddening as a function of radial distance is shown in Fig. 7. These diagrams clearly indicate a lack of reddening material in the central region of the cluster. However, we did not find any reddening variation in the NS or EW direction as evident from Fig. 8.

In Fig. 9 the reddening E(B-V) is plotted as a function of luminosity in two different regions, having $r\leq 400\hbox {$^{\prime \prime }$ }$ and $400\hbox{$^{\prime\prime}$ }\leq r \leq 700\hbox{$^{\prime\prime}$ }$, of the cluster field. In the inner and intermediate region of the cluster (i.e., $r\leq 400\hbox {$^{\prime \prime }$ }$) the brightest stars ( $V_{0}\leq 10.0$) show in general a higher value of reddening. However no such type of dependence is observed in the outer region.

5 The extinction law

Numerous investigations have shown that the reddening law in terms of $R={\rm A}_v/E(B-V)=3.1$ is valid in many parts of our Galaxy. However young clusters associated with gas and dust may show a large value of R (cf. Hillenbrand et al. 1993 and references therein). It has been shown by Chini & Wargau (1990) that two-colour-diagrams (TCDs) of the form (V-X) vs. (B-V), where X denotes one of the broad band filters (R,I,J,H,K,L) between 0.7 and 3.7 $\mu$, provide an effective method of separating the abnormal extinction arising within such clusters from the normal extinction produced by general interstellar medium. In those TCDs the unreddened main-sequence and the path of the normal reddening make practically identical lines. This makes these diagrams useless for the determination of the amount of reddening, but, instead very useful for detecting anomalies in the reddening law. To derive the value of $R_{\rm cluster}$(ratio of total to selective extinction in the cluster region) we use the approximate relation (cf. Neckel & Chini 1981),

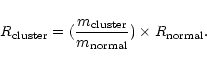
\begin{eqnarray*}R_{\rm cluster}=(\frac{m_{\rm cluster}}{m_{\rm normal}})\times R_{\rm normal}. \end{eqnarray*}


Here $m_{\rm cluster}$ and $m_{\rm normal}$ are the slopes of the lines followed by the cluster stars and field stars, respectively, and $R_{\rm normal}$ = 3.1.

Figure 10 shows the (V-I)/(B-V) TCD for all the stars measured in the inner+intermediate region of the cluster (i.e., $r\leq 400\hbox {$^{\prime \prime }$ }$). In Fig. 10 we can identify two distinct group of objects.

i)
Stars having $1.1 \leq (B-V) \leq 2.0$. Most of these star should be field stars;

ii)
Stars having $0.4 \leq (B-V) \leq 1.1$. Most of these stars are cluster members and fall below the distribution of field stars.

However it is difficult to clearly differentiate the cluster stars from the field stars with the help of this diagram. To derive $m_{\rm cluster}$ we performed a least square fit to the data having $(B-V) \leq $ 1.1, however, we have to keep in mind that the sample is contaminated by field stars. For the above mentioned sample $m_{\rm clusters}$ comes out to be 1.31$\pm$0.03. The $m_{\rm normal}$ is estimated from the stars outside the cluster region i.e., $r \geq 700\hbox{$^{\prime\prime}$ }$ having same range in colour ( $B-V \leq 1.1$) as in case of stars in the cluster region and comes out to be $1.15\pm0.02$. Then the value of $R_{\rm cluster}$ comes out to be 3.5 $\pm$ 0.1.

6 Colour magnitude diagrams

In Fig. 11 we have plotted V/(B-V), V/(U-B) and V/(V-I) colour-magnitude diagrams (CMDs) for stars lying in three different regions of the cluster. In the innermost region we see a very well defined main-sequence (MS). The effect of field stars on the MS can be seen easily as we move towards outer regions. The broadening of the (MS) may be due to:

(i)
variable reddening in the cluster region;
(ii)
presence of field stars in the sample;
(iii)
internal error of the photometry;
(iv)
presence of binaries and peculiar stars in the cluster.


  \begin{figure} \par\includegraphics[width=16.1cm,clip]{MS1127fig6.ps} \end{figure} Figure 6: The frequency distribution of the E(B-V) in various regions of the cluster.
Open with DEXTER

Since the error in magnitude estimation is $\sim$0.04 mag for stars having $V\leq $ 17.0, the third point is not the main factor for broadening of the MS. However, the errors increase rapidly for star having V> 17.0 and the effect of photometric errors is obvious in the CMDs. As we have discussed earlier that the cluster region shows a variable reddening, the interstellar reddening should be a cause of broadening of the MS. It is difficult to separate field stars from the cluster stars, however we can reduce the contamination of field stars if we restrict ourselves to the central portion of the cluster. Thus on the basis of the above discussions we can conclude that the variable reddening, probable binaries and the presence of field stars are the main cause for broadening of the MS below $V\sim$ 17 mag.

6.1 Cluster membership


 

 
Table 5: Luminosity function for the three cluster subregions. The $n_{\rm c}, n_{\rm f}$ are the number of stars (corrected for the data incompleteness) in the subregions of the cluster & the number of expected field stars, respectively and $n_{\rm p}$ is the number of probable cluster members.

Range in		 Inner region Intermediate region Outer region
V mag $n_{\rm c}$ $n_{\rm f}$ $n_{\rm p}$ $n_{\rm c}$ $n_{\rm f}$ $n_{\rm p}$ $n_{\rm c}$ $n_{\rm f}$ $n_{\rm p}$
10.5-11.5 3.0 0.3 2.7 8.0 1.0 7.0 - 2.8 -
11.5-12.5 9.0 0.6 8.4 17.0 2.3 14.7 9.0 6.0 3.0
12.5-13.5 18.0 1.0 17.0 27.0 3.8 23.2 20.0 10.0 10.0
13.5-14.5 25.0 2.1 22.9 50.0 8.3 41.7 52.0 22.0 30.0
14.5-15.5 31.4 4.8 26.6 70.1 18.6 51.5 90.8 49.5 41.3
15.5-16.5 43.7 11.8 31.9 84.6 46.0 38.6 138.1 122.4 15.7
16.5-17.5 61.0 25.9 35.1 171.4 101.7 69.7 283.3 270.3 13.0
17.5-18.5 144.0 76.1 67.9 422.6 298.0 124.6 766.1 792.6 -
18.5-19.5 411.7 421.2 - 1843.8 1650.6 193.2 4038.9 4390.0 -


In order to determine cluster parameters precisely, it is important to identify the stars which are actually cluster members. Membership determination is also crucial for assessing the presence of pre-main sequence (PMS) stars, since PMS stars and dwarf foreground stars both occupy positions above the ZAMS in a CMD. The most valuable method to decide cluster membership is the proper motion studies. Other methods of estimating cluster membership are: i) expected range of colour excess, ii) reddening slopes, iii) position on the CMDs and iv) spectroscopic observations. Since proper motions and spectroscopic observations are not available, we will use only photometric criteria to identify the cluster members. The membership for individual stars brighter than V=15 can be obtained after dereddening the magnitude and colours of the stars and inspecting their positions on the CMDs. However, membership for stars fainter than $V\le 15$ could not be established as individual reddening is not available due to the inapplicability of the Q-method for these stars.

The cluster members thus identified are used to estimate the age and the age spread in the cluster. As stated above it is difficult to separate the cluster members fainter than $V\sim 15$ from field stars. However, the contamination due to field stars is greatly reduced if we select a sample of stars which are located near the well defined main-sequence. We defined blue and red envelopes for the main-sequence on the V/(B-V) CMD for stars lying within the cluster boundary i.e., $r\leq 700\hbox {$^{\prime \prime }$ }$ and these are shown in Fig. 12. Stars located outside the area having $r>700\hbox{$^{\prime\prime}$ }$ are considered as field stars. After normalizing the area we can find the number of field stars present per unit area in each magnitude bin. Thus after subtracting the contribution of field stars (corrected for data incompleteness) from each magnitude bin of the contaminated sample of MS stars (also corrected for data incompleteness) we can estimate the number of probable MS cluster members. The number of probable cluster members in the three subregions of the cluster thus obtained are given in Table 5. As expected field star contamination increases from the inner region to the outer region.


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{MS1127fig7.ps} \end{figure} Figure 7: The radial variation of the reddening E(B-V) in the cluster field. The error bars represent standard errors.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.4cm,clip]{MS1127fig8.ps} \end{figure} Figure 8: Distribution of the reddening E(B-V) in the NGC 7654 region. The numbers given in parentheses are the number of stars. The coordinates are given in pixels. The coordinates of the cluster centre are X=855, Y=755.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{MS1127fig9.ps} \end{figure} Figure 9: The plot of reddening E(B-V) as a function of luminosity. The bright stars ( $V_{0}\leq 10.0$) in the upper panel have been differentiated for the first epoch (open circles) and second epoch (filled circle) (for details see text).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{MS1127fig10.ps} \end{figure} Figure 10: The (V-I)/(B-V) diagram for all the stars measured in the region having $r\leq 400\hbox {$^{\prime \prime }$ }$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=17cm,clip]{MS1127fig11.ps} \end{figure} Figure 11: The CMDs in the three subregions of the cluster. The isochrones by Bertelli et al. (1994) for log age = 8.0, 8.2 and 8.4 are also shown.
Open with DEXTER

6.2 Age and distance of the cluster

Recently Viskum et al. (1997) and Choi et al. (1999) reported an age of 158 Myr and 100 Myr, respectively for NGC 7654, whereas, Danford & Thomas (1981) and Harris (1976) assigned a younger age, 65 Myr and 25 Myr, respectively, to the cluster. By combining their data with those of Bouigue (1959) and Hoag et al. (1961), Viskum et al. (1997) tried to investigate the discrepancy in the age determination using the isochrones for younger ages, but could not fit them with the entire sample. They concluded that there is an older cluster behind a group of younger stars. We tried to fit the isochrones by Bertelli et al. (1994) for z = 0.008 assuming a mean reddening E(B-V)= 0.57, in Fig. 11 and found a mean age $\sim$160 Myr and a mean distance modulus $(m-M_v) = 12.50 \pm 0.10$which corresponds to a distance of 1380 $\pm$ 70 pc. Viskum et al. (1997) and Choi et al. (1999) reported a distance of 1400 $\pm$ 200 pc and $1500 \pm 100$ pc, respectively, for the cluster. Although the age and distance obtained here are in good agreement with the results by Viskum et al. (1997) and Choi et al. (1999), we will illustrate in the ensuing discussions how the analysis gives errant results if the reddening correction is not applied properly especially where the reddening is variable.

In Fig. 13, we have plotted dereddened colour-magnitude diagrams for the cluster stars in the area having $r\leq 400\hbox {$^{\prime \prime }$ }$ to reduce the contamination due to field stars. The dereddened magnitude V0 (= V - Av) has been obtained for a normal extinction law i.e., R = 3.1, though we have indication for a slightly different extinction law in the NGC 7654 region. One bright star (star no 2 of Hoag et al. 1961) was saturated even in our shortest exposures. The data for this star have been taken from Hoag et al. (1961). The dereddened magnitude and colours of this star are obtained by using mean E(B-V) value (=0.75) of nearby stars. The star is located in the central region, therefore the probability of being a cluster member is high. If it is a cluster member, it can be assigned a spectral class as $\sim$F5Ib and it nicely follows the isochrone of age 63 Myr.


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1127fig12.ps} \end{figure} Figure 12: The V, (B-V) CMD for stars lying within the cluster boundary (i.e., $r\leq 700\hbox {$^{\prime \prime }$ }$) with blue and red envelopes delimiting the MS stars (see text).
Open with DEXTER

The dereddened CMDs present an entirely different picture for the cluster age. The distribution of 15 bright stars ( $V_{0}\leq 10.0$) in the CMDs shows a large spread in colour which cannot be explained only on the basis of photometric errors and presence of binaries etc. The statistics for the bright stars ( $V \leq 12.5$) given in Table 5 indicate a contamination of about 10% due to the field stars in the cluster region having $r\leq 400\hbox {$^{\prime \prime }$ }$. Statistically we expect that at most 2 field stars may contaminate the sample of 15 stars. Thus the distribution of stars in the CMDs indicates that the star formation within the cluster is not coeval and has a large age spread $(30<\tau\leq100$ Myr). Such a large age spread has not been reported in the open clusters. The Pleiades cluster has been claimed to have a prolonged star formation period, perhaps 30 Myr (Siess et al. 1997; Belikov et al. 1998). Recently, Elmegreen (2000) has reported that the total duration of star formation in most of the clouds is only 1-2 dynamical times ($\sim$2-4 Myr) once star formation begins. However, some clusters have larger age spreads than the dynamical time, which could be the result of multiple and independent star formation (Elmegreen 2000).

The dereddened CMDs give a distance modulus (m-Mv)0 = 10.4 which corresponds to a distance of 1200 pc. However, Fig. 11, where we applied an average value of E(B-V) = 0.57, gives a distance of $1380 \pm 70$ pc. We prefer this distance (1380 pc) as compared to that obtained from Fig. 13 (1200 pc), where we used only the upper portion of the CMDs as E(B-V) values are not available for fainter stars. Most of these stars are showing evolutionary effects, whereas in Fig. 11 it is easy to compare the theoretical MS with the observed one.

7 Mass function


 

 
Table 6: The mass function of the cluster NGC 7654. The numbers of probable cluster members (N) have been obtained after subtracting the expected contribution of field stars in each magnitude range. $\log \phi$ represents $\log N(\log m)$.

Range		 Mass Mean Inner region Intermediate region Outer region
V mag $M_{\odot}$ $\log M_\odot $ N $\log \phi$ N $\log \phi$ N $\log \phi$
10.5-11.5 5.13-4.49 0.682 2.7 1.668 7.0 2.082 - -
11.5-12.5 4.49-3.58 0.606 8.4 1.933 14.7 2.176 3.0 1.486
12.5-13.5 3.58-2.58 0.489 17.0 2.078 23.2 2.213 10.0 1.848
13.5-14.5 2.58-1.84 0.344 22.9 2.193 41.7 2.452 30.0 2.310
14.5-15.5 1.84-1.42 0.212 26.6 2.371 51.5 2.659 41.3 2.563
15.5-16.5 1.42-1.19 0.116 31.9 2.623 38.6 2.706 15.7 2.315
16.5-17.5 1.19-1.00 0.039 35.1 2.665 69.7 2.962 13.0 2.233
17.5-18.5 1.00-0.84 -0.036 67.9 2.951 124.6 3.215 - -



  \begin{figure} \par\includegraphics[width=8.3cm,clip]{MS1127fig13.ps} \end{figure} Figure 13: The dereddened CMDs for the stars in the cluster region having $r\leq 400\hbox {$^{\prime \prime }$ }$. The isochrones for Z=0.008 by Bertelli et al. (1994) for various ages have also been plotted.
Open with DEXTER

The distribution of stellar masses at the time of birth of the cluster is known as the initial mass function (IMF). Studies of IMF of star clusters are important to constrain star formation theories and also to understand the early stages of evolution of star clusters. A fundamental question about the IMF is whether the shape of the IMF is universal in time or space. Scalo (1986) in a detailed review of IMF did not find any convincing logic to support a variable IMF. However after a period of twelve years, he cited much evidence that does NOT support a universal IMF (Scalo 1998). On the other hand, Sagar (2000) indicates a universal Salpeter type MF above $M > 1~M_\odot$. The most important contribution to the studies of IMF in the last twelve years is the advent of CCDs. The CCDs combined with a moderate size telescope are giving deeper insights into low mass stars that can change the scenario of the IMF studies. One of the important studies was by Phelps & Janes (1993) who estimated IMF for eight clusters with ages $10-70\times10^{6}$. The slope of the mass function they obtained varies from 0.4 to 1.8. However some of the clusters in their sample, as pointed out by Scalo (1998), do not cover a large area. Pandey et al. (1992) and Sagar et al. (1986) have found that the nature of mass function does not remain the same over the entire region of the cluster and the slope of the mass function steepens as the radial distances increase. In the present observations we have imaged a sufficiently large area that covers the cluster including its coronal region where most of the low mass stars are expected to present. With the help of CMD's we can derive the observed luminosity function LF of the probable main sequence cluster members and then the mass function (MF) using the theoretical evolutionary model of Bertelli et al. (1994). As the IMF is the frequency distribution of stellar masses in an ensemble of newly formed stars in a stellar system or region, it is assumed safe to say that the IMF can be estimated for young star clusters as they contain a nearly coeval set of stars formed from a parental cloud. However the star formation in the present case as well as in the case of some other clusters (e.g., Pandey et al. 1991) is found to be a continuous process. Therefore, the term IMF cannot be strictly applicable in the case of NGC 7654 and we can estimate only the present day mass function.

The mass function is often expressed by the power law, $N(\log m) \propto m^{\Gamma}$ and the slope of the mass function is given as:

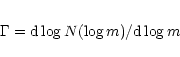
\begin{eqnarray*}\Gamma = {\rm d} \log N(\log m)/{\rm d} \log m \end{eqnarray*}


where $N (\log m)$ is the number of star per unit logarithmic mass interval. The classical value derived by Salpeter (1955) for the slope of IMF is $\Gamma = -1.35$. The LFs of the three subregions of the cluster NGC 7654 (given in Table 5) have been converted to the MFs using the theoretical model of Bertelli et al. (1994) and the resultant mass function data are given in Table 6.


  \begin{figure} \par\includegraphics[height=12.4cm,width=8cm,clip]{MS1127fig14.ps} \end{figure} Figure 14: A plot of the mass function for the entire cluster region i.e., $r\leq 700\hbox {$^{\prime \prime }$ }$ (uppermost panel). The brightest point has not been included in the least-squares fit. Other three panels show the mass functions in three subregions of the cluster. The error bars represent 1/$\sqrt {N}$ errors.
Open with DEXTER

Figure 14 (uppermost panel) shows a plot of $\log N(\log m)$ vs. $\log m$ for the entire cluster region, i.e., $r\leq 700\hbox {$^{\prime \prime }$ }$. The mass function can be represented by a power law with a slope $\Gamma = -1.40\pm - 0.07$, which is in good agreement with the Salpeter value. Thus prima facie the mass function of the NGC 7654 looks a normal one, however in reality it turns out not to be so if we plot the mass function for three subregions, also shown in Fig. 14. Figure 14 shows that the mass function is NOT uniform in the whole cluster region and it can NOT be represented by a single power law. The slopes of the mass function for the three subregions are given in Table 7, which indicates that in the inner and intermediate regions the slope $\Gamma $ for stars $M >\sim$ $1.5~M_{\odot}$, is the same within errors, whereas it becomes steeper for the low mass stars in the intermediate region. However there is no indication for a truncation of the slope of mass function at lower mass end ($\sim$0.9 $M_{\odot}$). The mass function in the outer region is quite different from the inner and intermediate regions. In the outer region a truncation of mass function occurs at $M \sim 1.6~M_{\odot}$. Since the data have been corrected for their incompleteness which is not very severe (CF $\sim$ 0.9), we believe that the truncation in mass function is a real feature. In the outer region the slope of the mass function in the mass range 1.6 $< M_{\odot} < $ 4.0 is quite steeper as compared to those obtained in the inner and intermediate regions. These findings are in agreement with those reported by Pandey et al. (1992), where they have reported that slope of the MF becomes steeper in the outer region of the clusters.


 

 
Table 7: The slope of mass function $\Gamma $ in various regions/subregions of the cluster NGC 7654.
  Mass range ($M_{\odot}$) $\Gamma \pm \sigma$
Inner region 0.92-1.63 -2.17 $\pm$ 0.39
  1.63-4.04 -1.07 $\pm$ 0.08
Intermediate region 0.92-1.31 -3.18 $\pm$ 0.10
  1.31-4.04 -1.28 $\pm$ 0.20
Outer region 1.63-4.04 -2.78 $\pm$ 0.21
Whole cluster region 0.92-4.04 -1.40 $\pm$ 0.07


As discussed in Sect. 6, the star formation seems to be a prolonged process in the cluster NGC 7654. To study the star formation in different phases, we overplotted two isochrones for age 32 Myr and 100 Myr representing the extreme stages of the star formation. The proximity of the stars to the isochrones was the criterion to decide the phase. The stars (mostly fainter than $V_{0} \sim 10.0$) lying significantly away from the isochrones in both the V0/(B-V)0 and V0/(U-B)0 CMDs are probably field stars and were not included in the sample. The V0/(U-B)0 CMD thus obtained is shown in Fig 15. A cumulative distribution of stars in these two phases as a function of luminosity is shown in Fig. 16. The Kolmogorov-Smirnov test at a confidence level  0.75, indicates that the distribution of stars during the early phase of star formation was relatively biased towards bright (i.e. relatively massive) stars.


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{MS1127fig15.ps} \end{figure} Figure 15: The dereddened V/(U-B) CMD for probable cluster members formed during different phases of star formation (see text).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{MS1127fig16.ps} \end{figure} Figure 16: The cumulative distribution of stars as a function of luminosity. Phases I and II represents early and later stages of star formation process, respectively.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1127fig17.ps} \end{figure} Figure 17: The massive end of the mass function of the cluster for two different phases of star formation (see text).
Open with DEXTER

For both the samples the stars were counted as a function of one magnitude bin of the V passband. The obtained luminosity functions (LFs) were converted to the mass functions using the theoretical models of Bertelli et al. (1994), in the same manner as described in Sect. 7. The difference in the mass bins of the two samples arises due to conversion of V luminosity to the mass using the isochrones of log age =7.5 and 8.0 respectively. The obtained MFs, shown in Fig. 17, also indicate that during the early phase star formation was biased towards relatively high mass stars whereas most of the low mass stars should have been formed later on.

8 Mass segregation

There are clear evidences for mass segregation in a few galactic star clusters, with the highest mass stars preferentially found towards the center of the cluster (see e.g., Pandey et al. 1992 and references therein). Star clusters in the LMC also show a large number of low-mass stars relative to high mass stars at larger radii (Fisher et al. 1998 and references therein). To characterize the degree of mass segregation in the NGC 7654 we subdivided the sample into three mass groups ( $ 5.2\le M_{\odot}<2.6,\, 2.6\le M_{\odot}<1.2$ and $1.2\le M_{\odot}\le 0.7$). Figure 18 shows the cumulative distribution as a function of radius in three different mass groups. These normalized cumulative distributions are corrected for the incompleteness and the probable contamination due to field stars has also been removed. Figure 18 clearly indicates an effect of mass segregation in the cumulative distribution in the sense that most massive stars tend to lie near the cluster centre. The Kolmogorov-Smirnov test confirms the statement that the cumulative distribution of most massive stars in the cluster ( $5.2 \le M_{\odot} < 2.6$) is different at a confidence level better than 99% from the cumulative distribution of relatively less massive stars. However, the cumulative radial distributions for the lower mass bins cannot be distinguished from one another. This indicates that the mass segregation is less evident in the lowest mass stars of the cluster. This phenomenon was noticed by Van Leeuwen (1983) and also found in the Hyades (Mathieu 1985) and Pleiades (Raboud & Mermilliod 1998). It could be a general phenomenon because low mass star population is the most spatially extended, due to energy equipartition, and therefore is the most severely truncated by the galactic tidal field (Mathieu 1985).


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{MS1127fig18.ps} \end{figure} Figure 18: Cumulative distribution function for different mass intervals.
Open with DEXTER

To decide whether the mass segregation discussed above is primordial or due to dynamical relaxation, we have to estimate the relaxation time. Because of the dynamical relation low mass stars in a cluster may possess the largest random velocities, consequently these will try to occupy a large volume than high stars (cf. Mathieu & Latham 1986; McNamara & Sekiguchi 1986; Mathieu 1985). The dynamical relaxation time $T_{\rm E}$, of the clusters can be estimated using the relation,

\begin{eqnarray*}T_{\rm E} = \frac {8.9\times 10^{5}(NR_{\rm h}^{3}/\bar{m})^{1/2}} {\log(0.4N)} \end{eqnarray*}


where N is the number of cluster members, $R_{\rm h}$ is the radius containing half of the cluster mass and $\bar{m}$ is the average mass of cluster stars (cf. Spitzer & Hart 1971). We estimated a total number of main-sequence stars in the mass range 0.8 $\le M_{\odot} \le$ 5.1, $N \sim$ 670. The total mass of the MS stars in the mass range 0.8 $\le M_{\odot} \le$ 5.1, obtained with the help of luminosity function, is $\sim$1100  $M_{\odot}$. This mass should be considered as a lower limit to the total mass of the cluster. Thus the mean mass of the cluster stars is $\bar{m}$ = 1.6 $M_{\odot}$. For the half mass radius, we used half of the cluster extent i.e., $R_{\rm h} = 2.3$ pc. Using these numbers the relaxation time $T_{\rm E}$ comes out to be $\sim$ $3\times10^{7}$ yr. The obtained relaxation time $T_{\rm E}$ is comparable to the ages of the stars formed during the second epoch of star formation.

9 Effect of change in the cluster center on the analysis


 

 
Table 8: The mass function slope $\Gamma $ for various regions/subregions of the cluster NGC 7654 for the new center (X= 825, Y= 795). The values given in brackets are for the MF obtained in Sect. 7 (see Table 7).
  mass range($M_{\odot}$)        $\Gamma \pm \sigma$
Inner region 0.92-1.63 $-1.73\pm0.43$ ( $-2.17\pm0.39$)
  1.63-4.04 $-0.70\pm0.15$ ( $-1.07\pm 0.08$)
     
Intermediate region 0.92-1.31 $-2.59\pm0.07$ ( $-3.18\pm0.10$)
  1.31-4.04 $-1.59\pm0.19$ ( $-1.28\pm 0.20$)
     
Outer region 1.63-4.04 $-3.35\pm0.89$ ( $-2.78\pm0.21$)
     
Total region 0.92-4.04 $-1.53\pm0.08$ ( $-1.40\pm0.07$)


Sometimes, estimation of the center in star clusters is a tricky job. The determination of cluster center may depend on various parameters e.g., the distribution of the stars of different luminosity may have different centers for their distribution. The statistics given in Table 5 indicate that there may be many cluster members as faint as $V\sim 19.5$, therefore in the present work we preferred a center (X= 855, Y= 755) obtained for the stars having luminosity $ V \le 20$ (cf. Sect. 3). However, the center coordinates for the cluster shifts towards the North-East direction for the distribution of bright stars. For the stars having $V \le$ 18.5 the pixel coordinates for the cluster center comes out to be X=825, Y=795. In this section we try to find out possible effects on the analysis presented above due to the change of the adopted cluster center. We obtained the radial surface density distribution, the spatial distribution of reddening and the spatial variation of mass function for the cluster center having the above pixel coordinates. The density and reddening distributions are shown in Fig. 19. The comparison of the distributions obtained for two different centers of the cluster, also shown in Fig. 19, are nearly the same. The slope of the mass function (in the mass range $0.8 \le M_{\odot} \le 4.5$) for the whole cluster region i.e., $r\le 700{\hbox{$^{\prime\prime}$ }}$ around the new center can be represented by a single power law with a slope $\Gamma = -1.53 \pm 0.08$, which is in fair agreement with the $\Gamma = -1.40 \pm 0.08$ obtained in Sect. 7. Although the mass function also indicates a same type of spatial variation as discussed in Sect. 7, the values of mass function slopes are slightly different. The slopes of the mass function obtained for the new center are compared with those obtained in Sect. 7 in Table 8.


  \begin{figure} \par\includegraphics[height=9.8cm,width=8.1cm,clip]{MS1127fig19.ps} \end{figure} Figure 19: The reddening and density distributions obtained for the cluster centre having pixel coordinates X=825, Y=795 (filled circles). Density is given as number of stars/ ${\rm arcsec}^2$. In the upper panel the small dashed curve with open circles shows radial variation of the reddening displayed in Fig. 7, whereas in the lower panel the small dashed curve shows the radial variation of the projected stellar density displayed in Fig. 4, for stars $ V\leq 20$. Dashed line, in the lower panel, shows the density of field stars.
Open with DEXTER

On the basis of above discussion we may conclude that a change in the cluster center by about 1 arcmin does not affect the analysis presented in the paper.


  \begin{figure} \par\includegraphics[angle=270,width=8.2cm,clip]{MS1127fig20.ps} \end{figure} Figure 20: The distribution of mean reddening and bright stars in the cluster. The mark * shows the adopted cluster center with pixel coordinates X=855, Y=755. The X and Y coordinates are given in pixels.
Open with DEXTER

10 Discussion

The distribution of interstellar matter inside the cluster (cf. Fig. 7) indicates a slight lack of interstellar matter at the center. In the case of very young clusters, e.g., NGC 3603 and 30 Dor, Pandey et al. (2000) and Brandl et al. (1996), respectively, have also found that the stars in the core of these clusters show almost no reddening. Stellar winds or a supernova explosion may be a probable explanation for the lack of dust (and gas) at the center of these clusters. It is interesting to mention that there is a deficiency of bright (i.e. massive) stars in the central region of the NGC 7654. The bright stars are distributed in an arc at about $ r \sim 225\hbox{$^{\prime\prime}$ }$ and all these show in general a higher value of reddening (Fig. 20). The bright stars (V0<10.0) discriminated for different epochs of star formation have been plotted as a function of luminosity in Fig. 9 (Sect. 4) as open circle (first generation star) and filled circle (second generation star), respectively. Statistically $\sim$2 field stars are expected to contaminate the cluster region in the range $V_{0}\leq 10.0$. We expect that 2-3 stars which have reddening $E(B-V)\sim$ 0.65-0.67 may be foreground stars. The reddening E(B-V) especially for the second generation stars shows a dependence on the luminosity in the sense that brighter (i.e., massive) stars have a higher value of E(B-V). This suggests that some bright stars may still have a dust shell around them.


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{MS1127fig21.ps} \end{figure} Figure 21: The distribution of stars having $V_0\geq 10.0$ as a function of reddening.
Open with DEXTER

A few faint stars having luminosity V0 >10.0 also show higher reddening. In Fig. 21 the positional distribution of stars having V0 >10.0 and $E(B-V) \geq 0.72$, $0.72 < E(B-V) \leq 0.6$ and E(B-V) < 0.6 has been shown by filled triangles, open circles and crosses, respectively. There is no trend apparent in the diagram. The location of stars having V0 > 10.0 and $E(B-V) \geq 0.72$, on the CMDs indicates that these are background stars. The distribution of bright stars ( $V_{0}\leq 10.0$) and an increase in interstellar matter towards the outer region of the cluster which becomes rather constant at $r > 400\hbox{$^{\prime\prime}$ }$ (Fig. 7) poses an interesting question. As we have discussed in Sect. 7 the star formation was biased towards massive stars during the early phase, an extrapolation of the MF indicates a good number of massive stars must have been formed and may have already turned into supernovae. Because of the supernovae explosions the gas and dust from the central region would have been pushed toward the outer region of the cluster, thereby increasing the density of gas and dust in that region. Although we cannot estimate the number of these massive stars because of the uncertainty due to small-number statistics in deriving the MF of the early phase of star formation, still we can speculate a few supernovae events in the history of NGC 7654. Those supernovae explosions might have triggered the star formation in the second epoch. Since more interstellar matter was available towards the outer region, the activity of star formation was higher in that region. Considering the fact that the star formation was biased towards low mass stars during the end of star formation (cf. Sect. 7), more low mass stars should have been formed in the outer region, this fact along with the dynamical relaxation of the cluster (cf. Sect. 8) explains the excess of low mass stars in the intermediate region ( $180\hbox{$^{\prime\prime}$ }< r \leq 400\hbox{$^{\prime\prime}$ }$).


  \begin{figure} \par\includegraphics[width=8cm,clip]{MS1127fig22.ps} \end{figure} Figure 22: The distribution of massive stars in the cluster as a function of age. Open and filled circles represent stars formed during the first and the second epoch respectively.
Open with DEXTER

Figure 22 shows that formation of massive stars took place sequentially, in the sense that low mass stars formed first. The age and mass of individual stars were estimated from the isochrones. The star formation history in the cluster NGC 7654 supports the conventional picture of star formation in clusters that "low mass stars'' form first and that star formation continues over a long period of time ($\sim$20 Myr). The star formation within the cluster was terminated with the formation of the most massive star in the cluster. In the literature we can find several observational supports for the conventional theory, including the study of the Hyades and Pleiades by Herbig (1962), which revealed low mass (<2$M_{\odot}$) stars on the ZAMS, despite the fact that their contraction time is much larger than the nuclear burning life time of higher mass stars that dominate these clusters. In the case of NGC 3293 Herbst & Miller (1982) also found 2 $M_{\odot}$ stars on or near the ZAMS with the presence of massive O stars within the cluster. The mass distribution of brighter (i.e., massive) stars in NGC 7654 as a function of age (see Fig. 22) supports the conventional theory where star formation was terminated by the formation of most massive stars in each epoch. However, this scenario is in contradiction with some recent observations which showed that star formation does not cease after the formation of most massive star in the cluster (Hillenbrand et al. 1993; Massey et al. 1995; Pandey et al. 2000 and references therein).

The mass function of NGC 7654 in various subregions, for the entire observed mass range ($\sim$5 - 0.8 $M_{\odot}$), cannot be represented by a single power law. The slope of the mass function becomes steeper for $M\leq 1.6~M_{\odot}$. This is probably due to the abundant formation of less massive stars during the later phase of star formation. Moreover, the slope of the mass function for stars having $M < 1.6~M_{\odot}$ becomes steeper in the outer part of the cluster. Thus the mass function of NGC 7654 does not support the three component model recently proposed by Scalo (1998), where he gives a slope of mass function as $\Gamma= -1.7$ for the mass range $1< M_{\odot} <10$. Here it is interesting to mention that the mass function in the entire cluster (i.e., $r\leq 700\hbox {$^{\prime \prime }$ }$), in the mass range $0.8 \leq M_{\odot} \leq 4.5$, can be represented by a single power law with a slope of $\Gamma= -1.40 \pm 0.07$.

Thus on the basis of the above discussions it seems that star formation in star cluster is highly localized and and that it depends on the prevailing conditions in different parts of the cloud/cluster. In the future we plan to carry out a detailed study of those parameters which affect star formation in star clusters using the Kiso Schmidt telescope.

11 Summary and conclusion

The current paper is the first of a series where we plan to carry out wide field CCD photometry around open clusters using the Kiso Schmidt telescope to study in detail the structure, star formation history, and mass function of open clusters. In this contribution we present a detailed study of the cluster NGC 7654, which is based on a deep CCD photometry of $\sim$17860 stars in a wide area of $\sim$ $40 \times 40 ~{\rm arcmin}^2$. The completeness of the present CCD data has been determined empirically as a function of brightness in different regions of the cluster field. The observed LFs after correcting for both the data incompleteness and the field star contamination were converted to MF using the theoretical isochrones given by Bertelli et al. (1994). Following are the main conclusions of the present work:

1.
The mass function of the cluster NGC 7654 in the mass range $0.8 \leq M_{\odot} \leq 4.5$ cannot be represented by a single power law. The slope $\Gamma $ becomes steeper in the outermost region of the cluster;

2.
A mean age of $\sim$160 Myr and a distance of $\sim$ $1380 \pm 70$ pc is obtained by applying a mean reddening E(B-V)= 0.57 which are in good agreement with those obtained by Viskum et al. (1997) and Choi et al. (1999). The scenario changes if reddening is applied to individual stars. Looking at the upper part of the CMDs (Fig. 13) we find a large range in the age of the stars ( $30< \tau < 100$ Myr);

3.
The star formation was biased towards relatively massive stars during the early phase of star formation whereas more low mass stars were formed in the last phase;

4.
Supernovae explosion of massive stars formed during the early phase may be a probable explanation for the lack of interstellar matter at the centre of the cluster;

5.
The majority of the excess low mass stars ( $ V \geq 17, M \sim1~M_{\odot}$) in the intermediate region of the cluster were formed during the last phase of star formation;
6.
The mean age ($\sim$50 Myr) of the cluster is comparable to the two-body relaxation time-scale of the NGC 7654. The dynamical relaxation along with the star formation process in the NGC 7654 as discussed above explain the excess of low mass stars in the intermediate region of the cluster;

7.
The star formation seems to be a gradual process in which low mass stars are formed slowly over a long period of time and the process terminated with the formation of the most massive stars;

8.
(B-V)/(V-I) TCDs indicate (although weakly) a possibility for an anomalous reddening law in the cluster region ( $R \sim 3.5$).

Acknowledgements
AKP is thankful to the DST (India) and JSPS (Japan) for providing funds to visit KISO observatory to take observations and to the staff of KISO observatory for their generous help during the stay. AKP is also thankful to Prof. K. Ishida (Ex-director of the Kiso observatory) who encouraged us to pursue wide field photometry around open clusters through the KISO Schmidt telescope. The authors are thankful to Dr. Debra Elmegreen for useful comments which improved the contents of the paper.

References

 

Copyright ESO 2001