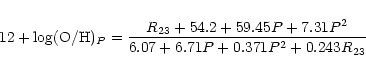A&A 374, 412-420 (2001)
DOI: 10.1051/0004-6361:20010732
Oxygen abundances in dwarf irregular galaxies
and the
metallicity-luminosity relationship
L. S. Pilyugin
Main Astronomical Observatory
of National Academy of Sciences of Ukraine,
Goloseevo, 03680 Kiev-127, Ukraine
Received 20 December 2000 / Accepted 2 May 2001
Abstract
The low-luminosity dwarf irregular galaxies are considered.
The oxygen abundances in H II regions of dwarf irregular galaxies were
recalculated from published spectra through the recently suggested P-method. It has been found that the metallicity of low-luminosity dwarf
irregular galaxies, with a few exceptions, correlates well with galaxy
luminosity. The dispersion of oxygen abundances around the metallicity-luminosity relationship increases with decreasing galaxy luminosity, as was
found by Richer & McCall (1995). The absence of a relationship between the
oxygen abundance and the absolute magnitude in the blue band for irregular
galaxies obtained by Hidalgo-Gámez & Olofsson (1998) can be explained by the
large uncertainties in the oxygen abundances derived through the  -method, that in turn can be explained by the large uncertainties in the
measurements of the strengths of the weak oxygen line
-method, that in turn can be explained by the large uncertainties in the
measurements of the strengths of the weak oxygen line
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) used in the
used in the  -method.
-method.
Key words: galaxies: abundances - galaxies: ISM -
galaxies: irregular - galaxies: individual: NGC 6822
Twenty years ago Lequeux et al. (1979) revealed that the oxygen abundance
correlates with total galaxy mass for irregular galaxies, in the sense that
the higher the total mass, the higher the heavy element content. Since the
galaxy mass is a poorly known parameter, the metallicity-luminosity relation
instead of the mass-metallicity relation is usually considered (Skillman et al. 1989a; Richer & McCall 1995; Hidalgo-Gámez & Olofsson 1998; Hunter &
Hoffman 2000; Pilyugin & Ferrini 2000b; among others). It has been found that
the characteristic gas-phase abundances (the oxygen abundance at a predetermined
galactocentric distance) and luminosities of spiral galaxies are also correlated
(Garnett & Shields 1987; Vila-Costas & Edmunds 1992; Zaritsky et al. 1994;
Garnett et al. 1997), and this relationship maps almost directly on to the
metallicity-luminosity relationship of irregular galaxies (Zaritsky et al.
1994; Garnett et al. 1997).
Richer & McCall (1995) have revealed a prominent feature of their
metallicity-luminosity relation for irregular galaxies: they have found more
scatter at low luminosities, though they found less at high luminosities. The
onset of this scatter seems to occur at
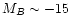 or
or
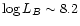 .
Moreover, Hidalgo-Gámez & Olofsson (1998) have found that there is no
relationship between the oxygen abundance and the absolute magnitude in the blue
band for dwarf irregular galaxies (
MB > - 17 or
.
Moreover, Hidalgo-Gámez & Olofsson (1998) have found that there is no
relationship between the oxygen abundance and the absolute magnitude in the blue
band for dwarf irregular galaxies (
MB > - 17 or
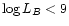 ). Hunter &
Hoffman (2000) have found that their samples do generally cluster around the
relationship between MB and O/H derived by Richer & McCall (1995) but do
not themselves define a linear relationship very well, appearing more as a cloud
of points with a large scatter around the line. In particular, the scatter
becomes larger for
MB> -16. Hunter & Hoffman (2000) have concluded
that the relationship between O/H and MB is very general over the Hubble
sequence but the scatter is very large and discerning the trend over a limited
parameter range is hard. They noted that perhaps the interesting science lies in
this scatter, although a part of this scatter is undoubtedly due to the
uncertainties in determining O/H and MB.
). Hunter &
Hoffman (2000) have found that their samples do generally cluster around the
relationship between MB and O/H derived by Richer & McCall (1995) but do
not themselves define a linear relationship very well, appearing more as a cloud
of points with a large scatter around the line. In particular, the scatter
becomes larger for
MB> -16. Hunter & Hoffman (2000) have concluded
that the relationship between O/H and MB is very general over the Hubble
sequence but the scatter is very large and discerning the trend over a limited
parameter range is hard. They noted that perhaps the interesting science lies in
this scatter, although a part of this scatter is undoubtedly due to the
uncertainties in determining O/H and MB.
The most precise method of determining the abundances of H II regions
requires the detection of
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) emission line (the
emission line (the  -method). The
-method). The
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) emission line appears in high excitation
spectra of oxygen-poor H II regions and is usually undetectable in
spectra of oxygen-rich H II regions. Then, in the general case, the
precision of the oxygen abundance determination in oxygen-poor H II
regions is higher than in oxygen-rich H II regions. The derived oxygen
abundances of metal-poor H II regions in blue compact galaxies possessing
very bright emission lines are accurate to within 0.05 dex (Izotov & Thuan
1999). However, many irregular galaxies have no bright H II regions with
readily measured emission lines. As was noted by Hidalgo-Gámez & Olofsson
(1998) the uncertainties in the intensity of the line
emission line appears in high excitation
spectra of oxygen-poor H II regions and is usually undetectable in
spectra of oxygen-rich H II regions. Then, in the general case, the
precision of the oxygen abundance determination in oxygen-poor H II
regions is higher than in oxygen-rich H II regions. The derived oxygen
abundances of metal-poor H II regions in blue compact galaxies possessing
very bright emission lines are accurate to within 0.05 dex (Izotov & Thuan
1999). However, many irregular galaxies have no bright H II regions with
readily measured emission lines. As was noted by Hidalgo-Gámez & Olofsson
(1998) the uncertainties in the intensity of the line
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) in
spectra of H II regions in dwarf irregular galaxies reported in the
literature fluctuate between 11
in
spectra of H II regions in dwarf irregular galaxies reported in the
literature fluctuate between 11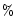 and 120
and 120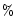 .
Thus, in reality, the precision
of oxygen abundance determination in dwarf irregular galaxies seems to be
rather low.
.
Thus, in reality, the precision
of oxygen abundance determination in dwarf irregular galaxies seems to be
rather low.
In our recent work (Pilyugin 2000 Paper I, 2001 Paper II) a new method for
oxygen abundance determination in H II regions (the P-method) has been
constructed, starting from the idea of McGaugh (1991) that the strong oxygen
lines (
![$\rm [OII] \lambda \lambda 3727, 3729$](/articles/aa/full/2001/29/aa10586/img11.gif) and
and
![$\rm [OIII] \lambda \lambda 4959, 5007$](/articles/aa/full/2001/29/aa10586/img12.gif) )
contain the necessary information for determination of accurate abundances in
H II regions. By comparing oxygen abundances in bright H II
regions derived (with high precision) through the
)
contain the necessary information for determination of accurate abundances in
H II regions. By comparing oxygen abundances in bright H II
regions derived (with high precision) through the  -method,
O/H
-method,
O/H
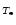 ,
and those derived through the suggested P-method, O/HP, it
has been found that the precision of oxygen abundance determination with the
P-method is comparable to that of the
,
and those derived through the suggested P-method, O/HP, it
has been found that the precision of oxygen abundance determination with the
P-method is comparable to that of the  -method. Then it can be
expected that in faint H II regions, in which the temperature-sensitive
line
-method. Then it can be
expected that in faint H II regions, in which the temperature-sensitive
line
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) is measured with large uncertainty, the P-method
provides more realistic oxygen abundances than the
is measured with large uncertainty, the P-method
provides more realistic oxygen abundances than the  -method since
only the strong (and as a consequence, more readily measurable) oxygen lines
are used in the P-method. Moreover, the P-method is workable in the
cases when the temperature-sensitive line
-method since
only the strong (and as a consequence, more readily measurable) oxygen lines
are used in the P-method. Moreover, the P-method is workable in the
cases when the temperature-sensitive line
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) is undetectable.
Thus, we can expect that the application of the P-method to the oxygen
abundance determination in faint H II regions of dwarf irregular galaxies
allows us to refine the oxygen abundances in H II regions with
low-precision measurements of line
is undetectable.
Thus, we can expect that the application of the P-method to the oxygen
abundance determination in faint H II regions of dwarf irregular galaxies
allows us to refine the oxygen abundances in H II regions with
low-precision measurements of line
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) and to determine the
realistic oxygen abundances in H II regions with undetectable line
and to determine the
realistic oxygen abundances in H II regions with undetectable line
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) .
We hope that it can clarify whether the luminosity-metallicity relationship for irregular galaxies still persists or disappears
at the low-luminosity end. This is a goal of the present study.
.
We hope that it can clarify whether the luminosity-metallicity relationship for irregular galaxies still persists or disappears
at the low-luminosity end. This is a goal of the present study.
The relation of the type
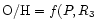 )
between oxygen abundance and the
values of P and R3 has been derived empirically in Papers I and II using
the available oxygen abundances determined via measurement of the
temperature-sensitive line ratio [OIII]4959, 5007/[OIII]4363. Notations similar
to those in Papers I and II will be adopted here:
)
between oxygen abundance and the
values of P and R3 has been derived empirically in Papers I and II using
the available oxygen abundances determined via measurement of the
temperature-sensitive line ratio [OIII]4959, 5007/[OIII]4363. Notations similar
to those in Papers I and II will be adopted here:
![$R_{2} = I_{\rm [OII] \lambda 3727+ \lambda 3729} /I_{\rm H\beta }$](/articles/aa/full/2001/29/aa10586/img17.gif) ,
R3 =
,
R3 =
![$I_{\rm [OIII] \lambda 4959+ \lambda 5007} /I_{\rm H\beta }$](/articles/aa/full/2001/29/aa10586/img18.gif) ,
R =
,
R =
![$I_{\rm [OIII] \lambda 4363} /I_{\rm H\beta }$](/articles/aa/full/2001/29/aa10586/img19.gif) ,
R23 =R2 + R3,
,
R23 =R2 + R3,
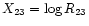 ,
and
P = R3/R23. The excitation index P used in Paper II and indexes
p2 and p3 used in Paper I are related through simple expressions:
,
and
P = R3/R23. The excitation index P used in Paper II and indexes
p2 and p3 used in Paper I are related through simple expressions:
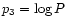 and
and
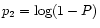 .
The following equations for the oxygen
abundance determination in low-metallicity H II regions have been
suggested in Paper I
.
The following equations for the oxygen
abundance determination in low-metallicity H II regions have been
suggested in Paper I
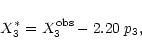 |
(1) |
and
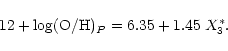 |
(2) |
Equations (1) and (2) can be rewritten as
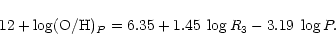 |
(3) |
Equation (3) shows that the positions in the R3-P
diagram can be calibrated in terms of oxygen abundance (Fig. 1).
The relationship between oxygen abundance and strong line intensities is double
valued with two distinctive parts named usually as the lower and upper branches
of the R23-O/H diagram, and so one has to know in advance on which
branch of the R23-O/H diagram the H II region lies. The above
expression for the oxygen abundance determination in H II regions,
Eq. (3), is valid for H II regions with 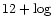 (O/H) less
than around 8 (Paper I). According to the metallicity-luminosity relationship
for irregular galaxies after Richer & McCall (1995), the oxygen abundances in
the low-luminosity irregular galaxies (
(O/H) less
than around 8 (Paper I). According to the metallicity-luminosity relationship
for irregular galaxies after Richer & McCall (1995), the oxygen abundances in
the low-luminosity irregular galaxies (
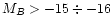 )
are expected
to lie in this range. Then it has been adopted here that the H II regions
in the low-luminosity irregular galaxies (
)
are expected
to lie in this range. Then it has been adopted here that the H II regions
in the low-luminosity irregular galaxies (
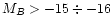 )
lie on
the lower branch of the R23-O/H diagram. Furthermore, only the
high-excition (P > 0.5) H II regions will be considered here because
Eqs. (1) and (2) (linear approximation)
have been derived based on the high-excition H II regions.
)
lie on
the lower branch of the R23-O/H diagram. Furthermore, only the
high-excition (P > 0.5) H II regions will be considered here because
Eqs. (1) and (2) (linear approximation)
have been derived based on the high-excition H II regions.
Firstly the Hidalgo-Gámez & Olofsson (1998) sample of irregular galaxies will
be considered. The R3- P diagram for H II regions with MB>-16 from Hidalgo-Gámez & Oloffson (1998) sample is shown in the
Fig. 1 (panel a). The squares are H II regions with
12+log O/H < 7.4, the pluses are those with 7.4 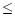 12+log O/H < 7.6, the
triangles are those with 7.6
12+log O/H < 7.6, the
triangles are those with 7.6 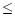 12+log O/H < 7.8, the crosses are those
with 7.8
12+log O/H < 7.8, the crosses are those
with 7.8 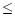 12+log O/H < 8.0, and the circles are those with 12+log O/H
12+log O/H < 8.0, and the circles are those with 12+log O/H
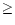 8.0. The dashed curves are the R3-P relations obtained from
Eq. (3) for fixed values of O/H. Each curve is labeled with the
corresponding value of 12+log O/H. For comparison the R3-P diagram for
"calibrating H II regions'' from Paper I is also shown in
Fig. 1 (panel b). Examination of Fig. 1
(panel a) shows that the oxygen abundances O/H
8.0. The dashed curves are the R3-P relations obtained from
Eq. (3) for fixed values of O/H. Each curve is labeled with the
corresponding value of 12+log O/H. For comparison the R3-P diagram for
"calibrating H II regions'' from Paper I is also shown in
Fig. 1 (panel b). Examination of Fig. 1
(panel a) shows that the oxygen abundances O/H
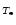 derived through
the classical
derived through
the classical  -method are in conflict with the oxygen abundances
corresponding to their positions in the R3-P for a number of H II
regions from the Hidalgo-Gámez & Olofsson (1998) sample of irregular galaxies.
It can be explained by the large uncertainties in the oxygen abundances derived
through the
-method are in conflict with the oxygen abundances
corresponding to their positions in the R3-P for a number of H II
regions from the Hidalgo-Gámez & Olofsson (1998) sample of irregular galaxies.
It can be explained by the large uncertainties in the oxygen abundances derived
through the  -method, that in turn can be explained by the large
uncertainties in the measurements of the strengths of the weak oxygen line
-method, that in turn can be explained by the large
uncertainties in the measurements of the strengths of the weak oxygen line
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) used in the
used in the  -method.
-method.
![\begin{figure}
\par\resizebox{1.00\hsize}{!}{\includegraphics[angle=0]{10586f1.eps}}\end{figure}](/articles/aa/full/2001/29/aa10586/Timg28.gif) |
Figure 1:
The R3-P diagram for H II regions with MB>-16 from
Hidalgo-Gámez & Oloffson (1998) sample (panel a) and for "calibrating
H II regions" from Paper I (panel b). The squares are H II
regions with 12+log O/H < 7.4, the pluses are those with 7.4 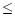 12+log O/H
< 7.6, the triangles are those with 7.6
12+log O/H
< 7.6, the triangles are those with 7.6 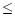 12+log O/H < 7.8, the crosses
are those with 7.8
12+log O/H < 7.8, the crosses
are those with 7.8 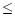 12+log O/H < 8.0, and the circles are those with
12+log O/H
12+log O/H < 8.0, and the circles are those with
12+log O/H 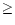 8.0. The dashed curves are R3-P relations predicted
by the calibration for fixed values of O/H. Each curve is labeled with
the corresponding value of 12+log O/H.
8.0. The dashed curves are R3-P relations predicted
by the calibration for fixed values of O/H. Each curve is labeled with
the corresponding value of 12+log O/H. |
The oxygen abundances in H II regions of low-luminosity (MB>-16) irregular galaxies have been recalculated through the P-method. The
intensities of
![$\rm [OII] \lambda \lambda 3727, 3729$](/articles/aa/full/2001/29/aa10586/img11.gif) and
and
![$\rm [OIII] \lambda \lambda 4959, 5007$](/articles/aa/full/2001/29/aa10586/img12.gif) lines were taken from the sources cited by
Hidalgo-Gámez & Olofsson (1998): Skillman et al. (1989)
(DDO 47, Leo A, Sext A); Moles et al. (1990) (Sext B, GR 8);
González-Riestra et al. (1988) (Mkn 178); Heydari-Malayeri et al. (1990) (IC 4662); Webster et al. (1983) (IC 5152);
Hodge & Miller (1995) (WLM). The NGC 6822 is excluded from consideration here,
this galaxy will be discussed below. The oxygen abundances have been recalculated
with the P-method in 12 H II regions of 9 dwarf irregular galaxies.
The H II regions A1 and A2 in IC 4662 have oxygen abundances 12+log O/HP
= 7.97 and 8.08, respectively. These H II regions seems to belong to the
transition zone of the R23-O/H diagram, and in the strict sense
Eq. (3) cannot be used for oxygen abundance determination in
these H II regions since Eq. (3) was derived for
H II regions with 12+log O/H
lines were taken from the sources cited by
Hidalgo-Gámez & Olofsson (1998): Skillman et al. (1989)
(DDO 47, Leo A, Sext A); Moles et al. (1990) (Sext B, GR 8);
González-Riestra et al. (1988) (Mkn 178); Heydari-Malayeri et al. (1990) (IC 4662); Webster et al. (1983) (IC 5152);
Hodge & Miller (1995) (WLM). The NGC 6822 is excluded from consideration here,
this galaxy will be discussed below. The oxygen abundances have been recalculated
with the P-method in 12 H II regions of 9 dwarf irregular galaxies.
The H II regions A1 and A2 in IC 4662 have oxygen abundances 12+log O/HP
= 7.97 and 8.08, respectively. These H II regions seems to belong to the
transition zone of the R23-O/H diagram, and in the strict sense
Eq. (3) cannot be used for oxygen abundance determination in
these H II regions since Eq. (3) was derived for
H II regions with 12+log O/H 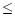 7.95 (the lower branch of the R23-O/H diagram). The metallicity-luminosity diagram for dwarf irregular
galaxies from Hidalgo-Gámez & Olofsson (1998) is represented in
Fig. 2 by the pluses. The metallicity-luminosity diagram
for dwarf irregular galaxies with
MB>- 16 with the oxygen abundances
recalculated through Eq. (3) is shown in Fig. 2
by the filled circles. In order to clearly recognize the influence of the oxygen
abundance redetermination on the metallicity-luminosity diagram, the same
values of MB as in Hidalgo-Gámez & Olofsson were used.
7.95 (the lower branch of the R23-O/H diagram). The metallicity-luminosity diagram for dwarf irregular
galaxies from Hidalgo-Gámez & Olofsson (1998) is represented in
Fig. 2 by the pluses. The metallicity-luminosity diagram
for dwarf irregular galaxies with
MB>- 16 with the oxygen abundances
recalculated through Eq. (3) is shown in Fig. 2
by the filled circles. In order to clearly recognize the influence of the oxygen
abundance redetermination on the metallicity-luminosity diagram, the same
values of MB as in Hidalgo-Gámez & Olofsson were used.
![\begin{figure}
\par\resizebox{1.00\hsize}{!}{\includegraphics[angle=0]{10586f2.eps}}\end{figure}](/articles/aa/full/2001/29/aa10586/Timg29.gif) |
Figure 2:
The metallicity-luminosity diagram for dwarf irregular galaxies. The
metallicity-luminosity diagram after Hidalgo-Gámez & Olofsson (1998) based
on the oxygen abundances determined with the  -method is presented by
the pluses. The metallicity-luminosity diagram based on the oxygen abundances
derived with the P-method is shown by the filled circles. The positions of
Leo A with luminosity from Hidalgo-Gámez & Olofsson and with luminosity adopted
here (triangle) are connected with dashed line. The solid line is the L-Z
relationship after Richer & McCall (1995). -method is presented by
the pluses. The metallicity-luminosity diagram based on the oxygen abundances
derived with the P-method is shown by the filled circles. The positions of
Leo A with luminosity from Hidalgo-Gámez & Olofsson and with luminosity adopted
here (triangle) are connected with dashed line. The solid line is the L-Z
relationship after Richer & McCall (1995). |
It can be easily seen in Fig. 2 that the metallicity-luminosity relation for dwarf irregular galaxies based on the oxygen abundances
derived with the P-method shows appreciably less scatter than that based on
the oxygen abundances derived with the  -method. It is strong evidence
in favor of the large scatter in the low-luminosity end of the metallicity- luminosity relation for irregular galaxies being explained mainly by the
uncertainty in oxygen abundance determination with the
-method. It is strong evidence
in favor of the large scatter in the low-luminosity end of the metallicity- luminosity relation for irregular galaxies being explained mainly by the
uncertainty in oxygen abundance determination with the  -method.
-method.
It should be noted that the abundances used by Hidalgo-Gámez & Olofsson were
not taken directly from the sources listed but have been recalculated in a
consistent way and as a consequence the differences in techniques and atomic
data do not contribute to the scatter. Then, the increased scatter in oxygen
abundances derived with the  -method, compared to the scatter in
oxygen abundances derived with the P-method seems to be explained by the
observational uncertainties in the
-method, compared to the scatter in
oxygen abundances derived with the P-method seems to be explained by the
observational uncertainties in the
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) line strengths.
line strengths.
A well defined trend is seen between MB and O/HP,
Fig. 2. The deviations of O/HP from a linear
relationship for all, with one exception, of the H II regions are within
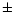 0.1 dex. The point with a large deviation (in excess of 0.4 dex) corresponds
to the dwarf galaxy Leo A. The H II region observed in Leo A is a
planetary nebula with no detectable
0.1 dex. The point with a large deviation (in excess of 0.4 dex) corresponds
to the dwarf galaxy Leo A. The H II region observed in Leo A is a
planetary nebula with no detectable
![$\rm [OII] \lambda \lambda 3727, 3729$](/articles/aa/full/2001/29/aa10586/img11.gif) lines;
P = 1 was adopted in the oxygen abundance determination through the P-method.
It cannot be excluded that the P-method calibrated on the basis of
H II regions is inapplicable in the case of planetary nebulae. It should
be noted, however, that the oxygen abundance in Leo A derived with the P-method agrees remarkably with the oxygen abundance derived by Skilman, et al. (1989). The deviation of Leo A from the relationship seems to be
caused by the uncertainty in the integrated B-band absolute magnitude adopted by
Hidalgo-Gámez & Olofsson rather than the uncertainty in the oxygen abundance.
The position of Leo A with a new integrated B-band absolute magnitude (see next
section) is shown in Fig. 2 by triangles (the positions of
Leo A in the Z-L diagram with a new absolute magnitude and with absolute
magnitude adopted by Hidalgo-Gámez & Olofsson are connected with a dashed line).
lines;
P = 1 was adopted in the oxygen abundance determination through the P-method.
It cannot be excluded that the P-method calibrated on the basis of
H II regions is inapplicable in the case of planetary nebulae. It should
be noted, however, that the oxygen abundance in Leo A derived with the P-method agrees remarkably with the oxygen abundance derived by Skilman, et al. (1989). The deviation of Leo A from the relationship seems to be
caused by the uncertainty in the integrated B-band absolute magnitude adopted by
Hidalgo-Gámez & Olofsson rather than the uncertainty in the oxygen abundance.
The position of Leo A with a new integrated B-band absolute magnitude (see next
section) is shown in Fig. 2 by triangles (the positions of
Leo A in the Z-L diagram with a new absolute magnitude and with absolute
magnitude adopted by Hidalgo-Gámez & Olofsson are connected with a dashed line).
Thus, the determination of oxygen abundances in H II regions of
low-luminosity irregular galaxies from the Hidalgo-Gámez & Olofsson sample with
the P-method suggests that there is a well defined trend between MB and
O/HP, and the large scatter in the low-luminosity end of the metallicity-luminosity relation obtained by Hidalgo-Gámez & Olofsson (1998) is explained
mainly by the uncertainty in oxygen abundance determination with the  -method. In order to verify this conclusion, a larger sample of low-luminosity
irregular galaxies will be considered in the next section.
-method. In order to verify this conclusion, a larger sample of low-luminosity
irregular galaxies will be considered in the next section.
Table 1:
Characteristics of the galaxies in the present sample.
| galaxy |
other name |
H II region |
MB |
reference |
O/H1 |
reference |
(O/H)P1 |
(O/H)P1 |
| |
|
or spectrum |
|
|
|
|
individual |
average |
| |
|
label |
|
|
|
|
H II region |
for galaxy |
| Sextans B |
DDO 70 |
|
-13.8 |
M |
8.11 |
MAM |
7.87 |
7.86 |
| |
|
No 2 |
|
|
7.56* (7.54-7.57) |
SKH |
7.85 |
|
| Sextans A |
DDO 75 |
No 1 |
-14.2 |
M |
7.40 (6.70-7.65) |
SKH |
7.76 |
7.71 |
| |
|
No 1h |
|
|
7.58 (6.90-7.83) |
SKH |
7.65 |
|
| GR 8 |
DDO 155 |
H2a |
-11.2 |
M |
7.66 |
MAM |
7.61 |
7.60 |
| |
|
H2b |
|
|
7.71 |
MAM |
7.60 |
|
| WLM |
DDO 221 |
No 7 |
-13.9 |
M |
7.72 (7.64-7.78) |
HM |
7.71 |
7.78 |
| |
|
No 9 |
|
|
7.81 (7.73-7.88) |
HM |
7.69 |
|
| |
|
No 1 |
|
|
7.78 (7.48-7.95) |
STM |
7.79 |
|
| |
|
No 2 |
|
|
7.70 (7.30-7.90) |
STM |
7.89 |
|
| UGC 4483 |
|
INT |
-12.8 |
STKGT |
7.50 (7.46-7.54) |
STKGT |
7.45 |
7.47 |
| |
|
McD |
|
|
7.48 (7.42-7.54) |
STKGT |
7.46 |
|
| |
|
WHT |
|
|
7.57 (7.51-7.62) |
STKGT |
7.50 |
|
| Mkn 178 |
|
A |
-14.36 |
H-GO |
7.72 |
G-RRZ |
7.83 |
7.88 |
| |
|
B |
|
|
7.73 |
G-RRZ |
7.92 |
|
| M81dB |
UGC 5423 |
|
-12.9 |
MH94 |
7.98 (7.70-8.15) |
MH |
7.81 |
7.81 |
| UGC 6456 |
|
Case 1 |
-13.24 |
RM |
7.77 |
TBDS |
7.68 |
7.71 |
| |
|
Case 2 |
|
|
7.76 |
TBDS |
7.75 |
|
| Leo A |
DDO 69 |
|
-11.3 |
M |
7.28 (7.08-7.42) |
SKH |
7.27 |
7.27 |
| DDO 187 |
|
|
-13.4 |
SKH |
7.36* (7.23-7.46) |
SKH |
7.62 |
7.62 |
| DDO 47 |
|
No 1 |
-14.4 |
H-GO |
7.89 (7.64-8.05) |
SKH |
7.84 |
7.86 |
| |
|
No 3 |
|
|
7.71* (7.66-7.75) |
SKH |
7.87 |
|
| UGCA 292 |
|
No 1 |
-11.43 |
vZ |
7.28 (7.23-7.33) |
vZ |
7.26 |
7.22 |
| |
|
No 2 |
|
|
7.32 (7.26-7.38) |
vZ |
7.17 |
|
| DDO 167 |
|
|
-13.3 |
SKH |
7.66 (7.23-7.88) |
SKH |
7.81 |
7.81 |
| SagDIG |
|
|
-12.1 |
M |
7.36* |
STM |
7.48 |
7.48 |
| A1116+51 |
|
|
-14.992 |
KD |
7.55 (7.35-7.75) |
KD |
7.76 |
7.76 |
| A1228+12 |
|
|
-14.572 |
KD |
7.64 (7.57-7.71) |
KD |
7.79 |
7.79 |
| A2228-00 |
|
|
-14.852 |
KD |
7.62 (7.56-7.68) |
KD |
7.81 |
7.81 |
| ESO 245-G05 |
|
19 |
-15.5 |
H-G99 |
7.80 (7.79-7.81) |
H-G99 |
7.98 |
7.94 |
| |
|
12 |
|
H-G99 |
7.59 (7.57-7.61) |
H-G99 |
7.89 |
|
| DDO 53 |
|
A |
-13.35 |
H-G99 |
7.46 (7.39-7.53) |
H-G99 |
7.76 |
7.75 |
| |
|
B |
|
H-G99 |
7.55 (7.50-7.60) |
H-G99 |
7.74 |
|
| DDO 190 |
|
|
-15.10 |
H-G99 |
7.94 (7.88-8.00) |
H-G99 |
7.74 |
7.74 |
1 - In units of 12 + log(O/H).
2 -
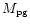
was taken as
MB.
*-Oxygen abundance was derived not through the

-method.
List of references to MB:
H-G99 - Hidalgo-Gámez (1999);
H-GO - Hidalgo-Gámez & Olofsson (1998);
KD - Kinman & Davidson (1981);
M -
Mateo (1998);
MH94 - Miller & Hodge (1994);
RM - Richer & McCall (1995);
SKH -
Skillman et al. (1989);
STKGT - Skillman et al. (1994);
vZ - van Zee (2000)
List of references to oxygen abundances:
G-RRZ - González-Riestra et al. (1988);
H-G99 - Hidalgo-Gámez (1999);
HM - Hodge & Miller (1995);
KD -
Kinman & Davidson (1981);
MAM - Moles et al. (1990);
MH - Miller & Hodge (1996);
SKH - Skillman et al. (1989);
STKGT - Skillman et al. (1994);
STM - Skillman et al. (1989);
TBDS - Tully et al. (1981);
vZ - van Zee (2000).
The data used in this study consists of published absolute magnitudes of
irregular galaxies in B band and the intensities of
![$\rm [OII] \lambda \lambda 3727, 3729$](/articles/aa/full/2001/29/aa10586/img11.gif) and
and
![$\rm [OIII] \lambda \lambda 4959, 5007$](/articles/aa/full/2001/29/aa10586/img12.gif) emission lines. Our sample
includes 34 data points in 20 irregular galaxies for which we have collected
the relevant observational data, listed with references in Table 1.
The commonly used name(s) of the galaxy are given in Cols. 1 and 2 and the
label of the H II region or spectrum is given in Col. 3. The absolute
blue magnitude MB is listed in Col. 4 (references in Col. 5). The
original oxygen abundance is given in Col. 6 (references in Col. 7). If the
error range of the oxygen abundance determination was indicated by the author(s),
this range is given in parentheses (Col. 6). If a method other than the
emission lines. Our sample
includes 34 data points in 20 irregular galaxies for which we have collected
the relevant observational data, listed with references in Table 1.
The commonly used name(s) of the galaxy are given in Cols. 1 and 2 and the
label of the H II region or spectrum is given in Col. 3. The absolute
blue magnitude MB is listed in Col. 4 (references in Col. 5). The
original oxygen abundance is given in Col. 6 (references in Col. 7). If the
error range of the oxygen abundance determination was indicated by the author(s),
this range is given in parentheses (Col. 6). If a method other than the
 -method has been used for the oxygen abundance determination, this
oxygen abundance is labeled with an asterisk.
-method has been used for the oxygen abundance determination, this
oxygen abundance is labeled with an asterisk.
The oxygen abundances in H II regions have been calculated with the P-method using the published intensities (references in Col. 7) of
![$\rm [OII] \lambda \lambda 3727, 3729$](/articles/aa/full/2001/29/aa10586/img11.gif) and
and
![$\rm [OIII] \lambda \lambda 4959, 5007$](/articles/aa/full/2001/29/aa10586/img12.gif) emission lines. The derived oxygen abundances for individual H II regions
are given in Col. 8 of Table 1. The metallicity-luminosity diagram for
dwarf irregular galaxies based on the oxygen abundances derived here through
the P-method is presented in Fig. 3 (panel b). The
line is the best fit. For comparison, the metallicity-luminosity diagram for
dwarf irregular galaxies based on the oxygen abundances derived through the
emission lines. The derived oxygen abundances for individual H II regions
are given in Col. 8 of Table 1. The metallicity-luminosity diagram for
dwarf irregular galaxies based on the oxygen abundances derived here through
the P-method is presented in Fig. 3 (panel b). The
line is the best fit. For comparison, the metallicity-luminosity diagram for
dwarf irregular galaxies based on the oxygen abundances derived through the
 -method or empirical method (data from the Col. 6 of Table 1) is
also presented in Fig. 3 (panel a). The line is the
best fit.
-method or empirical method (data from the Col. 6 of Table 1) is
also presented in Fig. 3 (panel a). The line is the
best fit.
![\begin{figure}
\par\resizebox{1.00\hsize}{!}{\includegraphics[angle=0]{10586f3.eps}}\end{figure}](/articles/aa/full/2001/29/aa10586/Timg32.gif) |
Figure 3:
The metallicity-luminosity diagram for dwarf irregular galaxies.
The oxygen abundances for individual H II regions are shown. a)
The L-Z diagram based on the oxygen abundances derived with the  -method or the empirical method (see Table 1). The line is the best fit.
b) The L-Z diagram based on the oxygen abundances determined here
with the P-method. The line is the best fit. -method or the empirical method (see Table 1). The line is the best fit.
b) The L-Z diagram based on the oxygen abundances determined here
with the P-method. The line is the best fit. |
Inspection of Fig. 3 shows that the metallicity-luminosity
diagram for dwarf irregular galaxies based on the oxygen abundances derived
with the P-method shows relatively small scatter. It confirms the above
conclusion that the large scatter in the low-luminosity end of the metallicity-luminosity relation for irregular galaxies obtained by Hidalgo-Gámez & Olofsson
(1998) is explained mainly by the uncertainty in oxygen abundance determination
with  -method.
-method.
The uncertainty in the integrated B-band absolute magnitudes MB for
irregular galaxies can also contribute to the dispersion in the Z-L diagram.
The uncertainty in the distance determinations is the major source of
uncertainty in the determination of the integrated B-band absolute magnitudes
MB for irregular galaxies. Therefore accurate distances to irregular
galaxies are necessary in the construction of the Z-L diagram.
Most galaxies considered here are members of the Local Group. The compilation
of the recent information on distances for all the dwarf members and candidates
of the Local Group is given by Mateo (1998). Nearly all of the members of the
Local Group have reasonable distance determinations based on one or more
high-precision distance indicator, including Cepheid variables. There are
exceptions. In the case of Leo A there is a large discrepancy in the determined
distances; Hoessel et al. (1994) found a value of 2.2 Mpc on the basis of
Cepheid variables. More recently, Tolstoy et al. (1998) (based on the position
of the red clump, the helium-burning blue loops, and the tip of the red giant
branch) obtained the value of
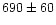 kpc. The short distance resolves
the problems which appear for Leo A in the case of long distance, (see discussion
in Mateo 1998, and references therein). The short distance makes the position
of Leo A much closer to the metallicity-luminosity relationship
(see Fig. 2).
kpc. The short distance resolves
the problems which appear for Leo A in the case of long distance, (see discussion
in Mateo 1998, and references therein). The short distance makes the position
of Leo A much closer to the metallicity-luminosity relationship
(see Fig. 2).
![\begin{figure}
\par\resizebox{1.00\hsize}{!}{\includegraphics[angle=0]{10586f4.eps}}\end{figure}](/articles/aa/full/2001/29/aa10586/Timg34.gif) |
Figure 4:
The metallicity-luminosity diagram for dwarf irregular galaxies. The
metallicity-luminosity diagram of Richer & McCall (1995) is represented by
pluses. The metallicity-luminosity diagram based on the oxygen abundances
derived with the P-method is shown by filled circles. The positions of
Sextans B, GR8, and NGC 6822 with our data and their positions with Richer and
McCall's data are connected by dashed lines. The open circle is the position
of NGC 6822 with oxygen abundance from Eq. (4). |
The comparison of our Z-L diagram with that of Richer & McCall (1995) is given
in Fig. 4. The pluses are data of Richer & McCall (1995),
the filled circles are the data for irregular galaxies from the present sample.
The oxygen abundances O/HP used in the construction of the Z-L diagram in
Fig. 4 are the values obtained by averaging all the available
determinations for a given galaxy (Col. 9 in Table 1). The solid line is the
metallicity-luminosity relationship obtained by Richer & McCall (1995) for
the luminous (
MB< -15) irregular galaxies. As can be seen in
Fig. 4, the metallicity-luminosity relation for
low-luminosity dwarf irregular galaxies derived here is in good agreement with
the metallicity-luminosity relation obtained by Richer & McCall (1995).
However, the positions of some galaxies in our metallicity-luminosity
diagram and in the diagram of Richer & McCall are appreciable different.
According to the data of Richer & McCall the positions of three galaxies
(Sextans B, GR8, and NGC 6822) in the Z-L diagram have large deviations
from the metallicity-luminosity relationship (Fig. 4).
The positions of Sextans B and GR8 in the Z-L diagram with our data show
significantly smaller deviations from the metallicity-luminosity relationship
than their positions with Richer and McCall's data. (The positions of Sextans B,
GR8, and NGC 6822 in the Z-L diagram with our data and positions with Richer
and McCall's data are connected with dashed lines in Fig. 4.)
There are two determinations of oxygen abundance in Sextans B
(Table 1) which result in different values of oxygen abundance:
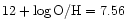 according to Skillman et al. (1989a) and
according to Skillman et al. (1989a) and
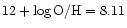 according
to Moles et al. (1990). The value of oxygen abundances from Moles et al. (1990)
has been adopted by Richer & McCall (1995). The oxygen abundances derived
through the P-method with the line intensities measurements from
Skillman et al. (1989a) and from Moles et al. (1990) are in good argeement:
according
to Moles et al. (1990). The value of oxygen abundances from Moles et al. (1990)
has been adopted by Richer & McCall (1995). The oxygen abundances derived
through the P-method with the line intensities measurements from
Skillman et al. (1989a) and from Moles et al. (1990) are in good argeement:
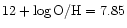 for the Skillman et al.'s data and
for the Skillman et al.'s data and
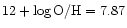 for the
Moles et al.'s data (Table 1). This value of oxygen abundance
in the Sextans B is in agreement with oxygen abundance corresponding
to its luminosity according to the metallicity-luminosity relationship.
A large deviation of the position of GR8 in the Richer and McCall Z-L diagram
from the metallicity-luminosity relationship is caused mainly by the
uncertainty in the value of the luminosity, Fig. 4. The case of
NGC 6822 will be considered in the next subsection.
for the
Moles et al.'s data (Table 1). This value of oxygen abundance
in the Sextans B is in agreement with oxygen abundance corresponding
to its luminosity according to the metallicity-luminosity relationship.
A large deviation of the position of GR8 in the Richer and McCall Z-L diagram
from the metallicity-luminosity relationship is caused mainly by the
uncertainty in the value of the luminosity, Fig. 4. The case of
NGC 6822 will be considered in the next subsection.
Thus, the metallicity-luminosity diagram for low-luminosity dwarf irregular
galaxies constructed here on the base of oxygen abundances derived through the
P-method is in good agreement with the metallicity-luminosity relation
obtained by Richer & McCall (1995). It should be particularly emphasized that
Richer & McCall have determined their metallicity-luminosity relation
using only the best available data for dwarf irregulars. In contrast, we
have constructed the metallicity-luminosity diagram using all the available
data for dwarf irregulars. As a consequance of this, the number of points at the
low-luminosity end of the metallicity-luminosity relation increases by
about a factor of two. As this takes place, the scatter at low luminosities in
our diagram is not in excess of that in Richer and McCall's diagram, although
the dispersion of oxygen abundances around the metallicity-luminosity
relationship seems to increase with decreasing galaxy luminosity, as was
found by Richer & McCall (1995).
The position of NGC 6822 in the Z-L diagram shows a large deviation from the
metallicity-luminosity relationship (Fig. 4). The oxygen
abundance determinations both in individual stars and in H II regions in
the NGC 6822 are now available. The mean stellar oxygen abundance derived from
high resolution spectra of two stars is
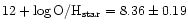 (Venn et al. 2001). Twelve determinations of oxygen abundances in H II
regions of the NGC 6822 (Lequeux et al. 1979; Pagel et al. 1980; Skillman et al.
1989b; Hidalgo-Gámez 1999) result in a mean value of gas oxygen abundance
(Venn et al. 2001). Twelve determinations of oxygen abundances in H II
regions of the NGC 6822 (Lequeux et al. 1979; Pagel et al. 1980; Skillman et al.
1989b; Hidalgo-Gámez 1999) result in a mean value of gas oxygen abundance
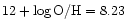 (Table 2). If this value of gas oxygen
abundance in the NGC 6822 is correct, then the position of NGC 6822 in the
metallicity-luminosity diagram deviates considerably from the metallicity-luminosity relationship, i.e. this value of oxygen abundance in the NGC 6822 is
significantly (by around 0.3 dex) higher than the oxygen abundance corresponding
to its luminosity, Fig. 4.
(Table 2). If this value of gas oxygen
abundance in the NGC 6822 is correct, then the position of NGC 6822 in the
metallicity-luminosity diagram deviates considerably from the metallicity-luminosity relationship, i.e. this value of oxygen abundance in the NGC 6822 is
significantly (by around 0.3 dex) higher than the oxygen abundance corresponding
to its luminosity, Fig. 4.
| List of references: |
H-G - Hidalgo-Gámez (1999);
Letal - Lequeux et al. (1979);
Petal -
Pagel et al. (1980);
STM - Skillman et al. (1989) |
If H II regions in NGC 6822 lie on the lower branch of the R23-O/H
diagram then, Eq. (3) can be used for the oxygen abundance
determination in H II regions of NGC 6822. The mean value of oxygen
abundances obtained via Eq. (3) is around 7.90. In this case
the position of the NGC 6822 in the Z-L diagram is close to the metallicity-luminosity relationship, Fig. 4, but this value of oxygen
abundance is in conflict with a stellar oxygen abundance 12+log O/H
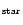 and with the oxygen abundances of O/H
and with the oxygen abundances of O/H
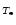 derived through the
derived through the  -method (Table 2).
-method (Table 2).
![\begin{figure}
\par\resizebox{1.00\hsize}{!}{\includegraphics[angle=0]{10586f5.eps}}\end{figure}](/articles/aa/full/2001/29/aa10586/Timg54.gif) |
Figure 5:
The radial abundance gradient within NGC 6822. The original oxygen abundances
of H II regions (Col. 2 of Table 2) are represented by open circles
with error bars. The stellar data (with error bars) are shown by filled
triangles. Our oxygen abundances O/HP for H II regions
(Col. 4 of Table 2) are shown by filled circles. The line is the best fit
to our data for H II regions and to the original data for stars. |
The stellar oxygen abundances and oxygen abundances derived through the  -method suggest that the H II regions in NGC 6822 lie on the upper
branch of the R23-O/H diagram. Then, the corresponding equation from
Paper II
-method suggest that the H II regions in NGC 6822 lie on the upper
branch of the R23-O/H diagram. Then, the corresponding equation from
Paper II
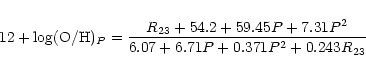 |
(4) |
should be used for the oxygen abundance determination in H II regions
of NGC 6822. In this case the mean oxygen abundance for 11 H II regions in
NGC 6822 is
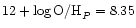 ,
Table 2 (the value of
O/HP obtained in the H II region Ho 14 from the sample of Pagel
et al. (1980) is in conflict with the suggestion that this H II region
belongs to the upper branch of the R23-O/H diagram, and this H II
region is excluded from the consideration). The mean value of O/HP is in
agreement with the mean value of the stellar oxygen abundance. But in this case
the position of the NGC 6822 in the Z-L diagram deviates considerably from the
metallicity-luminosity relationship (open circle in Fig. 4).
,
Table 2 (the value of
O/HP obtained in the H II region Ho 14 from the sample of Pagel
et al. (1980) is in conflict with the suggestion that this H II region
belongs to the upper branch of the R23-O/H diagram, and this H II
region is excluded from the consideration). The mean value of O/HP is in
agreement with the mean value of the stellar oxygen abundance. But in this case
the position of the NGC 6822 in the Z-L diagram deviates considerably from the
metallicity-luminosity relationship (open circle in Fig. 4).
The values of the distance modulus of NGC 6822 determined with different
distance indicators (Cepheids, the tip of the red giant branch) are in good
agreement (Lee et al. 1993; Gallart et al. 1996; Ferrarese et al. 2000); the
uncertainty seems to be not in excess of 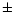 0.15. Therefore the deviation of
NGC 6822 from the metallicity-luminosity relation cannot be caused by the
uncertainty in the luminosity determination. Thus, the large deviation of
NGC 6822 from the metallicity-luminosity relationship seems to be real,
although the actual value of the deviation is not clear.
0.15. Therefore the deviation of
NGC 6822 from the metallicity-luminosity relation cannot be caused by the
uncertainty in the luminosity determination. Thus, the large deviation of
NGC 6822 from the metallicity-luminosity relationship seems to be real,
although the actual value of the deviation is not clear.
In Fig. 5 we show our oxygen abundances O/HP
for H II regions from Table 2, as a function of galactocentric
distance, together with the original oxygen abundances in H II regions and
with data for stars. The original oxygen abundances are presented
by open circles with error bars. The stellar data (with error bars) are
shown by filled triangles. Our data are shown with filled circles.
The galactocentric distances for H II regions and stars were taken from
Venn et al. (2001). The line is the best fit to our data for H II regions
and to the original data for stars. From examination of the O/HP in the
H II regions together with the stellar data, it is evident that there is no
significant radial abundance gradient within the NGC 6822. The slope of the
formal best fit is about -0.035 dex/kpc. The data are also consistent
with no gradient at all. Thus, our data confirm the conclusion of Pagel et al.
(1980) that if there is an actual radial abundance gradient within NGC 6822,
the slope of the gradient is small and the trend is entirely masked by the errors.
Thus, the metallicity-luminosity relation for irregular galaxies extends into
the region of low luminosities up to
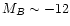 .
It is widely suggested
that the metallicity-luminosity relation for irregular galaxies is caused by
galactic winds of different efficiencies. In other words, the metallicity-luminosity relation represents the ability of a given galaxy to keep the products
of its own evolution rather than their ability to produce metals (Larson 1974).
On the other hand, it has been found that the astration level is higher in
massive irregular galaxies than in dwarf ones (Lequeux et al. 1979; Vigroux
et al. 1987). Then, it is suggested that the systematic increase of the
astration level with luminosity can aslo play a role in the origin of the
metallicity-luminosity relationship for irregular galaxies.
.
It is widely suggested
that the metallicity-luminosity relation for irregular galaxies is caused by
galactic winds of different efficiencies. In other words, the metallicity-luminosity relation represents the ability of a given galaxy to keep the products
of its own evolution rather than their ability to produce metals (Larson 1974).
On the other hand, it has been found that the astration level is higher in
massive irregular galaxies than in dwarf ones (Lequeux et al. 1979; Vigroux
et al. 1987). Then, it is suggested that the systematic increase of the
astration level with luminosity can aslo play a role in the origin of the
metallicity-luminosity relationship for irregular galaxies.
The values of the gas mass fraction 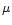 and oxygen abundance deficiency (which
is a good indicator of the efficiency of mass exchange between a galaxy and its
environment) have been derived for a number of late-type spiral (Pilyugin &
Ferrini 1998) and irregular (Pilyugin & Ferrini 2000a) galaxies. Using these
data, the roles of two hypothesed mechanisms as causes of the
metallicity-luminosity correlation among late-type spiral and irregular
galaxies have been examined in our recent study (Pilyugin & Ferrini 2000b).
It was found that both the increase in astration level and the decreasing
efficiency of heavy element loss with increasing luminosity, make comparable
contributions to the metallicity-luminosity correlation. The fact that the
metallicity-luminosity relation for irregular galaxies extends up to low
luminosity can be considered as evidence that the tendency for the decrease
in astration level and the increasing efficiency of heavy element loss with
decreasing luminosity remains at the low-luminosity end.
and oxygen abundance deficiency (which
is a good indicator of the efficiency of mass exchange between a galaxy and its
environment) have been derived for a number of late-type spiral (Pilyugin &
Ferrini 1998) and irregular (Pilyugin & Ferrini 2000a) galaxies. Using these
data, the roles of two hypothesed mechanisms as causes of the
metallicity-luminosity correlation among late-type spiral and irregular
galaxies have been examined in our recent study (Pilyugin & Ferrini 2000b).
It was found that both the increase in astration level and the decreasing
efficiency of heavy element loss with increasing luminosity, make comparable
contributions to the metallicity-luminosity correlation. The fact that the
metallicity-luminosity relation for irregular galaxies extends up to low
luminosity can be considered as evidence that the tendency for the decrease
in astration level and the increasing efficiency of heavy element loss with
decreasing luminosity remains at the low-luminosity end.
A prominent feature of the metallicity-luminosity relation for irregular
galaxies is the increased scatter at low luminosities in comparison to that at
high luminosities. Part of this scatter is undoubtedly due to uncertainties in
the oxygen abundances and luminosities. But another part is likely to be real.
Since there is no apparent reason to suggest that the uncertainties in oxygen
abundances and/or in luminosities increase systematically with decreasing
galaxy luminosity, the increase of the dispersion of oxygen abundances
around the metallicity-luminosity relationship with decreasing galaxy
luminosity seems to be real. The increase in the scatter of oxygen abundances
with luminosity can be explained by the fluctuations in values
of the gas mass fraction among irregular galaxies of a given luminosity.
There is a correlation between the gas mass fraction 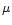 and the galaxy's
luminosity, decreasing from
and the galaxy's
luminosity, decreasing from 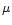
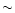 0.8 at MB = -12 or
0.8 at MB = -12 or
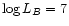 to
to
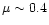 at MB = -18 or
at MB = -18 or
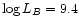 (Pilyugin &
Ferrini 2000a). According to the simple model for the chemical evolution
of galaxies, the relation between oxygen abundance and gas mass fraction is given
by a logarithmic relationship,
(Pilyugin &
Ferrini 2000a). According to the simple model for the chemical evolution
of galaxies, the relation between oxygen abundance and gas mass fraction is given
by a logarithmic relationship,
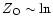 (1/
(1/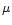 ), then the
O/H-
), then the
O/H-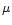 curve is significantly steeper at large than at small
curve is significantly steeper at large than at small 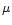 .
Therefore, the equal fluctuations in values of the gas mass fraction, say
.
Therefore, the equal fluctuations in values of the gas mass fraction, say
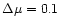 ,
result in an appreciably larger dispersion
of oxygen abundances among low-luminosity irregular galaxies with high values
of the gas mass fraction (the change of
,
result in an appreciably larger dispersion
of oxygen abundances among low-luminosity irregular galaxies with high values
of the gas mass fraction (the change of 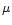 from 0.9 to 0.8 results in
from 0.9 to 0.8 results in
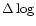 O/H
O/H 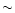 0.33) than among luminous irregular galaxies with low
values of the gas mass fraction (the change of
0.33) than among luminous irregular galaxies with low
values of the gas mass fraction (the change of 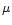 from 0.5 to 0.4 results in
from 0.5 to 0.4 results in
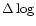 O/H
O/H 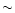 0.12). Thus, the increase in the scatter of oxygen
abundances with luminosity is not surprising.
0.12). Thus, the increase in the scatter of oxygen
abundances with luminosity is not surprising.
In summary:
The low-luminosity dwarf irregular galaxies are considered.
The oxygen abundances in H II regions of dwarf irregular galaxies were
recalculated from published spectra through the recently suggested P-method. It has been found that the metallicity of low-luminosity dwarf
irregular galaxies, with a few exceptions, correlates well with galaxy
luminosity. The dispersion of oxygen abundances around the luminosity-metallicity relationship increases with decreasing galaxy luminosity,
as was found by Richer & McCall (1995). The lack of relationship between the
oxygen abundance and the absolute magnitude in the blue band for irregular
galaxies obtained by Hidalgo-Gámez & Olofsson (1998) can be explained by the
large uncertainties in the oxygen abundances derived through the  -method, that in turn can be explained by the large uncertainties in the
measurements of the strengths of the weak oxygen line
-method, that in turn can be explained by the large uncertainties in the
measurements of the strengths of the weak oxygen line
![$\rm [OIII] \lambda 4363$](/articles/aa/full/2001/29/aa10586/img6.gif) used in the
used in the  -method.
-method.
Acknowledgements
It is a pleasure to thank the referee, Dr. N. Arimoto, for his comments on this
work. This study was partly supported by the NATO grant PST.CLG.976036 and
the Joint Research Project between Eastern Europe and Switzerland (SCOPE)
No. 7UKPJ62178.
-
Ferrarese, L., Mould, J. R., Kennicutt, R. C., et al. 2000,
ApJ, 529, 745
NASA ADS
-
Gallart, C., Aparicio, A., & Vilchez, J. M. 1996, AJ, 112, 1928
In the text
NASA ADS
-
Garnett, D. R., & Shields, G. A. 1987, ApJ, 317, 82
In the text
NASA ADS
-
Garnett, D. R., Shields, G. A., Skillman, E. D., Sagan, S. P., & Dufour, R. J.
1997, ApJ, 489, 63
In the text
NASA ADS
-
González-Riestra, R., Rego, M., & Zamorano, J. 1988, A&A, 202, 27
In the text
NASA ADS
-
Heydari-Malayeri, M., Melnick, J., & Martin, J.-M. 1990, A&A, 234, 99
In the text
NASA ADS
-
Hidalgo-Gámez, A. M. 1999, Dissertation for the Degree of Doctor of
Philosophy in Astronomy, Uppsala University
In the text
-
Hidalgo-Gámez, A. M., & Olofsson, K. 1998, A&A, 334, 45
In the text
NASA ADS
-
Hodge, P., & Miller, B. W. 1995, ApJ, 451, 176
In the text
NASA ADS
-
Hoessel, J. G., Saha, A., Krist, J., & Danielson, G. E. 1998, AJ, 108, 645
NASA ADS
-
Hunter, D. A., & Hoffman, L. 2000, AJ, 117, 2789
NASA ADS
-
Izotov, Y. I., & Thuan, T. X. 1999, ApJ, 511, 639
In the text
NASA ADS
-
Larson, R. B. 1974, MNRAS, 169, 229
In the text
NASA ADS
-
Lee, M. G., Freedman, W. L., & Madore, B. F. 1993, ApJ, 417, 553
In the text
NASA ADS
-
Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S.
1979, A&A, 80, 155
In the text
NASA ADS
-
Kinman, T. D., & Davidson, K. 1981, ApJ, 243, 127
In the text
NASA ADS
-
Mateo, M. 1998, ARA&A, 36, 435
In the text
NASA ADS
-
McGaugh, S. S. 1991, ApJ, 380, 140
In the text
NASA ADS
-
Miller, B. W., & Hodge, P. 1994, ApJ, 427, 656
In the text
NASA ADS
-
Miller, B. W., & Hodge, P. 1996, ApJ, 458, 467
In the text
NASA ADS
-
Moles, M., Aparicio, A., & Masegosa, J. 1990, A&A, 228, 310
In the text
NASA ADS
-
Pagel, B. E. J., Edmunds, M. G., & Smith, G. 1980, MNRAS, 193, 219
In the text
NASA ADS
-
Pilyugin, L. S. 2000, A&A, 362, 325 (Paper I)
NASA ADS
-
Pilyugin, L. S. 2001, A&A, 369, 594 (Paper II)
NASA ADS
-
Pilyugin, L. S., & Ferrini, F. 1998, A&A, 336, 103
In the text
NASA ADS
-
Pilyugin, L. S., & Ferrini, F. 2000a, A&A, 354, 874
NASA ADS
-
Pilyugin, L. S., & Ferrini, F. 2000b, A&A, 358, 72
NASA ADS
-
Richer, M. G., & McCall, M. L. 1995, ApJ, 445, 642
In the text
NASA ADS
-
Skillman, E. D., Kennicutt, R. C., & Hodge, P. W. 1989a, ApJ, 347, 875
In the text
NASA ADS
-
Skillman, E. D., Terlevich, R., Kennicutt, R. C., Garnett, D. R., & Terlevich, E.
1994, ApJ, 431, 172
In the text
NASA ADS
-
Skillman, E. D., Terlevich, R., & Melnick, J. 1989b, MNRAS, 240, 563
In the text
NASA ADS
-
Tolstoy, E., Gallagher, J. S., Cole, A. A., et al. 1998, AJ, 116, 1244
In the text
NASA ADS
-
Tully, R. B., Boesgaard, A. M., Dyck, H. M., & Schempp, W. V. 1981, ApJ, 246, 38
In the text
NASA ADS
-
van Zee, L. 2000, ApJL, 543, 31L
In the text
-
Venn, K. A., Lennon, D. J., Kaufer, A., et al. 2001,
ApJ, 547, 765
NASA ADS
-
Vigroux, L., Stasinska, G., & Comte, G. 1987, A&A, 172, 15
In the text
NASA ADS
-
Vila-Costas, M. B., & Edmunds, M. G. 1992, MNRAS, 259, 121
In the text
NASA ADS
-
Webster, B. L., Longmore, A. J., Hawarden, T. G., & Mebold, U. 1983, MNRAS,
205, 643
In the text
NASA ADS
-
Zaritsky, D., Kennicutt, R. C., & Huchra, J. P. 1994, ApJ, 420, 87
In the text
NASA ADS
Copyright ESO 2001
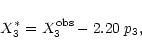
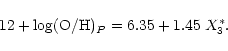
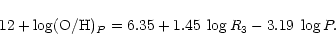
![\begin{figure}
\par\resizebox{1.00\hsize}{!}{\includegraphics[angle=0]{10586f1.eps}}\end{figure}](/articles/aa/full/2001/29/aa10586/Timg28.gif)
![\begin{figure}
\par\resizebox{1.00\hsize}{!}{\includegraphics[angle=0]{10586f2.eps}}\end{figure}](/articles/aa/full/2001/29/aa10586/Timg29.gif)
![\begin{figure}
\par\resizebox{1.00\hsize}{!}{\includegraphics[angle=0]{10586f3.eps}}\end{figure}](/articles/aa/full/2001/29/aa10586/Timg32.gif)
![\begin{figure}
\par\resizebox{1.00\hsize}{!}{\includegraphics[angle=0]{10586f4.eps}}\end{figure}](/articles/aa/full/2001/29/aa10586/Timg34.gif)