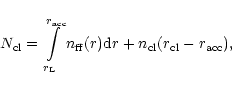 |
(3) |
We now discuss some consequences of our proposal that the braking of PSR B1509-58 is mostly due to the interaction of the pulsar's magnetosphere with the dense matter of a circumstellar clump.
First, we consider the contribution of the circumstellar matter to the
neutral hydrogen absorption toward the pulsar.
The low covering factor of clumps (see Sect. 3)
implies that this contribution is
It was pointed out by Strom (1994) that a ROSAT observation
of the SNR MSH15-52 indicates a larger absorption towards PSR
B1509-58 than seen from the bright northwest part of the
SNR's shell (known as RCW89). The comparison of neutral
hydrogen absorption data
(see Greiveldinger et al. 1995; Trussoni et al.
1996; Tamura et al. 1996;
Marsden et al. 1997; Rots et al. 1998) shows that the excess of absorption towards
the pulsar could be as large as ![]() (1-5)
(1-5)
![]() .
This discrepancy could be interpreted as a sign that
the pulsar is more distant than the SNR, and therefore that these
two objects are not physically associated with each other (Strom
1994). It is also possible that "the spectral analysis is
not detailed enough to provide the correct parameters"
(Trussoni et al. 1996). Another possibility is that the HI column density
distribution is really inhomogeneous across the SNR (cf.
Trussoni et al. 1996). We favour the last possibility and suggest that the
excess of absorption towards PSR B1509-58 is due to the dense
neutral gas around the pulsar. One can use Eq. (3) to set an
upper limit on
.
This discrepancy could be interpreted as a sign that
the pulsar is more distant than the SNR, and therefore that these
two objects are not physically associated with each other (Strom
1994). It is also possible that "the spectral analysis is
not detailed enough to provide the correct parameters"
(Trussoni et al. 1996). Another possibility is that the HI column density
distribution is really inhomogeneous across the SNR (cf.
Trussoni et al. 1996). We favour the last possibility and suggest that the
excess of absorption towards PSR B1509-58 is due to the dense
neutral gas around the pulsar. One can use Eq. (3) to set an
upper limit on
![]() .
For the parameters adopted above, and
assuming that
.
For the parameters adopted above, and
assuming that
![]() (1-5)
(1-5)
![]() ,
one has
,
one has
![]() (0.2-1.2)
(0.2-1.2)
![]() cm. This estimate shows that if our explanation of the
age discrepancy is correct, then one might expect that in the near
future (i.e. after a lapse of
cm. This estimate shows that if our explanation of the
age discrepancy is correct, then one might expect that in the near
future (i.e. after a lapse of ![]()
![]() ,
where
,
where
![]() is the line of sight component of
is the line of sight component of ![]() )
the
first derivative of the pulsar's spin period will suffer a
significant decrease.
)
the
first derivative of the pulsar's spin period will suffer a
significant decrease.
Second, let us discuss the candidate optical counterpart for PSR
B1509-58 proposed by Caraveo et al. (1994). Caraveo et al.
pointed out that the luminosity of the optical counterpart
(
![]() )
exceeds by a few orders of magnitude the value derived
for magnetospheric optical emission of young pulsars (Pacini
1971). This fact together with the negative result of
searching of optical pulsations at the radio period led to the
conclusion that the proposed identification could be erroneous
(Mignami et al. 1998; see also Shearer et al. 1998; Chakrabarti & Kaspi 1998). We suggest,
however, that the observed optical emission should rather be
attributed to the bow shock around the pulsar than to the pulsar
itself. This suggestion is supported by the estimate of the total
luminosity of the bow shock,
)
exceeds by a few orders of magnitude the value derived
for magnetospheric optical emission of young pulsars (Pacini
1971). This fact together with the negative result of
searching of optical pulsations at the radio period led to the
conclusion that the proposed identification could be erroneous
(Mignami et al. 1998; see also Shearer et al. 1998; Chakrabarti & Kaspi 1998). We suggest,
however, that the observed optical emission should rather be
attributed to the bow shock around the pulsar than to the pulsar
itself. This suggestion is supported by the estimate of the total
luminosity of the bow shock,
![]() ,
where
,
where
![]() and
and
![]() are the area and the
characteristic radius of the bow shock, respectively. For the
adopted parameters
are the area and the
characteristic radius of the bow shock, respectively. For the
adopted parameters![]() this
gives
this
gives
![]() ,
i.e.
,
i.e.
![]() for
for
![]() .
It is obvious that if our suggestion is correct, there can be no
correspondence between the observed luminosity and the luminosity
expected from the results of Pacini (1971). The optical
pulsations should be absent as well.
.
It is obvious that if our suggestion is correct, there can be no
correspondence between the observed luminosity and the luminosity
expected from the results of Pacini (1971). The optical
pulsations should be absent as well.
To conclude, we point out a curious coincidence of the accretion rate derived in Sect. 2 with accretion rates required in accretion-based models to explain high spin-down rates of anomalous X-ray pulsars and soft gamma-ray repeaters (e.g. Mereghetti & Stella 1995; Ghosh et al. 1997; Chatterjee et al. 2000; Alpar 2000). This coincidence allows us to believe (Gvaramadze 1999a, 2000b) that these objects could lose a significant part of their rotational energy due to the process discussed in this paper, and that their "true" ages could be much larger than the respective characteristic spin-down ones.
Acknowledgements
I am grateful to N. D'Amico and A. D'Ercole for discussions, to D. Page (the referee) for comments, and to J. K. Katgert-Merkelijn (the Deputy Editor) for carefully reading the manuscript. This work was partially supported by NPS.
Copyright ESO 2001