A&A 374, 204-212 (2001)
DOI: 10.1051/0004-6361:20010609

Eclipsing binaries with candidate CP stars

II. Parameters of the system V392 Carinae[*] [*]

Y. Debernardi - P. North

Institut d'Astronomie de l'Université de Lausanne, 1290 Chavannes-des-Bois, Switzerland

Received 12 April 2001 / Accepted 26 April 2001

Abstract
We present a detailed study of an eclipsing binary which had been classified Ap SrCrEu (Hartoog 1976) before being known as a binary. Radial velocities measured at the times of both quadratures allow us to obtain precise masses for both components, while the light curve yields the radii. The following ephemeris and fundamental parameters of the system were obtained: ${\rm HJD} = (2447999.7656\pm 0.0041) + (3.174990 \pm 0.000001) E$, e = 0.00, $i = 81.9\pm 0.1$$^\circ$, $M_1 = 1.90 \pm 0.02~M_{\odot}$, $M_2 = 1.85 \pm 0.02~M_{\odot}$, $R_1 = 1.63\pm 0.03~R_{\odot}$, $R_2 = 1.60\pm 0.03~R_{\odot}$, $v\sin i_1 = 27.6\pm 3.5$ kms-1, $v\sin i_2 = 23.6\pm 3.6$ kms-1. The projected rotational velocities were determined by fitting a synthetic spectrum convolved with a rotational profile to the observed spectrum. A comparison of the spectra of V392 Car and of the normal A star Cox 98, which has the same colour indices, shows that Sr is not overabundant and the metallicity of V392 Car is the same as that of the other cluster members. Therefore, V392 Car is a normal A2 star rather than an Ap star. The position of V392 Car in the HR diagram is entirely consistent with membership of the cluster NGC 2516. An independent estimate of the distance to this cluster was done using the parameters of the eclipsing system, and found to be in agreement with the Hipparcos one. A comparison of the parameters obtained from observations with predictions of internal structure models leads to a metallicity estimate ${\rm [M/H]}=0\pm 0.10$ dex for NGC 2516. This estimate is completely independent of any spectroscopic or photometric method (except for the $T_{\rm eff}$ determination) but relies on stellar structure models.

Key words: stars: peculiar - stars: eclipsing binaries - stars: spectroscopic binaries


1 Introduction

Magnetic Ap stars, i.e. late B and A stars of type Si, Cr or SrCrEu, are peculiar not only regarding their atmospheric abundances, but also regarding fundamental properties such as rotation and binarity. Rotation is statistically slower than for normal stars of similar mass and luminosity class, while binarity is peculiar in the sense that orbital periods shorter than three days are practically not found among them.

This paper is the second one dedicated to candidate chemically peculiar stars in eclipsing binaries. The first paper in the series (North et al. 1997) examined the case of three eclipsing systems, one of which had been classified Ap and another Am, the third one being interesting in this context because of its relatively slow rotation. The Ap classification of the first system seems to have been spurious.

V392 Car belongs to the open cluster NGC 2516, which has an age of log(t) = 8.15 and is located at a distance of 373 pc (Mermilliod 1999 http://obswww.unige.ch/webda). V392 Car is also designated under the number 38 in NGC 2516 by Cox (1955).

Cox 38 in NGC 2516 was discovered by PN (North et al. 1982; North 1984) to be an eclipsing system in early 1982, in the course of a systematic search for photometric variability in Ap stars. It did not show any smooth variability typical of such objects, but eclipses were found and the star received its designation V392 Car. The lack of intrinsic variability, though disappointing, was not an argument sufficient to deny the Ap nature of at least one of the components, since many Ap stars have a vanishingly small photometric amplitude, which in this case might have been further diluted by the flux of the normal component. Furthermore, Maitzen & Hensberge (1981) had found a marginal photometric peculiarity $\Delta a = 0.014$ in Maitzen's y g1 g2 system, which gave some hope that this system might host a magnetic Ap star. At the time, therefore, this object appeared to be the first known eclipsing magnetic Ap star, and this was an exciting perspective because it offered the possibility of mapping the surface of the Ap component (which is expected to present overabundance patches) by taking spectra during eclipses. Another interest of this object was that it belongs to a cluster, so that independent constraints exist on its age and luminosity. These reasons explain why we devoted much time to monitor it in the Geneva photometric system.

To obtain all fundamental parameters, it is necessary to have a radial velocity curve available. According to Andersen & Nordström (1983), the Sr II line at 421.5 nm is an appropriate one for deriving radial velocities in SB2 binaries without bias. This lead us to examine the wavelength range 419.4 nm to 422.8 nm centered on this line to measure the radial velocity (RV); in our case, another advantage of this line is to allow a check of the peculiar nature of each component of the binary.

In this paper we derive the orbit and fundamental physical parameters of the system, check the possible peculiar nature of each component and take advantage of its membership of the open cluster NGC 2516 to provide an independent distance estimate of the latter. In addition, we provide a metallicity estimate of the binary components, hence of NGC 2516, through comparison with stellar structure models.

2 Observations and reduction

The photometric observations were done in the GENEVA photometric system (Golay 1980; Rufener & Nicolet 1988; Cramer 1999) between January 1978 and January 1991, at the European Southern Observatory, La Silla, Chile, with the "P7'' double-beam photometer (Burnet & Rufener 1979) attached to the 70 cm Swiss telescope at La Silla (ESO Chile). The discovery was made in 1982, but most of the lightcurve was acquired in 1985 and a few complementary data collected a few years later to check the orbital period. Although the early measurements were made in a differential way relative to the comparison star NGC 2516-129 (CpD -60$^\circ$982), the other ones are all-sky measurements, but made with a standard star at the same airmass just before or after. The reduction of the data went through the standard procedure performed systematically at the Geneva Observatory. The 734 photometric data are displayed in Table 1 (available at the CDS). The photometric data in the GENEVA system are collected in the General Catalogue (Rufener 1988) and its up-to-date database (Burki 2001).

The spectroscopic observations were performed on the nights of 3-4 and 8-9 February 1991 with the CES spectrograph attached to the 1.4 m CAT telescope at ESO, La Silla, Chile, in remote control mode from Garching. The two nights were planned to fall at the times of both quadratures, in order to obtain good estimates of the RV amplitudes and systemic velocity, even though all phases could not be covered. This was judged enough, because both the lightcurve and the short period suggested a circular orbit and this hypothesis also appears justified a posteriori.

The star Cox 98 in NGC 2516 (CpD -60$^\circ$958) was measured once on the first night for comparison purpose. Indeed, this star lies in the same photometric "box'' as V392 Car, i.e. its six Geneva colours are the same within 0.02 mag. It also lies close to V392 Car in the HR diagram, except that it is 0.707 mag below it, exactly as expected for a single star compared to an SB2 binary. The strength of its Sr II line provides a reference for that of both components of V392 Car. The central wavelength was 4212 Å and the resolving power was $R=50\,000$. The detector was the ESO CCD#9; we adopted a binning factor of 2 in the direction perpendicular to dispersion, in order to increase the S/N ratio slightly. One-hour exposures of V392 Car were done in succession, each one being followed by a calibration exposure using an internal thorium lamp. Ten flat-field exposures (made with an internal lamp) were done just before each night, and averaged to yield a high S/N 2-D frame. Short (2-5 mn) exposures were done to check the bias level; the dark current was considered negligible.

The reduction of the data was performed in Garching with the IHAP software. The 2-D frames were bias subtracted and divided by the bias-subtracted average flat-field. The spectra were then extracted by simple addition of the pixel columns carrying a significant signal (the spectrum being sufficiently parallel to the pixel columns). The wavelength calibration was updated for each exposure, using the average of the two thorium exposures taken just before and after the science one. The rms scatter of the residuals around the fitted dispersion curve was typically about 2.6 mÅ. After extraction and rebinning, the spectra were interactively normalized to the continuum using a spline fit to the continuum points.

A single observation was kindly performed by M. Burnet with the CORALIE high-resolution fiber-fed echelle spectrograph (Queloz et al. 2000) mounted on the Nasmyth focus on the 120$\,$cm New Swiss telescope at La Silla (ESO, Chile). CORALIE is an improved version of the ELODIE spectrograph (Baranne et al. 1996). Thanks to a slightly different optical combination at the entrance of the spectrograph and the use of a 2k by 2k CCD camera with smaller pixels ( $15~{\rm\mu m}$), CORALIE has a larger resolution than ELODIE. The CORALIE spectra were reduced at the telescope, using a software package called INTER-TACOS (INTERpreter for the Treatment, the Analysis and the COrrelation of Spectra), developed by D. Queloz and L. Weber at Geneva Observatory (Baranne et al. 1996). They cover the wavelength range 3875-6820 Å.

3 Spectral type classification

V392 Car was first classified as an Ap star by Hartoog (1976). Another star belonging to the same cluster, Cox 98, is located in the same photometric box as V392 Car and its spectrum can be compared with that of Cox 98, as mentioned in Sect. 2. Unfortunately, the only available spectral classification for Cox 98 is the HD one (A0), and this object was not measured in the $\Delta a$ system by Maitzen & Hensberge (1981), so there is no clear indication in the literature that it is a normal A star rather than an Ap one. However, its colours in the Geneva system do not indicate any photometric peculiarity ( $\Delta(V1-G)=-0.010$, see e.g. Hauck & North 1982 for the definition of this peculiarity index), and synthetic spectra computed for near-solar abundances with a modified version of the ADRS code (Berthet 1991; Chmielewsky 1979; Lanz 1987) well represent the observed one (atmosphere models from Kurucz 1979 were used). Therefore, it seems safe to conclude that the comparison star Cox 98 is a normal A star.

In order to test whether any component of V392 Car is peculiar or not, we compared the equivalent width (EW) of the Sr II (421.5 nm) line with that of Cox 98. Because of the binary nature of V392 Car (dilution by the continuum flux of the companion), the observed EW of the Sr line of each component is roughly half the real one; taking that into account, the EW of each component of V392 Car was found to be very close to that of Cox 98, suggesting that both components of V392 Car are normal stars as well. In addition, two synthetic spectra properly shifted in RV and added together were able to reproduce well the observed spectra of the binary. Besides, no line variation could be observed, so that no abundance patch exist on the surface of either component, as already suggested by the lack of photometric out-of-eclipse variation. Yet another argument against the peculiarity of V392 Car is that no correlation dip was seen with the Coravel spectrovelocimeter (Baranne et al. 1979) attached to the Danish 1.54 m telescope at ESO, la Silla, when Dr. Willy Benz kindly attempted a RV measurement for us on the night of 18 February 1982: generally, magnetic Ap stars do show a correlation dip with this instrument when they are cooler than about 10000 K and have a $v\sin i$ smaller than about 30 kms-1, which is the case here. All this is consistent with the lack of photometric peculiarity in the Geneva system, even though the sensitivity of this indicator is not as good for Ap stars cooler than 9000-10000 K.

These conclusions may be illustrated by the (Y, Z) diagram of the Geneva photometry (Cramer & Maeder 1979) shown in Fig. 1, which is useful to discriminate Ap stars from the normal ones in open clusters. In the plot, the well known Ap stars Cox 127, Cox 15, Cox 26, Cox 24 and Cox 230 are clearly distinguished from standard stars, while V392 Car (= Cox 38) lies right in the middle of the sequence of normal stars.

From another point of view, the $\Delta m_2$ parameter of V392 Car is normal ( $\Delta m_2 = -0.013$), showing that it is not an Am star.

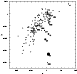  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms1383f1.eps}}\end{figure} Figure 1: Position of V392 Car (Cox 38) in the (Y, Z) colour colour diagram of NGC 2516. The sizes of the points represent the intensity of $\Delta a$ (Maitzen & Hensberge 1981).
Open with DEXTER

Thus, we can no longer consider V392 Car as hosting an Ap Sr or SrCrEu star; both components are normal A2V stars.

4 Spectroscopic variations

4.1 circularization

This eclipsing binary is a short period binary system: $P=3\hbox{$.\!\!^{\rm d}$ }17499$ was derived from the photometric observations (see next section). In such a case, the tidal forces are big enough to alter the orbital and rotational motions of both stars. For typical A star masses, the tidal cut off of this effect is roughly 10 days (Mathieu & Mazeh 1988). So here, tidal effects have been strong enough to synchronize the rotational and orbital periods and to circularize the orbit (e=0), which is an important starting hypothesis to determine the spectroscopic orbit.

4.2 Radial and rotational velocity determination

Two different methods were used to determine the radial velocities of each component from the CAT observations. The first one, adopted here, consisted simply of fitting a gaussian to the Sr II (421.5 nm) line to determine its shift relative to the laboratory value. The second method relied on the correlation between V392 Car and Cox 98, which have the same colours and hence, presumably, the same spectral type. This correlation implicitly assumes that the RV of Cox 98 is representative of the average RV of the NGC 2516 cluster, and is equal to the systemic velocity of V392 Car. These two different methods gave consistants results for all observations, which is not very surprising because much of the information lies in the Sr II line. Nevertheless, this good agreement leads us to estimate a mean error of 1.5 kms-1 for the primary and of 1.7 kms-1 for the secondary. The resulting radial velocities are listed in Table 2.


 

 
Table 2: The first column is the Julian date of the observation. The radial velocities are related to the CORALIE standard system. The mean errors are 1.5 km s-1 for the primary and 1.7 km s-1 for the secondary.

Date [HJD-2400000]		 $V_{\rm A}$ [km s-1] $V_{\rm B}$ [km s-1]

48291.561		 -71.43 113.94
48291.609 -78.11 119.83
48291.656 -81.50 124.06
48291.752 -87.06 129.14
48291.797 -89.60 130.40
48291.867 -90.35 130.65
48296.565 135.42 -85.28
48296.612 135.71 -86.09
48296.662 135.58 -87.12
48296.713 133.75 -86.15
48296.770 130.63 -83.67
48296.817 126.96 -81.96
48296.864 120.82 -81.02
51557.725 102.69 -54.33


To determine the rotational velocities, we fitted synthetic spectra convolved with a rotational profile to the observed ones. With the only useful line being the Sr II one, the accuracy of these estimates is not very high. The two values are $v\sin i_{\rm A} = 27.6\pm3.5$ kms-1 and $v\sin i_{\rm B} = 23.6\ \pm\ 3.6$ kms-1 and agree quite well with a synchronized orbit, provided that the secondary has a smaller radius than the primary. The latter condition itself agrees with the fact that the secondary is less massive than the primary, both stars being unevolved. Using the physical parameters obtained in the next section, the synchronized rotational-velocity is calculated from the relation $v\sin i = \frac{2\,\pi}{P_{\rm orb}}R\, {\sin}\, i$. Thus the synchronized rotational-velocities for the respective components are $v\sin i_{\rm Async} = 25.9\pm0.5$ kms-1 and $v\sin i_{\rm Bsync} = 25.5\pm0.5$ kms-1. The errors are estimated from the value of the rotational period which is the same as the orbital period due to synchronization, and from the radii determination in Table 5. The observational results are in complete agreement with the calculated values, thus showing that the orbital and rotational motions are synchronized.

4.3 Spectroscopic orbit and parameters

Since the photometric period, which is identical to the orbital one, is precisely known, and since the eccentricity can be considered as zero, due to synchonization and circularization effects, it is possible to determine the spectroscopic orbit in spite of the poor phase sampling of RV. More precisely, the determination is based on fixed parameters, the photometrical period and T0, the eccentricity (e=0) and the accurate determination of the radial velocities fitted to the CORALIE RV system. Thus 4 parameters are free: $\gamma$, K1, K2 and $\Delta RV$, which is the zero point shift between the two different instruments. We adopted CORALIE as the reference instrument, since it is very precisely calibrated and stable. The resulting orbital parameters are listed in Table 3 and give the radial velocity curves shown in Fig. 2.

   \begin{figure} \par\includegraphics[angle=-90,width=8.8cm,clip]{ms1383f2.eps}\end{figure} Figure 2: Radial-velocity curve of V392 Car phased with the period $P=3\hbox{$.\!\!^{\rm d}$ }174990 \pm 0\hbox{$.\!\!^{\rm d}$ }000001$.
Open with DEXTER


 

 
Table 3: Orbital elements of V392 Car deduced from the radial velocity orbit. The scatter of the residuals is $\sigma $(O-C) = 2.2 km s-1.
P [J] 3.174990 $\pm$ 0.000001
T [HJD-2400000] 47999.7625 $\pm$ 0.0041
e 0
$\gamma$ [km s-1] 22.09 $\pm$ 0.77
$\omega_1$ [$^\circ$] -
$\omega_2$ [$^\circ$] -
K1 [km s-1] 110.04 $\pm$ 0.49
K2 [km s-1] 112.84 $\pm$ 0.49
q=K2/K1 0.975 $\pm$ 0.008
a1sin(i) [$R_{\odot}$] 7.088 $\pm$ 0.023
a2sin(i) [$R_{\odot}$] 6.913 $\pm$ 0.021
M1sin3(i) [$M_{\odot}$] 1.798 $\pm$ 0.018
M2sin3(i) [$M_{\odot}$] 1.844 $\pm$ 0.018


5 Photometric variability

Snowden (1975), Maitzen & Hensberge (1981) and Rufener & Bartholdi (1982) have discussed the possible variability or microvariabilty of V392 Car. Antonello & Mantegazza (1986) did not observe any variability in their study of variable stars in NGC 2516. In the Geneva measurements, however, the brightness of V392 Car clearly undergoes periodic variations which are quite well defined in spite of their small amplitude, about 0.15 mag in the V filter. The B and U magnitudes show luminosity variations at the same time as the V one, and with the same amplitude. All this unambiguously points to an eclipsing binary system.

5.1 Period determination

The period of the eclipsing binary was determined using the $\theta_1$statistical test for period search proposed by Renson (1978), in its modified form $\theta_1^{-1}$ (Manfroid et al. 1991). This test proves very efficient for precise determination of periods of eclipsing binaries; it was applied to each of the [U], [B] and V magnitudes and gave a period $P=3\hbox{$.\!\!^{\rm d}$ }174990$. The system is well detached, so the period will not change during the several years of the photometric observations.

5.2 Effective temperature

The effective temperature of the system is derived using the Geneva photometric colours and the calibration of Künzli et al. (1997). The equivalent photometric effective temperature, i.e. that of a single star with same colours as the binary, is 8746 K. There is no significant colour variation during the eclipses, which implies that both components very nearly have the same effective temperature.

Taking into account the masses of both components (derived in next section) and theoretical stellar models (Schaller et al. 1992) at $\log(t) = 8.15$ and ${\rm [Fe/H]} = 0$, which are the age and metallicity of NGC 2516, the theoretical difference of effective temperature between the two components is 200 K.

Thus, thanks to models allowing us to estimate a precise difference of effective temperatures and to observed colours giving access to a precise mean effective temperature, we can assume that $T_{\rm eff1}=8850$ K and $T_{\rm eff2} = 8650$ K.

5.3 Light curve

The light curve does not show deep eclipses ($\Delta$V$\sim$0.15mag), but the corresponding phases are well sampled by the observations. The well defined shapes of both eclipses (Fig. 3) do not show any flat part in the bottom, which implies that the eclipses are only partial. Only the V-light curve is drawn in this paper, since the [U], [B] and V light curves show the same behaviour due to similar $T_{\rm eff}$.

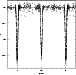  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms1383f3.eps}}\end{figure} Figure 3: V-light curve of V392 Car with a period $P=3\hbox{$.\!\!^{\rm d}$ }174990 \pm 0\hbox{$.\!\!^{\rm d}$ }000001$.
Open with DEXTER

To fit the V light curve, some parameters were fixed in the following way:

Each photometric minimum is shown in detail in Fig. 4 and in Fig. 5 for the primary and secondary component respectively. The analysis of the system was done using an interactive version (by PN) of the EBOP16 code of Paul Etzel (1980, 1989). This relatively simple programme is ideal for our case of a well detached binary, where no detectable proximity effect exists.
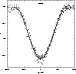  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms1383f4.eps}}\end{figure} Figure 4: V light-curve of V392 Car around the primary minimum. The less accurate observations are represented by empty triangles, while the more accurate ones are represented by empty circles, filled triangles and filled circle, in order of increasing accuracy (photometric weights 1 to 4).
Open with DEXTER


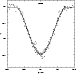  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms1383f5.eps}}\end{figure} Figure 5: V light-curve of V392 Car around the secondary minimum. Same codes as in Fig. 4.
Open with DEXTER

5.4 Parameters of the fitted light-curve

The photometric parameters of the system (Table 4) were obtained using data in the V band.

 

 
Table 4: Solution of the light-curve. $\sigma $(O-C) = 0.0062 mag.
P [J] 3.174990 $\pm$ 0.000001
i [$^\circ$] 81.89 $\pm$ 0.05
J2(V)/J1(V) 0.929 $\pm$ 0.007
L1(V) 0.527 $\pm$ 0.004
L2(V) 0.473 $\pm$ 0.004
r1 [a-1 $R_{\odot}$] 0.1149 $\pm$ 0.0005
r2 [a-1 $R_{\odot}$] 0.1132 $\pm$ 0.0005


The inclination i is well defined in spite of the partial eclipses. A small variation of the inclination significantly increases the residuals.

The ratio of surface brightnesses J2(V)/J1(V) is close to one and in good agreement with the ratio of effective temperatures.

The radii r are expressed in units of semi-major axis a of the relative orbit, thus the absolute radii can only be calculated by combining the photometric and spectroscopic solutions.

6 Physical parameters of both components

The physical parameters of V342 Car obtained from both photometric and spectroscopic data are listed in Table 5.

 

 
Table 5: Physical parameters of V342 Car.
P [J] 3.174990 $\pm$ 0.000001
T [HJD-2400000] 47999.7656 $\pm$ 0.0041
i [$^\circ$] 81.89 $\pm$ 0.05
e 0.0
a1 [$R_{\odot}$] 7.160 $\pm$ 0.023
a2 [$R_{\odot}$] 6.982 $\pm$ 0.022
a [$R_{\odot}$] 14.142 $\pm$ 0.051
M1 [$M_{\odot}$] 1.900 $\pm$ 0.024
M2 [$M_{\odot}$] 1.853 $\pm$ 0.024
R1 [$R_{\odot}$] 1.625 $\pm$ 0.030
R2 [$R_{\odot}$] 1.601 $\pm$ 0.031
Log(g)1 4.286 $\pm$ 0.017
Log(g)2 4.310 $\pm$ 0.024
$T_{\rm eff1}$ [K] 8850 $\pm$ 200
$T_{\rm eff2}$ [K] 8650 $\pm$ 200


7 V392 Car and NGC 2516

We can now discuss the membership of V392 Car in the NGC 2516 open cluster, and its belonging to the photometric Ap group.

7.1 Membership of V392 Car

The usual membership criteria are discussed below:


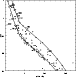  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms1383f6.eps}}\end{figure} Figure 6: Position of V392 Car (Cox 38) in the (mV, B2-V1) color magnitude diagram.
Open with DEXTER

7.2 Distance to NGC 2516

The distance of V392 Car could be derived for each of the components of the system. The method is to compare the observed luminosity with the one derived from the effective temperatures and the radii. To translate the luminosity into absolute visual magnitude, we used the bolometric correction of Flower (1996). The visual absorption AV is derived from the average colour excess of the cluster E(B-V)=0.101 (Mermilliod 1999) through the relation of Olson (1975), adopting (B-V) = 0.21 (Dachs & Kabus 1988). For all solar parameters, such as effective temperature, surface gravity and bolometric luminosity, we used the values by Cayrel de Ströbel (1996).

From the distances derived for each component of V392 Car and assuming that this binary is indeed a member of the cluster, a weighted average yields an estimate of the distance to NGC 2516. The result is $349.1\pm27.9$ pc, in good agreement with the HIPPARCOS distance d =  346+27.1-23.4 pc given by Robichon et al. (1999). Thus, our analysis of this single binary provides the distance to NGC 2516 with an accuracy similar to that of Hipparcos, i.e. about 8%.

7.3 Metallicity of NGC 2516

From the location of the components of V392 Car in the HR diagram, shown in Fig. 7, one can obtain a good estimate of the metallicity from a comparison with theoretical predictions. We have interpolated the evolutionary tracks of Schaller et al. (1992) for the empirical masses. These models are built for a metal content Z=0.020, i.e. very slightly above solar (Z=0.018). Another set of evolutionary tracks, computed for Z=0.008 (Schaerer et al. 1993), were interpolated for the same masses. Clearly, Fig. 7 shows that the metallicity of the binary is very close to solar, as far as the models are realistic. A linear interpolation leads to Z=0.018 or ${\rm [M/H]}=0.0\pm 0.1$ dex. It is interesting to compare this estimate with metallicities published in the literature for NGC 2516: ${\rm [M/H]}=-0.32\pm 0.06$ dex (Jeffries et al. 1997), ${\rm [M/H]}=-0.28$ dex (Lynga & Wramdemark 1984), ${\rm [M/H]}=-0.18\pm 0.08$ dex (Jeffries et al. 1998) and ${\rm [M/H]}=+0.06$ dex (Twarog et al. 1997). These recent estimates are all based on photometric methods, not spectroscopic ones.

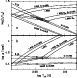  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{ms1383f7.eps}}\end{figure} Figure 7: a) Position of the components in the theoretical HR diagram. Full heavy lines: ZAMS and evolutionary tracks interpolated for the measured masses in the models of Schaller et al. (1992) for a metal content Z=0.020. Heavy broken line: isochrone for $\log t=8.15$. The thin lines are the same, but for Z=0.008 (Schaerer et al. 1993), which corresponds to ${\rm [M/H]}=-0.35$. Dotted lines: linear interpolation between models with Z=0.008 and Z=0.020 for each component. b) Same as a), but with surface gravity instead of luminosity.
Open with DEXTER

Jeffries et al. (1997) asked for an urgent detailed analysis of the chemical abundances, which become more important because of the great disagreement between the fit of ZAMS performed by Jeffries (1997, 1998) and by this analysis on one particular pair of stars. The Mermilliod (1999) correlation between MVand ${\rm [M/H]}$ is mostly deduced from the assumed metal deficiency of NGC 2516. Thus the correlation between ${\rm [M/H]}$ and $\Delta M_V$ must be further investigated. This study is based on a single system, so spectroscopic determination of the metallicity of solar type stars of NGC 2516 would be welcome to settle the question.

8 Conclusion

The case of this binary is interesting, in that both components appear to be normal stars in spite of their slow equatorial velocities. Indeed, Abt & Morrell (1995) proposed that all A stars with slow rotational velocities have abnormal spectra, while all rapidly rotating A stars have normal spectra. This view is held anew by Abt (2000). Though our data allow us to exclude an Ap peculiarity of the Sr type for V392 Car, they do not exclude some more subtle anomaly such as weak MgII $\lambda 4481$. But, in any case, any strong peculiarity of the Am or Ap type would have left its footprints in the photometric characteristics; such footprints are not observed, so any peculiarity, if present, can only be very mild. The orbital period is slightly longer than the shortest ones observed for systems hosting Am or Ap stars, and synchronism has already taken place, so this system seems to be in a very stable configuration. The question why its components have remained normal, rather than becoming Am or Ap, remains open, especially if Abt & Morrell (1995) are right. The very existence of such stars, which appear at least superficially normal although they are slow rotators, suggests that slow rotation is not a sufficient condition to make peculiar stars. Some additional initial condition seems necessary, which might be linked with the presence and structure of magnetic fields at the surface of the star, since such fields have been found in some Am stars (Mathys & Lanz 1990; Lanz & Mathys 1993; Savanov & Savelyeva 1996).

Acknowledgements
Preliminary studies of the system V392 Car had been done by two students, P. Sturzenegger and E. Schoepfer, in the course of their diploma theses. We thank the Swiss National Science Foundation for its support and ESO for the allocation of two nights centered on the quadratures. We also thank Dr. Noël Cramer for complementary photometric measurements, Dr. Michel Burnet for a spectroscopic observation with CORALIE and Dr. Willy Benz for a tentative observation with CORAVEL.

References

 

Copyright ESO 2001