A&A 374, 337-347 (2001)
DOI: 10.1051/0004-6361:20010724
G. Bodo1 - S. Poedts2,![]() - A. Rogava3,4,
- A. Rogava3,4,![]() - P. Rossi1
- P. Rossi1
1 - Osservatorio Astronomico di Torino, Strada
dell'Osservatorio 20, 10025 Pino Torinese, Italy
2 - Centre for Plasma Astrophysics, K.U. Leuven,
Celestijnenlaan 200B, 3001 Heverlee, Belgium
3 - Dipartimento di Fisica Generale,
Universitá degli Studi di Torino, Via Pietro Giuria 1,
10125 Torino, Italy
4 - Abdus Salam International Centre for Theoretical Physics, 34014
Trieste, Italy
Received 28 March 2001 / Accepted 17 May 2001
Abstract
The phenomenon of Shear Induced wave Transformations
(SITs) (Chagelishvili et al. 1996), is a common feature of flows,
sustaining n>1 mode of wave motion. Until now this "nonmodal''
phenomenon was described only in terms of the time evolution of
individual Fourier harmonics of perturbations in the space of wave
numbers (k-space). In this paper we present the results of
the first, direct numerical simulations of SITs, giving
compelling evidence in favor of the robust and recognizable
character of SITs. The importance of these results for an
understanding of physical processes in astrophysical shear flows
is pointed out. Namely, concrete astrophysical situations (solar
plasma flows, galactic gaseous disks, accretion disks and
accretion-ejection flows), where
this approach may help to shed some light on observational
appearances of related objects, are indicated and discussed.
Key words: magnetohydrodynamics (MHD) - waves
In astrophysics we are frequently challenged to consider physical processes in shear flows: flows of astrophysical plasmas with spatially inhomogeneous rates. Recent studies of the physics of shear flows have revealed a number of peculiar, shear-induced processes, that might be observationally important in the astrophysical context (see Rogava et al. 2000 and references therein). Therefore, the study of astrophysical shear flows (ASF) is important both from physical and astronomical points of view. For the physical theory, these studies could provide ample range of observational tests, since ASF are so diverse in terms of physical conditions and a spectrum of physical parameters. For astronomy, these studies could possibly provide a clue to the understanding of observational appearances of related astronomical objects.
In many cases of practical importance ASF maintain different modes
of collective behavior: vortices, waves and instabilities. When a
flow sustains more than one mode of collective behavior, for
instance two or more different kinds of wave modes, then the
velocity shear may couple these waves with each other and may
lead to their mutual transformation. Originally, this effect was
discovered for a magnetohydrodynamic (MHD), two-dimensional (2-D)
shear flow: it was shown that the shear couples the slow
magnetosonic waves (SMWs) and the fast magnetosonic waves (FMWs)
and that under favorable conditions, namely, when the speed of
sound ![]() and the Alfvén speed
and the Alfvén speed ![]() are of the same order of
magnitude, the coupling leads to the efficient reciprocal
transformations of these waves (Chagelishvili et al. 1996).
are of the same order of
magnitude, the coupling leads to the efficient reciprocal
transformations of these waves (Chagelishvili et al. 1996).
It was apparent from the very beginning that the SITs may easily
occur in a number at astrophysical situations and may have diverse
and characteristic observational appearances. One of the first
attempts of astrophysical application was related to pulsar
physics. Namely, it was shown that SITs couple Langmuir
oscillations with electromagnetic waves in relativistic
electron-positron plasmas and the process was suggested (Mahajan
et al. 1997) as an alternative mechanism for the generation of
pulsar radio emission. Later it was shown that in the solar wind
there exist favorable conditions for the mutual transformation of
MHD waves and it was argued that the observed large-amplitude
Alfvén waves (AWs) in the solar wind may be generated as a result
of the SITs of photospheric SMWs and FMWs (Poedts et al. 1998). It
was surmised that the SITs may play an important role in the
generation of MHD waves, coronal heating and the acceleration of
the solar wind (Rogava et al. 2000). Another prominent
astrophysical example of a magnetized ASF is a galactic gaseous
disk that sustains both slow (
![]() kms-1) and fast
(
kms-1) and fast
(
![]() kms-1) MHD density waves (Fan & Lou 1996).
Theoretical studies imply (Fan & Lou 1997; Rogava et al. 1999)
that these waves may be coupled by the shear and may transform
into each other.
kms-1) MHD density waves (Fan & Lou 1996).
Theoretical studies imply (Fan & Lou 1997; Rogava et al. 1999)
that these waves may be coupled by the shear and may transform
into each other.
The mathematical aspect of the SITs is nontrivial - it
belongs to the so called "nonmodal processes''. These
phenomena are not accessible by means of the traditional normal
modes approach because of a fundamental quality of shear flow
systems: non-self-adjointness, or "non-normality" (Trefethen et al. 1993) of their linear dynamics. These systems exhibit some
interesting physics on finite time scales associated with
existing modes of collective behavior and/or appearance
of completely new processes
(see, e.g., Rogava et al. 2000 and references therein).
The so called nonmodal
approach became a convenient instrument for the disclosure of
these phenomena (Mahajan & Rogava 1999; Rogava et al. 2000). This
method allows one to reduce the original system of partial
differential equations for physical perturbation variables
F(x,y,z;t) to the set of non-autonomous ordinary differential
equations (ODEs) for the functions
![]() -
amplitudes of individual Fourier harmonics corresponding to the
Fourier decomposition of perturbations.
-
amplitudes of individual Fourier harmonics corresponding to the
Fourier decomposition of perturbations.
However, an important disadvantage of all "nonmodal" schemes is that although they help to disclose new phenomena, providing us with basic understanding of a temporal span of involved processes; they do not give us any information about the spatial appearance of these phenomena. We do know that SITs are taking place in shear flows, but we still know next to nothing about the appearance of these phenomena in real physical space. This is a non-trivial step ahead, because, when we talk about real space, we have to consider the superposition of many Fourier components that undergo the process of mode conversion at different moments in time and we have also to take into account the effects of wave propagation. Therefore, before addressing in detail the concrete situations pertaining to the different astrophysical contexts described above, we think that an essential step is to consider an ideal case in which we can examine whether mode transformation can indeed be observed also in real space and for which we can develop the tools for analysing the process. This is the aim of the present paper and in the next section we describe a simple 2-D MHD setup, corresponding to Chagelishvili et al. (1996) where SITs were originally identified, which allows as to study mutual transformations of SMWs and FMWs. We write down the system of partial differential equations for the perturbations of physical variables and describe briefly the "nonmodal" evolution of the amplitudes of individual Fourier harmonics. The third section contains a description of the numerical simulation of the initial set of partial differential equations. Detailed analysis of the results shows that the initial compact "package'' of SMWs undergoes an efficient transformation into FMWs. The latter waves manage to persist and even augment their strength despite the presence of nonzero viscous dissipation in the system. The latter fact clearly indicates that the transformed FMWs, in full accordance with the nonmodal behaviour of Fourier amplitudes, efficiently extract energy from the mean flow.
In the final section we discuss the importance of these results that give the first direct and firm evidence, obtained by means of numerical simulations, in favor of the efficiency of SITs. Possible applications of these results in astrophysics are outlined and critically discussed. We think that solar plasma flows, galactic gaseous disks, accretion-ejection flows and pulsar magnetospheric plasmas are astrophysical instances where one may look for SITs and their observational appearances.
We consider a standard MHD system:
| (1) |
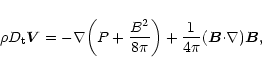 |
(2) |
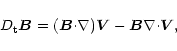 |
(3) |
| (4) |
We study the evolution of 2D waves in compressible, unbounded
parallel flow with uniform velocity shear contained in an external
regular magnetic field
![]() .
The mean
velocity field is given by:
.
The mean
velocity field is given by:
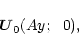 |
(5) |
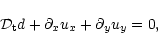 |
(6) |
| (7a) |
| (7b) |
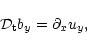 |
(8) |
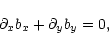 |
(9) |
The set of Eqs. (6)-(9) forms our basic system of equations.
Before employing nonmodal techniques, we can derive from (6)-(9),
still staying in the "physical space'', a pair of second order
partial differential equations, which describes the coupling
between the SMWs and the FMWs. Taking into account (6)-(9) we
easily get:
| (10) |
![\begin{displaymath}{\cal
D}_{\rm t}^2b_{y}-[C_{\rm A}^2\partial_x^2+
(C_{\rm s}^2+C_{\rm A}^2)\partial_y^2]b_y=-C_{\rm s}^2\partial_y{\Psi},
\end{displaymath}](/articles/aa/full/2001/28/aa1313/img30.gif) |
(11) |
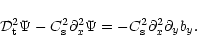 |
(12) |
At this stage we can employ standard "nonmodal" approach (see
e.g., Chagelishvili et al. 1996).
For the flow described by Eq. (5) the only nonzero component of the shear
matrix (Mahajan & Rogava 1999) in this case is
![]() and, therefore, kx stays constant while the transverse
component of the wave vector varies linearly in time:
and, therefore, kx stays constant while the transverse
component of the wave vector varies linearly in time:
| Ky(t)=ky - Akxt. | (13) |
| (14a) |
| (14b) |
| (15a) |
| (15b) |
| (16a) |
| (16b) |
| (17a) |
| (17b) |
| (17c) |
![\begin{figure}
\par\resizebox{8.4cm}{!}{\includegraphics[angle=90]{MS1313f1.eps}} \end{figure}](/articles/aa/full/2001/28/aa1313/Timg48.gif) |
Figure 1:
The evolution of the density (solid line) and the longitudinal
(bx) magnetic field (dashed line) perturbations. The values of
parameters are: ky/kx=3,
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{8.1cm}{!}{\includegraphics[angle=90]{MS1313f2.eps}} \end{figure}](/articles/aa/full/2001/28/aa1313/Timg49.gif) |
Figure 2: The evolution of the total energy of perturbations (solid line) plotted together with the graphs for the time-dependent dispersion curves of the SMW (dashed line) and the FMW (dashed-dotted line) effective normal frequencies. The values of the parameters are the same as for Fig. 1. |
| Open with DEXTER | |
In order to illustrate how this method of the initial
separation of wave modes works we present here an example of the
solution when ky/kx=3,
![]() ,
and
,
and
![]() .
Figure 1 displays the evolution of the density (solid line) and
the longitudinal (bx) magnetic field (dashed line)
perturbations. It is clear that the initial perturbation is a pure
SMW with phase difference being almost
.
Figure 1 displays the evolution of the density (solid line) and
the longitudinal (bx) magnetic field (dashed line)
perturbations. It is clear that the initial perturbation is a pure
SMW with phase difference being almost ![]() between these two
oscillations. This "anticorrelation" of the density and the
magnetic field perturbations is a "bona fide'' signature of the SMW
(Fan & Lou 1997) and helps to distinguish the SMW from the FMW. The
latter MHD mode, on the contrary, is characterized by an exact
correlation between these oscillations. Obviously Fig. 1
clearly shows that around the time
between these two
oscillations. This "anticorrelation" of the density and the
magnetic field perturbations is a "bona fide'' signature of the SMW
(Fan & Lou 1997) and helps to distinguish the SMW from the FMW. The
latter MHD mode, on the contrary, is characterized by an exact
correlation between these oscillations. Obviously Fig. 1
clearly shows that around the time
![]() a
drastic change of the oscillation mode occurs and the initial pure
SMW transforms into the FMW.
a
drastic change of the oscillation mode occurs and the initial pure
SMW transforms into the FMW.
One of the notable features of the SITs is that in the case of
sufficiently low shearing rates (
![]() )
the temporal evolution
of the perturbations stays adiabatic both before and after the
transformations. This is related to the fact that the
shear-induced change of the oscillation frequencies is a
much slower process than the oscillation time scales
associated with both modes. This is illustrated by
Fig. 2. The
)
the temporal evolution
of the perturbations stays adiabatic both before and after the
transformations. This is related to the fact that the
shear-induced change of the oscillation frequencies is a
much slower process than the oscillation time scales
associated with both modes. This is illustrated by
Fig. 2. The ![]() graph is plotted together with
the graphs for the time-dependent dispersion curves of the SMW
(dashed line) and the FMW (dashed-dotted line) effective normal
frequencies. The energy evolution is adiabatic, following
the SMW/FMW dispersion curve before/after the transformation.
graph is plotted together with
the graphs for the time-dependent dispersion curves of the SMW
(dashed line) and the FMW (dashed-dotted line) effective normal
frequencies. The energy evolution is adiabatic, following
the SMW/FMW dispersion curve before/after the transformation.
The theory of SITs in Fourier space, summarized in the previous Sections, gives us important information on the process. However, a complete and vivid picture of the phenomenon can be obtained by examining the behavior of the solutions in real space for a wave-packet - superposition of different Fourier harmonics.
In this section we adopt this perspective and we approach the problem with two different methods: by a numerical solution of the full set of MHD equations and by a semi-analytical approach based on asymptotic expansions (Whitham 1974). These two methods will be described in the next two subsections.
We have solved numerically the fully nonlinear viscous and resistive MHD equations by using a central differencing scheme with fourth order spatial accuracy.
As an initial condition, we superimpose on the basic shear flow (5)
a wave packet, that we define in k-space centered
around a value
(kx(0) = kx0, ky(0) = ky0). The form of the
perturbations for the different physical variables in real space
can be then obtained through the inverse Fourier transform and
expressed in the following form:
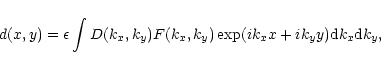 |
(18a) |
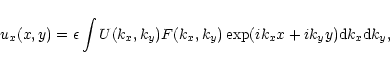 |
(18b) |
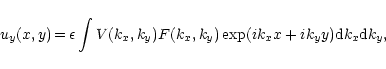 |
(18c) |
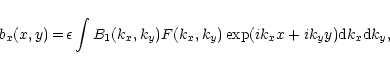 |
(18d) |
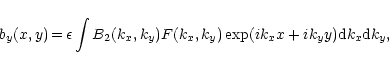 |
(18e) |
The system we are considering does not have any characteristic scale,
we have only the constraint that the characteristic length scale of
perturbations
![]() has to be much less than the size of
the computational domain L. This is because we want to avoid the
influence of domain boundaries on the shear-induced processes,
which we are intending to simulate. We have therefore chosen an arbitrary
unit of length and in this unit we have fixed
kx0 = 2 and
ky0 = 6,
so that the central wavenumber of the wave-packet corresponds
to the case we have presented in the previous section.
Our unit of time will then be the sound crossing time over the
unit of length. The Reynolds and magnetic Reynolds numbers are both equal
to 500. The computational domain, defined by
(-L < x < L, -L < y < L),
with L = 40, is divided in
has to be much less than the size of
the computational domain L. This is because we want to avoid the
influence of domain boundaries on the shear-induced processes,
which we are intending to simulate. We have therefore chosen an arbitrary
unit of length and in this unit we have fixed
kx0 = 2 and
ky0 = 6,
so that the central wavenumber of the wave-packet corresponds
to the case we have presented in the previous section.
Our unit of time will then be the sound crossing time over the
unit of length. The Reynolds and magnetic Reynolds numbers are both equal
to 500. The computational domain, defined by
(-L < x < L, -L < y < L),
with L = 40, is divided in
![]() grid points and the
boundary conditions are periodic along the direction of the basic
flow and outflow in the transverse direction.
grid points and the
boundary conditions are periodic along the direction of the basic
flow and outflow in the transverse direction.
We can follow the propagation of a wave packet using the theory of ray tracing
described by Whitham (1974) and Lighthill (1978),
under the assumption that the wavelengths are much
smaller than the scale of variation of the basic flow. In this case we can
describe the solution in terms of a slowly varying wavetrain, writing each
quantity in the form
![\begin{displaymath}{\cal A}(\vec{r}, t) \exp \left[ i \theta (\vec{r}, t) \right],
\end{displaymath}](/articles/aa/full/2001/28/aa1313/img63.gif) |
(19) |
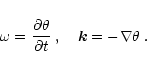
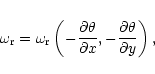
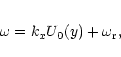
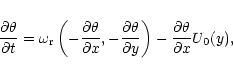
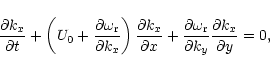 |
(20) |
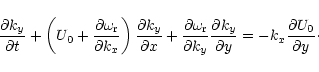 |
(21) |
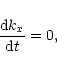 |
(22) |
 |
(23) |
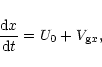 |
(24) |
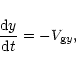 |
(25) |
This method allows us to capture the propagation properties of FMWs and SMWs but not their transformation, since the solutions of the previous section show that the transformation process occurs quite abruptly when ky = 0, thus violating the adiabatic assumption made in the derivation above. Following the wave packet we have, therefore, assumed that each wave number initially starts as a FMW or a SMW (appropriate for the considered case) and then, during the propagation, when ky = 0 it switches to the other kind of wave.
The study of the dynamics of a single Fourier harmonic, described in
Sect. 2, allows us to analyze the process of mode conversion, but cannot
capture the effects related to the wave propagation and their interplay
with the process of conversion. This can only be achieved by studying the
behavior of solutions in real space and in this Section we will indeed
follow, as an example, the evolution of a wave packet, analyzing
propagation and conversion effects. As discussed in Sect. 3,
this has been done through a numerical solution of the full system
of MHD equations. The initial conditions for the wave packet are
described in Sect. 3. Initially, as we have discussed, the
packet is composed mainly of slow waves and the amplitude of the
perturbation of the x component of velocity is
![]() (small enough to consider it linear).
Saying "mainly" we want to emphasize that the method of
initial preparation of "pure" normal modes is valid only approximately. It
is exact only for oscillatory systems with constant characteristics, while
the parameters of our system vary adiabatically. Therefore,
the initial wave package, "baked" according to the approximate "recipe", will
be mainly a package of SMWs with a small dash of FMWs.
Since group velocities
of these two wave modes are quite different, this initial FMW impurity
will drift
much faster than the bulk of the package, composed of SMWs, and the two of them
will be spatially separated.
(small enough to consider it linear).
Saying "mainly" we want to emphasize that the method of
initial preparation of "pure" normal modes is valid only approximately. It
is exact only for oscillatory systems with constant characteristics, while
the parameters of our system vary adiabatically. Therefore,
the initial wave package, "baked" according to the approximate "recipe", will
be mainly a package of SMWs with a small dash of FMWs.
Since group velocities
of these two wave modes are quite different, this initial FMW impurity
will drift
much faster than the bulk of the package, composed of SMWs, and the two of them
will be spatially separated.
![\begin{figure}
\par {\includegraphics[angle=90,width=16.4cm]{MS1313f3.eps} }
\end{figure}](/articles/aa/full/2001/28/aa1313/Timg80.gif) |
Figure 3: Real-space evolution of initial (predominantly SMW) perturbation package, given by eight panels for eight different moments of time: t = 0, 8, 16, 24, 32, 40, 48 and 56, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=90,width=16.7cm]{MS1313f4.eps} }
\end{figure}](/articles/aa/full/2001/28/aa1313/Timg81.gif) |
Figure 4: The shapes of the wave-packets, calculated by means of analytical approximation, at the same moments of time, for which the numerical solution is displayed in Fig. 3. Different tonalities of grey are used to distinguishing between: SMW transformed into FMW (the darkest), SMW that stays SMW (lighter), FMW transformed into SMW (still lighter), and FMW staying FMW (the lightest). |
| Open with DEXTER | |
The general evolution can be seen in Fig. 3, where we show images of the distribution of the y-component of velocity at eight different times. From the figure, we can see that initially the wave packet splits in four parts. The two central parts slowly propagate along the positive and negative x-direction. These two packets, as they propagate, also rotate in the clockwise direction. The rotation of the packet is associated with the drift of ky induced by the shear and discussed in the previous section (see Eqs. (22)-(23)). The group velocity for slow waves with wavenumber equal to the central value of the packet is mainly directed along the x-direction and this explains the propagation of the packet in this direction. The Fourier harmonics composing the packet evolve separately, each one follows its ky-drift described by Eq. (23) and, at different times, they will reach the value ky = 0 around which transformation to fast waves occurs. Fast waves have a large component of the group velocity along the y-direction and, therefore, as soon as transformation begins to occur, around t = 30, the packet begins to get an elongated component in the y-direction. The fast waves propagating along the y-direction are also dragged forward for positive y (or backward for negative y) by the increasing x-velocity component of the shear flow and thus the packet takes a curved shape (see panels 5-6-7-8 in Fig. 3).
In panel 2-3, alongside the slow packets that propagate along the x-direction, we observe also the presence of two other packets with a higher y-component of their propagation velocity. Their propagation can also be followed in the successive panels. The presence of these additional packets is due to the fact that, as we have discussed, the initial conditions we have imposed do not correspond exactly to pure slow waves but contain a small mixture of fast waves.
The changes in the shape of the wave-packet can be also captured
using the ray-tracing approach described in the previous section. We start
assuming that initially, at t = 0, all the wave number
components of the packet are concentrated at the origin. Then we
follow the propagation of each wave number according to
Eqs. (22)-(25), and the shape of the packet at a given time is
reconstructed from the position of all wave numbers at that time.
We assume that initially in the wave-packet both slow
and fast waves are present and we follow their propagation and their mutual
transformations. Initially, the propagation velocities for each
wave number of the slow and fast components are given by
Eqs. (24)-(25) where ![]() is taken to be the slow or the
fast group velocity for that wave number, respectively.
is taken to be the slow or the
fast group velocity for that wave number, respectively.
As time progresses, Eq. (23) shows that ky changes its value and, when ky = 0, we assume that the transformation of slow to fast or of fast to slow waves may occur (as discussed above). Accordingly, hereafter, the group velocity is switched from slow to fast or from fast to slow. The transformation, however, is not complete. Slow waves are not totally transformed to fast waves or, conversely, fast waves are not totally transformed to slow waves. Therefore, we have followed also the propagation of slow and fast waves that do not undergo the transformation process. In Fig. 4 we show the shapes of the wave-packets at the same moments of time, for which the numerical solution is displayed in Fig. 3, so that a comparison between the exact numerical solution and the analytical approximation can be performed. Originally, when transformation has not yet occurred, we observe only the presence of two pairs of wave-packets (fast and slow waves), but, from the time when transformation begins to occur, we observe the presence of four pairs of wave packets (slow transformed into fast, slow that stays slow, fast transformed into slow and fast that stays fast). To distinguish between the different wave packets we have used for each of them a different tonality of grey: the darkest for slow transformed into fast, lighter for slow that stays slow, still lighter for fast transformed into slow and the lightest for fast that stays fast.
In comparing the numerical and analytical solutions, we have to keep in mind that we have somewhat different initial conditions, since for the analytical solution we assume essentially a point source at t = 0. However, we can see that the characteristics of the solution are captured quite well by the analytical approach. The comparison also allows a better interpretation of the numerical results since it enables the identification of the different components. For example, we can notice that in the numerical solution it is also possible to observe the transformation of the fast wave-packets in slow wave-packets.
![\begin{figure}
\par {\includegraphics[angle=90,width=17.1cm]{MS1313f5a.eps} }
...
...e*{6mm}
{\includegraphics[angle=90,width=17.1cm]{MS1313f5b.eps} }
\end{figure}](/articles/aa/full/2001/28/aa1313/Timg83.gif) |
Figure 5: The distribution of the y-component of the perturbed velocity for four different times, t = 5, 20, 35, 50, respectively. The distribution at each time (shown in the first column) is decomposed in its slow (second column) and fast (third column) components. The arrows and letters show the points where we have taken the cuts that are shown in Fig. 6. |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[angle=90,width=18cm]{MS1313f6.eps} }
\end{figure}](/articles/aa/full/2001/28/aa1313/Timg84.gif) |
Figure 6: Cuts of the density and Bx perturbations, in the positions and along the directions shown by the arrows marked in Figure 5. In the positions of slow waves there is a substantial phase difference between density and magnetic field perturbations (see panels A, B, C, E), while at the location of fast waves the perturbations are almost in phase (see panels D, F). |
| Open with DEXTER | |
The firm evidence of the occurrence of the SITs is demonstrated by Fig. 5, where we show images of the distribution of the y-component of the perturbed velocity for four different times. The distribution at each time (shown in the first column) has been decomposed in to its slow and fast components and these are shown respectively in the second and third column of images of the figure. The decomposition has been obtained first projecting the Fourier components of the perturbation onto the eigenvectors for the slow and fast modes and then transforming back in real space the slow and fast components separately. We can see that initially the four wave-packets can be easily separated in their slow and fast components. At later times, we see that the elongated arcs extending in the y direction can be effectively identified as fast waves and a remnant of the slow mode is still found slowly "creeping" in the x direction.
Another strong signature of the SITs - drastic change of the phase characteristics of MHD waves (Fan & Lou 1997; Rogava et al. 1999) before and after the transformation - is illustrated in Fig. 6, where we plot cuts of the density and Bx perturbations, in the positions and along the directions shown by the arrows marked in Fig. 5. From the plots we can see that in the positions of slow waves we indeed find a substantial phase difference (opposition of phases) between density and magnetic field perturbations, in complete accordance with the theoretical expectations (see panels A, B, C, E). While at the location of fast waves, density and magnetic field perturbations are almost in phase (see panels D, F).
In Fig. 7 we show the behavior of the total perturbation energy defined as
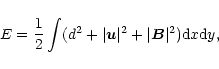 |
(26) |
Several years ago "nonmodal" study of MHD perturbations led to the discovery of velocity shear-induced wave transformations (SITs). This phenomenon, despite its linear nature, was suspected to be quite persistent and universal. However, direct numerical simulations that could confirm these expectations, could display SITs explicitly and could show their appearance within real physical space, were dramatically lacking.
In this article we report the first real-space simulations of the SITs. We found that the effect is indeed robust - it persists and it is strongly pronounced even in the presence of the nonzero dissipation. This allows us to assume that in real shear flows - laboratory MHD devices, terrestrial and astrophysical situations - this effect will not be obliterated by the presence of other physical phenomena.
Where, in astrophysics, could we expect to observe manifestations of the SITs? Below we discuss three classes of ASF - solar plasma flows, galactic gaseous disks and accretion-ejection flows - where theoretical modeling of these objects and the interpretation of their observational features might lead to the identification of the SITs.
The solar atmosphere is known to be particularly rich in diverse
kinds of complicated oscillatory, transient or sustained motions
throughout different kinds of flow patterns within the solar
photosphere, chromosphere, transition region and corona (Pneuman
& Orrall 1986; Thomas 1996). Solar plasma flows of different
nature and geometry can sustain all three kinds of MHD waves, but
only Alfvén waves seem to be capable of making the whole trip
through the chromosphere, penetrate through the transition region
and reach the low coronal layers. Recent observational results
(Grall et al. 1996) indicate that the acceleration of the polar
wind is almost completed by
![]() ,
implying that the
acceleration of the solar wind and the heating of the solar corona
occur in approximately the same region, where plasma motions,
coupled with magnetic fields, are having significant impact on
physical processes.
,
implying that the
acceleration of the solar wind and the heating of the solar corona
occur in approximately the same region, where plasma motions,
coupled with magnetic fields, are having significant impact on
physical processes.
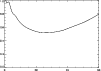 |
Figure 7: Temporal evolution of the total perturbation energy normalized to its initial value. |
| Open with DEXTER | |
Therefore, it is reasonable to admit that solar plasma flows might exhibit SITs (Poedts et al. 1998). Recently it was argued (Rogava et al. 2000) that FMWs, produced by high-frequency photospheric motions within isolated intense magnetic flux tubes, could become subject to shear-induced FMW-AW transformations in the chromosphere. The Alfvén waves, being weakly dissipative, and channelized by spicules, could penetrate through the transition region and reach those "heights" of the solar corona, where the main bulk of the coronal heating and the solar wind acceleration processes take place. The pressure of these waves, as well as compressional damping of "secondary" fast waves (the outcome of the opposite (AW-FMW) transformation processes) might contribute to the acceleration of the solar wind.
Now, having first encouraging results of direct MHD simulations, showing robust character of SITs, we could develop a detailed, 3-D numerical MHD model and check whether the regime of shear-induced MHD wave oscillations can indeed be realized in the solar wind (Poedts et al. 1998), in the inner corona and in various kinds of solar flux tube flows (Rogava et al. 2000). Can SITs help to generate large amplitude Alfvén waves penetrating through the transition region? The analysis of this problem involves a quite broad program, because it requires one to perform high-resolution simulations of the SITs with a properly chosen equilibrium setup, boundary conditions and realistic values of the solar plasma physical parameters.
Another challenging task would be to see how SITs behave? in galactic gaseous disks. It is believed that
shear-induced processes play a significant role in the generation
and maintenance of the galactic MHD density waves for gas-rich
spiral galaxies (Fan & Lou 1996, 1997), where physical conditions
seem to be favorable for the SITs. Thermal and magnetic energy
densities are of comparable magnitude: for typical nearby galaxies
the Alfvén (![]() )
and sound (
)
and sound (![]() )
speeds are comparable and
fall in the range
)
speeds are comparable and
fall in the range ![]() 10-20 km s-1. This supports the
existence of both fast (
10-20 km s-1. This supports the
existence of both fast (![]() 20 km s-1) and slow (
20 km s-1) and slow (![]() 0.2 km s-1) MHD density waves in such a disk system. Phase
characteristics of mass density and azimuthal magnetic field
perturbations help to distinguish galactic MHD density waves from
one another (Fan & Lou 1997). In particular, for a FMW the
enhancement of the surface density and parallel magnetic field
are more or less in phase, while for a SMW there is a significant
(
0.2 km s-1) MHD density waves in such a disk system. Phase
characteristics of mass density and azimuthal magnetic field
perturbations help to distinguish galactic MHD density waves from
one another (Fan & Lou 1997). In particular, for a FMW the
enhancement of the surface density and parallel magnetic field
are more or less in phase, while for a SMW there is a significant
(
![]() )
phase difference between these perturbations. The
"Whirlpool galaxy" M 51, for instance, has been identified as a
clear case of a galactic disk with FMWs, while in NGC 6946 coherent
large-scale magnetic spiral arms are located between the
optical spiral arms leading us to believe that here we observe SMWs.
Moreover, there is at least one example of a spiral galaxy where
optical and radio continuum observations indicate the presence of
both kinds of MHD density waves! This is the galaxy IC 342,
where observations show the presence of SMWs in the inner (rigidly
rotating) region of the galactic gaseous disk and FMWs in the outer
(differentially rotating) region. Recently it was argued (Poedts
& Rogava 2000) that this galaxy features the very first
observational evidence of the SITs. Real-space simulations, with
due consideration of the rotation curve and all its physical
characteristics, taking into account the influence of Coriolis
forces and the self-gravity, might result in the numerical spatial
portrait of the wave evolution, which could be compared with
existing observational data about magnetic field structure of this
galaxy.
)
phase difference between these perturbations. The
"Whirlpool galaxy" M 51, for instance, has been identified as a
clear case of a galactic disk with FMWs, while in NGC 6946 coherent
large-scale magnetic spiral arms are located between the
optical spiral arms leading us to believe that here we observe SMWs.
Moreover, there is at least one example of a spiral galaxy where
optical and radio continuum observations indicate the presence of
both kinds of MHD density waves! This is the galaxy IC 342,
where observations show the presence of SMWs in the inner (rigidly
rotating) region of the galactic gaseous disk and FMWs in the outer
(differentially rotating) region. Recently it was argued (Poedts
& Rogava 2000) that this galaxy features the very first
observational evidence of the SITs. Real-space simulations, with
due consideration of the rotation curve and all its physical
characteristics, taking into account the influence of Coriolis
forces and the self-gravity, might result in the numerical spatial
portrait of the wave evolution, which could be compared with
existing observational data about magnetic field structure of this
galaxy.
Yet another broad class of ASF, where SITs can be modeled numerically, are accretion-ejection flows. The possible role of SITs in the generation of ``mixed'' MHD turbulence in accretion disks has already been indicated (Rogava et al. 2000). Numerical models may help to understand what role is played by the SITs in the generation of the disk wind and the appearance of ejectional outflows in different kinds of accretion-ejection systems (Balbus & Hawley 1998; Ferrari 1998).
Therefore, apart from the general importance of the obtained results, which constitute the first, real-space simulations and verification of the SITs, they may serve as a steppingstone for the further, comprehensive study of shear-induced phenomena in different astrophysical situations. The attractive advantage of the real-space simulations in the astrophysical context is that they are much closer to the real observational picture than the analysis of the same phenomena in the space of wave numbers. In this way we may come much closer to the interpretation and understanding of some puzzling observational features and appearances of related astronomical objects.
Acknowledgements
Our work was supported, in part, by the INTAS grant No. 97-0504. Andria Rogava wishes to thank Abdus Salam International Centre for Theoretical Physics and Universitá degli Studi di Torino for supporting him, in part, through the Regular Associate Membership Award and the Assegno di Ricerca A02.070./99, respectively. The calculations have been performed on the Cray T3E at CINECA in Bologna, Italy, thanks to the support of CNAA.
In order to excite "pure'' modes in a coupled linear oscillatory
system with two degrees of freedom, described by (16), one needs
to calculate fundamental (normal) frequencies for t=0, given by
the standard expressions (Magnus 1976):
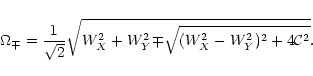 |
(A.1) |
When coefficients are constant, the general solution of (16) is a
certain mixture of the normal modes:
| (A.2a) |
| (A.2b) |
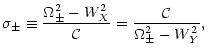 |
(A.3) |
From these expressions we see that the system exhibits simple
harmonic motion with one of the fundamental (normal) frequencies
(![]() or
or ![]() )
when either X+ or X- is equal to
zero. It immediately follows that:
)
when either X+ or X- is equal to
zero. It immediately follows that:
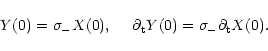 |
(A.4) |
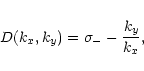
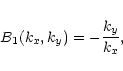
![\begin{displaymath}F(k_x, k_y) =
\left\{
\begin{array}{ll}
\textrm{atan($\xi$...
... [4pt]
0 &\quad \hbox{if} \;\;\xi < 0
\end{array} \right. ,
\end{displaymath}](/articles/aa/full/2001/28/aa1313/img114.gif) |
(A.5) |
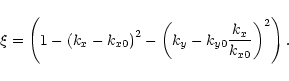 |
(A.6) |