A&A 374, 243-249 (2001)
DOI: 10.1051/0004-6361:20010728

Apsidal motion in eccentric eclipsing binaries:
TV Ceti and V451 Ophiuchi[*]

M. Wolf 1 - R. Diethelm 2 - K. Hornoch 1


1 - Astronomical Institute, Charles University Prague, 180 00 Praha 8, V Holesovickách 2, Czech Republic
2 - Astronomical Institute, University of Basel, Venusstrasse 7, 4102 Binningen, Switzerland

Received 6 March 2001 / Accepted 21 May 2001

Abstract
Several new times of minimum light recorded with photoelectric means have been gathered for two bright eccentric eclipsing binaries TV Cet ( $P = 9\hbox{$.\!\!^{\rm d}$ }1, e = 0.055$) and V451 Oph ( $P = 2\hbox{$.\!\!^{\rm d}$ }2, e = 0.013$). Analysis of all available eclipse timings of TV Ceti has revealed a small motion of the line of apsides of $\dot{\omega} = 0.000\,30\, \pm\, 0.000\,08$ deg cycle-1, corresponding to an apsidal period of $U = 30\,000\, \pm\, 8\,000$ years. The contribution from the general relativity effects is dominant ( $\dot{\omega}_{\rm rel} / \dot{\omega} \sim 80 \% $). In this system, the third body on an eccentric orbit with a period of 28.5 years is also predicted. The more precise values for the apsidal motion elements were computed for V451 Oph, where apsidal motion with a period of $170 \pm 5$ years was confirmed. The corresponding internal structure constants log k2 were derived.

Key words: stars: binaries: eclipsing - stars: individual: TV Cet - stars: individual: V451 Oph - stars: fundamental parameters - relativity


1 Introduction

Eclipsing binaries are excellent laboratories for studying a wide variety of processes in stellar astrophysics. Their usefulness extends far beyond their textbook role in the determination of stellar masses and radii. The study of apsidal motion in detached eclipsing binary systems with eccentric orbit is known as an important source of information for the stellar internal structure as well as the possibility of verification of general relativity. Suitable objects for this research were recently collected by Giménez (1994).

In this paper, we report new results for our observational project initiated in 1993 with the main purpose of monitoring eclipsing binaries with eccentric orbits, see also Wolf et al. (1999) or Wolf (2000). In this paper, we compare observational data of apsidal motion rates for two eclipsing systems with significant relativistic contribution. The two relatively bright equatorial objects, TV Cet and V451 Oph, are analysed here. V451 Oph is a well studied early-type eclipsing binary, whose orbit has been known to be eccentric and to exhibit apsidal motion. On the other hand, TV Ceti, due to its rather long orbital period, is a rarely investigated system of similar brightness.


 

 
Table 1: New precise times of minimum light.

System

 JD Hel.- Error Epoch Method Reference
  2400000 [day]   Filter Observatory

TV Cet		 46687.8088* 0.0093 549.5 pe, R Caton & Hawkins (1987)
  47147.58576 0.00022 600.0 pe, V Caton et al. (1989)
  47566.338 0.001 646.0 pe, B Diethelm (1989)
  48135.2339 0.0020 708.5 pe, H Hipparcos
  48622.3207 0.0020 762.0 pe, B Diethelm (1992)
  50470.2868* 0.0004 965.0 CCD, - Agerer & Hübscher (1998)
  51421.5165 0.0003 1069.5 pe, UBV this paper, SAAO
  51776.544 0.001 1108.5 CCD, R this paper, Ondrejov
  51899.5004 0.0001 1122.0 CCD, R this paper, Lelekovice
           
V451 Oph 46210.530 0.002 147.5 pe, B Diethelm (1985)
  46298.392 0.002 187.5 pe, B Diethelm (1985)
  47307.73282 0.00035 647.0 pe, V Caton et al. (1989)
  47437.3303 0.000 706.0 pe Isles (1991)
  47654.79386 0.00028 805.0 pe, V Caton et al. (1989)
  47696.5275 0.000 824.0 pe Isles (1992)
  48108.3891 0.0005 1011.5 pe, B Diethelm (1990)
  48476.3240 0.000 1179.0 pe, BV Isles (1997)
  48499.3838 0.0008 1189.5 pe Blättler (1992)
  48655.342 0.002 1260.5 pe, H Hipparcos
  49560.3397 0.0004 1672.5 pe, UBV Müyesseroglu et al. (1996)
  51415.3614 0.0003 2517.0 pe, BV this paper, SAAO
  51773.4089** 0.0006 2680.0 CCD, - this paper, Metzerlen
  51774.5105 0.0001 2680.5 CCD, R this paper, Lelekovice
  51806.3563 0.0001 2695.0 CCD, R this paper, Lelekovice

Notes: * recalculated original data, ** published also in BBSAG Bull. No. 123.

2 Observations of minimum light

In order to enlarge the number of times of minimum light, new observations for both systems were carried out. Our new photoelectric photometry was performed at four observatories with the aim of securing several well-covered primary and secondary minima for each variable:

$\bullet$
Ondrejov Observatory, Czech Republic: 65 cm reflecting telescope with CCD camera SBIG ST-8 and Cousins Rfilter;

$\bullet$
South Africa Astronomical Obsevatory (SAAO), Sutherland, South Africa: 50 cm Cassegrain telescope with Johnsons UBV filters and classical photometer;

$\bullet$
R. Szafraniec Observatory, Metzerlen, Switzerland: 35 cm Schmidt-Cassegrain telescope with photoelectric photometer STARLIGHT-1 and Johnsons B filter or CCD camera SBIG ST-6;

$\bullet$
private observatory of K.H. at Lelekovice, Czech Republic: 35 cm Newtonian telescope with CCD camera SBIG ST-6V and R filter.

The CCD measurements in Ondrejov and Lelekovice were done using the standard Cousins R filter. Flat fields for the reduction of the CCD frames were routinely obtained from exposures of regions of the sky taken at dusk or dawn. Several comparison stars were chosen in the same frame as the variables. During the observations, no variations in the brightness of these stars exceeding the possible error of measurements (typically $\sigma \simeq$ 0.005 mag) were detected. No correction was allowed for differential extinction, due to the proximity of the comparison stars to the variable and the resulting negligible differences in the air mass.

Photoelectric observations at SAAO were obtained with the modular photometer utilizing a Hamamatsu GaAs R943-02 photomultiplier during two weeks in August 1999. Each observation of an eclipsing binary was accompanied by observation of a local comparison star. The photoelectric measurements were done in the UBV filters of the Johnson photometric system with 10 s integration time. All observations were reduced to the Cousins E-region standard system (Menzies et al. 1989).

The new times of primary and secondary minimum and their errors were determined using the least squares fit of the data, by the bisecting cord method or the Kwee-van Woerden algorithm. Only the lower part of the eclipse was used. These times of minimum are presented in Table 1. Some of the published moments were newly determined using only the lower part of its observed light curve.

3 Apsidal motion analysis

The apsidal motion in both systems was studied by means of an O-C diagram analysis. We have collected all reliable times of minimum light gathered from the literature as well as from current databases of BAV and BBSAG observers or from the Besançon Double and Multiple Star Database. All photoelectric times of minimum were used with a weight of 10 in our computation. The current less precise measurements were weighted with a factor of 5, while the earlier visual and photographic times of minimum were given a weight of 1 or 0 due to the large scatter in these data.

4 TV Cet

The detached eclipsing binary TV Cet (also HD 20173, BD  $+02^{\circ}$ 502, SAO 111068, HIP 15090, PPM 146367, AN 270.1934, FL 266; $\alpha_{2000} = 3^{\rm h} 14^{\rm m} 36.5^{\rm s}$, $\delta_{2000} = +2^{\circ}45'16.4''$, $V_{\max} = 8.6$ mag; Sp. F2+F5) is a rarely investigated binary with an eccentric orbit (e = 0.055) and relatively long orbital period of about 9.1 days. It was discovered to be a variable by Martynov (1951), who derived the first light elements

\begin{displaymath}{\rm Pri.~Min. = HJD~24~ 26692.494 ~+~ 9\hbox{$.\!\!^{\rm d}$ }1032 \cdot} E. \end{displaymath}

Spectroscopically TV Ceti was studied by Popper (1967, 1968), who obtained the radial velocity curves with semiamplitudes K1 = 67.4 kms-1 and K2 = 73.8 kms-1. Four-color ubvy photometry was obtained by Jørgensen (1979) at ESO, Chile, between November 1972 and December 1974. He derived photometric elements and absolute dimensions of this binary ( $M_1 = 1.39 \pm 0.05~M_{\odot}$, $M_2 = 1.27 \pm 0.04~M_{\odot}$). He also presented three new times of minimum and refined light elements

\begin{displaymath}{\rm Pri.~ Min. = HJD~ 24~ 41685.6112~ +~ 9\hbox{$.\!\!^{\rm d}$ }103291 \cdot} E. \end{displaymath}

From its spectral type and other known properties, TV Cet was listed by Giménez (1985) as a good candidate for the study of the contribution of general relativity to the secular displacement of the line of apsides, given that the relativistic effect is expected to be dominant in this particular case. More moments of minimum light obtained photoelectrically were published by Meyer (1972) and later by Caton & Hawkins (1987), Caton et al. (1989) and Agerer & Hübscher (1998). Aside from these occasional measurements of the times of eclipse, TV Ceti has remained a rather neglected system until recently. More than 20 years have elapsed since its last study, thus TV Cet was also included in our photometric program. From the Hipparcos photometry (Perryman 1997), we were able to determine one additional moment of minimum light. It is also given in Table 1, where epochs are calculated according to the light elements given by Jørgensen (1979).

All photoelectric times of minimum light published in Meyer (1972), Jørgensen (1979), Caton & Hawkins (1987), Caton et al. (1989) as well as Agerer & Hübscher (1998) were incorporated in our analysis. A total of 20 times of minimum light were used in our analysis, with 9 secondary eclipses among them.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{TVCET.EPS} \end{figure} Figure 1: O-C graph for the times of minimum of TV Cet. The continuous and dashed lines represent predictions for primary and secondary eclipses, respectively. The individual primary and secondary minima are denoted by circles and triangles, respectively. Larger symbols correspond to the photoelectric measurements which were included in calculations with higher weight.
Open with DEXTER

The eclipse timings listed partially in Table 1 allow the determination of linear ephemerides indepedently for primary and secondary eclipses with the following results(numbers between parentheses indicate errors in the last digits and E is the number of cycles):

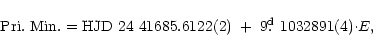
\begin{displaymath}{\rm Pri.~Min. = HJD~ 24~ 41685.6122(2)~ + ~9\hbox{$.\!\!^{\rm d}$ }1032891(4) \cdot} E, \end{displaymath}


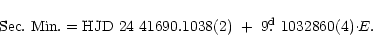
\begin{displaymath}{\rm Sec.~Min. = HJD~ 24~ 41690.1038(2) ~+~ 9\hbox{$.\!\!^{\rm d}$ }1032860(4) \cdot} E. \end{displaymath}

These linear ephemerides we propose also for current use. The difference in the apparent periods is of course a clear indication of the presence of significant apsidal motion. The method described by Giménez & García-Pelayo (1983), with equations revised by Giménez & Bastero (1995), was used for a more accurate calculation of the apsidal motion rate. The apsidal motion resulting from the final fit is $\dot{\omega} = 0.000\,30 \pm 0.000\,08$ deg cycle-1, which is significant at the 3 $\sigma$ level.

Adopting the orbital inclination derived from the light curve solution of $i = 89.15^{\circ}$ (Jørgensen 1979), the apsidal motion elements can be computed. The parameters found and their internal errors of the least squares fit (in brackets) are given in Table 2. In this table $P_{\rm s}$ denotes the sidereal period, $P_{\rm a}$ the anomalistic period, e represents the eccentricity and $\dot{\omega}$ is the rate of periastron advance (in degrees per cycle or in degrees per year). The zero epoch is given by T0 and corresponding position of the periastron is represented by $\omega_0$.

The relation between the sidereal and the anomalistic period, $P_{\rm s}$ and $P_{\rm a}$, is given by

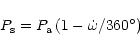
\begin{displaymath}P_{\rm s} = P_{\rm a} \,(1 - \dot{\omega}/360^\circ) \end{displaymath}

and resulting apsidal motion period U, directly given by  $\dot{\omega}$ is,

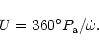
\begin{displaymath}U = 360^\circ P_{\rm a}/\dot{\omega}. \end{displaymath}

The O-C residuals for all times of minimum with respect to the linear part of the apsidal motion equation are shown in Fig. 1. The quasi-linear predictions, corresponding to the fitted parameters, are plotted as continuous and dashed lines for primary and secondary eclipses, respectively.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{tv3.eps} \end{figure} Figure 2: O-C2 diagram for the times of minimum of TV Cet after substraction the terms of apsidal motion. The curve represents a light-time effect for the third body orbit with a period of 28.5 years and an amplitude of about 0.003 days. The individual primary and secondary minima are denoted by circles and triangles, respectively.
Open with DEXTER

Subtracting the influence of apsidal motion, the O-C2 diagram in Fig. 2 can be plotted. The sinusoidal variation of these values are remarkable and could be caused by a light-time effect. A preliminary analysis of the possible third body orbit gives the following parameters:

P3 (period) = $10\,415 \pm 80$ days
  = 28.5 years
T3 (time of periastron) = JD $24\,50505 \pm 40$
A (semiamplitude) = $ 0\hbox{$.\!\!^{\rm d}$ }0027 \pm 0\hbox{$.\!\!^{\rm d}$ }0004 $
e3 (eccentricity) = $ 0.25 \pm 0.03 $
$\omega_3$ (lenght of periastron) = $ 148\hbox{$.\!\!^\circ$ }1 \pm 1\hbox{$.\!\!^\circ$ }4 .$

These values were obtained together with the new mean linear ephemeris

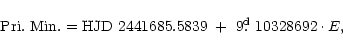
\begin{displaymath}% {\rm Pri.~Min.} ={\rm HJD~ 24 41685.5839} ~+~ 9\hbox{$.\!\!^{\rm d}$ }10328692 \cdot E, \end{displaymath}


\begin{displaymath}~~~~~~~~~~~~~~~~~~~~~~~~~~~~\,\pm0.0004~~~\pm0.00000032 \end{displaymath}

by the least squares method. Assuming a coplanar orbit ( $i_3 = 90^{\circ}$) and a total mass of the eclipsing pair $M_1 + M_2 = 2.66~M_{\odot}$(Jørgensen 1979), we can obtain a lower limit for the mass of the third component $M_{3, \min}$. The value of the mass function is $f(M) = 0.000\,13~M_{\odot}$, from which the minimum mass of the third body follows as $0.10~M_{\odot}$. A possible third component of spectral type M8 with the bolometric magnitude about +12 mag could be practically invisible in the system with a F2 primary ( $M_{\rm bol} = +3.2$ mag, Harmanec 1988). Therefore, new high-accuracy timings of this eclipsing binary are necessary in order to confirm the light-time effect in this system.

The acceleration of the rate of apsidal motion caused by the presence of the third body $\dot{\omega}$(Martynov 1973) is

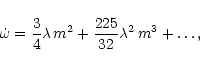\begin{displaymath}\dot{\omega} = \frac{3}{4} \lambda \, m^2 + \frac{225}{32} \lambda^2 \, m^3 + \dots , \end{displaymath} (1)

where

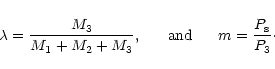\begin{displaymath}\lambda = \frac{M_3}{M_1 + M_2 + M_3} , {\rm ~~~~~and~~~~~} m = \frac{P_{\rm s}}{P_3}\cdot \end{displaymath} (2)

This correction for the apsidal motion is negligible in this system due to the relatively long period P3 of the third body orbit.

More precise non-linear light elements of the eclipsing pair including the term of the light-time effect with the circular orbit are

\begin{displaymath}{\rm Pri.~ Min. = HJD~ 24 41685\hbox{$.\!\!^{\rm d}$ }6122~ +~ 9\hbox{$.\!\!^{\rm d}$ }1032891 \cdot} E \end{displaymath}


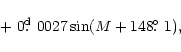
\begin{displaymath}\hspace{2.7cm}+~ 0\hbox{$.\!\!^{\rm d}$ }0027 \sin (M + 148\hbox{$.\!\!^\circ$ }1 ), \end{displaymath}


\begin{displaymath}{\rm Sec.~ Min. = HJD~ 24 41690\hbox{$.\!\!^{\rm d}$ }1038 ~+~ 9\hbox{$.\!\!^{\rm d}$ }1032860 \cdot} E \end{displaymath}


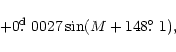
\begin{displaymath}\hspace{2.7cm}+ 0\hbox{$.\!\!^{\rm d}$ }0027\sin (M + 148\hbox{$.\!\!^\circ$ }1 ), \end{displaymath}

where

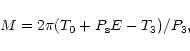
\begin{displaymath}M = 2 \pi (T_0 + P_{\rm s} E - T_3)/P_3, \end{displaymath}

is a mean anomaly of the third body.


 

 
Table 2: Apsidal motion elements of TV Cet and V451 Oph.
Element TV Cet V451 Oph
T0 [HJD] 24 41685.5839 (3) 24 45886.5310 (2)
$P_{\rm s}$ [days] 9.10328692 (8) 2.19659703 (12)
$P_{\rm a}$ [days] 9.10329452 (8) 2.19667490 (12)
e 0.0545 (4) 0.0120 (5)
$\dot{\omega}$ [deg $\:\rm {cycle^{-1}}$] 0.00030 (8) 0.0128 (4)
$\dot{\omega}$ [deg $\:\rm {yr^{-1}}$] 0.012 (3) 2.12 (6)
$\omega_0$ [deg] 100.9 (0.2) 253.4 (0.5)
U [years] 30000 (8000) 170 (5)


5 V451 Oph

The double-lined detached eclipsing binary V451 Oph (also HD 170470, BD $+10^{\circ}$ 3528, SAO 103766, HIP 90599, PPM 134790, AN 104.1935, FL 2483; $\alpha_{2000} = 18^{\rm h} 29^{\rm m} 14.0^{\rm s}$, $\delta_{2000} = +10^{\circ}53'31.4''$, $V_{\max} = 7.87$ mag; Sp. B9-A0) is a relatively bright and well-known binary with a slightly eccentric orbit (e=0.0125). It was discovered to be variable by Hoffmeister (1935). Colacevich (1953) obtained the first photoelectric light curve, determined the photomeric elements and found the correct period of the system $P = 2\hbox{$.\!\!^{\rm d}$ }1965962$.

The first spectroscopic study was presented by Heard & Morton (1962), who derived the absolute parameters of this system ( $M_1 = 2.38~M_{\odot}$, $M_2 = 1.98~M_{\odot}$, $R_1 = 2.51~R_{\odot}$, $R_2 = 2.01~R_{\odot}$). Next spectroscopic study was carried out by Popper (1971), who obtained the radial velocity curves with semiamplitudes K1 = 129.3 kms-1 and K2 = 152.3 kms-1.

Apsidal motion in V451 Oph was first announced by Plavec et al. (1960). Several studies have been made of the apsidal motion rate of V451 Oph since its discovery as an eccentric eclipsing binary. Other photometric study has been published by Giuricin et al. (1980). Khaliullin & Kozyreva (1984) obtained four-colour WBVR photometry at the Tian-Shan Observatory, finding an apsidal motion with a period of U = 170 yr, the internal structure constant $k_2 = 0.0045 ~\pm~ 0.0015$and an eccentricity of e = 0.012.

Complete simultaneous Strömgren four-colour photometry of V451 Oph was obtained in 1983-84 at Sierra Nevada in Spain (Clausen et al. 1987). The most detailed analysis is that by Clausen et al. (1986) using those data. They obtained separately way and using different methods, apsidal motion rates of $0.0120 \,\pm\, 0.0007$ deg/cycle, with the period of $U = 180\, \pm\, 30$ yr and a value for orbital eccentricity of $e = 0.0125~ \pm~ 0.0015$, in good agreement with each other given their expected mean errors. The internal structure constant log $\,k_2 = -2.48$ was also calculated. In that paper the following linear ephemerides were obtained for primary and secondary eclipses, respectively:

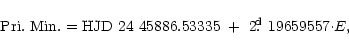
\begin{displaymath}{\rm Pri.~ Min. = HJD~ 24~ 45886.53335 ~+~ 2\hbox{$.\!\!^{\rm d}$ }19659557 \cdot} E, \end{displaymath}


\begin{displaymath}{\rm Sec.~ Min. = HJD ~24~ 45887.62673 ~+~ 2\hbox{$.\!\!^{\rm d}$ }19659863 \cdot} E. \end{displaymath}


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{451oph.eps}\end{figure} Figure 3: O-C diagram for V451 Oph. See legend for Fig. 1.
Open with DEXTER

The system is known, moreover, to have a large relativistic contribution to the observed apsidal motion rate. This made V451 Oph a case of special interest from the point of view of the orbit rotation. Since the mentioned papers, several new times of minima have been measured and thus allow us to decrease the involved observational uncertainties.

Recently, the relativistic apsidal motion in this binary was discussed by Claret (1997), who found excellent agreement of observational data with theoretical prediction based on stellar theoretical models.

All photoelectric times of minimum light given in Pohl & Kizilirmak (1970, 1975), Kizilirmak & Pohl (1971, 1974), Batistini et al. (1974), Khaliullin & Kozyreva (1984) and Clausen et al. (1986, their Table 2) were incorporated in our calculation. From the Hipparcos photometry (Perryman 1997), we were able to determine one additional time of minimum light. A total of 67 photoelectric times of minimum light were used in our analysis, with 29 secondary eclipses among them. The orbital inclination was adopted to be $i = 85.9^{\circ}$ based on the photometric analysis (Clausen et al. 1986). The computed apsidal motion elements and their internal errors of the least squares fit are given in Table 2. The O-C diagram is shown in Fig. 3.

More precise non-linear light elements including one term in e are

\begin{displaymath}{\rm Pri.~Min. = HJD~24~ 45886\hbox{$.\!\!^{\rm d}$ }5310 ~+ ~2\hbox{$.\!\!^{\rm d}$ }19659703 \cdot} E \end{displaymath}


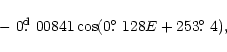
\begin{displaymath}\hspace{2.7cm}-~ 0\hbox{$.\!\!^{\rm d}$ }00841\cos (0\hbox{$.\!\!^\circ$ }128 E + 253\hbox{$.\!\!^\circ$ }4 ), \end{displaymath}


\begin{displaymath}{\rm Sec.~ Min. = HJD~ 24~ 45887\hbox{$.\!\!^{\rm d}$ }6293 ~+~ 2\hbox{$.\!\!^{\rm d}$ }19659703 \cdot} E \end{displaymath}


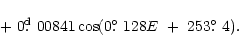
\begin{displaymath}\hspace{2.7cm}+~ 0\hbox{$.\!\!^{\rm d}$ }00841\cos (0\hbox{$.\!\!^\circ$ }128 E ~+~ 253\hbox{$.\!\!^\circ$ }4 ). \end{displaymath}


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{451OPH3.EPS} \end{figure} Figure 4: O-C2 diagram for the times of minimum of V451 Oph after substraction the terms of apsidal motion. The individual primary and secondary photoelectric minima are denoted by circles and triangles, respectively.
Open with DEXTER


 

 
Table 3: Adopted parameters of the components and derived results.
Parameter Unit TV Cet V451 Oph
M1 $M_{\odot}$ 1.39 (5) 2.78 (6)
M2 $M_{\odot}$ 1.27 (4) 2.36 (5)
r1   0.05872 (13) 0.2155 (20)
r2   0.05029 (15) 0.1655 (20)
Source   Jørgensen Clausen et al.
    (1979) (1986)
$\dot{\omega}_{\rm rel}$ deg $\:\rm {cycle^{-1}}$ 0.00024 0.0010
$\dot{\omega}_{\rm rel} / \dot{\omega}$ % 80.2 7.8
$\dot{\omega}_{\rm cl}$ deg $\:\rm {cycle^{-1}}$ 0.00006 0.0118
log $k_{2, \rm obs}$   -2.03 (15) -2.477 (45)
log $k_{2, \rm theo}$   -2.23 -2.48


6 Internal structure constant

Observations of binary systems allow us to determine the internal structure constant, k2, which is related to the variation of density within the star and is an important parameter of stellar evolution models. It is best studied in binary systems with eccentric orbits that show apsidal motion. The period of rotation of the periastron in eccentric eclipsing binaries does not allow us to derive the individual internal stellar constant of the component stars.


 

 
Table 4: Triple eccentric eclipsing binaries with the AM and LTE.
System Spectral e P U e3 P3 Source
  type   [days] [years]   [years]  
HS Her B4+A4 0.021 1.637 72.4 0.7 74.1 Wolf (2001)
U Oph B5+B5 0.003 1.677 21.2 0.22 38.7 Kämper (1986)
DR Vul B0+B0.5 0.095 2.251 36.3 0.73 62.8 Wolf et al. (1999)
YY Sgr B6+B5 0.159 2.628 290.4 0.44 44.3 Wolf (2000)
RU Mon B7+B7 0.396 3.585 347 0.46 73.3 Wolf et al. (1999)
TV Cet F2+F5 0.055 9.103 30000 0.25 28.5 this paper


The observational average value of $k_{2, \rm obs}$ is given by the relation

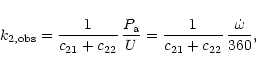\begin{displaymath}k_{2, \rm obs} = \frac{1}{c_{21} + c_{22}} \, \frac{P_{\rm a}}{U} = \frac{1}{c_{21} + c_{22}} \, \frac{\dot{\omega}}{360} , \end{displaymath} (3)

where c21 and c22 are functions of the orbital eccentricity, fractional radii, the masses of the components and the ratio between rotational velocity of the stars and Keplerian velocity (Kopal 1978).

Taking into account the value of the eccentricity and the masses of the components, one has to subtract from $\dot{\omega}$ a relativistic correction $\dot{\omega}_{\rm rel}$ (Levi-Civita 1937; Giménez 1985)

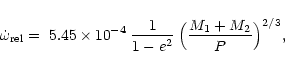\begin{displaymath}\dot{\omega}_{\rm rel} = \; 5.45 \times 10^{-4} \: \frac{1}{1-e^2} \: \Bigl( \frac{M_1 + M_2}{P} \Bigr) ^{2/3}, \end{displaymath} (4)

where Mi denotes the individual masses of the components in solar units, or

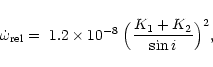\begin{displaymath}\dot{\omega}_{\rm rel} = \; 1.2 \times 10^{-8} \: \Bigl( \frac {K_1 + K_2} {\sin i} \Bigr) ^2, \end{displaymath} (5)

if Ki is expressed in kms-1.

The values of $\dot{\omega}_{\rm rel}$ and resulting mean internal structure constants $k_{2, \rm obs}$ are given in Table 3. Theoretical values $k_{2, \rm theo}$ according to available theoretical models for the internal stellar structure along the main sequence, computed by Claret & Giménez (1992) for a variety of masses and chemical compositions, are also given.

7 Conclusions

We derive updated apsidal motion elements for two eccentric eclipsing binaries by means of an O-C diagram analysis. Both systems analysed here present important relativistic contributions to the total apsidal motion.

Concerning TV Cet, we have detected apsidal motion at a rate $\dot{\omega}_{\rm obs} = 0.000\,30 \pm 000\,08$ deg cycle-1. A substantial fraction of this ($\sim$80%) is due to the contribution from general relativity and our measurement is consistent with theory. The difference between theoretical and observed values of the internal structure constants is caused probably by the relatively high uncertainty of the observed rate of apsidal motion.

In the case of V451 Oph, our resulting orbital eccentricity and the period of apsidal motion is in a good agreement with elements previously obtained by Khaliullin & Kozyreva (1984) and Clausen et al. (1987). A few more times of minimum added over the next decade will make V451 Oph one of the best investigated systems in the observational check of stellar structure models. Nevertheless, the scatter of O-C values seems to be relatively high for the detached eclipsing system. Substracting the influence of apsidal motion, the O-C2 diagram in Fig. 4 can be plotted. From this diagram, no other phenomenon (i.e. presence of a third body in the system) can be simply derived. The differences from the zero line are substantially larger than the standard errors of many observed times of minimum.

A small group of triple eccentric eclipsing binaries presenting apsidal motion and light-time effects, is given in Table 4. These excellent labratories of celestial mechanics deserve a continuous monitoring. More high-accuracy timings of these systems are necessary in the future in order to enlarge the time span for a better analysis of the apsidal motion, especially in TV Cet, where the light-time effect is only poorly determined.

Acknowledgements
This investigation was supported by allocation of SAAO observing time, in part by the Grant Agency of the Czech Reublic, grant No. 205/99/0255 and by the research plan J13/98: 113200004 Investigation of the Earth and the Universe. MW wishes to thank Dr. David Kilkenny, SAAO, for help with the photometric data reductions. We are also thankful to Mr. Wilhelm Kleikamp, BAV, for sending his original data of TV Ceti, and to Dr. Valentina Kozyreva, SAI, Moscow, for supplying us with her photoelectric measurements of V451 Oph. RD wishes to thank the Emilia Guggenheim-Schnurr Foundation for financial support. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France, and of NASA's Astrophysics Data System Bibliographic Services.

References

 
Copyright ESO 2001