The thermal structure of neutron stars with magnetized envelopes is studied using modern physics input. The relation between the internal (
A&A 374, 213-226 (2001)
DOI: 10.1051/0004-6361:20010698
A. Y. Potekhin - D. G. Yakovlev
Ioffe Physico-Technical Institute, Politekhnicheskaya 26, 194021 St. Petersburg, Russia
Received 19 February 2001 / Accepted 17 April 2001
Abstract
The thermal structure of neutron stars with magnetized envelopes
is studied using modern physics input.
The relation between the internal (
![]() )
and local surface temperatures is calculated
and fitted by analytic expressions
for magnetic field strengths B from 0 to 1016 G
and arbitrary inclination of the field lines to the surface.
The luminosity of a neutron star with dipole magnetic field
is calculated and fitted as a function
of B,
)
and local surface temperatures is calculated
and fitted by analytic expressions
for magnetic field strengths B from 0 to 1016 G
and arbitrary inclination of the field lines to the surface.
The luminosity of a neutron star with dipole magnetic field
is calculated and fitted as a function
of B,
![]() ,
stellar mass and radius.
In addition, we simulate cooling
of neutron stars with magnetized envelopes.
In particular, we analyse ultramagnetized envelopes
of magnetars and also the effects of the magnetic field
of the Vela pulsar on the determination of
critical temperatures of neutron and proton superfluids
in its core.
,
stellar mass and radius.
In addition, we simulate cooling
of neutron stars with magnetized envelopes.
In particular, we analyse ultramagnetized envelopes
of magnetars and also the effects of the magnetic field
of the Vela pulsar on the determination of
critical temperatures of neutron and proton superfluids
in its core.
Key words: stars: neutron - dense matter - conduction - magnetic fields
Most of the observed NSs
possess magnetic fields
![]() -1013 G
(e.g., Taylor et al. 1993).
Some NSs are possibly magnetars, with B>1014 G
(e.g., Thompson & Duncan 1995;
Kouveliotou et al. 1998,1999;
Mereghetti 2001).
The internal NS magnetic field can be even higher.
The strong magnetic field affects physical
properties of all NS layers in many ways.
For instance, the field
-1013 G
(e.g., Taylor et al. 1993).
Some NSs are possibly magnetars, with B>1014 G
(e.g., Thompson & Duncan 1995;
Kouveliotou et al. 1998,1999;
Mereghetti 2001).
The internal NS magnetic field can be even higher.
The strong magnetic field affects physical
properties of all NS layers in many ways.
For instance, the field
![]() G
may affect the neutrino emissivity in the NS core
(e.g., Baiko & Yakovlev 1999). The field
G
may affect the neutrino emissivity in the NS core
(e.g., Baiko & Yakovlev 1999). The field
![]() G
may change the electrical resistivity of NS cores,
accelerating evolution of the internal field. In principle
the thermal evolution may be coupled to the
magnetic one (e.g., Urpin & Shalybkov 1995).
G
may change the electrical resistivity of NS cores,
accelerating evolution of the internal field. In principle
the thermal evolution may be coupled to the
magnetic one (e.g., Urpin & Shalybkov 1995).
Thus modelling of the thermal structure
and evolution of the magnetized NSs is a complicated
task. In this paper we focus on two problems.
First we consider the thermal structure of the
outer magnetized NS envelope of density
![]() g cm-3with the magnetic field
g cm-3with the magnetic field
![]() G.
These envelopes produce thermal insulation
(blanketing) of NS interiors.
We solve this problem using updated physics
input described in Sect. 2.
The solution (Sect. 3) relates
the internal NS temperature
G.
These envelopes produce thermal insulation
(blanketing) of NS interiors.
We solve this problem using updated physics
input described in Sect. 2.
The solution (Sect. 3) relates
the internal NS temperature
![]() with the local effective surface temperature
with the local effective surface temperature ![]() and, therefore, with the integrated NS luminosity (or
the mean effective surface temperature,
and, therefore, with the integrated NS luminosity (or
the mean effective surface temperature, ![]() ).
Second, in order to illustrate
the obtained
).
Second, in order to illustrate
the obtained
![]() relation,
we simulate (Sect. 4)
cooling of NSs which possess a
given dipole or radial magnetic field
in the outer envelopes.
relation,
we simulate (Sect. 4)
cooling of NSs which possess a
given dipole or radial magnetic field
in the outer envelopes.
The effects of a strong magnetic field
on thermodynamic and kinetic properties
of the outer NS layers
have been reviewed, for instance, by
Yakovlev & Kaminker (1994) and
Ventura & Potekhin (2001).
The field affects the properties
of all plasma components, the electron
component usually being affected most strongly.
Motion of free electrons perpendicular to the field lines
is quantized in Landau orbitals
with a characteristic transverse scale equal to
the magnetic length
![]() ,
where
,
where
![]() is the electron Compton wavelength,
is the electron Compton wavelength,
![]() is the magnetic field strength expressed in relativistic units,
is the magnetic field strength expressed in relativistic units,
![]() is the electron cyclotron frequency,
and
is the electron cyclotron frequency,
and
![]() G).
Except for the outermost parts of the NS envelopes,
the electrons constitute degenerate, almost ideal gas.
The electron entropy,
magnetization, thermal and electrical conductivities,
and other quantities
exhibit quantum oscillations of the de Haas-van Alphen type.
The oscillations occur under variations of density
G).
Except for the outermost parts of the NS envelopes,
the electrons constitute degenerate, almost ideal gas.
The electron entropy,
magnetization, thermal and electrical conductivities,
and other quantities
exhibit quantum oscillations of the de Haas-van Alphen type.
The oscillations occur under variations of density ![]() or Bwhenever the electron Fermi momentum reaches the characteristic values
or Bwhenever the electron Fermi momentum reaches the characteristic values
![]() associated with occupation of Landau levels
n=1,2,...These oscillations appreciably change the properties
of degenerate electrons in the
limit of a strongly quantizing field
(e.g., Yakovlev & Kaminker 1994)
in which almost all electrons populate the ground Landau level.
The latter case takes place
at temperature
associated with occupation of Landau levels
n=1,2,...These oscillations appreciably change the properties
of degenerate electrons in the
limit of a strongly quantizing field
(e.g., Yakovlev & Kaminker 1994)
in which almost all electrons populate the ground Landau level.
The latter case takes place
at temperature
![]() and density
and density
![]() ,
where
,
where
The thermal structure of magnetized NS
envelopes has been studied
by a number of authors mainly using a
plane-parallel approximation.
More attention has been paid to the
case of the radial magnetic field (normal to the surface).
It has been thoroughly considered by Hernquist (1985),
Van Riper (1988), Schaaf (1990a),
Heyl & Hernquist (1998b) for
![]() G.
In another paper
Heyl & Hernquist (1998a)
analysed the case of higher fields,
G.
In another paper
Heyl & Hernquist (1998a)
analysed the case of higher fields,
![]() -1016 G.
One can consult the cited papers for references to
earlier works. The principal conclusion
of these studies is that
the magnetic field reduces thermal insulation
of the blanketing envelope by increasing
the longitudinal (along the field lines) thermal
conductivity of degenerate electrons due to Landau
quantization of electron motion.
-1016 G.
One can consult the cited papers for references to
earlier works. The principal conclusion
of these studies is that
the magnetic field reduces thermal insulation
of the blanketing envelope by increasing
the longitudinal (along the field lines) thermal
conductivity of degenerate electrons due to Landau
quantization of electron motion.
The thermal structure of the envelope with the magnetic field
tangential to the surface has been analysed by
Hernquist (1985), Schaaf (1990a),
and Heyl & Hernquist (1998a) for
![]() G.
In this case the field increases thermal insulation
of the blanketing envelope due to the classical
effect of reduction of the electron thermal conductivity
transverse to the field because of the Larmor rotation.
G.
In this case the field increases thermal insulation
of the blanketing envelope due to the classical
effect of reduction of the electron thermal conductivity
transverse to the field because of the Larmor rotation.
The case of arbitrary inclination of the field to
the surface was studied by Greenstein &
Hartke (1983) in the approximation
of constant (density and temperature independent)
longitudinal and transverse thermal conductivities.
The authors proposed a very simple formula (Sect. 3.3)
which relates the local
surface and internal stellar temperatures, ![]() and
and
![]() .
It is constructed from two
.
It is constructed from two
![]() relations obtained
for the radial and tangential magnetic fields.
Page (1995) presented arguments that the formula
of Greenstein & Hartke is valid also for realistic,
variable thermal conductivities. If so, one
immediately gets the required
relations obtained
for the radial and tangential magnetic fields.
Page (1995) presented arguments that the formula
of Greenstein & Hartke is valid also for realistic,
variable thermal conductivities. If so, one
immediately gets the required
![]() relation for any magnetic field
inclination using the realistic relations for the radial
and tangential fields.
This method has been used by several authors
(e.g., Shibanov & Yakovlev 1996).
Recently, the case of arbitrary field inclination
has been studied also by Heyl & Hernquist (1998b).
In Sect. 3 we reconsider the
thermal structure of the blanketing envelopes
for any magnetic field inclination and compare our results
with those of earlier studies.
relation for any magnetic field
inclination using the realistic relations for the radial
and tangential fields.
This method has been used by several authors
(e.g., Shibanov & Yakovlev 1996).
Recently, the case of arbitrary field inclination
has been studied also by Heyl & Hernquist (1998b).
In Sect. 3 we reconsider the
thermal structure of the blanketing envelopes
for any magnetic field inclination and compare our results
with those of earlier studies.
Early simulations of cooling of magnetized NSs
were performed assuming the radial magnetic field
everywhere over the stellar surface
(e.g., Nomoto & Tsuruta 1987; Van Riper 1991).
Since the radial magnetic field reduces the thermal insulation,
these theories predicted acceleration of cooling
of the magnetized NS accompanied by enhanced
NS luminosity at the early (neutrino-dominated) cooling stage
(at stellar ages
![]() yr).
Page (1995) and
Shibanov & Yakovlev (1996) simulated cooling
of NSs with dipole magnetic fields.
They showed that the decrease of thermal
insulation of the stellar envelope near the magnetic
equator partly compensated by its increase near the pole,
and the magnetic field did not necessarily accelerate the cooling,
in agreement with an earlier conjecture of Hernquist (1985).
In a series of papers Heyl & Hernquist
(1997a,1997b,1998a,1998b) proposed simplified
models of cooling of magnetized NSs including the cases
of ultrahigh surface magnetic fields,
yr).
Page (1995) and
Shibanov & Yakovlev (1996) simulated cooling
of NSs with dipole magnetic fields.
They showed that the decrease of thermal
insulation of the stellar envelope near the magnetic
equator partly compensated by its increase near the pole,
and the magnetic field did not necessarily accelerate the cooling,
in agreement with an earlier conjecture of Hernquist (1985).
In a series of papers Heyl & Hernquist
(1997a,1997b,1998a,1998b) proposed simplified
models of cooling of magnetized NSs including the cases
of ultrahigh surface magnetic fields,
![]() G.
G.
We illustrate our new models of magnetized NS envelopes with simulation of cooling of NSs (Sect. 4). We briefly discuss cooling of ultramagnetized NSs as well as cooling models of the Vela pulsar with the dipole magnetic field and superfluid core.
Integration of Eq. (6) gives a temperature profile
![]() where
where
![]() is the
optical depth,
and the integration constant corresponds to the Eddington
approximation (
is the
optical depth,
and the integration constant corresponds to the Eddington
approximation (
![]() at the radiative surface,
where
at the radiative surface,
where
![]() ).
A more accurate boundary condition
requires solution of the radiative transfer equation in
the NS atmosphere (e.g., Shibanov et al. 1998).
).
A more accurate boundary condition
requires solution of the radiative transfer equation in
the NS atmosphere (e.g., Shibanov et al. 1998).
At ![]() the general relativistic equation of hydrostatic equilibrium
can be reduced to the Newtonian form:
the general relativistic equation of hydrostatic equilibrium
can be reduced to the Newtonian form:
![]() ,
where
,
where
![]() is the surface gravity.
Together with Eq. (6), it leads to the thermal structure equation
is the surface gravity.
Together with Eq. (6), it leads to the thermal structure equation
The thermal conductivity tensor of magnetized plasma is anisotropic.
It is characterized by the conductivities parallel (![]() )
and transverse (
)
and transverse (
![]() )
to the field, and by the
off-diagonal (Hall) component.
In the plane-parallel approximation Eq. (6)
contains the effective thermal conductivity
)
to the field, and by the
off-diagonal (Hall) component.
In the plane-parallel approximation Eq. (6)
contains the effective thermal conductivity
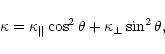 |
(8) |
Assuming the dipole field, we
can use the general-relativistic solution
(Ginzburg & Ozernoy 1964)
![$\displaystyle a = - {(1-x) \ln(1-x) + x - 0.5 x^2
\over [ \ln(1-x)+x + 0.5 x^2] \sqrt{1-x}},$](/articles/aa/full/2001/28/aa1164/img98.gif) |
(11) |
The quantities ![]() ,
,
![]() and Lrefer to a local reference frame at the NS surface.
The redshifted ("apparent'') quantities
as detected by a distant observer are (Thorne 1977):
and Lrefer to a local reference frame at the NS surface.
The redshifted ("apparent'') quantities
as detected by a distant observer are (Thorne 1977):
![]() ,
,
![]() ,
,
![]() .
.
Crucial for the thermal evolution is the relation between
![]() and
and
![]() .
For non-magnetic blanketing envelopes composed of iron,
this relation was studied by Gudmundsson et al. (1983),
while the non-magnetic envelopes of various chemical compositions
were analysed by PCY.
Ventura & Potekhin (2001)
presented an analytic analysis of
the
.
For non-magnetic blanketing envelopes composed of iron,
this relation was studied by Gudmundsson et al. (1983),
while the non-magnetic envelopes of various chemical compositions
were analysed by PCY.
Ventura & Potekhin (2001)
presented an analytic analysis of
the
![]() relation
for the envelopes without magnetic fields and with
strong magnetic fields; Heyl & Hernquist (1998a)
performed a
semianalytic investigation of the case of strong magnetic field.
The results of Ventura & Potekhin (2001)
and Heyl & Hernquist (1998a)
are rather approximate because of a number
of simplifying assumptions discussed
by Ventura & Potekhin (2001).
relation
for the envelopes without magnetic fields and with
strong magnetic fields; Heyl & Hernquist (1998a)
performed a
semianalytic investigation of the case of strong magnetic field.
The results of Ventura & Potekhin (2001)
and Heyl & Hernquist (1998a)
are rather approximate because of a number
of simplifying assumptions discussed
by Ventura & Potekhin (2001).
The validity of the one-dimensional approximation can be checked by direct two-dimensional simulation of the heat transport in the blanketing envelope. Such simulation has been attempted by Schaaf (1990b) for a homogeneously magnetized NS under many simplified assumptions, so that a more realistic study is required. The heat conduction from hotter to cooler zones along the surface or possible meridional and convective motions can smooth the temperature variations over the NS surface. Nevertheless, the one-dimensional approximation seems to be sufficient for our cooling calculations presented below.
The outer envelope is assumed to be composed of iron,
which can be partially ionized at
![]() .
Following PCY,
we employ the mean-ion approximation
and adjust an effective ion charge
to a more elaborate EOS:
the Opacity Library (OPAL)
EOS (Rogers et al. 1996) at B=0 and
the Thomas-Fermi EOS of Thorolfsson et al. (1998)
at
B=(1010-1013) G.
The tabular entries of these EOSs in
.
Following PCY,
we employ the mean-ion approximation
and adjust an effective ion charge
to a more elaborate EOS:
the Opacity Library (OPAL)
EOS (Rogers et al. 1996) at B=0 and
the Thomas-Fermi EOS of Thorolfsson et al. (1998)
at
B=(1010-1013) G.
The tabular entries of these EOSs in ![]() and T are interpolated
in the same way as in PCY.
When necessary, we interpolate the effective charge at intermediate B.
Since no reliable EOS of iron has been published for B>1013 G,
we use the effective charge obtained at B=1013 G for
higher B.
and T are interpolated
in the same way as in PCY.
When necessary, we interpolate the effective charge at intermediate B.
Since no reliable EOS of iron has been published for B>1013 G,
we use the effective charge obtained at B=1013 G for
higher B.
Thus, in our model of the outer envelope, the pressure
is produced by magnetized Fermi gas of electrons and
by the gas of classical ions
with an effective charge.
We neglect the anomalous magnetic moments
of the nuclei, which is a good approximation at
![]() G
(cf. Broderick et al. 2000; Suh & Mathews 2001).
The electron pressure can be expressed through
the chemical potential
G
(cf. Broderick et al. 2000; Suh & Mathews 2001).
The electron pressure can be expressed through
the chemical potential ![]() and T
(e.g., Blandford & Hernquist 1982):
and T
(e.g., Blandford & Hernquist 1982):
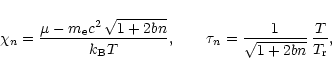
Typically, the radiative conduction dominates
(
![]() )
in
the outermost non-degenerate layers of a NS,
whereas the electron conduction
dominates (
)
in
the outermost non-degenerate layers of a NS,
whereas the electron conduction
dominates (
![]() )
in deeper, moderately and strongly degenerate layers.
The
)
in deeper, moderately and strongly degenerate layers.
The
![]() relation depends mainly on the conductivities in the
sensitivity strip on the
relation depends mainly on the conductivities in the
sensitivity strip on the ![]() plane
(Gudmundsson et al. 1983)
placed near the turning point,
where
plane
(Gudmundsson et al. 1983)
placed near the turning point,
where
![]() .
.
At B=0, the second process is described by
the well-known Thomson cross section
![]() in the non-relativistic limit
in the non-relativistic limit
![]() (e.g., Berestetskii et al. 1992).
The corresponding opacity is
(e.g., Berestetskii et al. 1992).
The corresponding opacity is
The free-free absorption coefficient
at B=0 was calculated
by Karzas & Latter (1961)
as a function of the electron
velocity and photon frequency ![]() .
Hummer (1988) produced an accurate fit to
its thermal average in the range
.
Hummer (1988) produced an accurate fit to
its thermal average in the range
![]() and
and
![]() ,
where
,
where
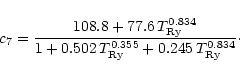 |
(18) |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{MS1164f1.ps}\end{figure}](/articles/aa/full/2001/28/aa1164/Timg149.gif) |
Figure 1:
|
| Open with DEXTER | |
Interaction of photons with magnetized plasma
depends on their polarization and propagation direction.
Accordingly, radiative thermal conductivities
and associated opacities along and across the field
become different.
Rosseland mean opacities
![]() and
and
![]() were calculated by Silant'ev & Yakovlev (1980)
for various values
of T and B.
We have fitted their numerical results by
were calculated by Silant'ev & Yakovlev (1980)
for various values
of T and B.
We have fitted their numerical results by
| n | 1 | 2 | 3 | 4 | 5 | 6 |
| an | 0.0949 | 0.1619 | 0.2587 | 0.3418 | 0.4760 | 0.2533 |
| bn | 0.0610 | 0.1400 | 0.1941 | 0.0415 | 0.3115 | 0.1547 |
| cn | 0.090 | 0.0993 | 0.0533 | 2.15 | 0.2377 | 0.231 |
Asymptotic behaviour of Eqs. (21) and (22)
at
![]() agrees with theoretical results of Silant'ev & Yakovlev
(1980):
agrees with theoretical results of Silant'ev & Yakovlev
(1980):
![]() at f=0 (Thomson scattering);
at f=0 (Thomson scattering);
![]() at f=1 (free-free transitions);
and
at f=1 (free-free transitions);
and
![]() at any f.
at any f.
At finite but large uthe radiative opacities of fully ionized matter
are strongly reduced.
The reduction is ![]() 10 times
stronger for scattering than for free-free transitions.
Inserting this factor 10 into Eq. (16)
and taking into account that,
at
10 times
stronger for scattering than for free-free transitions.
Inserting this factor 10 into Eq. (16)
and taking into account that,
at
![]() G, the NS radiative surface
is pushed to
G, the NS radiative surface
is pushed to
![]() (Ventura & Potekhin 2001),
one can see that in deep, strongly magnetized photospheric layers
Thomson scattering dominates the opacity only
at
(Ventura & Potekhin 2001),
one can see that in deep, strongly magnetized photospheric layers
Thomson scattering dominates the opacity only
at
![]() .
.
We note that the Rosseland
mean opacity due to scattering by free ions,
![]() ,
can be obtained from that for electrons,
,
can be obtained from that for electrons, ![]() ,
by the simple scaling:
,
by the simple scaling:
From the asymptote of ![]() at large u we see that
the Thomson opacity of ions
is
at large u we see that
the Thomson opacity of ions
is ![]() times larger than that of electrons,
if the ions are strongly quantized into Landau levels,
which occurs at
times larger than that of electrons,
if the ions are strongly quantized into Landau levels,
which occurs at
![]() .
Since the main contribution into the radiative opacity
at sufficiently low temperature
comes from free-free processes (see above),
we can conclude that
the Thomson ion scattering cannot contribute appreciably
to the Rosseland mean opacity of the photosphere
unless
.
Since the main contribution into the radiative opacity
at sufficiently low temperature
comes from free-free processes (see above),
we can conclude that
the Thomson ion scattering cannot contribute appreciably
to the Rosseland mean opacity of the photosphere
unless
![]() .
.
Recently, Baiko et al. (1998)
considerably improved the
treatment of ![]() by taking into account
multiphonon absorption and emission processes
in Coulomb crystals and
incipient quasiordering in a Coulomb liquid of ions.
Using these results, Potekhin et al. (1999)
constructed an effective scattering potential
which allowed them to calculate the non-magnetic
conductivity in the relaxation time approximation
in an analytic form; these analytic expressions
described accurately numerical results obtained beyond
the framework of the relaxation time approximation.
The effective potential has been
used then at arbitrary magnetic fields in order to derive
practical expressions for evaluation of
electrical and thermal conductivities
of degenerate electrons
in magnetized outer envelopes of NSs
(Potekhin 1999).
Unlike previous treatments of the electrical conductivities
perpendicular to the quantizing magnetic fields
(Kaminker & Yakovlev 1981; Hernquist 1984;
Schaaf 1988), Potekhin (1999)
went beyond the assumption that
by taking into account
multiphonon absorption and emission processes
in Coulomb crystals and
incipient quasiordering in a Coulomb liquid of ions.
Using these results, Potekhin et al. (1999)
constructed an effective scattering potential
which allowed them to calculate the non-magnetic
conductivity in the relaxation time approximation
in an analytic form; these analytic expressions
described accurately numerical results obtained beyond
the framework of the relaxation time approximation.
The effective potential has been
used then at arbitrary magnetic fields in order to derive
practical expressions for evaluation of
electrical and thermal conductivities
of degenerate electrons
in magnetized outer envelopes of NSs
(Potekhin 1999).
Unlike previous treatments of the electrical conductivities
perpendicular to the quantizing magnetic fields
(Kaminker & Yakovlev 1981; Hernquist 1984;
Schaaf 1988), Potekhin (1999)
went beyond the assumption that
![]() by introducing an interpolation from the case
by introducing an interpolation from the case
![]() to
to
![]() .
All tensor components of the kinetic coefficients in magnetic fields
have been calculated and fitted by analytic formulae;
the corresponding Fortran
code is available electronically at
http://www.ioffe.rssi.ru/astro/conduct/.
This code is used here to calculate the temperature profile
in the outer envelope of a NS.
.
All tensor components of the kinetic coefficients in magnetic fields
have been calculated and fitted by analytic formulae;
the corresponding Fortran
code is available electronically at
http://www.ioffe.rssi.ru/astro/conduct/.
This code is used here to calculate the temperature profile
in the outer envelope of a NS.
In the inner envelope, we need to know
the thermal conductivity ![]() only in young NSs,
only in young NSs,
![]() yr, as long as the internal region (
yr, as long as the internal region (
![]() )
remains non-isothermal (GYP).
For this purpose, we will use
the non-magnetic
conductivities presented by GYP.
They generalize the expressions
by Potekhin et al. (1999) in two respects.
First, the atomic nuclei in the inner envelope
cannot be considered as pointlike:
the size and shape of nuclear charge distribution
significantly affect the conductivity.
Second, the electron-phonon
scattering in the inner crust at temperatures much below 108 K
changes its character: the so called umklapp processes cease to
dominate and the normal processes (with electron momentum
transfer within one Brillouin zone) become more important.
)
remains non-isothermal (GYP).
For this purpose, we will use
the non-magnetic
conductivities presented by GYP.
They generalize the expressions
by Potekhin et al. (1999) in two respects.
First, the atomic nuclei in the inner envelope
cannot be considered as pointlike:
the size and shape of nuclear charge distribution
significantly affect the conductivity.
Second, the electron-phonon
scattering in the inner crust at temperatures much below 108 K
changes its character: the so called umklapp processes cease to
dominate and the normal processes (with electron momentum
transfer within one Brillouin zone) become more important.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1164f2.ps}\end{figure}](/articles/aa/full/2001/28/aa1164/Timg176.gif) |
Figure 2:
Electron magnetization parameter
at the top and bottom of the inner crust
(solid lines) and in the outer envelope (dashed line).
The curves are marked with the values of |
| Open with DEXTER | |
The internal temperature in young NSs
is relatively high,
![]() K.
Our neglect of the effects of the magnetic fields
in the internal region
is strictly justified for the case of small
magnetization parameter,
K.
Our neglect of the effects of the magnetic fields
in the internal region
is strictly justified for the case of small
magnetization parameter,
![]() .
This parameter
is shown in Fig. 2 as a function of Tfor three values of density: near the top
and the bottom of the inner envelope (solid lines) and in
the middle of the outer envelope (dashed line).
We see that the use of non-magnetic
.
This parameter
is shown in Fig. 2 as a function of Tfor three values of density: near the top
and the bottom of the inner envelope (solid lines) and in
the middle of the outer envelope (dashed line).
We see that the use of non-magnetic ![]() is justified for the NSs with the
magnetic fields
is justified for the NSs with the
magnetic fields
![]() G in the inner envelope.
However it cannot be justified
for higher B in the inner envelope or
for
G in the inner envelope.
However it cannot be justified
for higher B in the inner envelope or
for
![]() G in the outer envelope.
In such cases the conductivity
across the field is suppressed by the large factor
G in the outer envelope.
In such cases the conductivity
across the field is suppressed by the large factor
![]() and
the Hall thermal conductivity may become important.
We neglect these effects in the inner envelope.
Therefore, our simulations
(Sect. 4) of cooling of young NSs (
and
the Hall thermal conductivity may become important.
We neglect these effects in the inner envelope.
Therefore, our simulations
(Sect. 4) of cooling of young NSs (
![]() yr)
are justified for
yr)
are justified for
![]() G
in the inner envelopes. The results for older NSs,
for which the inner envelope is isothermal,
are valid at larger B as well.
G
in the inner envelopes. The results for older NSs,
for which the inner envelope is isothermal,
are valid at larger B as well.
Figures 3 and 4
present the calculated
![]() profiles for a NS of mass
profiles for a NS of mass
![]() and radius R=10 km
(
and radius R=10 km
(
![]() and
and
![]() ). The curves in Fig. 3
are calculated at fixed
). The curves in Fig. 3
are calculated at fixed
![]() K.
The solid curves show the results of accurate calculations
for the magnetic field normal and tangential to the surface
(cases of parallel and transverse conduction, Sect. 2.1.2).
The dashed lines are obtained for the parallel conduction using
the classical thermal conductivity
(neglecting the Landau quantization).
This approximation becomes inaccurate with increasing B.
The dot-and-dash lines are calculated
for the tangential magnetic field
using the transverse conductivity in the limit of
K.
The solid curves show the results of accurate calculations
for the magnetic field normal and tangential to the surface
(cases of parallel and transverse conduction, Sect. 2.1.2).
The dashed lines are obtained for the parallel conduction using
the classical thermal conductivity
(neglecting the Landau quantization).
This approximation becomes inaccurate with increasing B.
The dot-and-dash lines are calculated
for the tangential magnetic field
using the transverse conductivity in the limit of
![]() ,
employed in previous papers
(e.g., Hernquist 1984,1985;
Schaaf 1988,1990a,1990b;
Heyl & Hernquist 1998a,1998b).
This approximation is inaccurate at lower B;
a more accurate approximation (solid line) is given by
the interpolation (Potekhin 1999)
mentioned in Sect. 2.3.2.
,
employed in previous papers
(e.g., Hernquist 1984,1985;
Schaaf 1988,1990a,1990b;
Heyl & Hernquist 1998a,1998b).
This approximation is inaccurate at lower B;
a more accurate approximation (solid line) is given by
the interpolation (Potekhin 1999)
mentioned in Sect. 2.3.2.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS1164f3.ps}\end{figure}](/articles/aa/full/2001/28/aa1164/Timg188.gif) |
Figure 3:
Temperature profiles through an iron envelope of
a NS with
|
| Open with DEXTER | |
| |
Figure 4:
Temperature profiles through an iron envelope of
a NS with
|
| Open with DEXTER | |
Figure 4 shows temperature profiles
at four field strengths B and five inclinations ![]() for
for
![]() and 109 K
(we do not present the curves for
and 109 K
(we do not present the curves for
![]() at B=1015 G
because the temperature
at B=1015 G
because the temperature ![]() is
too small near the surface in the transverse conduction case).
The curves show pronounced
is
too small near the surface in the transverse conduction case).
The curves show pronounced ![]() -dependence
at high densities starting from
the turning point (Sect. 2.3).
-dependence
at high densities starting from
the turning point (Sect. 2.3).
The endpoints of the curves in Figs. 3
and 4
lie at the radiative surface
![]() ,
where
,
where
![]() ,
and near the neutron drip point.
Their behaviour qualitatively agrees
with the results of the approximate analytic study of
Ventura & Potekhin (2001).
For instance, we confirm
the approximate linear dependence
,
and near the neutron drip point.
Their behaviour qualitatively agrees
with the results of the approximate analytic study of
Ventura & Potekhin (2001).
For instance, we confirm
the approximate linear dependence
![]() and the shift of the turning point to higher densities
with increasing B.
The density
and the shift of the turning point to higher densities
with increasing B.
The density
![]() marked on the graphs
is defined by Eq. (1). It
separates the strongly- and weakly-quantizing field regimes.
We see that the increase
of T at
marked on the graphs
is defined by Eq. (1). It
separates the strongly- and weakly-quantizing field regimes.
We see that the increase
of T at
![]() (neglected by Heyl & Hernquist 1998a)
can be significant.
(neglected by Heyl & Hernquist 1998a)
can be significant.
The higher the temperature, the wider
is the density region,
where ![]() and
and
![]() are of similar magnitude.
Therefore the dependence of the profiles on the inclination
are of similar magnitude.
Therefore the dependence of the profiles on the inclination ![]() and magnetic field strength Bis less pronounced at higher
and magnetic field strength Bis less pronounced at higher
![]() showing convergence to the B=0 case.
showing convergence to the B=0 case.
For the parallel and transverse conduction
cases (at the magnetic pole and equator)
we have, respectively,
![\begin{figure}
\includegraphics[width=11.8cm,clip]{MS1164f5.ps}\end{figure}](/articles/aa/full/2001/28/aa1164/Timg213.gif) |
Figure 5:
Dependence of the surface temperature |
| Open with DEXTER | |
Figure 6 shows the distribution of the effective
temperature from the magnetic pole to the equator.
Heavy dots show the results of numerical integration
of ![]() profiles.
Solid lines are obtained using our fit,
Eqs. (26)-(30),
while short-dashed lines correspond to the
approximation of Greenstein-Hartke (1983).
For comparison, dot-dashed lines
on the left panel represent the fitting formulae
of Schaaf (1990a,1990b).
profiles.
Solid lines are obtained using our fit,
Eqs. (26)-(30),
while short-dashed lines correspond to the
approximation of Greenstein-Hartke (1983).
For comparison, dot-dashed lines
on the left panel represent the fitting formulae
of Schaaf (1990a,1990b).
Horizontal long-dashed lines in Fig. 6
show ![]() which would have been observed at the same
which would have been observed at the same
![]() if the magnetic field were absent.
In qualitative agreement with the results
of earlier works (Sect. 1),
the thermal flux emergent from the NS interior
is suppressed by the magnetic fields
in the equatorial region and enhanced near the pole.
For a rotating NS, such distribution leads to a pulsating
light curve (e.g., Page 1995),
which may be observed, for instance, with Chandra
in soft X-rays (where the spectral flux of the
thermal NS radiation has maximum)
or with the HST in UV.
if the magnetic field were absent.
In qualitative agreement with the results
of earlier works (Sect. 1),
the thermal flux emergent from the NS interior
is suppressed by the magnetic fields
in the equatorial region and enhanced near the pole.
For a rotating NS, such distribution leads to a pulsating
light curve (e.g., Page 1995),
which may be observed, for instance, with Chandra
in soft X-rays (where the spectral flux of the
thermal NS radiation has maximum)
or with the HST in UV.
![\begin{figure}
\includegraphics[width=11.4cm,clip]{MS1164f6.ps}\end{figure}](/articles/aa/full/2001/28/aa1164/Timg227.gif) |
Figure 6:
Dependence of the surface temperature |
| Open with DEXTER | |
a1=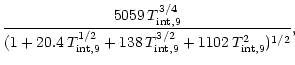 |
a2=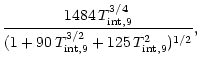 |
a3=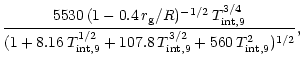 |
Note one important feature: the effect of the
magnetic field on the F(B)/F(0)ratio becomes weaker with growing
![]() .
It is explained by the arguments presented
in Sect. 3.1.
Accordingly, the luminosity
of a hot NS cannot be strongly affected even
by very high magnetic fields.
.
It is explained by the arguments presented
in Sect. 3.1.
Accordingly, the luminosity
of a hot NS cannot be strongly affected even
by very high magnetic fields.
Let us discuss briefly the effects of
magnetized envelopes on NS cooling.
For illustration, we take the models of
NSs with two masses, M=1.3 and
![]() .
For the chosen EOS in the stellar
core (Sect. 2),
the
.
For the chosen EOS in the stellar
core (Sect. 2),
the
![]() NS has the radius R=11.86 km.
Its central density
NS has the radius R=11.86 km.
Its central density
![]() g cm-3is lower than the density
g cm-3is lower than the density
![]() g cm-3 at which the powerful direct Urca process
of neutrino emission is switched on. Thus the
main neutrino emission mechanisms in the NS core are
a modified Urca process and neutrino bremsstrahlung in
nucleon-nucleon collisions. Accordingly, the
g cm-3 at which the powerful direct Urca process
of neutrino emission is switched on. Thus the
main neutrino emission mechanisms in the NS core are
a modified Urca process and neutrino bremsstrahlung in
nucleon-nucleon collisions. Accordingly, the
![]() model gives us the example of slow cooling.
For
model gives us the example of slow cooling.
For
![]() we have R=11.38 km
and
we have R=11.38 km
and
![]() g cm
g cm
![]() .
The direct Urca process is open in the central kernel
of mass
.
The direct Urca process is open in the central kernel
of mass
![]() and radius 2.84 km.
This is an example of fast cooling.
Further details of these NS models may be found
in GYP.
and radius 2.84 km.
This is an example of fast cooling.
Further details of these NS models may be found
in GYP.
We have calculated the cooling curves of NSs with magnetized envelopes, assuming the dipole magnetic field, Eq. (10). For comparison with earlier papers (Sect. 1), we also consider a familiar model of the field which is radial and constant in magnitude throughout the blanketing envelope. In addition, we have switched on and off superfluidity of neutrons and protons in stellar interiors to demonstrate the combined effects of magnetized envelopes and superfluid interiors on NS cooling.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{MS1164f7.eps}\end{figure}](/articles/aa/full/2001/28/aa1164/Timg245.gif) |
Figure 7:
Cooling curves of non-superfluid
|
| Open with DEXTER | |
The results for
![]() G are in good
qualitative agreement with those obtained
by Page (1995) and Shibanov & Yakovlev (1996).
The thermal state of the stellar interior
is almost independent of the magnetic field in the
NS envelope at the neutrino cooling stage
(
G are in good
qualitative agreement with those obtained
by Page (1995) and Shibanov & Yakovlev (1996).
The thermal state of the stellar interior
is almost independent of the magnetic field in the
NS envelope at the neutrino cooling stage
(
![]() yr), but is affected by
the magnetic field later, at the photon cooling stage.
On the contrary, the surface temperature
is always affected by the magnetic field.
The dipole field
yr), but is affected by
the magnetic field later, at the photon cooling stage.
On the contrary, the surface temperature
is always affected by the magnetic field.
The dipole field
![]() G makes
the blanketing envelope overall less heat-transparent.
This lowers
G makes
the blanketing envelope overall less heat-transparent.
This lowers ![]() at the neutrino cooling
stage and slows down cooling at the photon cooling stage.
The dipole field
at the neutrino cooling
stage and slows down cooling at the photon cooling stage.
The dipole field
![]() G makes the
blanketing envelope overall more transparent,
increasing
G makes the
blanketing envelope overall more transparent,
increasing ![]() at the neutrino cooling stage
and accelerating the cooling at the photon stage.
at the neutrino cooling stage
and accelerating the cooling at the photon stage.
Contrary to the case of the dipole magnetic field,
any radial field (e.g., Van Riper 1991)
would always lower the thermal insulation
of the blanketing envelope, increasing ![]() at the neutrino cooling stage and accelerating cooling
at the photon cooling stage. The radial field would affect
the cooling noticeably more than the
dipole field.
at the neutrino cooling stage and accelerating cooling
at the photon cooling stage. The radial field would affect
the cooling noticeably more than the
dipole field.
Even very strong magnetic fields do not change
significantly thermal insulation of a hot
blanketing envelope (Sect. 3.3).
Accordingly, the effects
of magnetic fields in a young and hot NSs
are not too strong. The strongest effects
take place in cold NSs, at the photon cooling
stage. Unfortunately, our knowledge of insulating
properties of the blanketing envelopes is the
poorest for these NSs (Sect. 2).
In addition, the magnetic field evolution
and reheating processes
may become
important for these stars, which we ignore for simplicity.
Notice that the fields
![]() G
appreciably accelerate the cooling and lower
the duration of the neutrino cooling stage.
G
appreciably accelerate the cooling and lower
the duration of the neutrino cooling stage.
For the dipole field, however, the detected flux depends
on observation direction.
The dipole field
![]() G reduces the
flux averaged over the entire NS surface (solid line)
by a factor of 1.3, while the fields
G reduces the
flux averaged over the entire NS surface (solid line)
by a factor of 1.3, while the fields
![]() and 1016 G
amplify it by factors of
about 2 and 4, respectively.
The dashed
and dotted lines in Fig. 8 refer to the fluxes detected
in the direction to the magnetic pole and equator,
respectively (assuming the magnetic axis coincides
with the rotational one, for simplicity). These
lines show the largest difference of the fluxes
detected under different angles.
They are obtained taking proper account of
the general relativity effect of bending of light rays
propagating from the NS surface to a distant observer,
in the same manner as was done by Page (1995).
For comparison, we present also the fluxes
calculated neglecting the gravitational ray-bending effect
(as if space-time outside the NS were flat).
In the absence of light
bending effects, the difference of fluxes
observed under different angles is quite
noticeable. For instance, at
and 1016 G
amplify it by factors of
about 2 and 4, respectively.
The dashed
and dotted lines in Fig. 8 refer to the fluxes detected
in the direction to the magnetic pole and equator,
respectively (assuming the magnetic axis coincides
with the rotational one, for simplicity). These
lines show the largest difference of the fluxes
detected under different angles.
They are obtained taking proper account of
the general relativity effect of bending of light rays
propagating from the NS surface to a distant observer,
in the same manner as was done by Page (1995).
For comparison, we present also the fluxes
calculated neglecting the gravitational ray-bending effect
(as if space-time outside the NS were flat).
In the absence of light
bending effects, the difference of fluxes
observed under different angles is quite
noticeable. For instance, at
![]() G
the largest difference would
be about 65%.
The light bending reduces
the largest difference to 14%
for
G
the largest difference would
be about 65%.
The light bending reduces
the largest difference to 14%
for
![]() G,
making it practically negligible.
This is explained
(e.g., Page 1995) by the fact that
gravitational bending of light rays increases
the fraction of the NS surface visible by
the observer. The observer detects the flux
from the larger portion of the surface, that
is closer to the flux averaged over observation directions.
The light bending effect is
strong for our
G,
making it practically negligible.
This is explained
(e.g., Page 1995) by the fact that
gravitational bending of light rays increases
the fraction of the NS surface visible by
the observer. The observer detects the flux
from the larger portion of the surface, that
is closer to the flux averaged over observation directions.
The light bending effect is
strong for our
![]() and
and
![]() NS models. Thus we will neglect weak dependence of
fluxes on the detection direction and use the
average fluxes and associated effective
temperatures
NS models. Thus we will neglect weak dependence of
fluxes on the detection direction and use the
average fluxes and associated effective
temperatures ![]() in our analysis.
Notice that here we mean total (spectral integrated)
fluxes but not the fluxes observed in selected
spectral bands taking into account interstellar
absorption.
in our analysis.
Notice that here we mean total (spectral integrated)
fluxes but not the fluxes observed in selected
spectral bands taking into account interstellar
absorption.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS1164f8.eps}\end{figure}](/articles/aa/full/2001/28/aa1164/Timg249.gif) |
Figure 8:
Effect of dipole
or radial surface
magnetic fields on the flux of electromagnetic
radiation F(B) detected from a
non-superfluid
|
| Open with DEXTER | |
Figure 9 shows the effective
temperatures
of young (1000 yr) non-superfluid
![]() and
and
![]() NSs with dipole and
radial magnetic fields of different strengths.
The effects of magnetic fields are similar to
those in Fig. 8.
Since the
NSs with dipole and
radial magnetic fields of different strengths.
The effects of magnetic fields are similar to
those in Fig. 8.
Since the
![]() NS undergoes fast cooling,
its internal temperature (
NS undergoes fast cooling,
its internal temperature (
![]() K)
is much lower
than in the
K)
is much lower
than in the
![]() star (
star (
![]() K).
Accordingly, the magnetic fields
affect the surface temperature of the
K).
Accordingly, the magnetic fields
affect the surface temperature of the
![]() NS more significantly. Previously,
it was suggested (e.g., Heyl & Hernquist 1997a)
that the models of
young and hot, slowly
cooling NSs with ultramagnetized envelopes
could serve as models of anomalous X-ray pulsars and
soft gamma repeaters.
Although those previous cooling models were rather simplified,
they are in qualitative agreement with our
more elaborate models.
The main outcome of these studies is that even
ultrahigh magnetic fields cannot change appreciably
the average surface temperatures of young
NSs with iron envelopes (as seen clearly
from Figs. 8 and 9).
We stress that the
local surface temperatures in narrow strips
near the magnetic equators appear to be much
lower than near the magnetic poles (Sect. 3),
but they do not contribute noticeably to the
NS luminosity integrated over the surface.
NS more significantly. Previously,
it was suggested (e.g., Heyl & Hernquist 1997a)
that the models of
young and hot, slowly
cooling NSs with ultramagnetized envelopes
could serve as models of anomalous X-ray pulsars and
soft gamma repeaters.
Although those previous cooling models were rather simplified,
they are in qualitative agreement with our
more elaborate models.
The main outcome of these studies is that even
ultrahigh magnetic fields cannot change appreciably
the average surface temperatures of young
NSs with iron envelopes (as seen clearly
from Figs. 8 and 9).
We stress that the
local surface temperatures in narrow strips
near the magnetic equators appear to be much
lower than near the magnetic poles (Sect. 3),
but they do not contribute noticeably to the
NS luminosity integrated over the surface.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS1164f9.eps}\end{figure}](/articles/aa/full/2001/28/aa1164/Timg252.gif) |
Figure 9:
Effect of dipole or radial surface
magnetic fields on the averaged
effective surface temperature
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{MS1164f10.eps}\end{figure}](/articles/aa/full/2001/28/aa1164/Timg257.gif) |
Figure 10:
Cooling of
|
| Open with DEXTER | |
It is well known that
neutron or proton superfluidity in the NS core
affects the cooling.
For illustration, we adopt the same simplified model
of nucleon superfluidity which has been used in
a number of previous works
(Yakovlev et al. 1999 and references therein).
In this model, the neutron pairing is
assumed to be in the triplet state, while the
proton pairing occurs in the singlet state of
a nucleon-nucleon pair.
The critical temperatures
![]() and
and
![]() of the neutron and proton superfluids are
assumed to be constant and treated as free parameters
to be adjusted to observational data.
Figure 10 demonstrates that taking
the neutron and proton superfluidities with certain
values of
of the neutron and proton superfluids are
assumed to be constant and treated as free parameters
to be adjusted to observational data.
Figure 10 demonstrates that taking
the neutron and proton superfluidities with certain
values of
![]() and
and
![]() we can lower
we can lower ![]() of our
Vela model to the observed values. This can be done for all
three models of the envelope, with B=0 as well as with the
dipole and radial fields. In the given examples,
the lowering of
of our
Vela model to the observed values. This can be done for all
three models of the envelope, with B=0 as well as with the
dipole and radial fields. In the given examples,
the lowering of ![]() for the dipole or field-free cases is
produced by neutrino emission due to Cooper
pairing of neutrons, while for the radial
field the lowering is produced by neutrino
emission due to Cooper pairing of neutrons and protons.
In these three cases
we need different critical temperatures
for the dipole or field-free cases is
produced by neutrino emission due to Cooper
pairing of neutrons, while for the radial
field the lowering is produced by neutrino
emission due to Cooper pairing of neutrons and protons.
In these three cases
we need different critical temperatures
![]() and
and
![]() .
In each case the choice of
.
In each case the choice of
![]() and
and
![]() is not unique.
is not unique.
Generally, if we fix the blanketing envelope model,
we can determine the domains of
![]() and
and
![]() values in the
values in the
![]() -
-
![]() plane
which force the NS
to have
plane
which force the NS
to have
![]() within the
given errorbar by the specified age t.
These domains (hatched regions) are shown in Fig. 11
for the Vela pulsar with a non-magnetic envelope,
and also for the envelope
with dipole and radial magnetic fields.
within the
given errorbar by the specified age t.
These domains (hatched regions) are shown in Fig. 11
for the Vela pulsar with a non-magnetic envelope,
and also for the envelope
with dipole and radial magnetic fields.
![\begin{figure}\par\epsfxsize=\hsize
\epsffile[35 175 470 590]{MS1164f11.eps}
\end{figure}](/articles/aa/full/2001/28/aa1164/Timg258.gif) |
Figure 11:
Domains (hatched)
of
|
| Open with DEXTER | |
The domain for the non-magnetic envelope
has a complicated X-shape.
The dipole magnetic field
facilitates a lowering of ![]() to the
required errorbar.
The domain of acceptable values
of
to the
required errorbar.
The domain of acceptable values
of
![]() and
and
![]() becomes narrower overall
and splits into two parts (Fig. 11).
In principle, in these two cases we do not need
proton superfluidity to explain the
observations (Fig. 10): the neutrino
emission due to Cooper pairing of neutrons is
sufficiently strong by itself to lower
becomes narrower overall
and splits into two parts (Fig. 11).
In principle, in these two cases we do not need
proton superfluidity to explain the
observations (Fig. 10): the neutrino
emission due to Cooper pairing of neutrons is
sufficiently strong by itself to lower ![]() .
On the other hand, were the magnetic field radial, it would
raise
.
On the other hand, were the magnetic field radial, it would
raise ![]() and complicate
the adjusting of
and complicate
the adjusting of ![]() to observations.
Neutrino emission due to Cooper pairing of neutrons is
insufficient to lower
to observations.
Neutrino emission due to Cooper pairing of neutrons is
insufficient to lower ![]() ,
and the
emission due to Cooper pairing of protons
is needed. The domain acquires a qualitatively
different shape: the proton superfluidity
cannot be too weak (
,
and the
emission due to Cooper pairing of protons
is needed. The domain acquires a qualitatively
different shape: the proton superfluidity
cannot be too weak (
![]() ).
).
The domains of
![]() and
and
![]() obtained
for the Vela pulsar
can be combined further with analogous domains
determined for other cooling NSs in attempt
to impose restrictions on the values of
obtained
for the Vela pulsar
can be combined further with analogous domains
determined for other cooling NSs in attempt
to impose restrictions on the values of
![]() and
and
![]() in the stellar cores.
A preliminary analysis of such a kind has been done
by Yakovlev et al. (1999).
However, further work remains to be done
to constrain strongly the critical temperatures:
one should take into account new observational data
on thermal radiation from isolated NSs and
new theoretical models of cooling NSs
with superfluid cores; particularly,
one has to incorporate density dependence of
in the stellar cores.
A preliminary analysis of such a kind has been done
by Yakovlev et al. (1999).
However, further work remains to be done
to constrain strongly the critical temperatures:
one should take into account new observational data
on thermal radiation from isolated NSs and
new theoretical models of cooling NSs
with superfluid cores; particularly,
one has to incorporate density dependence of
![]() and
and
![]() over the stellar core.
Such work is beyond the scope of the present
paper, but our illustrative examples show that
proper analysis of the NS superfluidity may require
consideration of
the effects of the magnetic field on the NS blanketing envelope.
over the stellar core.
Such work is beyond the scope of the present
paper, but our illustrative examples show that
proper analysis of the NS superfluidity may require
consideration of
the effects of the magnetic field on the NS blanketing envelope.
We have analysed the thermal structure of neutron star
envelopes with typical pulsar magnetic fields
1011-1013 G and with ultrahigh
magnetic fields up to 1016 G.
We have used (Sect. 2)
modern data on equation of state
and thermal conductivities of magnetized neutron star
envelopes. In particular, we have proposed
an analytic model of the radiative thermal
conductivity limited by the Thomson scattering
and free-free absorption of photons in a magnetized
plasma. We have used the values of thermal conductivity
of degenerate electrons, updated recently by
proper treatment of dynamical ion-ion
correlations which affect electron-ion scattering.
We have calculated the temperature profiles
(Sect. 3)
in the neutron star envelope for any
inclination of the magnetic field to the surface
and obtained a fit expression
which relates the internal temperature of the neutron
star to the local effective surface temperature.
We have also calculated and fitted the
relation between the internal temperature and
total surface luminosity (or effective
temperature) for the dipole magnetic fields
![]() G.
G.
Furthermore, we have performed (Sect. 4) simulations of cooling of neutron stars with dipole or radial magnetic fields in the envelopes. In agreement with the previous studies of Page (1995) and Shibanov & Yakovlev (1996), we have found that the effects of the two magnetic field configurations on neutron star cooling are qualitatively different. We have briefly discussed cooling of young and middle-aged neutron stars with ultramagnetized envelopes (magnetars as the models of soft gamma repeaters and anomalous X-ray pulsars) and the effect of surface magnetic fields on constraining critical temperatures of the neutron and proton superfluids in the cores of ordinary pulsars, considering the Vela pulsar as an example.
We stress that our results are less
reliable for cold neutron stars
(
![]() K) with
very strong magnetic fields
K) with
very strong magnetic fields
![]() G
because of lack of knowledge of ionization
state and thermal conductivity of
the outermost parts of the cold blanketing envelopes.
Further work is required to fill these gaps.
In this paper, we have considered
the blanketing envelope composed of
iron and have not analysed the envelopes
containing light elements.
The presence of light elements generally
reduces thermal insulation of the envelope.
This effect has been studied in detail
for non-magnetic envelopes (PCY)
and is expected to be important
for magnetic envelopes as well (Heyl &
Hernquist 1997a). We are planning to address
this matter in a future work.
G
because of lack of knowledge of ionization
state and thermal conductivity of
the outermost parts of the cold blanketing envelopes.
Further work is required to fill these gaps.
In this paper, we have considered
the blanketing envelope composed of
iron and have not analysed the envelopes
containing light elements.
The presence of light elements generally
reduces thermal insulation of the envelope.
This effect has been studied in detail
for non-magnetic envelopes (PCY)
and is expected to be important
for magnetic envelopes as well (Heyl &
Hernquist 1997a). We are planning to address
this matter in a future work.
Acknowledgements
We are grateful to G. Pavlov for encouragement and for providing us with the results of observations (Pavlov et al. 2001) before publication, to U. Geppert for stimulating suggestions, to Yu. A. Shibanov and K. P. Levenfish for helpful discussions, and to the referee, Dany Page, for useful remarks. This work was supported by RFBR (grant No. 99-02-18099).