A&A 374, 265-279 (2001)
DOI: 10.1051/0004-6361:20010735
LTE spectrum synthesis in magnetic stellar atmospheres
The interagreement of three independent polarised radiative transfer codes
G. A. Wade1 - S. Bagnulo2,3 - O. Kochukhov4 - J. D. Landstreet5 - N. Piskunov4 - M. J. Stift2
1 - Département de Physique,
Université de Montréal,
CP 6128 succ. Centre-Ville,
Montréal, QC, Canada H3C 3J7
2 -
Institut für Astronomie,
Universität Wien,
Türkenschanzstr. 17, 1180 Wien, Austria
3 -
European Southern Observatory,
Casilla 19001,
Santiago 19,
Chile
4 -
Uppsala Astronomical Observatory,
Box 515, 751 20 Uppsala, Sweden
5 -
Physics & Astronomy Department,
University of Western Ontario,
London, Ontario, Canada N6A 3K7
Received 10 November 2000 / Accepted 22 May 2001
Abstract
With the aim of establishing a benchmark for the detailed calculation
of the polarised line profiles of magnetic stars, we describe an
intercomparison of LTE Stokes profiles calculated using three
independent, state-of-the-art magnetic spectrum synthesis codes: COSSAM,
i10 and 2. We find, upon establishing a homogeneous basis for the
calculations (identical definitions of the Stokes parameters and the
magnetic and stellar reference frames, identical input model stellar
atmosphere, identical input atomic data, and identical chemical element abundances and
magnetic field distributions), that local and disc-integrated Stokes IQUV
profiles of Fe
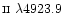 calculated using the three codes agree very
well. For the illustrative case of disc-integrated profiles
calculated for abundance
calculated using the three codes agree very
well. For the illustrative case of disc-integrated profiles
calculated for abundance
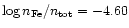 ,
dipole
magnetic field intensity
,
dipole
magnetic field intensity
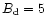 kG, and projected rotational
velocity
kG, and projected rotational
velocity
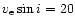 kms
kms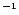 ,
Stokes I profiles (depth
,
Stokes I profiles (depth 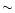 40% of
the continuum flux
40% of
the continuum flux 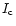 )
agree to within about 0.05% rms of
)
agree to within about 0.05% rms of 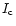 ,
Stokes V profiles (full amplitude
,
Stokes V profiles (full amplitude  10%) to within about 0.02% rms of
10%) to within about 0.02% rms of
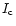 ,
and Stokes Q and U profiles (full amplitudes
,
and Stokes Q and U profiles (full amplitudes  2%) at the
sub-0.01% rms level. These differences are sufficiently small so as to allow
for congruent interpretation of the best spectropolarimetric data
available, as well as for any data likely to become available during the
near future. This indicates that uncertainties in modeling Stokes profiles
result overwhelmingly from uncertainties in input atomic and physical data,
especially the state and structure of model stellar atmospheres.
2%) at the
sub-0.01% rms level. These differences are sufficiently small so as to allow
for congruent interpretation of the best spectropolarimetric data
available, as well as for any data likely to become available during the
near future. This indicates that uncertainties in modeling Stokes profiles
result overwhelmingly from uncertainties in input atomic and physical data,
especially the state and structure of model stellar atmospheres.
Key words: line: profiles - polarisation - stars: magnetic fields -
stars: atmospheres
Magnetic fields have now been confidently detected in the atmospheres of stars
occupying most regions of the H-R diagram: on the pre-main sequence
(Donati et al. 1997; Johns-Krull et al. 1999), the lower (Johns-Krull et al. 1996),
middle (Babcock 1947, 1958) and upper (Bohlender et al. 1987)
main sequence, among evolved stars (Donati et al. 1997), and among
degenerate objects (Kemp et al. 1973). In order to study the detailed structure and
the origins of these fields, as well as their impact on other
physical processes operating in stellar atmospheres, accurate
calculations of spectral line profiles modified by the Zeeman effect are
necessary. Of particular diagnostic value are the variations of
circular and linear polarisation across spectral lines, often
referred to as the Stokes QUV profiles. Recently, the
first high-precision time-resolved observations of all the Stokes profiles of magnetic
stars were reported (Wade et al. 2000). Interpretation of these new data
requires the ability to confidently calculate synthetic Stokes profiles.
Spectrum synthesis for magnetic stars involves all the intricacies of
unpolarised spectrum synthesis - accurate atomic data, model
atmospheres, continuous opacities, and line opacities, consideration
of relevant broadening mechanisms, non-LTE effects, etc., plus a
number of other factors associated with the particular problems of
magnetic fields and polarised light: consistent definitions of the
Stokes parameters, magnetic field configuration and stellar model
geometry, accurate summation of the local Stokes IQUV profiles over the
visible stellar disc, and additional atomic data (Landé
factors and the intensities of Zeeman components). In addition, because the
amplitudes of the Stokes profiles of magnetic stars are often very
weak (of order 1% of the continuum flux) the requisite accuracy of
the calculation is substantially more stringent than is usually required for unpolarised
synthesis. Finally, polarised spectrum synthesis requires a much larger
number of calculations than does unpolarised synthesis, increasing the
computational demand and requiring faster hardware and/or more efficient
coding.
The existence of these intricacies implies that the potential exists
for substantial differences among independent calculations of
synthetic Stokes profiles. In this paper we describe a careful
intercomparison of Stokes profiles calculated using three independent
polarised spectrum synthesis codes, with the aim of quantifying their
agreement, establishing a benchmark for future calculations, and
identifying the main sources of uncertainty. Our
goal is to answer the question: how similar are the Stokes
profiles calculated by each of the three codes, under identical input
conditions (i.e. identical model stellar atmosphere, atomic data)?
As a secondary goal we examine the sensitivity of the calculated profiles to changes in the
input conditions. In Sect. 2 we introduce the three synthesis
codes, and in Sect. 3 we establish a consistent astrophysical basis for
the comparison. In Sect. 4 we describe an extensive series
of tests designed to evaluate the agreement among local and
disc-integrated synthetic Stokes profiles, and in Sect. 5 we discuss the
dependence of this agreement on changes in the input
conditions, and summarise our findings.
Modeling the spectral line profiles of non-magnetic stars in LTE requires
the solution of the unpolarised radiative transfer problem, which involves a
single first-order linear differential equation. Treatment of the spectral
lines of magnetic stars in LTE, on the other hand, requires the solution of
a set of four coupled
first-order linear differential equations, one for each Stokes parameter![[*]](/icons/foot_motif.gif) (e.g. Rees 1987).
The practical problem of computing the solution to this system of equations is the
polarised radiative transfer, or PRT, problem.
(e.g. Rees 1987).
The practical problem of computing the solution to this system of equations is the
polarised radiative transfer, or PRT, problem.
COSSAM stands for "Codice per la sintesi
spettrale nelle atmosfere magnetiche''.
It is the first object-oriented parallel code in the field of
(polarised) spectral line synthesis and is the result of a
major software engineering effort. COSSAM
is designed for the accurate direct calculation
of full Stokes IQUV spectra in the sun or in rotating
and/or pulsating stars whose magnetic fields are
represented by a tilted, eccentric dipole, or by
a dipole-quadrupole expansion.
Genealogists won't find it difficult to trace COSSAM back
to the ALGOL60 code Analyse65 by Baschek
et al. (1966) and its FORTRAN adaptation ADRS
(Peytremann et al. 1967). An evolved version ADRS3 by
Chmielewski (1979) was modified by Stift (1985) in
order to synthesise Stokes I and V profiles in
rotating and/or pulsating magnetic stars. Restricting the
scope of the code to the synthesis of a single Zeeman-split
line with an arbitrarily complex Zeeman pattern in intensity
and circular polarisation made it possible to employ the
fast polarised formal solver given in Hardorp et al. (1975);
the systematic investigation
of theoretical Stokes V profiles for magnetic stars was made feasible on a
VAX11/750.
The study of broadband linear polarisation (BBLP)
in CP stars by Landolfi et al. (1993) made it clear that, in
order to investigate and exploit the full diagnostic contents
of BBLP, there was an urgent need for a code that could
synthesise full Stokes profiles in (heavily) blended spectra.
An attempt to modify the existing FORTRAN-77 code in a
way as to be able to calculate full Stokes profiles for blends
was abandoned when it emerged that there would be no readable
and easily modifiable code without the radical rewriting of
the code in a language of less restricted expressive power.
The first software design solution for a Stokes code in Ada83
was presented in 1993 more or less in the guise of a Christmas
present by a student, G. Könighofer. The convincing design
and the impending revision of Ada which promised so many
powerful new language features (now all found in Ada95) never
left any doubt as to the desirability of exploring object-oriented
parallelism with Ada95. Ultimately this has led to the development
of a whole family of parallel codes including COSSAM, a
Zeeman Doppler Imaging code, and CARAT, a code for the
calculation of radiative accelerations in magnetic atmospheres.
Polarised spectral line synthesis in the Zeeman regime is
not overly complicated from the physical or numerical
point of view; the difficulties lie in software engineering
issues. The ultimate goal of portability, modifiability,
extensive software reuse and parallelism in addition to
computational efficiency can only be attained by using a
standardised object-oriented language with parallel constructs
(see Stift 1998a, for an introduction and code examples).
A data type is characterised by a set of values and
a set of operations that can be applied to those values.
There is no implicit type conversion in Ada95, in contrast to
FORTRAN. This strong typing implies that values of one
type cannot be assigned to variables of another type, enabling
incredibly extensive static compiler checks.
Values can be stored in objects, declared to be of a specific
type. Each type declaration introduces a new type totally
distinct from any other type; it subsequently has to be
exported (made visible) to other software modules. Data
types can be of almost arbitrary complexity (see e.g. Stift 1996).
Efficient "programming in the large'' must be based on
truly reusable software components ("verbatim reuse'').
The use of abstract data types, encapsulation, information
hiding, generics, inheritance and programming by extension
is essential for this purpose; we may loosely designate
it as object-orientation.
A large program - such as COSSAM - builds on numerous
user-defined data types and many subprograms. Type definitions
and their associated operations can be encapsulated in
packages, and it is also often useful to group together related
subprograms in packages. In order to facilitate software
reuse, packages (and subprograms) can be parameterised.
Generic packages are templates with formal
parameters which have to be instantiated with
actual parameters.
Any extension to a package which is used in many different programs
will lead to the necessity of recompiling all programs that use
this package; it may also introduce new bugs in a well tested,
trusted software component. Ada95 allows "incremental programming'':
you can extend existing packages without recompilation. Child
units have full access to all the declarations and subprograms in
their ancestors. Types and subprograms can be overloaded, i.e.
replaced by alternative ones of the same name.
In contrast to High Performance FORTRAN, Ada95 provides thread-parallel
task constructs. Tasks are program entities that perform a
sequence of actions and that can execute concurrently within
the same program on several processors. Tasks are declared as
task objects and start to execute upon elaboration of
the object declaration; each task has its own thread of control.
Protected objects, which do not have a thread of control of
their own, are accessed in mutual exclusion, i.e. only one
process can update a variable at a time. In the rendezvous
mechanism a task can call an entry of another task or
accept a call on one of its own entries. Protected objects
and the rendezvous are used for synchronisation between task and
calling program, or between different tasks.
COSSAM works under the assumption of LTE in a plane-parallel
atmosphere. The atomic transitions are taken from the VALD
database (Piskunov et al. 1995). The atomic partition functions
are normally calculated with the Kurucz (1993) routine rewritten
in Ada95, but one can also choose those by Traving et al. (1966),
Irwin (1981), or Cowley (1998). In the Saha equation the lowering
of the ionisation potential as a function of temperature and
electron density is taken into account. Radiation damping, Stark
broadening and van der Waals broadening constants are taken from
VALD. When experimental constants are unavailable, classical radiation damping and Unsöld van der Waals broadening respectively are assumed, and Stark broadening can be ignored or
approximated according to Gonzalez et al. (1995).
The Zeeman splitting and component strengths are calculated with the help of the Landé
factors and J-values of the respective lower and upper energy
levels provided by VALD. A classical Zeeman-triplet is assumed
whenever Landé factors are missing. Partial Paschen-Back
effect is not taken into account.
For the continuous opacity
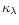 at a given
wavelength, COSSAM interpolates in a 2D table
(wavelength - depth) provided by ATLAS9 (Kurucz 1993).
The total line opacities required in the formal solver are
determined by full opacity sampling of the
at a given
wavelength, COSSAM interpolates in a 2D table
(wavelength - depth) provided by ATLAS9 (Kurucz 1993).
The total line opacities required in the formal solver are
determined by full opacity sampling of the
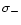 ,
the
,
the
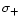 ,
and
,
and 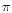 components separately.
components separately.
For metallic lines, COSSAM employs the rational approximation
to the Voigt and Faraday functions given in Landolt-Börnstein
(1982). The hydrogen line profiles are calculated by interpolation in the
tables given by Stehlé & Hutcheon (1999). As to the polarised
formal solver, the user has the choice between the Zeeman Feautrier
method (Auer et al. 1977) and the somewhat faster but less accurate
DELO method (Rees et al. 1989). Magneto-optical effects are normally
included in the formal solution but there is a runtime option to
suppress them.
In the "solar case'' (local case) the emerging spectrum is calculated for one
given point (with a given magnetic vector) on the solar surface,
whereas in the "stellar case'' (disc-integrated case), COSSAM integrates the emerging
spectrum over the visible hemisphere, taking into account rotation,
(non)radial pulsation and global (dipolar and/or quadrupolar)
magnetic field structure. A special algorithm discussed by Stift
(1985) and Fensl (1995) provides an optimum grid for this
2D-integration, thereby greatly reducing the number of quadrature
points required in comparison to fixed grids.
Task types and protected types are part of the Ada95 kernel
language, so COSSAM is perfectly transportable from any
PC to a 512-processor supercomputer: exactly 2 lines of code
have to be changed! No message passing libraries, no need to
delve into pthread-programming, no extra software to be bought
and/or installed. And there is a public version of COSSAM
which is free software, available for many platform/operating system
combinations; you can redistribute it and/or modify
it under the terms of the GNU General Public License as
published by the Free Software Foundation. Source code, data
files and documentation can be downloaded from:
http://fedelma.astro.univie.ac.at/web/cossam/index.html
INVERS10 is a Magnetic Doppler Imaging code designed for reconstructing
the distribution of magnetic field
vectors and abundance of one chemical
element over the surface of magnetic Ap stars. The maps are recovered from
a time series of the spectropolarimetric observations by solving a
regularised inverse problem.
The core of INVERS10 is a magnetic spectrum synthesis code that
solves the equation of radiative transfer for four Stokes parameters for
all visible elements on the stellar surface, and performs disc integration
to simulate the observed Stokes spectra. We have implemented two transfer
algorithms: magnetic (or Zeeman)
Feautrier and Diagonal Element Lambda Operator (DELO). Both algorithms
have advantages and problems and the final choice is unclear at this
stage.
The Feautrier method is well-established as a fast and very stable
radiative transfer solver for non-magnetic synthesis. Therefore, it was logical
to extend it to the case of magnetic synthesis. Such an algorithm was first
formulated by Auer et al. (1977). Similar to conventional
Feautrier, the vector of Stokes parameters throughout the atmosphere is
found by solving a system of linear equations with the right-hand side
dependent upon the source function and with a block tri-diagonal matrix.
Each matrix element consists of a 4 4 block dependent upon the
total opacity matrix. The magneto-optical effects are included as
cross-terms between the Q, U and V Stokes parameters in the opacity
matrix. During the course of multiple tests we discovered that the primary advantages of
the Feautrier techniques (stability and rapid convergence) are
preserved in the magnetic case. On the other hand, we found a problem with
numerical stability caused by the fact that the opacity matrix K can become nearly degenerate. This happens, for example, for a
strong magnetic field in the the cores of Zeeman sigma components
(Piskunov 1999). The solution is to use matrix pivoting when
inverting the opacity matrices, a procedure that is costly in terms of computing
time (factor of 2).
4 block dependent upon the
total opacity matrix. The magneto-optical effects are included as
cross-terms between the Q, U and V Stokes parameters in the opacity
matrix. During the course of multiple tests we discovered that the primary advantages of
the Feautrier techniques (stability and rapid convergence) are
preserved in the magnetic case. On the other hand, we found a problem with
numerical stability caused by the fact that the opacity matrix K can become nearly degenerate. This happens, for example, for a
strong magnetic field in the the cores of Zeeman sigma components
(Piskunov 1999). The solution is to use matrix pivoting when
inverting the opacity matrices, a procedure that is costly in terms of computing
time (factor of 2).
The alternative DELO method suggested by Rees et al. (1989)
replaces the opacity matrix with so-called pseudo-opacity matrix in
which the diagonal is always dominant. The formal solution of the
radiative transfer equation at each tabulated atmospheric depth is evaluated analytically
assuming a linear depth dependence of the source function. This allows the
construction of a one-way integrator for the Stokes parameters. At each
integration step this requires the inversion of a single 4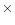 4 matrix, which can
be performed very efficiently without pivoting. For a modern
super-scalar workstation that translates into 2.5 times speed increase
compared to Feautrier. Unfortunately, the convergence properties (the
decrease of residual errors with the number of vertical integration steps) is noticeably
worse than for Feautrier. For this reason the Feautrier version of INVERS10
was used for all the tests in this paper.
4 matrix, which can
be performed very efficiently without pivoting. For a modern
super-scalar workstation that translates into 2.5 times speed increase
compared to Feautrier. Unfortunately, the convergence properties (the
decrease of residual errors with the number of vertical integration steps) is noticeably
worse than for Feautrier. For this reason the Feautrier version of INVERS10
was used for all the tests in this paper.
The calculations of the opacity matrix and the source function assume
LTE and an unpolarised continuum. The code is capable of calculating synthetic
spectrum over several wavelength intervals by combining the
opacity matrices of individual lines and interpolating the continuum
intensities between the two ends of each interval. The calculations of
continuous opacities and partition functions are adapted from the
ATLAS9 code (Kurucz 1993), with the exception of rare earth
elements for which the partition functions were provided by Cowley
(1998).
The main purpose of INVERS10 is to solve the inverse problem, which
means reconstructing the magnetic vector and abundance value at each point
on the visible stellar surface. This goal requires that the implementation of
the radiative transfer solver be both fast and accurate. We have
separated the program in two parts. The main part performs input/output,
constructs the surface grid and pre-calculates the line opacities and
damping in the center of each line throughout all atmospheric layers. We
assume the same atmosphere model to be suitable for all surface elements and the
abundance/magnetic field vector to be constant within each element (both horizontally and
vertically). The main program also performs disc integration and adjustment of the
abundance and magnetic field values based on comparison with the observations.
The surface grid employs fixed steps in latitude and variable steps in
longitude that preserve approximately the area of surface elements. The
radiative transfer is performed by a separate program (RT solver). Several
RT solvers can run in parallel. The main program initialises each RT
solver by passing the table of central line opacities and damping
parameters. During disc integration the main program passes the local
abundances and magnetic field vector, as well the orientation of the
surface element relative to the line-of-sight for all rotational phases.
After initiating the calculations for the first element the main program
continues distributing surface elements to available RT solvers until all are
busy. Each RT solver constructs the total opacity matrix and solves the
radiative transfer equation for 4 Stokes parameters on an adaptive wavelength grid
which ensures accurate linear interpolation between wavelength samples. The
calculations are repeated for all rotational phases. Next the polarisation
spectra are interpolated onto an equispaced wavelength grid and convolved with the
instrumental profile using a Fast Fourier Transform. Finally the spectra are
returned to the main program for disc integration.
The main program receives the data from the RT solver that first completes the
calculations and restarts that solver with the data for the next surface element
in the queue.
In this way an automatic load balance is achieved when INVERS10 is
used on a multi-CPU machine. The implementation of the RT solver as a
separate program allows experimentation with different numerical
algorithms without modification to the main component of INVERS10.
The typical size of the surface grid is between 300 and 2500 elements. The
disc integration takes into account rotational Doppler shifts for each rotational
phase and the transformation of the Q and U Stokes parameters to the
observer's frame.
The INVERS10 code can be used for simulating Stokes parameters for a
star with arbitrary field and surface abundance
distribution geometry (forward mode) or for Magnetic Doppler Imaging (inverse mode).
For inverse mode, high-quality spectropolarimetric observations for different
rotational phases are required. Based on numerical experiments, typically 30-40
iterations are required to
reconstruct both the magnetic field and abundance maps. For smooth global
fields we have developed a special type of multipolar regularization that
allows the use of a limited dataset (only Stokes I and V) (Piskunov &
Kochukhov 2000, in preparation).
ZEEMAN2 is the descendant of the original FORTRAN-77 LTE line
synthesis code ZEEMAN, described by Landstreet (1988). The code is
designed both for direct calculation of polarised spectra and for
modeling of data using a simple field description
and a simply parametrised element distribution.
Here we
provide a short history of the code and the motivation for its
development, and a description of its internal workings, especially
its scheme for integration of the polarised transfer equations.
In the early 1980's it was clear that interest in obtaining Doppler
abundance maps of magnetic Ap stars was increasing. However, mapping
was focussed on reconstructing equivalent width distributions in stars
with particularly weak fields, so that simple local line profiles
could be used. Therefore mapping was moving in the direction of
studying precisely the stars for which one knows the least about the
magnetic geometry. From the point of view of clarifying what diffusion
theory has to explain, this seemed relatively unhelpful. In fact, the
most interesting stars to model are the ones for which one has the
maximum of information about both the field and the abundance
patches. But clearly to model these stars one must be able to model
strongly magnetically-split lines.
The
intention of ZEEMAN was never to do detailed magnetic or abundance
mapping, but rather to obtain approximate models of both
magnetic field and abundance distributions for a few stars at a level
of detail suitable for comparison with diffusion theory.
It was decided from the outset to try to include as much physics as
was affordable, so as to have reasonable confidence that the
synthesis was physically reasonable. However, the slowness and cost of
computers made forward integration only (and small arrays and mimimal
CPU time) a necessity. It was planned initially to make comparisons
by eye and to adjust by hand; this was the procedure used by
Landstreet (1988) in modeling 53 Cam. However, after initial
experiments indicated that ZEEMAN ran some 50 (!) times faster on a Cray
than on a Cyber 835, the potential for automatic fitting became clear
and the code was modified to allow for control by a least-squares
optimisation routine. The subroutine responsible for integration of
the transfer equations was also rewritten to allow it to
vectorise on the Cray (another gain of 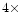 in speed).
in speed).
Besides the standalone line synthesis version of 2 (which is
capable of producing Stokes IQUV spectra for both the local
and disc-integrated cases) used for the calculations reported in this
paper, 2 is currently incorporated into a suite of tools for
modeling (in the simple ZEEMAN tradition) horizontal abundance
nonuniformities, vertical abundance stratification, and radial
pulsation simultaneously with recovery of the axisymmetric multipolar
magnetic field geometry, using observations in all 4 Stokes
parameters.
To numerically integrate the polarised transfer equations, both ZEEMAN and 2 employ the efficient quasi-analytic technique proposed by Martin
& Wickramasinghe (1979). This technique assumes that the coupled
transfer equations have constant coefficients between successive
tabulated atmospheric depths, so that the analytic Unno-Rachkovsky
solution may be used at depth m in the atmosphere to calculate the
values of the Stokes parameters from values at depth m+1. This
technique is essentially as accurate as, and is much faster than,
direct integration of the transfer equations.
Martin & Wickramasinghe present two general solutions to the
transfer problem: the "restricted'' solution for 3 Stokes parameters
ignoring anomalous dispersion, and the "full'' solution for 4 Stokes
parameters including anomalous dispersion. With the expectation that
anomalous dispersion would not strongly affect the calculated Stokes
profiles (and Stokes I in particular), Landstreet (1988) adopted
the "restricted'' solution; this solution requires about 50% less
time for execution than does the "full'' solution![[*]](/icons/foot_motif.gif) .
.
The most fundamental difference between ZEEMAN and 2 involves the
inclusion of anomalous dispersion in the solution to the polarised
transfer equations, accomplished by substituting the 4 Stokes
parameter solution of Martin & Wickramasinghe for their 3 Stokes
parameter solution. This turned out to be a highly nontrivial
exercise: even for the relatively simple 3 Stokes parameter solution,
Landstreet (1988) found that in the special case where the line
absorption coefficients 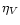 and
and 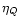 vanish, the transfer
equations decouple and a special subsolution (Landstreet 1988) must be
employed. In the case of the 4 Stokes parameter solution, the
potential for decoupling increases manyfold, and 9 independent
subsolutions (including the "full'' solution and the "restricted''
solution as special cases) are required. It was necessary to derive
these subsolutions in order to implement the 4 Stokes parameter
transfer solution in 2. Details regarding the particular
pathologies and requisite subsolutions of the Martin & Wickramasinghe 4
Stokes solution can be obtained by contacting JDL.
vanish, the transfer
equations decouple and a special subsolution (Landstreet 1988) must be
employed. In the case of the 4 Stokes parameter solution, the
potential for decoupling increases manyfold, and 9 independent
subsolutions (including the "full'' solution and the "restricted''
solution as special cases) are required. It was necessary to derive
these subsolutions in order to implement the 4 Stokes parameter
transfer solution in 2. Details regarding the particular
pathologies and requisite subsolutions of the Martin & Wickramasinghe 4
Stokes solution can be obtained by contacting JDL.
ZEEMAN2 employs pretabulated plane-parallel atmosphere
models (e.g. ATLAS models).
Atomic data is extracted from various sources (usually the
VALD database), and Zeeman patterns are calculated using the L, S and
J quantum numbers characterising the upper and lower levels of the
transitions to calculate splitting and Landé factors (assuming LS coupling).
Partition functions are
calculated from polynomial approximations taken from Bolton (1970,
1971) for elements up to Zr, and from Aller & Everett (1972), Cowley & Adelman
(1983) and Cowley (1994) for more massive elements, and partition functions from Irwin (1981)
are also available. Ionic populations are calculated for
(up to) the fourth ionisation state (i.e. up to state
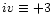 )
using the Saha equation. Radiation damping, van der
Waals broadening and quadratic Stark broadening are each taken into
account, usually using constants supplied from the literature
(usually VALD), and otherwise classical radiation damping and the
Unsöld approximation for van der Waals broadening are
assumed. Quadratic Stark effect is otherwise calculated using the
approximation described by Cowley (1971) for neutrals, and the
approximation of Griem (1968) as simplified and empirically
recalibrated by Gonzalez et al. (1995) for ions broadened by
electrons.
)
using the Saha equation. Radiation damping, van der
Waals broadening and quadratic Stark broadening are each taken into
account, usually using constants supplied from the literature
(usually VALD), and otherwise classical radiation damping and the
Unsöld approximation for van der Waals broadening are
assumed. Quadratic Stark effect is otherwise calculated using the
approximation described by Cowley (1971) for neutrals, and the
approximation of Griem (1968) as simplified and empirically
recalibrated by Gonzalez et al. (1995) for ions broadened by
electrons.
ZEEMAN2 does not presently calculate
lines of He or H (although implementation is currently underway).
Metallic line opacity and anomalous dispersion
profiles are described assuming the Voigt H(a,v) and Faraday-Voigt F(a,v) functions
calculated using the numerical recipe by Humlicek (1982). We note that the
Faraday-Voigt function produced using this formulation implicitly
includes a factor of 2, i.e. it in fact results in 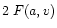 .
.
Continuous opacities are calculated for H I, H-, He I
bound-free (b-f) and free-free (f-f) transitions, Rayleigh scattering
by H I and electron scattering (both treated as
absorption). H I b-f Gaunt factors are from Carbon & Gingerich
(1969), while those for H I f-f are calculated from the
Menzel-Pekeris approximation (as quoted by Gray 1992). H- b-f and
f-f are calculated from the polynomial fits by Gingerich (1964),
which give results similar to those reported by Gray (1992). He
I b-f and f-f opacities are calculated using a hydrogenic
approximation, as discussed briefly by Gingerich (1964) and Mihalas
(1970). Rayleigh scattering by H I is calculated using an
expression from Dalgarno quoted by Gingerich (1964).
The magnetic field is described as a oblique axisymmetric linear
multipole including terms up to the octupole. Departures from
axisymmetry can be introduced by multiplying such an axisymmetric
field distribution by a series of spherical harmonics consistent with
those employed in the modeling by Leroy et al. (1996).
At each rotational phase, the visible stellar disc is divided into anywhere
from about 60
up to several thousand subelements of
approximately equal
projected area (Landstreet 1988), and in each
subelement the transfer equations are
integrated vertically through the atmosphere for the specific
local abundance and magnetic field
(assumed constant both
vertically and horizontally in each subelement) to
yield the surface Stokes intensities
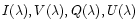 .
Because the transfer calculation occurs in the frame of
reference of the surface subelement, the surface intensities can be
summed for Doppler shifts corresponding to various macroscopic velocity
fields (in particular
projected rotational velocities,
.
Because the transfer calculation occurs in the frame of
reference of the surface subelement, the surface intensities can be
summed for Doppler shifts corresponding to various macroscopic velocity
fields (in particular
projected rotational velocities,
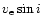 )
before convolution with
the (assumed Gaussian) instrumental profile.
)
before convolution with
the (assumed Gaussian) instrumental profile.
Spectral line synthesis is an "embarrassingly parallel''
problem. Sampling the opacity, solving the transfer
equation, and integrating the local Stokes
parameters over the stellar disc can be carried out in parallel for all line
frequencies.
INVERS10 is written in FORTRAN-77, and the communication
between the main program and the RT solvers is based on
the Message Passing Interface (MPI). MPI is available as
a public domain library as well as proprietary packages
for all major brands of high-performance computers.
COSSAM, developed in Ada95, relies on light-weight
synchronisation by means of protected objects which
provide exclusive read-write access or concurrent
read-only access to shared data. For more details on concurrency
and synchronisation with Ada95 in the context of
astrophysics the reader is referred to Stift (1998b).
Gene Amdahl in 1967 postulated that there is a maximum
speedup that can be achieved by using many processors
in parallel processing. Since the nature of the
synchronisation overhead in parallelism appears to be
sequential, the maximum speedup that can be achieved by
using P processors is given by
1/(F+(1-F)/P) where
F is the fraction of a calculation that is sequential
(essentially synchronisation). This is known as Amdahl's law.
The granularity of the parallel calculations by
i10 or COSSAM determines when Amdahl's law becomes
important. Several choices are possible which depend
on the way the supercomputer facilities are organised.
In Uppsala, on a Hewlett Packard V2500 server and a Cray T3E
with up to 128 CPUs, i10 is run on a number of CPUs
which are also used by other jobs. Thus the available resources
are constantly changing. The parallelisation scheme has
to be capable of always using all currently available resources;
we may refer to this as "dynamic load balance''. Even when the
various individual processes do not finish at the same time,
there is no waste of resources thanks to the other users.
It is therefore possible to employ coarse-grained
parallelism: i10
distributes calculations related to individual disc surface elements
among the available processors, so
synchronisation can take place only after a full local
Stokes profile has been calculated. With F as low
as 10-4 or 10-5, linear scaling is fulfilled up to
a few hundred CPUs.
COSSAM and CARAT, a code to calculate radiative accelerations,
have been devised to run on supercomputers of the SGI Origin
family. With the "Miser'' deterministic batch scheduling
facility a fixed number of CPUs must be reserved. It is
imperative to achieve almost perfect load balance among the
various Ada taks to avoid waste of resources allocated
exclusively to the job. This implies a more fine-grained
parallelism. COSSAM and CARAT distribute 1 Å wavelength
intervals rather than surface elements. Although only
1 protected is necessary for synchronisation
purposes, the value of F can go up to around 10-3. Amdahl's
law then implies that it does not make sense to use more than
typically 64 CPUs. Note that this fine-grained parallelism
will also achieve perfect load-balance on systems where CPUs
are not allocated exclusively to a single user.
Summarising this discussion, we want to emphasise that there
is no single optimum approach to parallelism, not even in the
restricted field of (polarised) spectrum synthesis. It is
relatively easy to obtain near perfect load balance. The
number of CPUs up to which speedup is linear depends on the
granularity of the approach, is given by Amdahl's law, and
strongly depends on how the supercomputing facility is organised.
As stated in the introduction, our goal is to examine
the agreement of the Stokes profiles
calculated by the three codes under identical input
conditions. This requires that we ensure the consistency of the
stellar model geometry, as well as the input model atmosphere and
input atomic data upon which each code relies. Once this has been
established we can begin to explore the level of agreement of the
additional data calculated implicitly by each code (atomic and ionic
populations, line and continuous opacities) which are furthermore
required for the radiative transfer calculation. This procedure
will aid in establishing the source of any differences between the Stokes profiles
calculated by the codes.
The calculation of Stokes profiles in the disc-integrated case
presents some obvious complications with respect to the local
case. The radiative transfer problem must be solved on a
two-dimensional spatial grid, which multiplies manyfold the
computational expense of the calculation. As well, definitions of the
(complex) stellar geometry and magnetic field configuration are
required.
In fact, for the non-magnetic case, when gravity-darkening
is not significant, the projected equatorial rotational velocity
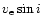 is the only parameter required to account for the
stellar orientation and rotational velocity. By contrast, in the
magnetic case, particular attention must be devoted to provide an
unambiguous description of both the orientation of the star's
rotation axis and the magnetic field configuration. The
photospheres of many magnetic Ap stars are permeated by a relatively
smooth magnetic field, usually not symmetric about the rotational
axis. A magnetic dipole, tilted with respect to the
rotational axis, represents a natural first approximation for the
magnetic morphology of this class of stars. Hence, we decided to adopt
this simple example of the oblique rotator model (ORM) as
representative of many real cases of astrophysical interest. A full
characterisation of the dipolar ORM requires six parameters. Three of
them specify the orientation of the star's rotation axis, and its rotational velocity:
is the only parameter required to account for the
stellar orientation and rotational velocity. By contrast, in the
magnetic case, particular attention must be devoted to provide an
unambiguous description of both the orientation of the star's
rotation axis and the magnetic field configuration. The
photospheres of many magnetic Ap stars are permeated by a relatively
smooth magnetic field, usually not symmetric about the rotational
axis. A magnetic dipole, tilted with respect to the
rotational axis, represents a natural first approximation for the
magnetic morphology of this class of stars. Hence, we decided to adopt
this simple example of the oblique rotator model (ORM) as
representative of many real cases of astrophysical interest. A full
characterisation of the dipolar ORM requires six parameters. Three of
them specify the orientation of the star's rotation axis, and its rotational velocity:
The (dipolar) magnetic field configuration is
specified by three additional parameters:
- the strength of the dipolar field, usually expressed in terms of
field strength at the positive magnetic pole,
 ;
;
- the obliquity
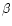 (
(
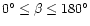 )
of the magnetic dipole axis with respect to the rotation axis, counted from the positive
rotational pole toward the positive magnetic pole;
)
of the magnetic dipole axis with respect to the rotation axis, counted from the positive
rotational pole toward the positive magnetic pole;
- the rotational phase f (
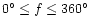 ); for its detailed
definition we refer the reader to Landolfi et al. (1993); in fact, the rotational phase
is commonly expressed as a fraction of the rotational cycle, sometimes normalised to
100 (e.g., Leroy 1995), or more often to 1 (e.g., Mathys 1993).
); for its detailed
definition we refer the reader to Landolfi et al. (1993); in fact, the rotational phase
is commonly expressed as a fraction of the rotational cycle, sometimes normalised to
100 (e.g., Leroy 1995), or more often to 1 (e.g., Mathys 1993).
As a step toward ensuring homogeneity of the input data, we have adopted
identical model atmospheres for all spectrum synthesis calculations
reported here. The adopted model atmosphere has effective temperature
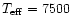 K, surface gravity (in cgs units)
K, surface gravity (in cgs units)
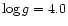 ,
solar metallicity, 2 kms
,
solar metallicity, 2 kms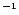 microturbulence, and has been calculated using ATLAS9 (Kurucz 1993) with standard convection treatment. For this adopted 72-level model, the
logarithmic standard optical depth
microturbulence, and has been calculated using ATLAS9 (Kurucz 1993) with standard convection treatment. For this adopted 72-level model, the
logarithmic standard optical depth
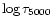 reaches 0.0 around level 58
(as measured from the top of the atmosphere).
reaches 0.0 around level 58
(as measured from the top of the atmosphere).
Most line synthesis calculations in this paper are for Fe
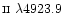 .
All
calculations of this line employ identical transition data.
The relevant atomic data has been extracted directly from the VALD
database, and is reported in Table 1
.
All
calculations of this line employ identical transition data.
The relevant atomic data has been extracted directly from the VALD
database, and is reported in Table 1![[*]](/icons/foot_motif.gif) .
.
To furthermore ensure homogeneity of the input data, we have adopted identical
partition functions u(T) for Fe II
for these tests. The adopted values of u(T) correspond to those reported by
Drawin & Felenbock (1965).
In the remainder of this section we employ the three codes, along
with this standardised input data, to compare the consistency of the
calculated ionic populations and continuous and line opacities.
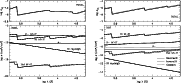 |
Figure 1:
Continuous opacity distributions for 2, COSSAM and i10. Left - selected
sources for the "cool'' conditions shown in Table 1: right - selected
sources for the "hot'' conditions shown in Table 1. The upper frames show the total opacity for the three codes due to all calculated sources. |
| Open with DEXTER |
Using the atmosphere model discussed above, the calculated
populations of all ionisation states of H and He among the three
codes agree to better than 0.01% of the total populations at
atmospheric depths above 40, and to better than 0.5% for deeper
layers.
As discussed in Sect. 2, 2 and i10 calculate continuous opacities
during execution, while COSSAM adopts opacities output from
ATLAS9. In Fig. 1 we compare continuous opacities for the three
codes, calculated for the two different sets of physical conditions
outlined in Table 2. The agreement for individual source and total
opacity appears fairly good on the logarithmic ordinate of Fig. 1. In
fact, the total continuous opacities employed by the three codes
differ systematically by less than 5% in the visible for the cool
conditions, but by about 10% for the hot conditions. In the near
infra-red the agreement worsens somewhat.
Among individual sources, the electron scattering opacity
employed by COSSAM for the hot conditions shows relatively
large differences from the other codes' calculations.
The line opacity
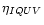 and
anomalous dispersion
and
anomalous dispersion
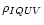 are related to the total
absorption and anomalous dispersion profiles of the
are related to the total
absorption and anomalous dispersion profiles of the 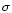 and
and
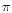 Zeeman components via the Voigt H(a,v) and Faraday-Voigt
F(a,v) functions. Both H and F as calculated by each of the
codes agree to within 0.2%.
Zeeman components via the Voigt H(a,v) and Faraday-Voigt
F(a,v) functions. Both H and F as calculated by each of the
codes agree to within 0.2%.
Differences in the calculated damping a will impact the calculated
wings of saturated lines. In Fig. 2 we compare for the three codes
radiative, van der Waals and quadratic Stark damping constants
calculated for all atmospheric levels for Fe
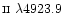 .
The typical spread in
total damping is smaller than 1%, although more important systematic
differences do exist among the individual damping contributors. The
most important systematic difference is associated with the quadratic
Stark calculation, where deeper in the atmosphere than level 68 the 2 calculation differs
from the others by a maximum of about 10%. Quadratic Stark is the
primary damping mechanism in these deepest layers of the atmosphere,
and this results in a difference in the 2 total damping below
level 68 of about 8% with respect to the others (which maintain
agreement to within 1%). However, the standard continuum optical
depth
.
The typical spread in
total damping is smaller than 1%, although more important systematic
differences do exist among the individual damping contributors. The
most important systematic difference is associated with the quadratic
Stark calculation, where deeper in the atmosphere than level 68 the 2 calculation differs
from the others by a maximum of about 10%. Quadratic Stark is the
primary damping mechanism in these deepest layers of the atmosphere,
and this results in a difference in the 2 total damping below
level 68 of about 8% with respect to the others (which maintain
agreement to within 1%). However, the standard continuum optical
depth
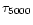 in these layers is greater than 20, and the
differences in damping have no significant effect on the line profile
calculation.
in these layers is greater than 20, and the
differences in damping have no significant effect on the line profile
calculation.
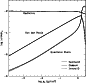 |
Figure 2:
Radiative, van der Waals and quadratic Stark effect damping coefficients for Fe
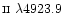 versus column mass, calculated for all levels of the test model atmosphere.
versus column mass, calculated for all levels of the test model atmosphere. |
| Open with DEXTER |
Having explored the uncertainties resulting from the basic physical data necessary for the synthesis, we now examine the agreement among synthetic Stokes profiles.
A comparison of the emergent Stokes profiles calculated at a single
point on the stellar surface, characterised by a single uniform
magnetic field vector, provides us with the most stringent test of
the results of the transfer calculations. We have performed a variety
of such tests for Fe
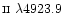 ,
for null, weak and strong magnetic fields with
various orientations, as
well as for various surface positions (limb angles) and Fe
abundances. The quantitative agreement among the local profiles is summarised in Table 3.
,
for null, weak and strong magnetic fields with
various orientations, as
well as for various surface positions (limb angles) and Fe
abundances. The quantitative agreement among the local profiles is summarised in Table 3.
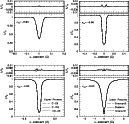 |
Figure 3:
Local disc-centre profiles of Fe
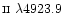 calculated for zero magnetic field and four abundances:
calculated for zero magnetic field and four abundances:
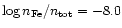 ,
-6.0, -4.6 and -3.0. The larger lower frames ( profile frames) compare the profiles calculated by i10, COSSAM and 2, while the smaller upper frames ( difference frames) show their pairwise differences COSSAM-2, COSSAM-i10 and i10-2. Ordinate is in units of the continuum intensity ,
-6.0, -4.6 and -3.0. The larger lower frames ( profile frames) compare the profiles calculated by i10, COSSAM and 2, while the smaller upper frames ( difference frames) show their pairwise differences COSSAM-2, COSSAM-i10 and i10-2. Ordinate is in units of the continuum intensity 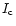 . . |
| Open with DEXTER |
Our first comparison examines the agreement of the calculated line
profiles in the absence of a magnetic field, for various values of
the abundance
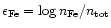 ,
at the centre of the
stellar disc
(
,
at the centre of the
stellar disc
(
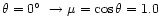 ). Such a test should
most clearly show any effects resulting from the differences in continuous
opacity and damping discussed in the previous section. Results of
this test are illustrated in Fig. 3.
). Such a test should
most clearly show any effects resulting from the differences in continuous
opacity and damping discussed in the previous section. Results of
this test are illustrated in Fig. 3.
Each frame in Fig. 3 shows the calculated profiles of Fe
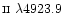 for zero
magnetic field and a given abundance in a lower subframe (which we will call
the profile frame), along with the pairwise
differences among the three calculations in the upper
subframe (which we will call the difference frame). Differences in continuous opacity and damping notwithstanding,
the calculated profiles agree remarkably well, at the level of about
0.1% rms of the continuum intensity
for zero
magnetic field and a given abundance in a lower subframe (which we will call
the profile frame), along with the pairwise
differences among the three calculations in the upper
subframe (which we will call the difference frame). Differences in continuous opacity and damping notwithstanding,
the calculated profiles agree remarkably well, at the level of about
0.1% rms of the continuum intensity 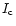 for all tests.
Similar comparisons were performed for profiles calculated at various
limb angles (
for all tests.
Similar comparisons were performed for profiles calculated at various
limb angles (
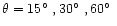 ). Profiles for all
limb angles show levels of agreement similar to those described above.
). Profiles for all
limb angles show levels of agreement similar to those described above.
This first test establishes
that local Stokes I profiles, calculated by the three codes, for Fe
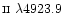 at various points
on the stellar disc, are essentially
identical throughout a range of abundance spanning at least 5 dex.
at various points
on the stellar disc, are essentially
identical throughout a range of abundance spanning at least 5 dex.
For abundances
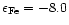 and -4.6 we have compared the
calculated local Fe
and -4.6 we have compared the
calculated local Fe
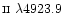 Stokes profiles from the three codes for three values
of the local magnetic field strength
B=0.1, 5, 20 kG, as well as
for three values of the magnetic field orientation,
Stokes profiles from the three codes for three values
of the local magnetic field strength
B=0.1, 5, 20 kG, as well as
for three values of the magnetic field orientation,
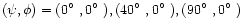 (where
(where 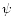 and
and 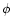 are respectively the polar and azimuthal angles of the magnetic field vector
as described by Landolfi et al. 1993).
To illustrate the results of these tests we show in Fig. 4
the calculations for magnetic field orientation
are respectively the polar and azimuthal angles of the magnetic field vector
as described by Landolfi et al. 1993).
To illustrate the results of these tests we show in Fig. 4
the calculations for magnetic field orientation
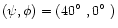 and an Fe abundance
and an Fe abundance
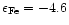 .
.
The Stokes I profiles calculated by the three codes and shown in
Fig. 4 show levels of agreement similar to those obtained
for the respective nonmagnetic case. Stokes V, Q and U profiles
agree to within 1% rms of their full amplitudes.
To facilitate explicit comparison with these calculations, we tabulate the Stokes
profiles shown in Fig. 4 in Table 4,
available only in electronic form
at the CDS via anonymous ftp to
cdsarc.u-strasbg.fr (130.79.128.5)
or via http://cdsweb.u-strasbg.fr/cgi-bin/qcat?JA+A/374/265.
Table 3:
Local profile calculations summary. Summary of root mean square (rms) and maximum pairwise deviations for calculations with
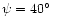 ,
,
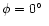 .
Considering all pixels with intensity lower than 1% of maximum Stokes I profile depth. First value is rms deviation, second is maximum deviation. Values in brackets are full amplitude of the respective profile and the full amplitude expressed in units of the maximum deviation. Values are in percent of
.
Considering all pixels with intensity lower than 1% of maximum Stokes I profile depth. First value is rms deviation, second is maximum deviation. Values in brackets are full amplitude of the respective profile and the full amplitude expressed in units of the maximum deviation. Values are in percent of  .
.
|
Model |
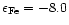 |
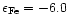 |
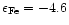 |
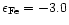 |
|
0 kG |
0.070 0.155 (12.8,83) |
0.134 0.455 (80.7,177) |
0.091 0.404 (89.2,221) |
0.095 0.405 (92.8,229) |
|
Model |
I |
V |
Q |
U |
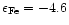 |
|
0.1 kG |
0.084 0.381 (89.2,234) |
8.99E-3 6.48E-2 (8.00,123) |
2.57E-4 1.89E-3 (0.057,30) |
3.07E-4 2.48E-3 (0.051,21) |
| 5 kG |
0.055 0.242 (82.2,216) |
3.36E-2 1.42E-1 (72.2,508) |
1.17E-2 4.47E-2 (11.0,246) |
4.73E-3 1.67E-2 (1.96,117) |
| 20 kG |
0.085 0.422 (77.3,184) |
6.10E-2 4.58E-1 (81.2,177) |
4.59E-2 6.25E-1 (26.4,42.2) |
3.20E-2 4.43E-1 (12.9,29.1) |
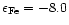 |
|
0.1 kG |
0.019 0.043 (12.8,298) |
3.62E-3 7.23E-3 (1.31,182) |
5.98E-5 1.61E-4 (0.023,143) |
2.54E-6 6.24E-6 (1.16E-4,19) |
| 5 kG |
0.020 0.043 (3.62,84) |
1.70E-2 4.14E-2 (6.98,169) |
7.55E-3 1.95E-2 (2.48,127) |
2.43E-4 6.01E-4 (1.96E-2,33) |
| 20 kG |
0.009 0.036 (2.78,77) |
7.96E-3 3.46E-2 (5.34,148) |
3.29E-3 1.10E-2 (1.61,148) |
2.28E-5 8.42E-5 (2.67E-3,31.7) |
Table 5:
Disc integrated profile calculations summary.
Summary of root mean square (rms) and maximum pairwise deviations.
Considering all pixels with intensity lower than 1% of maximum Stokes
I profile depth. First value is rms deviation, second is maximum
deviation. Values in brackets are full amplitude of the respective
profile and the full amplitude expressed in units of the maximum deviation.
Values are in percent of 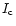 .
For the 4915-4930 Å calculation,
"homogeneous'' and "heterogeneous'' refer to calculations performed with/without
verifying identical partition functions and ionisation potentials.
.
For the 4915-4930 Å calculation,
"homogeneous'' and "heterogeneous'' refer to calculations performed with/without
verifying identical partition functions and ionisation potentials.
|
Model |
I |
0 kG,
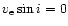 kms kms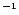 |
7.39E-2 3.25E-1 (87.6,270) |
0 kG,
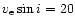 kms kms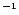 |
4.72E-2 1.57E-1 (27.8,177) |
0 kG,
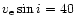 kms kms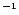 |
3.41E-2 1.35E-1 (14.7,109) |
0 kG,
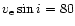 kms kms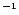 |
2.68E-2 8.44E-2 (7.54, 89) |
|
Model |
I |
V |
Q |
U |
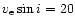 kms kms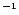 ,
dipole field with ,
dipole field with
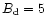 kG kG |
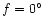 |
4.43E-2 1.03E-1 (40.2,390) |
1.67E-2 6.60E-2 (9.6,146) |
6.46E-3 2.99E-2 (1.7,57) |
4.59E-3 1.87E-2 (1.7,91) |
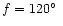 |
4.46E-2 1.42E-1 (39.5,278) |
1.57E-2 6.84E-2 (9.8,143) |
4.52E-3 2.00E-2 (1.4,70) |
7.81E-3 3.31E-2 (1.9,57) |
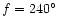 |
4.38E-2 1.34E-1 (39.5,295) |
2.05E-2 9.74E-2 (9.8,101) |
5.21E-3 1.75E-2 (1.4,80) |
7.69E-3 3.32E-2 (1.9,57) |
4915-4930 Å,
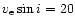 kms kms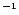 , ,
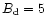 kG kG |
|
heterogeneous |
7.74E-2 2.13E-1 |
2.64E-2 9.76E-2 |
1.39E-2 5.45E-2 |
6.80E-3 3.50E-2 |
 homogeneous
homogeneous |
3.10E-2 1.04E-1 |
1.70E-2 6.04E-2 |
1.16E-2 4.40E-2 |
8.92E-3 5.60E-2 |
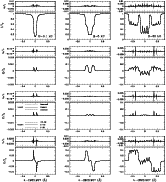 |
Figure 4:
Local disc-centre profiles of Fe
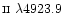 for abundance
for abundance
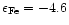 calculated for 0.1, 5.0 and 20.0 kG magnetic
field strengths, with orientation
calculated for 0.1, 5.0 and 20.0 kG magnetic
field strengths, with orientation
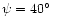 , ,
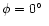 .
The vertical scale of the small upper difference frames for Stokes Q,
U and V corresponds to 2% of that of the respective larger lower profile
frame. Note the different scales for the different Stokes
parameters and field strengths. .
The vertical scale of the small upper difference frames for Stokes Q,
U and V corresponds to 2% of that of the respective larger lower profile
frame. Note the different scales for the different Stokes
parameters and field strengths. |
| Open with DEXTER |
This second test establishes that local Stokes I profiles
calculated by the three codes, for Fe
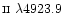 under the influence of a
magnetic field, maintain the level of agreement obtained in the case
of a null field, and that the associated Stokes V, Q and U profiles agree to within 1% rms of their respective amplitudes,
throughout a range of field strengths from 0.1 to 20 kG.
under the influence of a
magnetic field, maintain the level of agreement obtained in the case
of a null field, and that the associated Stokes V, Q and U profiles agree to within 1% rms of their respective amplitudes,
throughout a range of field strengths from 0.1 to 20 kG.
It is the Stokes I, Q, U and V flux profiles, obtained by
weighting and integrating the local profiles over the stellar disc,
that will be ultimately compared with spectropolarimetric
observations. From this standpoint flux profiles represent
the most important test of the agreement of the three synthesis codes.
In this section we compare calculated disc-integrated profiles for
both non-magnetic and magnetic scenarios. A quantitative summary of this
comparison is provided in Table 5.
As in the local case, we begin with a comparison of
profiles calculated in the absence of a magnetic
field. Such a comparison includes the effects of the (very small) differences in the
local profiles established in Sect. 4.1, but furthermore examines the accuracy of the disc
integration. Profiles have been calculated for Fe
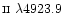 for the adopted
model atmosphere, abundance
for the adopted
model atmosphere, abundance
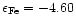 ,
and assuming
projected rotational velocities (
,
and assuming
projected rotational velocities (
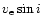 )
of 0, 20, 40 and
80 kms
)
of 0, 20, 40 and
80 kms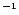 .
.
Agreement for
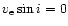 kms
kms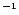 is at the sub-0.1% rms level,
and is essentially the same as that observed for local
profiles calculated for this abundance. For increasing
is at the sub-0.1% rms level,
and is essentially the same as that observed for local
profiles calculated for this abundance. For increasing
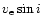 the absolute level of agreement improves somewhat. We point out that, were these
calculations convolved with an instrumental profile (as would
commonly be performed for comparison with real observations),
small-scale structure in the pairwise differences frames (resulting from differences
in the disc integration grids employed by the three codes) would essentially
disappear, and the agreement would improve correspondingly.
the absolute level of agreement improves somewhat. We point out that, were these
calculations convolved with an instrumental profile (as would
commonly be performed for comparison with real observations),
small-scale structure in the pairwise differences frames (resulting from differences
in the disc integration grids employed by the three codes) would essentially
disappear, and the agreement would improve correspondingly.
We have also compared disc-integrated profiles of Fe
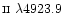 calculated
assuming a dipolar surface magnetic field configuration, observed
from three different aspects (i.e. at three difference rotational
phases f). The profiles correspond to
calculated
assuming a dipolar surface magnetic field configuration, observed
from three different aspects (i.e. at three difference rotational
phases f). The profiles correspond to
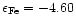 and
and
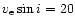 kms
kms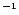 .
Agreement among the Stokes I profiles
is similar to that obtained in the null field case (better than 0.05% rms,
corresponding to agreement to better than 0.2% of the profile depth),
while agreement for Stokes V is at the level of
0.02% rms (0.2% of the profile full amplitude), and Stokes Q/U agree
at the sub-0.01% rms level (0.4% of the profile amplitude).
.
Agreement among the Stokes I profiles
is similar to that obtained in the null field case (better than 0.05% rms,
corresponding to agreement to better than 0.2% of the profile depth),
while agreement for Stokes V is at the level of
0.02% rms (0.2% of the profile full amplitude), and Stokes Q/U agree
at the sub-0.01% rms level (0.4% of the profile amplitude).
These tests establish that the differences in disc-integrated
Stokes profiles of Fe
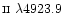 calculated by the three codes, for
homogeneous input conditions, both in the presence and absence of a
magnetic field, remain at or below the levels of agreement obtained
for local Stokes profiles. The observed levels of agreement for
disc-integrated Stokes V, Q and U profiles all correpond to
congruence to within better than 1% rms of the profile amplitude,
and this agreement is maintained for various field configurations.
calculated by the three codes, for
homogeneous input conditions, both in the presence and absence of a
magnetic field, remain at or below the levels of agreement obtained
for local Stokes profiles. The observed levels of agreement for
disc-integrated Stokes V, Q and U profiles all correpond to
congruence to within better than 1% rms of the profile amplitude,
and this agreement is maintained for various field configurations.
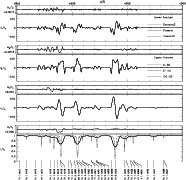 |
Figure 5:
Synthetic disc-integrated spectrum for the region 4915-4930 Å, including
the effects of 34 spectral lines (identified at bottom). The abundance table
is solar, the magnetic field is dipolar with
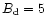 kG, kG,
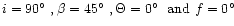 .
The projected rotational
velocity is .
The projected rotational
velocity is
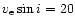 kms kms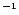 .
The disc-centre spectrum, calculated in the
absence of a magnetic field by COSSAM, has been overlayed on Stokes I to clarify the
distribution of spectral lines. Nearly all of the visible structure in the difference
frames results from Landé factor discrepancies. .
The disc-centre spectrum, calculated in the
absence of a magnetic field by COSSAM, has been overlayed on Stokes I to clarify the
distribution of spectral lines. Nearly all of the visible structure in the difference
frames results from Landé factor discrepancies. |
| Open with DEXTER |
Is such good agreement maintained in the more realistic case of
synthetic spectrum calculated including multiple blended ions? To
answer this question we have compared calculations of the spectral
region 4915-4930 Å, including the effects of 34 spectral lines
formed by 12 different
ions (with data obtained from the VALD database),
as well as a dipolar magnetic field. This
comparison is illustrated in Fig. 5. Our first such calculations
showed important systematic differences between 2 and the other
codes, especially for Stokes I (up to more than 1% of 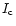 ). Some of these differences were found to be due to differences in
adopted partition functions and, for trace ions (e.g. Fe I), very small
differences in adopted ionisation potentials. (These differences trace
the close connection of COSSAM and i10 to Kurucz's ATLAS codes and
data, and the lack of such a connection for 2.) After homogenising
partition functions and relevant ionisation potentials, the
systematic differences essentially disappeared, but obvious
differences still remained for a few apparently unrelated lines. This
can be seen in Fig. 5. (e.g. Fe
). Some of these differences were found to be due to differences in
adopted partition functions and, for trace ions (e.g. Fe I), very small
differences in adopted ionisation potentials. (These differences trace
the close connection of COSSAM and i10 to Kurucz's ATLAS codes and
data, and the lack of such a connection for 2.) After homogenising
partition functions and relevant ionisation potentials, the
systematic differences essentially disappeared, but obvious
differences still remained for a few apparently unrelated lines. This
can be seen in Fig. 5. (e.g. Fe
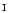
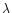 4918.0, Fe
4918.0, Fe
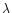 4918.9,
Fe I/II + Cr I
4918.9,
Fe I/II + Cr I 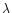 4922.2).
Examination of spectra calculated for this
wavelength region for null magnetic field, as well as examination of the
experimental versus LS coupling Landé factors for these lines,
showed clearly that these discrepancies result from frequent
differences between observed and calculated Landé factors (e.g. as
large as a factor of two for Fe
4922.2).
Examination of spectra calculated for this
wavelength region for null magnetic field, as well as examination of the
experimental versus LS coupling Landé factors for these lines,
showed clearly that these discrepancies result from frequent
differences between observed and calculated Landé factors (e.g. as
large as a factor of two for Fe
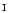
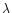 4918.0). The remaining differences
in Fig. 5 are therefore a direct consequence of the (clearly
hazardous) 2 strategy of calculating Landé factors.
4918.0). The remaining differences
in Fig. 5 are therefore a direct consequence of the (clearly
hazardous) 2 strategy of calculating Landé factors.
This test shows that, apart from differences resulting from
calculated versus experimental Landé factors, the codes continue
to maintain good agreement even for calculations including various
blended ions.
The comparisons performed in Sect. 4 show, for identical input data,
that the differences between Stokes profiles calculated using COSSAM,
i10 and 2 are sufficiently small so as to allow for congruent
interpretation of the highest quality stellar Stokes IQUV data presently
available (
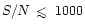 ,
,
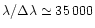 ). As the next generation of high-resolution spectropolarimeters
(such as the ESPaDOnS instrument; Donati et al. 1998) begin to see
light on medium- and large-class telescopes this situation will remain
unchanged for all but the brightest sources. Therefore our basic
ability to solve the PRT problem and to calculate precise
disc-integrated Stokes IQUV profiles is not an important limitation
for modeling observations. This is the primary conclusion of this
paper.
). As the next generation of high-resolution spectropolarimeters
(such as the ESPaDOnS instrument; Donati et al. 1998) begin to see
light on medium- and large-class telescopes this situation will remain
unchanged for all but the brightest sources. Therefore our basic
ability to solve the PRT problem and to calculate precise
disc-integrated Stokes IQUV profiles is not an important limitation
for modeling observations. This is the primary conclusion of this
paper.
On the other hand, as is aptly illustrated in Sect. 4.2.2,
uncertainties in input atomic and astrophysical data can have an
important impact on the shapes and amplitudes of Stokes
profiles. Atomic data are often subject to important errors:
gf-values, Landé factors, Zeeman component intensities, damping
coefficients, partition functions, and excitation and ionisation
potentials all exhibit uncertainties of varying degree. Even more
important are uncertainties in the input astrophysical data,
particularly the state and structure of the model stellar
atmosphere. Such uncertainties are especially critical for magnetic
stars: surface features (starspots on cool stars, abundance
nonuniformities on tepid stars) indicate that no single model of the
vertical run of temperature and pressure is valid at all stellar
surface locations. The convective state of magnetic atmospheres is
uncertain due to possible suppression of velocity fields by the
magnetic field.
The atmospheric chemical composition of magnetic tepid
stars is frequently strongly nonsolar, and elements may furthermore be
strongly stratified; a unique abundance of each chemical element may
not characterise all atmospheric depths (let alone all surface
locations). Although the impact of these physical complexities is
widely recognised, they are not generally included in stellar
atmosphere models (but see Piskunov & Kupka 2001 for some steps in
this direction). In fact, the overwhelming majority of line profile
modeling to date (polarised and unpolarised) has been accomplished
using atmosphere models characterised by scaled solar abundance tables.
Of course, all of these unaccounted-for model atmosphere errors
contribute to errors in calculated Stokes profiles (errors which can
potentially be very much larger than those discussed in Sect. 4). Such
profiles are frequently used to recover stellar magnetic field topologies
by comparing the calculations with observations. A number of such modeling strategies
are presently under development.
For example, Bagnulo & Wade (2001) are attempting to fit Stokes
IQUV profile variations within the context of a low-order multipolar framework.
Kochukhov et al. (2001), on the other hand, employ a method based on Doppler Imaging
principles to accomplish the same goal. At this point, it is not clear
to what degree uncertainties in calculated Stokes profiles may
lead to an inability to accurately reproduce observed profiles or to inaccurate
recovery of the parent magnetic field. Neither is it clear how this will
depend on the modeling strategy employed.
Therefore, while we have shown that Stokes IQUV profiles of
magnetic stars can in principle be calculated to very high precision,
in practice this agreement means little in terms of the accuracy of
such profiles, which will be limited overwhelmingly by uncertainties
in input atomic and astrophysical data, in particular model stellar
atmospheres.
Acknowledgements
GAW acknowledges support during 1998-2000 from the
Natural Sciences and Engineering Research Council of Canada (NSERC)
in the form of an NSERC postdoctoral fellowship, as well as support
from the NSERC operating grants of J. B. Lester and C. T. Bolton
(University of Toronto). JDL acknowledges support from NSERC
in the form of an operating grant. S. Bagnulo and M. J. Stift gratefully
acknowledge financial support
by the Austrian Fonds zur Förderung der Wissenschaftlichen
Forschung, project P12101-AST. Research in scientific programming
with Ada has been funded by the Hochschuljubiläumsstiftung
der Stadt Wien, project Software Engineering with Ada95. We thank F. Leone for taking time to provide ATLAS9 continuous opacity calculations.
- Aller, M. F., & Everett, C. H. M. 1972, ApJ, 172, 447
In the text
NASA ADS
- Auer, L. H., Heasley, J. N., & House, L. L. 1977, ApJ, 216, 531
In the text
NASA ADS
- Bagnulo, S. & Wade, G. A. 2001, in Proceedings of Magnetic Fields Across the H-R Diagram, PASP Conf. Ser., ed. G. Mathys, S. Solanki, & D. Wickramasinghe, in press
In the text
- Baschek, B., Holweger, H., & Traving, G. 1966, Abh. Hamburger
Sternwarte, Band VIII, 26
In the text
- Babcock, H. W. 1947, ApJ, 105, 105
In the text
NASA ADS
- Babcock, H. W. 1958, ApJ, 128, 228
In the text
NASA ADS
- Bohlender, D. A., Brown, D. N., Landstreet, J. D., & Thompson, I. B. 1987, ApJ, 323, 325
In the text
NASA ADS
- Bolton, C. T. 1970, ApJ, 161, 1187
In the text
NASA ADS
- Bolton, C. T. 1971, A&A, 14, 233
In the text
NASA ADS
- Carbon, & Gingerich, O. 1969, in Theory and Observation of Normal Stellar Atmospheres, 399
In the text
- Chmielewski, Y. 1979, Publ. Obs. de Genève,
Série B, Fasc. 7
In the text
- Cowley, C. R. 1971, Obs., 91, 139
In the text
NASA ADS
- Cowley, C. R. 1994, Obs., 114, 308
In the text
NASA ADS
- Cowley, C. R. 1998, In the text
ftp://astro.lsa.umich.edu/pub/get/cowley
/partition/bolpfn.f
- Cowley, C. R., & Adelman, S. J. 1983, QJRAS, 24, 393
In the text
NASA ADS
- Donati, J. F., Semel, M., Carter, B. D., Rees, D. E., & Cameron, A. C.
1997, MNRAS, 291, 658
In the text
NASA ADS
- Donati, J.-F., Catala, C., & Landstreet, J. D. 1998, in Proceedings of the fifth CFHT user's meeting, 50
In the text
- Drawin, H. W., & Felenbok, P. 1965, Z. Astrophys., 63, 62
In the text
NASA ADS
- Fensl, R. M. 1995, A&AS, 112, 191
In the text
NASA ADS
- Gingerich, O. 1964, SAO Report #167
In the text
- Gonzalez, J.-F., Artru, M.-C., & Michaud, G. 1995, A&A, 302, 788
In the text
NASA ADS
- Gray, D. F. 1992, The Observation and Analysis of Stellar Photo
spheres (Cambridge University Press)
In the text
- Griem, H. R., 1968, ApJ, 154, 1111
In the text
NASA ADS
- Hardorp, J., Shore, S. N.,
& Wittmann, A. 1975, in Proc. IAU Coll. No. 32, Physics of Ap Stars, ed. W. W. Weiss, H. Jenkner, & H. J. Wood, Universitätssternwarte
Wien, 419
In the text
- Humlicek 1982, J. Quant. Spec. Rad. Trans. 27, 437
In the text
- Irwin, A. W. 1981, ApJS, 45, 621
In the text
NASA ADS
- Johns-Krull, C. M., & Valenti, J. A. 1996, ApJ, 459, 95
In the text
- Johns-Krull, C. M., Valenti, J. A., & Koresko, C. 1999, ApJ, 516, 900
In the text
NASA ADS
- Kemp, J. C., Swedlund, J. B., Landstreet, J. D., & Angel, J. R. P. 1970, ApJL, 161, 77
- Kochukhov, O., Piskunov, N., Ilyin, I., Ilyina, S., & Tuominen, I. 2001, in Proceedings of Magnetic Fields Across the H-R Diagram, PASP Conf. Ser., ed. G. Mathys, S. Solanki, & D. Wickramasinghe, in press
In the text
- Kurucz, R. 1993, CDROM Model Distribution, Smithsonian
Astrophys. Obs.
In the text
- Landolfi, M., Landi Degl'Innocenti, E., Landi
Degl'Innocenti, M., & Leroy, J.-L. 1993, A&A, 272, 285
In the text
NASA ADS
- Landolt-Börnstein 1982, Zahlenwerte und Funktionen
aus Naturwissenschaften und Technik, Neue Serie,
Gruppe VI: Astronomie, Astrophysik und Weltraumforschung,
Band 2, Teilband b, ed. K. Schaifers, & H. H. Voigt, 107
In the text
- Landstreet, J. D. 1982, ApJ, 258, 639
NASA ADS
- Landstreet, J. D. 1988, ApJ, 326, 967
In the text
NASA ADS
- Leroy, J.-L. 1995, A&AS, 114, 79
In the text
NASA ADS
- Leroy, J.-L., Landolfi, M., & Landi Degl'Innocenti, E. 1996, A&A, 311,
513
In the text
NASA ADS
- Martin, B., & Wickramasinghe, D. T. 1979, MNRAS, 189, 883
In the text
NASA ADS
- Mathys, G. 1993, A&AS, 108, 547
In the text
NASA ADS
- Mihalas, D. 1970, Stellar Atmospheres
In the text
- Peytremann, E., Baschek, B., Holweger, H., & Traving, G.
1967, Rapport Interne, Obs. de Genève
In the text
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W.,
& Jeffery, C. S. 1995, A&AS, 112, 525
In the text
NASA ADS
- Piskunov, N. 1999, in
Proceedings of the 2nd Workshop on Solar Polarisation, ed.
J. Stenflo, & K. N. Nagendra, 1998, Bangalore,
India (Kluwer Acad. Publ. ASSL), 243, 515
In the text
- Piskunov, N. E., & Kupka, F. 2001, ApJ, 547, 1040
In the text
NASA ADS
- Putney, A. 1999, in 11th
European Workshop on White Dwarfs, ASP Conf. Ser. #169, ed. S.-E. Solheim,
& E. G. Meistas, 195
- Rees, D. E., Murphy, G. A., & Durrant, C. J. 1989, ApJ, 339, 1093
In the text
NASA ADS
- Rees, D. E. 1987, in Numerical Radiative Transfer, ed. Kalkofen W.
(Cambridge University Press), 213
In the text
- Shurcliff, W. A. 1962, Polarized light (Harvard University Press, Cambridge)
- Stehlé, C., & Hutcheon, R. 1999, A&AS, 140, 93
In the text
NASA ADS
- Stift, M. J. 1985, MNRAS, 217, 55
In the text
NASA ADS
- Stift, M. J. 1996, in Model Atmospheres
and Spectrum Synthesis, ed. S. J. Adelman, F. Kupka,
& W. W. Weiss, ASP Conf. Ser., 108, 217
In the text
- Stift, M. J. 1998a, Comp. Phys., 12, 150
In the text
- Stift, M. J. 1998b, in Reliable
Software Technologies - Ada-Europe '98, ed. L. Asplund,
Lecture Notes in Computer Science, 1411 (Springer), 128
In the text
- Traving, G., Baschek, B., & Holweger,
H. 1966, Abh. Hamburger
Sternwarte, Band, VIII, 1
In the text
- Wade, G. A., Donati, J.-F.,
Landstreet, J. D., & Shorlin, S. L. S. 2000, MNRAS, 313, 823
In the text
NASA ADS
Copyright ESO 2001




