A&A 374, 294-300 (2001)
DOI: 10.1051/0004-6361:20010701
Relationship in sign between tilt and twist
in active region magnetic fields
L. Tian
- S. Bao
- H. Zhang
- H. Wang
National Astronomical Observatories,
Chinese Academy of Sciences, Beijing 100012, PR China
Received 15 September 2000 / Accepted 24 April 2001
Abstract
In this paper, we analyze the photospheric vector magnetograms of 286
active regions (ARs) which were observed from 1988-1996
during the 22nd solar cycle at Huairou Solar Observing Station in Beijing. Among
these active regions, which are
dominated by bipolar magnetic fields, 203 ARs exhibit a simple configuration of magnetic
fields, while 83 ARs show a more complicated configuration of magnetic fields. When we
explore the relationship between the sign of the tilt angle of magnetic polarity axis and
the sign of the mean current helicity defined by
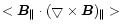 ,
we find that:
(1) There is a negative correlation between the sign of the tilt angle and the sign
of the current helicity if the tilt angle is set a positive value (0-90
,
we find that:
(1) There is a negative correlation between the sign of the tilt angle and the sign
of the current helicity if the tilt angle is set a positive value (0-90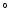 )
in the northern hemisphere and a negative value (0-90
)
in the northern hemisphere and a negative value (0-90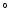 )
in the southern hemisphere for
active regions following Joy's law. In other words, about 60% of the bipolar active regions
have a positive/negative
tilt angle with respect to solar equator and a negative/positive current
helicity in the northern/southern hemisphere.
(2) In about one-third of the bipolar active regions, the tilt angle and the current
helicity have the same sign in both hemispheres. They are abnormal active regions with
an "abnormal chirality''. These active regions are located preferentially in
some longitudinal
bins.
(3) Most of the 62 X-ray flares larger than M-class during the 22nd solar cycle have
a tendency to locate in some longitudinal bins, where active regions with "abnormal
chirality'' appear frequently.
)
in the southern hemisphere for
active regions following Joy's law. In other words, about 60% of the bipolar active regions
have a positive/negative
tilt angle with respect to solar equator and a negative/positive current
helicity in the northern/southern hemisphere.
(2) In about one-third of the bipolar active regions, the tilt angle and the current
helicity have the same sign in both hemispheres. They are abnormal active regions with
an "abnormal chirality''. These active regions are located preferentially in
some longitudinal
bins.
(3) Most of the 62 X-ray flares larger than M-class during the 22nd solar cycle have
a tendency to locate in some longitudinal bins, where active regions with "abnormal
chirality'' appear frequently.
Key words: Sun: magnetic field - Sun: photosphere - Sun: interior
It is commonly believed that magnetic fields in the solar atmosphere are caused by a
dynamo operating at or beneath the bottom of the convection zone and then emerge as
 flux tubes on the solar surface to form solar active regions. Joy's Law (Hale et al.
1919) states that in many active regions of bipolar magnetic fields, the
magnetic polarity axis has a particular inclination, with the preceding spot closer to the
solar equator than
the following spot. The angle between the magnetic polarity axis and the solar
equator is defined as the "tilt angle''. Observational studies of the tilt angle have been published in
many papers (Howard 1989, 1991; Wang & Sheeley 1989; Tian et al. 1999). The physical
origin of the tilt angle has been discussed by following authors: Babcock (1961) proposed
that, if the interior field has a purely toroidal orientation, Coriolis forces acting on the
upwelling fluid associated with an active region would produce a tilt in the sense that is
measured. Schmidt (1968) and Wang & Sheeley (1991) suggested that the tilts of active
regions are formed by the Coriolis force acting on the expanding plasma contained
within a buoyant, rising flux tube, rather than on the surrounding fields. On the other
hand, the solar magnetic fields are twisted. The twist has been inferred by a number
of methods including studying the morphology of filaments (Martin et al. 1994) and
coronal loops (Rust & Kumar 1996), in situ measurements of flux ropes (Burlaga 1988)
and interplanetary fields (Bieber et al. 1987), computing the force-free parameter
flux tubes on the solar surface to form solar active regions. Joy's Law (Hale et al.
1919) states that in many active regions of bipolar magnetic fields, the
magnetic polarity axis has a particular inclination, with the preceding spot closer to the
solar equator than
the following spot. The angle between the magnetic polarity axis and the solar
equator is defined as the "tilt angle''. Observational studies of the tilt angle have been published in
many papers (Howard 1989, 1991; Wang & Sheeley 1989; Tian et al. 1999). The physical
origin of the tilt angle has been discussed by following authors: Babcock (1961) proposed
that, if the interior field has a purely toroidal orientation, Coriolis forces acting on the
upwelling fluid associated with an active region would produce a tilt in the sense that is
measured. Schmidt (1968) and Wang & Sheeley (1991) suggested that the tilts of active
regions are formed by the Coriolis force acting on the expanding plasma contained
within a buoyant, rising flux tube, rather than on the surrounding fields. On the other
hand, the solar magnetic fields are twisted. The twist has been inferred by a number
of methods including studying the morphology of filaments (Martin et al. 1994) and
coronal loops (Rust & Kumar 1996), in situ measurements of flux ropes (Burlaga 1988)
and interplanetary fields (Bieber et al. 1987), computing the force-free parameter
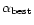 (Pevtsov et al. 1995) and mean current helicity density
(Pevtsov et al. 1995) and mean current helicity density
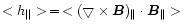 (Abramenko et al. 1996; Bao & Zhang 1998). Results from these methods reveal the
dominance of negative/positive helicity in the northern/southern hemisphere, which is
defined as "a rule of helicity sign''.
(Abramenko et al. 1996; Bao & Zhang 1998). Results from these methods reveal the
dominance of negative/positive helicity in the northern/southern hemisphere, which is
defined as "a rule of helicity sign''.
In studying the origin of the twist, Wang et al. (1994) and Leka et al. (1996) used
photospheric observation of magnetic fields to probe sub-photospheric fields. They
concluded that some active regions were carrying electric currents prior to their emergence.
In other words, the twist of the active region magnetic fields was present in a flux
tube below the photosphere. There are many models explaining the origin of the twist of
magnetic lines in sub-photospheric magnetic flux tubes. Longcope et al. (1996),
Moreno-Insertis & Emonet (1996) and Fan et al. (1998) proposed that twist presented in a
flux tube is produced by a solar dynamo before the tube rises. Rust & Kumar (1994)
considered that the current helicity is caused by the subphotospheric differential rotation
in the convection zone. Longcope & Klapper (1997) suggested that the twist could
be given rise to by the tilt of the magnetic polarity axis, which is caused by the
Coriolis force acting on the buoyant,
rising flux tube as a 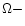 loop in the convection
zone.
In a recent paper,
Longcope et al. (1998) proposed that the twist
is imparted to the flux tube through
the deformation of the axis of the flux tube, which is caused by
turbulent motions with a non-zero kinetic
helicity
loop in the convection
zone.
In a recent paper,
Longcope et al. (1998) proposed that the twist
is imparted to the flux tube through
the deformation of the axis of the flux tube, which is caused by
turbulent motions with a non-zero kinetic
helicity
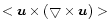 in the convection zone.
in the convection zone.
The force-free parameter 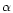 and the mean current helicity
< h|| > calculated in the
photosphere carry some information on the twist of magnetic lines in a flux
tube rising
to the photosphere from the view of observations (Seehafer 1990; Pevtsov et al. 1995;
Abramenko et al. 1996; Bao & Zhang 1998). Positive/negative values of these parameters
correspond to the twist of magnetic lines in the right/left-handedness. We
use
< h|| > as a parameter to describe the twist of an active region magnetic fields in
this paper.
and the mean current helicity
< h|| > calculated in the
photosphere carry some information on the twist of magnetic lines in a flux
tube rising
to the photosphere from the view of observations (Seehafer 1990; Pevtsov et al. 1995;
Abramenko et al. 1996; Bao & Zhang 1998). Positive/negative values of these parameters
correspond to the twist of magnetic lines in the right/left-handedness. We
use
< h|| > as a parameter to describe the twist of an active region magnetic fields in
this paper.
It is important for some dynamo and flux tube models to study the origin of the twist
of magnetic fields in the active regions. Perhaps, the relationship between the twist of
the magnetic field and the tilt angle of an active region could shed light on this problem,
as Longcope & Klapper (1997) and Longcope et al. (1998) have proposed. After considering
helicity conservation in a flux tube with zero helicity, helicity modifies both twist and
writhe in the tube. However, the writhe will be opposite in sign to the twist (Moffatt &
Ricca 1992) if the Coriolis force produced a twist in originally untwisted flux tubes.
Canfield & Pevtsov (1998) first studied the relationship in sign of both the force-free parameter
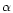 and tilt per unit length (
and tilt per unit length (
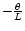 ),
where L is the separation between sunspots of opposite
polarity. Their data show no reliable anticorrelation in sign between twist and writhe
(see Fig. 6 of their paper), as one would expect.
),
where L is the separation between sunspots of opposite
polarity. Their data show no reliable anticorrelation in sign between twist and writhe
(see Fig. 6 of their paper), as one would expect.
However, the mean current helicity < h||> was measured by Bao & Zhang (1998)
for 422 active regions in the 22nd cycle. They found that almost 80% of active regions
adhere to the hemispheric helicity rule, being negative in the northern hemisphere and positive in
the southern hemisphere. The tilt angle 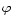 was measured by Tian et al. (1999) for 203
bipolar regions among the 422 active regions. They found that almost 70% of bipolar
active regions adhere to the Hale-Nickolson Law. What is the relationship in sign between the
tilt and the twist using these data? In the present paper, we will use this relationship
to investigate where the helicity is produced. Observational techniques and data chosen
are described in Sect. 2. Definitions and calculations of tilt angle and current helicity
are given in Sect. 3. In Sect. 4, we present the relationship between the sign of the
tilt angle of magnetic polarity axis and the sign of the mean current helicity
< h|| > for
286 bipolar active regions. In Sect. 5, we examine the distribution of active regions
with "abnormal chirality''. Distribution of 62 X-ray flares larger than M-class is given in
Sect. 6. Finally, conclusions and discussions are given in Sect. 7.
was measured by Tian et al. (1999) for 203
bipolar regions among the 422 active regions. They found that almost 70% of bipolar
active regions adhere to the Hale-Nickolson Law. What is the relationship in sign between the
tilt and the twist using these data? In the present paper, we will use this relationship
to investigate where the helicity is produced. Observational techniques and data chosen
are described in Sect. 2. Definitions and calculations of tilt angle and current helicity
are given in Sect. 3. In Sect. 4, we present the relationship between the sign of the
tilt angle of magnetic polarity axis and the sign of the mean current helicity
< h|| > for
286 bipolar active regions. In Sect. 5, we examine the distribution of active regions
with "abnormal chirality''. Distribution of 62 X-ray flares larger than M-class is given in
Sect. 6. Finally, conclusions and discussions are given in Sect. 7.
We use the data of vector magnetic fields obtained by the Solar Magnetic Field Telescope,
an imaging vector magnetograph installed at Huairou Solar Observing Station of the Beijing
Astronomical Observatory, with a field of view of about 5
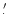
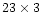
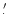 63
(
63
(
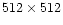 pixels
of the CCD). The temporal and spatial resolution of the vector magnetograms depend on
the number of video frames that are integrated to make one magnetogram. Each
magnetogram used in this paper is the sum of 256 individual frames for both line-of-sight and
transverse fields. Temporal resolution is about 5 min for each vector magnetogram.
Each pixel is about 0
pixels
of the CCD). The temporal and spatial resolution of the vector magnetograms depend on
the number of video frames that are integrated to make one magnetogram. Each
magnetogram used in this paper is the sum of 256 individual frames for both line-of-sight and
transverse fields. Temporal resolution is about 5 min for each vector magnetogram.
Each pixel is about 0
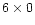
 4.
After performing a
4.
After performing a 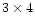 pixels smoothing average,
the spatial
resolution is 2
pixels smoothing average,
the spatial
resolution is 2
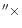 2
2
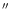 .
.
The vector magnetic field in the photosphere was obtained on the basis of narrow-band
images (filtergrams) of four Stokes parameters I, V, Q, U in FeI 5324.191 Å. The
longitudinal magnetic field strength (B||) and transverse magnetic field strength ( )
are given, respectively, by
)
are given, respectively, by
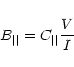 |
(1) |
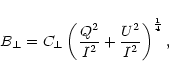 |
(2) |
where C|| and 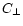 are the calibration coefficients for line-of-sight and transverse
components
of the magnetic fields.
However, a precise calibration of a vector magnetograph
is very complicated and difficult. Both theoretical and empirical methods are used to
calibrate the vector magnetograms (Ai et al. 1982; Wang et al. 1996).
are the calibration coefficients for line-of-sight and transverse
components
of the magnetic fields.
However, a precise calibration of a vector magnetograph
is very complicated and difficult. Both theoretical and empirical methods are used to
calibrate the vector magnetograms (Ai et al. 1982; Wang et al. 1996).
The 180-degree azimuthal ambiguity in determining the transverse field direction is
an intrinsic defect of the Zeeman effect (Harvey 1969). It may be resolved according to the
potential field approximation method (Wang & Lin 1993; Wang et al. 1994) taking
into account the evolution of active regions and the orientation of chromospheric fibrils.
After the 3 4 pixel smoothing average of V, Q and U was made, the noise level
was less than 10 G for the line-of-sight field and 100 G for the transverse field over the same
integration time.
4 pixel smoothing average of V, Q and U was made, the noise level
was less than 10 G for the line-of-sight field and 100 G for the transverse field over the same
integration time.
It should be mentioned that magneto-optical effects (Faraday rotation) is insignificant
(Wang et al. 1996) in FeI 5324.191 Å. Several tests were made particularly to compare
the measured field azimuth for a few sunspots when switching the bandpass from line
center to line wing, and differences in the observed azimuth were less than 10 .
On the
other hand, after Bao et al. (2000) compared the vector magnetograms of an active
region, NOAA 5747, from Huairou and Mees Solar Observation, they found a qualitative
agreement between them. Then, they estimated that Faraday rotation in the Huairou
magnetogram contributes about 12
.
On the
other hand, after Bao et al. (2000) compared the vector magnetograms of an active
region, NOAA 5747, from Huairou and Mees Solar Observation, they found a qualitative
agreement between them. Then, they estimated that Faraday rotation in the Huairou
magnetogram contributes about 12 in the azimuth difference when possible sources of error
are taken into account. After considering the role of Faraday rotation in computation of
< h|| >, Bao et al. (2000) conclude that it does not affect the strength of the hemispheric
helicity rule.
in the azimuth difference when possible sources of error
are taken into account. After considering the role of Faraday rotation in computation of
< h|| >, Bao et al. (2000) conclude that it does not affect the strength of the hemispheric
helicity rule.
In our study, we have chosen 286 active regions which belong to 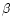 sunspots in the
magnetic classification. Most of the active regions are formed by two main bigger spots.
Among them, 203 active regions have simpler magnetic configuration (i.e. the magnetic
fields in these regions can be simply divided into areas with N and S polarities) and 83
are more complicated (i.e. there is some small scale inverse regions in
the dominated polarities).
sunspots in the
magnetic classification. Most of the active regions are formed by two main bigger spots.
Among them, 203 active regions have simpler magnetic configuration (i.e. the magnetic
fields in these regions can be simply divided into areas with N and S polarities) and 83
are more complicated (i.e. there is some small scale inverse regions in
the dominated polarities).
We analyze the vector magnetograms of these active regions obtained from 1988 to
1996 at Huairou Solar Observing Station of the Beijing Astronomy Observatory, and
compare them with their images of sunspots in the photosphere and fulldisk magnetograms
published in the SGD. It is found that these active region are much better bipolar regions
and are isolated from others. The magnetograms always cover the entire active region. All
the vector magnetic field data included in this study were carefully chosen and acquired
with favorable weather and seeing conditions during the observations. Thus, the noise
level could be lowered to 6 G for the line-of-sight field and 60 G for the transverse
field in the photosphere. When an active region developed maturely and was located near the
central meridian, it is included in the sample. Therefore, most of the active
regions are not new emerging and young active regions. We then calculate tilts and
current helicity of those active regions using the best magnetograms. The projection
effect for high latitude active regions were removed according to the formulae given by
Gary & Hagyard (1990).
In calculation of the tilt angle, the magnetic flux-weighted center is determined as the position
of each magnetic polarity. This position could be approximately indicated by the magnetic flux
weighted center of each magnetic polarity in the line-of-sight as:
where,
 is the area of each pixel. The tilt angle (
is the area of each pixel. The tilt angle (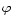 )
of an active region is defined as
the angle between the line joining opposite polarities and the solar equator. The tangent
of the tilt angle (tan
)
of an active region is defined as
the angle between the line joining opposite polarities and the solar equator. The tangent
of the tilt angle (tan 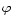 )
is given by
)
is given by
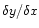 (Gary & Hagyard 1990; Wang & Sheeley 1989; Howard 1989; Tian et al. 1999), where
(Gary & Hagyard 1990; Wang & Sheeley 1989; Howard 1989; Tian et al. 1999), where 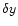 and
and 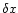 are the distances between the leading polarity and the following polarity along the Y- and X-axis, respectively, in Cartesian coordinates in the heliographic plane.
are the distances between the leading polarity and the following polarity along the Y- and X-axis, respectively, in Cartesian coordinates in the heliographic plane.
We determinate the sign of the tilt angle of the magnetic polarity axis in an active
region magnetic field such that: in the northern hemisphere, if the S polarity is closer to
the solar equator, the tilt of the active region is positive (
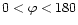 degree), otherwise
the tilt is negative (
degree), otherwise
the tilt is negative (
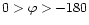 degree); in the southern hemisphere, the tilt
is negative (
degree); in the southern hemisphere, the tilt
is negative (
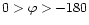 degree) when the N polarity is closer to the equator,
and otherwise the tilt is positive (
degree) when the N polarity is closer to the equator,
and otherwise the tilt is positive (
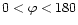 degree). Note that in the 22nd solar cycle,
the leading spot
should be S/N-polarity in the northern/southern hemisphere. Thus, active regions with
a tilt angle
degree). Note that in the 22nd solar cycle,
the leading spot
should be S/N-polarity in the northern/southern hemisphere. Thus, active regions with
a tilt angle
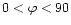 degree in the northern hemisphere, or
degree in the northern hemisphere, or
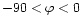 degree in the southern hemisphere, all adhere to Joy's Law.
Figure 1 shows the sign convention of the tilt angles (
degree in the southern hemisphere, all adhere to Joy's Law.
Figure 1 shows the sign convention of the tilt angles (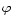 )
in the 22nd solar cycle.
)
in the 22nd solar cycle.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f1.eps}\par\mbox{In the Northern Hemisphere
~~~In the Southern Hemisphere}
\par\end{figure}](/articles/aa/full/2001/28/aa10281/Timg41.gif) |
Figure 1:
Convention for the sign of the tilt angle of the magnetic polarity axis.
Active regions
with a tilt angle
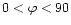 degree in the northern hemisphere,
or degree in the northern hemisphere,
or
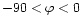 degree
in the northern hemisphere, follow Joy's law. degree
in the northern hemisphere, follow Joy's law. |
| Open with DEXTER |
In order to obtain the flux-weighted center closer to the center of the sunspot and then the
tilt of active regions, a magnetic field of 160 G was selected as a criterion of the
minimum of magnetic strength, so that the effect of some other weak
magnetic fields around main polarities would be minimized. It is useful for us to
calculate the flux-weighted center and tilt angle of magnetic polarity axis by this method
(Tian et al. 1999).
Current helicity plays an important role in the study of twisted magnetic
fields in the solar atmosphere. Its density can be split into two parts,
h|| is the parallel component in the direction of the line of sight which can
be inferred from photospheric vector magnetograms. 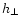 is the transverse component
which is hard to compute because we have magnetic measurement only at a single height
in the solar atmosphere.
is the transverse component
which is hard to compute because we have magnetic measurement only at a single height
in the solar atmosphere.
In the approximation of the force-free magnetic field:
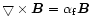 ,
there is,
,
there is,
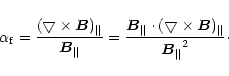 |
(4) |
Thus, the density of current helicity is:
Here, we define
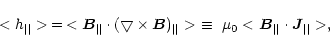 |
(6) |
as mean of h|| distribution over an active region, where
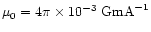 ,
and the vertical current density J|| can be expressed by
,
and the vertical current density J|| can be expressed by
(Wang et al. 1994).
In order to minimize the effect of observational error, the current helicity h|| is
calculated only in pixels as
B|| > 20 G,
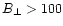 G and current density
J||> 0.001 Am-2, with the noise level of
J||(j,i). Eventually, Bao et al. (1998)
determined an average of the current helicity for each active region.
In this case, the uncertainty of magnetic fields affects <h||> very little.
We evaluated the error in 2
G and current density
J||> 0.001 Am-2, with the noise level of
J||(j,i). Eventually, Bao et al. (1998)
determined an average of the current helicity for each active region.
In this case, the uncertainty of magnetic fields affects <h||> very little.
We evaluated the error in 2 in Figs. 2 and 3. However,
although an active region develops over days, the sign of < h||>and the sign of the tilt angle of the active region
do not change.
in Figs. 2 and 3. However,
although an active region develops over days, the sign of < h||>and the sign of the tilt angle of the active region
do not change.
We have calculated the tilt angle 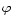 in the paper by Tian et al. (1999) and current
helicity
< h|| > in the paper by Bao & Zhang (1998) for the 286 active regions. Thus, we
can investigate the relationship between the sign of the tilt angle of the magnetic polarity
axis and the sign of the current helicity
< h|| >. Figure 2 illustrates this relationship for
203 bipolar active regions with relatively simple configurations of magnetic fields.
in the paper by Tian et al. (1999) and current
helicity
< h|| > in the paper by Bao & Zhang (1998) for the 286 active regions. Thus, we
can investigate the relationship between the sign of the tilt angle of the magnetic polarity
axis and the sign of the current helicity
< h|| >. Figure 2 illustrates this relationship for
203 bipolar active regions with relatively simple configurations of magnetic fields.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f2.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg56.gif) |
Figure 2:
Relationship between the tilt angle 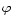 and the mean current helicity
and the mean current helicity
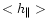 =
=
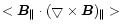 for 203 bipolar active regions.
In these active regions, the magnetic configuration is
simple. Each point denotes an active region. The length of error bars is determined 2
for 203 bipolar active regions.
In these active regions, the magnetic configuration is
simple. Each point denotes an active region. The length of error bars is determined 2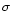 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f3.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg58.gif) |
Figure 3:
The relationship between the tilt angles
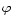 and the mean current helicity
and the mean current helicity
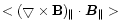 for 83 bipolar active regions.
In these active regions, magnetic configurations are more complicated.
The sign convention of the tilt angle and the current helicity is same as in
Fig. 2. The length of error bars is determined 2
for 83 bipolar active regions.
In these active regions, magnetic configurations are more complicated.
The sign convention of the tilt angle and the current helicity is same as in
Fig. 2. The length of error bars is determined 2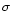 .
Each point denotes an active region. .
Each point denotes an active region. |
| Open with DEXTER |
Figure 3 shows such relationship for the other 83 bipolar active regions with relatively
more complicated magnetic fields than the 203 active regions. We find that in both
kinds of bipolar active regions, about 60% of the regions have a positive/negative tilt angle
and a negative/positive current helicity in the northern/southern hemisphere. In other
words, there is a negative correlation between the sign of the tilt angle and the sign of
the mean twist. These active regions adhere not only to Joy's Law (Hale et al. 1919), but
also to the hemispheric helicity rule (Bao & Zhang 1998; Pevtsov et al. 1995). Thus, we call
these active regions "normal active regions''.
If we consider an active region as
an 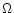 -flux tube rising through the convection zone (Babcock 1961) to the photosphere,
the tube acquires writhe through the Coriolis force on internal flow (Fan et al. 1993). The
tilt of active regions with respect to the equator is an observable manifestation of such writhe,
at photospheric level. A positive/negative tilt angle corresponds to the right/left-handed
writhe of the flux tube in the northern/southern hemisphere on the basis of our sign convention for the tilt angle in Fig. 1. On the whole, a negative/positive mean current helicity
-flux tube rising through the convection zone (Babcock 1961) to the photosphere,
the tube acquires writhe through the Coriolis force on internal flow (Fan et al. 1993). The
tilt of active regions with respect to the equator is an observable manifestation of such writhe,
at photospheric level. A positive/negative tilt angle corresponds to the right/left-handed
writhe of the flux tube in the northern/southern hemisphere on the basis of our sign convention for the tilt angle in Fig. 1. On the whole, a negative/positive mean current helicity
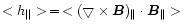 approximately reflects a left/right-handed mean twist of magnetic lines. Thus, these normal active regions are in a stable condition because of the minimization of total helicity.
approximately reflects a left/right-handed mean twist of magnetic lines. Thus, these normal active regions are in a stable condition because of the minimization of total helicity.
Figures 2 and 3 show that most of the active regions in the northern/southern hemisphere
have a positive/negative tilt angle and a negative/positive mean twist <h||> of the
magnetic field lines. These active regions are regarded as "normal active regions'' with
"normal chirality'' due to adhering to both Joy's Law and the hemispheric helicity rule.
While in some other active regions, as in Figs. 2 and 3, we see
the sign of the tilt angle is the same as the sign of the mean twist <h||>. These
active regions disobey either Joy's Law or the hemispheric helicity rule. We regard these
regions as "abnormal active regions'' with "abnormal chirality''. Our results show that in
both the northern and southern hemisphere, about 60% of the active regions are of "normal
chirality'', and about one-third of the active regions are of "abnormal chirality''.
In our data, there are a third kind of active region which has a negative/positive
tilt angle with a positive/negative twist in the northern/southern hemisphere, i.e.
adhering to neither Joy's Law nor the hemispheric helicity rule. They do not belong to
either of the two groups defined above and are a tiny fraction of the active regions (less than 5%).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f4.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg60.gif) |
Figure 4:
Longitudinal distribution of the active regions with Carrington rotation. The sign "+''
denotes active regions with a "normal chirality'', "-'' denotes active regions with an "abnormal
chirality'', and "*'' denotes active regions with neither a "normal chirality'' nor an "abnormal
chirality'' (see text). Each point indicates one active region. |
| Open with DEXTER |
In Fig. 4 we give the distribution of the studied active regions with Carrington
rotation. In the figure, the sign "+'' denotes active regions with "normal chirality'', i.e.,
active regions with a positive/negative tilt angle 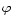 and a negative/positive twist
< h|| >of magnetic lines in the northern/southern hemisphere; "-'' denotes active regions with
an "abnormal chirality'', i.e., active regions in which the tilt angle
and a negative/positive twist
< h|| >of magnetic lines in the northern/southern hemisphere; "-'' denotes active regions with
an "abnormal chirality'', i.e., active regions in which the tilt angle 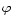 and the mean twist
< h|| > have the same sign. The third kind of active region with a negative/positive
tilt angle
and the mean twist
< h|| > have the same sign. The third kind of active region with a negative/positive
tilt angle 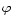 and a positive/negative twist
< h|| > in the northern/southern hemisphere,
which have neither a "normal chirality'' nor an "abnormal chirality'', are denoted by "*''.
Figure 4 show that some areas keep the same sign for many rotations, implying that the helicity of the magnetic fields
has been generated at great depths. This result is in agreement with Canfield & Pevtsov (1998). We especially find
that those active regions with "abnormal chirality'', denoted by "-'' sign, tend to be located
at some special heliospheric longitudes, such as 0-30
and a positive/negative twist
< h|| > in the northern/southern hemisphere,
which have neither a "normal chirality'' nor an "abnormal chirality'', are denoted by "*''.
Figure 4 show that some areas keep the same sign for many rotations, implying that the helicity of the magnetic fields
has been generated at great depths. This result is in agreement with Canfield & Pevtsov (1998). We especially find
that those active regions with "abnormal chirality'', denoted by "-'' sign, tend to be located
at some special heliospheric longitudes, such as 0-30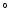 ,
120
,
120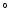 ,
240
,
240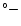 270
270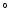 and 330
and 330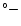 360
360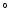 in the northern hemisphere and 30
in the northern hemisphere and 30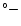 90
90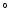 ,
180
,
180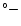 270
270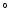 in the southern hemisphere.
in the southern hemisphere.
Bai (1988) examined the distribution of some active regions which produced eruptive flare
during the 19th, 20th and 21st solar cycles. He found that these flares were located
at some special longitudes. We also examine the longitudinal distribution of active regions
that produced major flares with proton events in the 22nd solar cycle. Figure 5 shows the
distribution of these active regions with major flares in the heliosphere. It is found that
these active regions with major flares also tend to be located at some special longitudes.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f5.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg62.gif) |
Figure 5:
Distribution of 62 > M-class X-ray flares with proton event in the 22nd activity
cycle. Each point denotes an active region. |
| Open with DEXTER |
Figure 6a is the histogram used to show the number of the major flares in 30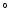 longitudinal bins. We note
that most of the major flares tend to occur in the longitudinal bins 15
longitudinal bins. We note
that most of the major flares tend to occur in the longitudinal bins 15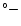 45
45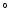 ,
225
,
225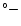 285
285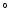 and 315
and 315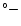 345
345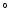 in the northern hemisphere and bins 15
in the northern hemisphere and bins 15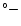 105
105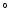 ,
165
,
165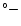 225
225 and 285
and 285 in the southern hemisphere.
Figure 6b is the histogram used to show the number of active regions
in the 30
in the southern hemisphere.
Figure 6b is the histogram used to show the number of active regions
in the 30 longitudinal bins. Solid line denotes the distribution of the active regions
with "abnormal chirality'', shown as "-'' sign in Fig. 4. The dotted line denotes the
distribution of the active regions with "normal chirality'', shown as "+'' in Fig. 4.
We notice that in the longitudinal bins with more major flares, there are more
active regions with "abnormal chirality'' (shown as shadowed regions A to F). These active
regions with "normal chirality'' have their longitudinal bins preferred.
longitudinal bins. Solid line denotes the distribution of the active regions
with "abnormal chirality'', shown as "-'' sign in Fig. 4. The dotted line denotes the
distribution of the active regions with "normal chirality'', shown as "+'' in Fig. 4.
We notice that in the longitudinal bins with more major flares, there are more
active regions with "abnormal chirality'' (shown as shadowed regions A to F). These active
regions with "normal chirality'' have their longitudinal bins preferred.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f6.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg63.gif) |
Figure 6:
a) Histogram of distribution of the 62 > M-class X-ray flares in the 22nd cycle in the 30 longitudinal bins. b) Histogram of distribution of the active regions. Solid line denotes the active
regions with "abnormal chirality'', shown as "-'' sign in Fig. 4. Dotted line denotes the active
regions with "normal chirality'', showed as "+'' sign in the Fig. 4.
longitudinal bins. b) Histogram of distribution of the active regions. Solid line denotes the active
regions with "abnormal chirality'', shown as "-'' sign in Fig. 4. Dotted line denotes the active
regions with "normal chirality'', showed as "+'' sign in the Fig. 4. |
| Open with DEXTER |
We note the following results from this study:
(1) About 60% of studied bipolar active regions are normal active regions with
"normal chirality''. It is inferred that the tilt angle of the magnetic polarity axis and the
mean current helicity
< h|| > have opposite signs. In other words, there is a negative
correlation between the sign of the tilt angle and the sign of the mean twist.
(2) About one-third of bipolar active regions are abnormal active regions with the
"abnormal chirality''. In these active regions, the tilt angles and the current helicity have the
same sign. These active regions tend to be located at particular longitudes in the heliosphere.
(3) Most of the 62 X-ray flares larger than M-class in the 22nd cycle also tend to
occur in particular longitudinal bins, where active regions with "abnormal chirality'' appear
frequently.
We know that total helicity H of a flux tube can be separated into the twist helicity
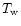 of magnetic lines in the tube and the writhe helicity
of magnetic lines in the tube and the writhe helicity 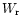 of the tube (Moffatt & Ricca
1992). Therefore, an active region with a "normal chirality'' (i.e., a left/right handed twist
accompanied by a right/left handed writhe) is likely to be in a lower energy state due
to a negative/positive twist helicity and a positive/negative writhe helicity. This is a
relatively stable tube because the total helicity is minimized. An active region
with an "abnormal chirality'' (i.e., a left or right handed twist and a same handed writhe)
is likely to be in a higher energy state due to the same sign of twist and writhe helicity.
There is much more chance of magnetic reconnection in this kind of active region.
Therefore, we propose that the "abnormal chirality'' of active regions is a possible source
of instability able to produce some eruptive phenomena as seen in the Fig. 6.
Fisher et al. (2000) predict that the
twist and writhe in
of the tube (Moffatt & Ricca
1992). Therefore, an active region with a "normal chirality'' (i.e., a left/right handed twist
accompanied by a right/left handed writhe) is likely to be in a lower energy state due
to a negative/positive twist helicity and a positive/negative writhe helicity. This is a
relatively stable tube because the total helicity is minimized. An active region
with an "abnormal chirality'' (i.e., a left or right handed twist and a same handed writhe)
is likely to be in a higher energy state due to the same sign of twist and writhe helicity.
There is much more chance of magnetic reconnection in this kind of active region.
Therefore, we propose that the "abnormal chirality'' of active regions is a possible source
of instability able to produce some eruptive phenomena as seen in the Fig. 6.
Fisher et al. (2000) predict that the
twist and writhe in 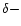 spot active regions should have the same sign because of the kink
hypothesis for
spot active regions should have the same sign because of the kink
hypothesis for 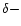 spot active regions. The active region with an "abnormal chirality'' may
represent these kinked regions. However, the relevance between the distribution of the
flares and that of the active regions with "abnormal chirality'' is not high (shown in
the Fig. 6). We believe that it is probably because the number of cases is relatively low
for statistical significance.
spot active regions. The active region with an "abnormal chirality'' may
represent these kinked regions. However, the relevance between the distribution of the
flares and that of the active regions with "abnormal chirality'' is not high (shown in
the Fig. 6). We believe that it is probably because the number of cases is relatively low
for statistical significance.
From Figs. 2 and 3, we find that there is a roughly fixed percentage in each quarter.
We believe this is not a coincidence and that there must be a physical reason. Canfield & Pevtsov
(1998) use a different twist indicator, the force-free parameter 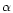 ,
to investigate the
relationship
in sign between the tilt and the twist of magnetic fields. They obtain important and some what
different results from ours. What is the reason? Is it because they use different twist
parameters of magnetic fields? Is there another physical meaning? Figure 4 shows us that
some longitudes keep the same or opposite sign between the tilt and twist for many rotations,
that tells us that the twist of magnetic fields is produced at great depths, not on the surface.
What is real
origin of the twist of the magnetic fields?
,
to investigate the
relationship
in sign between the tilt and the twist of magnetic fields. They obtain important and some what
different results from ours. What is the reason? Is it because they use different twist
parameters of magnetic fields? Is there another physical meaning? Figure 4 shows us that
some longitudes keep the same or opposite sign between the tilt and twist for many rotations,
that tells us that the twist of magnetic fields is produced at great depths, not on the surface.
What is real
origin of the twist of the magnetic fields?
This study could give us some information on the chirality of the magnetic fields in the
sub-photospheric convection zone. We will further investigate the origin and development
of the magnetic field twist and the tilt of active regions, which is an important respect
of some dynamic models of sub-photospheric flux tubes and the dynamo theory as well.
A following paper will discuss this question.
Acknowledgements
The authors are grateful to Drs. T. J. Wang, Y. H. Yan, and Y. Y. Deng for useful
discussions, valuable comments and suggestions. They specially acknowlede
Dr. Jiong Qiu who helped us to improve this paper. The authors are grateful to the referee
for his/her helpful suggestions. This research is supported by NSFC Grant Nos. 19791090 and
10073013.
-
Abramenko, V. I., Wang, T. J., & Yurchishin, V. B. 1996, Solar Phys., 168, 75
In the text
NASA ADS
-
Ai, G. X., Li, W., & Zhang, H. Q. 1982, Chinese Astron. & Astrophys., 6, 129
In the text
NASA ADS
-
Babcock, H. W. 1961, ApJ, 133, 572
In the text
NASA ADS
-
Bai, T. 1988, ApJ, 328, 860
In the text
NASA ADS
-
Bao, S. D., & Zhang, H. Q. 1998, ApJ, 496, L43
In the text
NASA ADS
-
Bao, S. D., Pevtsov, A. A., Wang, T. J., & Zhang, H. Q. 2000,
Solar Phys., 195, 75
In the text
NASA ADS
-
Bieber, J. W., Evenson, P. A., & Matthaeus, W. H. 1987, ApJ, 315, 700
In the text
NASA ADS
-
Burlaga, L. F. 1988, Geophys. J. Res., 93(A7), 7217
In the text
NASA ADS
-
Canfield, R., & Pevtsov, A. 1998, Synoptic Solar Physics, ASP Conf. Ser. 140,
ed. K. Balasubramaniam, J. Harvey, & D. Rabin, 131
In the text
-
Fan, Y., Fisher, G. H., & DeLuca, E. E. 1993, ApJ, 405, 390
In the text
NASA ADS
-
Fan, Y., Zweibel, E. G., & Lantz, S. R. 1998, ApJ, 493, 480
In the text
NASA ADS
-
Fisher, G., Fan, Y., Longcope, D., Linton, M., & Pevtsov, A. 2000, Solar Phys., 192, 119
In the text
NASA ADS
-
Gary, G. A., & Hagyard, M. J. 1990, Solar Phys., 126, 21
In the text
NASA ADS
-
Hale, G. E., Ellerman, F., Nicholson, S. B., & Joy, A. H. 1919, ApJ, 49, 153
In the text
NASA ADS
-
Hagyard, M., & Pevtsov, A. 1999, Solar Phys., 189, 25
NASA ADS
-
Harvey, J. W. 1969, Ph.D. Thesis, Univ. of Colorado
In the text
-
Howard, R. F. 1989, Solar Phys., 123, 271
In the text
NASA ADS
-
Howard, R. F. 1991, Solar Phys., 132, 49
In the text
NASA ADS
-
Leka, K. D. , Canfield, R. C., McClymont, A. N., & Van Driel-Gesztelyi, L. 1996, ApJ, 426, 547
In the text
-
Longcope, D. W., Fisher, G. H., & Arendt, S. 1996, ApJ, 464, 999
In the text
NASA ADS
-
Longcope, D. W., & Klapper, I. 1997, ApJ, 488, 443
In the text
NASA ADS
-
Longcope, D. W., Fisher, G. H., & Pevtsov, A. A. 1998, ApJ, 507, 417
In the text
NASA ADS
-
Martin, S. F., Billamoria, R., & Tracadas, P. W. 1994, in Solar Surface Magnetism, ed. R. J. Rutten,
& C. J. Schrijver (Dordrecht: Kluwer), 303
In the text
-
Moffatt, H. K., & Ricca, R. L. 1992, Proc. R. Soc. Lond. A, 439, 411
In the text
-
Moreno-Insertis, F., & Emonet, T. 1996, ApJ, 472, L53
In the text
NASA ADS
-
Pevtsov, A. A., Canfield, R. C., & Metcalf, T. R. 1995, ApJ, 440, L109
In the text
NASA ADS
-
Rust, D. M., & Kumar, A. 1994, Solar Phys., 155, 69
In the text
NASA ADS
-
Rust, D. M., & Kumar, A. 1996, ApJ, 464, L199
In the text
NASA ADS
-
Schmidt, H. U. 1968, in IAU Symp., 35, Structure and Development of Solar Active Regions, ed.
K. O. Kiepeuheuer, 95
In the text
-
Seehafer, N. 1990, Solar Phys., 125, 219
In the text
NASA ADS
-
Tian, L., Zhang, H., Tong, Y., & Jing, H. 1999, Solar Phys., 189, 305
In the text
NASA ADS
-
Wang, H. N., & Lin, Y. 1993, Chin. Astron. Astrophys., 17, 423
In the text
NASA ADS
-
Wang, J. X., Shi, Z. X., Wang, H. N., & Lü, Y. P. 1996, ApJ, 456, 861
In the text
NASA ADS
-
Wang, T. J., Xu, A. A., & Zhang, H. Q. 1994, Solar Phys., 155, 99
In the text
NASA ADS
-
Wang, T. J., Ai, G. X., Deng, Y. Y. 1996, Publ. Beijing Astron. Obs., 28, 31
-
Wang, Y.- M., & Sheeley, N. R. 1989, Solar Phys., 124, 81
In the text
NASA ADS
-
Wang, Y. M., & Sheeley, N. R. 1991, ApJ, 375, 761
In the text
NASA ADS
Copyright ESO 2001
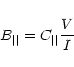
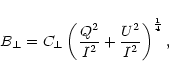
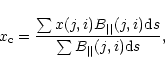
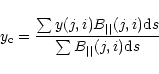
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f1.eps}\par\mbox{In the Northern Hemisphere
~~~In the Southern Hemisphere}
\par\end{figure}](/articles/aa/full/2001/28/aa10281/Timg41.gif)
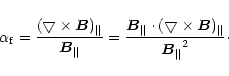
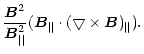
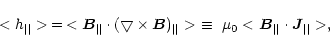
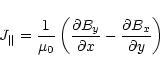
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f2.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f3.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg58.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f4.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg60.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f5.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg62.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10281f6.eps}\end{figure}](/articles/aa/full/2001/28/aa10281/Timg63.gif)