A&A 374, 13-27 (2001)
DOI: 10.1051/0004-6361:20010699
Dipartimento di Scienze Fisiche E.R. Caianiello, Università di Salerno, 84081 Baronissi, Salerno, Italy - Istituto Nazionale di Fisica Nucleare, Sezione di Napoli, Gruppo Collegato di Salerno, Italy
Received 3 July 2000 / Accepted 12 April 2001
Abstract
We study in detail the trajectories followed by single images
during binary microlensing events. Starting from perturbative
resolutions of the lens equation, we explore the full parameter
space by continuity arguments. We see that the images created
during the caustic crossing can recombine with the others in
different ways. This leads to a new classification of the
microlensing events according to the behaviour of the images. We
show that the images involved in these combinations depend on the
folds that are crossed at the entry and at the exit from the
caustic. Non-trivial trajectories can be classified into four main
types. Some consequences for the motion of the center of light of
the source in astrometric measurements are also examined.
Key words: gravitational lensing - stars: binaries - astrometry
The theoretical study of binary lenses started in 1986, with the paper by Schneider & Weiß, where the equal masses case was considered in detail. The caustics were derived and they started to explore the non-trivial image dynamics underlying this model. Their results were extended by Erdl & Schneider (1993) and Witt & Petters (1993) to an arbitrary mass ratio. These works contain two independent analytical derivations of the caustic structure of the binary lens.
On the contrary, the direct inversion of the binary lens equation can only be performed numerically, as it can be reduced to a fifth order complex equation (Witt 1990). This point poses a major difficulty in the extraction of analytical results about the images of the binary lens. Two successful examples are the minimum amplification during the caustic crossing, computed by Rhie (1997) and the shape of the light curves in the caustic crossing by a limb darkened source (Rhie & Bennett 1999). In practice, numerical methods are applied to fit experimental curves (Mao & di Stefano 1995; Albrow et al. 1999) and to make empirical investigations about what should be expected in several cases (Di Stefano & Perna 1997; Dominik 1995, 1998). Obviously, this lack of analytical results prevents a full understanding of the problem, so that almost all we know of the images and their magnification relies on numerical results whose generality cannot be proved.
A new interest in the study of the trajectories of the images has recently risen with the possibility of exploiting space interferometry to measure the astrometric displacements of the source stars being microlensed (Walker 1995; Dominik & Sahu 2000). These researches are encouraged by several projects of space missions that will bring the resolution down to few microarcsecs (Allen et al. 1997; Lindegren & Perryman 1996). In the case of binary microlensing, astrometric observations can lead to a complete break of the degenerations affecting the light curves, since paths giving similar light curves would be discriminated (Han et al. 1999; Gould & Han 2000). Following the motion of the center of light (CoL) of the source can also help in the detection of extrasolar planets with a more accurate determination of the parameters of the system (Safizadeh et al. 1999). It is likely that in the near future it will be possible to follow the images in microlensing events independently, at least when the source is not too large.
With this paper, we mean to bring new analytical knowledge to this field, going beyond numerical studies, opening a discussion about the generality of the results and studying the relations between the observables and the parameters of the system. In Sect. 2, we give analytical resolutions of the lens equation in special cases where perturbative approximations are possible. In Sect. 3, we review the gravitational lensing near cusps, looking at the local structure of the lens equation. Then, in Sect. 4, we consider the full lens equation and, by continuity arguments, we exploit the results of Sect. 3 to investigate the trajectories of the images globally. This leads to a new classification of the microlensing events, according to the continuity of the trajectories of the images involved in the caustic crossing. We shall also identify the features distinguishing each topology from the others. Finally, in Sect. 5, we give the summary.
Perturbative solutions show several interesting aspects of the inversion problem, giving insight to some questions and opening new ones. Moreover, they provide some starting points for a global investigation of the images.
We introduce the Einstein radius of the total mass M:
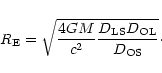 |
(1) |
The lens equation reads
y1 = 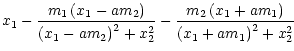 |
(2a) |
| y2 = |
(2b) |
The simplest case, where perturbative resolution of the lens
equation is possible, is when the source is very far from the
lenses. We consider the inverse of the modulus of the source
position
![]() as a perturbative parameter. In the limit
as a perturbative parameter. In the limit
![]() going to infinity, the predominant
image is the source itself, i.e.
going to infinity, the predominant
image is the source itself, i.e.
![]() ,
since
the lens effects vanish. Expanding the lens
Eq. (2) starting from this image, we get corrections to its
position in the form of a series in inverse powers of
,
since
the lens effects vanish. Expanding the lens
Eq. (2) starting from this image, we get corrections to its
position in the form of a series in inverse powers of
![]() .
Stopping at the first order, we have
.
Stopping at the first order, we have
| x1 = |
(3a) |
| x2 = |
(3b) |
with positive parity.
We get the same solution if we expand the exact solutions for a single lens with mass equal to the total mass of the system, placed at the origin. In the following, this image will be referred to as the principal image of the system.
Besides the principal image, two more expansions of the lens
equation are possible, starting from the two mass positions. They
lead to the same solutions we get by expanding the single lens
secondary images for each mass. We write here the secondary image
of the first mass. A similar expression holds for the other:
| x1 = |
(4a) |
| x2 = |
(4b) |
They have negative parity.
So, at least when the source is far from the lenses, we can identify a principal image and a secondary image for each mass.
The images of planetary systems were already found in Bozza (1999), where they were used to build analytical light curves for planetary microlensing events. It is easy to build an analytic expression for the center of light motion during a planetary microlensing event as well.
The three images found in the limit
![]() can be easily
reported to the far source labeling introduced in Sect. 2.1. Two
images are just the single lens images of the star, slightly
displaced by the planet. The third image is the secondary image of
the planet. The latter gives a negligible contribution to the
light curve and CoL trajectory.
can be easily
reported to the far source labeling introduced in Sect. 2.1. Two
images are just the single lens images of the star, slightly
displaced by the planet. The third image is the secondary image of
the planet. The latter gives a negligible contribution to the
light curve and CoL trajectory.
In this case, the perturbative parameter is the inverse of the
distance a-1. We put the first lens in the origin and the
other in the position
![]() .
.
For the principal image and the secondary image of the first mass,
we can start from the single lens images
![$\displaystyle \frac{m_2}{a\left(m_1^2-\left\vert{\vec I}
\right\vert^4\right)} \left[ m_1 \left( I_2^2- I_1^2 \right)+
\left\vert{\vec I} \right\vert^4
\right]$](/articles/aa/full/2001/28/aa10066/img18.gif) |
(6a) |
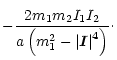 |
(6b) |
For the secondary image of the second mass, we can proceed in the same way as for the planetary image. Up to the second order, we have
| (7a) | |
| (7b) |
Even if we can calculate positions and magnifications of all images, the light curves and CoL trajectories built by these quantities do not prove to be as good as those of the planetary case. The problem is that to have any significant modulation on a light curve or CoL trajectory, we need the source to pass very close to the caustic of the first mass. But, in this regime, the two main images lie very close to the critical curve of the first mass where the magnification diverges. This fact rules out the possibility of employing these results in a reliable way. In the planetary case, on the contrary, when the source is close to the planetary caustic, the two main images are far from the critical curve and can be approximated efficiently.
Deriving the formulae for wide binaries, we have considered the separation of the lenses to be much greater than all other lengths, including |y|. Thus they are valid for a source close to the first mass. If the source is far from the first mass as well, then the formulae of Sect. 2.1 hold.
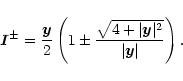 |
(8) |
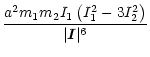 |
(9a) |
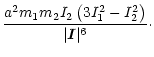 |
(9b) |
Then, the perturbations to the images are given by
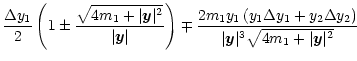 |
(10a) |
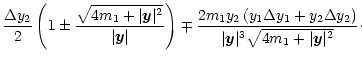 |
(10b) |
A third image of negative parity can be found if we start from the
origin. This central image has coordinates
| (11a) | |
| (11b) |
but is highly demagnified.
Also for close binaries, apparent modulations to light curves and CoL trajectories are achieved in a regime where the two main images are too close to singularities. We cannot use these results to study these curves analytically.
The secondary images of a close binary system are drastically different from those of the far source regime. Rather than left and right secondary images, we have a global secondary image and a central one.
To understand the transition between the two regimes, consider two
lenses of equal mass. If the source is on the y2 axis, i.e. on
the axis of symmetry of the system, the calculations of this
section show that the secondary and the central image would be
placed on the x2 axis. If we move the source away along the
y2 axis, in the limit of a far source, two secondary images are
formed close to the two lenses which are off-axis. Then, it seems
to be non-trivial how the transition between these two regimes
occurs. However, the secondary and the central image become very
close when
![]() .
This is the order of distance
of the secondary caustics in close binary systems (Bozza 2000a).
We will see in Sect. 4 that these small singularities play a
fundamental role in the transition between the two regimes.
.
This is the order of distance
of the secondary caustics in close binary systems (Bozza 2000a).
We will see in Sect. 4 that these small singularities play a
fundamental role in the transition between the two regimes.
Having explored the lens equation in the cases where it is possible to resort to analytical approximations, we want to bring our attention to the general case. To get any comprehension of the global shape of the trajectories of the images, it is necessary to look at the local behaviour first. As will be explained in the next section, the cusps play an important role in this comprehension. So, it is useful to review some general aspects of lensing near cusps in order to develop further studies.
In the standard treatment (Schneider & Weiß 1992), the cusp
is at the origin of the source plane, while the point of the
critical curve generating the cusp (cusp point) is at the origin
of the lens plane. With a suitable rotation, the lens map can be
generically written in the following form:
| y1 = |
(12a) |
| y2 = bx1x2+ax23, | (12b) |
where the coefficients a, b, c are related to the derivatives of the Fermat potential. The sign of the cusp, defined as the sign of the quantity 2ac-b2 (Blandford & Narayan 1986), determines the parities of the images involved in the cusp lensing.
The lens Eq. (12) can be exactly
solved. In particular, along the cusp axis (i.e. when y2=0),
the solutions take a simple form:
| x1 = |
(13a) |
x1 =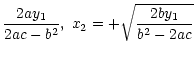 |
(13b) |
x1 =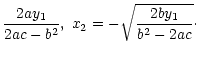 |
(13c) |
We see that, for positive cusps, when y1>0, there is one image with positive parity on the x1 axis. After the cusp crossing (i.e. when y1<0), this image has changed parity, while two positive images are formed off-axis in specular positions (Fig. 1b). The situation is reversed for negative cusps.
If we slightly displace the source by a small constant y2, the caustic is crossed on a fold. Then, analyzing the exact solutions and their parity, we see that the original image merges with the top positive image, giving a fully continuous trajectory, without changes of parity, moving along the critical curve on its positive side on the top (Fig. 1a). The negative parity branch of the former on-axis solution is slightly displaced towards negative x2. It starts below the cusp point on the critical curve, together with the remaining positive image.
Of course, if we consider a small negative y2, the plots are reversed around the horizontal axis (Fig. 1c). We see that the creation process occurs on the opposite side of the fold crossing point (with respect to the cusp axis). So, if we go from source trajectories crossing the caustic on the upper fold to cusp crossing and then to trajectories crossing the lower fold, we see that the continuous image changes side. It passes on the top of the critical curve when the upper fold is crossed and passes on the bottom when the lower fold is crossed. Meanwhile, the creation point rises from below to above. A similar process can be done for negative cusps.
After these preparatory sections, we are ready to compare with the
global properties of the image trajectories. It must be stressed
that we are considering microlensing of a point source and
consequently examine the trajectories of point images. This
discussion would apply to every area element of an extended image,
but not to the image as a whole, since different area elements may
follow quite different trajectories and it is impossible to define
the trajectory of the whole extended image.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{10066f1.eps} \end{figure}](/articles/aa/full/2001/28/aa10066/Timg42.gif) |
Figure 1:
Images in the neighborhood of a positive cusp. On the right,
the cusp and the source trajectory are shown.
On the left, the corresponding
images and the critical curve are plotted. The
critical curve and the caustic are represented by the thick
lines. The trajectories are described by dot-dashed lines
before the caustic crossing and by dashed lines after. The sign of |
| Open with DEXTER | |
To deduce global properties of point image trajectories from local ones, we resort to several continuity arguments:
The topology of the trajectories of the images only depends on the folds intercepted by the source trajectory. The topology of the trajectories does not change when the parameters of the binary lens are changed (if the folds crossed remain the same) even when transition through different topologies of the critical curves occur.
This justifies a classification of the trajectories of the images based on the folds crossed by the source at the entry and at the exit from the caustic.
For the observations exposed in the previous subsection, we are entitled to extend the labeling of Sect. 2 to each source trajectory that can be continuously transported to infinity without crossing any caustics. In fact, for these trajectories, there is always one positive image to be identified with the principal image. The two negative images start their trajectories and end each at the same mass without exchanging, since this exchange would need a discontinuous jump. So they can be identified with the secondary images of each mass.
There are two kinds of source trajectories not crossing caustics that are not homotopic to far source trajectories. In wide binaries, if the source passes in the middle of the two caustics, it cannot be transformed into a far source trajectory continuously without intersecting any caustics. The two negative images live inside the two separate critical curves and cannot mix. So, even in this case, they can be identified with the secondary images of the two masses. The other source trajectories non-homotopic to far sources are those passing between the central caustic and one secondary caustic of a close binary configuration. Since, in this case, the two negative images live in the same critical curve, in principle they can exchange. So we need further investigation about what happens inside a secondary critical curve. We will come back to this case in Sect. 4.1.4.
Once we have established that the discriminators in our classification are the folds intercepted by the source, we can choose the parameters of the binary system in the most convenient way, since their specific value is not essential. The natural choice is the equal masses case.
To investigate the shapes of the trajectories of the images in caustic crossing events, we need some well known starting point where a full analytical description is available. The full binary lens equation can be exactly solved for a source on the axis joining the two lenses, i.e. when y2=0. In the equal masses case, it can also be solved on the symmetry axis orthogonal to the latter, i.e. when y1=0. The fifth degree complex equation is separated in a second degree and a third degree equation. The solutions can be easily studied to find the trajectories of the images in these particular cases. They will provide the basis for the complete classification of the trajectories, so we discuss them in detail.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{10066f2.eps} \end{figure}](/articles/aa/full/2001/28/aa10066/Timg43.gif) |
Figure 2: Trajectories of the images (left) corresponding to the source trajectory on the right, lying on the horizontal axis. a) wide binary, b) intermediate binary, c) close binary. To make the time sequence evident, we have displayed the positions of the images and the source by dots of increasing size. Moreover, letters mark the positions of the images and the source in the most important passages: a is the starting point, b is the entrance into the caustic, c is the exit from the caustic, d is the end of the trajectory. |
| Open with DEXTER | |
In Fig. 2 we have represented the solutions for a source on the horizontal axis in the three topologies of an equal masses binary system. We recall that the cusps on the y1 axis are positive and the others are negative, as proved in (Bozza 2000b).
In the wide binary case (Fig. 2a), we have shown the right caustic crossing, since the other is obviously symmetric. The source threads the caustic from left to right. At the beginning, we have an image in the middle of the two critical curves of positive parity and two negative parity images in each of the two critical curves (time a). At time b the source meets the first cusp of the right caustic. It is a positive cusp, so the positive image is substituted by a negative one, inside the right critical curve and two positive images are formed at the same point moving perpendicularly. At time c the source leaves the caustic. The two positive images meet again in the right extremity of the critical curve to disappear. The original negative image of the right critical curve is destroyed and a positive image leaves the critical curve at the same point. Finally (time d) there is a positive image on the right and again a negative image in each critical curve.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{10066f3.eps} \end{figure}](/articles/aa/full/2001/28/aa10066/Timg44.gif) |
Figure 3: Trajectories of the images for a source on the vertical axis: in the intermediate case a), close binary case (central caustic crossing) b), close binary case (secondary caustic crossing) c). |
| Open with DEXTER | |
In the same way, we can discuss the intermediate configuration (Fig. 2b). At the beginning (time a), there is a positive image on the left and two negative images close to each mass inside the critical curve. When the source enters the caustic (time b), the positive image enters the critical curve and two positive images are formed as in the previous case. At time c, the two positive images, after having passed the whole critical curve, one on the top and one on the bottom, annihilate in the cusp point on the right. The right negative image disappears and a positive one leaves the critical curve. At the end (time d), we have the positive image on the right and again two negative images close to each mass. We see that the secondary image of the left mass has become the secondary image of the right mass, without taking part in the creation/destruction processes. So, in this case, there is an exchange of secondary images between the two masses. One of the two images is exchanged directly, while the other is exchanged via creation/destruction processes.
For the close binary system (Fig. 2c), the discussion is similar to that of the intermediate case, since the two cusps crossed are the same (in the sense of continuous transformations of the lens configuration) of the former case. So, here as well, there is an exchange of secondary images.
Now we come to the exact solutions on the vertical axis, represented in Fig. 3. In the case of wide binaries, it is not a caustic crossing curve, so we do not take it into consideration.
We start from the intermediate case (Fig. 3a). The source threads a fold in the entrance and in the exit from the caustic. The two secondary images of the two masses do not participate in the creation/destruction processes and do not exchange. At time b, a pair of images with opposite parities is created in the lower part of the critical curve. The positive image just created survives at the end playing the role of principal image when the source exits from the caustic (time c). At this time, the former principal image is destroyed with the negative image temporarily created. So, in this case, during the caustic crossing time, it is not possible to identify a unique principal image, because there are two positive images and each of them becomes the principal image in one of the two asymptotic regimes.
For close binary systems, the vertical trajectory meets both the central and the two secondary caustics. The second plot (Fig. 3b) deals with the central caustic crossing. At the beginning (time a), there is a positive image, a negative image at the centre to be identified with the central image of Sect. 2.4 and a negative image close to the opposite boundary of the main critical curve (global secondary image of Sect. 2.4). At time b, the source meets a negative cusp. The secondary image leaves the place to a positive image, and two negative images are formed. These negative images travel to the top, where they annihilate at time c. At the same point, the former principal image is destroyed and a negative one is born, playing the role of global secondary image at the end. The central image is not involved in any process.
Finally, we deal with the secondary caustic crossing (Fig. 3c). At time a, the source is above the top secondary caustic. There is a principal image and a secondary image for each mass. These can be unambiguously associated with their masses, since, for y2 going to infinity, they reach them. At time b the source reaches the secondary caustic in the upper fold. A pair of images is created at the top of the lower oval. The negative image just created goes towards the centre and finally plays the role of central image. The positive one goes to the bottom of the oval and at time c, when the source exits the secondary caustic through the lower negative cusp, it becomes negative, finally playing the role of global secondary image. The two former partial secondary images are destroyed at the cusp point at time c. So, it is clear now how the transition between the far source regime and the close binary regime happens, at least in the vertical trajectory case: first, the central image is created and then its temporary positive partner converts to the global secondary image while the partial secondary images disappear.
We have previously stated that the topology of the paths of the images depends on the folds crossed by the source during the microlensing event. We will derive these topologies starting from those of the exact solutions on the two axes of the system, by slightly perturbing the trajectory and applying the discussion of Sect. 3 to resolve the lens equation in the neighborhood of the cusps.
In general, a source trajectory can intersect the caustics more than once. In each caustic crossing, it has to enter through a fold and exit through another fold (it cannot be the same fold, since the folds seen from the inside are convex). So, we can decompose a trajectory in a succession of simple caustic crossings and study them separately. For this reason, we shall examine, in what follows, just simple caustic crossings. Multiple caustic crossings are obtained by putting together two or more simple crossings.
The two caustics of the wide binaries are equivalent for reflection on the vertical axis. Let's consider the right one. Each caustic has four folds. We number them from the upper left to the lower left clockwise. Obviously, we can pair the folds in six ways. Two pairs (3-4, 2-4) can be obtained from other two pairs (1-2, 1-3) by reflection around the horizontal axis, so we have to consider four possibilities for fold crossings. The trajectories intersecting the caustic in these pairs are shown in Fig. 4.
The caustic of the intermediate configuration has six folds. We number them in the same way as the wide binary caustic. By considering equivalent pairs that can be obtained by reflection on either axis, out of the fifteen pairs, we are left with six pairs (1-3, 1-4, 1-6, 2-3, 2-4, 2-5). The first three trajectories are shown in Fig. 5 and the other three in Fig. 6.
For the central caustic of close binaries there are three possibilities (1-2, 1-3, 1-4), shown in Fig. 7. We number the folds of the upper secondary caustic starting from the upper, clockwise. So we have two other possible fold crossings (5-6, 6-7) (Fig. 8).
![\begin{figure}
\par\includegraphics[width=10cm,clip]{10066f4.eps} \end{figure}](/articles/aa/full/2001/28/aa10066/Timg45.gif) |
Figure 4: The four inequivalent fold crossings in wide binaries. a) 1-4, b) 1-3, c) 1-2, d) 2-4. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{10066f5.eps} \end{figure}](/articles/aa/full/2001/28/aa10066/Timg46.gif) |
Figure 5: Three of the six inequivalent fold crossings for the caustic of intermediate binaries. a) 1-3, b) 1-4, c) 1-6. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{10066f6.eps} \end{figure}](/articles/aa/full/2001/28/aa10066/Timg47.gif) |
Figure 6: The other three of the six inequivalent fold crossings for the caustic of intermediate binaries. a) 2-3, b) 2-4, c) 2-5. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{10066f7.eps} \end{figure}](/articles/aa/full/2001/28/aa10066/Timg48.gif) |
Figure 7: The three inequivalent fold crossings for the central caustic of close binaries. a) 1-4, b) 1-3, c) 1-2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=10cm,clip]{10066f8.eps} \end{figure}](/articles/aa/full/2001/28/aa10066/Timg49.gif) |
Figure 8: The two inequivalent fold crossings for the upper secondary caustic of close binaries. a) 5-6, b) 6-7. |
| Open with DEXTER | |
Exploiting all the considerations done up to now, we are able to discuss these trajectories and derive their properties analytically.
The first fold crossing we want to discuss is wide binary 1-2, represented in Fig. 4c. It can be obtained by slightly displacing the horizontal trajectory (shown in Fig. 2a) towards the top. As the two cusps crossed in the horizontal trajectory are positive, following the discussion of Sect. 3 about the behaviour of positive cusps, we can say that the upper positive image created in the caustic crossing has to join with the positive image living before and after the crossing to form a unique continuous image. At the first fold crossing (time b), the two opposite images have to be created in the y2<0 half of the critical curve. At the second crossing (time c), the extra positive image is destroyed in the same half of the critical curve, near the right cusp point. We can observe that in this kind of fold crossing the principal image can be continuously followed from the beginning to the end of the event, even during the caustic crossing. The right secondary image passes from right to left through a creation/destruction process with an extra positive image. The left secondary image is unaffected.
Modifying the parameters of the system, we can derive other significant fold crossings from the wide binary 1-2. The intermediate binary 2-3 is obtained by lowering the separation between the lenses. The upper fold of the intermediate caustic is the result of the merging of wide binary fold 1 of the right caustic with the homologous of the left caustic. So, the trajectories of the images will not be topologically changed during the transition between the two regimes. So, in the intermediate binary 2-3 crossing, represented in Fig. 6a, there is a continuous principal image, a left secondary image unaffected and a right secondary image jumping via creation of a positive image.
The wide binary 1-3 (Fig. 4b) is derived by
displacing the horizontal trajectory by a
![]() with
with ![]() small and b is the position of the right
caustic. In this way, the left positive cusp is skipped from above
and the right from below. According to Sect. 3, the upper positive
image appearing during caustic crossing has to merge with the left
positive image existing before the crossing. This image has to
disappear at time c, where it meets the former right secondary
image. At the same time, the lower positive image appearing during
the caustic crossing merges with the right positive image existing
after the crossing. This image is created at time b with the
final right secondary image. So, in this case, the situation is
more complicated, since the original principal image is destroyed
and another positive image takes its place. The same happens for
the right secondary image. So, we can say that at time b a new
pair of principal and right secondary images are formed and the
preexisting ones are destroyed at time c.
small and b is the position of the right
caustic. In this way, the left positive cusp is skipped from above
and the right from below. According to Sect. 3, the upper positive
image appearing during caustic crossing has to merge with the left
positive image existing before the crossing. This image has to
disappear at time c, where it meets the former right secondary
image. At the same time, the lower positive image appearing during
the caustic crossing merges with the right positive image existing
after the crossing. This image is created at time b with the
final right secondary image. So, in this case, the situation is
more complicated, since the original principal image is destroyed
and another positive image takes its place. The same happens for
the right secondary image. So, we can say that at time b a new
pair of principal and right secondary images are formed and the
preexisting ones are destroyed at time c.
From wide binary 1-3, we can derive the intermediate binary 2-4 (Fig. 6b) in the same way as before for the intermediate 2-3.
The intermediate binary 1-3 is derived from the horizontal trajectory (Fig. 2b) adding a positive y2. Then, as in wide binary 1-2, the positive extra-image appearing during the caustic crossing joins with the positive images existing before and after to give a fully continuous principal image. The left secondary image becomes the secondary image of the right mass, as in the horizontal case, since it is not involved in singularities. At time b, a pair of opposite images is formed near the left cusp point. The negative image just produced becomes the left secondary image, while the positive annihilates with the former right secondary image at time c near the right cusp point.
The close binary 1-2 crossing (Fig. 7c) involves the same folds of intermediate binary 1-3, since the transition to close binaries separates the folds 1 and 3 of the intermediate caustic in two, with the separation of the secondary caustics from the central one. So, the discussion is similar to the previous. There is a continuous principal image. The left secondary image becomes the right one, but we can also identify it with the central image of this phase. The global secondary image is broken in two pieces joined by a temporary positive image.
The intermediate binary 1-4 is derived by the horizontal
trajectory by taking
![]() with
with ![]() small
(Fig. 5b). The upper positive image
during the caustic crossing merges with the positive one before
the crossing. So, the principal image is destroyed at time cwith the right secondary image. The lower positive image joins
with the one after the crossing. So the late time principal image
is born at time b along with the final left secondary image. The
initial left secondary image becomes the right one.
small
(Fig. 5b). The upper positive image
during the caustic crossing merges with the positive one before
the crossing. So, the principal image is destroyed at time cwith the right secondary image. The lower positive image joins
with the one after the crossing. So the late time principal image
is born at time b along with the final left secondary image. The
initial left secondary image becomes the right one.
The discussion is the same for close binary 1-3, that can be obtained from the latter case (Fig. 7b).
The intermediate 2-5 fold crossing (Fig. 6c) is described analytically by the vertical trajectory (Fig. 3a), already discussed.
The wide binary 1-4 case, shown in Fig. 4a, involves the same folds of the intermediate 2-5 case after their breaking in two pieces. So, in this case as well, the two secondary images are unaffected, while the principal image is broken into two pieces joined by a temporary negative image.
To attain the close binary 1-4 fold crossing, we have to displace the vertical trajectory of Fig. 3b towards the left. The two cusps intercepted were negative, so the right negative image living during the caustic crossing joins with the two pieces of the global secondary image to give a fully continuous trajectory. The central image remains unaffected. The left negative image deals with the joining of the two pieces of the principal image which remains interrupted. So, at time b, two opposite images are created at the bottom, on the left of the cusp point. The positive image becomes the final principal image, while the negative one travels to the top to destroy the former principal image at time c.
From this case, we can obtain, by continuous transformation of the separation between the lenses, the intermediate binary 1-6 (Fig. 5c). The roles of the two unaffected secondary images is here more defined. We have to remember that for a full definition of the two negative images in close binaries we have to consider the secondary caustic crossing.
The wide binary 2-3 case (Fig. 4d) is a transformation of the close binary 2-3 crossing, which is the reflection of 1-4 crossing, examined before. So, also in this case, the two negative images are not involved and the principal image is broken.
Last, we consider the two kinds of secondary caustic crossings. The 5-6 crossing (Fig. 8a) can be derived from the vertical trajectory (Fig. 3c) adding a small positive y1. The only cusp to resolve is negative. At the beginning, we have a secondary image for each mass (time a). At time b, the fold 5 is crossed and two images are formed on the top of the lower oval, as in the vertical trajectory. The negative image just formed becomes the central image, while the positive image annihilates with the right secondary image, according to the negative cusp resolution, as discussed in Sect. 3. The initial left secondary image is no longer involved in the negative cusp destruction and becomes the global secondary image. Finally, the transition between far source and close binary regime is achieved.
The secondary caustic crossing 6-7 (Fig. 8b) can be considered as a transformation from the intermediate 1-3 case, since the folds involved are pieces of the folds 1 and 3 broken after the transition to the close binary configuration. The principal image and the central image are unaffected and the global secondary image is broken in two pieces joined by a positive temporary image residing in the small lower oval.
After the study of all possible fold crossing curves, we can complete our classification by considering the non caustic crossing source trajectory passing between the central and the secondary caustic of the close binary system. If we start from the 6-7 crossing (Fig. 8b), we can obtain our trajectory by pushing the trajectory below the secondary caustic. The source will no longer intersect the caustic and the global secondary image will become continuous. So, the difference between this trajectory and a non caustic crossing one homotopic to far source trajectories is in the exchange between the two partial secondary images. This is the only exchange between secondary images where none of the two images is involved in creation/destruction processes.
Looking at Figs. 4-8, there exist four possible events characterizing a non-trivial trajectory.
About the continuity of the principal image, it is possible to draw a general conclusion. In fact, if a positive image has to be principal in both asymptotic regimes, it has to thread the horizontal axis (apart from the particular case of a source trajectory parallel to this axis). Obviously, the candidate to the principal image has to thread the horizontal axis out of the critical curves. But, as we have seen discussing the source trajectory along the y1 axis, the image positions on the x1axis outside of the critical curve all correspond to sources on the y1 axis outside the caustics. So, we can say that all source trajectories threading the y1 axis inside the caustics possess a discontinuous principal image. The converse is also true if we look at the outcomes of our classification.
| Source trajectory | Breaking | Exchange | Ext. exchange | Pair subst. |
|---|---|---|---|---|
| Non caustic crossing | ||||
| Homotopic to far source | ||||
| Non homotopic in wide binaries | ||||
| Non homotopic in close binaries | L
|
|||
| Caustic crossing | ||||
| Wide binaries | ||||
| Folds 1-2 | R | |||
| Folds 1-3 | PR | |||
| Folds 1-4 | P | |||
| Folds 2-3 | P | |||
| Intermediate binaries | ||||
| Folds 1-3 | L
|
R
|
||
| Folds 1-4 | L
|
PR
|
||
| Folds 1-6 | P | |||
| Folds 2-3 | R | |||
| Folds 2-4 | PR | |||
| Folds 2-5 | P | |||
| Close binaries | ||||
| Folds 1-2 | L
|
R
|
||
| Folds 1-3 | L
|
PR
|
||
| Folds 1-4 | P | |||
| Folds 5-6 | R | |||
| Folds 6-7 | L
|
R
|
In no case are two images created at time b destroyed together at time c. The pairs of destroyed images are never the two created previously. So, if we look at the union of all image trajectories, forgetting about time ordering, we will see three continuous curved lines. The extremities of these three curves are those of the far source regime: no other possible start or end points are available. Normally, the three curves will start and end at the same pole (we can treat infinity as an effective pole of the map in a one-point compactification of the image plane on a sphere), resulting in three loops. If an exchange or a pair substitution occurs, one curve will start on a pole and end on another, while the curve starting from the latter pole will end on the first. In this case, therefore, there will be two loops, since two curves will be joined together through the poles. Finally, if a pair substitution and an exchange occur simultaneously, there will be just one loop, starting from infinity, passing through the two masses and going back to infinity.
The behaviour of the images of gravitational lenses is almost an untouched field of investigation. The difficulties in the inversion of the lens equation is an obstacle to analytic statements. In this paper, we have studied the images produced by a binary lens. We started from particular cases where analytic solutions were available; then, studying the lens equation near cusps, we extended our results by continuity. In this way, we have attained a full investigation of images in microlensing events, with a complete classification of the topologies of the trajectories and an identification of the four phenomena related to topology changes. Many of our results have a more general validity and could be extended to other lenses just by examining the far source regime and the caustic structure which is, in general, easier to derive than the images. So, our method gives new insights into the study of the lens equation and the topologies of the trajectories of the images.
It would also be very interesting to try to exploit these results in the study of CoL motion in order to have an immediate connection to a quantity that will become observable in the near future. In principle, a complete classification of the light curves and the CoL motion with respect to the folds intercepted by the source is possible and would be a very useful tool for the interpretation of a binary microlensing event. The classification presented in this work is an important first step towards these objectives.
Acknowledgements
I would like to thank Gaetano Scarpetta and Salvatore Capozziello and Martin Dominik for their comments on the manuscript.Work supported by the European Social Fund through PO by MURST.