A&A 374, 116-131 (2001)
DOI: 10.1051/0004-6361:20010529
J. Ising - D. Koester
Institut für Theoretische Physik und Astrophysik, Universität Kiel, 24098 Kiel, Germany
Received 26 June 2000 / Accepted 2 April 2001
Abstract
Numerical simulations of light curves of variable DA white dwarfs (ZZ
Ceti stars) predict flux amplitudes with surface distributions different
from the spherical harmonics of the pulsation mode in deeper layers. In
contrast to the results of the perturbation analysis by Goldreich and Wu,
this is also true for the fundamental period of the flux variation. As a
consequence, normalized amplitude spectra depend not only on the mode
number l but also on pulsation amplitude and inclination. Another new
result is that with increasing amplitude of the pressure variation below
the convection zone, the flux variation at the surface goes through a
maximum and then decreases again.
Key words: stars: white dwarfs - stars: atmospheres - stars: interiors - convection - stars: variable: general
The ZZ Ceti stars are the coolest class of pulsating white
dwarfs. They are multi-periodic g-mode pulsators with periods in the
range of 100 s to 1000 s. In contrast to the PG 1159 objects
and the variable DB only a few modes are observed in each individual
ZZ Ceti star. The number of observed pulsation periods, the amplitudes
and the shape of the light curves of these stars change systematically
within the instability strip (see e.g. Clemens
1993). At the hot (blue) edge, small amplitude
pulsations are observed with sinusoidal light curves. The cooler
ZZ Ceti stars show more modes with large amplitudes of more than
![]() with overtones and additional frequencies, formed by sums and
differences of the fundamental frequencies of the modes.
with overtones and additional frequencies, formed by sums and
differences of the fundamental frequencies of the modes.
The small number of unstable modes forms an obstacle to standard mode identification techniques (identifying the "quantum numbers'' l and m of the spherical harmonics of a mode), which rely mostly on periods and period spacings of unstable frequencies in the power spectrum. In recent years, time-resolved spectroscopy of white dwarfs has become possible and was used to identify the spherical harmonics of the modes. This mode identification technique uses the wavelength dependence of normalized pulsation amplitudes and takes advantage of the wavelength dependence of the limb darkening and different cancellation of the flux variation for different spherical harmonics (Robinson et al. 1982; Brassard et al. 1995; Robinson et al. 1995; Kepler et al. 2000; Clemens & Kerkwijk 2000). This diagnostic technique depends on the assumption that the flux amplitude on the visible surface varies with the spherical harmonic (l, m) of the mode.
This assumption - which we will call "linear'' - is subject to criticism, at least for larger amplitudes. For large amplitudes, non-sinusoidal light curves are observed, in contrast to the sinusoidal light curves for small amplitudes. Because the ZZ Ceti stars are non-radial pulsators, the amplitude varies over the surface of the star and one would expect a variation of the shape of the light curves over the surface for large amplitudes as well. This is in contradiction to the assumption of a flux variation with spherical harmonics. For a quantitative description of the integrated light curve and spectra we will need a theoretical understanding of the reaction of the local surface flux to an imposed pressure variation at deeper layers. This theory should demonstrate how the surface variation becomes increasingly non-sinusoidal with increasing amplitude of the pressure variation.
Such a description was provided by Brickhill (1983), who proposed that the thin convection zone below the surface of the ZZ Ceti stars has an important effect on the light curves. Brickhill showed, in a series of papers, that numerical simulations of the light curves can qualitatively reproduce the observed flux variations. This result was confirmed by Wu (1998) and Wu (2000).
Goldreich & Wu (1999, 1999a) and Wu & Goldreich (1998a) studied the driving mechanism of the ZZ Ceti stars in a linear perturbation analysis. Their work lead to impressive progress in the understanding of the driving of the pulsation modes, but it their linear analysis they consider only the entropy change in a convection zone of constant depth. Wu (1998, 2000) extended this work to take into account the depth changes, but used only static models of convection zone.
The numerical integrations we have performed for this paper show that for larger amplitudes the depth varies significantly during one cycle. At each time step during the pulsation the structure remains different from any static structure, leading to modifications of the nonlinear effects, which appear already in the perturbation analysis using static structures, as described in this paper.
We extend Brickhill's work and show that the convection zone strongly influences the spatial distribution of surface amplitudes, which for larger amplitudes cannot anymore be described by spherical harmonics. This cannot be neglected in the technique of mode identification by time-resolved spectroscopy. In the next section we describe the model used for our numerical calculations. First we will introduce the relatively simple system of ordinary differential equations to solve the time-dependent structure of the envelope of ZZ Ceti stars, obtained by allowing only a restricted time dependence of the basic equations. To examine the validity of this restriction for large amplitude pulsation, we introduce the full time-dependent equations in the following subsection. The boundary conditions have a large influence on the results of the numerical simulations; the following subsection is devoted to this topic. Section 3 describes the results of a light curve simulation for a plane-parallel column with a fixed pulsation amplitude. In Sect. 4 we consider that the pulsation amplitude varies over the surface for non-radial pulsators like the ZZ Ceti stars, and describe the surface distribution of the flux for different maximum amplitudes and spherical harmonics. The technique used to calculate the total flux together with the expected consequences for the time-dependent spectroscopy are discussed in Sect. 5 Finally we give our main conclusion in Sect. 6.
Within her analysis, Wu (1998, 2000) calculates the local response of the surface flux to a sinusoidal variation of pressure and flux in a layer at the bottom of the convection zone. Due to the change in extent and structure of the convection zone its reaction to the perturbation of the input flux is nonlinear, leading to the appearance of higher harmonics in the surface flux (Wu 2000).
The main result is that the amplitude of the fundamental period depends linearly and that of the first overtone quadratically on the amplitude below the convection zone. The phase delays between surface flux and pressure variation are constant, independent of amplitude. This important result guarantees that the spatial distribution over the stellar surface for the fundamental period is still given by the same spherical harmonic, which describes the variation in the deeper layers. This justifies the usual assumptions made in the analysis of time-dependent spectroscopy.
The starting point of our own study is the numerical model of Brickhill. In this model the convective layer is considered as a plane-parallel column. The lower boundary of this column lies below the surface convection zone, the upper boundary is directly below the photosphere. The sinusoidal relative pressure variation is assumed to be constant through the whole column, an assumption justified in the work by Brickhill and Goldreich and Wu.
In the simulation we calculate the transfer of energy and the time-dependent temperature structure numerically in a way similar to Brickhill's work. Some improvements over his work are state-of-the-art equation of state from Saumon et al. (1995) and OPAL opacity data (Iglesias & Rogers 1996), and our own model atmosphere grids, which are described in Finley et al. (1997).
In this paper we want to show the principal effects for the analysis
of time-resolved spectroscopy. Since we are not aiming at a detailed
comparison with observations, it is sufficient to investigate only one
equilibrium model with one effective temperature and one pulsation
period. We take a stellar model with
![]() and
and
![]() and a pulsation period of
and a pulsation period of
![]() .
We use only one parameter for
the mixing length theory (ML2/
.
We use only one parameter for
the mixing length theory (ML2/
![]() ); the thermal
relaxation time scale is 4.5 s. With this choice our model is
representative for the conditions near the blue edge of the
instability strip. All our calculations and results of this study are
based on this set of parameters.
); the thermal
relaxation time scale is 4.5 s. With this choice our model is
representative for the conditions near the blue edge of the
instability strip. All our calculations and results of this study are
based on this set of parameters.
The main aim of the model calculation is to determine the temperature
structure as a function of time. The temperature disturbance ![]() for a static model can be calculated from
for a static model can be calculated from
To calculate the heat energy ![]() we consider a finite volume
element with the cross section A and a height
we consider a finite volume
element with the cross section A and a height ![]() .
Introducing a discretization and finite volume elements at this
point, we can avoid the use of partial differential equations. In a
plane-parallel symmetry, the flux has only a vertical component. If
.
Introducing a discretization and finite volume elements at this
point, we can avoid the use of partial differential equations. In a
plane-parallel symmetry, the flux has only a vertical component. If
![]() is the difference between the outgoing and the incoming
flux for a mass element, the heat energy accumulated in a time
interval
is the difference between the outgoing and the incoming
flux for a mass element, the heat energy accumulated in a time
interval ![]() is given by
is given by
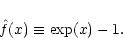
The rapid variation of the flux with the temperature leads to short relaxation time scales near the upper boundary of the column. This leads to a stiff behavior of the ODE. Consequently we use a Gear solver (Gear 1971) to integrate Eq. (6).
The differential formulation of (1) leads in principle to
reliable solutions for large perturbations as well. But to obtain
Eq. (6) we have ignored all time-dependencies except for
![]() ,
,
![]() and
and
![]() .
For large amplitudes (
.
For large amplitudes (
![]() ),
this cannot be justified any longer, since temperature and specific
heat capacity can change by large amounts. In a first step to correct
for this we can replace all quantities in Eq. (6) by
their current values instead of those of the equilibrium model. Since
this may not be sufficient for short pulsation periods (
),
this cannot be justified any longer, since temperature and specific
heat capacity can change by large amounts. In a first step to correct
for this we can replace all quantities in Eq. (6) by
their current values instead of those of the equilibrium model. Since
this may not be sufficient for short pulsation periods (![]() 100
100![]() ), we have modified Eq. (6) and taken into
account all terms produced by the derivative of (1) with
respect to time
), we have modified Eq. (6) and taken into
account all terms produced by the derivative of (1) with
respect to time
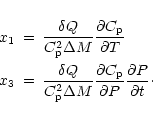
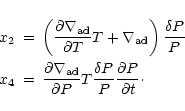
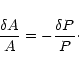
The contributions of x1 and x2 are important for large pulsation
amplitudes, caused by the large and rapid changing of the temperature,
whereas all terms including a derivative of
![]() are unimportant.
Table 1 compares the amplitudes of the fundamental and the
first overtone of the photospheric flux variation as a result of (6) with (8) for our model with a period of
are unimportant.
Table 1 compares the amplitudes of the fundamental and the
first overtone of the photospheric flux variation as a result of (6) with (8) for our model with a period of
![]() .
For (6) we take the current values of all quantities,
instead of the values of the equilibrium model.
.
For (6) we take the current values of all quantities,
instead of the values of the equilibrium model.
| ODE | IDE | |||
|
|
A1[%] | A2[%] | A1[%] | A2[%] |
| 0.02 | 1.71 | 0.24 | 1.71 | 0.25 |
| 0.04 | 3.64 | 1.17 | 3.65 | 1.23 |
| 0.06 | 5.14 | 2.01 | 5.18 | 2.13 |
| 0.08 | 6.17 | 2.61 | 6.29 | 2.83 |
| 0.10 | 6.78 | 2.95 | 7.04 | 3.32 |
| 0.12 | 6.97 | 2.97 | 7.45 | 3.56 |
| 0.14 | 6.74 | 2.67 | 7.54 | 3.54 |
| 0.16 | 6.09 | 2.01 | 7.31 | 3.25 |
| 0.18 | 5.17 | 1.17 | 6.78 | 2.68 |
The differences for large pressure amplitudes are significant in the solutions of (6) and (8), but the qualitative behavior is the same in both cases. Since the numerical effort is not very much larger for solving the IDE, this method will be implemented in future versions of our code. The ODE solution (6) is adequate for a qualitative discussion and all results given in this paper are based on (6) with current values for all quantities. One should remember, however, that the results for large amplitudes - though qualitatively correct - may be affected by this approximation.
The basic system of ODE (6) looks like an initial value problem, but this is only partially correct. To obtain Eq. (2) we have introduced a discretization of the column, to replace the spatial derivatives of the flux with finite differences. The mathematical structure of a partial differential equation survives in the coupling of the ODEs and the necessity to define boundary conditions for the flux.
For the lower boundary we assume the adiabatic approximation. The
matter in the region below the convection zone is well approximated as
a completely ionized hydrogen plasma. Under this assumption the flux
perturbation is given by (see Goldreich & Wu 1999)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{ising_fig1.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg52.gif) |
Figure 1:
The variation of the photospheric flux (solid line) and the flux variation
at the lower boundary (dashed line) are plotted for a |
| Open with DEXTER | |
We assume a column with a lower boundary much deeper than the bottom
of the convection zone with a constant pressure amplitude in the whole
column. The depth of the lower boundary is limited by the growing
computing costs, because a pulsation simulation has to be done for at
least one thermal time scale of the whole column to reach a stationary
situation. For our model we choose a thermal time scale of
![]() and a value of
and a value of
![]() to fix the lower boundary for this
experiment. At this lower boundary we apply a sinusoidal flux
perturbation and study the resulting flux at a point clearly below the
maximum extent of the convection zone, but far away from the lower
boundary. At this point the flux is no longer sinusoidal but shows a
fundamental with amplitude A1 and a first overtone with amplitude
A2. The phases are shifted relative to the bottom flux by
to fix the lower boundary for this
experiment. At this lower boundary we apply a sinusoidal flux
perturbation and study the resulting flux at a point clearly below the
maximum extent of the convection zone, but far away from the lower
boundary. At this point the flux is no longer sinusoidal but shows a
fundamental with amplitude A1 and a first overtone with amplitude
A2. The phases are shifted relative to the bottom flux by ![]() and
and ![]() respectively, where a positive phase means that the
variation is lagging behind the perturbation. One should note that
these effects would be absent in a completely radiative star; they are
caused by the delayed reaction of the convection zone, which
determines the outer boundary for the envelope structure.
respectively, where a positive phase means that the
variation is lagging behind the perturbation. One should note that
these effects would be absent in a completely radiative star; they are
caused by the delayed reaction of the convection zone, which
determines the outer boundary for the envelope structure.
Table 2 shows the results at the point with
![]() .
The first overtone at this point remains at least one order of
magnitude smaller than the fundamental amplitude and the phase shift
between pressure and flux variation remains small. We follow Brickhill
in our conclusion that the adiabatic flux variation at the lower
boundary is a good approximation if the propagation zone of the
g-modes is far away from the convective layer. This is true for
short period pulsations as considered in our model, which represents
the "blue edge'' of the instability strip. For our pulsation
simulations we then fixed our lower boundary at
.
The first overtone at this point remains at least one order of
magnitude smaller than the fundamental amplitude and the phase shift
between pressure and flux variation remains small. We follow Brickhill
in our conclusion that the adiabatic flux variation at the lower
boundary is a good approximation if the propagation zone of the
g-modes is far away from the convective layer. This is true for
short period pulsations as considered in our model, which represents
the "blue edge'' of the instability strip. For our pulsation
simulations we then fixed our lower boundary at
![]() .
.
|
|
|
A1[%] |
|
A2[%] |
|
| 0.02 | 4.40 | 4.72 | 2.67 | 0.05 | -98.43 |
| 0.04 | 8.80 | 9.43 | 2.67 | 0.19 | -97.35 |
| 0.06 | 13.20 | 14.09 | 2.84 | 0.40 | -97.80 |
| 0.08 | 17.60 | 18.62 | 3.12 | 0.69 | -97.80 |
| 0.10 | 22.00 | 23.05 | 3.43 | 1.08 | -97.52 |
| 0.12 | 26.40 | 27.39 | 3.75 | 1.56 | -97.35 |
| 0.14 | 30.80 | 31.59 | 4.09 | 2.10 | -97.92 |
| 0.16 | 35.20 | 35.61 | 4.47 | 2.72 | -99.01 |
| 0.18 | 39.60 | 39.45 | 4.88 | 3.44 | -100.32 |
To find an upper boundary condition we make the assumption, that the
photosphere reaches the static structure for each time step
instantaneously. As discussed e.g. by Brickhill (1983) this
approximation is valid for small thermal time scales compared with the
pulsation period. We choose the upper boundary at the pressure point
with the optical depth ![]() 10, where this condition is clearly
fulfilled. The advantage to take the optical depth clearly greater
than 1 at the upper boundary of the column is, that the
time-dependent calculations can be done with the diffusion
approximation for the radiative flux. The determination of the
photospheric structure requires a detailed radiative transfer
calculation, but without consideration of terms with
time-derivatives. To connect these two different calculations we
assume, that the combination of the actual flux, pressure and
temperature is the same at the upper boundary of the column as in one
specific static photospheric model. To find the flux we use a grid of
static models and find the known combination of pressure and
temperature in this grid for each time step separately and interpolate
the flux from these models. This procedure avoids a further
linearization at the upper boundary, but is in principle equivalent to
Brickhill's method.
10, where this condition is clearly
fulfilled. The advantage to take the optical depth clearly greater
than 1 at the upper boundary of the column is, that the
time-dependent calculations can be done with the diffusion
approximation for the radiative flux. The determination of the
photospheric structure requires a detailed radiative transfer
calculation, but without consideration of terms with
time-derivatives. To connect these two different calculations we
assume, that the combination of the actual flux, pressure and
temperature is the same at the upper boundary of the column as in one
specific static photospheric model. To find the flux we use a grid of
static models and find the known combination of pressure and
temperature in this grid for each time step separately and interpolate
the flux from these models. This procedure avoids a further
linearization at the upper boundary, but is in principle equivalent to
Brickhill's method.
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{ising_fig2.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg63.gif) |
Figure 2:
Shape of the flux variation for different pressure
amplitudes. The bottom line is the light curve for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{ising_fig3.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg64.gif) |
Figure 3: Amplitudes of the Fourier coefficients relative to the mean flux for a local column. The numerical results are labeled with the name of the harmonic. The curves marked with p.a. indicate the linear and quadratic relations predicted by the perturbation analysis. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{ising_fig4.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg65.gif) |
Figure 4: Phases of the fundamental and overtones relative to the pressure variation in a local column for the numerical results. The linear perturbation analysis predicts constant phases with values which depend on the equilibrium model. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{ising_fig5.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg66.gif) |
Figure 5: Time-averaged flux relative to the flux below the convection zone. |
| Open with DEXTER | |
In this section we study the reaction of the convection zone and the shape and amplitude of the surface flux variation for a column on the stellar surface.
For small amplitude pulsations with ![]() pressure variation (see
upper panel in Fig. 1), the photospheric flux (solid line) is
shifted in phase relative to the flux of the adiabatic layers (dashed
line) and the amplitude is reduced. As shown by Brickhill
(1983), the phase shift and the reduced amplitude is caused
by the delay in the heat transfer due to the necessary adjustment of
the convective layers to a change in the input flux. If the flux is
increased, the depth of the convective layer is shrinking as required
by a static envelope solution corresponding to a higher effective
temperature. A large amount of heat is necessary to change
convective into radiative layers and to increase the heat content of
the remaining convection zone, which has to be supplied by the input
flux. Consequently, the photospheric flux follows the input flux with
a delay of the order of the thermal time scale of the convective
layer. If the input flux varies periodically with a period comparable
to the thermal time scale, this delay results in a phase shift and an
amplitude reduction.
pressure variation (see
upper panel in Fig. 1), the photospheric flux (solid line) is
shifted in phase relative to the flux of the adiabatic layers (dashed
line) and the amplitude is reduced. As shown by Brickhill
(1983), the phase shift and the reduced amplitude is caused
by the delay in the heat transfer due to the necessary adjustment of
the convective layers to a change in the input flux. If the flux is
increased, the depth of the convective layer is shrinking as required
by a static envelope solution corresponding to a higher effective
temperature. A large amount of heat is necessary to change
convective into radiative layers and to increase the heat content of
the remaining convection zone, which has to be supplied by the input
flux. Consequently, the photospheric flux follows the input flux with
a delay of the order of the thermal time scale of the convective
layer. If the input flux varies periodically with a period comparable
to the thermal time scale, this delay results in a phase shift and an
amplitude reduction.
Figure 2 summarizes this variation of the light curves with changing pressure amplitudes.
For small amplitudes the variation of the surface flux remains sinusoidal and the amplitude increases linearly with the pressure amplitude as predicted by the perturbation analysis.
For larger amplitudes, e.g. ![]() (lower panel Fig. 1) the
extent of the the convective zone varies significantly during the
pulsation cycle, and the stratification may even become completely
radiative shortly after maximum compression. At that instant the
photospheric flux follows directly the adiabatic flux variation,
causing the steep increase and sharp maxima in the light curves.
(lower panel Fig. 1) the
extent of the the convective zone varies significantly during the
pulsation cycle, and the stratification may even become completely
radiative shortly after maximum compression. At that instant the
photospheric flux follows directly the adiabatic flux variation,
causing the steep increase and sharp maxima in the light curves.
Increasing the pressure amplitudes even further (![]() ), the surface
flux variation becomes sinusoidal again, with small amplitudes. In
this case, a large fraction of the heat flux is transformed into
mechanical energy, and the remaining average flux corresponds to a
model with lower (time-averaged) effective temperature and thicker
convection zone. The thermal time constant of this convection
zone becomes large compared to the pulsation period, resulting in a
strong reduction of the flux amplitude.
), the surface
flux variation becomes sinusoidal again, with small amplitudes. In
this case, a large fraction of the heat flux is transformed into
mechanical energy, and the remaining average flux corresponds to a
model with lower (time-averaged) effective temperature and thicker
convection zone. The thermal time constant of this convection
zone becomes large compared to the pulsation period, resulting in a
strong reduction of the flux amplitude.
We emphasize that this conversion of heat to mechanical energy in the
column (which remains qualitatively the same with the higher numerical
accuracy of the IDE method) does not directly tell us anything about
the global excitation or damping of the mode. Our calculation is based
on energy arguments in an open system: the enforced variations of the
pressure and column cross section carry away any difference of
incoming and outgoing heat flux. In order to really study the
excitation of the mode, one would need to calculate the behavior of the
mode throughout the whole star. It is quite possible that the increase
of the mechanical energy in the outer envelope is more than balanced
by a damping in the interior; it is also possible that the energy goes
into the excitation of other modes. This problem will be studied
further in future simulations, which include the study of the
![]() term in Eq. (1).
term in Eq. (1).
The sharp maxima in the light curves imply the appearance of higher
harmonics in the Fourier decomposition. Figure 3 demonstrates,
how the relative amplitudes of fundamental, first, and second overtone
increase with increasing pressure amplitude. For low amplitudes, the
results confirm the predictions of the perturbation analysis (linear
and quadratic dependence for fundamental and first overtone); for
amplitudes larger than ![]() ,
however, strong deviations become
apparent.
,
however, strong deviations become
apparent.
The sign and even the magnitude of the phase shifts in Fig. 4 approximately agree with the predictions of the perturbation analysis: the fundamental for the flux is lagging behind the pressure, whereas the in the first harmonic it is leading. However, quite unexpectedly from the predictions of Goldreich and Wu, for very small amplitudes the phases do not become constant. The shift demonstrates the change of the relative contributions from the compression in the convection zone, which is strictly in phase, and the flux variation below the convection zone, which is phase shifted during the propagation through the convective layer. While at very low amplitudes the numerical result may be questionable, we are confident that this is not the case for pressure amplitudes larger than about 1%. This result needs further study, and we will attempt in a future paper to reconcile the results of numerical and perturbational analysis.
Another difference to the perturbation analysis of Goldreich and Wu is the dependence of the mean local flux on the pressure amplitude (see Fig. 5). The flux from below the convection zone is reduced by a fraction of energy that is converted into mechanical energy to drive the pulsation mode. This fraction grows quadratically with the pressure amplitude. Consequently the mean flux is reduced very efficiently for large amplitudes.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{ising_fig6.ps}\\ [8mm]
\incl...
...g_fig7.ps}\\ [4mm]
\includegraphics[width=6.5cm,clip]{ising_fig8.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg69.gif) |
Figure 6:
Surface distribution of the effective temperature near the
maximum of the integrated flux. The gray-level of the plot (top, for
an l=2 mode) is normalized to the maximum
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{ising_fig9.ps}\\ [8mm]
\incl...
...fig10.ps}\\ [4mm]
\includegraphics[width=6.5cm,clip]{ising_fig11.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg70.gif) |
Figure 7: Similar to Fig. 6, but for a maximum pressure amplitude of 5%. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{ising_fig12.ps}\\ [8mm]
\inc...
...fig13.ps}\\ [4mm]
\includegraphics[width=6.5cm,clip]{ising_fig14.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg71.gif) |
Figure 8: Similar to Fig. 6, but for a maximum pressure amplitude of 20%. |
| Open with DEXTER | |
In the preceding sections we have discussed the local reaction of the photospheric flux to an assumed fixed pressure amplitude. In this section we consider the whole surface of the star, assuming that the spatial structure of the pressure perturbation as well as the flux perturbation below the convection zone is described by a spherical harmonic of mode numbers l and m.
For small amplitudes - because of the linear dependence of surface amplitudes on pressure amplitudes - the distribution of the surface flux amplitude follows directly the pressure and is therefore described by the same spherical harmonic. But this is only true if one ignores the small phase changes of the flux variation. Due to this phase shift the maximum flux amplitude is reached at a later time for smaller amplitudes. This effect leads to a deviation of the photospheric flux distribution from the spherical harmonic of the mode, but the flux amplitude at the surface is still a monotonous function of the pressure amplitude. This changes with increasing amplitude: because of the non-monotonous local relation the maximum flux amplitude at the surface does not coincide with the maximum of the pressure amplitude and e.g. for m=0 modes the maximum flux amplitude is not reached at the poles. Since also the phases change with amplitude, different latitudes on the surface reach the maximum flux at different times.
Figures 6 to 8 show the surface distribution for
l=1,2, m=0 modes as three-dimensional plot with gray-level
indicating the effective temperature, and in graphical form the
dependence on polar angle
![]() .
Shown are three
different cases for small, medium, and large pressure amplitudes.
.
Shown are three
different cases for small, medium, and large pressure amplitudes.
For l=2 modes the change due to the nonlinear relation between pressure amplitude and surface flux amplitude may be quite dramatic: whereas for small amplitudes the maximum amplitudes are at the poles, with a smaller relative maximum at the equator, the situation can be completely reversed at large amplitudes (see Fig. 8).
From these results it follows that the surface distribution of the flux variation in general has a much more complicated form than is assumed traditionally (meaning spherical harmonics describing all variations on the stellar surface). In this section we want to answer two questions: First, we want to find an optimal strategy to calculate the wavelength dependent amplitude spectra, and second, we want to discuss the major effects on time-resolved spectra one has to expect, if the linear assumption is no longer appropriate.
The general problem is to find the time-dependent flux
![]() ,
where
,
where
![]() is the direction to the
observer. To integrate the flux we need the specific intensity at each
point of the surface at each time in the direction
is the direction to the
observer. To integrate the flux we need the specific intensity at each
point of the surface at each time in the direction
![]() .
In
general, the specific intensity is a function of wavelength
.
In
general, the specific intensity is a function of wavelength ![]() ,
the spatial point
,
the spatial point ![]() ,
the direction
,
the direction
![]() and the time. We want
to restrict this to a simpler situation, where the intensity can be
calculated from a plane-parallel model atmosphere at each
point. Furthermore we assume, that the surface structure is equivalent
to a static model atmosphere down to optical depths larger than 1 for
each time step. In this case the specific intensity is only a function
of the wavelength, the local flux F and the cosine between
and the time. We want
to restrict this to a simpler situation, where the intensity can be
calculated from a plane-parallel model atmosphere at each
point. Furthermore we assume, that the surface structure is equivalent
to a static model atmosphere down to optical depths larger than 1 for
each time step. In this case the specific intensity is only a function
of the wavelength, the local flux F and the cosine between
![]() and the vector normal to the surface
and the vector normal to the surface ![]()
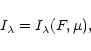
The surface coordinates
![]() can be taken as identical to
the coordinates in the spherical harmonic of the pulsation mode. For
the integrated flux it is convenient to introduce a coordinate system
with the axis oriented towards the observer. The system
can be taken as identical to
the coordinates in the spherical harmonic of the pulsation mode. For
the integrated flux it is convenient to introduce a coordinate system
with the axis oriented towards the observer. The system
![]() is defined by
is defined by
![\begin{displaymath}{\cal F}_\lambda(\Omega,t) = \frac{A_0}{2} + \sum_{n=1}^\infty \left[
A_n \cos n \omega t + B_n \sin n \omega t \right] \end{displaymath}](/articles/aa/full/2001/28/aa10057/img87.gif)
For the evaluation of Eq. (11) it is necessary to connect
the specific intensity with the total flux of a local column.
Using an expansion to first order we assume for this relation
![\begin{displaymath}F(t) = \frac{a_0}{2} + \sum_{n=1}^\infty \left[
a_n \cos n \omega t + b_n \sin n \omega t \right] \end{displaymath}](/articles/aa/full/2001/28/aa10057/img96.gif)
Using approximations similar to those of Robinson et al. (1982) we could simplify the relation for the intensity as
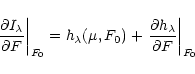 |
(21) |
The linear assumption is to specify the local flux by
| |
Figure 9:
Comparison of the amplitude spectra for an l=2 mode,
calculated with a limb darkening independent of
|
| Open with DEXTER | |
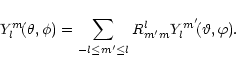
To test the accuracy of the linear approximation for the intensity
(Eq. (16)) we have calculated the
Fourier coefficients directly from the integrated light curve by means
of Eqs. (11), (12) and (13) and have
compared the result with the results from the linearized intensity. We
find a very good correspondence for all wavelengths for modes with ![]() and amplitudes less than
and amplitudes less than ![]() .
This range is much larger
than the range, where the total flux variation can be assumed to be
linear with
.
This range is much larger
than the range, where the total flux variation can be assumed to be
linear with
![]() .
For even larger amplitudes the amplitude spectrum
calculated directly from Eq. (11) becomes inclination and
amplitude dependent, because the function
.
For even larger amplitudes the amplitude spectrum
calculated directly from Eq. (11) becomes inclination and
amplitude dependent, because the function ![]() varies over the
surface for different flux amplitudes. Such large amplitudes are not
observed, however.
varies over the
surface for different flux amplitudes. Such large amplitudes are not
observed, however.
The Goldreich and Wu theory assumes - following Brickhill - a
pressure variation with a spatial and time-dependence described by the
spherical harmonic and period of the pulsation mode. They predict the
appearance of non-sinusoidal flux variations at the surface
The result for the fundamental is equivalent to the linear assumption Eq. (22) and as a consequence leads to the same results for the normalized spectra: they depend only on the mode number l.
The amplitude of the first overtone has a different behavior than the
spherical harmonic of the mode over the stellar surface. It can be written
as
The 2![]() overtone will not be discussed in detail. The local
flux amplitude
overtone will not be discussed in detail. The local
flux amplitude
![]() cannot be represented by a single
cannot be represented by a single
![]() and consequently the normalized amplitude
spectra become in general also amplitude dependent.
and consequently the normalized amplitude
spectra become in general also amplitude dependent.
To determine the normalized amplitude spectra from our numerical
results, it is possible to use the integration of the local Fourier
coefficients an and bn. However, because the phase is not
constant (see Fig. 4) over the surface and a0 is a
function of the coordinates
![]() (see Fig. 5) the
expression Eq. (23) is completely useless even for
m=0 modes and we have to calculate the coefficients An and Bnseparately. This means that there is no economical advantage to
calculate the Fourier series locally and then to integrate the
coefficients over the visible disk.
(see Fig. 5) the
expression Eq. (23) is completely useless even for
m=0 modes and we have to calculate the coefficients An and Bnseparately. This means that there is no economical advantage to
calculate the Fourier series locally and then to integrate the
coefficients over the visible disk.
We therefore decided to calculate the flux
![]() for each
time step completely numerically by using Eq. (11). This
method also avoids the disadvantage of having to use a linearization
like Eq. (16) to reach expressions for the Fourier
coefficients of the integrated flux
for each
time step completely numerically by using Eq. (11). This
method also avoids the disadvantage of having to use a linearization
like Eq. (16) to reach expressions for the Fourier
coefficients of the integrated flux
![]() .
From the time-dependent flux we can calculate the Fourier coefficient
with the aid of Eqs. (12) and (13). The numerical
results presented in the following section are based on such
integrations.
.
From the time-dependent flux we can calculate the Fourier coefficient
with the aid of Eqs. (12) and (13). The numerical
results presented in the following section are based on such
integrations.
On the other hand, in order to gain more insight into the qualitative behavior of the spectra for different amplitudes and inclinations, we will use simple fits for the numerical results of the local variation, which allow then analytic integrations for the total flux. Both approaches are complementary: with the completely numerical simulation we avoid simplifications, which may not be correct, but we can calculate the result only for very few combinations of parameters. The semi-analytical study, on the other hand, shows the functional dependence of the results on quantum numbers, inclination, etc.
The phase dependence of all local Fourier coefficients and the
nonlinear dependence on the pressure variation leads to deviations
from the assumptions made traditionally for the flux variation over
the stellar surface. The intention of this subsection is to show, how
this deviation affects the synthetic spectra for different
inclinations, pulsation amplitudes and mode numbers l.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ising_fig16.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg126.gif) |
Figure 10:
The amplitude dependence of the correction term
|
| Open with DEXTER | |
To find an expression for the error made when using the linear
assumption, we assume a flux independent limb darkening function and
the integrated Fourier coefficients given by Eqs. (18) and
(19). We define a correction term for the fundamental as
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ising_fig17.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg134.gif) |
Figure 11:
The factor |
| Open with DEXTER | |
The third term ![]() is the inclination dependent term. Besides
this it depends on the mode numbers and wavelength, but not on the
amplitude. The results for the factor
is the inclination dependent term. Besides
this it depends on the mode numbers and wavelength, but not on the
amplitude. The results for the factor ![]() for
for ![]() are plotted in Fig. 11. This factor is for most
inclinations very small for l=1 and moderate for l=2, if the
inclination is clearly different from the latitude of the
node lines. For l=3 the factor
are plotted in Fig. 11. This factor is for most
inclinations very small for l=1 and moderate for l=2, if the
inclination is clearly different from the latitude of the
node lines. For l=3 the factor ![]() is much larger and leads to
a large global deviation of the numerical results from those using the
linear assumptions for any inclination and amplitude.
is much larger and leads to
a large global deviation of the numerical results from those using the
linear assumptions for any inclination and amplitude.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ising_fig18.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg135.gif) |
Figure 12: Amplitude spectra for small pressure amplitude. The solid line and the dashed lines are results based on the spherical harmonics l=2 and l=1 respectively. The diamonds connected with the dotted line are the numerical results. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ising_fig19.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg136.gif) |
Figure 13: Phase spectra for small pressure amplitude. The solid line (l=1) and the dashed line (l=2) gives the predicted phase shift for the wavelength range from 2000 Å to 6000 Å. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ising_fig20.ps}\vspace*{-2mm}
\end{figure}](/articles/aa/full/2001/28/aa10057/Timg137.gif) |
Figure 14: Amplitude spectra for intermediate amplitude. The lines have the same meaning as in Fig. 12. |
| Open with DEXTER | |
In the previous section we discussed the effects of the nonlinear behavior of the light curves on the amplitude spectra of the fundamental with some approximations. To find the correct spectra we now calculate the Fourier coefficients directly from the integrated light curves in a strictly numerical way.
As an illustrating example we take the l=2 mode with a maximum
pressure amplitude of ![]() .
For this amplitude the light curves are
sinusoidal in a good approximation, so we can restrict the discussion
to the fundamental of the mode.
.
For this amplitude the light curves are
sinusoidal in a good approximation, so we can restrict the discussion
to the fundamental of the mode.
From Fig. 11 we do not expect very large deviations from
the linear result for most inclinations. To show the effect, we
take an inclination of
![]() near the latitude of the node line,
where we expect a moderate deviation. The numerical result is plotted
in Fig. 12, together with the result of the linear
assumption, that is supported by the theory of Goldreich and Wu.
All amplitudes in this and the following similar figures have been
normalized to 1 at 5500 Å.
Although the effect is not very large, it is important for mode
identification, because of the generally small differences between the
calculations for different mode numbers.
near the latitude of the node line,
where we expect a moderate deviation. The numerical result is plotted
in Fig. 12, together with the result of the linear
assumption, that is supported by the theory of Goldreich and Wu.
All amplitudes in this and the following similar figures have been
normalized to 1 at 5500 Å.
Although the effect is not very large, it is important for mode
identification, because of the generally small differences between the
calculations for different mode numbers.
Deviations in the spectra already for small amplitudes are suggested
by the analytical calculations in the previous subsection, but are not
obvious in the plot of the absolute amplitude Fig. 3, which
grows linearly with the pressure amplitudes up to ![]() 5% pressure amplitude. Consequently, the deviation has to be an
effect of the phase shift for small amplitudes. This phase shift
should be visible in the integrated light as well. Figure 13
gives the numerical prediction for the phase shift for the same mode
and modes with l=1. In contrast to the prediction of Goldreich and
Wu, we expect a small phase shift of a few degrees over the spectral
range for the l=2 modes.
5% pressure amplitude. Consequently, the deviation has to be an
effect of the phase shift for small amplitudes. This phase shift
should be visible in the integrated light as well. Figure 13
gives the numerical prediction for the phase shift for the same mode
and modes with l=1. In contrast to the prediction of Goldreich and
Wu, we expect a small phase shift of a few degrees over the spectral
range for the l=2 modes.
The amplitude dependent factor ![]() is very small in this region
and we expect practically no differences to the predictions of
Goldreich and Wu. Figure 14 shows the numerical result for
the same mode and inclination as Fig. 12, but for a
pressure amplitude of
is very small in this region
and we expect practically no differences to the predictions of
Goldreich and Wu. Figure 14 shows the numerical result for
the same mode and inclination as Fig. 12, but for a
pressure amplitude of ![]() .
The spectra for the numerical prediction
and the Goldreich and Wu theory are very similar.
.
The spectra for the numerical prediction
and the Goldreich and Wu theory are very similar.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ising_fig21.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg140.gif) |
Figure 15: Amplitude spectra for the first overtone and intermediate amplitude. The lines have the same meaning as in Fig. 12. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ising_fig22.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg141.gif) |
Figure 16: Amplitude spectra for large amplitude. The lines have the same meaning as in Fig. 12. |
| Open with DEXTER | |
In contrast to the small amplitude case, the light curves for ![]() pressure amplitude are non-sinusoidal with large flux amplitudes. We
can calculate the expected deviation from the predictions of Goldreich
and Wu analogous to Eq. (30) and find for this region a
small deviation for the first overtone as well. Figure 15
shows a comparison of the numerical result, with the predicted spectrum
for a quadratic dependence of the flux amplitude on the pressure
amplitude.
pressure amplitude are non-sinusoidal with large flux amplitudes. We
can calculate the expected deviation from the predictions of Goldreich
and Wu analogous to Eq. (30) and find for this region a
small deviation for the first overtone as well. Figure 15
shows a comparison of the numerical result, with the predicted spectrum
for a quadratic dependence of the flux amplitude on the pressure
amplitude.
For increasing maximum pressure amplitude the deviation factor
![]() becomes smaller and finally negative. For really large
pressure amplitude we expect again a significant deviation from the
Goldreich and Wu result. Figure 16 shows the numerical
result for a
becomes smaller and finally negative. For really large
pressure amplitude we expect again a significant deviation from the
Goldreich and Wu result. Figure 16 shows the numerical
result for a ![]() pressure amplitude. As expected from the
analytical result, the difference to the Goldreich and Wu result has
the opposite sign and the spectrum of the l=2 mode becomes very
similar to that of an l=1 mode. The numerical result for the l=1 mode
does not significantly change for an inclination of
pressure amplitude. As expected from the
analytical result, the difference to the Goldreich and Wu result has
the opposite sign and the spectrum of the l=2 mode becomes very
similar to that of an l=1 mode. The numerical result for the l=1 mode
does not significantly change for an inclination of
![]() (see
Fig. 11) and modes with l=2 can easily be confused with l=1.
(see
Fig. 11) and modes with l=2 can easily be confused with l=1.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ising_fig23.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg143.gif) |
Figure 17: Amplitude spectra for the first overtone and large amplitudes. The lines have the same meaning as in Fig. 12. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{ising_fig24.ps}\end{figure}](/articles/aa/full/2001/28/aa10057/Timg144.gif) |
Figure 18: Amplitude spectra for l=3 and large amplitudes. The lines have the same meaning as in Fig. 12. |
| Open with DEXTER | |
The first overtone is significant for large amplitudes as well. In contrast to the intermediate amplitudes, a difference from the predicted result of Goldreich and Wu appears. For our example Fig. 17 shows the numerical result in comparison with the quadratic dependence of the flux amplitude.
For l=3 the deviation of the numerical results from the results of the linear assumption is much larger. Figure 18 shows one example for a large deviation. In contrast to a rapidly increasing amplitude in the UV the amplitude remains almost constant. In this regime the prediction of the variation from Eq. (30) can be only qualitative. In general, the amplitude increase towards the UV is caused by the decreasing "effective visible area'' due to the larger limb darkening. This effect becomes significant, when the effective area is comparable in size to the spatial scale of the light variations on the surface of the star. For the large amplitudes the spatial structure of the l = 3 flux variation is more complex than the unperturbed spherical harmonic and the cancellation effects set in only farther in the UV.
In the past, the method of time-resolved spectroscopy has been based
on the assumption - called "linear'' throughout this paper - that
the flux varies with the spherical harmonic of the pulsation mode over
the surface of the ZZ Ceti stars. The numerical light curve simulation
shows that this assumption is questionable in many situations. For
small amplitudes with sinusoidal lightcurves, only the absolute
amplitude varies like the spherical harmonic of the mode. The phase
shift leads to normalized amplitude spectra, which depend on
inclination and pulsation (pressure) amplitude for mode numbers
l>2. For large amplitudes (>10% in pressure) the absolute
amplitude of the flux depends non-monotonously on the pressure
amplitude and the flux variation shows maxima at different latitudes
than the spherical harmonic of the mode. The numerical results show
relatively good correspondence to traditionally calculated amplitude
spectra for intermediate amplitudes (![]() 5%) in pressure, with
non-sinusoidal light curves. In this regime, the phase becomes
stationary and the absolute amplitude varies in good correspondence to
the spherical harmonic of the mode; the numerical results are close to
the results of the perturbation analysis of Goldreich and Wu.
5%) in pressure, with
non-sinusoidal light curves. In this regime, the phase becomes
stationary and the absolute amplitude varies in good correspondence to
the spherical harmonic of the mode; the numerical results are close to
the results of the perturbation analysis of Goldreich and Wu.
Another result of our simulations is the existence of a maximum surface flux amplitude. This is a reaction of the convection zone on a predefined pressure variation in deeper layers, and should not be confused with the amplitude saturation of the pulsation as studied by Goldreich & Wu (1999). The amplitude of the photospheric flux is reduced by the inert reaction of the temperature structure in the convective layer to the changing input flux. The decrease in the thermal heat flux is converted to kinetic energy of the pulsation as discussed above, and this convection region is therefore a driving region for the pulsation. The extent of this conversion depends on the thermal time scale of the convection zone.
In our model calculations for large amplitudes the time-averaged depth of the convection zone becomes much larger than in the corresponding static model. The thermal time scale then increases with the pulsation amplitude, leading to a reduction of the surface flux amplitude. This is the reason for the existence of a maximum amplitude for the surface flux. It also explains the return to sinusoidal variations for large pressure amplitudes: the convection zone becomes so thick that variations during one cycle do not decrease its depth enough for the appearance of higher overtones.
While our calculations cannot determine the maximum pressure amplitude
that can be reached in a pulsating star, one prediction is that
observable flux amplitudes should not exceed ![]() ,
for the
parameters used in this paper. The maximum flux amplitudes support the
dominance of small l in the observed light curves and lead to the
prediction that the dominant pulsation modes are l=1, if l=1modes and modes with larger l are unstable, for a large amplitude
range, independent of the actual amplitudes of the modes.
,
for the
parameters used in this paper. The maximum flux amplitudes support the
dominance of small l in the observed light curves and lead to the
prediction that the dominant pulsation modes are l=1, if l=1modes and modes with larger l are unstable, for a large amplitude
range, independent of the actual amplitudes of the modes.
While nonlinear effects are well known for large observed amplitude pulsations, the present study reaches the surprising conclusion that the amplitudes and phases can be described fairly accurately by the linear theory as developed by Robinson et al. (1982) for the fundamental and Wu (1998) for higher harmonics.
On the other hand, the observation of small amplitudes in the surface integrated light does not necessarily guarantee that these effects are absent. Deviations from the traditional interpretation could occur in spite of small observed amplitudes under the following conditions
All conclusions are obtained for a special set of stellar and
pulsational parameters. The effects discussed may be more or less
important for other ranges of ![]() and
and
![]() .
We have also not taken
into account that in general more than one pulsation mode is present
in a star. The modes will be influenced by the presence of other modes
and by their properties even well below the convection zone. These
effects are beyond the scope of the present analysis. We do not,
however, expect that the main conclusion will change: the mechanism
that leads to non-sinusoidal light curves for large flux variations
can be important for a correct identification of the pulsation modes
using time-resolved spectroscopy, for any observed amplitude of the
flux.
.
We have also not taken
into account that in general more than one pulsation mode is present
in a star. The modes will be influenced by the presence of other modes
and by their properties even well below the convection zone. These
effects are beyond the scope of the present analysis. We do not,
however, expect that the main conclusion will change: the mechanism
that leads to non-sinusoidal light curves for large flux variations
can be important for a correct identification of the pulsation modes
using time-resolved spectroscopy, for any observed amplitude of the
flux.
Acknowledgements
This work was made possible by a grant from the Deutsche Forschungsgemeinschaft. We want to thank Dr. Yanqin Wu, Dr. Marten van Kerkwijk, Prof. Dr. Rainer Wehrse and Dr. Günther Wuchterl for their helpful comments and recommendations. D.K. wants to thank Dr. J. Holberg of Lunar and Planetary Lab and Dr. J. Liebert of Steward Observatory for their hospitality during a stay at the University of Arizona in the summer of 2000 and the DFG for financial support.
To find a semi-analytic expression for the difference between
the synthetic amplitude spectra from the linear theory and
our numerical calculation, we approximate the local Fourier
coefficients a1 and b1 as a quadratic function of the
local pressure amplitude. Assuming a pressure variation
with the spherical harmonic of the mode on the stellar surface
we can write for the modes with l=0
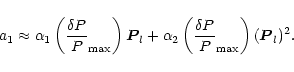 |
(31) |
In a similar way as for the spherical harmonics we can also expend
![]() with a finit number of
with a finit number of
![]() .
In this first
order approximation we only need the term with l'=0 of
this expansion (the next higher term belongs to l'=2 and
is strongly reduced by the cancelation effect). We can write
.
In this first
order approximation we only need the term with l'=0 of
this expansion (the next higher term belongs to l'=2 and
is strongly reduced by the cancelation effect). We can write
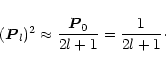 |
(32) |
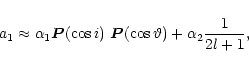 |
(33) |
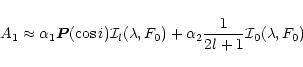 |
(34) |
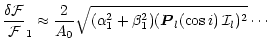 | |||
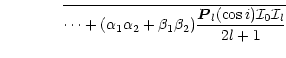 |
(36) | ||
Following the standard strategy to find an expression, which
eliminates the inclination dependence of the linear term, we normalize
Eq. (37) to the amplitude at a reference wavelength
![]() (e.g. =5500 Å) and obtain for the normalized spectrum
(e.g. =5500 Å) and obtain for the normalized spectrum
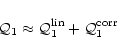
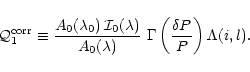 |
(39) |
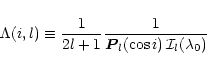 |
(40) |
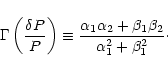 |
(41) |