

Up: Self-similar evolution of wind-blown
Subsections
2 Similarity solutions
The basic physics behind the hydrodynamic ablation of material from
dense clumps into the surrounding flow was presented by Hartquist et al.
(1986). It was proposed that if the flow around a clump
is subsonic, hydrodynamic mixing occurs as a result of the well-known
Bernoulli effect. For flow with a Mach number M with respect to the clump
of less than unity,
this leads to a volume mass injection rate,
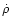 ,
proportional
to M4/3. For supersonic flow, mixing occurs largely as a result
of a low pressure region over the reverse face of the clump,
"shadowed'' from the flow. In this case the mass injection rate is Mach
number independent.
,
proportional
to M4/3. For supersonic flow, mixing occurs largely as a result
of a low pressure region over the reverse face of the clump,
"shadowed'' from the flow. In this case the mass injection rate is Mach
number independent.
In this paper we present similarity solutions for WBBs mass-loaded by
hydrodynamic ablation. Our solution method is very similar to that used by
PDH, and we refer the reader to that paper for a discussion of
many of the assumptions involved. As a starting point, we also assume the
same qualitative shock structure in the WBB as shown in Fig. 1 of PDH:
that is a central wind source surrounded by a region of
unshocked wind, separated from an outer region of shocked
wind by an inner shock. The swept-up ambient medium is
assumed to radiate efficiently and collapse to a negligibly thin shell
coincident with the contact discontinuity separating the stellar and ambient
gas (cf. Dyson & de Vries 1972).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f1.eps}\end{figure}](/articles/aa/full/2001/27/aa1222/Timg41.gif) |
Figure 1:
Results for
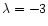 , ,
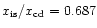 ,
and ,
and
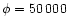 .
In the limit of large .
In the limit of large 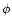 ( i.e. negligible mass loading),
the earlier results of Dyson (1973) are recovered. From the top
the panels indicate density, velocity, internal energy, and Mach number (with
respect to the stationary clumps) as a function of radius. Except for the
Mach number, the panels are normalized to values of 1.0 at the contact
discontinuity.
( i.e. negligible mass loading),
the earlier results of Dyson (1973) are recovered. From the top
the panels indicate density, velocity, internal energy, and Mach number (with
respect to the stationary clumps) as a function of radius. Except for the
Mach number, the panels are normalized to values of 1.0 at the contact
discontinuity. |
A central and fundamental difference between the conductive case
considered in PDH and the ablative case examined here, however,
is that here mass loading
may also occur in the unshocked stellar wind. The effect is to
heat this part of the flow, which leads to
reduced Mach numbers, and weaker jump conditions across the inner shock.
We shall see that for high mass loading rates, it is possible for the
unshocked mass-loaded wind to connect directly with the contact
discontinuity, without the presence of an inner shock.
In this work we assume that the flow can be treated as a single fluid.
This requires that the ablated clump material merges with the global flow
in the sense that its temperature, velocity, and density approach those of
the surrounding tenuous material. Ablation by itself might require that the
clump material mix microscopically with the wind to reach the density and
temperature of the wind. However, though the mass-loss rate may be controlled
by ablation, thermal conductivity will almost certainly be responsible for
material, once it is stripped from a clump, reaching the physical state of
the tenuous fast flowing medium. Thermal conduction accomplishes this
phase transition without microscopic mixing, and acceleration to the global
flow speed is effected by the response of stripped material to pressure
gradients and viscous coupling, which may arise from a host of mechanisms
including turbulence. Thus we envisage a two-stage process in which ablation
controls the rate at which mass is stripped from the clump but conductivity
becomes important for the merging into the global flow.
This receives support
from the comparison of the conductively driven evaporation time of a spherical
clump with
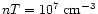 and T=104 K, embedded in a
medium with the same pressure (which is typical of planetary nebulae,
Wolf-Rayet wind-blown bubbles, and starburst superwinds) and T=107 K
(which is also typical of hot material in such regions) to the sound
crossing time in the clump. The sound crossing time is somewhat (but not
hugely) smaller than the conductively driven evaporation time for a large
range of clump sizes, if the Cowie & McKee (1977) estimate of the
mass-loss rate driven by saturated conduction is used. Consequently, ablation
initiates mass-loss because it causes an increase in the surface area of a
clump triggering more conductive heat transfer. Use of the analysis of
Cowie & McKee (1977) and McKee & Cowie (1977) shows
that for the assumptions given above, radiative losses do not hinder
conductively driven evaporation unless the clump radius is greater than
and T=104 K, embedded in a
medium with the same pressure (which is typical of planetary nebulae,
Wolf-Rayet wind-blown bubbles, and starburst superwinds) and T=107 K
(which is also typical of hot material in such regions) to the sound
crossing time in the clump. The sound crossing time is somewhat (but not
hugely) smaller than the conductively driven evaporation time for a large
range of clump sizes, if the Cowie & McKee (1977) estimate of the
mass-loss rate driven by saturated conduction is used. Consequently, ablation
initiates mass-loss because it causes an increase in the surface area of a
clump triggering more conductive heat transfer. Use of the analysis of
Cowie & McKee (1977) and McKee & Cowie (1977) shows
that for the assumptions given above, radiative losses do not hinder
conductively driven evaporation unless the clump radius is greater than
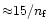 pc where
pc where 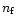 is the number density (
is the number density (
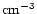 )
of the global tenuous flow. Of course, a clump that does not cool
radiatively after it is compressed by a shock will have a shorter sound
crossing time and be ablated more rapidly. However, by assuming a clump
temperature of 104 K above we have established that the two-stage
process is likely to be relevant in many environments if a clump radiatively
cools after being shocked.
)
of the global tenuous flow. Of course, a clump that does not cool
radiatively after it is compressed by a shock will have a shorter sound
crossing time and be ablated more rapidly. However, by assuming a clump
temperature of 104 K above we have established that the two-stage
process is likely to be relevant in many environments if a clump radiatively
cools after being shocked.
Observations of WBBs and PNe indicate that mass loading may not
necessarily begin at zero distance from the wind source. For
instance, in the young nebula Abell 30 the clumps appear almost all
of the way down to the central star (Borkowski et al.1995),
whilst in the more evolved Helix Nebula the clumps are all located closer
to its edge (e.g. Meaburn et al.1996). We therefore include
the radius at which mass-loading "switches on'' as a free parameter in our
models, and assume that the wind undergoes free expansion interior to this
radius. Hence each solution will consist of a region of supersonic wind
with no mass loading and an adjacent region with mass loading.
One can imagine two possible causes for this minimum "mass-loading'' radius.
In one scenario the clumps could have been ejected at low velocity
from the central star at an earlier evolutionary stage. The ejection of clumps
then abruptly stopped, so that at the time of observation they had
travelled a finite distance from the central star. By this process a
central region clear of clumps surrounded by a clumpy region can be
generated. A second possibility is that clumps interior to the mass-loading
radius have been completely destroyed by the wind. It seems reasonable to
suppose that clumps located closest to the central star will be
destroyed first, since they will have been subjected to the wind from the
central star for the longest time. Then as the bubble or nebula evolves,
clumps at ever increasing distance from the central star will be destroyed.
Timescales for the destruction of clumps by ablation can be estimated from
Hartquist et al.(1986) and Klein et al.(1994). Estimated
destruction timescales vary from significantly less than to greater than
the age of the bubble/PNe, in accord with the different spatial
distribution of clumps in objects of differing age.
Regardless of which of the above scenarios is responsible for the
existence of such a minimum mass-loading radius, this radius will
physically increase with time. Our similarity solution requires that it
increases in the same way as that of the contact discontinuity
(i.e.
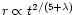 ,
where
,
where 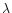 is the radial
dependence of the mass-loading). For most of the solutions presented in this
paper, the minimum mass-loading radius scales with or close to t. Since on
physical grounds we might expect it to scale as t, our solutions
closely match this requirement.
is the radial
dependence of the mass-loading). For most of the solutions presented in this
paper, the minimum mass-loading radius scales with or close to t. Since on
physical grounds we might expect it to scale as t, our solutions
closely match this requirement.
In our solutions an inner shock may or may not be present - in the
latter case the mass-loaded wind directly connects to the contact
discontinuity, and the mass loading may be strong enough for the wind to
become subsonic with respect to the clumps before the contact discontinuity
is reached. If an inner shock is present, the postshock flow is by definition
subsonic with respect to the shock, but may still be supersonic with respect
to the clumps. In this case a number of different profiles for the Mach
number are possible before the contact discontinuity is reached.
At the center of the bubble prior to the onset of mass loading,
we solve only the continuity and momentum equations, with the implicit
assumption that the thermal energy of the flow is negligible, whilst in
the mass loading regions we additionally solve the energy equation, and
include a source term for mass injection in the continuity equation. For
a
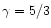 gas, the equations for the mass-loaded flow are:
gas, the equations for the mass-loaded flow are:
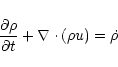 |
(1) |
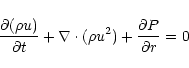 |
(2) |
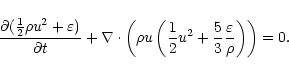 |
(3) |
In these equations the symbols have their usual meanings. In the
next sections we discuss appropriate similarity variables for these equations,
our treatment of the boundary conditions, and the scaling relationships
to normalize the resulting solutions. The reader is again referred to
PDH for a more in-depth discussion of the details.
2.1 The similarity variables
Let the interclump ambient medium have a density of the form
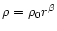 ,
and let us consider the case in which the
mass-ablation rate is also radially dependent:
,
and let us consider the case in which the
mass-ablation rate is also radially dependent:
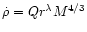 for subsonic ablation (M<1), and
for subsonic ablation (M<1), and
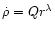 for supersonic ablation (M>1) (cf. Hartquist et al.
1986). A similarity solution demands that
for supersonic ablation (M>1) (cf. Hartquist et al.
1986). A similarity solution demands that
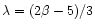 ,
and the "physical'' parameters
,
and the "physical'' parameters
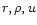 and
and
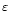 may be expressed in terms of the
dimensionless similarity variables x, f(x), g(x), and h(x) where
may be expressed in terms of the
dimensionless similarity variables x, f(x), g(x), and h(x) where
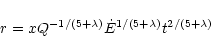 |
(4) |
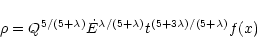 |
(5) |
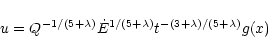 |
(6) |
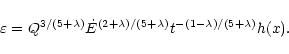 |
(7) |
Upon substituting the above similarity variables, the hydrodynamic
equations for the region of freely expanding wind become:
|
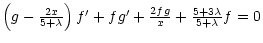 |
|
(8) |
| |
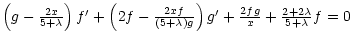 |
|
(9) |
where a prime denotes derivation with respect to x.
For the flow in the mass-loaded region we obtain:
where the Mach number,
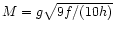 .
It is
simple to rearrange these equations to find f', g', and h' which may
then be integrated to obtain solutions.
.
It is
simple to rearrange these equations to find f', g', and h' which may
then be integrated to obtain solutions.
2.1.1 Boundary conditions
The values of f and g at
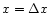 ,
the
inner boundary of our integration, are
,
the
inner boundary of our integration, are
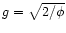 and
and
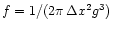 ,
where
,
where 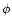 is a parameter which
specifies the relative amount of mass loading in the solution.
h is set to zero at this point. Equations (8)
and (9) are integrated to the radius at which mass loading
begins. From this point onwards we then integrate
Eqs. (10)-(12) instead.
The Mach number of the wind
rapidly decreases from its initial value of infinity and both the density
and velocity of the wind respond to the mass addition. Integration proceeds
until the contact discontinuity (CD) is reached. This occurs when the flow
velocity is equal to the coordinate velocity (i.e.
is a parameter which
specifies the relative amount of mass loading in the solution.
h is set to zero at this point. Equations (8)
and (9) are integrated to the radius at which mass loading
begins. From this point onwards we then integrate
Eqs. (10)-(12) instead.
The Mach number of the wind
rapidly decreases from its initial value of infinity and both the density
and velocity of the wind respond to the mass addition. Integration proceeds
until the contact discontinuity (CD) is reached. This occurs when the flow
velocity is equal to the coordinate velocity (i.e.
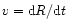 ),
which is where
),
which is where
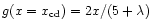 .
As previously discussed, this
can sometimes occur before the specified position of the inner shock
(
.
As previously discussed, this
can sometimes occur before the specified position of the inner shock
(
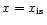 )
is reached, in which case the mass-loaded flow connects
directly to the CD. If an inner shock is present, its
velocity with respect to the bubble center is
)
is reached, in which case the mass-loaded flow connects
directly to the CD. If an inner shock is present, its
velocity with respect to the bubble center is
 ,
and the Mach number of the preshock flow
with respect to the shock is
,
and the Mach number of the preshock flow
with respect to the shock is
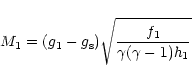 |
(13) |
where the subscript "1'' indicates the preshock values.
Because (unlike for the evaporative case) M1 is not necessarily
large, we cannot assume that
the strong shock jump conditions apply and therefore must use the full
Rankine-Hugoniot relations. The postshock values are then:
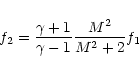 |
(14) |
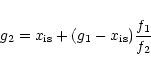 |
(15) |
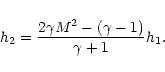 |
(16) |
Even if the flow velocity has not converged to the
coordinate velocity, an inner shock may not exist. This can occur if the
mass loading interior to the proposed position of the inner shock is
strong, resulting in M1 being less than unity. In such a scenario, the
jump conditions are not applied and the integration proceeds as before.
At the CD, we must also satisfy conservation of momentum. We take
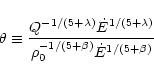 |
(17) |
as a measure of the ablated mass to the mass in the swept-up
shell. It follows that at the contact discontinuity,
![\begin{displaymath}%
\theta = \left(\frac{(\gamma-1) h}{x^{\beta}\left[g^{2} - \...
...mbda}
{(5+\lambda)(3+\beta)} xg\right]}\right)^{1/(5+\beta)}.
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img82.gif) |
(18) |
The rate of massloss from the star is
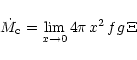 |
(19) |
where
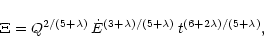 |
(20) |
which differs from the definition in the conductively driven
case.
The mass loading parameter 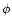 ,
which is a measure of the ratio of
ablated mass to wind mass is given by
,
which is a measure of the ratio of
ablated mass to wind mass is given by
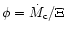 .
.
Table 1:
The influence of
 on solutions with
on solutions with
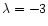 .
Two
cases are considered: minor mass loading (
.
Two
cases are considered: minor mass loading (
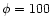 )
whereby the
value of
)
whereby the
value of
 is relatively unimportant, and appreciable mass loading
(
is relatively unimportant, and appreciable mass loading
(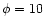 )
where
)
where
 exerts a major influence.
From left to right, the columns
indicate: i) the value of
exerts a major influence.
From left to right, the columns
indicate: i) the value of
 ,
ii) the ratio of the shock radii and CD,
iii-vi) the fractions of energy that are thermal and kinetic
in the bubble, kinetic in the swept-up shell, and radiated,
vii) the value of
,
ii) the ratio of the shock radii and CD,
iii-vi) the fractions of energy that are thermal and kinetic
in the bubble, kinetic in the swept-up shell, and radiated,
vii) the value of 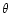 ,
viii) the ratio of mass within the bubble to the total mass injected by
the wind (values greater than unity indicate mass loading), ix) the ratio
of mass in
the swept-up shell to mass in the bubble, x) the preshock Mach number
of the unshocked wind.
,
viii) the ratio of mass within the bubble to the total mass injected by
the wind (values greater than unity indicate mass loading), ix) the ratio
of mass in
the swept-up shell to mass in the bubble, x) the preshock Mach number
of the unshocked wind.
 |
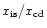 |
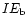 |
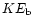 |
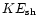 |
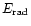 |
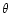 |
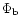 |
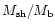 |
M1 |
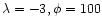 |
|
|
|
|
|
|
|
|
|
| 0.1 |
0.271 |
0.46 |
0.014 |
0.469 |
0.059 |
102 |
1.454 |
376 |
4.79 |
| 0.2 |
0.268 |
0.46 |
0.013 |
0.469 |
0.059 |
101 |
1.371 |
390 |
4.79 |
| 0.33 |
0.266 |
0.46 |
0.013 |
0.469 |
0.059 |
99.7 |
1.289 |
408 |
5.00 |
| 0.5 |
0.268 |
0.46 |
0.013 |
0.469 |
0.059 |
99.2 |
1.223 |
426 |
5.56 |
| 0.9 |
0.264 |
0.46 |
0.013 |
0.469 |
0.059 |
99.0 |
1.152 |
450 |
11.9 |
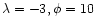 |
|
|
|
|
|
|
|
|
|
| 0.02 |
0.82 |
0.17 |
0.63 |
0.18 |
0.022 |
2.95 |
6.50 |
0.51 |
1.60 |
| 0.1 |
0.76 |
0.22 |
0.53 |
0.22 |
0.028 |
2.95 |
4.48 |
0.80 |
1.45 |
| 0.2 |
0.73 |
0.24 |
0.49 |
0.24 |
0.030 |
2.90 |
3.84 |
0.92 |
1.34 |
| 0.5 |
0.66 |
0.25 |
0.45 |
0.27 |
0.033 |
2.67 |
2.55 |
1.23 |
1.12 |
| 0.9 |
0.67 |
0.24 |
0.39 |
0.33 |
0.041 |
2.85 |
1.75 |
2.17 |
2.53 |
2.2 Scale transformation and normalization
The dimensionless Eqs. (10)-(12) are invariant
under the following transformation, which we shall call a normalization:
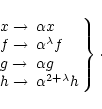 |
(21) |
These can be combined to obtain the normalizations for the
mass, and for the kinetic and internal energies of the bubble:
![\begin{displaymath}%
m = 4 \pi \int f x^{2} {\rm d}x
\hspace{15mm} [\alpha^{3+\lambda}]
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img95.gif) |
(22) |
![\begin{displaymath}%
k = 4 \pi \int \frac{1}{2} f g^{2} x^{2} {\rm d}x
\hspace{10mm} [\alpha^{5+\lambda}]
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img96.gif) |
(23) |
![\begin{displaymath}%
i = 4 \pi \int h x^{2} {\rm d}x
\hspace{17mm} [\alpha^{5+\lambda}].
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img97.gif) |
(24) |
The full equation for the mass in the bubble is:
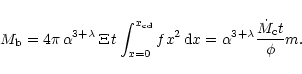 |
(25) |
The total mass lost by the star during its lifetime is
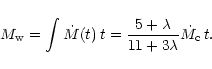 |
(26) |
The degree of mass loading in the bubble,
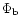 ,
is defined
as the ratio
,
is defined
as the ratio
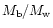 .
The mass-swept up into the shell,
.
The mass-swept up into the shell,
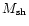 ,
the ratio of swept-up mass to bubble mass,
,
the ratio of swept-up mass to bubble mass,
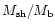 ,
the kinetic energy of the shell,
,
the kinetic energy of the shell,
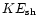 ,
and the pdV work on the
shocked ambient gas, are all identical to the corresponding forms in
PDH.
,
and the pdV work on the
shocked ambient gas, are all identical to the corresponding forms in
PDH.
2.3 Solution procedure
If an inner shock exists, three main parameters determine
the form of a given similarity solution (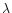 ,
,
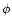 and
and
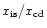 ). However, the ratio of the radius of the onset of
mass loading to the radius of the inner shock is an additional parameter
unique to the ablative solutions, and its value (
). However, the ratio of the radius of the onset of
mass loading to the radius of the inner shock is an additional parameter
unique to the ablative solutions, and its value (
 )
may also
influence the form of the solution. We find that if the mass loading of
the bubble is minor,
)
may also
influence the form of the solution. We find that if the mass loading of
the bubble is minor,
 has relatively little influence, and
vice-versa (since
has relatively little influence, and
vice-versa (since
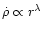 and
and
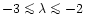 for most of the solutions presented,
most of the mass-loading occurs close to the minimum mass-loading radius).
Alternatively, if an inner shock does not exist,
for most of the solutions presented,
most of the mass-loading occurs close to the minimum mass-loading radius).
Alternatively, if an inner shock does not exist,
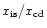 and
and
 have no meaning as we have defined them.
In this case we report the ratio of the onset radius of
mass loading to the radius of the contact discontinuity as the parameter
have no meaning as we have defined them.
In this case we report the ratio of the onset radius of
mass loading to the radius of the contact discontinuity as the parameter
 .
.
The ratio of mass pick-up from the clumps to the mass swept-up from the
interclump medium (which is related to the value of 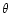 )
is
obtained only after a particular solution has been found. For bubbles whose
evolution is significantly altered by mass loading, we require that
simultaneously
)
is
obtained only after a particular solution has been found. For bubbles whose
evolution is significantly altered by mass loading, we require that
simultaneously 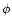 and
and 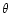 are both small.
are both small.
The similarity equations were integrated with a fifth-order accurate
adaptive step-size Bulirsch-Stoer method using polynomial
extrapolation to infinitesimal step size. Once the CD was reached,
the similarity variables were rescaled
using the relationships defined in Eq. (21) so
that
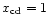 .
The mass, and kinetic and thermal energies
of the bubble were calculated, as were the kinetic energy of the shell
and the energy radiated from it. The correct normalization to satisfy
global energy conservation was then obtained. Finally, for given values of
.
The mass, and kinetic and thermal energies
of the bubble were calculated, as were the kinetic energy of the shell
and the energy radiated from it. The correct normalization to satisfy
global energy conservation was then obtained. Finally, for given values of
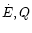 and t, the similarity variables x, f, g and h may be
scaled into the physical variables
and t, the similarity variables x, f, g and h may be
scaled into the physical variables
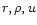 and
and
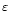 .
.


Up: Self-similar evolution of wind-blown
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f1.eps}\end{figure}](/articles/aa/full/2001/27/aa1222/Timg41.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f1.eps}\end{figure}](/articles/aa/full/2001/27/aa1222/Timg41.gif)
![]() and T=104 K, embedded in a
medium with the same pressure (which is typical of planetary nebulae,
Wolf-Rayet wind-blown bubbles, and starburst superwinds) and T=107 K
(which is also typical of hot material in such regions) to the sound
crossing time in the clump. The sound crossing time is somewhat (but not
hugely) smaller than the conductively driven evaporation time for a large
range of clump sizes, if the Cowie & McKee (1977) estimate of the
mass-loss rate driven by saturated conduction is used. Consequently, ablation
initiates mass-loss because it causes an increase in the surface area of a
clump triggering more conductive heat transfer. Use of the analysis of
Cowie & McKee (1977) and McKee & Cowie (1977) shows
that for the assumptions given above, radiative losses do not hinder
conductively driven evaporation unless the clump radius is greater than
and T=104 K, embedded in a
medium with the same pressure (which is typical of planetary nebulae,
Wolf-Rayet wind-blown bubbles, and starburst superwinds) and T=107 K
(which is also typical of hot material in such regions) to the sound
crossing time in the clump. The sound crossing time is somewhat (but not
hugely) smaller than the conductively driven evaporation time for a large
range of clump sizes, if the Cowie & McKee (1977) estimate of the
mass-loss rate driven by saturated conduction is used. Consequently, ablation
initiates mass-loss because it causes an increase in the surface area of a
clump triggering more conductive heat transfer. Use of the analysis of
Cowie & McKee (1977) and McKee & Cowie (1977) shows
that for the assumptions given above, radiative losses do not hinder
conductively driven evaporation unless the clump radius is greater than
![]() pc where
pc where ![]() is the number density (
is the number density (
![]() )
of the global tenuous flow. Of course, a clump that does not cool
radiatively after it is compressed by a shock will have a shorter sound
crossing time and be ablated more rapidly. However, by assuming a clump
temperature of 104 K above we have established that the two-stage
process is likely to be relevant in many environments if a clump radiatively
cools after being shocked.
)
of the global tenuous flow. Of course, a clump that does not cool
radiatively after it is compressed by a shock will have a shorter sound
crossing time and be ablated more rapidly. However, by assuming a clump
temperature of 104 K above we have established that the two-stage
process is likely to be relevant in many environments if a clump radiatively
cools after being shocked.
![]() ,
where
,
where ![]() is the radial
dependence of the mass-loading). For most of the solutions presented in this
paper, the minimum mass-loading radius scales with or close to t. Since on
physical grounds we might expect it to scale as t, our solutions
closely match this requirement.
is the radial
dependence of the mass-loading). For most of the solutions presented in this
paper, the minimum mass-loading radius scales with or close to t. Since on
physical grounds we might expect it to scale as t, our solutions
closely match this requirement.
![]() gas, the equations for the mass-loaded flow are:
gas, the equations for the mass-loaded flow are:
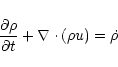
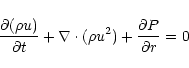
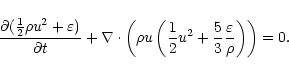
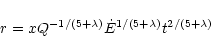
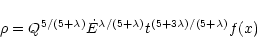
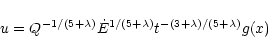
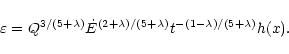
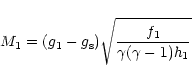
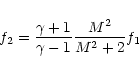
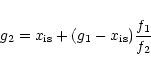
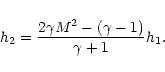
![\begin{displaymath}%
\theta = \left(\frac{(\gamma-1) h}{x^{\beta}\left[g^{2} - \...
...mbda}
{(5+\lambda)(3+\beta)} xg\right]}\right)^{1/(5+\beta)}.
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img82.gif)
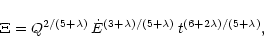
![\begin{displaymath}%
m = 4 \pi \int f x^{2} {\rm d}x
\hspace{15mm} [\alpha^{3+\lambda}]
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img95.gif)
![\begin{displaymath}%
k = 4 \pi \int \frac{1}{2} f g^{2} x^{2} {\rm d}x
\hspace{10mm} [\alpha^{5+\lambda}]
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img96.gif)
![\begin{displaymath}%
i = 4 \pi \int h x^{2} {\rm d}x
\hspace{17mm} [\alpha^{5+\lambda}].
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img97.gif)
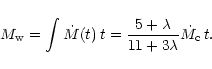
![]() )
is
obtained only after a particular solution has been found. For bubbles whose
evolution is significantly altered by mass loading, we require that
simultaneously
)
is
obtained only after a particular solution has been found. For bubbles whose
evolution is significantly altered by mass loading, we require that
simultaneously ![]() and
and ![]() are both small.
are both small.
![]() .
The mass, and kinetic and thermal energies
of the bubble were calculated, as were the kinetic energy of the shell
and the energy radiated from it. The correct normalization to satisfy
global energy conservation was then obtained. Finally, for given values of
.
The mass, and kinetic and thermal energies
of the bubble were calculated, as were the kinetic energy of the shell
and the energy radiated from it. The correct normalization to satisfy
global energy conservation was then obtained. Finally, for given values of
![]() and t, the similarity variables x, f, g and h may be
scaled into the physical variables
and t, the similarity variables x, f, g and h may be
scaled into the physical variables
![]() and
and
![]() .
.