A&A 373, 1043-1055 (2001)
DOI: 10.1051/0004-6361:20010673
Self-similar evolution of wind-blown bubbles with mass loading
by hydrodynamic ablation
J. M. Pittard - T. W. Hartquist - J. E. Dyson
Department of Physics & Astronomy, The University of Leeds,
Woodhouse Lane, Leeds, LS2 9JT, UK
Received 6 March 2001 / Accepted 2 May 2001
Abstract
We present similarity solutions for adiabatic bubbles that are blown by
winds having time independent mechanical luminosities and that are each
mass-loaded by the hydrodynamic ablation of
distributed clumps. The mass loading is "switched-on'' at a specified
radius (with free-expansion of the wind interior to this point) and
injects mass
at a rate per unit volume proportional to
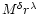 where
where
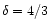 (1) if the flow is subsonic (supersonic) with respect to
the clumps.
In the limit of negligible mass loading a similarity solution found by
Dyson (1973) for expansion into a smooth ambient medium is
recovered. The presence of mass loading heats the flow, which
leads to a reduction in the Mach number of the supersonic
freely-expanding flow, and weaker jump conditions across
the inner shock. In solutions with large mass loading, it is possible for
the wind to connect directly to the contact discontinuity without first
passing through an inner shock, in agreement with previous hydrodynamic
simulations. In such circumstances, the flow may or
may not remain continuously supersonic with respect to the clumps.
For a solution that gives the mass of swept-up ambient gas to be less than
the sum of the masses of the wind and ablated material,
(1) if the flow is subsonic (supersonic) with respect to
the clumps.
In the limit of negligible mass loading a similarity solution found by
Dyson (1973) for expansion into a smooth ambient medium is
recovered. The presence of mass loading heats the flow, which
leads to a reduction in the Mach number of the supersonic
freely-expanding flow, and weaker jump conditions across
the inner shock. In solutions with large mass loading, it is possible for
the wind to connect directly to the contact discontinuity without first
passing through an inner shock, in agreement with previous hydrodynamic
simulations. In such circumstances, the flow may or
may not remain continuously supersonic with respect to the clumps.
For a solution that gives the mass of swept-up ambient gas to be less than
the sum of the masses of the wind and ablated material,
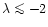 ,
meaning that the exponent of the density profile
of the interclump medium must be at most slightly positive, with negative
values preferred. Maximum possible values for the ratio of ablated mass
to wind mass occur when mass loading
starts very close to the bubble center and when the flow is supersonic
with respect to the clumps over the entire bubble radius.
Whilst mass loading always reduces the temperature of the shocked wind,
it also tends to reduce the emissivity in the interior of the
bubble relative to its limb, whilst simultaneously increasing the central
temperature relative to the limb temperature. The maximum temperature in
the bubble often occurs near the onset of mass loading, and in some cases
can be many times greater than the post-inner-shock temperature.
Our solutions are potentially relevant to a wide range of astrophysical
objects, including stellar wind-blown bubbles, galactic winds, starburst
galaxy superwinds, and the impact of an AGN wind on its surrounding
environment. This work complements the earlier work of Pittard et al.
(2001) in which it was assumed that clumps were evaporated
through conductive energy transport.
,
meaning that the exponent of the density profile
of the interclump medium must be at most slightly positive, with negative
values preferred. Maximum possible values for the ratio of ablated mass
to wind mass occur when mass loading
starts very close to the bubble center and when the flow is supersonic
with respect to the clumps over the entire bubble radius.
Whilst mass loading always reduces the temperature of the shocked wind,
it also tends to reduce the emissivity in the interior of the
bubble relative to its limb, whilst simultaneously increasing the central
temperature relative to the limb temperature. The maximum temperature in
the bubble often occurs near the onset of mass loading, and in some cases
can be many times greater than the post-inner-shock temperature.
Our solutions are potentially relevant to a wide range of astrophysical
objects, including stellar wind-blown bubbles, galactic winds, starburst
galaxy superwinds, and the impact of an AGN wind on its surrounding
environment. This work complements the earlier work of Pittard et al.
(2001) in which it was assumed that clumps were evaporated
through conductive energy transport.
Key words: hydrodynamics - shock waves - stars: mass-loss -
ISM: bubbles - galaxies: active
1 Introduction
Numerous observations of wind-blown bubbles (WBBs) have led to the
conclusion that their structures and evolution are significantly affected
by mass entrainment from embedded clumps. As a case in point, bubbles
blown by the winds of highly evolved stars can be mass-loaded from
clumps of stellar material ejected during prior stages of massloss
(Smith et al.1984; Hartquist et al.1986;
Meaburn et al.1991; Dyson & Hartquist 1992;
Hartquist & Dyson 1993). The properties of winds mass-loaded by
material from clumps (or stellar sources) has also received theoretical
attention in the context of ultracompact H II regions (Dyson et al.
1995), globular cluster
winds (Durisen & Burns 1981), galactic winds and starburst
galaxy superwinds (Strickland & Stevens 2000), and accretion flow
structures at the centers of active galactic nuclei (David & Durisen
1989; Toniazzo et al.2001).
Investigations into the self-similar nature of supernova remnant (McKee &
Ostriker 1977; Chièze & Lazareff 1981; Dyson &
Hartquist 1987) and stellar wind-blown bubble
(Pittard et al.2001) evolution in
tenuous media with embedded clumps have been performed. Detailed
one-dimensional, time-dependent hydrodynamic models of specific WBBs
associated with evolved stars have also been constructed (Arthur et al.
1993, 1994, 1996). In at least some isothermal
mass-loaded winds, Arthur et al.(1994) and Williams et al.
(1995, 1999) showed that a global shock does not
occur in the region where the Mach number is large. Instead, a global shock
occurs only after the wind has travelled far enough for mass loading to
decelerate it sufficiently that its Mach number is less than a few. In
some of these cases, a global shock within the mass loading region does not
exist at all, and the wind continues until it encounters a termination
shock caused by the interaction of the wind with an external medium.
Observations supporting mass loading in WBBs include the detection of
blue-shifted absorption features of species with a range of ionization
potentials in the spectrum of the central star of the Wolf-Rayet nebula
RCW 58. Smith et al.(1984) argued that the observed velocity
spread for the detected features is much larger than would be expected
for
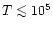 K gas consisting only of stellar wind material
decelerated through a terminal shock, and suggested that the velocity
spread originates due to mass loading of the shocked wind through the
entrainment of material from clumps. Crucially, one can obtain an estimate
for the ratio of wind mass to entrained clump mass: the observed velocity
spread implies a value of 40 or 50 to one. A detailed time-dependent,
hydrodynamic model including nonequilibrium ionization structure is
consistent with these conclusions (Arthur et al.1996).
Spectroscopic data also provide evidence for transonic flows in the halo
of core-halo planetary nebula (Meaburn et al.1991),
again consistent with high mass loading rates. Finally, it is also
suspected that
the gradual deceleration of a wind by mass loading and the associated
weakening of an inner shock may in fact contribute to the radio quietness
of some WBBs, although this is a conjecture which currently cannot be proven
(see Williams et al.1995, 1999).
In Pittard et al.(2001, hereafter PDH), similarity solutions were
derived for the structures and evolution of mass-loaded WBBs, under the
assumption that conductive evaporation from embedded clumps was the dominant
mass loading process, and that both evaporation from the cold swept-up
shell and radiative losses were negligible. To obtain a similarity solution
with these conditions, specific radial power-laws on the clump and
interclump density distribution, and temporal power-laws on the wind
mass-loss rate and terminal velocity, were required. Approximate
similarity solutions for evaporatively mass-loaded WBBs with the assumptions
of constant mass-loss rate and wind velocity, and an isobaric shocked
wind region have previously been obtained by Weaver et al.(1977;
evaporation from the cool swept-up shell) and Hanami & Sakashita
(1987; mass-loading from clumps). A central assumption in both
of these papers was that the shocked wind was approximately isobaric.
However, PDH demonstrated that this was not necessarily a good assumption
(e.g. see their Fig. 4). Indeed, imposing this condition is likely to
set a limit to the amount of mass loading that can occur.
K gas consisting only of stellar wind material
decelerated through a terminal shock, and suggested that the velocity
spread originates due to mass loading of the shocked wind through the
entrainment of material from clumps. Crucially, one can obtain an estimate
for the ratio of wind mass to entrained clump mass: the observed velocity
spread implies a value of 40 or 50 to one. A detailed time-dependent,
hydrodynamic model including nonequilibrium ionization structure is
consistent with these conclusions (Arthur et al.1996).
Spectroscopic data also provide evidence for transonic flows in the halo
of core-halo planetary nebula (Meaburn et al.1991),
again consistent with high mass loading rates. Finally, it is also
suspected that
the gradual deceleration of a wind by mass loading and the associated
weakening of an inner shock may in fact contribute to the radio quietness
of some WBBs, although this is a conjecture which currently cannot be proven
(see Williams et al.1995, 1999).
In Pittard et al.(2001, hereafter PDH), similarity solutions were
derived for the structures and evolution of mass-loaded WBBs, under the
assumption that conductive evaporation from embedded clumps was the dominant
mass loading process, and that both evaporation from the cold swept-up
shell and radiative losses were negligible. To obtain a similarity solution
with these conditions, specific radial power-laws on the clump and
interclump density distribution, and temporal power-laws on the wind
mass-loss rate and terminal velocity, were required. Approximate
similarity solutions for evaporatively mass-loaded WBBs with the assumptions
of constant mass-loss rate and wind velocity, and an isobaric shocked
wind region have previously been obtained by Weaver et al.(1977;
evaporation from the cool swept-up shell) and Hanami & Sakashita
(1987; mass-loading from clumps). A central assumption in both
of these papers was that the shocked wind was approximately isobaric.
However, PDH demonstrated that this was not necessarily a good assumption
(e.g. see their Fig. 4). Indeed, imposing this condition is likely to
set a limit to the amount of mass loading that can occur.
A central conclusion of PDH was that there exist maximum possible values
for the ratio of evaporated mass to stellar wind mass, as a consequence of
the evaporation rates dependence on temperature and the lowering of
temperature by mass loading. In particular it was difficult to find ratios
approaching what was observationally required.
The work in this paper complements PDH by considering the case in which
hydrodynamic ablation is the dominant mass addition process. As conductively
driven evaporation has a very temperature sensitive rate, ablation is
likely to regulate clump dispersal into lower temperature media.
Our solutions are again potentially relevant to such diverse objects as
WBBs created by a faster wind interacting with a
clumpy AGB superwind, by the wind of a young star interacting
with surrounding molecular material, and the wind of an active galactic
nucleus impacting its environment.
2 Similarity solutions
The basic physics behind the hydrodynamic ablation of material from
dense clumps into the surrounding flow was presented by Hartquist et al.
(1986). It was proposed that if the flow around a clump
is subsonic, hydrodynamic mixing occurs as a result of the well-known
Bernoulli effect. For flow with a Mach number M with respect to the clump
of less than unity,
this leads to a volume mass injection rate,
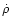 ,
proportional
to M4/3. For supersonic flow, mixing occurs largely as a result
of a low pressure region over the reverse face of the clump,
"shadowed'' from the flow. In this case the mass injection rate is Mach
number independent.
,
proportional
to M4/3. For supersonic flow, mixing occurs largely as a result
of a low pressure region over the reverse face of the clump,
"shadowed'' from the flow. In this case the mass injection rate is Mach
number independent.
In this paper we present similarity solutions for WBBs mass-loaded by
hydrodynamic ablation. Our solution method is very similar to that used by
PDH, and we refer the reader to that paper for a discussion of
many of the assumptions involved. As a starting point, we also assume the
same qualitative shock structure in the WBB as shown in Fig. 1 of PDH:
that is a central wind source surrounded by a region of
unshocked wind, separated from an outer region of shocked
wind by an inner shock. The swept-up ambient medium is
assumed to radiate efficiently and collapse to a negligibly thin shell
coincident with the contact discontinuity separating the stellar and ambient
gas (cf. Dyson & de Vries 1972).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f1.eps}\end{figure}](/articles/aa/full/2001/27/aa1222/Timg41.gif) |
Figure 1:
Results for
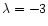 , ,
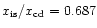 ,
and ,
and
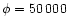 .
In the limit of large .
In the limit of large 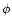 ( i.e. negligible mass loading),
the earlier results of Dyson (1973) are recovered. From the top
the panels indicate density, velocity, internal energy, and Mach number (with
respect to the stationary clumps) as a function of radius. Except for the
Mach number, the panels are normalized to values of 1.0 at the contact
discontinuity.
( i.e. negligible mass loading),
the earlier results of Dyson (1973) are recovered. From the top
the panels indicate density, velocity, internal energy, and Mach number (with
respect to the stationary clumps) as a function of radius. Except for the
Mach number, the panels are normalized to values of 1.0 at the contact
discontinuity. |
| Open with DEXTER |
A central and fundamental difference between the conductive case
considered in PDH and the ablative case examined here, however,
is that here mass loading
may also occur in the unshocked stellar wind. The effect is to
heat this part of the flow, which leads to
reduced Mach numbers, and weaker jump conditions across the inner shock.
We shall see that for high mass loading rates, it is possible for the
unshocked mass-loaded wind to connect directly with the contact
discontinuity, without the presence of an inner shock.
In this work we assume that the flow can be treated as a single fluid.
This requires that the ablated clump material merges with the global flow
in the sense that its temperature, velocity, and density approach those of
the surrounding tenuous material. Ablation by itself might require that the
clump material mix microscopically with the wind to reach the density and
temperature of the wind. However, though the mass-loss rate may be controlled
by ablation, thermal conductivity will almost certainly be responsible for
material, once it is stripped from a clump, reaching the physical state of
the tenuous fast flowing medium. Thermal conduction accomplishes this
phase transition without microscopic mixing, and acceleration to the global
flow speed is effected by the response of stripped material to pressure
gradients and viscous coupling, which may arise from a host of mechanisms
including turbulence. Thus we envisage a two-stage process in which ablation
controls the rate at which mass is stripped from the clump but conductivity
becomes important for the merging into the global flow.
This receives support
from the comparison of the conductively driven evaporation time of a spherical
clump with
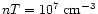 and T=104 K, embedded in a
medium with the same pressure (which is typical of planetary nebulae,
Wolf-Rayet wind-blown bubbles, and starburst superwinds) and T=107 K
(which is also typical of hot material in such regions) to the sound
crossing time in the clump. The sound crossing time is somewhat (but not
hugely) smaller than the conductively driven evaporation time for a large
range of clump sizes, if the Cowie & McKee (1977) estimate of the
mass-loss rate driven by saturated conduction is used. Consequently, ablation
initiates mass-loss because it causes an increase in the surface area of a
clump triggering more conductive heat transfer. Use of the analysis of
Cowie & McKee (1977) and McKee & Cowie (1977) shows
that for the assumptions given above, radiative losses do not hinder
conductively driven evaporation unless the clump radius is greater than
and T=104 K, embedded in a
medium with the same pressure (which is typical of planetary nebulae,
Wolf-Rayet wind-blown bubbles, and starburst superwinds) and T=107 K
(which is also typical of hot material in such regions) to the sound
crossing time in the clump. The sound crossing time is somewhat (but not
hugely) smaller than the conductively driven evaporation time for a large
range of clump sizes, if the Cowie & McKee (1977) estimate of the
mass-loss rate driven by saturated conduction is used. Consequently, ablation
initiates mass-loss because it causes an increase in the surface area of a
clump triggering more conductive heat transfer. Use of the analysis of
Cowie & McKee (1977) and McKee & Cowie (1977) shows
that for the assumptions given above, radiative losses do not hinder
conductively driven evaporation unless the clump radius is greater than
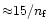 pc where
pc where 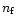 is the number density (
is the number density (
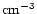 )
of the global tenuous flow. Of course, a clump that does not cool
radiatively after it is compressed by a shock will have a shorter sound
crossing time and be ablated more rapidly. However, by assuming a clump
temperature of 104 K above we have established that the two-stage
process is likely to be relevant in many environments if a clump radiatively
cools after being shocked.
)
of the global tenuous flow. Of course, a clump that does not cool
radiatively after it is compressed by a shock will have a shorter sound
crossing time and be ablated more rapidly. However, by assuming a clump
temperature of 104 K above we have established that the two-stage
process is likely to be relevant in many environments if a clump radiatively
cools after being shocked.
Observations of WBBs and PNe indicate that mass loading may not
necessarily begin at zero distance from the wind source. For
instance, in the young nebula Abell 30 the clumps appear almost all
of the way down to the central star (Borkowski et al.1995),
whilst in the more evolved Helix Nebula the clumps are all located closer
to its edge (e.g. Meaburn et al.1996). We therefore include
the radius at which mass-loading "switches on'' as a free parameter in our
models, and assume that the wind undergoes free expansion interior to this
radius. Hence each solution will consist of a region of supersonic wind
with no mass loading and an adjacent region with mass loading.
One can imagine two possible causes for this minimum "mass-loading'' radius.
In one scenario the clumps could have been ejected at low velocity
from the central star at an earlier evolutionary stage. The ejection of clumps
then abruptly stopped, so that at the time of observation they had
travelled a finite distance from the central star. By this process a
central region clear of clumps surrounded by a clumpy region can be
generated. A second possibility is that clumps interior to the mass-loading
radius have been completely destroyed by the wind. It seems reasonable to
suppose that clumps located closest to the central star will be
destroyed first, since they will have been subjected to the wind from the
central star for the longest time. Then as the bubble or nebula evolves,
clumps at ever increasing distance from the central star will be destroyed.
Timescales for the destruction of clumps by ablation can be estimated from
Hartquist et al.(1986) and Klein et al.(1994). Estimated
destruction timescales vary from significantly less than to greater than
the age of the bubble/PNe, in accord with the different spatial
distribution of clumps in objects of differing age.
Regardless of which of the above scenarios is responsible for the
existence of such a minimum mass-loading radius, this radius will
physically increase with time. Our similarity solution requires that it
increases in the same way as that of the contact discontinuity
(i.e.
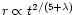 ,
where
,
where 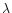 is the radial
dependence of the mass-loading). For most of the solutions presented in this
paper, the minimum mass-loading radius scales with or close to t. Since on
physical grounds we might expect it to scale as t, our solutions
closely match this requirement.
is the radial
dependence of the mass-loading). For most of the solutions presented in this
paper, the minimum mass-loading radius scales with or close to t. Since on
physical grounds we might expect it to scale as t, our solutions
closely match this requirement.
In our solutions an inner shock may or may not be present - in the
latter case the mass-loaded wind directly connects to the contact
discontinuity, and the mass loading may be strong enough for the wind to
become subsonic with respect to the clumps before the contact discontinuity
is reached. If an inner shock is present, the postshock flow is by definition
subsonic with respect to the shock, but may still be supersonic with respect
to the clumps. In this case a number of different profiles for the Mach
number are possible before the contact discontinuity is reached.
At the center of the bubble prior to the onset of mass loading,
we solve only the continuity and momentum equations, with the implicit
assumption that the thermal energy of the flow is negligible, whilst in
the mass loading regions we additionally solve the energy equation, and
include a source term for mass injection in the continuity equation. For
a
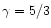 gas, the equations for the mass-loaded flow are:
gas, the equations for the mass-loaded flow are:
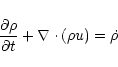 |
(1) |
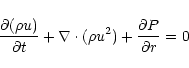 |
(2) |
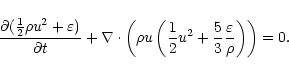 |
(3) |
In these equations the symbols have their usual meanings. In the
next sections we discuss appropriate similarity variables for these equations,
our treatment of the boundary conditions, and the scaling relationships
to normalize the resulting solutions. The reader is again referred to
PDH for a more in-depth discussion of the details.
2.1 The similarity variables
Let the interclump ambient medium have a density of the form
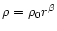 ,
and let us consider the case in which the
mass-ablation rate is also radially dependent:
,
and let us consider the case in which the
mass-ablation rate is also radially dependent:
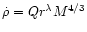 for subsonic ablation (M<1), and
for subsonic ablation (M<1), and
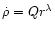 for supersonic ablation (M>1) (cf. Hartquist et al.
1986). A similarity solution demands that
for supersonic ablation (M>1) (cf. Hartquist et al.
1986). A similarity solution demands that
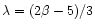 ,
and the "physical'' parameters
,
and the "physical'' parameters
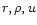 and
and
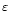 may be expressed in terms of the
dimensionless similarity variables x, f(x), g(x), and h(x) where
may be expressed in terms of the
dimensionless similarity variables x, f(x), g(x), and h(x) where
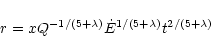 |
(4) |
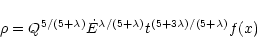 |
(5) |
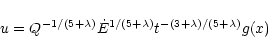 |
(6) |
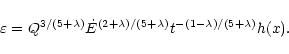 |
(7) |
Upon substituting the above similarity variables, the hydrodynamic
equations for the region of freely expanding wind become:
|
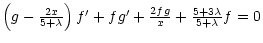 |
|
(8) |
| |
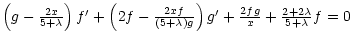 |
|
(9) |
where a prime denotes derivation with respect to x.
For the flow in the mass-loaded region we obtain:
where the Mach number,
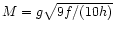 .
It is
simple to rearrange these equations to find f', g', and h' which may
then be integrated to obtain solutions.
.
It is
simple to rearrange these equations to find f', g', and h' which may
then be integrated to obtain solutions.
2.1.1 Boundary conditions
The values of f and g at
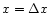 ,
the
inner boundary of our integration, are
,
the
inner boundary of our integration, are
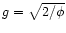 and
and
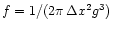 ,
where
,
where 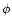 is a parameter which
specifies the relative amount of mass loading in the solution.
h is set to zero at this point. Equations (8)
and (9) are integrated to the radius at which mass loading
begins. From this point onwards we then integrate
Eqs. (10)-(12) instead.
The Mach number of the wind
rapidly decreases from its initial value of infinity and both the density
and velocity of the wind respond to the mass addition. Integration proceeds
until the contact discontinuity (CD) is reached. This occurs when the flow
velocity is equal to the coordinate velocity (i.e.
is a parameter which
specifies the relative amount of mass loading in the solution.
h is set to zero at this point. Equations (8)
and (9) are integrated to the radius at which mass loading
begins. From this point onwards we then integrate
Eqs. (10)-(12) instead.
The Mach number of the wind
rapidly decreases from its initial value of infinity and both the density
and velocity of the wind respond to the mass addition. Integration proceeds
until the contact discontinuity (CD) is reached. This occurs when the flow
velocity is equal to the coordinate velocity (i.e.
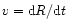 ),
which is where
),
which is where
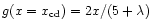 .
As previously discussed, this
can sometimes occur before the specified position of the inner shock
(
.
As previously discussed, this
can sometimes occur before the specified position of the inner shock
(
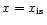 )
is reached, in which case the mass-loaded flow connects
directly to the CD. If an inner shock is present, its
velocity with respect to the bubble center is
)
is reached, in which case the mass-loaded flow connects
directly to the CD. If an inner shock is present, its
velocity with respect to the bubble center is
 ,
and the Mach number of the preshock flow
with respect to the shock is
,
and the Mach number of the preshock flow
with respect to the shock is
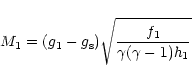 |
(13) |
where the subscript "1'' indicates the preshock values.
Because (unlike for the evaporative case) M1 is not necessarily
large, we cannot assume that
the strong shock jump conditions apply and therefore must use the full
Rankine-Hugoniot relations. The postshock values are then:
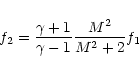 |
(14) |
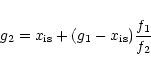 |
(15) |
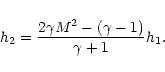 |
(16) |
Even if the flow velocity has not converged to the
coordinate velocity, an inner shock may not exist. This can occur if the
mass loading interior to the proposed position of the inner shock is
strong, resulting in M1 being less than unity. In such a scenario, the
jump conditions are not applied and the integration proceeds as before.
At the CD, we must also satisfy conservation of momentum. We take
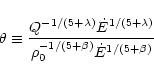 |
(17) |
as a measure of the ablated mass to the mass in the swept-up
shell. It follows that at the contact discontinuity,
![\begin{displaymath}%
\theta = \left(\frac{(\gamma-1) h}{x^{\beta}\left[g^{2} - \...
...mbda}
{(5+\lambda)(3+\beta)} xg\right]}\right)^{1/(5+\beta)}.
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img82.gif) |
(18) |
The rate of massloss from the star is
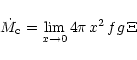 |
(19) |
where
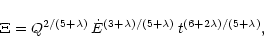 |
(20) |
which differs from the definition in the conductively driven
case.
The mass loading parameter 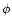 ,
which is a measure of the ratio of
ablated mass to wind mass is given by
,
which is a measure of the ratio of
ablated mass to wind mass is given by
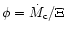 .
.
Table 1:
The influence of
 on solutions with
on solutions with
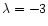 .
Two
cases are considered: minor mass loading (
.
Two
cases are considered: minor mass loading (
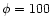 )
whereby the
value of
)
whereby the
value of
 is relatively unimportant, and appreciable mass loading
(
is relatively unimportant, and appreciable mass loading
(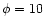 )
where
)
where
 exerts a major influence.
From left to right, the columns
indicate: i) the value of
exerts a major influence.
From left to right, the columns
indicate: i) the value of
 ,
ii) the ratio of the shock radii and CD,
iii-vi) the fractions of energy that are thermal and kinetic
in the bubble, kinetic in the swept-up shell, and radiated,
vii) the value of
,
ii) the ratio of the shock radii and CD,
iii-vi) the fractions of energy that are thermal and kinetic
in the bubble, kinetic in the swept-up shell, and radiated,
vii) the value of 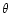 ,
viii) the ratio of mass within the bubble to the total mass injected by
the wind (values greater than unity indicate mass loading), ix) the ratio
of mass in
the swept-up shell to mass in the bubble, x) the preshock Mach number
of the unshocked wind.
,
viii) the ratio of mass within the bubble to the total mass injected by
the wind (values greater than unity indicate mass loading), ix) the ratio
of mass in
the swept-up shell to mass in the bubble, x) the preshock Mach number
of the unshocked wind.
 |
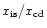 |
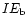 |
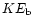 |
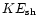 |
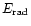 |
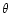 |
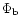 |
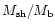 |
M1 |
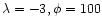 |
|
|
|
|
|
|
|
|
|
| 0.1 |
0.271 |
0.46 |
0.014 |
0.469 |
0.059 |
102 |
1.454 |
376 |
4.79 |
| 0.2 |
0.268 |
0.46 |
0.013 |
0.469 |
0.059 |
101 |
1.371 |
390 |
4.79 |
| 0.33 |
0.266 |
0.46 |
0.013 |
0.469 |
0.059 |
99.7 |
1.289 |
408 |
5.00 |
| 0.5 |
0.268 |
0.46 |
0.013 |
0.469 |
0.059 |
99.2 |
1.223 |
426 |
5.56 |
| 0.9 |
0.264 |
0.46 |
0.013 |
0.469 |
0.059 |
99.0 |
1.152 |
450 |
11.9 |
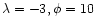 |
|
|
|
|
|
|
|
|
|
| 0.02 |
0.82 |
0.17 |
0.63 |
0.18 |
0.022 |
2.95 |
6.50 |
0.51 |
1.60 |
| 0.1 |
0.76 |
0.22 |
0.53 |
0.22 |
0.028 |
2.95 |
4.48 |
0.80 |
1.45 |
| 0.2 |
0.73 |
0.24 |
0.49 |
0.24 |
0.030 |
2.90 |
3.84 |
0.92 |
1.34 |
| 0.5 |
0.66 |
0.25 |
0.45 |
0.27 |
0.033 |
2.67 |
2.55 |
1.23 |
1.12 |
| 0.9 |
0.67 |
0.24 |
0.39 |
0.33 |
0.041 |
2.85 |
1.75 |
2.17 |
2.53 |
2.2 Scale transformation and normalization
The dimensionless Eqs. (10)-(12) are invariant
under the following transformation, which we shall call a normalization:
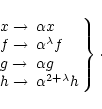 |
(21) |
These can be combined to obtain the normalizations for the
mass, and for the kinetic and internal energies of the bubble:
![\begin{displaymath}%
m = 4 \pi \int f x^{2} {\rm d}x
\hspace{15mm} [\alpha^{3+\lambda}]
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img95.gif) |
(22) |
![\begin{displaymath}%
k = 4 \pi \int \frac{1}{2} f g^{2} x^{2} {\rm d}x
\hspace{10mm} [\alpha^{5+\lambda}]
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img96.gif) |
(23) |
![\begin{displaymath}%
i = 4 \pi \int h x^{2} {\rm d}x
\hspace{17mm} [\alpha^{5+\lambda}].
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img97.gif) |
(24) |
The full equation for the mass in the bubble is:
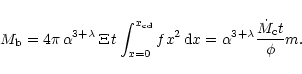 |
(25) |
The total mass lost by the star during its lifetime is
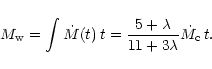 |
(26) |
The degree of mass loading in the bubble,
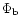 ,
is defined
as the ratio
,
is defined
as the ratio
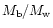 .
The mass-swept up into the shell,
.
The mass-swept up into the shell,
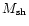 ,
the ratio of swept-up mass to bubble mass,
,
the ratio of swept-up mass to bubble mass,
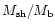 ,
the kinetic energy of the shell,
,
the kinetic energy of the shell,
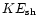 ,
and the pdV work on the
shocked ambient gas, are all identical to the corresponding forms in
PDH.
,
and the pdV work on the
shocked ambient gas, are all identical to the corresponding forms in
PDH.
2.3 Solution procedure
If an inner shock exists, three main parameters determine
the form of a given similarity solution (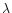 ,
,
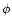 and
and
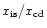 ). However, the ratio of the radius of the onset of
mass loading to the radius of the inner shock is an additional parameter
unique to the ablative solutions, and its value (
). However, the ratio of the radius of the onset of
mass loading to the radius of the inner shock is an additional parameter
unique to the ablative solutions, and its value (
 )
may also
influence the form of the solution. We find that if the mass loading of
the bubble is minor,
)
may also
influence the form of the solution. We find that if the mass loading of
the bubble is minor,
 has relatively little influence, and
vice-versa (since
has relatively little influence, and
vice-versa (since
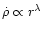 and
and
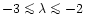 for most of the solutions presented,
most of the mass-loading occurs close to the minimum mass-loading radius).
Alternatively, if an inner shock does not exist,
for most of the solutions presented,
most of the mass-loading occurs close to the minimum mass-loading radius).
Alternatively, if an inner shock does not exist,
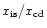 and
and
 have no meaning as we have defined them.
In this case we report the ratio of the onset radius of
mass loading to the radius of the contact discontinuity as the parameter
have no meaning as we have defined them.
In this case we report the ratio of the onset radius of
mass loading to the radius of the contact discontinuity as the parameter
 .
.
The ratio of mass pick-up from the clumps to the mass swept-up from the
interclump medium (which is related to the value of 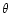 )
is
obtained only after a particular solution has been found. For bubbles whose
evolution is significantly altered by mass loading, we require that
simultaneously
)
is
obtained only after a particular solution has been found. For bubbles whose
evolution is significantly altered by mass loading, we require that
simultaneously 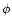 and
and 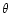 are both small.
are both small.
The similarity equations were integrated with a fifth-order accurate
adaptive step-size Bulirsch-Stoer method using polynomial
extrapolation to infinitesimal step size. Once the CD was reached,
the similarity variables were rescaled
using the relationships defined in Eq. (21) so
that
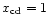 .
The mass, and kinetic and thermal energies
of the bubble were calculated, as were the kinetic energy of the shell
and the energy radiated from it. The correct normalization to satisfy
global energy conservation was then obtained. Finally, for given values of
.
The mass, and kinetic and thermal energies
of the bubble were calculated, as were the kinetic energy of the shell
and the energy radiated from it. The correct normalization to satisfy
global energy conservation was then obtained. Finally, for given values of
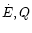 and t, the similarity variables x, f, g and h may be
scaled into the physical variables
and t, the similarity variables x, f, g and h may be
scaled into the physical variables
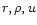 and
and
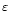 .
.
3 Results
We first checked our work against the solutions obtained by Dyson
(1973) for WBBs with no mass loading. For this comparison it was
required that
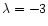 and that
and that 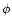 was large. For
was large. For
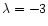 the radius of minimum mass loading increases as t.
Excellent agreement with Dyson (1973) was found
over a large range of
the radius of minimum mass loading increases as t.
Excellent agreement with Dyson (1973) was found
over a large range of
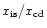 .
For large
.
For large 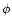 (i.e. negligible
mass loading) the value of
(i.e. negligible
mass loading) the value of
 has no effect on the resulting
solution. Figure 1 shows a sample solution.
has no effect on the resulting
solution. Figure 1 shows a sample solution.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f2.eps} %
\end{figure}](/articles/aa/full/2001/27/aa1222/Timg106.gif) |
Figure 2:
Results for
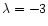 , ,
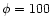 ,
and various values
of ,
and various values
of
 .
For these parameters the mass loading is small but
non-negligible, and hence demonstrates .
For these parameters the mass loading is small but
non-negligible, and hence demonstrates
 having a minor influence
on the results. Results for five values of
having a minor influence
on the results. Results for five values of
 are shown: 0.1 (solid),
0.2 (dots), 0.33 (dashes), 0.5 (dot-dash), and 0.9 (dot-dot-dot-dash).
The panels are the same as in Fig. 1. In Fig. 3 we
show solutions where the value of
are shown: 0.1 (solid),
0.2 (dots), 0.33 (dashes), 0.5 (dot-dash), and 0.9 (dot-dot-dot-dash).
The panels are the same as in Fig. 1. In Fig. 3 we
show solutions where the value of
 has a much greater influence.
has a much greater influence. |
| Open with DEXTER |
In Fig. 2 we show results for
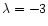 ,
,
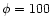 ,
with different values of
,
with different values of
 .
The mass loading in these results is
small, but not negligible, so that the precise value of
.
The mass loading in these results is
small, but not negligible, so that the precise value of
 has
minor consequences for the
solution obtained. In Table 1 we tabulate important
parameters from these solutions. In particular, we find that values for
the ratio
has
minor consequences for the
solution obtained. In Table 1 we tabulate important
parameters from these solutions. In particular, we find that values for
the ratio
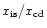 and
the energy fractions are very similar. The fractional mass loading of
the bubble,
and
the energy fractions are very similar. The fractional mass loading of
the bubble,
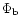 ,
is somewhat more sensitive to the value of
,
is somewhat more sensitive to the value of
 ,
and increases when the "turn-on'' radius for mass loading is decreased, as
one would expect. The preshock Mach number also reflects the degree of
preshock mass loading, again as expected. Interestingly, the profiles
of postshock Mach number are, however, very insensitive to the preshock
Mach number. With the assumption of constant
,
and increases when the "turn-on'' radius for mass loading is decreased, as
one would expect. The preshock Mach number also reflects the degree of
preshock mass loading, again as expected. Interestingly, the profiles
of postshock Mach number are, however, very insensitive to the preshock
Mach number. With the assumption of constant 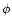 ,
we note that since
,
we note that since
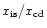 varies for the above results it was important to see
whether this was a possible factor for some of the differences in these
solutions. Therefore we also investigated the effect of different values
of
varies for the above results it was important to see
whether this was a possible factor for some of the differences in these
solutions. Therefore we also investigated the effect of different values
of
 whilst keeping
whilst keeping
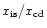 constant and varying
constant and varying 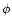 as
necessary. We find
that the resulting solutions are again fairly similar, and differ at about
the same level as the results in the top half of Table 1.
Therefore it seems that varying
as
necessary. We find
that the resulting solutions are again fairly similar, and differ at about
the same level as the results in the top half of Table 1.
Therefore it seems that varying
 has a direct effect on the
results, and not just an indirect influence through changes induced in
has a direct effect on the
results, and not just an indirect influence through changes induced in
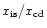 and/or
and/or 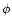 .
In the following, therefore, we will vary
.
In the following, therefore, we will vary
 whilst keeping
whilst keeping 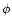 fixed.
fixed.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f3.eps} %
\end{figure}](/articles/aa/full/2001/27/aa1222/Timg107.gif) |
Figure 3:
Results for
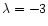 , ,
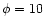 ,
and various values
of ,
and various values
of
 .
For this value of .
For this value of 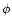 ,
the mass loading is appreciable,
and hence the solutions shown demonstrate ,
the mass loading is appreciable,
and hence the solutions shown demonstrate
 having a major influence.
Results for four values of
having a major influence.
Results for four values of
 are shown: 0.02 (solid), 0.1 (dots),
0.5 (dot-dash), and 0.9 (dot-dot-dot-dash).
The panels again represent density, velocity, internal energy and Mach number.
are shown: 0.02 (solid), 0.1 (dots),
0.5 (dot-dash), and 0.9 (dot-dot-dot-dash).
The panels again represent density, velocity, internal energy and Mach number. |
| Open with DEXTER |
At the other extreme, Fig. 3 shows results where the value
of
 can have large consequences for the solutions obtained. This
occurs for values of
can have large consequences for the solutions obtained. This
occurs for values of 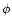 for which the resulting mass loading of the bubble
is important. Parameters from these solutions are tabulated in the lower
half of Table 1.
Although the ratio
for which the resulting mass loading of the bubble
is important. Parameters from these solutions are tabulated in the lower
half of Table 1.
Although the ratio
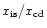 remains relatively insensitive to the
value of
remains relatively insensitive to the
value of
 ,
the fractional mass loading
,
the fractional mass loading
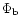 ,
the ratio of the
shell mass to the bubble mass
,
the ratio of the
shell mass to the bubble mass
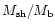 ,
and the energy partition are
all significantly affected, as Table 1 shows. This is
expected given that most of the mass loading occurs near the minimum mass
loading radius for
,
and the energy partition are
all significantly affected, as Table 1 shows. This is
expected given that most of the mass loading occurs near the minimum mass
loading radius for
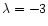 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f4.eps} %
\end{figure}](/articles/aa/full/2001/27/aa1222/Timg108.gif) |
Figure 4:
Results for
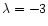 , ,
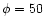 .
Here mass loading is
so severe that the flow directly connects to the contact discontinuity.
For the solution
shown, the onset of mass loading occurs at .
Here mass loading is
so severe that the flow directly connects to the contact discontinuity.
For the solution
shown, the onset of mass loading occurs at
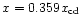 .
Once
the flow starts mass loading, its velocity drops, its relative density
increases, its kinetic energy drops, and its thermal energy increases. .
Once
the flow starts mass loading, its velocity drops, its relative density
increases, its kinetic energy drops, and its thermal energy increases. |
| Open with DEXTER |
An interesting consequence of mass loading the wind prior to the inner shock
is that if the mass loading is large, the Mach number of the flow can be
reduced so much that the flow directly connects to the contact discontinuity
without the presence of an inner shock. In Fig. 4
we show one solution where this happens. In this example,
the flow is continuously supersonic with respect to the clumps, and we
obtain
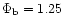 and
and
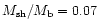 .
This perhaps indicates
that this morphology is most favoured at early stages of the evolution of
the bubble before a significant amount of ambient medium is swept-up. In
another example of "direct connection'', we find a solution where the Mach
number of the flow with respect to the clumps drops below unity (see
panel f of Fig. 6). In this case,
.
This perhaps indicates
that this morphology is most favoured at early stages of the evolution of
the bubble before a significant amount of ambient medium is swept-up. In
another example of "direct connection'', we find a solution where the Mach
number of the flow with respect to the clumps drops below unity (see
panel f of Fig. 6). In this case,
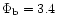 and
and
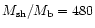 ,
suggesting a much older bubble.
We also find that low values of
,
suggesting a much older bubble.
We also find that low values of 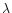 (
(
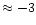 )
are apparently
needed to obtain directly-connected solutions.
)
are apparently
needed to obtain directly-connected solutions.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f5.eps} %
\end{figure}](/articles/aa/full/2001/27/aa1222/Timg115.gif) |
Figure 5:
Comparison of solutions with negligible (solid)
and high (dots) mass loading rates, for a given value of 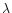 (-2) and
(-2) and
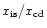 (0.606). The ratio of swept-up mass to bubble mass is
12.3 and 0.96 respectively, whilst the ratio of ablated mass to wind mass is
7.54 for the mass-loaded solution. The preshock Mach number for the
mass-loaded solution is 1.006. In both cases, the similarity solution has
been scaled such that the current wind parameters are appropriate for a
WR star:
(0.606). The ratio of swept-up mass to bubble mass is
12.3 and 0.96 respectively, whilst the ratio of ablated mass to wind mass is
7.54 for the mass-loaded solution. The preshock Mach number for the
mass-loaded solution is 1.006. In both cases, the similarity solution has
been scaled such that the current wind parameters are appropriate for a
WR star:
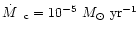 and
and
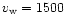 km s-1. km s-1. |
| Open with DEXTER |
In Fig. 5 we compare solution profiles for the
case where
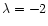 and for negligible and high mass loading rates.
A
and for negligible and high mass loading rates.
A
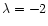 clump distribution is the most physically
plausible for many astrophysical objects. For this distribution
the minimum mass loading radius increases as t2/3, which is not far
removed from a linear increase with t.
The solutions have been scaled from the similarity results by assuming
current values for the wind parameters appropriate for a WR star:
clump distribution is the most physically
plausible for many astrophysical objects. For this distribution
the minimum mass loading radius increases as t2/3, which is not far
removed from a linear increase with t.
The solutions have been scaled from the similarity results by assuming
current values for the wind parameters appropriate for a WR star:
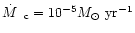 and
and
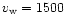 km s-1. The mass-loss rate
increases with time as t2/3 whilst the wind velocity decreases as
t-1/3, so the wind has evolved from a case more suitable to an O-star.
The assumed bubble age is
t = 104 yr. The interclump medium varies
as
km s-1. The mass-loss rate
increases with time as t2/3 whilst the wind velocity decreases as
t-1/3, so the wind has evolved from a case more suitable to an O-star.
The assumed bubble age is
t = 104 yr. The interclump medium varies
as
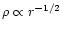 (i.e.
(i.e.
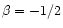 )
which is a flatter
distribution than for a constant velocity wind (r-2). However,
since the wind mass-loss rate is increasing and the velocity decreasing,
an r-1/2 interclump density profile is physically realistic for
such a scenario.
In comparison with the negligibly mass-loaded solution, the increase in
density inside the bubble for the highly mass-loaded solution can be
clearly seen, along with a decrease in preshock velocity, preshock Mach
number, and postshock temperature. Interestingly, the Mach number of the
postshock flow is higher for the heavily mass-loaded solution.
Note also that the heavily mass-loaded solution extends to a larger bubble
radius. This is a consequence of the different preshock interclump densities:
for the heavily mass-loaded solution
)
which is a flatter
distribution than for a constant velocity wind (r-2). However,
since the wind mass-loss rate is increasing and the velocity decreasing,
an r-1/2 interclump density profile is physically realistic for
such a scenario.
In comparison with the negligibly mass-loaded solution, the increase in
density inside the bubble for the highly mass-loaded solution can be
clearly seen, along with a decrease in preshock velocity, preshock Mach
number, and postshock temperature. Interestingly, the Mach number of the
postshock flow is higher for the heavily mass-loaded solution.
Note also that the heavily mass-loaded solution extends to a larger bubble
radius. This is a consequence of the different preshock interclump densities:
for the heavily mass-loaded solution
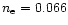 ,
whilst
,
whilst
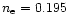 for the negligibly mass-loaded solution.
for the negligibly mass-loaded solution.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{fig6.eps}\end{figure}](/articles/aa/full/2001/27/aa1222/Timg121.gif) |
Figure 6:
The Mach number as a function of x for a number of different
solutions. With respect to the clumps, the shocked region can be either
entirely subsonic, entirely supersonic, or have one (or maybe more)
sonic points.
The panels show: a) shocked region with a monotonic
decrease in Mach number (
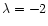 , ,
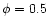 , ,
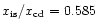 , ,
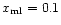 ); b) shocked region entirely supersonic with
a monotonic increase in Mach number ( ); b) shocked region entirely supersonic with
a monotonic increase in Mach number (
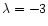 , ,
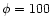 , ,
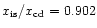 , ,
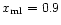 ); c) postshock Mach
number initially subsonic and decreasing, before levelling off and
subsequently increasing through a sonic point ( ); c) postshock Mach
number initially subsonic and decreasing, before levelling off and
subsequently increasing through a sonic point (
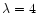 , ,
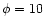 , ,
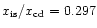 , ,
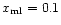 ); d) shocked region entirely
subsonic with a decreasing Mach number followed by a modest increase close
to the contact discontinuity ( ); d) shocked region entirely
subsonic with a decreasing Mach number followed by a modest increase close
to the contact discontinuity (
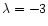 , ,
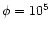 , ,
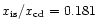 , ,
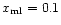 ); e) postshock flow
continuously supersonic though with an initial decrease in Mach number
( ); e) postshock flow
continuously supersonic though with an initial decrease in Mach number
(
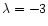 , ,
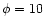 , ,
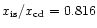 , ,
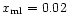 ); f) continuously supersonic flow (solid) directly
connected to the contact discontinuity ( i.e. no inner shock)
( ); f) continuously supersonic flow (solid) directly
connected to the contact discontinuity ( i.e. no inner shock)
(
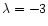 , ,
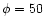 , ,
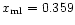 )
and a
flow becoming subsonic (dots) directly connected to the contact discontinuity
( )
and a
flow becoming subsonic (dots) directly connected to the contact discontinuity
(
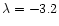 , ,
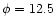 , ,
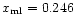 ). ). |
| Open with DEXTER |
In PDH it was shown that there is a
negative feed-back mechanism caused by the evaporation of mass from
embedded clumps, which set a maximum limit to the amount that a bubble
could be massloaded. Additionally, for the bubble mass to be greater than
the mass of the swept-up shell, a large radial dependence of the
mass loading was required (
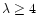 ). In this work we instead
find that small values of
). In this work we instead
find that small values of 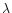 are required to satisfy this condition.
Our simulations show that it is impossible to obtain a similarity solution
with
are required to satisfy this condition.
Our simulations show that it is impossible to obtain a similarity solution
with
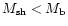 for
for
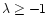 (e.g. for
(e.g. for
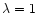 ,
,
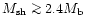 ). However, for smaller values of
). However, for smaller values of 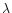 ,
solutions satisfying
,
solutions satisfying
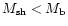 can be found (e.g. for
can be found (e.g. for
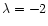 (-3), we can obtain
(-3), we can obtain
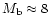 (29)
(29)
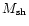 ,
where
,
where
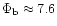 (15)).
For a given value of
(15)).
For a given value of
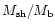 there appears to be a maximum
value for
there appears to be a maximum
value for
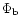 .
It occurs when mass loading
starts very close to the bubble centre (i.e.
.
It occurs when mass loading
starts very close to the bubble centre (i.e.
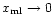 )
and
when the flow remains supersonic relative to the clumps over the entire
bubble radius.
)
and
when the flow remains supersonic relative to the clumps over the entire
bubble radius.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS1222f7.eps}\end{figure}](/articles/aa/full/2001/27/aa1222/Timg130.gif) |
Figure 7:
Radial profiles of emissivity per unit volume and temperature,
normalized to values of 1.0 at the limb. The upper panels show results
where an inner shock is present, whilst the bottom
panels show results where the mass loading region directly connects to the
contact discontinuity. For the upper panels the results shown are for:
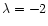 , ,
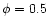 , ,
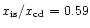 , ,
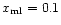 (solid);
(solid);
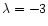 , ,
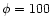 , ,
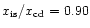 , ,
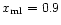 (dots);
(dots);
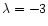 , ,
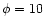 , ,
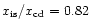 , ,
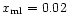 (dashes). For the lower panels the
results are for:
(dashes). For the lower panels the
results are for:
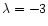 , ,
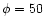 , ,
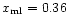 (solid);
(solid);
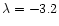 , ,
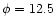 , ,
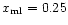 (dots).
(dots). |
| Open with DEXTER |
We have also investigated the Mach number profile of the solutions that
we obtain, of which some are already shown in Figs. 2
and 3. As for the evaporative mass loading in
PDH, we note that a number of different forms
are possible, and summarize these in Fig. 6.
Finally, radial profiles of the X-ray emissivity per unit volume and
temperature have been calculated (Fig. 7).
We assume that the emissivity
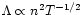 ,
which is a
good approximation over the temperature range
,
which is a
good approximation over the temperature range
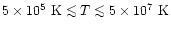 (cf. Kahn 1976). The upper
panels show results where an inner shock is present, and we will discuss these
first. The solution with the solid line displays relatively constant values
of
(cf. Kahn 1976). The upper
panels show results where an inner shock is present, and we will discuss these
first. The solution with the solid line displays relatively constant values
of  and T, and is characterized by a high degree of mass loading
(
and T, and is characterized by a high degree of mass loading
(
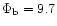 ). Note that the highest temperature in the bubble does
not occur postshock, but rather shortly after mass loading begins. The very
high emissivity at the onset of mass loading is a consequence of the low
temperature at this point and the assumed T-1/2 dependence of our
emissivity, and is not physical. The solution with the dotted line has an
interior dominated by free-expansion of the wind source. Mass loading
only occurs over the final 20 per cent of the radius, and is
relatively weak, and the maximum temperature in the bubble occurs
immediately postshock. The solution with the dashed line has some
characteristics of each of the other solutions. It is mass-loaded
from small radius which again leads to the maximum bubble temperature
occurring near the center. However, the mass loading is less severe
(
). Note that the highest temperature in the bubble does
not occur postshock, but rather shortly after mass loading begins. The very
high emissivity at the onset of mass loading is a consequence of the low
temperature at this point and the assumed T-1/2 dependence of our
emissivity, and is not physical. The solution with the dotted line has an
interior dominated by free-expansion of the wind source. Mass loading
only occurs over the final 20 per cent of the radius, and is
relatively weak, and the maximum temperature in the bubble occurs
immediately postshock. The solution with the dashed line has some
characteristics of each of the other solutions. It is mass-loaded
from small radius which again leads to the maximum bubble temperature
occurring near the center. However, the mass loading is less severe
(
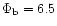 )
and its radial dependence steeper (
)
and its radial dependence steeper (
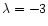 )
than
for the solution with the solid line, so that there is a large fall in
density between the switch-on radius for mass loading and
)
than
for the solution with the solid line, so that there is a large fall in
density between the switch-on radius for mass loading and
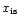 .
This leads
to a steep rise in emissivity from the inner shock to the bubble center in
a similar fashion to the solution with the dotted line.
.
This leads
to a steep rise in emissivity from the inner shock to the bubble center in
a similar fashion to the solution with the dotted line.
The bottom panels of Fig. 7 show results where there is no
inner shock and where the mass loading region directly connects to the
contact discontinuity. The Mach number profiles for these solutions are
displayed in the bottom-right panel of Fig. 6. As
can be seen, the temperature profiles are approximately flat over their
respective mass loading regions, and are very similar in shape to each other.
This contrasts with the behaviour of their emissivity profiles, where it
is clear that the solution represented by the solid (dotted) line has
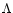 generally decreasing (increasing) with radius.
generally decreasing (increasing) with radius.
A general result from Fig. 7, which was also found in the
evaporatively mass-loaded bubbles of PDH, is that higher mass loading
tends to decrease the central emissivity and increase the
central temperature relative to the limb.
3.1 Comparison with observations and other theoretical work
Although our work cannot be directly compared to the hydrodynamic
simulations of Arthur et al. (1993, 1996), a number
of similarities exist. These include a sharp increase in temperature
at the onset of mass loading, and often
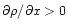 over the mass-loaded region. A noticeable achievement of the work of
Arthur et al. (1996) was the reproduction of the observed correlation
between the velocity and ionization potential of ultraviolet absorption
features towards the central star (Smith et al. 1984). Our
solutions also often reproduce this correlation (e.g. see
Fig. 5 which shows the velocity and temperature
decreasing together for the heavily mass-loaded solution), as do those
of Hanami & Sakashita (1987). Interestingly, solutions with
mass-loading from conductive evaporation of the swept-up shell do not
reproduce this correlation (see Weaver et al. 1977).
over the mass-loaded region. A noticeable achievement of the work of
Arthur et al. (1996) was the reproduction of the observed correlation
between the velocity and ionization potential of ultraviolet absorption
features towards the central star (Smith et al. 1984). Our
solutions also often reproduce this correlation (e.g. see
Fig. 5 which shows the velocity and temperature
decreasing together for the heavily mass-loaded solution), as do those
of Hanami & Sakashita (1987). Interestingly, solutions with
mass-loading from conductive evaporation of the swept-up shell do not
reproduce this correlation (see Weaver et al. 1977).
4 Summary
We have investigated the evolution of a mass-loaded wind blown bubble
with a constant rate of injection of mechanical energy from a central wind
source. The mass loading occurs due to the
hydrodynamic ablation of distributed clumps, and is "switched-on'' at a
specified radius, interior to which the wind expands freely.
The requirement that the solution be self-similar imposes a link
between the radial variation of the interclump density
(
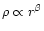 )
and the rate of mass loading from the clumps
(
)
and the rate of mass loading from the clumps
(
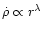 )
which forces
)
which forces
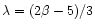 .
.
We first produced solutions with negligible mass loading and 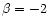 (which correspond to constant
(which correspond to constant
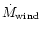 and
and
 ),
which we compared with results obtained by Dyson (1973).
Excellent agreement for the structure of the bubble was found.
We also confirmed that for negligible mass loading, the value of
),
which we compared with results obtained by Dyson (1973).
Excellent agreement for the structure of the bubble was found.
We also confirmed that for negligible mass loading, the value of
 had no effect on the resulting solutions, as desired.
had no effect on the resulting solutions, as desired.
We then investigated the changes in the structure of the bubble for
different values of  ,
,
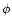 ,
,
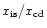 ,
and
,
and
 .
The central conclusions are:
.
The central conclusions are:
- Substantial mass loading of the wind-blown bubble can occur over
a wide range of
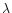 .
However, to additionally satisfy
the requirement that the bubble mass is larger than the mass of
the swept-up shell, low values of
.
However, to additionally satisfy
the requirement that the bubble mass is larger than the mass of
the swept-up shell, low values of 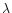 are needed (e.g.
are needed (e.g.
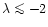 ).
).
- The profiles of the flow variables are significantly altered under
conditions of large mass loading. With respect to solutions with negligible
mass loading, the density and temperature profiles increase, and the
velocity and Mach number profiles drop. Changes to the profiles can be
very rapid. Mass loading of the wind also reduces the Mach number prior
to the inner shock.
- The mass-loaded wind may also connect directly to the contact
discontinuity without the need for a global inner shock.
- The Mach number of the flow relative to the
clumps which are injecting the mass can take several different forms.
The flow can be either entirely supersonic, or have one (or maybe more)
sonic points.
- Whilst mass loading reduces the bubble temperature, it also
tends to reduce the emissivity in the interior of the
bubble relative to its limb, whilst simultaneously increasing the central
temperature relative to the limb temperature. The maximum temperature in
the bubble is often not the post-inner-shock temperature, but occurs near
the onset of mass loading. In some cases this can be many times greater
than the post-inner-shock temperature.
Acknowledgements
JMP would like to thank PPARC for the funding of a PDRA position, and
Sam Falle and Rob Coker for helpful discussions. We would also like
to thank an anonymous referee whose suggestions improved this paper. This
work has made use of Nasa's Astrophysics Data System Abstract Service.
- Arthur, S. J., Dyson, J. E., & Hartquist, T. W. 1993,
MNRAS, 261, 425
In the text
NASA ADS
- Arthur, S. J., Dyson, J. E., & Hartquist, T. W. 1994,
MNRAS, 269, 1117
In the text
NASA ADS
- Arthur, S. J., Henney, W. J., & Dyson, J. E. 1996,
A&A, 313, 897
In the text
NASA ADS
- Borkowski, K. J., Harrington, J. P., & Tsvetanov, Z. I. 1995, ApJ, 449, L143
In the text
NASA ADS
- Chièze, J. P., & Lazareff, B. 1981, A&A, 95, 194
In the text
NASA ADS
- Cowie, L. L., & McKee, C. F. 1977, ApJ, 211, 135
In the text
NASA ADS
- David, L. P., & Durisen, R. H. 1989, ApJ, 346, 618
In the text
- Durisen, R. H., & Burns, J. O. 1981, MNRAS, 195, 535
In the text
NASA ADS
- Dyson, J. E. 1973, A&A, 23, 381
In the text
NASA ADS
- Dyson, J. E., & de Vries, J. 1972, A&A, 20, 223
In the text
NASA ADS
- Dyson, J. E., & Hartquist, T. W. 1987, MNRAS, 228, 453
In the text
NASA ADS
- Dyson, J. E., & Hartquist, T. W. 1992, Ap. Lett. Comm.,
28, 301
In the text
- Dyson, J. E., Williams, R. J. R., & Redman, M. P. 1995,
MNRAS, 237, 700
In the text
NASA ADS
- Hanami, H., & Sakahita, S. 1987, A&A, 181, 343
In the text
NASA ADS
- Hartquist, T. W., Dyson, J. E., Pettini, M.,
& Smith, L. J. 1986, MNRAS, 221, 715
In the text
NASA ADS
- Hartquist, T. W., & Dyson, J. E. 1993, QJRAS, 34, 57
In the text
NASA ADS
- Kahn, F. D. 1976, A&A, 50, 145
In the text
NASA ADS
- Klein, R. I., McKee, C. F., & Colella, P. 1994, ApJ,
420, 213
In the text
NASA ADS
- McKee, C. F., & Cowie, L. L. 1977, ApJ, 215, 213
In the text
NASA ADS
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148
In the text
NASA ADS
- Meaburn, J., Clayton, C. A., Bryce, M., & Walsh, J. R.
1996, MNRAS, 281, L57
In the text
NASA ADS
- Meaburn, J., Nicholson, R. A., Bryce, M.,
Dyson, J. E., & Walsh, J. R. 1991, MNRAS, 252, 535
In the text
NASA ADS
- Pittard, J. M., Dyson, J. E., & Hartquist, T. W. 2001,
A&A, 367, 1000
In the text
NASA ADS
- Smith, L. J., Pettini, M., Dyson, J. E.,
& Hartquist, T. W. 1984, MNRAS, 211, 679
In the text
NASA ADS
- Strickland, D. K., & Stevens, I. R. 2000, MNRAS, 314, 511
In the text
NASA ADS
- Toniazzo, T., Hartquist, T. W., & Durisen, R. H. 2001,
MNRAS, 322, 149
In the text
NASA ADS
- Weaver, R., McCray, R., Castor, J., Shapiro, P.,
& Moore, R. 1977, ApJ, 218, 377
In the text
NASA ADS
- Williams, R. J. R., Dyson, J. E., & Hartquist, T. W. 1999,
A&A, 344, 675
In the text
NASA ADS
- Williams, R. J. R., Hartquist, T. W., & Dyson, J. E. 1995,
ApJ, 446, 759
In the text
NASA ADS
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f1.eps}\end{figure}](/articles/aa/full/2001/27/aa1222/Timg41.gif)
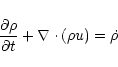
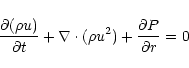
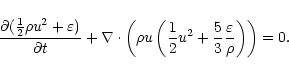
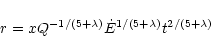
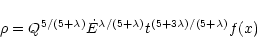
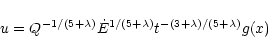
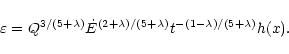
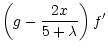
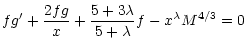
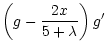
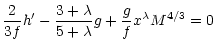
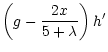
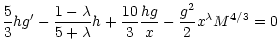
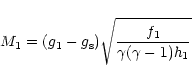
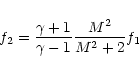
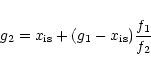
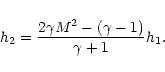
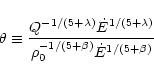
![\begin{displaymath}%
\theta = \left(\frac{(\gamma-1) h}{x^{\beta}\left[g^{2} - \...
...mbda}
{(5+\lambda)(3+\beta)} xg\right]}\right)^{1/(5+\beta)}.
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img82.gif)
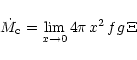
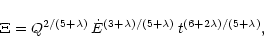
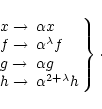
![\begin{displaymath}%
m = 4 \pi \int f x^{2} {\rm d}x
\hspace{15mm} [\alpha^{3+\lambda}]
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img95.gif)
![\begin{displaymath}%
k = 4 \pi \int \frac{1}{2} f g^{2} x^{2} {\rm d}x
\hspace{10mm} [\alpha^{5+\lambda}]
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img96.gif)
![\begin{displaymath}%
i = 4 \pi \int h x^{2} {\rm d}x
\hspace{17mm} [\alpha^{5+\lambda}].
\end{displaymath}](/articles/aa/full/2001/27/aa1222/img97.gif)
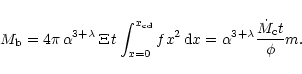
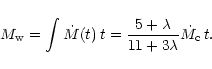
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f2.eps} %
\end{figure}](/articles/aa/full/2001/27/aa1222/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f3.eps} %
\end{figure}](/articles/aa/full/2001/27/aa1222/Timg107.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f4.eps} %
\end{figure}](/articles/aa/full/2001/27/aa1222/Timg108.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{MS1222f5.eps} %
\end{figure}](/articles/aa/full/2001/27/aa1222/Timg115.gif)
![\begin{figure}
\par\includegraphics[width=10cm,clip]{fig6.eps}\end{figure}](/articles/aa/full/2001/27/aa1222/Timg121.gif)
![\begin{figure}
\par\includegraphics[width=10cm,clip]{MS1222f7.eps}\end{figure}](/articles/aa/full/2001/27/aa1222/Timg130.gif)