A&A 373, 1099-1109 (2001)
DOI: 10.1051/0004-6361:20010941

Systematic relations between the HIPPARCOS catalogue and major (fundamental) catalogues
of the 20th century (Paper I)

H. Schwan[*]

Astronomisches Rechen-Institut, Moenchhofstrasse 12-14, 69120 Heidelberg, Germany

Received 22 February 2001 / Accepted 2 May 2001

Abstract
This paper presents the systematic relations between the HIPPARCOS catalogue and some major catalogues of the 20th century, preferentially fundamental catalogues. These relations allow one to reduce observations given in the system of one of these catalogues to the HIPPARCOS system. Software for performing such a transition can be downloaded from http://www.ari.uni-heidelberg.de/fk6/sysdiff. It is planned to add more catalogues from time to time.

Key words: reference systems - systematic differences - HIPPARCOS catalogue - fundamental catalogues


1 Introduction

The HIPPARCOS catalogue by the European Space Agency ESA (1997) has provided a reference system in optical wave-lengths which coincides globally (i.e. with respect to the orientation of the coordinate axes) with the International Celestial Reference System (ICRS) at a positional accuracy of about $\pm 0.6$ mas at the epoch 1991.25 and of about $\pm 0.25$ mas/yr for the proper motions (see HIPPARCOS catalogue, Vol. 1, p. 22). In addition, the HIPPARCOS system is expected to be free of regional systematic errors at the level of 0.1-0.2 mas (HIPPARCOS catalogue, Vol. III, p. 415) at the mean epoch 1991.25 of the HIPPARCOS observations, a level much lower than for any other existing catalogue. The internal precision of the HIPPARCOS positions at 1991.25 (about 0.8 mas, averaged over both coordinates) is extremely high and the precision of the proper motions (about 0.9 mas/yr) is significantly superior to all catalogues preceding the FK5. This is a formal precision estimated from the internal consistency of the observations. It depends on the number of observations per star which is correlated with the position on the sphere.

In view of this highly accurate reference frame, the problem of how to reduce (old) observations into the HIPPARCOS system arises. Since a complete rediscussion of old observations will in most cases not be possible, there should be available at least practical means for transforming such positions (and proper motions, if available) from their original reference system to the HIPPARCOS system, thus providing data in a highly accurate and homogenous reference frame. In addition, it is of some historical interest to see the increase in systematic accuracy for the various fundamental systems in the course of the 20th century.

There are a few important catalogues which have served as reference systems in the 20th century. In this paper we start deriving and presenting the systematic differences between the HIPPARCOS catalogue and such ground based catalogues, beginning with the PGC (L. Boss 1910), the GC (B. Boss 1937), the N30 (Morgan 1952), the NFK (Peters 1907), the FK3 by Kopff (Part 1, 1937 and Part 2, 1938), the FK4 (Fricke & Kopff 1963), the FK5 Part 1 (Fricke et al. 1988), the FK5 Extension (Fricke et al. 1991), the supplementary stars to the FK5 (Schwan et al. 1993), the PPM North (Roeser & Bastian 1991), the PPM South (Bastian & Roeser 1993) and the Perth 70 catalogue (Hoeg et al. 1976).

There are other important catalogues such as the SAO (1968), the AGK3 (Heckmann & Dieckvoss 1975), the ACRS (Corbin & Urban 1991) or the IRS (Corbin 1991). These catalogues and other ones will be compared with the HIPPARCOS catalogue in a forthcoming Paper II.

The main purposes of the present paper are therefore first, to derive and present the systematic relations between the HIPPARCOS system and some major catalogues of the 20th century, second, to give information on the increase of systematic accuracy achieved in the 20th century, and third, to provide software for the transformation of observations given in one of these catalogue systems to the HIPPARCOS system.

The software will be made available via the internet at http://www.ari.uni-heidelberg.de/fk6/sysdiff

In Sect. 2 we discuss various sources of systematic errors, Sect. 3 describes the global corrections necessary for the reduction of astrometric catalogues to the IAU(1976) System of Astronomical Constants, in Sect. 4 we present the additional (regional) corrections depending on the right ascension, declination and apparent magnitude needed for the transition to the HIPPARCOS system, Sect. 5 describes the practical transformation of a fundamental and an observational catalogue, respectively, and Sect. 6 gives some numerical and graphical results. In using the wording HIPPARCOS system, we mean the HCRF as defined in the IAU resolution B1.2 adopted at the General Assembly in Manchester (IAU 2001). This resolution exludes all stars form the optical realization of the International Celestial Reference System which have shown up as problematic cases in the derivation of the HIPPARCOS catalogue.

2 Sources of systematic errors

There are several sources introducing systematic errors into astrometric catalogues. Some of these errors arise from errors in the constants used or from approximations in the procedure applied for the construction of a catalogue. With improved knowledge of these shortcomings, such errors can be modelled and eliminated a priori. Other errors arise from systematic errors in the original observations (e.g. effects of flexure or refraction not completely eliminated). These errors have to be determined by a statistical treatment of the catalogue positions and proper motions before they can be eliminated.

It is advantageous to first model and eliminate the systematic errors of the first type (errors which are, in principle, known a priori). Residual errors of this type are, in a second step, automatically treated and eliminated within the determination of systematic errors of the second type.

All statistically determined corrections in the following discussion are derived at the mean epoch of each respective catalogue, since the positions and proper motions are much less correlated at that epoch than at the HIPPARCOS epoch, where the comparatively large errors in the proper motion system of an "old'' catalogue would contribute significantly. In the case of observational catalogues without proper motions this is the only possible way in any case. The choice of the mean catalogue epoch as the preferred epoch of comparison has been discussed in more detail by Schwan (2001).

3 Global corrections (Transition to the IAU (1976) conventions)

In this section we describe the "a priori known'' systematic corrections. These corrections arise from the use of constants, zero points or reduction procedures (e.g. the treatment of elliptic aberration) different from the IAU (1976) System of Astronomical Constants (Trans. I.A.U. 16B, 58-60 (1976), Trans. I.A.U. 18B, 72 (1982)). The necessary corrections have to be applied to practically all catalogues preceding the FK5. There was much controversy in the past on how to transform from FK4 based positions and proper motions to ones based on the FK5 (which refers to the new IAU (1976) system). Since all these minor differences between the various procedures are automatically included and absorbed in the final determination of the regional systematic errors, we do not need to enter again those discussions.

The result of applying the following corrections is a catalogue which is in accordance with the conventions adopted with the IAU (1976) System of Astronomical Constants. The necessary corrections are as follows.

3.1 Elimination of the E-terms

All mean catalogue positions prior to the FK5 contain the so-called E-terms of elliptic aberration which depend on the excentricity of the Earth's orbit. Based on the expressions given in the "Explanatory Supplement'' (1961) we compute for the epoch and equinox $T_{\rm C}$ of the catalogue the longitude $\tilde{\omega}$ of the perihelion of the Earth's orbit, the excentricity e of the Earth's orbit and the obliquity $\epsilon$ of the ecliptic. With the quantities

\begin{displaymath}c_{0} = \kappa \, e \, \cos \tilde{\omega} \, \cos \,\epsilon \end{displaymath} (1)


\begin{displaymath}d_{0} = \kappa \, e \, \sin \tilde{\omega} \end{displaymath} (2)

($\kappa$ denotes the constant of aberration) and the star numbers

$ c \, = \cos \alpha / \cos \delta $

$ d \, = \sin \alpha / \cos \delta $

                  $ c'= \tan \alpha \, \cos \delta - \sin \alpha \, \sin \delta $

$ d' = \cos \alpha / \sin \delta $


we compute the corrections

\begin{displaymath}\Delta \alpha = c \cdot c_{0} + d \cdot d_{0} \end{displaymath} (3)


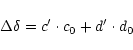\begin{displaymath}\Delta \delta = c' \cdot c_{0} + d' \cdot d_{0} \end{displaymath} (4)

which have to be subtracted from the catalogue positions (e.g. from an FK4 based position).

3.2 Precessional corrections

The adoption of a new precessional quantity implies a corresponding correction of the proper motions. From a comparison of the precessional expressions as defined in the IAU (1976) system with the formerly used Newcomb precession, we find the following corrections which have to be applied to the proper motions in catalogues based on the Newcomb precession:

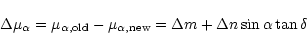\begin{displaymath}\Delta \mu_{\alpha} = \mu_{\alpha, {\rm old}} - \mu_{\alpha, {\rm new}} = \Delta m + \Delta n \sin \alpha \tan \delta \end{displaymath} (5)


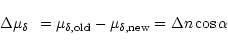\begin{displaymath}\Delta \mu_{\delta} \hspace*{1.5mm} = \mu_{\delta,{\rm old}} - \mu_{\delta,{\rm new}} = \Delta n \cos \alpha \end{displaymath} (6)

where

$\Delta m = m_{\rm new} - m_{\rm old} = 1\rlap.{''}0368 - 0\rlap.{''}00176 \tau - 0\rlap.{''}000398 \tau^{2} $

$\Delta n \hspace{1.0mm} = n_{\rm new} - n_{\rm old} \hspace{1.8mm} = 0\rlap.{''}4363 + 0\rlap.{''}00075 \tau + 0\rlap.{''}000153 \tau^{2}$


$m_{\rm new}, n_{\rm new}, (m_{\rm old}, n_{\rm old})$ are the new (old) rates of precession, $\tau$ is the time difference in Julian centuries between the epoch $T_{\rm C}$ of the catalogue equinox and J2000.

3.3 Equinox correction

The right ascensions and proper motions in right ascension in an astrometric catalogue should be referred to the dynamical equinox. In practice we find, however, that each catalogue has, more or less, a zero point deviating from the dynamical equinox. The reason is that there are considerable observational difficulties for the Solar System objects which have to be observed to relate the star positions to the dynamical equinox. The determination of the equinox correction was one of the major problems in the construction of the FK5 catalogue. The correction $ E = 0\rlap.{^{\rm s}}035 = 0\rlap.{''}525$ to the FK4 right ascensions at the epoch 1950 and the correction $ e = 0\rlap.{^{\rm s}}085$/cy to the FK4 proper motions in right ascension were finally adopted. This proper motion correction is also denoted as the "fictitious motion of the equinox''.

It may be useful to mention that the correction e of the "motion of the equinox'' and the precessional correction are highly correlated and partly cancel each other.

We have used in the following reduction procedure zero point corrections which are given either in the literature (see e.g. the introduction to the FK4 catalogue), or we have made an independent estimate by computing the mean differences HIPPARCOS - Catalogue in position and proper motion for the common stars in the equatorial zone. Some corrections were found to be of comparable size and near to the "classical'' corrections $0\rlap.{^{\rm s}}035$ and $0\rlap.{^{\rm s}}085/$cy which were used in the transition from the FK4 to the FK5. For all these catalogues we have adopted the "classical corrections''. The corrections E at the epoch $T_{\rm E}$ and e used for the various catalogues are given in Table 1. As already mentioned, any residual zero point correction is included either in an additional global rotation of the catalogue onto the HIPPARCOS system or finally in the determination of the regional systematic errors.

3.4 Change from tropical to Julian century

With the adoption of the Julian century instead of the tropical century, all proper motions in the "old'' catalogues have to be multiplied by the factor 1.000021356.

3.5 Transformation to J2000

The catalogue positions and proper motions obtained with the corrections described above are in the IAU (1976) System of Astronomical Constants. In a final step they are referred to the standard equinox J2000, and, in the case of a fundamental catalogue also, transformed to the epoch J2000 using the corrected proper motions in the catalogue. The new catalogue data have now the conventions of the IAU(1976) system of Astronomical Constants.


 

 
Table 1: Characteristic data in the reduction process of the various catalogues to the HIPPARCOS system.
 FK5BA FK5BXRS FK5FX FK4 FK3 NFK N30 PGC GC PPM Perth70
 
$N_{\rm tot} $1535 1987 2125 1535 1535 925 5268 6188 33342 378910 24900
$N_{\rm used, pos} $1151 1675 1859 1148 1149 626 5066 5906 19253 107425 22206
$N_{\rm used, pm } $1151 1687 1869 1168 1149 642 5179 5971 19109 108020 -
$T_{\rm C}$2000.0 2000.0 2000.0 1950.0 1950.0 1875.0 1950.0 1900.0 1950.0 2000.0 1950.0
T01949.4 1956.1 1940.1 1915.9 1903.3 1875.0 1930.0 1900.0 1900.9 1950.0 1970.0
$T_{\rm E}$- - - 1950.0 1950.0 1875.0 1950.0 1900.0 1950.0 - 1970.0
$\epsilon_{x}(T_{0}) $ [mas]-3.01 -5.61 +8.39 +5.25 +14.73 +19.98 -11.45 -6.45 0.00 +4.70 -11.74
$\epsilon_{y}(T_{0})$ [mas]-41.00 -34.97 -45.84 -65.67 -63.21 -55.38 -54.89 +65.74 0.00 -41.70 -27.31
$\epsilon_{z}(T_{0}) $ [mas]-19.12 -8.91 -23.72 -55.29 -82.93 +4.91 -4.88 -44.60 0.00 +11.00 +11.35
$\omega_{x}$ [mas/yr]-0.34 -0.54 -0.56 -0.43 -0.43 -0.16 -0.79 -0.16 0.00 -0.66 -
$\omega_{y}$ [mas/yr]+0.74 +0.68 +0.55 +0.30 -0.12 +1.41 +0.05 +0.12 0.00 +0.84 -
$\omega_{z}$ [mas/yr]+0.89 +0.84 +1.34 +1.09 +0.28 -0.11 -0.24 -0.84 0.00 +0.14 -
$E(T_{\rm E})$ [s]- - - +0.035 +0.035 -0.070 +0.010 -0.050 +0.035 - +0.050
e [s/cy]- - - +0.085 +0.085 +0.085 +0.070 +0.070 +0.085 - -
$N_{\rm sig}(\alpha) $42 33 23 25 16 19 31 43 65 37 32
$n_{\rm sig,max}(\alpha)$30 20 17 30 23 10 23 18 26 35 12
$m_{\rm sig,max}(\alpha)$10 6 5 6 4 4 5 6 4 4 6
$p_{\rm sig,max}(\alpha)$0 1 2 0 2 1 2 1 2 1 0
$N_{\rm sig}(\delta) $23 28 16 14 19 13 26 28 57 35 70
$n_{\rm sig,max}(\delta)$22 18 18 5 12 7 23 13 30 33 40
$m_{\rm sig,max}(\delta)$6 5 5 6 5 4 6 5 6 5 6
$p_{\rm sig,max}(\delta)$0 0 1 0 0 0 0 1 2 0 0
$N_{\rm sig}(\mu_{\alpha})$46 27 38 41 27 31 32 44 50 31 -
$n_{\rm sig,max}(\mu_{\alpha})$29 18 19 18 18 16 26 15 28 18 -
$m_{\rm sig,max}(\mu_{\alpha})$8 4 3 6 6 6 5 6 4 3 -
$p_{\rm sig,max}(\mu_{\alpha})$0 1 2 2 2 1 1 1 1 2 -
$N_{\rm sig}(\mu_{\delta})$23 15 20 23 20 27 37 42 55 26 -
$n_{\rm sig,max}(\mu_{\delta})$19 19 26 30 30 19 20 20 25 32 -
$m_{\rm sig,max}(\mu_{\delta})$2 4 3 5 6 6 6 6 4 3 -
$p_{\rm sig,max}(\mu_{\delta})$0 0 0 0 0 0 2 2 2 1 -
$\sigma_{\rm res}(\Delta\alpha)$ [mas]52.26 60.54 105.69 97.55 120.33 186.57 143.77 322.36 214.17 138.35 112.75
$\sigma_{\rm res}(\Delta\delta)$ [mas]56.82 71.63 105.24 92.50 112.46 171.94 138.91 287.85 195.56 134.68 209.80
$\sigma_{\rm res}(\Delta\mu_{\alpha})$ [mas/yr]1.65 2.75 3.70 2.74 4.19 6.46 6.14 9.17 11.43 5.15 -
$\sigma_{\rm res}(\Delta\mu_{\delta})$ [mas/yr]1.61 2.96 3.96 2.61 3.79 5.63 5.70 8.07 9.81 5.10 -
$\sigma_{\rm sys}(\Delta\alpha)$ [mas]37.05 35.62 51.74 61.96 81.66 174.16 71.17 202.03 166.98 37.78 51.01
$\sigma_{\rm sys}(\Delta\delta)$ [mas]48.07 49.05 50.13 35.57 56.66 128.58 64.36 286.92 119.06 59.61 109.87
$\sigma_{\rm sys}(\Delta\mu_{\alpha})$ [mas/yr]1.87 2.11 2.29 2.20 2.96 6.62 3.24 3.92 2.72 1.68 -
$\sigma_{\rm sys}(\Delta \mu_{\delta})$ [mas/yr]1.01 1.25 1.69 1.22 1.37 6.01 1.70 5.49 4.14 1.61 -
$<\Delta_{\alpha}>$ [mas]-3.35 -0.58 -7.34 -5.64 -4.43 +8.03 -14.47 -81.13 -61.80 -0.07 -7.70
$<\Delta_{\delta}>$ [mas]+36.79 +33.41 +29.63 +21.86 +12.78 +40.03 +40.89 +245.97 +43.15 +38.45 +71.65
$<\Delta_{\mu_{\alpha}}>$ [mas/yr]+0.32 +0.39 +0.35 +0.00 -0.08 +0.73 -0.25 +0.90 -0.17 +0.01 -
$<\Delta_{\mu_{\delta}}>$ [mas/yr]+0.22 +0.24 +0.37 +0.35 -0.22 +3.60 +0.01 +4.40 +2.73 +0.47 -



  \begin{figure} \par\includegraphics[width=7cm,clip]{allfk5rd.eps}\end{figure} Figure 1: Systematic proper motion differences $\Delta \mu _{\alpha *}$ [mas/yr] between HIPPARCOS and the various parts of the FK5 (and the PPM) as a function of $\delta $.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{allfk5dd.eps}\end{figure} Figure 2: Systematic proper motion differences $\Delta \mu _{\delta }$ [mas/yr] between HIPPARCOS and the various parts of the FK5 (and the PPM) as a function of $\delta $.
Open with DEXTER


  \begin{figure} \includegraphics[width=7cm,clip]{allfkrd.eps}\end{figure} Figure 3: Systematic proper motion differences $\Delta \mu _{\alpha *}$ [mas/yr] between HIPPARCOS and the series of German fundamental catalogues as a function of $\delta $.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{allfkdd.eps}\end{figure} Figure 4: Systematic proper motion differences $\Delta \mu _{\delta }$ [mas/yr] between HIPPARCOS and the series of German fundamental catalogues as a function of $\delta $.
Open with DEXTER

4 Transition from the IAU(1976) System to the HIPPARCOS system


  \begin{figure} \par\includegraphics[width=7cm,clip]{oldcatrd.eps}\end{figure} Figure 5: Systematic proper motion differences $\Delta \mu _{\alpha *}$ [mas/yr] between HIPPARCOS and various "old'' catalogues as afunction of $\delta $.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{oldcatdd.eps}\end{figure} Figure 6: Systematic proper motion differences $\Delta \mu _{\delta }$ [mas/yr] between HIPPARCOS and various "old'' catalogues as afunction of $\delta $.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{per70dddif.eps}\end{figure} Figure 7: Total differences $\Delta \delta $ [mas] between HIPPARCOS and the Perth 70 catalogue versus the declination.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7cm,clip]{per70ddfit.eps}\end{figure} Figure 8: Systematic differences $\Delta \delta $ [mas] between HIPPARCOS and the Perth 70 catalogue as a function of $\delta $.
Open with DEXTER

4.1 Residual global rotations

The HIPPARCOS reference frame was globally linked to the Extragalactic System as described in detail in the HIPPARCOS Catalogue (Vol. 3, Sect. 18). Since this procedure makes only indirect use of the dynamical equinox, we have to expect that residual rotations exist between the HIPPARCOS system and a catalogue which is reduced to the IAU(1976) system according to Sect. 3. In addition, we have used in many cases only rough estimates for the zero point corrections in right ascension and the proper motions in right ascension. In order to be, in a global sense, as accurate as possible in the HIPPARCOS system, we determine and apply therefore an additional rotation of the reduced catalogue positions (and proper motions, if available) onto the HIPPARCOS system.

We have derived such statistically determined corrections, namely the rotational parameters and the regional corrections (see Sect. 4.2) at the mean epoch T0 of the respective catalogue and not at the mean HIPPARCOS epoch 1991.25; the reasons are given in Sect. 2.

Let

\begin{displaymath}\Delta = \Delta \alpha, \Delta \delta, \Delta \mu_{\alpha}~~~ {\rm or}~~~~ \Delta \mu_{\delta} \end{displaymath}

denote a difference between a position or proper motion as given in the HIPPARCOS catalogue on the one hand and the respective catalogue (in the IAU(1976) System according to Sect. 3) on the other hand, computed at the mean epoch T0 of the catalogue (e.g. 1949.4 in the case of the Basic FK5). We use the differences $\Delta$always in the sense HIPPARCOS-Catalogue. This means that the results derived and presented for instance in Table 1 or in Figs. 1 through 8 describe the corrections which have to be added to the positions (and proper motions) in the respective catalogue in order to reduce the catalogue to the HIPPARCOS system.

The equations of condition for the rotational parameters $ \epsilon_{x}, \epsilon_{y}, \epsilon_{z}$ in position around the three coordinate axis are

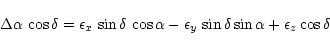\begin{displaymath}\Delta \alpha \, \cos\delta = \epsilon_{x}\,\sin\delta \, \co... ... \epsilon_{y} \, \sin\delta\sin\alpha + \epsilon_{z}\cos\delta \end{displaymath} (7)


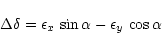\begin{displaymath}\Delta \delta = \epsilon_{x}\,\sin\alpha - \epsilon_{y} \,\cos\alpha \end{displaymath} (8)

and correspondingly for the rotation parameters $ \omega_{x}, \omega_{y}, \omega_{z}$ of the proper motions:

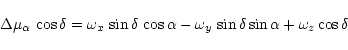\begin{displaymath}\Delta \mu_{\alpha} \, \cos\delta = \omega_{x}\,\sin\delta \,... ...ha - \omega_{y} \, \sin\delta\sin\alpha + \omega_{z}\cos\delta \end{displaymath} (9)


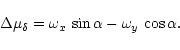\begin{displaymath}\Delta \mu_{\delta} = \omega_{x}\,\sin\alpha - \omega_{y} \,\cos\alpha. \end{displaymath} (10)

Stars with discordant differences were eliminated from the determination. The parameters were determined with the method of least squares and the rotational effects were removed from the original differences. The new residuals are further analyzed as described in the next step.

4.2 Regional corrections

After having corrected the catalogue for global systematic errors (Sect. 3) and after the rotation onto the HIPPARCOS system (Sect. 4.1), there remain additional systematic errors depending on the right ascension, the declination and the apparent magnitude of a star. These regional errors are determined from an analysis of the differences between the HIPPARCOS positions and proper motions and those in the respective catalogue which have already been corrected as described in Sects. 3 and 4.1. We determine the regional errors with the aid of the analytical method developed by Brosche (1966), extended by Schwan (1977) for the inclusion of a magnitude equation, and modified by Bien et al. (1978). The method splits a difference $\Delta$ into a systematic part $\Delta_{\rm sys}$and a random part $\Delta_{\rm res}$

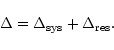\begin{displaymath}\Delta = \Delta_{\rm sys} + \Delta_{\rm res}. \end{displaymath} (11)

The systematic part $\Delta_{\rm sys}$ is developed into a series of statistically significant functions $Y_{j}(\alpha,\delta,m)$

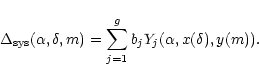\begin{displaymath}\Delta_{\rm sys} (\alpha,\delta,m) = \sum_{j=1}^{g}b_{j}Y_{j}(\alpha,x(\delta),y(m)). \end{displaymath} (12)

Each Yj is the product of a Legendre polynomial $ L_{n}(x(\delta)) $, a Fourier term $F_{m,l}(\alpha)$ and a Hermite polynomial $H_{p}(y(\delta))$. The letters p and n denote the degree of the Hermite and Legendre polynomial, respectively; m is the frequency of the Fourier term. $x(\delta), y(m)$ are transformed declinations and magnitudes which are introduced in order to improve the numerical orthogonality of the functions. Please note the double use of the letter m as the frequency in the Fourier terms and as the apparent magnitude in the Hermite polynomials. For more detail, see Bien et al. (1978).

The dispersion of the N (N = Number of stars included in the catalogue comparison) residuals $\Delta_{{\rm res},i}\, (i=1,...,N)$ around the system is given by

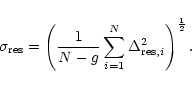\begin{displaymath}\sigma_{\rm res} = \left(\frac{1}{N-g} \sum_{i=1}^{N} \Delta_{{\rm res},i}^{2} \right)^\frac{1}{2}. \end{displaymath} (13)

Similar to the dispersion $\sigma_{\rm res}$ of the residuals which characterizes the scatter of the data around the system we can introduce the quantity $\sigma_{\rm sys}$ which is a measure of the typical variation of the systematic differences. In analogy to $\sigma_{\rm res}$ we define $\sigma_{\rm sys}$ as the rms-value of the systematic part $\Delta_{\rm sys}$ of our differences:

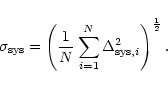\begin{displaymath}\sigma_{\rm sys} = \left(\frac{1}{N} \sum_{i=1}^{N} \Delta_{{\rm sys},i}^{2}\right)^\frac{1}{2}. \end{displaymath} (14)

We add an approximate formula for computing the mean error $\sigma(\Delta_{\rm sys}) $ of the systematic differences. A correct computation requires the use of the complete covariance matrix of the coefficients bj. For reasons of economy we use in the provided software merely the coefficients with their mean errors and estimate the accuracy of the system by the expression

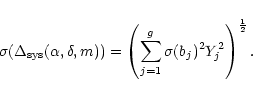\begin{displaymath}\sigma(\Delta_{\rm sys}(\alpha,\delta,m)) = \left(\sum_{j=1}^{g} \sigma(b_{j})^{2} Y_{j}^{2}\right)^\frac{1}{2}. \end{displaymath} (15)

This approximation is in most cases sufficiently accurate because the correlations between the coefficients bj are comparatively small. The reason is that with our transformed positions $x(\delta)$ and magnitudes y(m) we get functions which are approximately orthogonal also in the numerical applications where the data are given only for discrete values of $\alpha$, $\delta $ and m. A comparison of the correct results where the full covariance matrix is used (requiring rather time-consuming computations) with the results obtained by the approximation (15) was made for the comparison of the Basic FK5 with HIPPARCOS (Schwan 2001). It had been found that the approximate values differ from the correct ones by less than about 5 percent in the region $-70^{\circ}< \delta < +70 ^{\circ}$. For $\vert\delta\vert > 80^{\circ}$differences significantly exceeding 10 percent may occur, however.

5 Reduction of catalogues with and without proper motions

In the following we describe the reductions of (1) catalogues of positions and proper motions given at the epoch of the catalogue equinox (e.g. fundamental catalogues), and (2) catalogues of star positions given at the individual mean epochs of observation of a star (observational catalogues where no proper motion has been applied).

We assume that we have determined the various corrections as described in Sects. 3.3 and 4. That means that we have determined the zero point corrections for the right ascensions and the proper motions in right ascension, the global rotation parameters and also the regional corrections in position (and proper motion, if available).

5.1 Reduction of a catalogue with proper motions

This section describes the reduction of catalogues where proper motions have also been derived within the catalogue construction (e.g. fundamental catalogues as the FK4, FK5, or non-fundamental catalogues with derived proper motions as the PPM catalogue). The positions are reduced in the catalogue to the adopted catalogue epoch and equinox $T_{\rm C}$ with the aid of the given catalogue proper motions. The reduction of such a catalogue is performed as follows:

1.
elimination of the elliptic aberration from the catalogue positions according to Eqs. (1)-(4). The quantities c0, d0in Eqs. (1) and (2) are computed with $T_{\rm C}$ as the time argument;
2.
elimination of the equinox corrections E and e in right ascension and the proper motions in right ascension at the epoch $T_{\rm C}$. The equinox correction E at the epoch $T_{\rm C}$is obtained as $E(T_{\rm C}) = E(T_{\rm E}) + e\cdot(T_{\rm C}-T_{\rm E})$ where $T_{\rm E}$denotes the epoch at which $E(T_{\rm E})$ is given in Table 1;
3.
transformation of the proper motions to the IAU (1976) System of Constants using Eqs. (5) and (6) and considering Sect. 3.3;
4.
global rotation of the catalogue onto the HIPPARCOS system (see Eqs. (7)-(10)). Since the correction is applied at the epoch $T_{\rm C}$ (as in the case of the equinox corrections) we have to apply also the rotation in proper motion for the respective time interval to the positions;
5.
elimination of the regional corrections in position and proper motion at the equinox $T_{\rm C}$ of the "old'' catalogue. Since we determine our corrections primarily at the mean epoch T0 we have to add the systematic proper motion corrections to the corrections in position for the time interval $(T_{\rm C}-T_{0})$, i.e. we have to compute expressions like $\Delta_{{\rm sys},\delta}(T_{\rm C}) = \Delta_{{\rm sys},\delta}(T_{0}) + \Delta_{{\rm sys},\mu_{\delta}}(T_{\rm C}-T_{0})$. This is in analogy to the procedure for the equinox correction in Step 2 and the global rotation in Step 3;
6.
transformation of the corrected catalogue to the mean epoch and equinox J2000.
In the case of the FK5 or PPM, which are already on the IAU(1976) system, the reduction to the HIPPARCOS system reduces to the steps (4)-(6).

5.2 Reduction of a catalogue without proper motions

We assume that the catalogue positions are given at the star's individual mean epoch of observation $T_{\rm i}$ and referred to the equinox and equator for the epoch $T_{\rm C}$ adopted in the catalogue. The reduction of such catalogue positions to the HIPPARCOS system is performed as follows:

1.
elimination of the elliptic aberration from the catalogue positions;
2.
precession of the catalogue positions to the mean equinox and equator at the mean epochs $T_{\rm i}$ using the precessional quantities adopted in the catalogue. The resulting positions are practically independent of precessional quantities;
3.
removal of the equinox correction in position;
4.
elimination of the regional errors in the observational catalogue at the mean epoch $T_{0} =\, <T_{\rm i}>$ of the catalogue;
5.
reduction of the catalogue positions to the equinox and equator J2000. The individual epoch of a catalogue position is kept.
The results of this procedure are the positions at the mean epoch of observation of each star, reduced to the HIPPARCOS system and referred to the mean equinox and equator J2000.

6 Results and discussion

6.1 Numerical results and general remarks

A significance level of 5% was chosen for a merely accidental inclusion of a function into the development (12). The only exception was the PPM catalogue (see Sect. 6.4).

Some of the characteristic data used for the reduction or resulting from the catalogue comparison are compiled in Table 1. For the various catalogues we give the total number $N_{\rm tot} $ of the stars in the catalogue, the number of stars used in position ( $N_{\rm used, pos} $) and proper motion ( $N_{\rm used, pm } $) for deriving the systematic differences, the epoch $T_{\rm C}$of the catalogue equinox at which some the corrections are applied in the case of catalogues with proper motions, the mean epoch T0 at which the comparison was made, the epoch $T_{\rm E}$ for which the equinox correction holds, the rotational parameters $ \epsilon_{x}, \epsilon_{y}, \epsilon_{z}$ in position at the epoch T0 and $ \omega_{x}, \omega_{y}, \omega_{z}$ in proper motion, the equinox correction E at the epoch $T_{\rm E}$and the motion of the equinox e, the number $N_{\rm sig}$ of significant functions included in the series development of the systematic differences in $\alpha*, \delta, \mu_{\alpha*}$and $\mu_{\delta}$, the highest degree $n_{\rm sig,max}, p_{\rm sig,max}$ of the significant Legendre and Hermite polynomials, the highest frequency $m_{\rm sig,max}$ of the Fourier terms, the dispersions $\sigma_{\rm res}(\Delta \alpha*), \sigma_{\rm res}(\Delta \delta), \sigma_{\rm res}(\Delta \mu_{\alpha*}) $and $\sigma_{\rm res}(\Delta\mu_{\delta})$ of the residuals, similarly the mean quadratic deviations $\sigma_{\rm sys}(\Delta \alpha*), \sigma_{\rm sys}(\Delta \delta), \sigma_{\rm sys}(\Delta\mu_{\alpha*}), \sigma_{\rm sys}(\Delta\mu_{\delta})$of the systematic differences, and finally the mean deviations $<\Delta\alpha*>, <\Delta\delta*>, <\Delta\mu_{\alpha*}>, <\Delta\mu_{\delta}>$ between the HIPPARCOS system and the system of the globally reduced catalogue (i.e. before determining the regional errors).

The number of significant functions and, even more, the highest degree of those functions, give some information on how "complicated'' the systematic relations are. The more functions needed and the higher their degree, the more complicated is the system. Catalogues for which functions with $p \ne 0$occur are affected with a magnitude equation.

Since the positions are, in general, of lower interest, we restrict the figures and the discussion below to the proper motions only. The $\delta $-dependent systematic errors describe in most cases the major contribution to the systematic differences. We give therefore merely graphical representations of these errors. Not included in the regional errors are the corrections made for the transition to the IAU (1976) System, the equinox corrections and the global rotations.

6.2 The FK5 catalogue

In the case of the FK5 we follow the procedure applied in the construction of the FK6, Part 3 (Wielen et al. 2000). We have adopted in this paper the systematic relations used in the construction of the FK6 for the transformation of the various subsamples of the FK5 to the HIPPARCOS system. As explained in the introductory part to the FK6 systematic corrections, HIPPARCOS-FK5 were derived and used for the following three subsamples:

1) Basic FK5 (abbreviated as FK5 BA), consisting of the classical fundamental stars (which are already included in the FK3 and FK4).

2) FK5 Bright Extension (abbreviated as FK5 BX) combined with the remaining 995 stars from the FK4 Sup catalogue (abbreviated as FK5 RSup), which were not included in the FK5 Extension. The combined sample (abbreviated as "FK5 BXRS'') consists effectively of the stars published in the FK4 Supplement (Fricke 1963) but, of course, with new improved astrometric parameters. In the construction of the FK5, all these stars were treated in the same way. At the end of the full reduction process of these stars, the selection of the stars to be included in the FK5 (Part 2) was made. The remaining non-FK5 stars were published separately (Schwan et al. 1993).
Since it was found in the derivation of the FK6 (Part 3) that the systems of the two subgroups FK5BX and FK5RSup do not differ significantly, both subgroups were combined into the sample denoted as "FK5 BXRS'', and the systematic relation between this combined sample FK5BXRS and the HIPPARCOS catalogue was derived and used in the FK6.

3) The FK5 Faint Extension (abbreviated as FK5 FX), consists of 2125 stars selected from the IRS list (Scott 1967; Corbin 1991). These stars were included in the FK5 with the aim to extend the fundamental system to about 9.5th magnitude, nearly 3 mag fainter than the magnitudes of the FK4 stars. The extension of the system to these fainter magnitudes was a difficult task which is described in some detail in Corbin (1985) and Corbin & Urban (1990). Because of the completely different construction of the system of these faint stars we have derived their systematic relation to the HIPPARCOS independently.

The systematic differences in proper motion are presented in Figs. 1 and 2 for the three parts of the FK5. From these figures one can conclude that the systems of the sample FK5BXRS and also the Faint Extension agree rather well with the system of the Basic FK5.

Since the PPM catalogue has adopted the system of the FK5 we have included the $\delta $-dependent systematic proper motion errors for the PPM also in Figs. 1 and 2 (discussion of the PPM catalogue follows in Sect. 6.4).

6.3 The FK-catalogues

The systematic differences in proper motion for the whole series of FK catalogues are shown in the Figs. 3 and 4. If we exclude the very early catalogue NFK one is inclined to conclude that the increase in systematic accuracy was comparatively moderate. This presumption is, however, not really true, as can be concluded from the rms-values $\sigma_{\rm sys}$ of the systematic differences given in Table 1. In the case of the $\mu_{\alpha}$-system the rms-values $\sigma_{\rm sys}(\mu_{\alpha*})$, which describe the typical variation of the system, decrease significantly from 2.96 mas/yr for the FK3, 2.20 mas/yr for the FK4 to 1.87 mas/yr for the Basic FK5. On the other hand, the corresponding decrease 1.37, 1.22 and 1.01 for the $\mu_{\delta}$-system is not so pronounced. If we restrict, however, the computation of the $\sigma_{\rm sys}$-values to the region $\left\vert\delta\right\vert < 60^{\circ}$ we still find a very significant improvement for the $\mu_{\alpha}$-system (2.28, 1.95 and 1.22 mas/yr in the sequence FK3, FK4, Basic FK5), but no improvement in systematic accuracy for $\mu_{\delta}$ (1.02, 1.08, 1.05 in the same sequence).

6.4 The PPM catalogue

Nearly 110000 PPM stars in the HIPPARCOS catalogue could be used for the determination of the systematic differences. Because of this large number, many functions occur there with extremely high significance. If we would retain the significance level of 5% used for the other catalogues, then a large number of functions would be included in the development, most of them, however, with very small amplitudes. We have therefore decided to include merely a "reasonable'' number of functions, i.e. a number comparable to that for the other catalogues and with coefficients still essentially contributing. This was achieved by choosing a significance level of 10-8.

The PPM catalogue has been derived by making significant use of photographic observations. The treatment of these observations needs a reduction plate by plate. From this, one has to expect systematic errors down to the scale of a contributing plate. Such small-scale errors are not modelled within the present investigation. We have tested functions up to the degree $n_{\max} = 40$, corresponding to a binning in strips of about $4.6^{\circ}$ in declination, and of $m_{\max} = 25$, corresponding to strips of $7.2^{\circ}$ width in right ascension. With this selection we are, in principle, able to model systematic features on the scale of about $\Delta \alpha_{*}\times\Delta \delta = 4.5^{\circ}\times7.2^{\circ}$. The most complicated functions which were included in the final development had (n,m) = (35,1), (23,2) and (14, 3). These functions model features on the scale of $\Delta \alpha_{*}\times\Delta \delta = 5^{\circ}\times180^{\circ}$, $8^{\circ}\times90^{\circ}$, and $13^{\circ}\times60^{\circ}$ respectively. The function with the highest frequency in right ascension was (n,m) = (4,6) and resolves features on the scale of $\Delta \alpha_{*}\times\Delta \delta = 45^{\circ}\times30^{\circ}$.

The $\delta $-dependent systematic proper motion errors are also included in Figs. 1 and 2 because the PPM should be on the system of the FK5. For the proper motions in right ascension we find merely in the region south of $-50^{\circ}$significant deviations from the FK5 system, for the proper motions in declination we have north of $+50^{\circ}$ larger discrepancies.

6.5 PGC, GC and N30 catalogues

In the case of the GC we had already determined systematic differences HIPPARCOS-GC for the detection of so-called $\Delta \mu$ binaries in the GC catalogue (Wielen et al. 2001). Since we had at that time included the (small) rotations into the regional systematic differences, and since we want to remain as close as possible to those earlier results, we have adopted the former results without any changes.

These catalogues do not belong to a series of fundamental catalogues as the FK-series. Just for completeness we have added the graphical representation of the $\delta $-dependent systematic proper motion differences in Figs. 5 and 6 without any further comment. The FK3 has been added for comparison as an "old'' catalogue of the FK-series.

6.6 The Perth 70 catalogue

The Perth 70 catalogue (Hoeg et al. 1976) was derived from observations made within the International Southern Reference Star program. It was one of the most important catalogues in the southern sky, yielding mean positions for about 24900 stars. The observations were made from 1967 through 1972 resulting in the average mean epoch 1970. This catalogue has provided an important reference frame near that epoch, although many users of reference catalogues went on using SAO in the south until PPM and ACRS appeared. Comparisons of SAO and ACRS with HIPPARCOS will be provided in a forthcoming paper.

We have therefore used this catalogue as an example for the reduction of an observational catalogue, giving observed mean positions at the stars's mean epochs with no proper motions applied.

An exceptional stucture of the systematic errors in declination has been found for the Perth 70 catalogue. Up to our standard limit $n_{\max} = 30$ only three functions were found not to be significant, but 27 were included as significant, i.e. practically all functions depending only on the declination were significant. A plot of the differences $\Delta \delta $ versus the declination has shown a very striped structure on an extremely small scale. This structure is shown in Fig. 7. In order to model such features one would have to develop up to an extremely high order in n. In a development up to the order n = 200 we have found 118 significant functions, the functions with n = 194, 195, ..., 200 were all significant. This means that the spectrum of significant functions was still extremely dense and many further significant functions of much higher degree have to be expected. The development of systematic differences $\Delta \delta $ up to the degree n=200 is shown graphically in Fig. 8. If one superimposes this development onto the differences in Fig. 7 one finds that the spikes in both figures fit rather well. On the other hand, it seems to be questionable whether these extremely small-scale structures are of practical importance in using the Perth 70 catalogue as a reference frame. We have therefore cut the development at the highest degree $n_{\max} = 40$.

No similar pecularity in right ascension has been found.

From Table 1 we find that the dispersion $\sigma_{\rm res}(\Delta\delta)$ of the residuals in declination and also the typical variation $\sigma_{\rm sys}(\Delta\delta)$ of the systematic differences are about twice the corresponding values in right ascension. Problems related to circle errors may be responsible for those features.

7 Final remarks

The systematic relations between the HIPPARCOS catalogue and the following catalogues of the 20th century were derived: the FK5 (various subsamples), the FK4, FK3, NFK, the PGC, GC, N30, the PPM and the observational catalogue Perth 70. These relations include the transition from the catalogue system to the IAU (1976) system, a global rotation of the catalogue onto the HIPPARCOS system and the determination of regional errors depending on the right ascension, declination and also the apparent magnitude. The relations allow one to transform positions and proper motions given in one of these systems to the HIPPARCOS system. We provide software (FORTRAN programs and the required input data) via the Internet for performing the described reductions. We have used the offered computer program to transform the mentioned catalogue. An analysis of the differences between these reduced catalogues and the HIPPARCOS catalogue has shown no significant systematic trends.

It is planned to add the systematic relations for more catalogues from time to time.

References

 

Copyright ESO 2001