A&A 373, 998-1008 (2001)
DOI: 10.1051/0004-6361:20010663

Statistical equilibrium and photospheric abundance of silicon in the Sun and in Vega[*]

S. Wedemeyer

Institut für Theoretische Physik und Astrophysik, Universität Kiel, 24098 Kiel, Germany

Received 12 February 2001 / Accepted 2 May 2001

Abstract
Based on detailed non-LTE calculations, an updated determination of the abundance of silicon in the Sun and Vega is presented. The model atom includes neutral and singly ionized stages of silicon with 115 energy levels and 84 line transitions. Non-LTE effects are found to be quite small in the Sun. The mean non-LTE abundance correction is -0.010 dex with respect to standard LTE calculations, leading to a solar abundance of $\log \epsilon_{\rm NLTE} = 7.550 \pm 0.056$. For the prototype A0 V star Vega the non-LTE effects are small, too. With a non-LTE abundance correction of $\Delta \log \epsilon = -0.054$, a silicon abundance of $\log \epsilon_{\rm NLTE} = 6.951 \pm 0.100$ is derived, implying a deficiency of -0.599 dex with respect to the Sun. This confirms the classification of Vega as a mild $\lambda$ Boo star.

Key words: Sun: abundances - stars: abundances - atomic data


   
1 Introduction

For many astrophysical applications, an accurate knowledge of the silicon abundance is required. Silicon is not only an important reference element for comparing various types of cosmic matter (e.g. meteorites) with the Sun but also one of the main electron contributors (next to Fe and Mg) and opacity sources in the near UV in the atmospheres of cool stars. Furthermore, the C/Si abundance ratio is an indicator of gas-dust separation in A stars with superficial abundance anomalies like $\lambda$ Boo stars (Stürenburg 1993).
The most widely used sources of solar (photospheric) abundances, the compilation by Anders & Grevesse (1989) and its updates (e.g. Grevesse & Sauval 1998), are based on standard abundance analyses employing 1D solar models and, in most cases, assuming LTE (local thermodynamic equilibrium). But for a accurate abundance determination, the simplifying assumption of LTE should be replaced by a detailed non-LTE study.
In the Sun, abundance deviations due to non-LTE effects are generally small, as can be seen from former calculations: +0.05 dex for Fe I (Steenbock 1985), -0.07 dex for C I (Stürenburg & Holweger 1991) and -0.05 dex ( $-0.01 \,...\, -0.06$ dex) for N I/II (Rentzsch-Holm 1996). Nevertheless, exact solar values are indispensable, as the Sun serves as a reference for investigations of other stars.
The A0V star Vega (HR 7001) is well studied in the context of abundance determination, and non-LTE calculations have been carried out for various elements (e.g. Gigas 1988; Takeda 1992). Its chemical composition shows a metal deficiency with respect to the Sun resembling the pattern of $\lambda$ Boo stars (Venn & Lambert 1990; Holweger & Rentzsch-Holm 1995). Therefore the former standard star Vega has turned into an important example of A stars with abundance anomalies.
For most elements, non-LTE corrections are small but not negligible, for example -0.05 dex ( $-0.16 \,...\, 0.00$ dex) for C I (Stürenburg & Holweger 1990), -0.32 dex
($-0.16 \,...\, -0.53$ dex) for N I/II (Rentzsch-Holm 1996), $-1 \,...\, -0.02$ dex for O I (Takeda 1992).
The presented calculations were carried out with the Kiel non-LTE code (Steenbock & Holweger 1984) which uses the computational scheme developed by Auer & Heasley (1976). Non-LTE calculations require various input data, such as a stellar atmosphere and a model atom which accounts for the relevant atomic properties. The resulting silicon abundances were derived with the program LINFOR, an updated and augmented Fortran version of the program by Baschek et al. (1966) devised by H. Holweger, M. Steffen and W. Steenbock at Kiel.
In Sect. 2 the atomic data used for the model atom are described. In Sects. 3 and 4 the non-LTE calculations and abundance determination are outlined for the Sun and for Vega, respectively.

   
2 Atomic data

The silicon model atom accounts for the most important levels and transitions of Si I and Si II and comprises 115 energy levels and 84 line transitions. For Si I (ionization limit at 8.15 eV) 75 energy levels up to 7.77 eV and 53 line transitions were included, for Si II (ionization limit at 16.35 eV) 40 energy levels up to 15.65 eV and 31 line transitions were taken into account. The atomic data are listed in Tables 1 and 2,

 

 
Table 1: Energy levels included in the model atom.
no. config. term $E ({\rm eV})$ gi   no. config. term $E ({\rm eV})$ gi  
                       
Si I 1 3s$^2\, 3$p$^2\, $ 3P 0.0186 9   59 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$f $^2\lbrack9/2\rbrack $ 7.6394 20  
2 3s$^2\, 3$p$^2\, $ 1D 0.7810 5   60 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$g $^2\lbrack9/2\rbrack^{\rm o}$ 7.6398 20 *
3 3s$^2\, 3$p$^2\, $ 1S 1.9087 1   61 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$g $^2\lbrack7/2\rbrack^{\rm o}$ 7.6411 16 *
4 3s$ \, 3$p$^3\, (^4$P$ )\, $ 5S$^{\rm o} $ 4.1319 5   62 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$g $^2\lbrack11/2\rbrack^{\rm o}$ 7.6429 24 *
5 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\, 4$s 3P$^{\rm o} $ 4.9420 9   63 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$f $^2\lbrack3/2\rbrack $ 7.6434 8  
6 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\, 4$s 1P$^{\rm o} $ 5.0824 3   64 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$g $^2\lbrack5/2\rbrack^{\rm o}$ 7.6442 12 *
7 3s$ \, 3$p$^3\, $ 3D$^{\rm o} $ 5.6169 15   65 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,7$s $(3/2,1/2)^{\rm o}$ 7.6679 8  
8 3s$^2\, 3$p$ \, 4$p 1P 5.8625 3   66 3s$^2\, 3$p$ \,5$d 3P$^{\rm o} $ 7.6730 9 *
9 3s$^2\, 3$p$ \, 3$d 1D$^{\rm o} $ 5.8708 5   67 3s$^2\, 3$p$ \,6$d 1D$^{\rm o} $ 7.7065 5  
10 3s$^2\, 3$p$ \, 4$p 3D 5.9713 15   68 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,7$p (1/2,1/2) 7.7101 4  
11 3s$^2\, 3$p$ \, 4$p 3P 6.0911 9   69 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,7$p (1/2,3/2) 7.7156 8  
12 3s$^2\, 3$p$ \, 4$p 3S 6.1248 3   70 3s$^2\, 3$p$ \,6$d 3F$^{\rm o} $ 7.7414 21  
13 3s$^2\, 3$p$ \, 3$d 3F$^{\rm o} $ 6.1959 21   71 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,7$p (3/2,3/2) 7.7491 16  
14 3s$^2\, 3$p$ \, 4$p 1D 6.2227 5   72 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,7$p (3/2,1/2) 7.7527 8  
15 3s$^2\, 3$p$ \, 3$d 3P$^{\rm o} $ 6.2653 9   73 3s$^2\, 3$p$ \,6$d 1P$^{\rm o} $ 7.7697 3  
16 3s$^2\, 3$p$ \, 4$p 1S 6.3990 1   74 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,6$f $^2\lbrack7/2\rbrack $ 7.7700 16  
17 3s$^2\, 3$p$ \, 3$d 1F$^{\rm o} $ 6.6161 7   75 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,6$f $^2\lbrack5/2\rbrack $ 7.7701 12  
18 3s$^2\, 3$p$ \, 3$d 1P$^{\rm o} $ 6.6192 3              
19 3s$^2\, 3$p$ \, 3$d 3D$^{\rm o} $ 6.7232 15   Si II 76 3s $^2\, (^1$S$ )\, 3$p 2P$^{\rm o} $ 0.0237 6  
20 3s$^2\, 3$p$ \,5$s 3P$^{\rm o} $ 6.7478 9   77 3s$ \, 3$p$^2\, $ 4P 5.3316 12 *
21 3s$^2\, 3$p$ \,5$s 1P$^{\rm o} $ 6.8031 3   78 3s$ \, 3$p$^2\, $ 2D 6.8587 10  
22 3s$^2\, 3$p$ \, 4$d 1D$^{\rm o} $ 7.0055 5   79 3s $^2\, (^1$S$ )\, 4$s 2S 8.1210 2  
23 3s$^2\, 3$p$ \, 4$d 3P$^{\rm o} $ 7.0298 9   80 3s$ \, 3$p$^2\, $ 2S 9.5054 2  
24 3s$^2\, 3$p$ \,5$p 1P 7.0399 3   81 3s $^2\, (^1$S$ )\, 3$d 2D 9.8380 10  
25 3s$^2\, 3$p$ \,5$p 3D 7.0787 15   82 3s $^2\, (^1$S$ )\, 4$p 2P$^{\rm o} $ 10.0715 6  
26 3s$^2\, 3$p$ \,5$p 3P 7.1170 9   83 3s$ \, 3$p$^2\, $ 2P 10.4069 6  
27 3s$^2\, 3$p$ \, 4$d 3F$^{\rm o} $ 7.1277 21   84 3s $^2\, (^1$S$ )\, 5$s 2S 12.1471 2  
28 3s$^2\, 3$p$ \,5$p 3S 7.1343 3   85 3s $^2\, (^1$S$ )\, 4$d 2D 12.5255 10  
29 3s$^2\, 3$p$ \,5$p 1D 7.1660 5   86 3s $^2\, (^1$S$ )\, 4$f 2F$^{\rm o} $ 12.8394 14  
30 3s$^2\, 3$p$ \,5$p 1S 7.2297 1   87 3s $^2\, (^1$S$ )\, 5$p 2P$^{\rm o} $ 12.8792 6  
31 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\, 4$f $^2\lbrack5/2\rbrack $ 7.2872 12   88 3s$ \, 3$p$ \, (^3$P $^{\rm o} )\, 3$d 2D$^{\rm o} $ 13.4901 10  
32 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\, 4$f 3F 7.2888 16   89 3s $^2\, (^1$S$ )\, 6$s 2S 13.7852 2  
33 3s$^2\, 3$p$ \, 4$d 1P$^{\rm o} $ 7.2905 3   90 3s $^2\, (^1$S$ )\, 5$d 2D 13.9353 10  
34 3s$^2\, 3$p$ \, 4$d 1F$^{\rm o} $ 7.3019 7   91 3s $^2\, (^1$S$ )\, 5$f 2F$^{\rm o} $ 14.1046 14  
35 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\, 4$f 3G 7.3196 16   92 3s $^2\, (^1$S$ )\, 6$p 2P$^{\rm o} $ 14.1308 6  
36 3s$^2\, 3$p$ \, 4$d 3D$^{\rm o} $ 7.3247 15   93 3s $^2\, (^1$S$ )\, 5$g 2G 14.1563 18  
37 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\, 4$f $^2\lbrack5/2\rbrack $ 7.3288 12   94 3s$ \, 3$p$ \, (^3$P $^{\rm o} )\, 3$d 4F$^{\rm o} $ 14.1858 28 *
38 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\, 4$f $^2\lbrack9/2\rbrack $ 7.3312 20   95 3s$ \, 3$p$ \, (^3$P $^{\rm o} )\, 4$s 4P$^{\rm o} $ 14.5136 12 *
39 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\, 4$f $^2\lbrack3/2\rbrack $ 7.3388 8   96 3s$^2\, (^1$S$ )\,7$s 2S 14.6196 2  
40 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,6$s 3P$^{\rm o} $ 7.3474 4   97 3s$^2\, (^1$S$ )\, 6$d 2D 14.6951 10  
41 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,6$s $(3/2,1/2)^{\rm o}$ 7.3840 8   98 3s$^2\, (^1$S$ )\,7$p 2P$^{\rm o} $ 14.7870 6  
42 3s$^2\, 3$p$ \, $nd 3P$^{\rm o} $ 7.4344 9   99 3s$^2\, (^1$S$ )\, 6$f 2F$^{\rm o} $ 14.7928 14  
43 3s$^2\, 3$p$ \,5$d 1D$^{\rm o} $ 7.4764 5   100 3s$^2\, (^1$S$ )\, 6$g 2G 14.8258 18  
44 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,6$p (1/2,1/2) 7.4938 4   101 3s$ \, 3$p$ \, (^3$P $^{\rm o} )\, 4$s 2P$^{\rm o} $ 15.0693 6  
45 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,6$p (1/2,3/2) 7.5002 8   102 3s$^2\, (^1$S$ )\, 8$s 2S 15.1031 2  
46 3s$^2\, 3$p$ \,5$d 3F$^{\rm o} $ 7.5324 21   103 3s$^2\, (^1$S$ )\,7$d 2D 15.1463 10  
47 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,6$p (3/2,3/2) 7.5403 16   104 3s$^2\, (^1$S$ )\,7$f 2F$^{\rm o} $ 15.2073 14  
48 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,6$p (3/2,1/2) 7.5422 8   105 3s$^2\, (^1$S$ )\,7$g 2G 15.2296 18  
49 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$f $^2\lbrack5/2\rbrack $ 7.6008 12   106 3p$^3\, $ 4S$^{\rm o} $ 15.2542 4 *
50 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$f 3F 7.6010 16   107 3s $^2\, (^1$S$ )\, 8$p 2P$^{\rm o} $ 15.2656 6  
51 3s$^2\, 3$p$ \,5$d 1P$^{\rm o} $ 7.6011 3   108 3s $^2\, (^1$S$ )\, 9$s 2S 15.4084 2  
52 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$g $^2\lbrack7/2\rbrack^{\rm o}$ 7.6060 16   109 3s$ \, 3$p$ \, (^3$P $^{\rm o} )\, 3$d 4D$^{\rm o} $ 15.4204 20 *
53 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$g $^2\lbrack9/2\rbrack^{\rm o}$ 7.6061 20   110 3s $^2\, (^1$S$ )\, 8$d 2D 15.4355 10  
54 3s$^2\, 3$p$ \,5$d 1F$^{\rm o} $ 7.6156 7   111 3s$ \, 3$p$ \, (^3$P $^{\rm o} )\, 3$d 4P$^{\rm o} $ 15.4479 12 *
55 3s$^2\, 3$p$ \,5$d 3D$^{\rm o} $ 7.6276 15   112 3s $^2\, (^1$S$ )\, 8$f 2F$^{\rm o} $ 15.4760 14  
56 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$f 3G 7.6329 16   113 3s $^2\, (^1$S$ )\, 8$g 2G 15.4916 18  
57 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,7$s 3P$^{\rm o} $ 7.6351 4   114 3s $^2\, (^1$S$ )\, 9$p 2P$^{\rm o} $ 15.5018 6  
58 3s$^2\, 3$p$ \,(^2$P $^{\rm o} )\,5$f 3D 7.6372 12   115 3s$ \, 3$p$ \, (^3$P $^{\rm o} )\, 3$d 2P$^{\rm o} $ 15.6531 6  



 

 
Table 2: Line transitions used in the model atom.
no. mult. i k $\lambda$ (Å) $\log gf$     no. mult. i k $\lambda$ (Å) $\log gf$  
Si I-1 0.01F 1 2 16263.251 -9.126 F   Si I-43 31 8 22 10846.829 +0.150 F
Si I-2 1F 1 3 6567.708 -9.634 F   Si I-44 32.02 8 33 8680.080 -3.191 F
Si I-3 0.01 1 4 3014.243 -4.522 F   Si I-45 34 8 41 8093.231 -1.354 F
Si I-4 UV 1 1 5 2517.485 +0.173 F   Si I-46 36 8 43 7680.265 -0.691 F
Si I-5 UV 2 1 6 2448.510 -2.264 F   Si I-47 38 8 67 6721.840 -0.938 F
Si I-6 UV 3 1 7 2213.972 -0.217 F   Si I-48 42.21 10 20 15964.678 +0.456 F
Si I-7 UV 7 1 15 1984.967 -0.314 V   Si I-49 53 10 27 10720.959 +0.672 F
Si I-8 UV 8 1 17 1881.854 -1.922 V   Si I-50 57 10 46 7939.870 +0.061 F
Si I-9 UV 10 1 19 1849.336 +0.387 V   Si I-51 60 10 70 7002.660 -0.380 F
Si I-10 UV 11 1 20 1842.489 -0.663 V   Si I-52   11 21 17205.800 -1.450 L
Si I-11 2F 2 3 10991.400 -7.839 F   Si I-53   12 20 20343.900 -0.810 L
Si I-12 1 2 5 2979.674 -2.045 F   Si II-1 UV 0.01 76 77 2325.848 -4.193 F
Si I-13 UV 43 2 6 2881.577 -0.151 F   Si II-2 UV 1 76 78 1813.980 -1.474 F
Si I-14 UV 45 2 9 2435.154 -0.680 V   Si II-3 UV 2 76 79 1531.183 -0.108 F
Si I-15 UV 48 2 17 2124.111 +0.533 V   Si II-4 UV 3 76 80 1307.636 -0.249 F
Si I-16 UV 49 2 18 2122.990 -0.915 V   Si II-5 UV 4 76 81 1263.313 +0.759 F
Si I-17 UV 50 2 19 2084.462 -1.573 V   Si II-6 UV 5 76 83 1194.096 +0.742 F
Si I-18 UV 51 2 20 2082.021 -2.229 V   Si II-7 UV 5.01 76 84 1022.698 -0.902 F
Si I-19 UV 52 2 21 2058.133 -1.030 V   Si II-8 UV 6 76 85 991.745 +0.072 F
Si I-20 UV 53 2 22 1991.853 -2.189 V   Si II-9   77 82 2618.212 -4.135 F
Si I-21 2 3 5 4102.935 -2.916 F   Si II-10   77 86 1652.411 -3.759 F
Si I-22 3 3 6 3905.521 -1.092 F   Si II-11   77 106 1249.510 +0.551 F
Si I-23 UV 82 3 15 2842.333 -3.274 V   Si II-12 1 78 82 3858.050 -0.426 F
Si I-24 UV 83 3 18 2631.282 -0.520 V   Si II-13 UV 9 78 86 2072.430 -0.045 F
Si I-25 UV 86 3 21 2532.381 -1.200 V   Si II-14 2 79 82 6355.200 +0.406 F
Si I-26 4 5 10 12045.959 +0.744 F   Si II-15 3 81 86 4129.760 +0.706 F
Si I-27 5 5 11 10789.570 +0.539 F   Si II-16 UV 17 81 91 2905.130 +0.100 F
Si I-28 6 5 12 10482.452 +0.074 F   Si II-17 UV 18 81 99 2501.570 -0.269 F
Si I-29   5 14 9768.400 -2.300 L   Si II-18 4 82 84 5971.800 +0.109 F
Si I-30 9 5 25 5800.880 -0.866 F   Si II-19 5 82 85 5051.010 +0.662 F
Si I-31 10 5 26 5698.800 -0.867 F   Si II-20 6 82 89 3337.590 -0.823 F
Si I-32 11 5 28 5653.900 -1.170 F   Si II-21 7 82 90 3207.970 -0.149 F
Si I-33 11.04 5 45 4846.646 -1.527 F   Si II-22 UV 19 82 96 2725.220 -1.272 F
Si I-34 11.06 5 48 4768.462 -1.155 F   Si II-23   83 86 5113.168 -3.514 F
Si I-35 11.12 6 8 15892.767 -0.036 F   Si II-24 7.02 85 91 7849.400 +0.735 F
Si I-36   6 11 12390.200 -1.710 L   Si II-25 7.03 85 99 5466.720 +0.213 F
Si I-37   6 12 11890.500 -2.090 L   Si II-26 7.05 85 104 4621.600 -0.144 F
Si I-38 13 6 14 10872.520 +0.309 F   Si II-27 7.12 86 97 6679.650 -1.028 F
Si I-39 14 6 16 9413.506 -0.445 F   Si II-28 7.19 87 96 7121.700 -0.642 F
Si I-40 14.01 6 24 6331.957 -3.744 F   Si II-29 7.20 87 97 6826.000 -0.042 F
Si I-41 16 6 29 5948.540 -1.234 F   Si II-30 7.21 87 102 5573.430 -1.096 F
Si I-42 17 6 30 5772.145 -1.745 F   Si II-31 7.23 87 108 4900.700 -1.418 F
F = Fuhr & Wiese (1998), L = Lambert & Luck (1978), V = VALD (Piskunov et al. 1995 ; Kurucz 1993).


while Fig. 1 shows the corresponding Grotrian diagrams.

The data for the energy levels were adopted from a compilation of Martin & Zalubas (1983) which is available from the internet server of the National Institute of Standards and Technology (NIST, http://physics.nist.gov). This source also includes some unpublished measurements. It should be mentioned that apart from LS coupling, other schemes ( $Jl(j_{\rm c} \lbrack K \rbrack ^\pi_J$), $Jj((j,J)^\pi$) were found for Si I. For consistency and practical reasons the concerned energy levels were designated to LS coupling if possible (Table 1).

Data for the line transitions used in the model atom (Table 2) were obtained from the NIST server, the Vienna Atomic Line Data Base (Piskunov et al. 1995; Kurucz 1993) and Lambert & Luck (1978). The NIST data refer to the compilation of Wiese et al. (1969) and the newer version by Fuhr & Wiese (1998). The latter provides improved transition probabilities for some line transitions.
Photoionization cross-sections were taken from the Opacity Project (Seaton et al. 1992, 1994) for almost all energy levels with the exception of eleven mostly high excited ones (marked with * in Table 1). In these cases the Kramers Gaunt aproximation for hydrogen-like atoms as given by Allen (1973) was used.

  \begin{figure} \par\resizebox{10cm}{!}{\includegraphics{ms1145f1.ps}} \end{figure} Figure 1: Grotrian diagrams of the silicon model atom including Si I with 75 energy levels and 53 line transitions and Si II with 40 levels and 31 transitions.
Open with DEXTER

The majority of the more important electron collisional cross-sections of Si I were calculated using the tables given by Sobelman et al. (1981). Transistions not covered by the Sobelman tables were treated with the formulas compiled by Drawin (1967) but additionally needed to be scaled to the corresponding maximum cross-sections. For optically allowed transitions, the maximum cross-sections were calculated with the approximation of Van Regemorter (1962) using all available oscillator strengths and additional values from the Opacity Project. In all other cases, especially for optically forbidden transitions, the cross-sections were scaled with the collision strength formula described by Allen (1973).
Drawin (1967) also provides an estimate for collisional ionization by electrons, which was applied here, and for inelastic collisions with neutral hydrogen atoms. Cross-sections for the latter were calculated with the more generalized formula given by Steenbock & Holweger (1984). Due to a complete lack of data, the collisional parameter Q (maximum cross-section in units of $\pi\,a_0^2\,$) in this formula was set equal to the value of the respective electron collision (derived via the different approximations for optically allowed and forbidden bound-bound and bound-free collisions described above) and was additionally scaled with an empirical factor $S_{\rm H}=0.1$ (Holweger 1996).

   
3 Non-LTE calculations for the Sun

Our non-LTE calculations for the Sun are based on the model atom described above and employ the empirical model atmosphere of Holweger & Müller (1974).
In Figs. 2 and 3 the resulting departure coefficients $b_i = n_{i,{\rm NLTE}}/n_{i,{\rm LTE}}$ are shown for a calculation with the model atom for Si I and Si II, respectively. The numbers on the left of the diagrams correspond to energy level numbers specified in Table 1. In the solar photosphere at $\tau \approx 0.1$ about $\approx$$30\%$ of the silicon atoms are neutral while $\approx$$70\%$ are singly ionized. Our calculations show that most of Si II is present in the ground state. Therefore it is not surprising that the corresponding departure coefficient indicates almost perfect LTE conditions ( $b_i \approx 1$) in the Sun. The same is true for the ground state of Si I. Furthermore, throughout the photosphere ( $\log \tau_{5000} \geq -2$), deviations from LTE are almost negligible for excited levels of Si I. In contrast, most excited levels of Si II are overpopulated with respect to LTE. In both ionization stages there are groups of energy levels whose departure coefficients closely coincide. This is due to very small energy differences within these groups and consequently a strong collisional coupling.

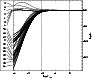  \begin{figure} \par\resizebox{8cm}{!}{\includegraphics{ms1145f2.ps}} \end{figure} Figure 2: Departure coefficients of Si I in the Sun.
Open with DEXTER


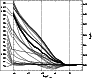  \begin{figure} \par\resizebox{8cm}{!}{\includegraphics{ms1145f3.ps}} \end{figure} Figure 3: Departure coefficients of Si II in the Sun.
Open with DEXTER

3.1 Abundance analysis

To enable a direct comparision between former LTE abundance determinations and the present work, the line list (Table 3) is essentially that adopted by Holweger (1973),

 

 
Table 3: Line list used for the abundance analysis in the Sun: wavelength, excitation potential $\chi _i$ of lower level, equivalent width $W_{\lambda }$ (center of disk), silicon abundances and non-LTE corrections $\Delta \log \epsilon = \log \epsilon_{\rm NLTE} - \log \epsilon_{\rm LTE}$. Oscillator strengths $\log gf$ of Si I: Garz (1973), corrected by Becker et al. (1980); Si II: Froese-Fischer (1968).
$\lambda$ mult. $\chi _i$ $\log gf$ $W_{\lambda }$ $\log \epsilon$ $\Delta \log \epsilon$
(Å) nr. (eV)   (mÅ)    
Si I:
5645.611 10 4.9296 -2.040 34 7.535 -0.004
5665.554 10 4.9201 -1.940 40 7.532 -0.004

5684.485

 11 4.9538 -1.550 60 7.485 -0.007
5690.427 10 4.9296 -1.770 52 7.563 -0.006
5701.105 10 4.9296 -1.950 38 7.514 -0.005
5708.397 10 4.9538 -1.370 78 7.550 -0.011

5772.145

 17 5.0823 -1.650 54 7.599 -0.008
5780.384 9 4.9201 -2.250 26 7.577 -0.004
5793.071 9 4.9296 -1.960 44 7.623 -0.005
5797.860 9 4.9538 -1.950 40 7.567 -0.005

5948.540

 16 5.0823 -1.130 86 7.508 -0.015
6976.520 60 5.9537 -1.070 43 7.532 $0.000\;^a$
7034.901 42.10 5.8708 -0.780 67 7.493 $-0.001\;^{a,b}$

7226.208

 21.05 5.6135 -1.410 36 7.498 -0.005
7680.265 36 5.8625 -0.590 98 7.626 $-0.003\;^b$
7918.382 57 5.9537 -0.510 95 7.565 $0.000\;^b$

7932.348

 57 5.9639 -0.370 97 7.451 $0.000\;^b$
7970.305 57 5.9639 -1.370 32 7.663 $0.000\;^a$
Si II:
6347.110 2 8.1210 0.260 56 7.639 $-0.097\;^c$
6371.370 2 8.1210 -0.040 36 7.521 $-0.064\;^c$

a Larger error in oscillator strength.
b Strongly sensitive to collisional line broadening.
c Susceptable to uncertainties in model atom.


except for the lines for which no departure coefficients were available from the non-LTE calculations. The present sample consists of 18 Si I lines from 10 different multiplets and two Si II lines from the same multiplet. The wavelengths and energy values $\chi _i$ of the lower levels of a line transition are taken from Fuhr & Wiese (1998) as found on the NIST server. The equivalent widths of Holweger (1973) refer to the center of the solar disk. Therefore the present abundance determination was carried out for the center of the disk ($\mu=1$) and a constant microturbulence of $\xi = 1.0\,{\rm km}\,{\rm s}^{-1}$ was used.
Line broadening by collisions with hydrogen atoms is treated as pure van der Waals broadening. The broadening parameter C6 for the individual lines was calculated from the mean square atomic radii of the corresponding energy levels, based on the approximation given by Unsöld (1955). In many applications, this approximation has turned out to underestimate the real damping constants, resulting in a systematic increase of abundance with equivalent width. This was corrected by applying a correction $\Delta \log C_6$, either derived empirically or from quantum mechanical calculations (Steffen 1985; O'Mara 1976). However, no increase with equivalent width is present for the silicon abundances, as can be seen from Fig. 4. For this reason, no correction is necessary and a value of $\Delta \log C_6 = 0$ was adopted for this abundance determination. This agrees with Holweger (1973) and, moreover, confirms the upper limit of $\Delta \log C_6 \approx 0.3$ given in that work.
  \begin{figure} \par\resizebox{13cm}{!}{\includegraphics{ms1145f4.ps}} \end{figure} Figure 4: Solar silicon abundance for the lines in Table 3 over equivalent width $W_{\lambda }$. Filled symbols represent non-LTE values, unfilled LTE abundances (circles for Si I, squares for Si II). The horizontal lines illustrate the weighted mean and the standard deviation (solid).
Open with DEXTER

For line broadening by electron collisions, the approximations according to Griem (1968) (ions) and Cowley (1971) (neutrals) were applied. For the Si I and Si II lines used here, radiation damping is small compared to collisional broadening, and the classical approximation for $\gamma_{\rm rad}$ is used. Oscillator strengths for all lines except for $\lambda 7034$ (9-56) and $\lambda 7226$ (7-37) are tabulated in the recent compilation by Fuhr & Wiese (1998). The derived abundances however show a large scatter with a standard deviation of $\pm 0.26$ dex. The mean silicon abundance is $\log \epsilon_{\rm LTE}= 7.468$ (LTE) and $\log \epsilon_{\rm NLTE}=7.456$ (non-LTE), respectively (Fig. 5b). Taking the oscillator strengths of Wiese et al. (1969) leads to a somewhat lower non-LTE abundance of $\log \epsilon_{\rm NLTE}= 7.405$ and a slightly smaller abundance scatter of 0.24 dex. From former investigations it is known that a much higher accuracy is possible for abundance determinations in the Sun. Obviously the internal accuracy of the Si I f-values in the Wiese et al./Fuhr & Wiese compilations is rather low. Consequently, these values were not taken into account any further. Nevertheless this set of $\log gf$-values can still be applied for the model atom. More satisfactory results were achieved with the older experimental oscillator strenghts of Garz (1973) which apparently have been adopted in the compilation by Kurucz (1993) and in the database VALD. Becker et al. (1980) have revised the absolute scale for Garz's $\log gf$-values which resulted in a general correction of +0.1 dex. Because of the small intrinsic scatter of abundances, the Garz/Becker et al. f-values are used for all Si I lines in this abundance analysis.
For the two Si II lines, different sources for the $\log gf$-values were found to agree within 0.07 dex. The oscillator strengths of Wiese et al. (1969)/Fuhr & Wiese (1998) were not used, instead those derived by Froese-Fischer (1968) were choosen.
The silicon abundances determined with LINFOR from the equivalent widths of the individual lines are listed in Table 3 and illustrated in Fig. 5a.

  \begin{figure} \par\resizebox{7.6cm}{!}{\includegraphics{ms1145f5.ps}} \end{figure} Figure 5: Solar silicon abundance for the lines in Table 3: a) Corrected oscillator strengths by Garz (1973) and Becker et al. (1980). b) Oscillator strengths by Fuhr & Wiese (1998). Filled symbols represent non-LTE values, unfilled LTE abundances (circles for Si I, squares for Si II). The horizontal lines illustrate the weighted mean and the standard deviation (solid) and the former (and confirmed) abundance of $\log \epsilon_{\rm Si} = 7.55$ (dashed).
Open with DEXTER

To account for larger uncertainties in oscillator strengths quoted for some Si I lines with wavelengths $\lambda > 6000$ Å, these lines have been entered with a half weight in the final abundance. Furthermore, the strongest Si I lines with equivalent widths $W_{\lambda} > 90$ mÅ were found to be extremely sensitive to collisional line broadening (van der Waals, Stark), with comparatively large uncertainties in abundance. Consequently the affected lines $\lambda\lambda$ 7680, 7918 and 7932 were half weighted, too. The two Si II lines are much more susceptible to uncertainties in the atomic data for the non-LTE calculations. Hence they were given half weight as well.
With the mentioned weights, an LTE abundance of $\log \epsilon_{\rm LTE} = 7.560 \pm 0.066$ and a non-LTE abundance of $\log \epsilon_{\rm NLTE} = 7.550 \pm 0.056$ was derived, implying a mean non-LTE correction of $\Delta \log \epsilon = -0.010$. Holweger (1973) used almost the same line list but with the original oscillator strenghts measured by Garz (1973) leading to a LTE abundance of $\log \epsilon=7.65$. With the systematic correction of the $\log gf$-values, the abundance was redetermined to $\log \epsilon=7.55$ (Becker et al. 1980). Their line sample is very similar to that used in the present work and the f-values were taken from the same source. There are only small differences in the atmosphere applied by Holweger (1973), mainly slightly different abundances of the main electron donors Fe, Mg and Si, and a depth-dependent microturbulence (see Holweger 1971). Since the present study showed that for Si II and especially Si I lines in the Sun, non-LTE effects are generally small, it is not surprising that the former silicon abundance could be reproduced almost exactly.
Several parameters have been varied to investigate their influence on the silicon abundance. Table 4 shows the deviations from the abundance derived for the above described standard model.
 

 
Table 4: Abundance differences due to different model assumptions for the Sun. Silicon non-LTE mean abundances, mean non-LTE corrections and deviations $(\Delta \log \epsilon)_{\rm d}$ from the result for the standard model.
model assumption $\log \epsilon$ $\Delta \log \epsilon$ $(\Delta \log \epsilon)_{\rm d}$
standard model $7.550 \pm 0.056$ -0.010  
Non-LTE calculations:
no Stark broadening $7.550 \pm 0.056$ -0.010 0.000
$\Delta\log C_6=-1.0$ $7.550 \pm 0.056$ -0.010 0.000
$\Delta\log C_6=+0.5$ $7.549 \pm 0.056$ -0.011 -0.001
no line transitions $7.565 \pm 0.065$ +0.005 +0.015
all $\gamma_{\rm rad} \times 5$ $7.549 \pm 0.056$ -0.011 -0.001
all $\sigma_{\rm PI} \times 0.75$ $7.549 \pm 0.056$ -0.011 -0.001
all $\sigma_{\rm PI} \times 1.25$ $7.551 \pm 0.056$ -0.009 +0.001
all $\sigma_{\rm e} \times 0.1$ $7.543 \pm 0.055$ -0.017 -0.007
all $\sigma_{\rm e} \times 10$ $7.557 \pm 0.061$ -0.003 +0.007
all $\sigma_{\rm H}: S_{\rm H} = 0.01$ $7.545 \pm 0.056$ -0.015 -0.005
all $\sigma_{\rm H}: S_{\rm H} = 10$ $7.556 \pm 0.060$ -0.004 +0.006
Abundance analysis:
$\Delta\log \gamma_{\rm rad} = -1.0$ $7.550 \pm 0.056$ -0.010 0.000
$\Delta\log \gamma_{\rm rad} = +1.0$ $7.543 \pm 0.056$ -0.009 -0.007
$\Delta\log C_4=-0.5$ $7.565 \pm 0.057$ -0.010 +0.015
$\Delta\log C_4=+0.5$ $7.525 \pm 0.063$ -0.009 -0.025
no Stark broadening $7.582 \pm 0.061$ -0.011 +0.032
$\Delta\log C_6=0.6$ $7.519 \pm 0.061$ -0.009 -0.031
$\Delta\log C_6=1.0$ $7.493 \pm 0.071$ -0.008 -0.056
$\xi= 0.8\,{\rm km}\,{\rm }s^{-1}$ $7.562 \pm 0.057$ -0.010 +0.012
ATLAS $7.448 \pm 0.058$ -0.008 -0.102


In general, the uncertainties of atomic data for the non-LTE calculations like line broadening parameters, photoionization and collision cross-sections have only a minor effect on the resulting departure coefficients. However, uncertainties in the parameters for the abundance determination produce larger, altough still small, abundance deviations. Radiative damping has only little effect on the result. As already noticed by Holweger (1973) some Si I lines are quite sensitive to Stark broadening. If Stark broadening is completely neglected, the abundances for $\lambda\lambda$ 7680, 7918 and 7932 increase by 0.11 dex and by 0.08 dex for $\lambda$ 7034. This effect is smaller (<0.03 dex) for most of the remaining lines. Much stronger is the influence of the van der Waals broadening parameter $\log C_6$. A value of $\Delta \log C_6 = +1.0$ would lead to a decrease in abundance by -0.056 dex. Again, the spectral lines $\lambda\lambda$ 7680, 7918 and 7932 are most sensitive. Adopting a microturbulence of $\xi= 0.8\,{\rm km}\,{\rm }s^{-1}$ instead of $\xi = 1.0\,{\rm km}\,{\rm s}^{-1}$ would lead to a small increase of the non-LTE abundance by +0.012 dex. Replacing the Holweger & Müller photospheric model by an ATLAS9 model (Kurucz 1992) ( $T_{\rm eff}= 5780~ {\rm K},\, \log g = 4.44$) results in a considerably lower mean non-LTE abundance of 7.448 dex. Note that the described variations of the model parameters do not represent real error limits but rather demonstrate their different influence on the resulting abundance.

   
3.2 Abundance correction due to granulation

For the present calculations, always static, plane-parallel models are applied which cannot account for horizontal temperature inhomogeneities associated with convection. These inhomogeneities are believed to have a small but non-negligible effect on the photospheric abundances, making further corrections necessary. In a first attempt, Steffen (2000a) determined abundance corrections for various elements from 2D hydrodynamics simulations which yield temperature and pressure fluctuations of the solar surface. Through comparison of 1D and 2D models, both with a depth-independent microturbulence of $1.0\,{\rm km}\,{\rm s}^{-1}$, the effect of temperature inhomogenities on the abundance can be determined. A first application is reported in Aellig et al. (1999). A more detailed description will be given in Steffen & Holweger (2001).
For the case of silicon, M. Steffen (2000b) kindly provided granulation abundance corrections for 10 representative line transistions which permitted an interpolation for the remaining lines in Table 3. The resulting abundance corrections depend on the excitation potential $\chi _i$ and equivalent width. The mean granulation abundance correction for Si I line transitions with $\chi_i \approx 5$ eV is +0.023 and increases to 0.029 dex for $\chi_i \approx 6$ eV. The abundance corrections for the two Si II lines are -0.014. Considering the same weights as in the abundance determination above, a total correction of +0.021 due to granulation results. Finally, the photospheric silicon abundance becomes $\log \epsilon_{\rm GC} = 7.571$, including granulation effects. In 3D simulations, temperature fluctuations are in general smaller than in 2D. Therefore the granulation abundance correction described here should be considered as an upper limit.

   
4 Non-LTE calculations for Vega

The Vega model atmosphere is the same as used in the non-LTE abundance analysis of nitrogen (Rentzsch-Holm 1996). It was generated with the ATLAS9 code (Kurucz 1992), adopting $T_{\rm eff} = 9500$ K, $\log g = 3.90$, $[{\rm M}/{\rm H}] = -0.5$, and a depth-independent microturbulence $\xi = 2.0$kms-1. The adopted subsolar metallicity is in accordance with recent non-LTE analyses (see Rentzsch-Holm 1996), e.g. $[{\rm C}/{\rm H}] = -0.30 \pm 0.18$ for carbon (Stürenburg & Holweger 1991). The applied model atom is the same as for the Sun.
The resulting departure coefficients of Si I (Fig. 6) show that low-lying energy levels are strongly underpopulated with respect to LTE,

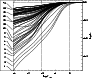  \begin{figure} \par\resizebox{8cm}{!}{\includegraphics{ms1145f6.ps}} \end{figure} Figure 6: Departure coefficients of Si I in Vega.
Open with DEXTER

implying substantial overionisation. Most of the silicon is in the singly ionized stage. The two lowest energy levels of Si II are almost perfectly in LTE (Fig. 7) but most of the excited Si II levels are overpopulated with respect to LTE. The ground state of Si III is also illustrated in Fig. 7.
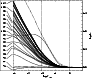  \begin{figure} \par\resizebox{8cm}{!}{\includegraphics{ms1145f7.ps}} \end{figure} Figure 7: Departure coefficients of Si II in Vega. The dashed line represents the ground state of Si III.
Open with DEXTER

Again, strong overpopulation is obvious. However, the fraction of silicon present as Si III is still small compared to Si II.

4.1 Abundance analysis

The abundance analysis of Vega is based on low-noise high-resolution photographic spectra kindly provided by R. Griffin (Griffin & Griffin 1977) covering the visible spectral region. Seven Si II lines (Table 5) were found to be suitable for a reliable abundance determination,

 

 
Table 5: Si II line list used for the abundance analysis in Vega: Wavelength, excitation potential $\chi _i$ of lower level, equivalent width $W_{\lambda }$, silicon abundances and non-LTE corrections $\Delta \log \epsilon = \log \epsilon_{\rm NLTE} - \log \epsilon_{\rm LTE}$. Oscillator strengths: VALD.
$\lambda$ mult. $\chi _i$ $\log gf$ $W_{\lambda }$ $\log \epsilon$ $\Delta \log \epsilon$
(Å) nr. (eV)   (mÅ)    
3862.595 1 6.8575 -0.817 89 6.980 +0.050
4128.054 3 9.8367 0.316 67 6.911 -0.093
4130.872 3 9.8388 -0.824 84 6.928 $-0.106\;^a$
4130.894 3 9.8388 0.476 a 6.928 $-0.106\;^a$
5041.024 5 10.0664 0.291 43 6.980 $-0.062\;^b$
5055.984 5 10.0739 0.593 77 6.970 $-0.062\;^c$
5056.317 5 10.0739 -0.359 c 6.970 $-0.062\;^c$

a,c Si II blend, combined equivalent width.
b Blend with Fe I.


whereas all Si I lines are much too weak. Equivalent widths were measured directly from the tracings. Line broadening is treated in the same way as in the foregoing solar abundance determination. As for the Sun, the oscillator strengths compiled by Wiese et al. (1969) and Fuhr & Wiese (1998) produce a larger abundance scatter ( $\sigma = 0.094$ dex) than the values taken from VALD ( $\sigma = 0.029$ dex). For this reason the latter set is used. The lines marked with a and c in Table 5 are close blends of Si II lines. Consequently, the listed equivalent widths refer to the entire blend, and these blends are only considered with half weight. The line marked with b is also weighted half because it is blended with a Fe I line.
The non-LTE corrections are all negative with values between -0.062and -0.106 with the exception of $\lambda 3862$. For this particular line the non-LTE correction is positive (+0.05) because the departure coefficient of the upper level exceeds that of the lower level, contrary to the other lines.
From these 7 lines a weigthed LTE abundance of $\log \epsilon_{\rm LTE} = 7.005$ was derived. The small mean non-LTE correction of $\Delta \log \epsilon = -0.054$ finally leads to a silicon abundance of $\log \epsilon_{\rm NLTE} = 6.951$ with a standard deviation of 0.029 dex. The estimated error limits, including uncertainties in the equivalent widths, are $\approx$0.1 dex. Table 6 shows the influence of the line broadening parameters and the microturbulence on the mean non-LTE abundance compared to the described standard Vega model.
 

 
Table 6: Abundance differences due to different model assumptions for the abundance determination of Vega. Silicon non-LTE mean abundances, mean non-LTE corrections and deviations $(\Delta \log \epsilon)_{\rm d}$ from the result for the standard model.
model assumption $\log \epsilon$ $\Delta \log \epsilon$ $(\Delta \log \epsilon)_{\rm d}$
standard model $6.951 \pm 0.029$ -0.054  
$\Delta\log \gamma_{\rm rad} = -1.0$ $6.952 \pm 0.029$ -0.054 0.001
$\Delta\log \gamma_{\rm rad} = +1.0$ $6.935 \pm 0.028$ -0.054 -0.016
$\Delta\log C_4=-0.5$ $7.014 \pm 0.017$ -0.062 +0.063
$\Delta\log C_4=+0.5$ $6.861 \pm 0.052$ -0.044 -0.090
no Stark broadening $7.096 \pm 0.047$ -0.083 +0.145
$\Delta\log C_6=1.5$ $6.951 \pm 0.029$ -0.053 0.000
$\xi= 1.5\,{\rm km}\,{\rm s}^{-1}$ $7.179 \pm 0.077$ -0.089 +0.228


For a smaller microturbulence of $\xi= 1.5\,{\rm km}\,{\rm s}^{-1}$, the resulting non-LTE abundances increases by +0.228 dex. Unlike the Sun, van der Waals broadening is less important than Stark broadening, as expected for an A star. Completely neglecting the Stark broadening causes an abundance deviation of +0.119 dex from the standard model.
For comparison, Hill (1995) and Lemke (1990) obtained values of $\log \epsilon_{\rm Si} = 6.86$ and $\log \epsilon_{\rm Si} = 6.94$, respectively, which is in good agreement with the result of this work.
The abundance of silicon in Vega differs by -0.599 dex from the solar value, confirming the deficiency of Si found by other authors.

   
5 Conclusions

Non-LTE effects of silicon in the Sun were found to be small. The solar silicon abundance becomes $\log \epsilon_{\rm NLTE} = 7.550 \pm 0.056$ with a mean non-LTE correction of $\Delta \log \epsilon = -0.010$. This matches almost exactly the previous values (e.g. Becker et al. 1980; Holweger 1979).
The effect of horizontal temperature inhomogeneities associated with convection on the photospheric abundance of Si has also been considered. According to preliminary results by Steffen (2000b), based on 2D hydrodynamics simulations, a mean granulation abundance correction of +0.021 dex is probably a safe upper limit, leading to a silicon abundance of 7.571.
As a by-product of the solar analysis, an assessment of the accuracy of the f-values was possible. The internal accuracy of the f-values of Garz (1973) is superior to those compiled by Wiese et al. (1969) and Fuhr & Wiese (1998).
For Vega, a Si abundance of $\log \epsilon_{\rm NLTE} = 6.951 \pm 0.100$ and a non-LTE correction of only $\Delta \log \epsilon = -0.054$ was derived. This confirms the value $\log \epsilon_{\rm Si} = 6.94$ quoted by Lemke (1990). With respect to the Sun, an underabundance of -0.599 dex results, confirming the general metal deficiency of Vega.

Acknowledgements

The author wishes to thank H. Holweger for suggesting and supporting this work. Further thanks are due to I. Kamp and M. Hempel for their useful comments and help with non-LTE calculations and abundance analysis, M. Steffen for providing unpublished data for granulation abundance corrections and to the referee Y. Takeda for helpful comments.

References

 

Online Material


 

 
Table 7: LTE and non-LTE silicon abundances due to different model assumptions for the Sun for the Si I lines used in the abundance determination.
model assumption   $\lambda 5645.6$ $\lambda 5665.6$ $\lambda 5684.5$ $\lambda 5690.4$ $\lambda 5701.1$ $\lambda 5708.4$ $\lambda 5772.1$ $\lambda 5780.4$ $\lambda 5793.1$
                     
standard model LTE 7.539 7.536 7.492 7.569 7.519 7.561 7.607 7.581 7.628
  NLTE 7.535 7.532 7.485 7.563 7.514 7.550 7.599 7.577 7.623
                     
Non-LTE calculations:  
reference LTE 7.539 7.536 7.492 7.569 7.519 7.561 7.607 7.581 7.628
no line transitions NLTE 7.543 7.541 7.497 7.573 7.523 7.567 7.612 7.585 7.633
no Stark broadening NLTE 7.535 7.532 7.485 7.563 7.514 7.550 7.599 7.577 7.623
$\Delta\log C_6=-1.0$ NLTE 7.535 7.532 7.485 7.563 7.515 7.552 7.599 7.577 7.623
$\Delta\log C_6=+0.5$ NLTE 7.534 7.531 7.485 7.562 7.514 7.550 7.598 7.577 7.623
all $\gamma_{\rm rad} \times 5$ NLTE 7.534 7.531 7.484 7.562 7.513 7.550 7.597 7.576 7.622
all $\sigma_{\rm PI} \times 0.75$ NLTE 7.534 7.531 7.484 7.562 7.514 7.550 7.598 7.576 7.622
all $\sigma_{\rm PI} \times 1.25$ NLTE 7.535 7.532 7.486 7.563 7.515 7.553 7.600 7.578 7.624
all $\sigma_{\rm e} \times 0.1$ NLTE 7.530 7.527 7.479 7.558 7.510 7.545 7.593 7.573 7.618
all $\sigma_{\rm e} \times 10$ NLTE 7.538 7.536 7.490 7.568 7.518 7.559 7.605 7.581 7.627
all $\sigma_{\rm H}: S_{\rm H} = 0.01$ NLTE 7.532 7.529 7.481 7.560 7.512 7.546 7.591 7.575 7.619
all $\sigma_{\rm H}: S_{\rm H} = 10$ NLTE 7.538 7.535 7.490 7.567 7.518 7.559 7.605 7.580 7.627
Abundance analysis:  
$\Delta\log \gamma_{\rm rad} = -1.0$ LTE 7.539 7.537 7.493 7.569 7.519 7.563 7.608 7.581 7.629
  NLTE 7.535 7.532 7.486 7.563 7.515 7.554 7.599 7.577 7.623
$\Delta\log \gamma_{\rm rad} = +1.0$ LTE 7.536 7.532 7.481 7.563 7.515 7.545 7.600 7.573 7.623
  NLTE 7.531 7.527 7.475 7.557 7.511 7.537 7.592 7.569 7.618
$\Delta\log C_4=-0.5$ LTE 7.544 7.542 7.503 7.578 7.524 7.584 7.619 7.583 7.635
  NLTE 7.539 7.538 7.497 7.572 7.520 7.572 7.611 7.579 7.630
$\Delta\log C_4=+0.5$ LTE 7.530 7.526 7.459 7.552 7.509 7.523 7.577 7.569 7.616
  NLTE 7.526 7.521 7.453 7.545 7.505 7.515 7.575 7.565 7.611
no Stark broadening LTE 7.556 7.548 7.517 7.588 7.530 7.607 7.632 7.585 7.642
  NLTE 7.550 7.544 7.509 7.581 7.525 7.596 7.623 7.581 7.636
$\Delta\log C_6=0.6$ LTE 7.527 7.521 7.448 7.543 7.505 7.507 7.569 7.567 7.610
  NLTE 7.523 7.516 7.442 7.538 7.500 7.498 7.562 7.563 7.605
$\Delta\log C_6=1.0$ LTE 7.517 7.508 7.420 7.512 7.493 7.460 7.543 7.561 7.594
  NLTE 7.513 7.504 7.414 7.508 7.489 7.452 7.537 7.557 7.589
$\xi= 0.8\,{\rm km}\,{\rm }s^{-1}$ LTE 7.545 7.545 7.507 7.582 7.527 7.584 7.621 7.586 7.639
  NLTE 7.542 7.541 7.500 7.576 7.523 7.573 7.612 7.582 7.634
                     
ATLAS LTE 7.449 7.441 7.382 7.466 7.426 7.436 7.502 7.490 7.532
  NLTE 7.443 7.437 7.376 7.460 7.421 7.429 7.495 7.486 7.527



 

 
Table 7: continued.
model assumption   $\lambda 5797.9$ $\lambda 5948.5$ $\lambda 6976.5$ $\lambda 7034.9$ $\lambda 7226.2$ $\lambda 7680.3$ $\lambda 7918.4$ $\lambda 7932.3$ $\lambda 7970.3$
                     
standard model LTE 7.572 7.523 7.532 7.494 7.503 7.629 7.565 7.451 7.663
  NLTE 7.567 7.508 7.532 7.493 7.498 7.626 7.565 7.451 7.663
Non-LTE calculations:  
reference LTE 7.572 7.523 7.532 7.494 7.503 7.629 7.565 7.451 7.663
no line transitions NLTE 7.576 7.532 7.536 7.500 7.508 7.641 7.574 7.461 7.668
no Stark broadening NLTE 7.567 7.508 7.532 7.493 7.498 7.626 7.565 7.451 7.663
$\Delta\log C_6=-1.0$ NLTE 7.568 7.509 7.532 7.493 7.499 7.626 7.565 7.451 7.663
$\Delta\log C_6=+0.5$ NLTE 7.567 7.507 7.532 7.492 7.498 7.626 7.565 7.451 7.663
all $\gamma_{\rm rad} \times 5$ NLTE 7.566 7.506 7.531 7.491 7.497 7.624 7.564 7.450 7.662
all $\sigma_{\rm PI} \times 0.75$ NLTE 7.566 7.507 7.531 7.491 7.497 7.624 7.563 7.449 7.662
all $\sigma_{\rm PI} \times 1.25$ NLTE 7.568 7.509 7.532 7.494 7.499 7.627 7.567 7.453 7.664
all $\sigma_{\rm e} \times 0.1$ NLTE 7.562 7.500 7.529 7.489 7.493 7.621 7.561 7.447 7.660
all $\sigma_{\rm e} \times 10$ NLTE 7.571 7.519 7.532 7.494 7.502 7.629 7.566 7.452 7.664
all $\sigma_{\rm H}: S_{\rm H} = 0.01$ NLTE 7.564 7.494 7.532 7.491 7.496 7.618 7.564 7.450 7.663
all $\sigma_{\rm H}: S_{\rm H} = 10$ NLTE 7.571 7.520 7.532 7.494 7.502 7.629 7.565 7.452 7.663
                     
Abundance analysis:  
$\Delta\log \gamma_{\rm rad} = -1.0$ LTE 7.573 7.525 7.532 7.494 7.503 7.630 7.566 7.452 7.663
  NLTE 7.568 7.510 7.532 7.493 7.498 7.627 7.566 7.452 7.663
$\Delta\log \gamma_{\rm rad} = +1.0$ LTE 7.568 7.505 7.530 7.489 7.501 7.620 7.557 7.443 7.663
  NLTE 7.563 7.491 7.530 7.488 7.496 7.616 7.557 7.443 7.663
$\Delta\log C_4=-0.5$ LTE 7.578 7.550 7.550 7.529 7.511 7.691 7.618 7.499 7.671
  NLTE 7.573 7.536 7.552 7.527 7.506 7.687 7.617 7.499 7.672
$\Delta\log C_4=+0.5$ LTE 7.561 7.476 7.510 7.438 7.491 7.559 7.495 7.381 7.639
  NLTE 7.557 7.463 7.510 7.437 7.486 7.556 7.497 7.381 7.639
no Stark broadening LTE 7.584 7.578 7.592 7.573 7.519 7.741 7.678 7.569 7.681
  NLTE 7.579 7.559 7.592 7.572 7.514 7.736 7.678 7.569 7.681
$\Delta\log C_6=0.6$ LTE 7.557 7.456 7.514 7.456 7.490 7.555 7.495 7.381 7.639
  NLTE 7.553 7.443 7.514 7.455 7.486 7.552 7.495 7.381 7.639
$\Delta\log C_6=1.0$ LTE 7.543 7.403 7.503 7.415 7.468 7.499 7.444 7.328 7.628
  NLTE 7.539 7.392 7.503 7.414 7.464 7.496 7.444 7.328 7.629
$\xi= 0.8\,{\rm km}\,{\rm }s^{-1}$ LTE 7.582 7.547 7.535 7.503 7.510 7.646 7.578 7.464 7.668
  NLTE 7.576 7.533 7.536 7.502 7.505 7.642 7.578 7.464 7.668
                     
ATLAS LTE 7.479 7.395 7.448 7.391 7.424 7.516 7.457 7.342 7.579
  NLTE 7.475 7.382 7.448 7.390 7.419 7.513 7.456 7.341 7.579



 

 
Table 8: LTE and non-LTE silicon abundances due to different model assumptions for the Sun for the Si II lines used in the abundance determination.
model assumption   $\lambda 6347.1$ $\lambda 6371.4$   model assumption   $\lambda 6347.1$ $\lambda 6371.4$
                 
standard model LTE 7.736 7.585          
  NLTE 7.639 7.521          
                 
Non-LTE calculations:
reference LTE 7.736 7.585          
no line transitions NLTE 7.736 7.585   no Stark broadening NLTE 7.640 7.521
$\Delta\log C_6=-1.0$ NLTE 7.639 7.521   $\Delta\log C_6=+0.5$ NLTE 7.640 7.522
all $\gamma_{\rm rad} \times 5$ NLTE 7.641 7.522          
all $\sigma_{\rm PI} \times 0.75$ NLTE 7.640 7.521   all $\sigma_{\rm PI} \times 1.25$ NLTE 7.640 7.521
all $\sigma_{\rm e} \times 0.1$ NLTE 7.605 7.491   all $\sigma_{\rm e} \times 10$ NLTE 7.697 7.563
all $\sigma_{\rm H}: S_{\rm H} = 0.01$ NLTE 7.624 7.510   all $\sigma_{\rm H}: S_{\rm H} = 10$ NLTE 7.686 7.554
                 
Abundance analysis:
$\Delta\log \gamma_{\rm rad} = -1.0$ LTE 7.738 7.586   $\Delta\log \gamma_{\rm rad} = +1.0$ LTE 7.702 7.575
  NLTE 7.641 7.522     NLTE 7.622 7.513
$\Delta\log C_6=0.6$ LTE 7.684 7.566   $\Delta\log C_6=1.0$ LTE 7.647 7.548
  NLTE 7.597 7.505     NLTE 7.567 7.490
$\Delta\log C_4=-0.5$ LTE 7.745 7.592   $\Delta\log C_4=+0.5$ LTE 7.697 7.573
  NLTE 7.649 7.527     NLTE 7.618 7.509
no Stark broadening LTE 7.757 7.599   $\xi= 0.8\,{\rm km}\,{\rm }s^{-1}$ LTE 7.762 7.602
  NLTE 7.660 7.533     NLTE 7.664 7.536
                 
ATLAS LTE 7.571 7.440          
  NLTE 7.506 7.399          



 

 
Table 9: LTE and non-LTE silicon abundances due to different model assumptions for Vega for the Si II lines used in the abundance determination.
model assumption   $\lambda 3862.595$ $\lambda 4128.054$ $\lambda 4130.872$ $\lambda 5041.024$ $\lambda 5055.984$
        $\lambda 4130.894$   $\lambda 5056.317$
             
standard model LTE 6.930 7.004 7.034 7.042 7.032
  NLTE 6.980 6.911 6.928 6.980 6.970
             
Abundance analysis:
$\Delta\log \gamma_{\rm rad} = -1.0$ LTE 6.933 7.005 7.035 7.043 7.033
  NLTE 6.984 6.911 6.930 6.980 6.971
$\Delta\log \gamma_{\rm rad} = +1.0$ LTE 6.900 6.993 7.020 7.025 7.026
  NLTE 6.936 6.902 6.918 6.976 6.963
$\Delta\log C_4=-0.5$ LTE 6.976 7.092 7.149 7.080 7.087
  NLTE 7.037 6.981 7.022 7.011 7.016
$\Delta\log C_4=+0.5$ LTE 6.838 6.892 6.888 6.970 6.970
  NLTE 6.879 6.817 6.808 6.917 6.914
no Stark broadening LTE 7.031 7.226 7.347 7.122 7.139
  NLTE 7.105 7.080 7.160 7.048 7.061
$\Delta\log C_6=1.5$ LTE 6.930 7.004 7.033 7.042 7.032
  NLTE 6.980 6.910 6.928 6.980 6.970
$\xi= 1.5\,{\rm km}\,{\rm s}^{-1}$ LTE 7.162 7.309 7.463 7.167 7.189
  NLTE 7.257 7.146 7.251 7.088 7.109


Copyright ESO 2001