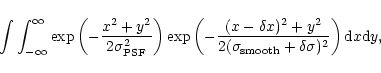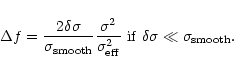A&A 373, 447-458 (2001)
DOI: 10.1051/0004-6361:20010593
HST optical spectral index map of the jet of 3C273![[*]](/icons/foot_motif.gif)
S. Jester 1
- H.-J. Röser 1
- K. Meisenheimer 1
- R. Perley 2
- R. Conway 3
1 - Max-Planck-Institut für Astronomie, Königstuhl 17,
69117 Heidelberg, Germany
2 - NRAO, PO Box 0, Socorro, NM 87801, USA
3 - Jodrell Bank Observatory, Macclesfield, Cheshire, SK11 9DL, UK
Received 26 March 2001 / Accepted 23 April 2001
Abstract
We present HST images at 622nm and 300nm of the jet in
3C273 and determine the run of the optical spectral index at
0
 2 along the jet. The smoothness of spectral index changes
shows that the physical conditions are varying smoothly across the
jet. There is no correlation between the optical flux and spectral
index, as would be expected for relativistic electrons suffering
strong cooling due to synchrotron emission. We find no evidence for
localized acceleration or loss sites. This suggests that the spectral
shape is not changing much throughout the jet. We show that
relativistic beaming and/or sub-equipartition magnetic fields cannot
remove the discrepancy between light-travel time along the jet and the
lifetime of electrons emitting optical synchrotron radiation. We
consider this further evidence in favour of a distributed electron
acceleration process.
2 along the jet. The smoothness of spectral index changes
shows that the physical conditions are varying smoothly across the
jet. There is no correlation between the optical flux and spectral
index, as would be expected for relativistic electrons suffering
strong cooling due to synchrotron emission. We find no evidence for
localized acceleration or loss sites. This suggests that the spectral
shape is not changing much throughout the jet. We show that
relativistic beaming and/or sub-equipartition magnetic fields cannot
remove the discrepancy between light-travel time along the jet and the
lifetime of electrons emitting optical synchrotron radiation. We
consider this further evidence in favour of a distributed electron
acceleration process.
Key words: galaxies: jets - quasars,
individual: 3C273
1 Introduction
While radio jets are a common feature of radio
galaxies and quasars, optical emission has to date been observed
from only about 15 extragalactic jets. As shown by polarimetric
observations (starting with Baade 1956 for M 87), both the radio
and optical emission is synchrotron continuum radiation. While
information on the source's magnetic field structure may be
obtained from the polarisation structure, the diagnostic tool for
the radiating particles is a study of the synchrotron continuum
over as broad a range of frequencies as possible, i.e., from radio
to UV or even X-ray wavelengths, and with sufficient resolution to
discern morphological details.
The radio and optical emission observed from hot spots in
radio jets can be well explained by first-order Fermi acceleration
at a strong shock in the jet (the bow shock)
(Meisenheimer & Heavens 1986; Heavens & Meisenheimer 1987;
Meisenheimer et al. 1989, 1997). But it is not clear that the
optical synchrotron emission from the jet body, extending
over tens of kiloparsecs in some cases, can be equally well
explained by acceleration at strong shocks inside the jet. As is
well known from standard synchrotron theory, electrons with the
highly relativistic energies required for the emission of
high-energy (optical and UV) synchrotron radiation have a very
short lifetime which is much less than the light-travel time down
the jet body in, e.g., 3C273. Observations of
optical synchrotron emission from such jets (Röser & Meisenheimer 1991; 1999) as
well as from the "filament'' near Pictor A's hot spot
(Röser & Meisenheimer 1987; Perley et al. 1997) suggest that both an extended, "jet-like'' and
a localized, "shock-like'' acceleration process are at work in
these objects in general and 3C273's jet in particular
(Meisenheimer et al. 1997). The extended mechanism may also be at work in the
lobes of radio galaxies, where the observed maximum particle
energies are above the values implied by the losses within the hot
spots (Meisenheimer et al. 1996) and by the dynamical ages of the lobes
(Blundell & Rawlings 2000).
The fundamental question is thus: how can we explain
high-frequency synchrotron emission far from obvious acceleration
sites in extragalactic jets? Although most of the known optical
jets are very small and faint (Scarpa & Urry 2000), there are a few jets
with sufficient angular size and surface brightness to be studied
in detail: those in M 87 (a radio galaxy), PKS
0521-365 (an
elliptical galaxy with a BLLac core), and 3C273 (a quasar).
We have embarked on a detailed study of the jet in 3C273 using
broad-band observations at various wavelengths obtained with
today's best observatories in terms of resolution: the VLA (in
combination with MERLIN data at  6cm) and the HST. Using
these observations, we will derive spatially resolved (at
0
6cm) and the HST. Using
these observations, we will derive spatially resolved (at
0
 2) synchrotron spectra for the jet. 3C273's radio jet
extends continuously from the quasar out to a terminal hot spot at
21
2) synchrotron spectra for the jet. 3C273's radio jet
extends continuously from the quasar out to a terminal hot spot at
21
 5 from the core, while optical emission has been observed
only from 10
5 from the core, while optical emission has been observed
only from 10
 outwards
outwards![[*]](/icons/foot_motif.gif) . On ground-based images, the optical jet appears to
consist of a series of bright knots with fainter emission
connecting them. So far, synchrotron spectra have been derived
for the hot spot and the brightest knots using ground-based
imaging in the radio (Conway et al. 1993), near-infrared
. On ground-based images, the optical jet appears to
consist of a series of bright knots with fainter emission
connecting them. So far, synchrotron spectra have been derived
for the hot spot and the brightest knots using ground-based
imaging in the radio (Conway et al. 1993), near-infrared
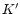 -band (Neumann et al. 1997) and optical I, R, B-bands
(Röser & Meisenheimer 1991) at a common resolution of 1
-band (Neumann et al. 1997) and optical I, R, B-bands
(Röser & Meisenheimer 1991) at a common resolution of 1
 3
(Meisenheimer et al. 1996a; Röser et al. 2000). The radio-to-optical continuum can be
explained by a single power-law electron population leading to a
constant radio spectral index
3
(Meisenheimer et al. 1996a; Röser et al. 2000). The radio-to-optical continuum can be
explained by a single power-law electron population leading to a
constant radio spectral index![[*]](/icons/foot_motif.gif) of -0.8,
but with a high-energy cutoff frequency decreasing from
of -0.8,
but with a high-energy cutoff frequency decreasing from
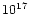 Hz to 1015Hz outwards along the jet. The aim of
the study is both the determination of the spectral shape of the
synchrotron emission, and by fitting synchrotron spectra according
to Meisenheimer et al. (1989), deriving the maximum particle energy
everywhere in the jet. The observed spectra can then be
compared to predictions from theoretical work.
Hz to 1015Hz outwards along the jet. The aim of
the study is both the determination of the spectral shape of the
synchrotron emission, and by fitting synchrotron spectra according
to Meisenheimer et al. (1989), deriving the maximum particle energy
everywhere in the jet. The observed spectra can then be
compared to predictions from theoretical work.
As an intermediate result of our study, we present HST WFPC2 images of
the jet in 3C273 in a red (F622W) and near-UV (F300W) broadband
filter. The near-UV observations constitute the highest-frequency
detection of synchrotron emission from 3C273 so far. (Extended X-ray
emission has also been observed, but it is unclear at present whether
this, too, is due to synchrotron radiation,
Röser et al. 2000;
Marshall et al. 2001; Sambruna et al. 2001.)
From these images, we construct an
optical spectral index map at 0
 2 resolution.
After a description of the observations and the data reduction in
Sects. 2 and 3, we examine the direct
images in Sect. 4. The creation and description of the
spectral index map follow in Sect. 5. We analyse the map
in Sect. 6 and conclude in Sect. 7. Details
regarding the alignment of HST images are found in
Appendix A.
2 resolution.
After a description of the observations and the data reduction in
Sects. 2 and 3, we examine the direct
images in Sect. 4. The creation and description of the
spectral index map follow in Sect. 5. We analyse the map
in Sect. 6 and conclude in Sect. 7. Details
regarding the alignment of HST images are found in
Appendix A.
2 Observations
Observations were made using the Planetary Camera of the second
Wide Field and Planetary Camera (WFPC2) (Biretta et al. 2000) on board the
HUBBLE SPACE TELESCOPE![[*]](/icons/foot_motif.gif) in three
sets of observations
on March 23rd and June 5th/6th, 1995, for 35500s
through filters F300W (ultra-violet, U) and
10000s through F622W (roughly
in three
sets of observations
on March 23rd and June 5th/6th, 1995, for 35500s
through filters F300W (ultra-violet, U) and
10000s through F622W (roughly 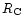 in the Kron-Cousins
system). The resulting limiting magnitudes are listed in
Table 1. The jet was imaged onto the center of the
Planetary Camera (PC) chip which has 800 by 800 pixels with a
nominal size of 0
in the Kron-Cousins
system). The resulting limiting magnitudes are listed in
Table 1. The jet was imaged onto the center of the
Planetary Camera (PC) chip which has 800 by 800 pixels with a
nominal size of 0
 0455 projected on the sky. The telescope
was oriented such that the position angle of the PC chip's y-axis
was
0455 projected on the sky. The telescope
was oriented such that the position angle of the PC chip's y-axis
was 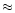
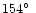 .
This way, the quasar itself is also mapped
on the PC, while each of three neighbouring astrometric reference
stars (see Table 3 in Röser & Meisenheimer 1991) was observed on one of the three
Wide Field chips. This choice gives distortion-free images of the
jet, while allowing the use of the quasar and the reference stars
for image alignment.
The total exposure time was split into individual exposures of about
2500s or one HST orbit, executed in three separate sets of observations. Each of
these exposures was done at a telescope pointing slightly offset from
all others (by up to 1
.
This way, the quasar itself is also mapped
on the PC, while each of three neighbouring astrometric reference
stars (see Table 3 in Röser & Meisenheimer 1991) was observed on one of the three
Wide Field chips. This choice gives distortion-free images of the
jet, while allowing the use of the quasar and the reference stars
for image alignment.
The total exposure time was split into individual exposures of about
2500s or one HST orbit, executed in three separate sets of observations. Each of
these exposures was done at a telescope pointing slightly offset from
all others (by up to 1
 )
to facilitate the correction for chip
artifacts. One short exposure was obtained in each set of observations and filter to
measure the positions of the quasar and reference stars, most of which
are saturated on the long exposures.
Our study of 3C273's jet will be conducted employing a 0
)
to facilitate the correction for chip
artifacts. One short exposure was obtained in each set of observations and filter to
measure the positions of the quasar and reference stars, most of which
are saturated on the long exposures.
Our study of 3C273's jet will be conducted employing a 0
 2
effective beam size. This results in a typical signal to noise ratio
(S/N) per resolution element in the red band of around 100 in the brightest
regions and 30-40 in inter-knot regions. Because both
the jet flux and the WFPC2 and telescope throughput decrease towards
the UV, the UV-band S/N is only about 40 in the brightest regions,
while the inter-knot regions are barely detected.
2
effective beam size. This results in a typical signal to noise ratio
(S/N) per resolution element in the red band of around 100 in the brightest
regions and 30-40 in inter-knot regions. Because both
the jet flux and the WFPC2 and telescope throughput decrease towards
the UV, the UV-band S/N is only about 40 in the brightest regions,
while the inter-knot regions are barely detected.
3 Data reduction
The data were re-calibrated under IRAF with the STSDAS
package provided by STScI, using the "most recent'' calibration
reference files as of December 1998, because some of the files had
changed since the original observations. The values of background
noise measured on the calibrated frames agree well with the values
expected from photon statistics, as calculated from the expected read
noise, dark current and sky background level.
One of the PC chip's charge traps (Whitmore & Wiggs 1995; Voit et al. 1998) lies inside
the jet image, in Col. 339. This has no observable effect on the
faint UV image, but the effect had to be corrected on the
well-exposed red-band images. This was done by replacing the
affected portion of each image by the corresponding pixels from an
offset image, as a correction according to Whitmore & Wiggs (1995) unduly
increased the noise in the corrected part of the image.
The images were initially registered using the commanded offsets to
the nearest pixels. This alignment is sufficient for the rejection of
cosmic rays as these only affect a small number of adjacent pixels.
Cosmic rays were rejected using a standard  -
- algorithm,
rejecting all pixel values deviating more than
algorithm,
rejecting all pixel values deviating more than 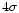 from the
local (low-biased) median in a first pass, and neighbouring pixels
with more than
from the
local (low-biased) median in a first pass, and neighbouring pixels
with more than
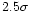 deviation in a second pass. The number of
pixels treated this way agrees with the expected cosmic ray hit rate
for the images.
A model of the sky background and "horizontal smear'' (increased
pixel values in rows containing saturated pixels from the quasar's
core, Chap. 4 of Biretta et al. 2000) was fitted in the part of the image containing the jet using
second-order polynomials along rows. The coefficients of the
polynomials were then smoothed in the perpendicular direction. The
conversion from photon count rate to physical flux units used the
throughput information provided by STScI which is valid after the 1997
deviation in a second pass. The number of
pixels treated this way agrees with the expected cosmic ray hit rate
for the images.
A model of the sky background and "horizontal smear'' (increased
pixel values in rows containing saturated pixels from the quasar's
core, Chap. 4 of Biretta et al. 2000) was fitted in the part of the image containing the jet using
second-order polynomials along rows. The coefficients of the
polynomials were then smoothed in the perpendicular direction. The
conversion from photon count rate to physical flux units used the
throughput information provided by STScI which is valid after the 1997
SYNPHOT update.
![\begin{figure}
\includegraphics[width=11cm,clip]{ms1311f1.eps} %
\end{figure}](/articles/aa/full/2001/26/aa1311/Timg33.gif) |
Figure 1:
The jet in red light (620nm) after background
subtraction. Logarithmic grey-levels run from 0 to
0.04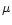 Jy/pixel, 0 Jy/pixel, 0
 08 effective beam size, 0 08 effective beam size, 0
 045 pixel
size. The quasar core lies 10 045 pixel
size. The quasar core lies 10
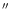 to the northeast
from A. The labelling of the jet features as introduced by
Lelièvre et al. (1984) and extended by Röser & Meisenheimer (1991), together with the hot spot nomenclature
from Flatters & Conway (1985) is also shown. Note that the
labelling used by Bahcall et al. (1995) is slightly
different.
to the northeast
from A. The labelling of the jet features as introduced by
Lelièvre et al. (1984) and extended by Röser & Meisenheimer (1991), together with the hot spot nomenclature
from Flatters & Conway (1985) is also shown. Note that the
labelling used by Bahcall et al. (1995) is slightly
different. |
| Open with DEXTER |
![\begin{figure}
\includegraphics[width=11cm,clip]{ms1311f2.eps} %
\end{figure}](/articles/aa/full/2001/26/aa1311/Timg34.gif) |
Figure 2:
The jet in UV light (300nm) after background
subtraction. Logarithmic grey-levels run from 0 to
0.014 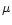 Jy/pixel, 0 Jy/pixel, 0
 06 effective beam size, 0 06 effective beam size, 0
 045 pixel size. 045 pixel size. |
| Open with DEXTER |
4 Maps of the optical brightness
The calibrated images are presented in
Figs. 1 and 2. The morphology of the jet is
identical in both images and appears rather similar to the morphology in
high-resolution radio maps (Conway et al. 1993; Bahcall et al. 1995). The exception to
this is the radio hot spot, being the dominant part in the radio but
fairly faint at high frequencies. Our images show structural details
of the optical jet which were not discernible on earlier, shallower
and undersampled HST WF images of 0
 1 pixel size
(Bahcall et al. 1995). Based on our new maps, the term "knots'' seems
inappropriate for the brightness enhancements inside the jet, as these
regions are resolved into filaments. The higher resolution
necessitates a new nomenclature for the jet features
(Fig. 1). For consistency with earlier work
(Lelièvre et al. 1984; Flatters & Conway 1985; Röser & Meisenheimer 1991), our nomenclature is partly at variance
with that introduced by Bahcall et al. (1995).
The jet is extremely well collimated - region A has an extent
(width at half the maximum intensity) of no more than 0
1 pixel size
(Bahcall et al. 1995). Based on our new maps, the term "knots'' seems
inappropriate for the brightness enhancements inside the jet, as these
regions are resolved into filaments. The higher resolution
necessitates a new nomenclature for the jet features
(Fig. 1). For consistency with earlier work
(Lelièvre et al. 1984; Flatters & Conway 1985; Röser & Meisenheimer 1991), our nomenclature is partly at variance
with that introduced by Bahcall et al. (1995).
The jet is extremely well collimated - region A has an extent
(width at half the maximum intensity) of no more than 0
 8
perpendicular to the average jet position angle of
8
perpendicular to the average jet position angle of
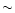
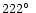 (opening angle
(opening angle
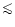
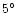 ). Even region D2/H3 is only 1
). Even region D2/H3 is only 1
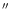 wide
(opening angle
wide
(opening angle 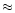
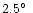 ). The optical jet
appears to narrow towards the hot spot, in the transition from H3
to H2.
Region A is now seen to extend further towards the core than
previously known. It may be noteworthy that Lelièvre et al. (1984)
reported the detection of an extension of knot A towards the
quasar, whose existence at the reported flux level was not,
however, confirmed by later work.
The criss-cross pattern visible in regions C1 and C2, and less
clearly in B1-2 and D1, is reminiscent of a (double?) helical
structure (Bahcall et al. 1995), but could also be explained by oblique
double shocks (Hardee & Norman 1989).
The jet has three "extensions'' (Fig. 1), none of
which has been detected at radio wavelengths. The morphology of
the outer extension supports the classification as a galaxy
based on its colours made by Röser & Meisenheimer (1991). The nature of the
other two extensions, however, remains unknown even with these
deeper, higher resolution images. The northern inner
extension was already resolved into two knots (In1, In2) on a
FAINT OBJECT CAMERA image (Thomson et al. 1993). The two knots are
extended sources and clearly connected to each other. The
southern extension is featureless and an extended source.
Comparing the direct images, we can immediately estimate that the jet's
colour slowly turns redder outwards from region A. The similarity of
the jet images in both filters shows that there are no abrupt colour
changes within the jet. For a quantitative assessment of the
extensions' and the jet's colour in the following, we derive an
optical spectral index map.
). The optical jet
appears to narrow towards the hot spot, in the transition from H3
to H2.
Region A is now seen to extend further towards the core than
previously known. It may be noteworthy that Lelièvre et al. (1984)
reported the detection of an extension of knot A towards the
quasar, whose existence at the reported flux level was not,
however, confirmed by later work.
The criss-cross pattern visible in regions C1 and C2, and less
clearly in B1-2 and D1, is reminiscent of a (double?) helical
structure (Bahcall et al. 1995), but could also be explained by oblique
double shocks (Hardee & Norman 1989).
The jet has three "extensions'' (Fig. 1), none of
which has been detected at radio wavelengths. The morphology of
the outer extension supports the classification as a galaxy
based on its colours made by Röser & Meisenheimer (1991). The nature of the
other two extensions, however, remains unknown even with these
deeper, higher resolution images. The northern inner
extension was already resolved into two knots (In1, In2) on a
FAINT OBJECT CAMERA image (Thomson et al. 1993). The two knots are
extended sources and clearly connected to each other. The
southern extension is featureless and an extended source.
Comparing the direct images, we can immediately estimate that the jet's
colour slowly turns redder outwards from region A. The similarity of
the jet images in both filters shows that there are no abrupt colour
changes within the jet. For a quantitative assessment of the
extensions' and the jet's colour in the following, we derive an
optical spectral index map.
5 Optical spectral index map
Firstly, we consider how to derive a map of the spectral index
 from the presented images, at a common effective beam
size of 0
from the presented images, at a common effective beam
size of 0
 2.
2.
5.1 Definition of optical spectral index
Independently of whether a spectrum actually does follow a power law
over any range of frequencies, a local two-point spectral index can be
defined between any two surface brightness measurements B1, B2 at
frequencies 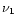 and
and 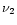 (with
(with
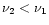 ),
respectively, as
),
respectively, as
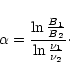 |
(1) |
The error on the spectral index is computed from the values of the
noise
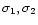 in the respective input images:
in the respective input images:
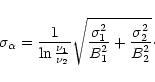 |
(2) |
This formula shows that the spectral index error depends on the S/N
of the input images and the "baseline'' between the wavelengths at
which the observations are made. In the following, we will use
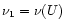 for the UV and
for the UV and
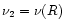 for the red, together with
B1 = BU, B2 = BR. With the mean wavelengths of the filters,
2942.8Å for F300W and 6162.8Å for F622W (Biretta et al. 2000), a cut
on the signal-to-noise ratio
for the red, together with
B1 = BU, B2 = BR. With the mean wavelengths of the filters,
2942.8Å for F300W and 6162.8Å for F622W (Biretta et al. 2000), a cut
on the signal-to-noise ratio
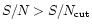 of the input
images limits the spectral index error to at most
of the input
images limits the spectral index error to at most
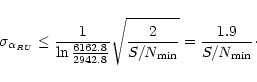 |
(3) |
In our case, the UV-band S/N is always much inferior to that in the
red band, so the error will actually be dominated by the UV noise and
hence smaller than the maximum from Eq. (3) for the most
part. The noise in the input images is calculated from the calibrated
images and includes shot noise due to both observed photons and dark
current as well as the read noise, but excludes systematic errors,
whose expected magnitude we now examine.
5.2 Systematic errors for a spectral index determination
We consider the systematic errors which may be introduced when
combining two images taken through different filters, or by different
instruments and telescopes. The main danger in a determination of
spectral gradients lies in a misalignment between the images which
would introduce spurious gradients; referring the flux to different
effective beam sizes will lead to wrong spectral index determinations
as well. Following considerations given in Sect. A.1,
we deduce that a 5% limit on the flux error due to misalignment
requires aligning the images to better than 10% of the effective PSF
full width. The error in the PSF determination is negligible when, as
in our case, the smoothing Gaussian is much wider than the PSF.
The 0
 2 effective resolution aimed for thus requires knowing the
relative alignment of all images in the data set to better than
20mas or 0.44 PC pixels. The absolute telescope pointing
does not need to be known for this purpose as we tie all positions
to the quasar core as origin.
After detailed investigations of all issues related to relative
alignment of HST images (see Sect. A.2), we used the
following procedure: as the first step, all exposures through one
filter and within one set of observations are summed up using the
relative positions from the "jitter files'' provided as part of
the observing data package (typical error 5 mas). The exposures
through F300W were distributed over three different sets of
observations, so we obtain three intermediate images. For
aligning these with each other, we use the average of the
positional shifts of the quasar and three astrometric stars
(observed on the Wide Field chips) measured on the intermediate
image or the short exposure in each set of observations (error
10 mas). The field flattener windows inside WFPC2 introduce a
wavelength dependence of the plate scale, which has to be removed
prior to combination of the images taken through different
filters. We therefore sample all four intermediate images (three
UV and one red) onto a grid of one tenth of their average plate
scale with a pixel size of 0
2 effective resolution aimed for thus requires knowing the
relative alignment of all images in the data set to better than
20mas or 0.44 PC pixels. The absolute telescope pointing
does not need to be known for this purpose as we tie all positions
to the quasar core as origin.
After detailed investigations of all issues related to relative
alignment of HST images (see Sect. A.2), we used the
following procedure: as the first step, all exposures through one
filter and within one set of observations are summed up using the
relative positions from the "jitter files'' provided as part of
the observing data package (typical error 5 mas). The exposures
through F300W were distributed over three different sets of
observations, so we obtain three intermediate images. For
aligning these with each other, we use the average of the
positional shifts of the quasar and three astrometric stars
(observed on the Wide Field chips) measured on the intermediate
image or the short exposure in each set of observations (error
10 mas). The field flattener windows inside WFPC2 introduce a
wavelength dependence of the plate scale, which has to be removed
prior to combination of the images taken through different
filters. We therefore sample all four intermediate images (three
UV and one red) onto a grid of one tenth of their average plate
scale with a pixel size of 0
 0045548. We sum the UV
intermediate images to give a UV final image. Because of the
scale change, we have to align this to the red image using the
quasar position only (estimated error 10 mas-15 mas). We then
rebin both images to the final pixel size of 0
0045548. We sum the UV
intermediate images to give a UV final image. Because of the
scale change, we have to align this to the red image using the
quasar position only (estimated error 10 mas-15 mas). We then
rebin both images to the final pixel size of 0
 045548. Adding
up all errors in quadrature, the error margin of 20 mas is just
kept.
045548. Adding
up all errors in quadrature, the error margin of 20 mas is just
kept.
 |
Figure 3:
Optical spectral index
 (
(
 )
at 0 )
at 0
 2 resolution. The contours show the
red-band image and are logarithmic
with a factor 2 resolution. The contours show the
red-band image and are logarithmic
with a factor 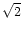 from 0.07
from 0.07 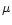 Jy/beam to
0.8 Jy/beam to
0.8 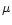 Jy/beam. Jy/beam. |
| Open with DEXTER |
Note that the rebinning has only matched the scales of the two images,
but not removed the geometric distortion of the focal plane. The
next-order wavelength-dependent term in the geometric distortion
solution is at least two orders of magnitudes smaller than the scale
difference. Both the red and the ultraviolet image can thus be
assumed to have identical distortion solutions. We therefore ignore
the geometric distortion for the remainder of this paper, but caution
that it must be taken into account when comparing these data with
data obtained at other instruments.
5.3 Calculation of the optical spectral index map
We have now aligned the images in the two
filters to better than 0
 02. When comparing flux measurements
on these images, they have to be referred to a common beam size.
The maps are therefore smoothed to a common 0
02. When comparing flux measurements
on these images, they have to be referred to a common beam size.
The maps are therefore smoothed to a common 0
 2 using
Gaussians with a width matched to the effective FWHM of the PSF in
each image. This operation retains the original pixel size. As
few point sources are available, the effective FWHM is determined
on PSF models generated using the
2 using
Gaussians with a width matched to the effective FWHM of the PSF in
each image. This operation retains the original pixel size. As
few point sources are available, the effective FWHM is determined
on PSF models generated using the TinyTIM
software (Krist 1999), resulting in 0
 08 on the red and
0
08 on the red and
0
 06 on the UV-band image. Because of sampling effects, the
measured widths are larger than the size of the Airy disk of the
HST's primary at the corresponding wavelengths.
Figure 3 shows the spectral index map obtained from the
images (Figs. 1 and 2) according to
Eq. (1). Only those points are shown in the map which
have an aperture S/N of at least 5 on both images. This limits
the error in the spectral index to 0.4 (Eq. (3)). The
error is less than 0.1 inside all knot regions, so that a colour
change indicates statistically significant variations of the
spectral index. Figure 4 shows the spectral index
along a tracing of the jet obtained from a rotated map with the
jet's mean position angle of 222
06 on the UV-band image. Because of sampling effects, the
measured widths are larger than the size of the Airy disk of the
HST's primary at the corresponding wavelengths.
Figure 3 shows the spectral index map obtained from the
images (Figs. 1 and 2) according to
Eq. (1). Only those points are shown in the map which
have an aperture S/N of at least 5 on both images. This limits
the error in the spectral index to 0.4 (Eq. (3)). The
error is less than 0.1 inside all knot regions, so that a colour
change indicates statistically significant variations of the
spectral index. Figure 4 shows the spectral index
along a tracing of the jet obtained from a rotated map with the
jet's mean position angle of 222
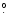 2 along the horizontal.
2 along the horizontal.
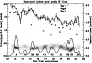 |
Figure 4:
Run of the red-band brightness and optical spectral index
along the outer half of the jet in 3C273, for a 0
 2
beam. 2
beam.
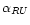 was determined from Figs. 1 and 2, while
was determined from Figs. 1 and 2, while
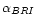 for a 1
for a 1
 3 beam is taken from
Röser & Meisenheimer (1991). For comparison, we show 3 beam is taken from
Röser & Meisenheimer (1991). For comparison, we show
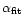 ,
the corresponding spectral
index obtained from synchrotron
spectra fitted by Meisenheimer et al. (1996a) and Röser et al. (2000). While the
observed spectral index agrees with older data, it is now clear that
the fit is inadequate for the optical part of the spectrum. The
steeper spectral index of the fit may either be
due to contamination of the infrared flux by a "backflow'' component
around the jet, or because of the presence of a second high-energy electron
population in the jet which is not included in the fit (see
Sect. 6.3.1 for a discussion of the discrepancies). ,
the corresponding spectral
index obtained from synchrotron
spectra fitted by Meisenheimer et al. (1996a) and Röser et al. (2000). While the
observed spectral index agrees with older data, it is now clear that
the fit is inadequate for the optical part of the spectrum. The
steeper spectral index of the fit may either be
due to contamination of the infrared flux by a "backflow'' component
around the jet, or because of the presence of a second high-energy electron
population in the jet which is not included in the fit (see
Sect. 6.3.1 for a discussion of the discrepancies). |
| Open with DEXTER |
5.4 Colours of the extensions
The outer extension is not
bright enough to show up on the map in its entirety. The
variation of
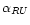 across it are consistent with a spiral
galaxy. The inner extension's two knots have markedly
different colours on the spectral index map. Knot In2 shows a
spectral index gradient,
across it are consistent with a spiral
galaxy. The inner extension's two knots have markedly
different colours on the spectral index map. Knot In2 shows a
spectral index gradient,
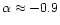 to -0.3 roughly
parallel to the jet and outwards from the quasar position. Knot
In1 has a much steeper spectral index of about -1.5 and shows no
gradient. Interestingly, the southern extension S has the
flattest spectrum (
to -0.3 roughly
parallel to the jet and outwards from the quasar position. Knot
In1 has a much steeper spectral index of about -1.5 and shows no
gradient. Interestingly, the southern extension S has the
flattest spectrum (
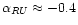 )
of all regions on
the map.
)
of all regions on
the map.
5.5 Spectral index of the jet
The optical spectral index declines globally outwards from -0.5 near
the onset of the optical jet at A to -1.6 in D2/H3. This trend does
not continue into the hot spot, again stressing the physical
distinction between jet and hot spot. The general steepening is in
agreement with previous determinations of the knots' synchrotron
spectrum which showed a decline of the cutoff frequency outwards
(Meisenheimer et al. 1996a; Röser et al. 2000). The optical spectral index
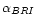 determined at 1
determined at 1
 3 resolution (Röser & Meisenheimer 1991)
agrees very well with
our new determination of
3 resolution (Röser & Meisenheimer 1991)
agrees very well with
our new determination of
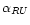 at the much higher resolution
(Fig. 4). The only discrepancy arises in C2/D1;
we defer a discussion to Sect. 6.3.1. The smooth
variations of the spectral index along the jet show that the physical
conditions in the jet change remarkably smoothly over scales of many
kpc. There is no strict correlation between red-band surface
brightness and spectral index like that found in the jet in M 87
(Meisenheimer et al. 1996a; Perlman et al. 2001).
There is a marginally significant flattening of the spectrum in the
transitions A-B1, B1-B2, C1-C2, and moving out of C2, consistent with
the absence of losses. In any case, the overall steepening of
the spectrum (from region A down do D2/H3) is less rapid than that
within individual regions (e.g., A and B2). There is no
significant steepening from D1 out to the bridge between H3 and H2,
despite large variations in surface brightness.
The criss-cross morphology in C1, C2, B1, B2 and D1 is reflected on
the spectral index map as a band of one colour crossing a second one.
This is most clearly seen in knot C1 which has a green band of
at the much higher resolution
(Fig. 4). The only discrepancy arises in C2/D1;
we defer a discussion to Sect. 6.3.1. The smooth
variations of the spectral index along the jet show that the physical
conditions in the jet change remarkably smoothly over scales of many
kpc. There is no strict correlation between red-band surface
brightness and spectral index like that found in the jet in M 87
(Meisenheimer et al. 1996a; Perlman et al. 2001).
There is a marginally significant flattening of the spectrum in the
transitions A-B1, B1-B2, C1-C2, and moving out of C2, consistent with
the absence of losses. In any case, the overall steepening of
the spectrum (from region A down do D2/H3) is less rapid than that
within individual regions (e.g., A and B2). There is no
significant steepening from D1 out to the bridge between H3 and H2,
despite large variations in surface brightness.
The criss-cross morphology in C1, C2, B1, B2 and D1 is reflected on
the spectral index map as a band of one colour crossing a second one.
This is most clearly seen in knot C1 which has a green band of
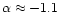 across an orange region of
across an orange region of
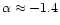 ,
supporting the interpretation of two emission regions appearing on top
of each other. The spectral index near the hot spot shows a flip from
flat (-1.0) to steep (-1.5).
,
supporting the interpretation of two emission regions appearing on top
of each other. The spectral index near the hot spot shows a flip from
flat (-1.0) to steep (-1.5).
6 Discussion
6.1 The jet's extensions
Before analysing the jet emission proper, we consider the relation of
the extensions to the jet. Our new images confirm the outer
extension's nature as spiral galaxy. The spectral index map gives us
few hints about the nature of the emission mechanism for the
inner and southern extensions. We have therefore measured
their integral fluxes at 300nm and 620nm (this paper) and
at 1.6 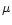 (HST NICMOS camera 2 imaging
(HST NICMOS camera 2 imaging![[*]](/icons/foot_motif.gif) ,
in prep.). Figure 5 shows the resulting
spectral energy distributions. In1, with the steepest
,
in prep.). Figure 5 shows the resulting
spectral energy distributions. In1, with the steepest
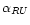 ,
is also the brightest in the infrared. The infrared flux points of
both extension S and of In2 lie on the continuation of the power law
with index -0.4, determined on the optical spectral index map. If
this power law were valid up to radio wavelengths, it would predict a
flux at
,
is also the brightest in the infrared. The infrared flux points of
both extension S and of In2 lie on the continuation of the power law
with index -0.4, determined on the optical spectral index map. If
this power law were valid up to radio wavelengths, it would predict a
flux at 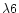 cm of about 50
cm of about 50 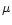 Jy for the northwestern knot
In1, and of about 45
Jy for the northwestern knot
In1, and of about 45 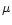 Jy for the southern extension S. This is a
factor of order 100 below the flux from the jet at this wavelength
(Conway et al. 1993), and any emission at this level would not be detected
even on our new VLA maps with an rms noise of
Jy for the southern extension S. This is a
factor of order 100 below the flux from the jet at this wavelength
(Conway et al. 1993), and any emission at this level would not be detected
even on our new VLA maps with an rms noise of  0.8mJy.
There is no similarly obvious extrapolation of In1's SED to radio
wavelengths. A full comparison will be presented in a future paper.
The inner extension shows a polarisation signal on unpublished
ground-based maps made by our group and on polarimetric images
obtained with the Faint Object Camera on board HST (Thomson et al. 1993). A
polarisation signal could be due to scattered quasar light
(Röser & Meisenheimer 1991) or, together with possible radio emission, synchrotron
radiation. We aim to clarify the nature of the inner extensions by
planned polarimetric and spectroscopic observations with the VLT.
0.8mJy.
There is no similarly obvious extrapolation of In1's SED to radio
wavelengths. A full comparison will be presented in a future paper.
The inner extension shows a polarisation signal on unpublished
ground-based maps made by our group and on polarimetric images
obtained with the Faint Object Camera on board HST (Thomson et al. 1993). A
polarisation signal could be due to scattered quasar light
(Röser & Meisenheimer 1991) or, together with possible radio emission, synchrotron
radiation. We aim to clarify the nature of the inner extensions by
planned polarimetric and spectroscopic observations with the VLT.
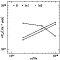 |
Figure 5:
Broad-band flux points for the radio-quiet extensions to
the jet from HST imaging at 1.6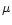 ,
620nm and 300nm. ,
620nm and 300nm. |
6.2 The hot spot
The optical counterpart to the radio hot
spot (H2) appears very faint on both images, and the spectral
index map shows a flip from flat to steep there. Both features
are explained by the Meisenheimer & Heavens (1986) hot spot model: the lifetime of
electrons emitting in the optical is quenched by the strong
magnetic field in the hot spot. The spectral index flip is
expected if there is an offset between the emission peaks at
different frequencies. This offset is predicted by the theory by
Meisenheimer & Heavens (1986) and is clearly seen when comparing optical and radio
images (Röser et al. 1997; a detailed comparison of all data will
be presented in a future paper). By its spectrum and morphology,
the hot spot appears exactly as expected for a high-loss
synchrotron emission region downstream of a localized strong shock
with first-order Fermi acceleration. Finally, we note that
although the term "hot spot'' is historically in use for this
part of the jet, the term is ill-defined and may have become
inadequate, but we defer a discussion of its adequacy to a future
paper.
6.3 Main body of the jet
Our HST images (Figs. 1 and 2) show a close
coincidence of the jet's morphology over a factor of 2 in frequency
(optical and UV). The spectral index map (Fig. 3) shows
amazingly smooth variations in the physical conditions over the entire
jet. The electrons' synchrotron cooling leaves little imprint on the
spectral index along the jet, contrary to expectations.
6.3.1 The spectral index at HST resolution
 |
Figure 6:
Optical spectral index against red-band brightness for the
outer half of the jet in 3C273 (data as in Fig. 4).
There is no strict correlation like that observed in the jet of M 87. |
| Open with DEXTER |
The two striking features of our spectral index map are the smooth
variation of the spectral index over the entire jet
(Fig. 4), and the lack of a strong correlation
between red-band brightness and spectral index
(Fig. 6) like that observed in the jet of M 87
(Meisenheimer et al. 1996a,b; Perlman et al. 2001). There are large but smooth variations
of the spectral index, while the surface brightness remains fairly
constant over the jet's projected extent of about 10
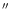 .
Conversely, there are large local variations of surface
brightness without strong changes in the spectral index. We do
not observe abrupt changes of the spectral index inside the jet
like we do in the hot spot. The run of the spectral index is thus
consistent with the complete absence of energy losses over scales
of many kiloparsecs, in spite of the large observed synchrotron
luminosity, which indicates the need for re-acceleration of
particles inside the jet. The mismatch between synchrotron
cooling scale and extent of the jet even led Guthrie & Napier (1975) to
conclude that the jet's emission could not be synchrotron
radiation.
The same lack of apparent synchrotron cooling is implied by the
surprising overall correspondence between
.
Conversely, there are large local variations of surface
brightness without strong changes in the spectral index. We do
not observe abrupt changes of the spectral index inside the jet
like we do in the hot spot. The run of the spectral index is thus
consistent with the complete absence of energy losses over scales
of many kiloparsecs, in spite of the large observed synchrotron
luminosity, which indicates the need for re-acceleration of
particles inside the jet. The mismatch between synchrotron
cooling scale and extent of the jet even led Guthrie & Napier (1975) to
conclude that the jet's emission could not be synchrotron
radiation.
The same lack of apparent synchrotron cooling is implied by the
surprising overall correspondence between
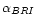 and
and
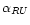 (Fig. 4) which have been determined at
vastly different resolutions (1
(Fig. 4) which have been determined at
vastly different resolutions (1
 3 and 0
3 and 0
 2, corresponding to
4.2h60kpc and 640h60pc, respectively). The small
differences (strongest in regions A and C2/D1) can be explained at
least in part by the different beam sizes: the spectral index
determined by smoothing the HST images to 1
2, corresponding to
4.2h60kpc and 640h60pc, respectively). The small
differences (strongest in regions A and C2/D1) can be explained at
least in part by the different beam sizes: the spectral index
determined by smoothing the HST images to 1
 3 makes the
discrepancy smaller. In addition, the emission region becomes wider
towards longer wavelengths, an effect already noticeable in the
near-infrared
3 makes the
discrepancy smaller. In addition, the emission region becomes wider
towards longer wavelengths, an effect already noticeable in the
near-infrared 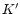 band (Neumann et al. 1997) and attributed to a
"backflow'' (Röser et al. 1996). The presence of such a steep-spectrum,
diffuse component more extended than the jet channel might also
explain the discrepancy.
The general agreement indicates a constancy of the shape of the
spectrum even at the scales resolved by HST. To first order, the
appearance of the jet at all wavelengths can be explained through such
a constant spectral shape consisting of a low-frequency power law and
a high-frequency curved cutoff. The assumed spectral shape is shifted
systematically in the
band (Neumann et al. 1997) and attributed to a
"backflow'' (Röser et al. 1996). The presence of such a steep-spectrum,
diffuse component more extended than the jet channel might also
explain the discrepancy.
The general agreement indicates a constancy of the shape of the
spectrum even at the scales resolved by HST. To first order, the
appearance of the jet at all wavelengths can be explained through such
a constant spectral shape consisting of a low-frequency power law and
a high-frequency curved cutoff. The assumed spectral shape is shifted
systematically in the
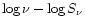 plane, passing different
parts of the curved cutoff through the optical flux point. This leads
to similar morphological features at all wavelengths, in accord with
observations (Conway et al. 1993; Bahcall et al. 1995). Moving the spectral shape
through a constant optical flux point leads to a correlation of
steeper optical spectral index with higher radio flux. This
correlation reproduces the observed tenfold increase of the radio
surface brightness from A to D2/H3 (Conway et al. 1993) and the overall
steepening of the optical spectral index. However, this steepening
happens on much longer time scales than expected from synchrotron
cooling alone.
Assuming an electron energy distribution with a fairly sharp cutoff,
drastic jumps in
plane, passing different
parts of the curved cutoff through the optical flux point. This leads
to similar morphological features at all wavelengths, in accord with
observations (Conway et al. 1993; Bahcall et al. 1995). Moving the spectral shape
through a constant optical flux point leads to a correlation of
steeper optical spectral index with higher radio flux. This
correlation reproduces the observed tenfold increase of the radio
surface brightness from A to D2/H3 (Conway et al. 1993) and the overall
steepening of the optical spectral index. However, this steepening
happens on much longer time scales than expected from synchrotron
cooling alone.
Assuming an electron energy distribution with a fairly sharp cutoff,
drastic jumps in
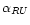 would be expected at the locations of
the shock fronts if the jet knots were (strong) shocks like the hot
spot without extended re-acceleration acting between them. The
absence of strong cooling makes it impossible to pinpoint localised
sites at which particles are either exclusively accelerated or
exclusively undergo strong losses. Any acceleration site must
therefore be considerably smaller than the beam size we used
(
640h60-1pc), and these acceleration sites must be
distributed over the entire jet to explain the absence of
cooling. This, together with the low-frequency spectral index of
would be expected at the locations of
the shock fronts if the jet knots were (strong) shocks like the hot
spot without extended re-acceleration acting between them. The
absence of strong cooling makes it impossible to pinpoint localised
sites at which particles are either exclusively accelerated or
exclusively undergo strong losses. Any acceleration site must
therefore be considerably smaller than the beam size we used
(
640h60-1pc), and these acceleration sites must be
distributed over the entire jet to explain the absence of
cooling. This, together with the low-frequency spectral index of
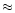 -0.8, corresponds to the jet-like acceleration mechanism
proposed by Meisenheimer et al. (1997).
Meisenheimer et al. (1996a) have presented fits of synchrotron continua to the
observed SEDs of knots A, B, C, D and the hot spot H at 1
-0.8, corresponds to the jet-like acceleration mechanism
proposed by Meisenheimer et al. (1997).
Meisenheimer et al. (1996a) have presented fits of synchrotron continua to the
observed SEDs of knots A, B, C, D and the hot spot H at 1
 3
which have also been used by Röser et al. (2000). It is noted that the
optical spectral index predicted from these spectra
(
3
which have also been used by Röser et al. (2000). It is noted that the
optical spectral index predicted from these spectra
(
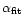 in Fig. 4) is always
steeper than the observed spectral index, that is below
in Fig. 4) is always
steeper than the observed spectral index, that is below
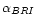 and
and
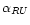 .
This indicates that the fitted
spectrum is not fully adequate at the highest frequencies. This
may again be due to contamination of the near-infrared flux by the
same "backflow'' component mentioned above. The contamination
would make the IR-optical spectral index (which dominates the run
of the spectrum at high frequencies) steeper than the optical
spectral index, as observed. Alternatively or additionally, there
could be deviations of the optical-UV spectral shape from a
standard synchrotron cutoff spectrum which may be interpreted as
the first observational hint towards the existence of a second,
higher-energy electron population producing the X-ray emission
(Röser et al. 2000). Detailed statements about the adequacy of model
spectra have to be deferred to a future paper considering the full
radio, infrared and optical data set.
.
This indicates that the fitted
spectrum is not fully adequate at the highest frequencies. This
may again be due to contamination of the near-infrared flux by the
same "backflow'' component mentioned above. The contamination
would make the IR-optical spectral index (which dominates the run
of the spectrum at high frequencies) steeper than the optical
spectral index, as observed. Alternatively or additionally, there
could be deviations of the optical-UV spectral shape from a
standard synchrotron cutoff spectrum which may be interpreted as
the first observational hint towards the existence of a second,
higher-energy electron population producing the X-ray emission
(Röser et al. 2000). Detailed statements about the adequacy of model
spectra have to be deferred to a future paper considering the full
radio, infrared and optical data set.
6.3.2 Can beaming account for the lack of cooling?
Heinz & Begelman (1997) proposed that sub-equipartition magnetic fields
combined with mildly relativistic beaming could explain the lack
of cooling in the jet of M 87 - which is, however, ten times
shorter than that of 3C273. As an alternative to postulating
re-acceleration, we consider whether low magnetic field values and
beaming could lead to electron lifetimes sufficient to allow
electrons to be accelerated at region A to illuminate the entire
jet down to the hot spot over a projected extent of
32
h60-1kpc (the argument will become even more stringent by
demanding acceleration in the quasar core). We consider the
electron lifetime against synchrotron and inverse Compton cooling
off cosmic microwave background photons; the synchrotron
self-Compton process is negligible for electrons in the jet
(Röser et al. 2000), as is Compton scattering off the host galaxy's star
light.
The total energy loss rate of an electron with energy E due to
synchrotron radiation and inverse Compton scattering, averaged
over many pitch-angle scattering events during its lifetime, is
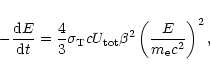 |
(4) |
where
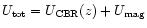 is the sum of the energy densities of the background
radiation and magnetic field, respectively, and
is the sum of the energy densities of the background
radiation and magnetic field, respectively, and
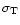 is the Thomson cross-section
(Longair 1994). We integrate this equation from
is the Thomson cross-section
(Longair 1994). We integrate this equation from 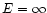 at t=0 to E(t), assuming
at t=0 to E(t), assuming 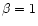 (appropriate for the
highly relativistic electrons required for optical synchrotron
radiation) and substitute for the electron's energy
(appropriate for the
highly relativistic electrons required for optical synchrotron
radiation) and substitute for the electron's energy
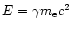 .
Inverting yields the maximum time that can have
elapsed since an electron was accelerated, given its Lorentz
factor
.
Inverting yields the maximum time that can have
elapsed since an electron was accelerated, given its Lorentz
factor 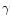 (van der Laan & Perola 1969):
(van der Laan & Perola 1969):
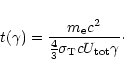 |
(5) |
This is the "electron lifetime'', inversely
proportional to both the energy density in which the electron has
been "ageing'', and the electron's own energy.
As most of the electron's energy is radiated at the synchrotron
characteristic frequency
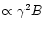 ,
we can substitute
for
,
we can substitute
for 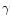 in Eq. (5) in terms of the observing
frequency and the magnetic field in the source. Hence,
Eq. (5) becomes (in convenient units)
in Eq. (5) in terms of the observing
frequency and the magnetic field in the source. Hence,
Eq. (5) becomes (in convenient units)
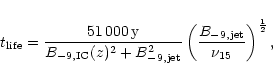 |
(6) |
where
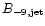 is the magnetic flux density in nT of the
jet field, the background radiation energy density has been
expressed in terms of an equivalent magnetic field,
is the magnetic flux density in nT of the
jet field, the background radiation energy density has been
expressed in terms of an equivalent magnetic field,
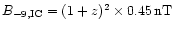 ,
and
,
and
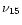 is the observing frequency in 1015Hz
(van der Laan & Perola 1969). Note that as the substituted
is the observing frequency in 1015Hz
(van der Laan & Perola 1969). Note that as the substituted
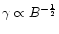 ,
setting
,
setting
 is now meaningless.
To be fully adequate for electrons in a relativistic jet at
cosmological distances, the equation needs to be modified. Firstly,
the frequency local to the source is (1+z) times the observing
frequency because of the cosmological redshift. Furthermore, the
radiating electron may be embedded in a relativistic flow with bulk
Lorentz factor
is now meaningless.
To be fully adequate for electrons in a relativistic jet at
cosmological distances, the equation needs to be modified. Firstly,
the frequency local to the source is (1+z) times the observing
frequency because of the cosmological redshift. Furthermore, the
radiating electron may be embedded in a relativistic flow with bulk
Lorentz factor 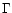 with three consequences: relativistic time
dilation and Doppler shift, and boost of the background radiation
energy density. The relativistic time dilation enhances the electron
lifetime in the jet frame by a factor
with three consequences: relativistic time
dilation and Doppler shift, and boost of the background radiation
energy density. The relativistic time dilation enhances the electron
lifetime in the jet frame by a factor 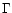 .
The Doppler shift
between the emission frequency
.
The Doppler shift
between the emission frequency
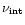 in the jet frame
(equal to the characteristic frequency) and the observation frequency
in the jet frame
(equal to the characteristic frequency) and the observation frequency
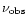 is given by
is given by
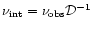 ,
where
,
where
![${\cal
D}(\Gamma,\theta) = [\Gamma(1-\beta_{{\rm jet}} \cos
\theta)]^{-1}$](/articles/aa/full/2001/26/aa1311/img81.gif) ,
the Doppler boosting factor for an angle
,
the Doppler boosting factor for an angle 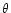 to
the line of sight (see Hughes & Miller 1991, e.g.). A relativistic
flow perceives the energy density of the background radiation field
boosted up by a factor
to
the line of sight (see Hughes & Miller 1991, e.g.). A relativistic
flow perceives the energy density of the background radiation field
boosted up by a factor 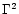 (Dermer 1995). Inserting these
yields
(Dermer 1995). Inserting these
yields
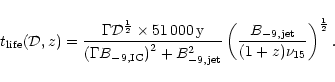 |
(7) |
The electron lifetime attains a maximum value at a certain value of
the jet's magnetic field (Fig. 7) (van der Laan & Perola 1969). On
either side of the maximum, the lifetime is decreased by larger losses
suffered before it is observed: for a higher magnetic field in
the jet, the synchrotron cooling is more rapid (
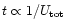 ,
Eq. (5)).
,
Eq. (5)).
 |
Figure 7:
Maximum
age against synchrotron and inverse Compton cooling (off microwave
background photons at 3C273's redshift) of an electron radiating at observed UV
wavelengths plotted against the jet magnetic field.
Solid line, no beaming; dashed line, relativistic
Doppler boosting with 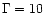 and a line-of-sight
angle
and a line-of-sight
angle
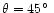 . . |
| Open with DEXTER |
A lower jet field requires an
electron of higher Lorentz factor for emission at the given frequency,
which also suffers more rapid losses (
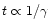 ,
Eq. (5)). By differentiation of Eq. (7), the
value of the maximum lifetime is
,
Eq. (5)). By differentiation of Eq. (7), the
value of the maximum lifetime is
![\begin{displaymath}%
t_{{\rm max}}(B_{{\rm IC}}, {\cal D}, z) = \sqrt{\frac{\cal...
...\frac{3}{2}} \left[(1+z)
\nu_{15}\right]^{\frac{1}{2}} }\cdot
\end{displaymath}](/articles/aa/full/2001/26/aa1311/img88.gif) |
(8) |
Note that
the largest possible value for the factor
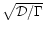 is
is
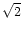 .
.
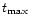 is a firm upper limit for the lifetime
of a synchrotron-radiating electron from a source at redshift z in a
flow of bulk Lorentz factor
is a firm upper limit for the lifetime
of a synchrotron-radiating electron from a source at redshift z in a
flow of bulk Lorentz factor 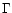 ,
whatever the magnetic field
strength in the source. It is deduced only from the fact that
synchrotron emission is observed at a certain frequency, and that
electrons which can radiate at this frequency suffer drastic energy
losses either by synchrotron or by inverse Compton cooling between the
time of acceleration and the time of emission. The only additional
assumptions are rapid pitch-angle scattering and a homogeneity of
conditions throughout the electron's lifetime.
,
whatever the magnetic field
strength in the source. It is deduced only from the fact that
synchrotron emission is observed at a certain frequency, and that
electrons which can radiate at this frequency suffer drastic energy
losses either by synchrotron or by inverse Compton cooling between the
time of acceleration and the time of emission. The only additional
assumptions are rapid pitch-angle scattering and a homogeneity of
conditions throughout the electron's lifetime.
The VLBI jet close to the core has a line-of-sight angle near
10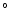 and a bulk Lorentz factor near 10 (Abraham & Romeo 1999). A
line-of-sight angle
and a bulk Lorentz factor near 10 (Abraham & Romeo 1999). A
line-of-sight angle
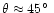 has been inferred for
the flow into the hot spot from independent considerations of the
jet's polarisation change there and the hot spot's morphology
(Conway & Davis 1994; Meisenheimer et al. 1997). We have plotted the lifetime of an electron
responsible for emission from the jet in 3C273 observed at
300nm as function of the jet's magnetic field in
Fig. 7 for the extreme cases of no beaming in the
optical jet and beaming identical to that in the VLBI jet with
has been inferred for
the flow into the hot spot from independent considerations of the
jet's polarisation change there and the hot spot's morphology
(Conway & Davis 1994; Meisenheimer et al. 1997). We have plotted the lifetime of an electron
responsible for emission from the jet in 3C273 observed at
300nm as function of the jet's magnetic field in
Fig. 7 for the extreme cases of no beaming in the
optical jet and beaming identical to that in the VLBI jet with
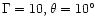 ,
and for an intermediate case with
,
and for an intermediate case with
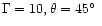 (though note that
(though note that
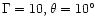 is unrealistic as there is a difference in position angle
between the VLBI jet at 244
is unrealistic as there is a difference in position angle
between the VLBI jet at 244 and the arcsecond jet at
222
and the arcsecond jet at
222 ).
The equipartition flux densities derived for the jet lie in the
range of 15nT (Neumann 1995) up to 67nT for regionA
(Röser et al. 2000), leading to maximum ages of 100-800 years, less
than the light travel time from one bright region to the next. In
the absence of beaming effects, the largest possible lifetime for
electrons in 3C273 from Eq. (8) is about
58000y, again short of the required values. The "boosted
lifetime'' can be at most
).
The equipartition flux densities derived for the jet lie in the
range of 15nT (Neumann 1995) up to 67nT for regionA
(Röser et al. 2000), leading to maximum ages of 100-800 years, less
than the light travel time from one bright region to the next. In
the absence of beaming effects, the largest possible lifetime for
electrons in 3C273 from Eq. (8) is about
58000y, again short of the required values. The "boosted
lifetime'' can be at most 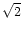 larger than this. There is
thus no combination of
larger than this. There is
thus no combination of
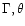 which enhances the
electron lifetime to the 100000y required for illumination of
the entire jet in 3C 273 by UV-radiating electrons.
Thus, the invocation of mild or even drastic beaming and/or
sub-equipartition fields cannot resolve the discrepancy between the
synchrotron loss scale and the extent of the optical jet of 3C273,
as has been possible for the jet in M 87 (Heinz & Begelman 1997). As another
alternative to invoking quasi-permanent re-acceleration, the existence
of a "loss-free channel'' in which electrons can travel down a jet
without synchrotron cooling has been proposed by Owen et al. (1989). As
an extreme version of this case, we assume that the electron travels
along the jet in zero magnetic field and is observed as soon as it
enters a filament with magnetic field
which enhances the
electron lifetime to the 100000y required for illumination of
the entire jet in 3C 273 by UV-radiating electrons.
Thus, the invocation of mild or even drastic beaming and/or
sub-equipartition fields cannot resolve the discrepancy between the
synchrotron loss scale and the extent of the optical jet of 3C273,
as has been possible for the jet in M 87 (Heinz & Begelman 1997). As another
alternative to invoking quasi-permanent re-acceleration, the existence
of a "loss-free channel'' in which electrons can travel down a jet
without synchrotron cooling has been proposed by Owen et al. (1989). As
an extreme version of this case, we assume that the electron travels
along the jet in zero magnetic field and is observed as soon as it
enters a filament with magnetic field
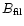 .
The energy
loss between acceleration and synchrotron emission is then only due to
inverse Compton scattering. The lifetime in 3C273 is then
130000y
.
The energy
loss between acceleration and synchrotron emission is then only due to
inverse Compton scattering. The lifetime in 3C273 is then
130000y
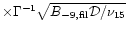 .
Again, if the jet flow in 3C273 is highly
relativistic, the electrons suffer heavy inverse Compton losses and
the lifetime mismatch persists. In any case, it remains to be shown
that the "loss-free channel'' is a physically feasible configuration
of an MHD jet.
.
Again, if the jet flow in 3C273 is highly
relativistic, the electrons suffer heavy inverse Compton losses and
the lifetime mismatch persists. In any case, it remains to be shown
that the "loss-free channel'' is a physically feasible configuration
of an MHD jet.
7 Conclusion
We have analysed deep HST images at 300nm and
600nm (Figs. 1 and 2) of the jet in
3C273 and constructed an optical spectral index map at 0
 2
resolution (Fig. 3). The optical spectral index varies smoothly
over the entire jet, indicating a smooth variation of the physical
conditions across the jet. Unlike in M 87 (Meisenheimer et al. 1996a; Perlman et al. 2001), there is
no strong correlation between optical brightness and spectral
index
(Figs. 4 and 6). The spectral
index map thus shows no signs of strong synchrotron cooling at any
location in the jet. Particle acceleration at a few localised sites
in the jet is not sufficient to explain the absence of strong cooling.
This does not preclude the possibility that the enhanced-brightness
regions are shocks - but even if they are, re-acceleration between
them is necessary to explain the observed spectral index features. We
have further shown that relativistic effects cannot lead to
significant enhancements of the electron lifetime in 3C273's jet,
whatever the bulk Lorentz factor (Sect. 6.3.2),
strengthening previous electron lifetime arguments. The need for a
continuous re-acceleration of electrons emitting high-frequency
synchrotron radiation in the jet of 3C273 is thus evident.
Mechanisms have been proposed which can explain the apparent lack of
cooling by distributed re-acceleration. These include acceleration by
reconnection in thin filaments (Lesch & Birk 1998) and turbulent acceleration
(Manolakou et al. 1999). Both processes manage to maintain the injection
spectrum over distances much larger than the loss scales, although the
latter so far only maintains cutoff frequencies in the range of
2
resolution (Fig. 3). The optical spectral index varies smoothly
over the entire jet, indicating a smooth variation of the physical
conditions across the jet. Unlike in M 87 (Meisenheimer et al. 1996a; Perlman et al. 2001), there is
no strong correlation between optical brightness and spectral
index
(Figs. 4 and 6). The spectral
index map thus shows no signs of strong synchrotron cooling at any
location in the jet. Particle acceleration at a few localised sites
in the jet is not sufficient to explain the absence of strong cooling.
This does not preclude the possibility that the enhanced-brightness
regions are shocks - but even if they are, re-acceleration between
them is necessary to explain the observed spectral index features. We
have further shown that relativistic effects cannot lead to
significant enhancements of the electron lifetime in 3C273's jet,
whatever the bulk Lorentz factor (Sect. 6.3.2),
strengthening previous electron lifetime arguments. The need for a
continuous re-acceleration of electrons emitting high-frequency
synchrotron radiation in the jet of 3C273 is thus evident.
Mechanisms have been proposed which can explain the apparent lack of
cooling by distributed re-acceleration. These include acceleration by
reconnection in thin filaments (Lesch & Birk 1998) and turbulent acceleration
(Manolakou et al. 1999). Both processes manage to maintain the injection
spectrum over distances much larger than the loss scales, although the
latter so far only maintains cutoff frequencies in the range of
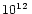 Hz-
Hz-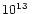 Hz, i.e., below the values
observed in 3C273.
We note that for those jets which are bulk relativistic flows
at high Lorentz factors, the increased inverse Compton losses form a
further sink of energy that has to be filled by re-energization
processes inside the jets. This requirement becomes more severe at
higher redshifts. As has been suggested previously (Celotti et al. 2001),
inverse Compton scattering off cosmic microwave background photons
might explain the so far unaccounted-for X-ray flux from 3C273's jet
(Röser et al. 2000; Marshall et al. 2001) and from Pictor A's jet and hot spot
(Wilson et al. 2001). If this is true, the outward-decreasing X-ray flux from
the jet in 3C273 indicates that the jet is still highly relativistic
near region A and slows down towards the hot spot. Recently, the
detection of extended X-ray emission from the jet in PKS 0637-752 by
the new X-ray observatory CHANDRA has been reported and a
similar explanation has been brought forward
(Chartas et al. 2000; Schwartz et al. 2000; Tavecchio et al. 2000; Celotti et al. 2001). Like for 3C273,
in situ
re-acceleration is required in PKS 0637-752 to explain the mismatch
between de-projected extent of the jet (>1Mpc) and inverse-Compton
loss scale (10kpc) (Tavecchio et al. 2000).
In order to understand the physical conditions in extragalactic jets
like that in 3C273, it is necessary to detect even the most subtle
variations in the parameters describing the synchrotron spectrum (that
is, cutoff frequency, break frequency and especially low-frequency
spectral index), which requires the deepest images at the highest
resolutions and in many wavelength bands to detect variations at all.
A theory of the physical processes at work in this jet initially has
to explain both the simple overall spectral shape, as well as its
constancy over scales of many kiloparsec. The details of this
physical process will be constrained by the subtle deviations from the
simple spectral shape, such as those tentatively identified in
Sect. 6.3.1. We aim to find these deviations with the
full data set, including new radio and near-infrared data in addition
to the presented optical and UV images.
Hz, i.e., below the values
observed in 3C273.
We note that for those jets which are bulk relativistic flows
at high Lorentz factors, the increased inverse Compton losses form a
further sink of energy that has to be filled by re-energization
processes inside the jets. This requirement becomes more severe at
higher redshifts. As has been suggested previously (Celotti et al. 2001),
inverse Compton scattering off cosmic microwave background photons
might explain the so far unaccounted-for X-ray flux from 3C273's jet
(Röser et al. 2000; Marshall et al. 2001) and from Pictor A's jet and hot spot
(Wilson et al. 2001). If this is true, the outward-decreasing X-ray flux from
the jet in 3C273 indicates that the jet is still highly relativistic
near region A and slows down towards the hot spot. Recently, the
detection of extended X-ray emission from the jet in PKS 0637-752 by
the new X-ray observatory CHANDRA has been reported and a
similar explanation has been brought forward
(Chartas et al. 2000; Schwartz et al. 2000; Tavecchio et al. 2000; Celotti et al. 2001). Like for 3C273,
in situ
re-acceleration is required in PKS 0637-752 to explain the mismatch
between de-projected extent of the jet (>1Mpc) and inverse-Compton
loss scale (10kpc) (Tavecchio et al. 2000).
In order to understand the physical conditions in extragalactic jets
like that in 3C273, it is necessary to detect even the most subtle
variations in the parameters describing the synchrotron spectrum (that
is, cutoff frequency, break frequency and especially low-frequency
spectral index), which requires the deepest images at the highest
resolutions and in many wavelength bands to detect variations at all.
A theory of the physical processes at work in this jet initially has
to explain both the simple overall spectral shape, as well as its
constancy over scales of many kiloparsec. The details of this
physical process will be constrained by the subtle deviations from the
simple spectral shape, such as those tentatively identified in
Sect. 6.3.1. We aim to find these deviations with the
full data set, including new radio and near-infrared data in addition
to the presented optical and UV images.
Acknowledgements
We are grateful to D. van Orsow for his
assistance with the HST observations. This research has made use of
NASA's Astrophysics Data System Abstract Service.
Appendix A: Image alignment
A.1 Flux errors from misalignment
Consider two images which are not registered correctly and which have
slightly different PSF widths. When performing photometry on these
images, we assume that they are registered perfectly and have
identical, known beam sizes. This amounts to making a flux
measurement in a certain aperture in one image, but in a slightly
offset aperture of slightly different size in the second image. The
error is largest in the steepest gradients in the image, which are the
flanks of the PSF of width 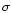 ,
smoothed to the desired effective
beam size
,
smoothed to the desired effective
beam size
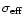 ,
with
,
with
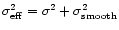 .
Its magnitude can be assessed
by considering the PSF as a Gaussian at given position and of given
width, and as smoothing filter a second Gaussian slightly displaced
from the PSF and of width slightly different from that achieving the
desired effective beam area. The result of the performed wrong
flux measurement is then proportional to the integral
.
Its magnitude can be assessed
by considering the PSF as a Gaussian at given position and of given
width, and as smoothing filter a second Gaussian slightly displaced
from the PSF and of width slightly different from that achieving the
desired effective beam area. The result of the performed wrong
flux measurement is then proportional to the integral
where 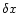 is the offset of the aperture from the correct
position and
is the offset of the aperture from the correct
position and
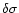 is the error in the determination of the
PSF width. The correct measurement is obtained by setting
is the error in the determination of the
PSF width. The correct measurement is obtained by setting
 and
and
 ,
and from this one obtains the fractional
flux error as a function of the two errors. The fractional flux error
,
and from this one obtains the fractional
flux error as a function of the two errors. The fractional flux error
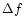 for a misalignment is
for a misalignment is
Hence, the relative flux error is better than 5% if the misalignment
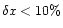 .
Similarly, for a wrong PSF width, the fractional error is
.
Similarly, for a wrong PSF width, the fractional error is
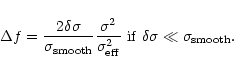 |
(A.3) |
This error is negligible if the desired effective PSF is much larger
than the intrinsic PSF of the input images, as is the case here.
A.2 Refined image alignment
 |
Figure A.1:
The
separation of a number of stars was measured both on a F336W (UV)
and a F673W (red) image of R136. This plot shows the difference in
separation between the frames, 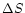 ,
plotted against the
separation on the "red'' image, S. The best-fitting straight line
is shown. ,
plotted against the
separation on the "red'' image, S. The best-fitting straight line
is shown. 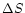 grows systematically with S, indicating a
differing scale between the frames. The slope of the line is
grows systematically with S, indicating a
differing scale between the frames. The slope of the line is
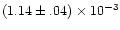 ,
the intercept with the ordinate is ,
the intercept with the ordinate is
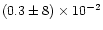 .
The slope is not changed within the
errors by forcing the line to pass through the origin. .
The slope is not changed within the
errors by forcing the line to pass through the origin. |
The two obvious ways to determine the relative shift between any two
images are measuring the positions of point sources on the various
images, or using the engineering files (also termed jitter
files) provided as part of the observing data package. If the
telescope pointing was known to be precise to better than 0
 02,
we could simply rely on the commanded shifts.
The HST has a pointing repeatability within a single
telescope visit
02,
we could simply rely on the commanded shifts.
The HST has a pointing repeatability within a single
telescope visit![[*]](/icons/foot_motif.gif) of about 5 milli-arcsecond (mas). The
offsets between individual exposures are accurate to 15 mas,
leading to a total error of about 16 mas. This is already
comparable to the demanded accuracy. The situation is expected to
be worse for relating exposures in different visits, when the
telescope has been pointing elsewhere in the mean time.
Unfortunately, measuring the positions of only a few (four, in our
case) astrometric reference stars does not immediately lead to accurate
measurements of the telescope's pointing - especially since in our
case, each star lies on a different chip. The undersampling of the
telescope PSF by the WFPC2 pixels and the so-called sub-pixel
scattering of the WFPC2 detectors lead to an additional scatter of the
centroid positions of point sources, approximately uniformly
distributed between +0.25 and -0.25 pixels and in excess of
statistical uncertainties (Lallo 1998, priv. comm.). With
only a small number of centroidable point sources available, the
centroiding errors are of the same magnitude as the intrinsic pointing
errors of the telescope.
It is therefore worth considering the pointing error sources
en détail to ensure that the alignment is at the required
0
of about 5 milli-arcsecond (mas). The
offsets between individual exposures are accurate to 15 mas,
leading to a total error of about 16 mas. This is already
comparable to the demanded accuracy. The situation is expected to
be worse for relating exposures in different visits, when the
telescope has been pointing elsewhere in the mean time.
Unfortunately, measuring the positions of only a few (four, in our
case) astrometric reference stars does not immediately lead to accurate
measurements of the telescope's pointing - especially since in our
case, each star lies on a different chip. The undersampling of the
telescope PSF by the WFPC2 pixels and the so-called sub-pixel
scattering of the WFPC2 detectors lead to an additional scatter of the
centroid positions of point sources, approximately uniformly
distributed between +0.25 and -0.25 pixels and in excess of
statistical uncertainties (Lallo 1998, priv. comm.). With
only a small number of centroidable point sources available, the
centroiding errors are of the same magnitude as the intrinsic pointing
errors of the telescope.
It is therefore worth considering the pointing error sources
en détail to ensure that the alignment is at the required
0
 02 level
02 level![[*]](/icons/foot_motif.gif) . Alignment errors can be caused by roll or pointing errors
and less obviously by a scale difference between exposures using
different filters in the same camera. The importance of the
various alignment error sources can be estimated by considering
the effect they have on the hot spot location if the quasar images
are assumed to coincide. The hot spot is separated by 22
. Alignment errors can be caused by roll or pointing errors
and less obviously by a scale difference between exposures using
different filters in the same camera. The importance of the
various alignment error sources can be estimated by considering
the effect they have on the hot spot location if the quasar images
are assumed to coincide. The hot spot is separated by 22
 from the quasar, corresponding to about 480 PC pixels.
The roll repeatability of the HST is at the 10
from the quasar, corresponding to about 480 PC pixels.
The roll repeatability of the HST is at the 10
 level. The
engineering data provided with HST exposures record roll angle
differences of about 6
level. The
engineering data provided with HST exposures record roll angle
differences of about 6
 .
This is well below the rotation of
3
.
This is well below the rotation of
3
 5 which would produce a 0.44 pixel difference over 480 pixels.
The telescope roll differences can thus be neglected.
The engineering files record the telescope pointing in
three-second intervals and can be used to calculate the offsets.
Their accuracy is only limited by the so-called "jitter'', vibrations
due to thermal effects. The jitter was below 10 mas in all exposures,
and below 5 mas in most. There is an additional uncertainty from the
transformation between the telescope's focal plane and the detector:
the location of a camera inside the telescope may change slightly over time
(shifts, rotations, or both). This uncertainty is irrelevant for
relative positions as long as the location and orientation of WFPC2
and the Fine Guidance Sensors (FGS, these perform the guiding
observations) inside the telescope is stable, which is the case for
the employed shifts of about 1
5 which would produce a 0.44 pixel difference over 480 pixels.
The telescope roll differences can thus be neglected.
The engineering files record the telescope pointing in
three-second intervals and can be used to calculate the offsets.
Their accuracy is only limited by the so-called "jitter'', vibrations
due to thermal effects. The jitter was below 10 mas in all exposures,
and below 5 mas in most. There is an additional uncertainty from the
transformation between the telescope's focal plane and the detector:
the location of a camera inside the telescope may change slightly over time
(shifts, rotations, or both). This uncertainty is irrelevant for
relative positions as long as the location and orientation of WFPC2
and the Fine Guidance Sensors (FGS, these perform the guiding
observations) inside the telescope is stable, which is the case for
the employed shifts of about 1
 and for the timescales between
the visits.
Within a single visit, the engineering file information is used to
obtain relative offsets, with a typical 5 mas error. The values
differ from the commanded shifts by a few milli-arcseconds at most.
All of these offsets are by an integer number of PC pixels.
Between the various visits, the telescope has been pointing to a
different part of the sky. One should therefore not assume that the
relative shifts between various visits as determined from the jitter
files are as accurate as shifts within one visit. We therefore
measured the positions of the four astrometric reference stars on each
of the short exposures (in fact, one of the stars is very faint in the
UV, so the position was determined on a long exposure for this one).
The shifts determined from the four point sources' positions have a
typical standard deviation (accuracy) of 15 mas in each coordinate.
On the three visits' sum images aligned this way, the scatter of the
quasar image position is less than 5 mas and 7 mas in x and y,
respectively. This means that although the measured shifts have a
fairly large scatter, the resulting value is precise to about
10 mas. Finally, we note that the observed shifts of the stellar
positions and those obtained from the jitter files agree to better
than 0
and for the timescales between
the visits.
Within a single visit, the engineering file information is used to
obtain relative offsets, with a typical 5 mas error. The values
differ from the commanded shifts by a few milli-arcseconds at most.
All of these offsets are by an integer number of PC pixels.
Between the various visits, the telescope has been pointing to a
different part of the sky. One should therefore not assume that the
relative shifts between various visits as determined from the jitter
files are as accurate as shifts within one visit. We therefore
measured the positions of the four astrometric reference stars on each
of the short exposures (in fact, one of the stars is very faint in the
UV, so the position was determined on a long exposure for this one).
The shifts determined from the four point sources' positions have a
typical standard deviation (accuracy) of 15 mas in each coordinate.
On the three visits' sum images aligned this way, the scatter of the
quasar image position is less than 5 mas and 7 mas in x and y,
respectively. This means that although the measured shifts have a
fairly large scatter, the resulting value is precise to about
10 mas. Finally, we note that the observed shifts of the stellar
positions and those obtained from the jitter files agree to better
than 0
 02 in all cases, with an rms value of 0
02 in all cases, with an rms value of 0
 01. There
are, however, systematic differences between these and the commanded
values. Hence, we do not blindly rely on the latter.
Because of differential refraction in the MgF2 field flattener
windows employed in WFPC2 (Trauger et al. 1995), the pixel scales of
images taken through the F622W and F300W filters differ by about
0.1%. This alone is enough to eat up the alignment error budget of
0.44 pixels over 480 pixels separation. The wavelength dependence was
expected from ray-tracing studies of the WFPC2 optics. Its presence
and magnitude were experimentally confirmed by comparing archival
images
01. There
are, however, systematic differences between these and the commanded
values. Hence, we do not blindly rely on the latter.
Because of differential refraction in the MgF2 field flattener
windows employed in WFPC2 (Trauger et al. 1995), the pixel scales of
images taken through the F622W and F300W filters differ by about
0.1%. This alone is enough to eat up the alignment error budget of
0.44 pixels over 480 pixels separation. The wavelength dependence was
expected from ray-tracing studies of the WFPC2 optics. Its presence
and magnitude were experimentally confirmed by comparing archival
images![[*]](/icons/foot_motif.gif) of the star
cluster R136 taken through similar filters as those employed in the
present work (F336W and F672N) (Fig. A.1). The scale
difference has to be removed before combining the images to a spectral
index map. This was done in the following manner: the plate scale of
each image was calculated using the parameters in
Trauger et al. (1995). All images were resampled to a grid with pixel
size of 0
of the star
cluster R136 taken through similar filters as those employed in the
present work (F336W and F672N) (Fig. A.1). The scale
difference has to be removed before combining the images to a spectral
index map. This was done in the following manner: the plate scale of
each image was calculated using the parameters in
Trauger et al. (1995). All images were resampled to a grid with pixel
size of 0
 0045548, which is one tenth of the average of the
original scales, using bilinear interpolation. The result was then
binned in blocks of
0045548, which is one tenth of the average of the
original scales, using bilinear interpolation. The result was then
binned in blocks of
 pixels to a common pixel size of
0
pixels to a common pixel size of
0
 045548. The scale of the two images is then identical to
better than 1 part in 10000.
The resampling required the use of the quasar image as common
reference point between the two filters. The QSO's position can be
determined to about 10-15 mas by centroiding routines on the unsaturated
images.
045548. The scale of the two images is then identical to
better than 1 part in 10000.
The resampling required the use of the quasar image as common
reference point between the two filters. The QSO's position can be
determined to about 10-15 mas by centroiding routines on the unsaturated
images.
-
Abraham, Z., & Romero, G. E. 1999, A&A, 344, 61
In the text
NASA ADS
-
Baade, W. 1956, ApJ, 123, 550
In the text
NASA ADS
-
Bahcall, J. N., Kirhakos, S., Schneider, D. P., et al. 1995, ApJ, 452,
L91
In the text
NASA ADS
-
Biretta, J. A., et al., eds. 2000, WFPC2 Instrument Handbook, Version 5.0
(Baltimore: STScI)
In the text
-
Blundell, K. M., & Rawlings, S. 2000, AJ, 119, 1111
In the text
NASA ADS
-
Celotti, A., Ghisellini, G., & Chiaberge, M. 2001, MNRAS, 321, L1
In the text
NASA ADS
-
Chartas, G., Worrall, D. M., Birkinshaw, M., et al. 2000, ApJ, 542, 655
In the text
NASA ADS
-
Conway, R. G., & Davis, R. J. 1994, A&A, 284, 724
In the text
NASA ADS
-
Conway, R. G., Garrington, S. T., Perley, R. A., & Biretta, J. A.
1993, A&A, 267, 347
In the text
NASA ADS
-
Dermer, C. D. 1995, ApJ, 446, L63
In the text
NASA ADS
-
Flatters, C., & Conway, R. G. 1985, Nature, 314, 425
In the text
NASA ADS
-
Guthrie, B. N. G., & Napier, W. M. 1975, MNRAS, 172, 85
In the text
NASA ADS
-
Hardee, P. E., & Norman, M. L. 1989, ApJ, 342, 680
In the text
NASA ADS
-
Heavens, A. F., & Meisenheimer, K. 1987, MNRAS, 225, 335
In the text
NASA ADS
-
Heinz, S., & Begelman, M. C. 1997, ApJ, 490, 653
In the text
NASA ADS
-
Hughes, P. A., & Miller, L. 1991, in Beams and jets in astrophysics, ed.
P. A. Hughes, Cambridge Astrophys. Ser., No. 19 (Cambridge University
Press), 1
In the text
-
Krist, J. 1999, Tiny Tim PSF modelling software,
In the text
http://scivax.stsci.edu/~krist/tinytim.html
-
Lelièvre, G., Nieto, J. L., Horville, D., Renard, L., & Servan,
B. 1984, A&A, 138, 49
In the text
NASA ADS
-
Lesch, H., & Birk, G. T. 1998, ApJ, 499, 167
In the text
NASA ADS
-
Longair, M. 1994, High-energy astrophysics, 2nd edn., vol. 2
(Cambridge: CUP), 276
In the text
-
Manolakou, K., Anastasiadis, A., & Vlahos, L. 1999, A&A, 345, 653
In the text
NASA ADS
-
Marshall, H. L., Harris, D. E., Grimes, J. P., et al. 2001, ApJ, 549,
L167
In the text
NASA ADS
-
Meisenheimer, K. 1996, in Lecture Notes in Physics, vol. 471, Jets from Stars
and Galactic Nuclei, ed. W. Kundt (Berlin Heidelberg New York: Springer
Verlag), 57
In the text
-
Meisenheimer, K., & Heavens, A. F. 1986, Nature, 323, 419
In the text
NASA ADS
-
Meisenheimer, K., Neumann, M., & Röser, H.-J. 1996a, in
Lecture Notes in Physics, vol. 471, Jets from Stars and Galactic Nuclei., ed.
W. Kundt (Berlin Heidelberg New York: Springer Verlag), 230
In the text
-
Meisenheimer, K., Röser, H.-J., Hiltner, P. R., et al. 1989, A&A,
219, 63
In the text
NASA ADS
-
Meisenheimer, K., Röser, H.-J., & Schlötelburg, M.
1996b, A&A, 307, 61
NASA ADS
-
Meisenheimer, K., Yates, M. G., & Röser, H.-J. 1997, A&A, 325, 57
In the text
NASA ADS
-
Neumann, M. 1995, Ph.D. Thesis, Universität Heidelberg
In the text
-
Neumann, M., Meisenheimer, K., & Röser, H.-J. 1997, A&A, 326, 69
In the text
NASA ADS
-
Owen, F. N., Hardee, P. E., & Cornwell, T. J. 1989, ApJ, 340, 698
In the text
NASA ADS
-
Perley, R. A., Röser, H.-J., & Meisenheimer, K. 1997, A&A, 328, 12
In the text
NASA ADS
-
Perlman, E. S., Biretta, J. A., Sparks, W. B., Macchetto, F. D., &
Leahy, J. P. 2001, ApJ, 551, 206
In the text
NASA ADS
-
Röser, H.-J., Conway, R. G., & Meisenheimer, K. 1996, A&A, 314, 414
NASA ADS
-
Röser, H.-J., & Meisenheimer, K. 1987, ApJ, 314, 70
In the text
NASA ADS
-
Röser, H.-J., & Meisenheimer, K. 1991, A&A, 252, 458
In the text
NASA ADS
-
Röser, H.-J., & Meisenheimer, K., eds. 1999, Lecture Notes in Physics,
vol. 530, The radio galaxy Messier 87, Proceedings of a conference held at
Schloß Ringberg (Springer-Verlag Berlin Heidelberg New York)
In the text
-
Röser, H. J., Meisenheimer, K., Neumann, M., Conway, R. G., &
Perley, R. A. 2000, A&A, 360, 99
In the text
NASA ADS
-
Röser, H.-J., Meisenheimer, K., Neumann, M., et al. 1997, Rev.
Mod. Astron., 10, 253
In the text
NASA ADS
-
Sambruna, R. M., Urry, C. M., Tavecchio, F., et al. 2001, ApJ, 549,
L161
In the text
NASA ADS
-
Scarpa, R., & Urry, C. M. 2000, preprint [astro-ph/9910417]
In the text
-
Schwartz, D. A., Marshall, H. L., Lovell, J. E. J., et al. 2000, ApJ,
540, L69
In the text
NASA ADS
-
Tavecchio, F., Maraschi, L., Sambruna, R. M., & Urry, C. M. 2000, ApJ,
544, L23
In the text
NASA ADS
-
Thomson, R. C., Mackay, C. D., & Wright, A. E. 1993, Nature, 365, 133
In the text
NASA ADS
-
Trauger, J. T., Vaughan, A. H., Evans, R. W., & Moody, D. C. 1995, in
Calibrating Hubble Space Telescope Post Servicing Mission, ed. A. Koratkar,
& C. Leitherer (Baltimore: STScI), 379
In the text
-
van der Laan, H., & Perola, G. C. 1969, A&A, 3, 468
In the text
NASA ADS
-
Voit, M., et al., eds. 1998, HST Data Handbook, Version 3.1 (Baltimore:
STScI)
In the text
-
Whitmore, B., & Wiggs, M. S. 1995, Charge Transfer Traps in the WFPC2,
Instrument Science Report WFPC2 95-03 (Baltimore: STScI)
In the text
-
Wilson, A. S., Young, A. J., & Shopbell, P. L. 2001, ApJ, 547, 740
In the text
NASA ADS
Copyright ESO 2001
![]() 2 along the jet. The smoothness of spectral index changes
shows that the physical conditions are varying smoothly across the
jet. There is no correlation between the optical flux and spectral
index, as would be expected for relativistic electrons suffering
strong cooling due to synchrotron emission. We find no evidence for
localized acceleration or loss sites. This suggests that the spectral
shape is not changing much throughout the jet. We show that
relativistic beaming and/or sub-equipartition magnetic fields cannot
remove the discrepancy between light-travel time along the jet and the
lifetime of electrons emitting optical synchrotron radiation. We
consider this further evidence in favour of a distributed electron
acceleration process.
2 along the jet. The smoothness of spectral index changes
shows that the physical conditions are varying smoothly across the
jet. There is no correlation between the optical flux and spectral
index, as would be expected for relativistic electrons suffering
strong cooling due to synchrotron emission. We find no evidence for
localized acceleration or loss sites. This suggests that the spectral
shape is not changing much throughout the jet. We show that
relativistic beaming and/or sub-equipartition magnetic fields cannot
remove the discrepancy between light-travel time along the jet and the
lifetime of electrons emitting optical synchrotron radiation. We
consider this further evidence in favour of a distributed electron
acceleration process.
![]() -
-![]() algorithm,
rejecting all pixel values deviating more than
algorithm,
rejecting all pixel values deviating more than ![]() from the
local (low-biased) median in a first pass, and neighbouring pixels
with more than
from the
local (low-biased) median in a first pass, and neighbouring pixels
with more than
![]() deviation in a second pass. The number of
pixels treated this way agrees with the expected cosmic ray hit rate
for the images.
A model of the sky background and "horizontal smear'' (increased
pixel values in rows containing saturated pixels from the quasar's
core, Chap. 4 of Biretta et al. 2000) was fitted in the part of the image containing the jet using
second-order polynomials along rows. The coefficients of the
polynomials were then smoothed in the perpendicular direction. The
conversion from photon count rate to physical flux units used the
throughput information provided by STScI which is valid after the 1997
deviation in a second pass. The number of
pixels treated this way agrees with the expected cosmic ray hit rate
for the images.
A model of the sky background and "horizontal smear'' (increased
pixel values in rows containing saturated pixels from the quasar's
core, Chap. 4 of Biretta et al. 2000) was fitted in the part of the image containing the jet using
second-order polynomials along rows. The coefficients of the
polynomials were then smoothed in the perpendicular direction. The
conversion from photon count rate to physical flux units used the
throughput information provided by STScI which is valid after the 1997
![\begin{figure}
\includegraphics[width=11cm,clip]{ms1311f1.eps} %
\end{figure}](/articles/aa/full/2001/26/aa1311/Timg33.gif)
![\begin{figure}
\includegraphics[width=11cm,clip]{ms1311f2.eps} %
\end{figure}](/articles/aa/full/2001/26/aa1311/Timg34.gif)





![]() and a bulk Lorentz factor near 10 (Abraham & Romeo 1999). A
line-of-sight angle
and a bulk Lorentz factor near 10 (Abraham & Romeo 1999). A
line-of-sight angle
![]() has been inferred for
the flow into the hot spot from independent considerations of the
jet's polarisation change there and the hot spot's morphology
(Conway & Davis 1994; Meisenheimer et al. 1997). We have plotted the lifetime of an electron
responsible for emission from the jet in 3C273 observed at
300nm as function of the jet's magnetic field in
Fig. 7 for the extreme cases of no beaming in the
optical jet and beaming identical to that in the VLBI jet with
has been inferred for
the flow into the hot spot from independent considerations of the
jet's polarisation change there and the hot spot's morphology
(Conway & Davis 1994; Meisenheimer et al. 1997). We have plotted the lifetime of an electron
responsible for emission from the jet in 3C273 observed at
300nm as function of the jet's magnetic field in
Fig. 7 for the extreme cases of no beaming in the
optical jet and beaming identical to that in the VLBI jet with
![]() ,
and for an intermediate case with
,
and for an intermediate case with
![]() (though note that
(though note that
![]() is unrealistic as there is a difference in position angle
between the VLBI jet at 244
is unrealistic as there is a difference in position angle
between the VLBI jet at 244![]() and the arcsecond jet at
222
and the arcsecond jet at
222![]() ).
The equipartition flux densities derived for the jet lie in the
range of 15nT (Neumann 1995) up to 67nT for regionA
(Röser et al. 2000), leading to maximum ages of 100-800 years, less
than the light travel time from one bright region to the next. In
the absence of beaming effects, the largest possible lifetime for
electrons in 3C273 from Eq. (8) is about
58000y, again short of the required values. The "boosted
lifetime'' can be at most
).
The equipartition flux densities derived for the jet lie in the
range of 15nT (Neumann 1995) up to 67nT for regionA
(Röser et al. 2000), leading to maximum ages of 100-800 years, less
than the light travel time from one bright region to the next. In
the absence of beaming effects, the largest possible lifetime for
electrons in 3C273 from Eq. (8) is about
58000y, again short of the required values. The "boosted
lifetime'' can be at most ![]() larger than this. There is
thus no combination of
larger than this. There is
thus no combination of
![]() which enhances the
electron lifetime to the 100000y required for illumination of
the entire jet in 3C 273 by UV-radiating electrons.
Thus, the invocation of mild or even drastic beaming and/or
sub-equipartition fields cannot resolve the discrepancy between the
synchrotron loss scale and the extent of the optical jet of 3C273,
as has been possible for the jet in M 87 (Heinz & Begelman 1997). As another
alternative to invoking quasi-permanent re-acceleration, the existence
of a "loss-free channel'' in which electrons can travel down a jet
without synchrotron cooling has been proposed by Owen et al. (1989). As
an extreme version of this case, we assume that the electron travels
along the jet in zero magnetic field and is observed as soon as it
enters a filament with magnetic field
which enhances the
electron lifetime to the 100000y required for illumination of
the entire jet in 3C 273 by UV-radiating electrons.
Thus, the invocation of mild or even drastic beaming and/or
sub-equipartition fields cannot resolve the discrepancy between the
synchrotron loss scale and the extent of the optical jet of 3C273,
as has been possible for the jet in M 87 (Heinz & Begelman 1997). As another
alternative to invoking quasi-permanent re-acceleration, the existence
of a "loss-free channel'' in which electrons can travel down a jet
without synchrotron cooling has been proposed by Owen et al. (1989). As
an extreme version of this case, we assume that the electron travels
along the jet in zero magnetic field and is observed as soon as it
enters a filament with magnetic field
![]() .
The energy
loss between acceleration and synchrotron emission is then only due to
inverse Compton scattering. The lifetime in 3C273 is then
130000y
.
The energy
loss between acceleration and synchrotron emission is then only due to
inverse Compton scattering. The lifetime in 3C273 is then
130000y
![]() .
Again, if the jet flow in 3C273 is highly
relativistic, the electrons suffer heavy inverse Compton losses and
the lifetime mismatch persists. In any case, it remains to be shown
that the "loss-free channel'' is a physically feasible configuration
of an MHD jet.
.
Again, if the jet flow in 3C273 is highly
relativistic, the electrons suffer heavy inverse Compton losses and
the lifetime mismatch persists. In any case, it remains to be shown
that the "loss-free channel'' is a physically feasible configuration
of an MHD jet.
![]() 2
resolution (Fig. 3). The optical spectral index varies smoothly
over the entire jet, indicating a smooth variation of the physical
conditions across the jet. Unlike in M 87 (Meisenheimer et al. 1996a; Perlman et al. 2001), there is
no strong correlation between optical brightness and spectral
index
(Figs. 4 and 6). The spectral
index map thus shows no signs of strong synchrotron cooling at any
location in the jet. Particle acceleration at a few localised sites
in the jet is not sufficient to explain the absence of strong cooling.
This does not preclude the possibility that the enhanced-brightness
regions are shocks - but even if they are, re-acceleration between
them is necessary to explain the observed spectral index features. We
have further shown that relativistic effects cannot lead to
significant enhancements of the electron lifetime in 3C273's jet,
whatever the bulk Lorentz factor (Sect. 6.3.2),
strengthening previous electron lifetime arguments. The need for a
continuous re-acceleration of electrons emitting high-frequency
synchrotron radiation in the jet of 3C273 is thus evident.
Mechanisms have been proposed which can explain the apparent lack of
cooling by distributed re-acceleration. These include acceleration by
reconnection in thin filaments (Lesch & Birk 1998) and turbulent acceleration
(Manolakou et al. 1999). Both processes manage to maintain the injection
spectrum over distances much larger than the loss scales, although the
latter so far only maintains cutoff frequencies in the range of
2
resolution (Fig. 3). The optical spectral index varies smoothly
over the entire jet, indicating a smooth variation of the physical
conditions across the jet. Unlike in M 87 (Meisenheimer et al. 1996a; Perlman et al. 2001), there is
no strong correlation between optical brightness and spectral
index
(Figs. 4 and 6). The spectral
index map thus shows no signs of strong synchrotron cooling at any
location in the jet. Particle acceleration at a few localised sites
in the jet is not sufficient to explain the absence of strong cooling.
This does not preclude the possibility that the enhanced-brightness
regions are shocks - but even if they are, re-acceleration between
them is necessary to explain the observed spectral index features. We
have further shown that relativistic effects cannot lead to
significant enhancements of the electron lifetime in 3C273's jet,
whatever the bulk Lorentz factor (Sect. 6.3.2),
strengthening previous electron lifetime arguments. The need for a
continuous re-acceleration of electrons emitting high-frequency
synchrotron radiation in the jet of 3C273 is thus evident.
Mechanisms have been proposed which can explain the apparent lack of
cooling by distributed re-acceleration. These include acceleration by
reconnection in thin filaments (Lesch & Birk 1998) and turbulent acceleration
(Manolakou et al. 1999). Both processes manage to maintain the injection
spectrum over distances much larger than the loss scales, although the
latter so far only maintains cutoff frequencies in the range of
![]() Hz-
Hz-![]() Hz, i.e., below the values
observed in 3C273.
We note that for those jets which are bulk relativistic flows
at high Lorentz factors, the increased inverse Compton losses form a
further sink of energy that has to be filled by re-energization
processes inside the jets. This requirement becomes more severe at
higher redshifts. As has been suggested previously (Celotti et al. 2001),
inverse Compton scattering off cosmic microwave background photons
might explain the so far unaccounted-for X-ray flux from 3C273's jet
(Röser et al. 2000; Marshall et al. 2001) and from Pictor A's jet and hot spot
(Wilson et al. 2001). If this is true, the outward-decreasing X-ray flux from
the jet in 3C273 indicates that the jet is still highly relativistic
near region A and slows down towards the hot spot. Recently, the
detection of extended X-ray emission from the jet in PKS 0637-752 by
the new X-ray observatory CHANDRA has been reported and a
similar explanation has been brought forward
(Chartas et al. 2000; Schwartz et al. 2000; Tavecchio et al. 2000; Celotti et al. 2001). Like for 3C273,
in situ
re-acceleration is required in PKS 0637-752 to explain the mismatch
between de-projected extent of the jet (>1Mpc) and inverse-Compton
loss scale (10kpc) (Tavecchio et al. 2000).
In order to understand the physical conditions in extragalactic jets
like that in 3C273, it is necessary to detect even the most subtle
variations in the parameters describing the synchrotron spectrum (that
is, cutoff frequency, break frequency and especially low-frequency
spectral index), which requires the deepest images at the highest
resolutions and in many wavelength bands to detect variations at all.
A theory of the physical processes at work in this jet initially has
to explain both the simple overall spectral shape, as well as its
constancy over scales of many kiloparsec. The details of this
physical process will be constrained by the subtle deviations from the
simple spectral shape, such as those tentatively identified in
Sect. 6.3.1. We aim to find these deviations with the
full data set, including new radio and near-infrared data in addition
to the presented optical and UV images.
Hz, i.e., below the values
observed in 3C273.
We note that for those jets which are bulk relativistic flows
at high Lorentz factors, the increased inverse Compton losses form a
further sink of energy that has to be filled by re-energization
processes inside the jets. This requirement becomes more severe at
higher redshifts. As has been suggested previously (Celotti et al. 2001),
inverse Compton scattering off cosmic microwave background photons
might explain the so far unaccounted-for X-ray flux from 3C273's jet
(Röser et al. 2000; Marshall et al. 2001) and from Pictor A's jet and hot spot
(Wilson et al. 2001). If this is true, the outward-decreasing X-ray flux from
the jet in 3C273 indicates that the jet is still highly relativistic
near region A and slows down towards the hot spot. Recently, the
detection of extended X-ray emission from the jet in PKS 0637-752 by
the new X-ray observatory CHANDRA has been reported and a
similar explanation has been brought forward
(Chartas et al. 2000; Schwartz et al. 2000; Tavecchio et al. 2000; Celotti et al. 2001). Like for 3C273,
in situ
re-acceleration is required in PKS 0637-752 to explain the mismatch
between de-projected extent of the jet (>1Mpc) and inverse-Compton
loss scale (10kpc) (Tavecchio et al. 2000).
In order to understand the physical conditions in extragalactic jets
like that in 3C273, it is necessary to detect even the most subtle
variations in the parameters describing the synchrotron spectrum (that
is, cutoff frequency, break frequency and especially low-frequency
spectral index), which requires the deepest images at the highest
resolutions and in many wavelength bands to detect variations at all.
A theory of the physical processes at work in this jet initially has
to explain both the simple overall spectral shape, as well as its
constancy over scales of many kiloparsec. The details of this
physical process will be constrained by the subtle deviations from the
simple spectral shape, such as those tentatively identified in
Sect. 6.3.1. We aim to find these deviations with the
full data set, including new radio and near-infrared data in addition
to the presented optical and UV images.
![]() ,
smoothed to the desired effective
beam size
,
smoothed to the desired effective
beam size
![]() ,
with
,
with
![]() .
Its magnitude can be assessed
by considering the PSF as a Gaussian at given position and of given
width, and as smoothing filter a second Gaussian slightly displaced
from the PSF and of width slightly different from that achieving the
desired effective beam area. The result of the performed wrong
flux measurement is then proportional to the integral
.
Its magnitude can be assessed
by considering the PSF as a Gaussian at given position and of given
width, and as smoothing filter a second Gaussian slightly displaced
from the PSF and of width slightly different from that achieving the
desired effective beam area. The result of the performed wrong
flux measurement is then proportional to the integral