A&A 373, 292-300 (2001)
DOI: 10.1051/0004-6361:20010591
F. A. Aharonian1 - A. G. Akhperjanian7 - J. A. Barrio2,3 - K. Bernlöhr1 - H. Börst5 - H. Bojahr6 - O. Bolz1 - J. L. Contreras3 - J. Cortina2 -
S. Denninghoff2 - V. Fonseca3 - J. C. Gonzalez3 - N. Götting4 - G. Heinzelmann4 -
G. Hermann1 - A. Heusler1 - W. Hofmann1 -
D. Horns4 - A. Ibarra3 - I. Jung1 - R. Kankanyan1,7 - M. Kestel2 -
J. Kettler1 - A. Kohnle1 - A. Konopelko1 -
H. Kornmeyer2 - D. Kranich2 -
H. Krawczynski1,![]() - H. Lampeitl1 -
E. Lorenz2 - F. Lucarelli3 - N. Magnussen6 -
O. Mang5 - H. Meyer6 - R. Mirzoyan2 -
A. Moralejo3 -
L. Padilla3 - M. Panter1 - R. Plaga2 -
A. Plyasheshnikov1,
- H. Lampeitl1 -
E. Lorenz2 - F. Lucarelli3 - N. Magnussen6 -
O. Mang5 - H. Meyer6 - R. Mirzoyan2 -
A. Moralejo3 -
L. Padilla3 - M. Panter1 - R. Plaga2 -
A. Plyasheshnikov1,![]() - J. Prahl4 - G. Pühlhofer1 - G. Rauterberg5 - A. Röhring4 -
W. Rhode6 - G. P. Rowell1 - V. Sahakian7 - M. Samorski5 - M. Schilling5 -
F. Schröder6 - W. Stamm5 - M. Tluczykont4 - H. J. Völk1 - C. Wiedner1 -
W. Wittek2
- J. Prahl4 - G. Pühlhofer1 - G. Rauterberg5 - A. Röhring4 -
W. Rhode6 - G. P. Rowell1 - V. Sahakian7 - M. Samorski5 - M. Schilling5 -
F. Schröder6 - W. Stamm5 - M. Tluczykont4 - H. J. Völk1 - C. Wiedner1 -
W. Wittek2
1 - Max-Planck-Institut für Kernphysik,
Postfach 103980, 69029 Heidelberg, Germany
2 -
Max-Planck-Institut für Physik, Föhringer Ring
6, 80805 München, Germany
3 -
Universidad Complutense, Facultad de Ciencias
Físicas, Ciudad Universitaria, 28040 Madrid, Spain
4 -
Universität Hamburg, II. Institut für
Experimentalphysik, Luruper Chaussee 149,
22761 Hamburg, Germany
5 -
Universität Kiel, Institut für Experimentelle und Angewandte Physik,
Leibnizstraße 15-19, 24118 Kiel, Germany
6 -
Universität Wuppertal, Fachbereich Physik,
Gaußstr.20, 42097 Wuppertal, Germany
7 -
Yerevan Physics Institute, Alikhanian Br. 2, 375036 Yerevan,
Armenia
![]() Present address: Astronomy Dept., Yale University,
PO Box 208101, New Haven, CT 06520-8101, USA
Present address: Astronomy Dept., Yale University,
PO Box 208101, New Haven, CT 06520-8101, USA
![]() On leave from
Altai State University, Dimitrov Street 66, 656099 Barnaul, Russia
On leave from
Altai State University, Dimitrov Street 66, 656099 Barnaul, Russia
Received 15 December 2000 / Accepted 24 April 2001
Abstract
Tycho's supernova remnant (SNR) was observed during 1997 and 1998 with the
HEGRA Cerenkov Telescope System in a search for gamma-ray emission at energies above
![]() 1 TeV. An analysis of these data,
1 TeV. An analysis of these data, ![]() 65 hours in total, resulted in
no evidence for TeV gamma-ray emission. The 3
65 hours in total, resulted in
no evidence for TeV gamma-ray emission. The 3![]() upper limit to the
gamma-ray flux (>1 TeV) from Tycho is estimated at
upper limit to the
gamma-ray flux (>1 TeV) from Tycho is estimated at
![]() photons cm-2 s-1, or 33 milli-Crab. We interpret our upper limit within the framework of the
following scenarios:
(1) that the observed hard X-ray tail is due to synchrotron emission. A lower limit on
the magnetic field within Tycho may be estimated
photons cm-2 s-1, or 33 milli-Crab. We interpret our upper limit within the framework of the
following scenarios:
(1) that the observed hard X-ray tail is due to synchrotron emission. A lower limit on
the magnetic field within Tycho may be estimated ![]()
![]() G, assuming that the
RXTE-detected
X-rays were due to synchrotron emission. However, using results from a detailed model
of the ASCA emission,
a more conservative lower limit
G, assuming that the
RXTE-detected
X-rays were due to synchrotron emission. However, using results from a detailed model
of the ASCA emission,
a more conservative lower limit ![]()
![]() G is derived.
(2) The hadronic model of Drury and (3) the more recent
time-dependent kinetic theory of Berezhko & Völk.
Our upper limit lies within the range of predicted values of both hadronic models,
according to uncertainties
in physical parameters of Tycho, and shock acceleration details. In the latter case,
the model was scaled
to suit the parameters of Tycho and re-normalised to account for a simplification of
the original model.
We find that we cannot rule out Tycho as a potential contributor at an average level
to the Galactic
cosmic-ray flux.
G is derived.
(2) The hadronic model of Drury and (3) the more recent
time-dependent kinetic theory of Berezhko & Völk.
Our upper limit lies within the range of predicted values of both hadronic models,
according to uncertainties
in physical parameters of Tycho, and shock acceleration details. In the latter case,
the model was scaled
to suit the parameters of Tycho and re-normalised to account for a simplification of
the original model.
We find that we cannot rule out Tycho as a potential contributor at an average level
to the Galactic
cosmic-ray flux.
Key words: gamma rays: observations - ISM: supernova remnants: individual objects: Tycho's SNR
The search for gamma-ray emission of TeV energies from supernova remnants (SNRs)
in recent years
is motivated by the need to explain the origin of Galactic cosmic-rays (CR). SNRs are
long-believed primarily responsible for the Galactic CR population, matching the CR
energetics and spectral index (Völk 1997;
Baring 2000a). The production of
![]() -rays in SNRs is thought to result from the interaction of
shock-accelerated particles (hadrons and electrons) with the interstellar medium (ISM) and
local soft photon fields. Being relatively unattenuated over long distances and
preserving the production site directionality, gamma radiation is one of the
most accessible tracers of CR acceleration in the universe.
-rays in SNRs is thought to result from the interaction of
shock-accelerated particles (hadrons and electrons) with the interstellar medium (ISM) and
local soft photon fields. Being relatively unattenuated over long distances and
preserving the production site directionality, gamma radiation is one of the
most accessible tracers of CR acceleration in the universe.
TeV gamma radiation is primarily expected from two channels (1) Collisions
of hadronic CRs, producing gamma-rays via ![]() decay and (2) CR electrons up-scattering
soft photons via the inverse Compton (IC) process, and CR electron collisions via Bremsstrahlung.
Detailed modelling of SNR environments has revealed distinct spectral features in the GeV/TeV regime for
these processes, and in combination with radio and X-ray observations, those in the TeV regime
are deemed vital in establishing SNRs as sites of CR production (Drury et al. 1994;
Naito & Takahara 1994; Berezhko & Völk 1997; Baring et al. 2000b).
decay and (2) CR electrons up-scattering
soft photons via the inverse Compton (IC) process, and CR electron collisions via Bremsstrahlung.
Detailed modelling of SNR environments has revealed distinct spectral features in the GeV/TeV regime for
these processes, and in combination with radio and X-ray observations, those in the TeV regime
are deemed vital in establishing SNRs as sites of CR production (Drury et al. 1994;
Naito & Takahara 1994; Berezhko & Völk 1997; Baring et al. 2000b).
So far, evidence for TeV emission has come from CANGAROO observations of two southern hemisphere SNRs, SN 1006, and SNR RX J1713.7-3946 (Tanimori et al. 1998; Muraishi et al. 2000), and the HEGRA Cerenkov Telescope CT-System (High Energy Gamma Ray Astronomy Cerenkov Telescope) after deep observations of Cas-A (Pühlhofer et al. 1999; Aharonian et al. 2000a). Upper limits are reported for those other promising SNR candidates observed so far in both the TeV and PeV regimes (Buckley et al. 1998; Prosch et al. 1996; Goret et al. 1999; Allen et al. 1995; Rowell et al. 2000), including Tycho's SNR, for which the Whipple Collaboration obtained 14.5 hours data. The CANGAROO and HEGRA detections might be interpreted in the framework of the SNR as a source of multi-TeV CR electrons by virtue of a strong non-thermal tail in their X-ray spectra above 1 keV (Koyama et al. 1995,1997; Allen et al. 1995). On the other hand as argued by Aharonian & Atoyan () and Berezkho et al. (1999) for SN 1006, and by Atoyan et al. (2000) for Cas-A, the TeV results do not rule out the hadron channel. It is nevertheless less clear at the moment as to the location of CR hadron accelerators in our galaxy.
Tycho's SNR (G120.1+1.4, 3C 10) is one of the most intensely studied SNRs. It is an archetypal shell-type
(radio & X-Ray) SNR, formed most likely from a type Ia supernova (SN 1572), and has expanded at ![]() 0.1% yr-1 to a radius
0.1% yr-1 to a radius
![]() 4
4![]() (Katz-Stone et al. 2000 and references therein). One estimate of distance is put at 2.2 kpc
(Albinson et al. 1986 and references therein) based on proper motion studies, absorption against field stars and the fact
that Tycho appears embedded in the Perseus arm of the Milky Way. A higher distance estimate of 4.5 kpc (Schwarz et al.
1995) is derived from a model of the HI spectrum and number of HI absorbing features in the region. The radio synchrotron
emission (20 & 90 cm) shows variation in photon index that appears correlated with edge filaments, perhaps tracing
regions of enhanced magnetic field and particle acceleration (Katz-Stone et al. 2000). Studies at the HI 21 cm line
indicate expansion on the eastern side of Tycho is slowed by a region of higher density (160-325 cm-3, Reynoso et al.
1999), suggesting that Tycho's SNR may not be expanding into such a homogeneous region as earlier believed.
The X-ray emission shows very strong line features and overall, is well fit by thermal bremsstrahlung components
(Fink et al. 1994; Petre et al. 1999). A power law however is necessary to fit a hard X-ray tail.
This presumably non-thermal tail above 1 keV suggests that Tycho may a source of electrons up to
(Katz-Stone et al. 2000 and references therein). One estimate of distance is put at 2.2 kpc
(Albinson et al. 1986 and references therein) based on proper motion studies, absorption against field stars and the fact
that Tycho appears embedded in the Perseus arm of the Milky Way. A higher distance estimate of 4.5 kpc (Schwarz et al.
1995) is derived from a model of the HI spectrum and number of HI absorbing features in the region. The radio synchrotron
emission (20 & 90 cm) shows variation in photon index that appears correlated with edge filaments, perhaps tracing
regions of enhanced magnetic field and particle acceleration (Katz-Stone et al. 2000). Studies at the HI 21 cm line
indicate expansion on the eastern side of Tycho is slowed by a region of higher density (160-325 cm-3, Reynoso et al.
1999), suggesting that Tycho's SNR may not be expanding into such a homogeneous region as earlier believed.
The X-ray emission shows very strong line features and overall, is well fit by thermal bremsstrahlung components
(Fink et al. 1994; Petre et al. 1999). A power law however is necessary to fit a hard X-ray tail.
This presumably non-thermal tail above 1 keV suggests that Tycho may a source of electrons up to ![]() 100 TeV, thereby
joining the growing number of SNRs that exhibit this feature (see Petre et al. 1999 for a review).
100 TeV, thereby
joining the growing number of SNRs that exhibit this feature (see Petre et al. 1999 for a review).
The observations of Tycho's SNR were made using the HEGRA CT-System
incorporating, at the time of data taking (1997 & 1998), four identical imaging air Cerenkov telescopes![]() (CT3-6).
The telescopes are operated in coincidence to achieve a stereoscopic view of Cerenkov light air showers induced by
(CT3-6).
The telescopes are operated in coincidence to achieve a stereoscopic view of Cerenkov light air showers induced by ![]() and
CR primaries. The CT-System is situated on the Roque de los Muchachos at La Palma
(2200 m asl,
and
CR primaries. The CT-System is situated on the Roque de los Muchachos at La Palma
(2200 m asl,
![]() N
N
![]() W) and at the zenith angles of these data, operates at an energy threshold for
W) and at the zenith angles of these data, operates at an energy threshold for ![]() -ray primaries of
-ray primaries of
![]() 1 TeV (see Konopelko et al. 1999 and references therein).
1 TeV (see Konopelko et al. 1999 and references therein).
| 1997 | 1998 | Total | |
| Obs. time (hrs) | 19.7 | 44.9 | 64.6 |
| Selected runs | 50 | 115 | 165(82%) |
| Configuration | CT3-6 | CT3-6 | |
| Zenith angle range | 32-41 |
32-45 |
|
| CR Event Rate (Hz) | 8.4 (10.3) | 8.5 | 8.5 |
The Tycho data were accumulated in Jul.-Sep. 1997 and Aug.-Dec. 1998 in 20-30 min runs utilising the wobble mode of
observation. In this mode, the source is offset
![]() in declination in alternating runs, enabling the background or OFF
source data to be estimated from the opposing position (or a series of positions) 1.0
in declination in alternating runs, enabling the background or OFF
source data to be estimated from the opposing position (or a series of positions) 1.0![]() away. Table 1 gives
a summary of these observations.
away. Table 1 gives
a summary of these observations.
Approximately 20% of all runs were rejected, due primarily to weather effects. Bad runs were identified
according to the criteria that the image width from each triggered telescope and stereo trigger rate match their expected values
accordingly, within 6% for width and 15% for rate (representing levels <4![]() outside their Gaussian distribution means).
The bad runs actually comprised the non-Gaussian tails of these distributions.
The trigger rate for CRs was significantly lower
in 1998 compared to 1997 (by
outside their Gaussian distribution means).
The bad runs actually comprised the non-Gaussian tails of these distributions.
The trigger rate for CRs was significantly lower
in 1998 compared to 1997 (by ![]() 25%), attributed mainly to photomultiplier tube (PMT) fatigue and mirror degradation.
We accounted for this threshold difference by artifically
raising the trigger threshold of 1997 data to 1998 levels by applying a 10 photoelectron threshold to the second-brightest
pixel in the image, mimicking the hardware trigger threshold, at 8 photoelectrons. The effect of this software trigger is to simplify
analysis and in particular, the estimation of upper limits. It may be justified given the negligible effect on the
25%), attributed mainly to photomultiplier tube (PMT) fatigue and mirror degradation.
We accounted for this threshold difference by artifically
raising the trigger threshold of 1997 data to 1998 levels by applying a 10 photoelectron threshold to the second-brightest
pixel in the image, mimicking the hardware trigger threshold, at 8 photoelectrons. The effect of this software trigger is to simplify
analysis and in particular, the estimation of upper limits. It may be justified given the negligible effect on the ![]() -ray
threshold of this cut (following the 40 photoelectron cut described below) and the fact that the 1997 observation time is
-ray
threshold of this cut (following the 40 photoelectron cut described below) and the fact that the 1997 observation time is ![]() 45%
that of 1998. The
45%
that of 1998. The ![]() -ray energy threshold
-ray energy threshold![]() for both years' data were found from simulations to be consistent within systematic errors (15%) to a value of 1 TeV.
for both years' data were found from simulations to be consistent within systematic errors (15%) to a value of 1 TeV.
Event filtering follows the standard method in that images containing more than 40 photoelectrons (size) are selected for
further analysis. The rejection of the CR background is achieved with cuts on the image shape and the location of its
reconstructed source position. The reconstruction is described as "Algorithm 1'' by Hofmann et al. (1999) and
the shape cut used is the so-called mean scaled width (msw).
The msw is the average of the scaled widths from each accepted image. Each image is scaled according to it's expected
value (![]() -ray hypothesis), dependent upon image size, zenith angle of observation and impact distance of the event from the
CT-System centre. Following cuts on msw and
-ray hypothesis), dependent upon image size, zenith angle of observation and impact distance of the event from the
CT-System centre. Following cuts on msw and ![]() ,
the difference between the reconstructed and actual source
positions, the stereoscopic method permits unprecedented angular and energy
resolution for
,
the difference between the reconstructed and actual source
positions, the stereoscopic method permits unprecedented angular and energy
resolution for ![]() -ray images on an event-by-event basis of
-ray images on an event-by-event basis of ![]() 6
6![]() and
and ![]() 20% respectively
(Aharonian et al. 2000b).
20% respectively
(Aharonian et al. 2000b).
We use a combination of "tight cuts'' in the shape (
0.4< msw<1.1) and direction
(
![]() deg2) criteria to preferentially select
deg2) criteria to preferentially select ![]() ray images against those from CR. Tight cuts are optimal
in the search for weak signals in background dominated statistics (3-5
ray images against those from CR. Tight cuts are optimal
in the search for weak signals in background dominated statistics (3-5![]() level), with the caveat that systematic effects may
become more important due to the cuts lying close to distribution tails. Tycho is a marginally extended source for the
HEGRA CT-System, and thus the optimal
level), with the caveat that systematic effects may
become more important due to the cuts lying close to distribution tails. Tycho is a marginally extended source for the
HEGRA CT-System, and thus the optimal ![]() cut will be slightly larger than that
for a point source at
cut will be slightly larger than that
for a point source at ![]() 0.015 deg2. A simple Monte Carlo, matching roughly the statistics of the background of our Tycho dataset,
was used to determine an optimal
0.015 deg2. A simple Monte Carlo, matching roughly the statistics of the background of our Tycho dataset,
was used to determine an optimal ![]() cut, assuming various morphologies for the SNR with the results displayed in
Fig. 1.
cut, assuming various morphologies for the SNR with the results displayed in
Fig. 1.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{h2595f1.eps} \end{figure}](/articles/aa/full/2001/25/aah2595/Timg42.gif) |
Figure 1:
Signal to noise ratios (unnormalised curves) from a Monte Carlo for sources of various morphologies. The HEGRA CT-System
point spread function (PSF, with |
| Open with DEXTER | |
A useful indicator of data quality is the CR acceptance (
![]() )
of the msw cut on a run-by-run basis
(Fig. 2).
)
of the msw cut on a run-by-run basis
(Fig. 2).
![\begin{figure}
\par\includegraphics[width=10cm,clip]{h2595f2.eps} \end{figure}](/articles/aa/full/2001/25/aah2595/Timg43.gif) |
Figure 2:
Cosmic ray acceptance (
|
| Open with DEXTER | |
We evaluate the statistical significance of the post-cut excess using Eq. (9) of Li & Ma (1983). The background or OFF source
counts are taken from three control regions at position angles 180![]() &
&
![]() ,
on a circle 0.5
,
on a circle 0.5![]() radius centred on
the tracking position, as the wobble mode of observation permits. A normalisation factor of
radius centred on
the tracking position, as the wobble mode of observation permits. A normalisation factor of
![]() is therefore used in the
significance calculation. By using more than one
background region, effects of skynoise, camera response and zenith angle difference are averaged out further (on
top of that already afforded by the stereoscopic technique), reducing somewhat any
systematics expected from such properties, and moreover, reducing the statistical error in the background.
A distribution of
is therefore used in the
significance calculation. By using more than one
background region, effects of skynoise, camera response and zenith angle difference are averaged out further (on
top of that already afforded by the stereoscopic technique), reducing somewhat any
systematics expected from such properties, and moreover, reducing the statistical error in the background.
A distribution of ![]() for the combined data after application of the msw cut discussed above is
presented in Fig. 3.
for the combined data after application of the msw cut discussed above is
presented in Fig. 3.
| |
Figure 3:
Distribution of |
| Open with DEXTER | |
| 1997 | 1998 | Total | |
| ON | 127 | 259 | 386 |
| OFF (
|
383 | 871 | 1254 |
| ON-OFF ( |
-0.7 | -1.6 | -1.4 |
| 3 |
0.033 | ||
| 3 |
5.78 | ||
Finally, we should point out that the method of Aharonian et al. (2000c)
(which downward fluctuates the Crab excess)
to estimate the UL in Crab units was tested for accuracy with a simple Monte Carlo
and found to overestimate a true 3![]() UL
(for the numbers of Table 2 by about 25%. This overestimate is
effectively canceled however by the negative
bias of our -1.4
UL
(for the numbers of Table 2 by about 25%. This overestimate is
effectively canceled however by the negative
bias of our -1.4![]() excess, an underestimate of
excess, an underestimate of ![]() 30% relative to a
zero excess result. We therefore may assume that our
3
30% relative to a
zero excess result. We therefore may assume that our
3![]() UL represents closely a true estimate. Secondly, any integral UL or flux
estimate quoted in absolute units will
naturally depend somewhat on the difference in photon index between the Crab and Tycho.
This uncertainty amounts
to
UL represents closely a true estimate. Secondly, any integral UL or flux
estimate quoted in absolute units will
naturally depend somewhat on the difference in photon index between the Crab and Tycho.
This uncertainty amounts
to ![]() 30% on the
UL estimation for a 20% uncertainty in the values of 1 TeV and -1.59 respectively
for energy and photon index.
30% on the
UL estimation for a 20% uncertainty in the values of 1 TeV and -1.59 respectively
for energy and photon index.
The evidence for a non-thermal tail (Fink et al. 1994, GINGA data;
Petre et al. 1999, RXTE data) may suggest that
Tycho's SNR is an accelerator of CR electrons to multi-TeV energies. In such a
framework, the synchrotron process is assumed to
account for these X-ray photons,
and the possibility of inverse Compton (IC) TeV ![]() -ray emission should be
considered. However, one must be careful
here since a power law fit is reasonable only at energies above
-ray emission should be
considered. However, one must be careful
here since a power law fit is reasonable only at energies above ![]() 10 keV and,
alternative physical explanations to the synchrotron scenario do exist (see for e.g.
Asvarov et al. 1990;
Laming 1998; Tatischeff et al. 1998).
10 keV and,
alternative physical explanations to the synchrotron scenario do exist (see for e.g.
Asvarov et al. 1990;
Laming 1998; Tatischeff et al. 1998).
Assuming that the synchrotron model is valid for Tycho, we may use the
direct relationship between the expected IC (
![]() )
and X-ray energy fluxes
)
and X-ray energy fluxes![]() (
(![]() )
arising
from the same electrons:
)
arising
from the same electrons:
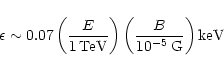 |
(2) |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{h2595f4.eps} \end{figure}](/articles/aa/full/2001/25/aah2595/Timg67.gif) |
Figure 4:
a) Optimal fit to the RXTE spectrum and radio normalisation using
Eq. (3) (thin solid line). (dashed line) A
fit when fixing
|
| Open with DEXTER | |
We will consider here the production of ![]() -radiation by the hadronic or
-radiation by the hadronic or ![]() -decay channel described in
two-fluid model by Drury et al. (1994), hereafter DAV, that has been used extensively in the past
(see also
Naito & Takahara 1994). The DAV prediction may be scaled simply according to
the energy budget of the SNR
-decay channel described in
two-fluid model by Drury et al. (1994), hereafter DAV, that has been used extensively in the past
(see also
Naito & Takahara 1994). The DAV prediction may be scaled simply according to
the energy budget of the SNR
![]() ,
density of the upstream target matter n, and distance to the remnant d:
,
density of the upstream target matter n, and distance to the remnant d:
Figure 5 highlights a comparison of this DAV prediction under limiting parameter-space selections as calculated by Völk (1997) with our present UL, and those of previous measurements (Whipple et al. 1998 & HEGRA AIROBICC, Prahl et al. 1997, and CASA-MIA, Borione et al. 1995).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{h2595f5.eps} \end{figure}](/articles/aa/full/2001/25/aah2595/Timg74.gif) |
Figure 5:
Upper limits from the present work (H-CT), and previous measurements (W - Whipple, H-A - HEGRA AIROBICC, CM - CASA-MIA.
See text for references)
with predictions of the |
| Open with DEXTER | |
An important parameter in view of the expected TeV emission from a SNR is it's evolutionary phase. Generally accepted is
the notion that the maximum TeV ![]() -ray emission occurs at the beginning of the Sedov phase and a broad maximum in the total CR
energy is reached during the Sedov phase. At the former time the mass of swept-up material will just exceed that ejected, and the outer
SNR shock begins to expand with
radius
-ray emission occurs at the beginning of the Sedov phase and a broad maximum in the total CR
energy is reached during the Sedov phase. At the former time the mass of swept-up material will just exceed that ejected, and the outer
SNR shock begins to expand with
radius
![]() .
Typical ages of Galactic SNRs for the onset of the Sedov phase are 500 to 1000 yrs. Tycho is a rather young SNR (428 yrs old)
expanding into an ISM with density typical of that expected within the Galactic plane and so it may not be clear as to exactly what phase Tycho is
presently in.
Observational evidence indicates that globally, Tycho's SNR is near to the Sedov phase (
.
Typical ages of Galactic SNRs for the onset of the Sedov phase are 500 to 1000 yrs. Tycho is a rather young SNR (428 yrs old)
expanding into an ISM with density typical of that expected within the Galactic plane and so it may not be clear as to exactly what phase Tycho is
presently in.
Observational evidence indicates that globally, Tycho's SNR is near to the Sedov phase (
![]() ,
,
![]() ,
Tan & Gull 1985),
and is expanding into, on a global scale at least, a homogeneous ISM. Reynoso et al. (1997) report a similar value,
from VLA data for the global expansion, but note that
,
Tan & Gull 1985),
and is expanding into, on a global scale at least, a homogeneous ISM. Reynoso et al. (1997) report a similar value,
from VLA data for the global expansion, but note that ![]() varies between 0.2 and 0.8 around the shell
and suggest the presence of
denser material along the eastern side
(see also recent 21 cm observations by Reynoso et al. 1999).
The expansion rate
at X-ray energies is significantly higher than at radio energies, but as in the radio, it also varies considerably azimuthally
(Hughes 2000). In contrast to the radio behaviour however, the expansion rate at X-ray energies varies radially,
supporting the idea of an ejecta-dominated, or pre-Sedov evolutionary state.
Taking these results together with the Rayleigh-Taylor
instabilities along the eastern side suggested by Velazquez et al. (1998), we may conclude that the global evolution state
of Tycho's SNR is pre-Sedov, although at regions of high density ISM, the evolutionary state will be locally advanced.
varies between 0.2 and 0.8 around the shell
and suggest the presence of
denser material along the eastern side
(see also recent 21 cm observations by Reynoso et al. 1999).
The expansion rate
at X-ray energies is significantly higher than at radio energies, but as in the radio, it also varies considerably azimuthally
(Hughes 2000). In contrast to the radio behaviour however, the expansion rate at X-ray energies varies radially,
supporting the idea of an ejecta-dominated, or pre-Sedov evolutionary state.
Taking these results together with the Rayleigh-Taylor
instabilities along the eastern side suggested by Velazquez et al. (1998), we may conclude that the global evolution state
of Tycho's SNR is pre-Sedov, although at regions of high density ISM, the evolutionary state will be locally advanced.
A comparison with DAV predictions should therefore allow for the current
evolutionary state of Tycho. The lower curve of Fig. 5
(nominal theory) may be lowered further
since the age of Tycho is likely less than the sweep-up time (t0=555 yrs) which signals the
onset of the Sedov phase. A reduction in the ![]() -ray emissivity for pre-Sedov epochs can be
manifested as a reduction in the
-ray emissivity for pre-Sedov epochs can be
manifested as a reduction in the ![]() parameter to values <0.1. A quantitative estimate for
parameter to values <0.1. A quantitative estimate for ![]() in this case is not trivial but generally one can expect a reduction by a factor
in this case is not trivial but generally one can expect a reduction by a factor ![]() 2 based on consideration of results
in Figs. 1 to 3 of DAV, describing different rates of luminosity increase with time.
In the next section comparisons to a model dealing with time-dependence in detail are made.
2 based on consideration of results
in Figs. 1 to 3 of DAV, describing different rates of luminosity increase with time.
In the next section comparisons to a model dealing with time-dependence in detail are made.
The most recent nonlinear kinetic models are the time-dependent, spherically symmetric
solution of Berezhko & Völk (1997), hereafter BV, and the Monte Carlo simulation of a quasistationary outer
SNR shock in plane parallel geometry by Baring et al. (1999). The BV model is
based on the numerical solution of Berezhko et al. (1994) and invokes a
distribution of ejecta velocities (e.g. Chevalier & Liang 1989 and references therein) that contains very high speed
components compared to the mean ejecta velocity. At early evolutionary phases this leads to much higher
shock speeds than implied by the mean ejecta velocity, and thus to much more intensive CR and ![]() -ray
production. We will in this paper make use of BV as it was calculated in their paper, scaling the parameters to those of Tycho's SNR.
As we shall note shortly, in addition, a physical re-normalisation of these results is necessary.
For a more complete treatment,
we refer to a companion paper elsewhere in which the BV model will be calculated assuming Tycho parameters.
-ray
production. We will in this paper make use of BV as it was calculated in their paper, scaling the parameters to those of Tycho's SNR.
As we shall note shortly, in addition, a physical re-normalisation of these results is necessary.
For a more complete treatment,
we refer to a companion paper elsewhere in which the BV model will be calculated assuming Tycho parameters.
A scaling of the original BV calculations is required since the start-up parameters
(in particular ejected mass
![]() and SNR energy
and SNR energy
![]() erg) may differ from those
one might expect for Tycho's SNR. For this scaling
we may reasonably assume, that the ejecta mass only effects the initial
normalisation in the form of the sweep-up time t0, and that other parameters will scale the flux
in the same way they do the DAV prediction, i.e. independent of time.
The first row of Table 3 presents a numerical comparison of our upper limit with
the predictions of the BV model,
erg) may differ from those
one might expect for Tycho's SNR. For this scaling
we may reasonably assume, that the ejecta mass only effects the initial
normalisation in the form of the sweep-up time t0, and that other parameters will scale the flux
in the same way they do the DAV prediction, i.e. independent of time.
The first row of Table 3 presents a numerical comparison of our upper limit with
the predictions of the BV model,
![]() (in units
of 10-13 ph cm-2 s-1), scaled to Tycho parameters.
(in units
of 10-13 ph cm-2 s-1), scaled to Tycho parameters.
![]() is the released fraction of energy available for CRs and
is the released fraction of energy available for CRs and
![]() is the value assumed for an average SNR, discussed previously.
is the value assumed for an average SNR, discussed previously.
| Case | a | b | c | |
| B ( |
5 | 30 | 5 | 5 |
| 10-3 | 10-3 | 10-4 | 10-4 | |
|
|
91.00 | 49.20 | 20.00 | 9.00 |
|
|
0.60 | 0.55 | 0.50 | 0.50 |
|
|
0.17 | 0.18 | 0.20 | 0.20 |
|
|
15.50 | 9.00 | 4.00 | 1.80 |
|
|
2.60 | 1.50 | 0.69 | 0.31 |
|
|
0.06 | 0.04 | 0.04 | 0.04 |
| HEGRA CT-System UL = 5.78 (10-13 ph cm-2 s-1). | ||||
![\begin{figure}
\par\includegraphics[width=9.2cm,clip]{h2595f6.eps}\end{figure}](/articles/aa/full/2001/25/aah2595/Timg87.gif) |
Figure 6:
Time dependence of the |
| Open with DEXTER | |
However, we must now invoke a further, physical re-normalisation of the Tycho-scaled BV
predictions for the following reason. The BV model assumes a parallel shock geometry
(shock normal parallel
to the average up-stream B field) over the entire spherical shock surface. For
spherical geometry expected of a SNR, such
an assumption will only apply for a limited part of the SNR shock surface.
Over
other parts the shock is quasi-perpendicular.
A strongly reduced injection efficiency below that derived from injection
theory for parallel shocks (
![]() )
along with a commensurate reduction of the particle production will
be noticed in such regions
(regarding the question of injection in general, see
Kirk & Dendy 2001 for a recent review).
Correcting for this effect in detail is
complicated, and will be discussed in a follow-up
paper. However, a rough, but empirically-argued
implementation of a re-normalisation is achieved by reducing the fluxes
)
along with a commensurate reduction of the particle production will
be noticed in such regions
(regarding the question of injection in general, see
Kirk & Dendy 2001 for a recent review).
Correcting for this effect in detail is
complicated, and will be discussed in a follow-up
paper. However, a rough, but empirically-argued
implementation of a re-normalisation is achieved by reducing the fluxes
![]() by the ratio
by the ratio
![]() to a re-normalised flux
to a re-normalised flux
![]() ,
where
,
where
![]() is
the empirically
expected value for an average Galactic SNR discussed earlier (and adopted by DAV), and
is
the empirically
expected value for an average Galactic SNR discussed earlier (and adopted by DAV), and
![]() is that value predicted by the BV model.
The re-normalised fluxes are those r-subscripted in
Table 3, and are rather close to our upper limit and the relative CR energy calculated
at the present age of Tycho.
is that value predicted by the BV model.
The re-normalised fluxes are those r-subscripted in
Table 3, and are rather close to our upper limit and the relative CR energy calculated
at the present age of Tycho.
![]() corresponds to values
of around 1049 ergs. Figure 6 graphically compares
corresponds to values
of around 1049 ergs. Figure 6 graphically compares
![]() for the different cases discussed. It appears that cases (c)
and (d), with a lower injection rate and B-field, are preferred. However, the combinations of B and
for the different cases discussed. It appears that cases (c)
and (d), with a lower injection rate and B-field, are preferred. However, the combinations of B and ![]() used here are not
exhaustive. For example a case assuming higher B (perhaps suggested by our inverse Compton interpretation in Sect. 4)
and low injection rate has not been tested by BV. More thorough comparisons will be made later. The uncertainties in
scaling parameters, d,
used here are not
exhaustive. For example a case assuming higher B (perhaps suggested by our inverse Compton interpretation in Sect. 4)
and low injection rate has not been tested by BV. More thorough comparisons will be made later. The uncertainties in
scaling parameters, d,
![]() and n will weaken of course the conclusion favouring cases (c) and (d), in which lower injection rates
and B fields are assumed.
The uncertainty in d, where roughly a factor of two above the
value used here (2.3 kpc) is published (Schwarz et al. 1995), will have strong influence. Also, a somewhat lower value of n=0.3 cm-3 derived by Seward et al. (1983) for the pre-shock density may also be preferable to the value given by Smith et al. (1988) used here. At this point we would conclude that a general consistency with the BV model is obtained, perhaps favouring lower injection rates and
higher B fields (noting the reduction in emissivity between cases (a) and (b), due to a change in B field), but
note that use of a wider parameter space under a dedicated BV calculation is required.
and n will weaken of course the conclusion favouring cases (c) and (d), in which lower injection rates
and B fields are assumed.
The uncertainty in d, where roughly a factor of two above the
value used here (2.3 kpc) is published (Schwarz et al. 1995), will have strong influence. Also, a somewhat lower value of n=0.3 cm-3 derived by Seward et al. (1983) for the pre-shock density may also be preferable to the value given by Smith et al. (1988) used here. At this point we would conclude that a general consistency with the BV model is obtained, perhaps favouring lower injection rates and
higher B fields (noting the reduction in emissivity between cases (a) and (b), due to a change in B field), but
note that use of a wider parameter space under a dedicated BV calculation is required.
A search for TeV ![]() -radiation from Tycho's SNR has been performed over two years (1997 & 1998) with the HEGRA
CT-system. We find no evidence for such emission
and the upper limit (3
-radiation from Tycho's SNR has been performed over two years (1997 & 1998) with the HEGRA
CT-system. We find no evidence for such emission
and the upper limit (3![]() level) to the TeV flux is estimated at 33 milli-Crab or
level) to the TeV flux is estimated at 33 milli-Crab or
![]() ph cm-2s-1,
a value which is a factor
ph cm-2s-1,
a value which is a factor ![]() 4
less than that previously published by the Whipple collaboration (when assuming a spectral index of -1.1 in for the comparison).
4
less than that previously published by the Whipple collaboration (when assuming a spectral index of -1.1 in for the comparison).
Making use of preliminary RXTE results, it is possible to set a lower limit on the magnetic
field in Tycho ![]()
![]() G under the assumption that the observed hard or non-thermal tail in the X-ray spectrum is
attributed to synchrotron radiation from multi-TeV electrons. A more conservative B field lower limit of
G under the assumption that the observed hard or non-thermal tail in the X-ray spectrum is
attributed to synchrotron radiation from multi-TeV electrons. A more conservative B field lower limit of ![]() 6
6 ![]() G is obtained
if we use the upper limit to the non-thermal
X-ray flux estimated by Hwang et al. (1998).
It may therefore be premature to draw conclusions about the minimum magnetic field until full analysis of RXTE data
are complete. Interestingly the upper limit to the non-thermal energetics of Hwang et al. (1998) is well below that implied by a
purely non-thermal interpretation of the RXTE and GINGA results.
Comparisons to a long-adopted model of TeV emission from the decay of
G is obtained
if we use the upper limit to the non-thermal
X-ray flux estimated by Hwang et al. (1998).
It may therefore be premature to draw conclusions about the minimum magnetic field until full analysis of RXTE data
are complete. Interestingly the upper limit to the non-thermal energetics of Hwang et al. (1998) is well below that implied by a
purely non-thermal interpretation of the RXTE and GINGA results.
Comparisons to a long-adopted model of TeV emission from the decay of ![]() were made (Drury et al. 1994, denoted DAV), in the initial case assuming that Tycho's SNR is well in to the
Sedov phase of evolution. Our upper limit is close to a conservative prediction of DAV.
Uncertainty in the global evolutionary state (Sedov, or pre Sedov)
of Tycho presents a complication upon comparison to the DAV
were made (Drury et al. 1994, denoted DAV), in the initial case assuming that Tycho's SNR is well in to the
Sedov phase of evolution. Our upper limit is close to a conservative prediction of DAV.
Uncertainty in the global evolutionary state (Sedov, or pre Sedov)
of Tycho presents a complication upon comparison to the DAV ![]() decay
decay ![]() -ray predictions.
As a function of time, advanced kinetic theory (Berezhko & Völk 1997, denoted BV) indicates a relatively early
rise in the
-ray predictions.
As a function of time, advanced kinetic theory (Berezhko & Völk 1997, denoted BV) indicates a relatively early
rise in the ![]() -ray emissivity of the hadronic channel for pre-Sedov epochs, in contrast to the less
realistic case of single-velocity ejecta, as adopted in the DAV model. We find that
after adjusting the predictions of BV, firstly scaling for Tycho's parameters and secondly, re-normalising to account for
quasi-perpendicular shock directions
expected in an SNR, a general consistency with our upper limit is found for a range of injection rates and B fields.
-ray emissivity of the hadronic channel for pre-Sedov epochs, in contrast to the less
realistic case of single-velocity ejecta, as adopted in the DAV model. We find that
after adjusting the predictions of BV, firstly scaling for Tycho's parameters and secondly, re-normalising to account for
quasi-perpendicular shock directions
expected in an SNR, a general consistency with our upper limit is found for a range of injection rates and B fields.
We conclude from this non-detection and the interpretation assuming Tycho to be a source of multi-TeV electrons and hadrons that Tycho's SNR is yet to be ruled out as an average accelerator of Galactic CRs. Our upper limit supports the notion that Tycho is in a pre-Sedov evolutionary state. A more complete investigation will be left to a companion paper in which a dedicated calculation in the framework of the BV model will be performed for the parameters (and their uncertainties) of Tycho's SNR.
Resulting from a type Ia supernova, Tycho's SNR in principle represents
the simplest category in terms of a theoretical understanding of the SNR dynamics and interaction with the
ISM. Yet, given the complexity in modeling non-thermal processes, the basic consistency between
experiment and theoretical predictions certainly encourages future observations of Tycho's SNR and other examples of it's
class.
Because of the ![]() dependence on instrument sensitivity, it is likely that further observations
at TeV energies of Tycho will have to wait for the
next generation of telescopes operating in the northern hemisphere (e.g.
MAGIC, Lorenz et al. 1999; VERITAS,
Krennrich et al. 1999). With roughly one order of magnitude
improvement in sensitivity for the next generation instruments over
that currently available, and the fact that current theory does not leave much room for non-detection at higher
instrument sensitivity, a decisive test of the question of whether or not Tycho's SNR
contributes to the Galactic CR population at an average level is expected within the next few years.
dependence on instrument sensitivity, it is likely that further observations
at TeV energies of Tycho will have to wait for the
next generation of telescopes operating in the northern hemisphere (e.g.
MAGIC, Lorenz et al. 1999; VERITAS,
Krennrich et al. 1999). With roughly one order of magnitude
improvement in sensitivity for the next generation instruments over
that currently available, and the fact that current theory does not leave much room for non-detection at higher
instrument sensitivity, a decisive test of the question of whether or not Tycho's SNR
contributes to the Galactic CR population at an average level is expected within the next few years.
Acknowledgements
We acknowledge the financial support of the German Ministry for Research and Technology (BMBF) and the Spanish Research Council. We thank the Instituto Astrofísica de Canarias for the use of their site and for the excellent working conditions at La Palma. The technical support staff of the Heidelberg, Kiel, Munich and Yerevan Institutes are also acknowledged. Glenn Allen is thanked for providing a fit to the RXTE Tycho data, and Anne Decourchelle for the model fit to the XMM data. GPR gratefully acknowledges receipt of a von Humboldt Fellowship. An anonymous referee is thanked for helpful comments.