A&A 373, 307-317 (2001)
DOI: 10.1051/0004-6361:20010494

Dynamics of the solar granulation

VII. A nonlinear approach

A. Nesis - R. Hammer - M. Roth - H. Schleicher

Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany

Received 8 December 2000 / Accepted 2 April 2001

Abstract
We investigate the attractor underlying the granular phenomenon by applying nonlinear methods to series of spectrograms from 1994 and 1999. In the three-dimensional phase space spanned by intensity, Doppler velocity, and turbulence (line broadening), the granulation attractor does not fill the entire phase space, as expected from the high Reynolds and Rayleigh numbers of the photospheric plasma, but rather shows a highly structured form. This could be due to the correlations between intensity, turbulence, and velocity, which represent also the Reynolds stress. To obtain insight into the dimensionality of the attractor, we use the time lag method, a nonlinear method that enables us to get information about the underlying attractor of a dynamical system (granulation) from the measurement of one physical quantity only. By applying this method to the observed Doppler velocities, we show that the granulation attractor can be described by three independent variables. The dimension of the granulation attractor seems to be independent of the appearance of big granules and shear flow. Furthermore, the power analysis of the Doppler velocity shows power down to the spatial resolution of the instrument (0.3 arcsec). In order to decide whether the power at the smallest scales is real or noise, we use again the time lag method in combination with either a high pass digital or wavelet filter, which filters out the large wave numbers. It appears that the power at the smallest scales represents a real signal.

Key words: Sun: photosphere - Sun: granulation

1 Introduction

Observables like Doppler velocity, intensity, and turbulence (line broadening) variations can provide insight into the physics of the granulation, i.e., into the physics of the upper solar convective layers. So far, measurements of these observables have been processed by means of a power and coherence analysis, which is actually connected with the physical concept of modes in linear theories: Nesis et al. (1993) studied the scaling law of small and large granular structures; Komm et al. (1991) and Espagnet et al. (1995) investigated the penetration of the granulation into the photosphere. Furthermore, Nesis et al. (1996) investigated the granular dynamics simultaneously in "plage'' and nonactive regions, and Nesis et al. (1997) repeated the study of the extension of the granular dynamics into the overshoot layers with better observations.

Figure 1: Part of our best spectrogram 99S4.Sp66, in the wavelength region $\lambda\lambda\!\! : 491.11$- $491.24~{\rm nm}$ with the corresponding slit-jaw white light picture attached at the right border. The dark line parallel to the x-axis, at 87 arcsec on the y-axis, is due to a calibration hair across the spectrograph slit. The dark line parallel to the y-axis corresponds to the spectrograph slit.

Open with DEXTER

Granules are dissipative structures and the end product of the convective processes in the upper solar layers: a highly nonlinear dissipative system operating far from thermodynamical equilibrium. According to Lorenz (1963), Ruelle & Takens (1971), and Hirsch & Smale (1974), such systems usually approach in time a strange attractor in its phase space. The attractor of a dynamical system can easily be obtained if the coupled differential equations for the relevant variables of the system are known. But, in many experimental situations neither the relevant variables nor even their total number are known, so that the attractor of the system is not a priori accessible. In this case, the attractor can be reconstructed in an artificial phase space, if a time series of one single variable is measured (Packard et al. 1980; Takens 1981). The embedding theorem of Takens (1981) ensures that the attractor is reliably reconstructed in the limit of a sufficiently large dimension $d\,\, (d \to \infty)$ of the artificial space. Based on this theorem, different procedures have been developed in order to determine dynamic as well as static invariants of attractors from experimental time series of single variables, e.g., the "correlation integral'' method (Grassberger & Procaccia 1983).

Nesis et al. (1999) found that during the evolution of granules the two dimensional phase portrait of the turbulence-granulation dynamical system shows notable changes in time, while the power spectra of the turbulence reveal a two-component character. These facts raise the question if the velocity field of the deep photospheric layers results from the superposition of many random events or whether it is governed by some global deterministic mechanism that can be effectively modeled by a small number of dynamical variables. In the latter case the signal may result from the superposition of two or more periodic effects, or it may be chaotic as a consequence of being associated with a low-dimensional attractor.

In the current investigation we address the granulation attractor and its dimension from the observational point of view, using the Doppler velocity, turbulence (line broadening), and intensity variations along the spectrograph slit as input data. Although these observables are functions of space instead of time, the results should nevertheless be reliable in view of the reasonable assumption that an ensemble of spatially neighbouring states is equivalent to a time trajectory of a single state over a sufficiently long period of time. Therefore, any physical state found along the slit at any given instant will be realized in time at a single point. This assumption is related to the ergodic hypothesis, which states that for an ensemble of strictly independent states, a large number of observations made on a single system at N arbitrary instants of time have the same statistical properties as observing simultaneously Narbitrarily chosen systems from the ensemble.

To obtain insight into the dimensionality of the attractor underlying the granulation, we apply the time-lag and "correlation integral'' method (cf. Grassberger & Procaccia 1983) to the Doppler velocity measurements. Here, we are interested to see (i) if the attractor corresponding to the granular Doppler velocity has a low or high dimensionality and (ii) if the dimensionality shows any change within the last 6 years, i.e., from solar minimum to solar maximum. We assert that the granulation attractor is a manifestation of the granulation dynamics and any of its mutual interactions with characteristic physical quantities; especially magnetic field and pressure stratification should be reflected by its dimension.

Furthermore, the investigation of the granular velocity power scaling law at scales comparable to the instrumental resolution confronts us with the problem of their recognition. We use wavelets methods and the correlation integral technique to examine the nature of the signal corresponding to the smallest recorded scales. The behavior of the attractor dimension enables us to distinguish between pure noise and signal.

   
2 Material and methods

2.1 Material

The current investigation is based on series of high spatial resolution spectrograms taken during periods of exceptional seeing conditions during 1994 May and 1999 August with the German Vacuum Tower Telescope (VTT) in Izaña (Tenerife).

The observational material of May 1994 consists of a series of long-slit photographic spectrograms taken every 15 s at a fixed position near the center of the solar disk, covering about 20 min in total. The exposure time was 4 s and the wavelength range was $\lambda\lambda\!\!: 491.00$- $491.40~{\rm nm}.$ In this work we discuss the spectrogram 94.A48. For a detailed description of this material see Nesis et al. (1996, 1997).

In August 1999 further series of spectrograms were taken, again at a fixed position near the center of the solar disk every 15 s, covering about 20 min in total. The associated slit jaw images define well the position of the spectrograph slit on the solar disk (see Fig. 1). The spectrograms were recorded by an electronic Xedar imaging camera, a $2048\times 2048$ pixel CCD system operated in frame selection mode, with an exposure time of 600 msec. By binning $2\times 2$ pixels we obtained a spatial resolution of 0.13 arcsec per pixel and a spectral resolution of 1.4 mÅ per pixel. In the current work we discuss the spectrogram, 99S4.Sp66, which turned out to be of particularly high quality (Fig. 1). It exhibits an intensity contrast of $\approx$7%. The wavelength range was again $\lambda\lambda\!\!: 491.00$- $491.40~{\rm nm}$ and included several absorption lines of different strength.

The quality of the spectra was judged both visually, on the basis of the crispness of line wiggles at large magnification, and numerically, based on the properties of power spectra.

   
2.2 Method

2.2.1 Filtering, power analysis and 3D correlation

The observables Doppler velocity $v_{{\rm conv}}$, line broadening FWHM, and continuum intensity $i_{{\rm gran}}$ were measured along the spectrograph slit at equidistant positions s_i. The $v_{{\rm conv}}$ variations were measured as Doppler shift fluctuations of the line core about its mean value along the spectrograph slit, while the line broadening fluctuations FWHM correspond to the full line width at half maximum (cf. Nesis et al. 1993). In the following the intensity variations $i_{{\rm gran}}$ along the spectrograph slit are also given relative to the mean intensity. By calculating the line profiles we verified that the lines have a small temperature sensitivity, as expected for neutral metal lines of ca. 4 eV excitation energy. Because the absorption lines are to first order also magnetically insensitive and the line asymmetry is negligible, the FWHM $w_{{\rm turb}}$ reflects an unresolved photospheric velocity field w which unambiguously includes photospheric turbulent velocity fluctuations; thus in the following we will refer to $w_{{\rm turb}}$ as turbulent velocity as opposed to the granular convective velocity $v_{{\rm conv}}$.

   
Wavelet filter.-

According to Meyer (1993) a wavelet transform presupposes the following necessities: the analyzing wavelet is required to have zero average, wavelets have to be continuous functions, and there should be a single, spatially localized "mother function'', which is translated to cover all positions and dilated to obtain the scale decomposition. Furthermore, a reconstruction formula has to exist for recovering the signal exactly from its wavelet coefficients. All analyzing wavelets are then mutually similar, and scale covariant with one another.

Wavelets can store separately the high and low frequency coefficients by the wavelet transformation (cf. Press et al. 1992). We use this property to remove the spatial high frequency noise. The inverse wavelet transformation, in addition, enables us to control the filtering process in such a way that the main features of the original signal remain intact. The wavelets which we use in this paper are the orthogonal Daubechies functions, which allow to separate a signal into a minimal number of independent coefficients. They are defined on the dyadic grid and are covariant with respect to discrete translations and dilatations only (see Press et al. 1992). As a consequence, the length of the data in pixels has to be a power of two, and the resolved scales are also powers of two. Therefore, in the case of the 94.A48 spectrogram we use only 512 out of the 676 digitized data points along the spectrograph slit.

   
Digital filter.-

In order to clarify the distinction between signal and noise in the power at sub-granular scales $\leq$0.40  ${\rm arcsec}$, we apply to the observables a low pass digital filter (cf. Nesis et al. 1992): a gently weighted running mean filter $\frac{1}{35}\left[-3,12,17,12,-3\right]$ (cf. Kendall & Stuart 1968). Since we are interested in signals beyond about 20 Mm^-1 in the wave number domain, corresponding to 0.43 arcsec, we constructed the numerical filter in such a way that its spatial frequency response shows a transmissivity of $\approx$55% of the original signal at 20 Mm^-1. We call the difference between the measured velocity along the slit $v_{{\rm conv}}$, and the output of the low pass filter residual velocity. The residual velocity, thus, corresponds to the output of a high pass filter.

   
Power analysis.-

The dynamical behavior of a complex system of dissipative nature can be studied by means of power spectra. Here, we use the power analysis in association with the digital filter described above and the time lag method in order to find out if the power assigned to the smallest scales is due to the granulation or to noise.

   
3D plot of the observables.-

The degree of the correlation between the intensity, Doppler velocity and turbulence is shown in the 3D phase portrait of the granulation (cf. Fig. 4 and Sect. 3).

2.2.2 Dynamical analysis

   
Reconstruction of the phase space.-

The existence of a chaotic attractor in a dissipative system can be demonstrated by analyzing a suitable single-variable time series. Packard et al. (1980) outline a simple method (time lag) developed by Ruelle & Takens (1971) for reconstructing a phase space from one dynamical variable: let $x_1, x_2,\dots,x_N$ be measurements of a physical variable at the time $t_i = t_0+i\Delta t ,\,\, i = 1,\dots,N$. From this sequence one can construct a set of m-dimensional vectors $v_i\,,\, i = 1,\dots,N-(m-1)T$, of the form

$$v_i = (x_i, x_{i+T}, x_{i+2T},\dots,x_{i+(m-1)T}),$$ (1)

where the time delay (time lag), T, is an integer multiple of $\Delta t$. This method, (time lag), fills the other dimensions with lagged versions of one dynamical variable.

Correlation integral and Attractor dimension.-

On the assumption that the dissipative system under study is associated with a chaotic attractor of the Hausdorff dimension D, Packard et al. (1980) show that the geometrical form of the attractor can be reconstructed from the set of vectors v_i, provided m is greater than D. The central idea is that if an attractor exists, the vectors v_i will lie on a D-dimensional subset of the embedding space R^m. The value of the time delay T is dictated in practice by the compromise between computation time and the accuracy of the results.

A lower limit on the dimension D of the attractor can be calculated by computing the correlation integral introduced by Grassberger & Procaccia (1983). It is defined as

$$C^{(m)}(r) = \frac{1}{N^2}\sum_{\scriptsize\begin{array}{l} i... ... j \neq i \end{array}}^{N} \theta(r - \vert v_i - v_j\vert),$$ (2)

where $\theta(x)$ is the Heavyside function

$$\theta(x) = \left\{\begin{array}{ll} 1 & \mbox{for $x\ge0$ ,} \\ 0 & \mbox{otherwise} \end{array} \right.$$

and

$$\begin{array}{lll} N & = \mbox{number of observations} \\ ... ...= \mbox{correlation integral for dimension $m$ .} \end{array}$$

The double sum in Eq. (2) counts the number of pairs of vectors v_i and v_j with a distance less than r. In other words the correlation integral is the probability that two points chosen at random are less than r units apart. The normalization constant has been chosen to make C^(m)(r)= 1 for large r.

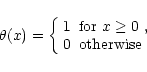
For a system with behavior governed by a D-dimensional attractor, Grassberger & Procaccia (1983) postulated that when ris less than the overall size of the attractor, $C^{(m)}(r)\propto r^\nu$, where $\nu$ is called the correlation dimension. They then showed that $D_{{\rm c}} \geq \nu$. In fact, for several model systems, Grassberger & Procaccia (1983) found that $\nu \simeq D_{{\rm c}}$ so that $\nu$is expected to be a good estimate of the exact dimensionality $D_{{\rm c}}$:

$$C^{({m})}(r) \propto \lim_{r \to 0} r^{D_{{\rm c}}(m)}$$ (3)

or

$$D_{{\rm c}}(m) \propto \lim_{r \to 0} \frac{\ln C^{({m})}(r)}{\ln r} \cdot$$ (4)

For a dimension m, we can calculate C^(m)(r)for increasing values of r. By finding the slope of a graph of the $\ln C^{({m})}(r)$ with $\ln r$, through a linear regression, we can estimate the correlation dimension $D_{{\rm c}}(m)$ for the embedding dimension m. By increasing m, $D_{{\rm c}}(m)$ will eventually converge to its true value. Usually, convergence occurs when the embedding dimension is three or more integer levels above the fractal dimension (cf. Figs. 6, 7 and Sect. 3).

There are, however, limitations to the Grassberger-Procaccia algorithm. The range [ $r_{{\rm min}},r_{{\rm max}}$] of values of r is limited ( $r_{{\rm min}}$ and $r_{{\rm max}}$ are the smallest and largest values of the distance of pairs $\left\vert v_i-v_j\right\vert$, in particular $r_{{\rm max}}$ is the diameter of the reconstructed attractor).

Choice of the space lag T.-

Based on the ergodic hypothesis we applied the time lag method, i.e., the method to reconstruct the phase space and to calculate the correlation integral and attractor dimension, to our series of measurements along the spectrograph slit. In this case T is a space lag instead of a time lag, and $\Delta t$ corresponds to the pixel size.

Now, to illustrate the choice of the space lag T, let us suppose that two vectors v_i and v_j have first components corresponding to the beginning of a granular structure. According to Hilborn (1994) the succeeding components of these vectors are reasonably well correlated as long as $mT \leq 3\tau$, where $\tau$ is an appropriate characteristic space lag of the autocorrelation decay for the original space series.

Komm et al. (1991) analyzed Doppler velocity space series and found a zero autocorrelation for $\tau \approx 725$ km. Mattig et al. (1969) studied the cross correlation between granular intensity and velocity series and found the first zero crossing at $\approx$725 km, i.e., at a spatial displacement of $\approx$725 km. Therefore, in our case $\tau \approx 725$ km should be a reasonable characteristic space lag.

Since the maximum embedding dimension is of order m = 7 (see below, Figs. 7, 10), the condition $mT\leq 3~\tau$ results in the choice of the space lag $T \approx 300~\mbox{km}$, which is approximately three times the pixel size of 90 km (cf. Sect. 2.1).

	Figure 2: Granular Doppler velocity variations $v_{{\rm conv}}$along the spectrograph slit derived from the line wiggles of the Ni absorption line (cf. $\lambda 491.24$ on the ordinate in Fig. 1). Abscissa: relative position on the solar surface (in arcsec). Ordinate: velocity variations in kms-1.
Open with DEXTER

	Figure 3: Log-log power spectrum of the granular Doppler velocity variations before ( grey curve, $v_{{\rm conv}}$) and after ( dark curve) applying a digital low pass velocity filter. The dark line shows the average gradient of the latter curve.
Open with DEXTER

Figure 4: 3D phase portrait of the granulation dynamics. The variations along the spectrograph slit of the Doppler velocity, turbulence, and intensity correspond to x, y, z axis, respectively. The planes xy, xz, and yz show qualitatively the correlations of the velocity - turbulence (dash-dot line), velocity - intensity (dash-dot-dot-dot line), and turbulence - intensity (dashed line), respectively.

Open with DEXTER

   
3 Results

The results that we present and discuss in the following are based on spectrogram 99S4.Sp66 taken in 1999, and spectrogram 94.A48 from 1994. The presentation of the results follows the order of the processing steps presented in Sect. 2.2.

   
3.1 Spectrogram $\mathsf{99S4.Sp66}$

In Fig. 1 we show part of the spectrogram 99S4.Sp66 with the corresponding slit jaw picture attached at its right border. The horizontal axis shows the wavelength range $\lambda\lambda\!\! : 491.11$- $491.24~ {\rm nm},$ which includes the absorption lines $\lambda\lambda$ Ti II 491.00, Fe IP 491.13, Fe I 491.78, and Ni I 491.20 nm. The vertical axis is parallel to the spectrograph slit and gives the relative positions along the slit in arcsec. On the slit jaw picture the dark line parallel to ordinate denotes the spectrograph slit.

Figure 1 shows clearly the correspondence between granule and intergranular space on the slit jaw picture, and bright and dark stripes on the spectrogram, respectively. Thus, we can trace clearly the Doppler shifts of the lines towards the blue and red parts of spectrum due to convective up- and downflows in granules and in the intergranular space, respectively. The dark line parallel to the abscissa, at 87 arcsec on the ordinate, is due to a fiducial hair across the spectrograph slit.

Figure 2 shows the Doppler velocity variations $v_{{\rm conv}}$ (about their mean value) along the spectrograph slit for the magnetically insensitive (g=0) absorption line Ni I 491.20 nm (cf. abscissa of Fig. 1). The abscissa of the plot is the length in arcsec along the slit, whereas the full line at the position 87 arcsec is due to the hair crossing the slit (cf. Fig. 1). On the ordinate positive velocities denote the granular upflow, while negative ones mark the downflow within the intergranular space. In Fig. 2 large amplitude variations within a distance of $\leq$0.7 arcsec or $\approx$500 km lead to shear flows and, thus, to the possibility of shear turbulence (cf. Nesis et al. (1997), for example at the intervals [40, 45] [52, 56], [74, 80] and [90, 95] on the x-axis. Noteworthy is also the behavior of the Doppler velocity along the slit in the interval [27, 38] and around the position 100 arcsec. Here the velocity $v_{{\rm conv}}$ shows small amplitude variations and the granulation on the slit jaw picture looks like a "jelly'' (cf. Fig. 1).

Power.-

In order to study the relationship of the variations of the velocity $v_{{\rm conv}}$ as a function of the various granular structures we calculated its power spectrum. Figure 3 exhibits the power spectral density of the measured granular velocity $v_{{\rm conv}}$ (grey line) as a function of the wavenumber $k[{\rm Mm}^{-1}] =2\pi/\Lambda$, where $\Lambda$ is spatial scale, in a log-log presentation. The power declines with the wavenumber and shows a minimum at $\log k \approx 1.30$; then it rises again with the wavenumber and shows a maximum of one log unit above the "zero level'' (dotted line) at $\log k \approx 1.45$. The logarithmic wavenumber interval [1.30, 1.45] corresponds to spatial structures within the interval [200, 300] km, which are comparable to the spatial resolution of the spectrograph. The finding of significant power in these structures raises the question about the origin of the signal causing this power; this shall be discussed later. In Fig. 3 we present also the power spectrum of $v_{{\rm conv}}$ after its digital filtering (dark line), i.e. the power of the velocity deprived of its high frequency variations. Remarkable is that both power curves show the same behavior down to $\log k \approx 1.3$ ( $\Lambda \approx 0.4$ Mm).

It is important to note that the slope of the power changes at $\log k \approx 0.7$ ( $\Lambda \approx 1.25$ Mm), from approximately -1.8 in the logarithmic wavenumber range [0.2, 0.7] to about -6.5 in the range [0.7, 1.3]. This raises the question of the underlying physical process causing the change of the slope.

3D plot of observables.-

Figure 4 shows the dynamics of the granulation in a space spanned by the three observables: Doppler velocity, turbulence, and intensity. The three observables are traced along the slit by means of the absorption line $\lambda$ Ni I 491.20 nm, and the continuum, respectively. Remarkable is in Fig. 4 the well structured plot (full line), which resembles an attractor within the 3D-state space and raises the question about its dimension. The correlations between the three observables correspond to the projections of the 3D-plot on the three phase planes. The velocity-intensity correlation (dash-dot-dot-dot line) is shown on the xz-plane, the velocity-turbulence correlation (dash-dot line) on the xy-plane, and the correlation between turbulence and intensity (dashed line) on the yz-plane.

3D reconstructed phase space.-

Figure 5 shows the three-dimensional phase portrait of the granulation, reconstructed by a single observable according to Eq. (1). The axis denoted Z_i shows the single observable $v_{{\rm conv}}$after the digital filtering. The time lag method fills the other dimensions with lagged versions of this observable, marked by Z_i+T, and Z_i+2T, respectively. Figure 5 implies a well formed attractor (full line) within the 3D reconstructed space. Its projections on the three planes xy, xz, and yz are also shown. They reflect the correlations <Z_i,Z_i+2T> (dash-dot line), <Z_i,Z_i+T> (dash-dot-dot-dot line), and <Z_i+2T,Z_i+T> (dashed line), respectively.

Correlation integral.-

Figure 6 shows the natural logarithm of the correlation integral C^(m)(r)calculated for 11 distances of increasing r and for different embedding dimensions m (see Eq. (2)). The correlation integral calculated for the velocity $v_{{\rm conv}}$ is shown in Fig. 6 up to the embedding dimension m=7. At this dimension the slope of the corresponding graph becomes practically equal to the slope of the preceding dimension m=6. The slope of the correlation integral refers to the scaling region, which is the linear part of the graphs, and changes with m (cf. Hilborn 1994). Dotted lines and the full line show the range of r where we measure the slope. For high values of the embedding dimension ($m \geq 4$) and small distances ( $\ln r \leq 5$), the correlation integral is almost constant. For large values of $\ln r$, on the other hand, the finite size of the attractor makes C^(m)(r)saturate at 1.

Figure 5: Three-dimensional phase portrait of the granulation, reconstructed by a single observable according to Eq. (1). The axis denoted by Zi represents this single observable: filtered $v_{{\rm conv}}$ measurements along the spectrograph slit. The time lag method fills the other dimensions with lagged versions of this observable, marked by Zi+T, and Zi+2T, respectively. The planes xy, xz, and yz show the correlations <Zi,Zi+2T> (dash-dot line), <Zi,Zi+T> (dash-dot-dot-dot), and <Zi+2T,Zi+T>(dash), respectively.

Open with DEXTER

	Figure 6: A plot of the natural logarithm of the correlation integral Cm(r) as a function of ${\rm ln}r$ for various embedding dimensions m for data derived from the filtering of the original measurements $v_{{\rm conv}}.$ The scaling region is denoted by lines of different style.
Open with DEXTER

Attractor dimension.-

In Fig. 7 we see the convergence correlation dimension $D_{{\rm c}}(m)$ as a function of the embedding dimension m (dark dots). $D_{{\rm c}}(m)$ is calculated for the filtered velocity variations $v_{{\rm conv}}$.

The dotted line parallel to the x-axis marks the convergence value, which defines the dimension of the attractor. The attractor dimension is found to be about 3.6. The convergence begins at the embedding dimension $m_{{\rm sat}}=6$, about twice the dimension of the attractor. We like to notice that white noise would provide a correlation dimension that does not converge (dotted line with crosses).

	Figure 7: The correlation dimension $D_{{\rm c}}(m)$ as a function of the embedding dimension m for data derived from the filtering of the original measurements $v_{{\rm conv}}.$ When the embedding dimension exceeds $m_{{\rm sat}}\approx 6$, the correlation dimension $D_{{\rm c}}(m)$ becomes independent of m. This is not the case for white noise (dotted line).
Open with DEXTER

3.2 Spectrogram $\mathsf{94.A48}$

Figure 8 shows the two-dimensional phase portrait of the attractor reconstructed for the convective velocity variations gained from spectrogram 94.A48. The x-axis denoted by X(i)shows velocity variations along the slit; the y-axis is the time-lagged version of this observable X(i+T). This plot corresponds to the attractor projection on the X(i), X(i+T)plane of the embedding space. The trajectory is seen to be smooth over long periods, concentrated towards the diagonal. This appears to reflect the fact that the trajectory belongs to a well structured attractor of low dimension for the convective velocity, which will be further discussed below.

	Figure 8: Two dimensional phase portrait calculated from the convective velocity variations $v_{{\rm conv}}$.
Open with DEXTER

	Figure 9: Same as Fig. 6, but for spectrogram 94.A48.
Open with DEXTER

Figure 9 shows the natural logarithm of the correlation integral C^(m)(r) calculated for 11 distances r and for different integer embedding dimensions m (see Eq. (2)) for the velocity $v_{{\rm conv}}$, traced from spectrogram 94.A48, up to the embedding dimension m=8. We stop the calculation when the slope of the graph becomes practically equal to the slope of the preceeding calculation, as can be seen with the aid of the dotted lines. These indicate also the range of r where we measure the line inclination. For high values of the embedding dimension ($m \geq 4$) and small distances ( $\ln r \leq 6$ ), the correlation integral is almost constant. For large values of $\ln r$, on the other hand, the finite size of the attractor makes C^(m)(r) saturate at 1.

	Figure 10: Same as Fig. 7, but for spectrogram 94.A48.
Open with DEXTER

Figure 10 demonstrates again the convergence of the correlation dimension $D_{{\rm c}}({\rm m})$ with increasing value of the embedding dimension m (dark dots). The dashed line parallel to the x-axis marks the convergence value, which defines also the dimension of the attractor. For the velocity variations $v_{{\rm conv}}$, gained from spectrogram 94.A48, the attractor dimension has again a fractal dimension of about 3.6. The convergence begins at the embedding dimension $m_{{\rm sat}}=7$, which is about twice the attractor dimension. We like to stress again that a white noise signal would give a correlation dimension that does not converge (dotted line with crosses).

4 Discussion

Figure 1 shows the dynamical behavior of the highly structured overshoot layers. The granule on the slit jaw pictures and the Doppler shifts of the absorption lines on the associated spectrogram show that the bright (hot) regions represent ascending, whereas the darker (colder) regions signify descending flow. But, on the other hand, theoretical considerations and model calculations of the granulation phenomenon regard these ordered layers as a highly turbulent hydrodynamical system, characterized by many degrees of freedom, thus provoking the continued quest for the physics of the granulation.

Important empirical insight in the physics of the granulation is provided by the power spectrum of the line of sight velocity $v_{{\rm conv}}$, measured along the spectrograph slit as shown in Fig. 2. The one-dimensional power spectrum in Fig. 3 (grey line) reflects the dynamical behavior of the granular structures (3.5 Mm down to 300 km). It is characterized by a change of its slope at ${{\rm log}k} \approx 0.7$; and an enhancement of the power at small granular scales. A literature survey shows that our finding concerning the change of the slope rests on a firm empirical basis. The velocity power spectra published by Durrant & Nesis (1982), Komm et al. (1990), Nesis et al. (1993), Espagnet et al. (1993), and Nesis et al. (1996) exhibit also a change of their slopes at practically the same granular scale as we find, of the order of $1.5 \pm 0.2$ Mm.

This finding means that the dynamical behavior of the granular spatial scales can not be described by a single power law of the form k^-q with a constant power exponent q. The slope change points to a division of the granular scales into groups, according to their dynamical behavior, and thus raises the question about the physical reasons underlying this change.

Keil (1980) showed a two-dimensional $k-\omega$ power spectrum of a line of sight velocity measurement in a medium-strength absorption line. In his Fig. 4, traces parallel to the k-axis represent the power as a function of the wavenumber at different frequencies. To compare our one-dimensional power spectrum (cf. Fig. 3, grey line) with that of Keil (1980, Fig. 4) we used a trace parallel to the k-axis at a frequency corresponding to a time period comparable to the mean life time of granules. This gives again a change of the power slope at a scale of 1.5 Mm: the slope at small scales seems to be steeper than that at larger scales. According to Keil (1980) the velocity variations at spatial scales of $\approx$2 Mm and smaller, show a great deal of power at frequencies corresponding to granular lifetimes, as well as the high-frequency power. However, at spatial scales smaller than 1.5 Mm the two-dimensional power is practically free from any oscillatory power.

Thus, the results presented by Keil (1980, Fig. 4) also support our findings concerning the change of the velocity power slope Fig. 3 (grey line) as well as the associated indication of the existence of separate regimes of granular scales with different dynamical behavior. Remarkable, however, is the coincidence of the oscillatory power with one of these two scale regimes.

Muller (1999) pointed out the existence of a critical granular size of the order of 1000 km, which divides the granular structures into two groups with clearly different behavior and different fractal dimensions associated with their geometry. Furthermore, he noticed that according to Mandelbrot (1977) these fractal dimensions prescribe the power law exponent and thus the dynamical state of the corresponding hydrodynamical system.

It is remarkable that our findings concerning the change of the power slope (cf. Fig. 3, grey line) are in a good agreement with those reported by Muller (1999) in spite of the different approach.

In Fig. 3 (grey line) the enhancement of the velocity power corresponding to small scale velocity fluctuations raises the question about the fitting of the observed power by a scaling law of the form k^-q with a constant power exponent q. To address this question we filtered out the small scale velocity fluctuations: first we applied a low pass digital filter to the original velocity fluctuations, with a cutoff wavenumber at $k \approx 20~ {\rm Mm}^{-1}$. Then we subtracted the low pass output from the original signal (the input of the low pass filter). This difference gives a series of fluctuations along the spectrograph slit associated with the small scales of the solar surface. The effectivity of the low pass digital filter to remove high wave numbers is demonstrated by the similarity between the two power plots in Fig. 3 (dark line and gray line) up to the cutoff wavenumber $k \approx 20~ {\rm Mm}^{-1}$. The power spectrum of the low pass velocity signal (dark line) and the original velocity fluctuations (gray line) can be expressed by a power law of the form k^-q with the exponent $q \approx -7$ for small granules [0.331.2] Mm and $q \approx -3.2$ for the large granules [1.23.2] Mm.

	Figure 11: The correlation dimension $D_{{\rm c}}(m)$ vs. the embedding dimension m for the residual velocity obtained from spectrogram 99-S4Sp66.
Open with DEXTER

The observational analysis of the dynamics of the granular layers is based mainly on three observables: Doppler velocity fluctuations, turbulence (line broadening), and intensity (see Sect. 2.2). The 3D plot in Fig. 4 shows the phase space spanned by these three observables, while on the three planes we see the correlations between the observables. It reflects in particular the high correlation between intensity and velocity and the moderate one between turbulence and velocity. The poor correlation between intensity and turbulence is likely due to the origin of the turbulence at the borders of granules in the dark intergranular lanes (cf. Nesis et al. 1997).

According to Bradshaw (1976), correlations between the observables describe sensitively the evolution of any convective flow, especially its transition to turbulence. From this point of view the significant correlation between the three observables implies a highly organized flow with few degrees of freedom, i.e., the existence of a low dimensional granulation attractor.

An organized flow with few degrees of freedom could be due to the presence of magnetic fields (e.g., Tennekes & Lumley 1972). Even though our measurements were taken in nonactive regions, weaker intergranular magnetic fields cannot be excluded. In fact, a large body of recent numerical work on magnetoconvection (Cattaneo 1999; Weiss & Proctor 2001) suggests that the solar granulation can act as an efficient dynamo source for small-scale magnetic fields of a strength determined by the balance between the rates of vorticity generation by buoyant and magnetic curvature forces (Galloway et al. 1978). This process would contribute to organizing the flow and reducing thus the number of degrees of freedom.

To learn more about the existence of a granular attractor and its dimension, we applied the time lag method for the reconstruction of the attractor embedding space and the correlation integral to measure its dimension, as described in Sect. 2.2.2.

In Fig. 5 we see the 3D phase portrait of the granular layers, reconstructed according to the time lag method from a single observable, namely the filtered, noise-free, velocity fluctuations. The axis denoted by Z_i corresponds to this observable, while the time lag method fills the other dimensions Z_i+T, and Z_i+2Twith lagged versions of the used observable, respectively. For more details see Sect. 2.2, Eq. (1). The plots on the planes xy, xz, and yz in Fig. 5 corresponds to the 2D phase portrait (the projections) of the attractor and represent the pairwise correlations between the observable Z_i and the lagged versions of this observable Z_i+T and Z_i+2T.

The resemblance between Figs. 4 and 5 is evident and corroborates the existence of a low dimensional attractor for the dynamical system underlying the granulation.

The plots in Fig. 6 display in a log-log presentation the correlation integral C^(m) as a function of r for various embedding dimensions m. Actually, by means of the correlation integral (cf. Eq. (2)) we measure the density of the points of the attractor trajectory within a definite distance r in a given embedding space m. We assign, thus, a probability measure to the various distances r. Towards large r the correlation integral approaches a constant value, which means that the calculation has included practically all the points of the trajectory of the attractor within the given embedding space. The saturation of the correlation integral begins at large embedding dimensions, which means that only up to a definite dimension m the calculation finds the same number of points of the attractor trajectory within the small distance r. The correlation integral as a function of r changes its slope with the embedding dimension m. This reflects the influence of the embedding space on the structure of the attractor size.

In Fig. 6 we see clearly the convergence of the slopes of the correlation integral (cf. Eq. (2)) as a function of distance r with increasing embedding dimension m. According to Eq. (4) the convergence limit defines the correlation dimension $D_{{\rm c}}$, which measures the size of the attractor in the corresponding embedding space.

To find the convergence limit we plotted in Fig. 7 the correlation dimension $D_{{\rm c}}$ as a function of m. $D_{{\rm c}}$ increases monotonically up to m=6 and then saturates at the level of $D_{{\rm c}} \approx 3.6$, which is the dimension of the attractor in an embedded space of the order of $\approx$6, twice the attractor dimension ( e.g., Argyris et al. 1995).

From a physical point of view this finding suggests that the evolution of the dissipative dynamical system underlying the granular structures has a low dimension strange attractor. The dimension $D_{{\rm c}} = 3.6$ indicates furthermore that the corresponding dynamical system can be described by only 3 to 4 observables. In other words, the system corresponding to the granulation layers is provided with a low dimensional (3 to 4) attractor - a finding that at first glance appears to contradict the description of parts of the granulation layer as turbulent.

We applied the time lag method (including the reconstruction of the phase space, the calculation of the correlation integral and of the attractor dimension) first to the velocity fluctuations traced by the spectrogram 99-S4Sp66 taken in 1999 (i.e, near solar maximum). Figures 5-7 exhibit the results of this calculation.

In a second step we applied the same method to the velocity fluctuations traced by the spectrogram 94.A48 taken in 1994 i.e., near solar minimum). The results of this calculation are displayed in Figs. 8-10. Interestingly they turn out to be very similar to those presented in Figs. 5-7. (We notice that the resemblance between Figs. 5 and 8 concerns the 2D plane Z_i,Z_i+T in Fig. 5 and the 2D plot in Fig. 8). This similarity of the results corresponding to data observed at completely different times and levels of solar activity reveals clearly the existence of a continuity of the physical behavior of the granulation layers over time.

In Fig. 3 (grey line) the enhancement of the velocity power at small scales raises the question about their convective nature. To address this question (actually the "noise'' problem of the velocity power spectrum) we used again the time lag method, applying it this time to the residual velocity fluctuations (the output of the high pass filter). Figure 11 shows the correlation dimension $D_{{\rm c}}$ as a function of the embedding dimension m for the residual velocity obtained from spectrogram 99-S4Sp66 (dashed line). The correlation dimension for the residual velocity does not show any saturation with increasing embedding dimension up to m=8, as it was the case in Figs. 7 and 10. On the other hand, however, the slope of $D_{{\rm c}}$ for the residual velocity (dashed line) is clearly different from its slope for white noise (dotted line). Thus the residual velocity variations associated with the velocity power enhancement at higher wave numbers in Fig. 3 (grey line) can not be considered as white noise. They reflect rather the existence of a high dimensional dynamical system (attractor), for example a turbulent flow within the intergranular space.

5 Conclusions

Our observational material probes the behavior of the granular dynamics of the deep photospheric layers near minimum and maximum solar activity. It reveals clearly that small and large granules are governed by different dynamics, as evidenced by different power slopes, with a well defined scale separating both types of granules. The application of a high pass digital or wavelet filter on the original data does not affect this result.

It is obvious that the dynamics of the granular structures is important for the production of photospheric turbulence and for the interaction with short period oscillations. To obtain insight into the dynamical system underlying the granulation we applied the time lag method to a single quantity: the observed velocity variations $v_{{\rm conv}}$. Based only on this observable we reconstructed the space within which the attractor of the dynamical system underlying the granulation is embedded; the attractor dimension defines the number of degrees of freedom of this system. We found that the granular structures are produced by a dynamical system with a low dimension (3-4) attractor. The significant correlation between the observed intensity, velocity, and turbulence variations infers a well organized flow.

The application of the time lag method to two sets of velocity variations observed near solar maximum and minimum, respectively, gave the same result. The reproducibility of the results points to a continuity of the dynamical behavior of the granulation layers and emphasizes the significance of our results.

The request to distinguish velocity variations associated with subgranular scales from variations due to photon statistics, numerical effects, and pixel impurities is evident. Using the time lag method we found that the velocity variations associated with intergranular structures do not behave like white noise. They rather appear to belong to turbulent flow coexisting with the flow of the granular structures or to represent turbulent flows within the intergranular space.

Acknowledgements

We are grateful to the referee, Dr. J. Brooke, for constructive comments.

References

 

• Argyris, J., Faust, G., & Haase, M. 1995, Die Erforschung des Chaos (Vieweg - Verlag, Braunschweig Wiesbaden), 230 In the text  
• Bradshaw, P. 1976, in Topics Appl. Phys. 12, ed. P. Bradshaw, Turbulence (Springer - Verlag, Berlin Heidelberg New York), 25 In the text  
• Cattaneo, F. 1999, ApJ, 515, L39 In the text NASA ADS  
• Durrant, C. J., & Nesis, A. 1982, A&A, 111, 272 In the text NASA ADS  
• Espagnet, O., Muller, R., Roudier, Th., & Mein, N. 1993, A&A, 271 589 In the text NASA ADS  
• Espagnet, O., Muller, R., Roudier, Th., Mein, P., & Mein, N. 1995, A&AS, 109, 79 In the text NASA ADS  
• Galloway, D. J., Proctor, M. R. E., & Weiss, N. O. 1978, J. Fluid Mech., 87, 243 In the text NASA ADS  
• Grassberger, P., & Procaccia, L. 1983, Phys. Rev. Lett., 50, 346 In the text NASA ADS  
• Hilborn, R. C. 1994, Chaos and Nonlinear Dynamics (Oxford University Press), 436 In the text  
• Hirsch, M. W. & Smale, S. 1974, Differential Equations, Dynamical Systems, and Linear Algebra (Academic Press, New York), 255 In the text  
• Keil, S. L. 1980, ApJ, 237, 1024 In the text NASA ADS  
• Kendall, M. G. & Stuart, A. 1968, The Advanced Theory of Statistics, vol. 3, 2nd ed. (Charles Griffin and Company Limited, London), 342 In the text  
• Komm, R., Mattig, W., & Nesis, A. 1990, A&A, 239, 340 In the text NASA ADS  
• Komm, R., Mattig, W., & Nesis, A. 1991, A&A, 252, 812 In the text NASA ADS  
• Lorenz, E. N. 1963, J. Atm. Sci., 20, 130 In the text  
• Mandelbrot, B. 1977, Fractals (Freeman, San Francisco) In the text  
• Mattig, W., Mehltretter, P., & Nesis, A. 1969, Solar Phys., 10, 254 In the text NASA ADS  
• Meyer, Y. 1993, Wavelets, Algorithms and Applications, Soc. for Industrial and Applied Math., Philadelphia In the text  
• Muller, R. 1999, in Motions in the Solar Atmosphere, Procs. of the Summerschool and Workshop held at the Solar Observatory Kanzelhöhe, Kärnten, Austria, Sep. 1-12, 1997, ed. A. Hanslmeier, & M. Messerotti, vol. 239 (Kluwer Acad. Publ., ASSL), 35 In the text  
• Nesis, A., Hanslmeier, A., Hammer, R., et al. 1992, A&A, 253, 561 In the text NASA ADS  
• Nesis, A., Hanslmeier, A., Hammer, R., et al. 1993, A&A, 279, 599 In the text NASA ADS  
• Nesis, A., Hammer, R., Hanslmeier, A., et al. 1996, A&A, 310, 973 In the text NASA ADS  
• Nesis, A., Hammer, R., Hanslmeier, A., et al. 1997, A&A, 326, 851 In the text NASA ADS  
• Nesis, A., Hammer, R., Kiefer, M., et al. 1999, A&A, 345, 265 In the text NASA ADS  
• Packard, N. H., Crutchfield, J. P., Farmer, J. D., & Shaw, R. S. 1980, Phys. Rev. Lett., 45, 712 In the text NASA ADS  
• Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1992, Numerical Recipes, 2nd ed. (Cambridge Univ. Press) In the text  
• Ruelle, D., & Takens, F. 1971, Commun. Math. Phys. 20, 167 In the text  
• Takens, F. 1981, in Lecture Notes in Mathematics, vol. 898, ed. D. A. Rand, & L. S. Young (Berlin: Springer), 366 In the text  
• Tennekes, H., & Lumley, J. L. 1972, A First Course in Turbulence (MIT Press, Cambridge, Mass) In the text  
• Weiss, N. O., & Proctor, M. R. E. 2001, in Recent Insights into the Physics of the Sun and Heliosphere: Highlights from SOHO and other Space Missions, ed. P. Brekke, B. Fleck, & J. Gurman, IAU Symp., No. 203, Publ. Astr. Soc. Pacific, in press In the text