A&A 373, 38-55 (2001)
DOI: 10.1051/0004-6361:20010590
J. Brunzendorf - H. Meusinger
Thüringer Landessternwarte Tautenburg, 07778 Tautenburg, Germany
Received 8 February 2001 / Accepted 11 April 2001
Abstract
The combination of variability and proper motion constraints
(VPM search) is believed to provide an unconventional yet efficient
search strategy for QSOs with selection effects quite different
from conventional optical QSO surveys. Previous studies in a
field of high galactic latitude have shown that the VPM method
is indeed an efficient search strategy. In the present paper, we
describe a further variability-proper motion (VPM) QSO survey on
Tautenburg Schmidt plates. The survey is based on an exceptionally
large number of 162 B plates centred on M 92
with a time-baseline of more than three decades.
Further U and V plates are used to measure time-averaged colour
indices, and morphology is evaluated on a deep R plate. Proper
motions with Hipparcos-like
accuracies as well as variability indices are derived for about 35000
star-like objects down to B=20.5. With regard to both the number
of plates and the number of objects to be investigated, this is the
largest VPM survey performed so far.
The present paper is focused on the description of the
observational material, the data reduction, the definition of the
selection parameters, and the construction of the QSO candidate sample.
Furthermore, the selection effects of the VPM-method are
discussed a priori. For the present survey, the selection effects
are shown to be dominated by the magnitude-dependence of the
photometric accuracy.
Down to the limiting magnitude of the survey
![]() ,
we
identify 62 high-priority QSO candidates and a further 57
candidates of medium priority.
Spectroscopic follow-up observations have been performed
for all these candidates as well as for additional selected candidates
of lower priority; the confirmed QSOs will be presented and discussed in a
forthcoming paper.
,
we
identify 62 high-priority QSO candidates and a further 57
candidates of medium priority.
Spectroscopic follow-up observations have been performed
for all these candidates as well as for additional selected candidates
of lower priority; the confirmed QSOs will be presented and discussed in a
forthcoming paper.
Key words: galaxies: active - galaxies: Seyfert - galaxies: statistics - quasars: general - globular clusters: individual: M 92
"Quasars cannot be studied until they are found'' (Weedman 1984).
Optical surveys for QSOs![]() can yield very high
completeness rates over a large redshift range - yet they are hampered by the
small fraction of QSOs among all objects visible in this wavelength range, with
most of the latter are foreground stars and galaxies. A straightforward identification
of all QSOs in a given survey field, which
requires spectroscopic observations of all objects up to
an adequate limiting magnitude with sufficient
spectral resolution and signal-to-noise ratio, would be a voluminous task with
low efficiency. Hence, optical QSO surveys are conducted in two steps:
1) selection of QSO candidates from all objects in the field, based on
criteria that are supposed to discriminate QSOs from non-QSOs, and 2) spectroscopic follow-up observations of all selected candidates. The properties
of the resulting QSO samples are constrained by the selection criteria of the
survey.
can yield very high
completeness rates over a large redshift range - yet they are hampered by the
small fraction of QSOs among all objects visible in this wavelength range, with
most of the latter are foreground stars and galaxies. A straightforward identification
of all QSOs in a given survey field, which
requires spectroscopic observations of all objects up to
an adequate limiting magnitude with sufficient
spectral resolution and signal-to-noise ratio, would be a voluminous task with
low efficiency. Hence, optical QSO surveys are conducted in two steps:
1) selection of QSO candidates from all objects in the field, based on
criteria that are supposed to discriminate QSOs from non-QSOs, and 2) spectroscopic follow-up observations of all selected candidates. The properties
of the resulting QSO samples are constrained by the selection criteria of the
survey.
Most selection criteria are based on the different spectral energy distribution (SED) of QSOs compared to stars and galaxies. The following properties have been proven to be particularly suited for the identification of QSO candidates: peculiar optical colours (e.g., intrinsic UV-excess, blue continuum), Lyman break (for QSOs with redshifts z>3), and prominent emission lines. Surveys based on these criteria are known to be biased in several ways (for an overview, see Wampler & Ponz 1985; Véron 1993; Hewett & Foltz 1994). Here we only note that their completeness depends (among others) on the QSO redshifts, colour indices, and emission line equivalent widths. It is widely believed that these conventional QSO surveys can reach a very high degree of completeness. However, such a claim can only be verified by means of alternative QSO surveys which are not based on the same or similar selection criteria. In fact, it is still a matter of debate whether conventional QSO surveys systematically overlook hitherto unknown and possibly substantial QSO populations (e.g., Webster et al. 1995; Drinkwater et al. 1997; Kim & Elvis 1999).
Due to their cosmological distances, QSOs have non-detectable proper motions for existing observation techniques. Therefore, the search for zero proper motion objects is expected to provide a bias-free QSO candidate sample (Sandage & Luyten 1967; Kron & Chiu 1981). However, a QSO search which is essentially based on the zero proper motion constraint is not very efficient, since the resulting sample will be dominated by faint galaxies and galactic foreground objects having insignificantly small proper motions by chance. Optical variability is a further general property of quasars (Ulrich et al. 1997; Netzer 1999), and the identification of the variable objects in a given field is a further, independent QSO search method (van den Bergh et al. 1973; Heckman 1976; Usher & Mitchell 1878; Hawkins 1983; Trevese et al. 1989; Véron & Hawkins 1993; Hook et al. 1994; Trevese et al. 1994; Meusinger et al. 1994; Véron & Hawkins 1995; Cristiani et al. 1996; Bershady et al. 1998). The combination of these two constraints, i.e. the search for variable objects with zero proper motion (VPM search = Variability and Proper Motion search), should therefore provide an alternative QSO search strategy which does not explicitely rely on the SEDs of QSOs. It has been speculated that "a search for objects which are both variable and stationary is a powerful technique for efficiently finding QSOs with no selection bias with regard to colour, redshift, spectral index, or emission line equivalent widths'' (Majewski et al. 1991; Véron 1993).
Apart from the experimental and comparably small survey by Majewski et al. (1991), the only VPM QSO survey so far is being performed by Meusinger, Scholz and Irwin on 85 Tautenburg Schmidt plates of a field near the North Galactic Pole (Meusinger et al. 1995; Scholz et al. 1997). According to a priori estimates, a high survey completeness of about 90%, in combination with a success rate of about 40%, is expected, which is confirmed by the preliminary results from spectroscopic follow-up observations (Meusinger et al. 1999).
Here, we present a new VPM QSO survey, which investigates a
![]() field centred on the globular cluster M 92. This is a
more ambitious project since a quasar search in this field faces
the problem of a stronger contamination by galactic foreground stars
than a search at high galactic latitudes, even though the direction of
the M 92 field is well off the galactic plane (
field centred on the globular cluster M 92. This is a
more ambitious project since a quasar search in this field faces
the problem of a stronger contamination by galactic foreground stars
than a search at high galactic latitudes, even though the direction of
the M 92 field is well off the galactic plane (
![]() ). On the
other hand, the field is one of the "Tautenburg Standard fields'',
characterized by a very large number of available plates. Further, this
area has never been surveyed for QSOs before. Our search is based on
208 selected, deep photographic Schmidt plates covering epoch
differences of up to 34 years. With regard to this large quantity of
observational data, the present project is the largest QSO survey based
on variability and/or proper motion criteria performed so far.
The main aims of this project are to improve the statistics of
VPM-selected QSOs and to enlarge the number of known QSOs with
well-sampled light-curves measured over a time baseline of several
decades. The combined sample from both VPM fields is expected to
contain more than hundred QSOs with
). On the
other hand, the field is one of the "Tautenburg Standard fields'',
characterized by a very large number of available plates. Further, this
area has never been surveyed for QSOs before. Our search is based on
208 selected, deep photographic Schmidt plates covering epoch
differences of up to 34 years. With regard to this large quantity of
observational data, the present project is the largest QSO survey based
on variability and/or proper motion criteria performed so far.
The main aims of this project are to improve the statistics of
VPM-selected QSOs and to enlarge the number of known QSOs with
well-sampled light-curves measured over a time baseline of several
decades. The combined sample from both VPM fields is expected to
contain more than hundred QSOs with ![]() and will be well-suited
both for the comparison with QSO samples from more traditional
methods and for statistical studies of quasar variability on timescales
of days to decades. In addition, the present study is aimed at the detailed
discussion of the selection effects of the VPM search.
and will be well-suited
both for the comparison with QSO samples from more traditional
methods and for statistical studies of quasar variability on timescales
of days to decades. In addition, the present study is aimed at the detailed
discussion of the selection effects of the VPM search.
The present paper is concerned with the description of the observational material (Sect. 2), the photometric and astrometric data reduction (Sect. 3), the definition of suitable indices for proper motion and variability, and the selection of the QSO candidates based on these indices (Sect. 4). The selection effects will be discussed in Sect. 5, and conclusions are summarized in Sect. 6. The identification of the QSOs among the candidates of high and medium priority by means of spectroscopic follow-up observations has been completed. The resulting QSO sample will be presented in a forthcoming paper along with the detailed discussion of the statistical properties of the VPM QSOs and the comparison with conventional optical QSO samples.
An efficient search for variable objects with zero proper motion
requires a large number of homogeneous (e.g., the same colour
system) observations of a large number of faint objects with high astrometric
and photometric accuracy, spanning a time-baseline of decades.
These requirements can be matched if a substantial number of deep
archival plates from a large wide-field imaging telescope is available.
The archive of the Tautenburg Schmidt telescope (134 cm free aperture,
4 m focal length,
![]() unvignetted field of view)
contains more than 9000 plates taken between 1960 and 1997.
For several "standard fields'', more than hundred archival plates are
available. With epoch differences of three decades and more,
this observational material is particularly well suited for a VPM QSO search,
since all plates were taken with the same telescope, through the same filters,
and onto very similar emulsions.
Moreover, thanks to its large focal length, compared to other
large Schmidt telescopes, the Tautenburg Schmidt has less problems
with distortions due to plate bending and has a better scale
for astrometric work
(e.g.,
Schilbach et al. 1995;
Scholz et al. 1993, 1994, 1996,
1997; Meusinger et al. 1996).
unvignetted field of view)
contains more than 9000 plates taken between 1960 and 1997.
For several "standard fields'', more than hundred archival plates are
available. With epoch differences of three decades and more,
this observational material is particularly well suited for a VPM QSO search,
since all plates were taken with the same telescope, through the same filters,
and onto very similar emulsions.
Moreover, thanks to its large focal length, compared to other
large Schmidt telescopes, the Tautenburg Schmidt has less problems
with distortions due to plate bending and has a better scale
for astrometric work
(e.g.,
Schilbach et al. 1995;
Scholz et al. 1993, 1994, 1996,
1997; Meusinger et al. 1996).
For the present VPM survey, the field centred on the globular
cluster M 92 was chosen (Table 1). In
preparation for this project, 56 plates were taken
in the years 1992 to 1997. Combined with the archival plates,
a total number of 332 plates of the M 92 field are available.
We selected 208 sufficiently
deep plates in the U, B, V or R band, among them 162 B plates
(Table 1). Only the B plates are used to measure
variabilities and proper motions; the measurements in the other
bands only provide additional colour information.
The plates were taken in the years 1963 to 1997. Compared
with our first VPM survey in the M 3 field, the present survey
comprises about three times more B plates with a better
time coverage and a slightly longer time baseline.
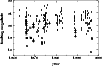 |
Figure 1: Individual limiting magnitudes of all 208 selected Schmidt plates of the M92 field versus epoch. Different symbols represent different colour bands in the Johnson system (open circle: U, filled circle: B, plus sign: V, cross: R). |
| Open with DEXTER | |
| plate centre: |
|
|
|
|
| (
|
|
| field size: |
|
| minus
|
|
| calibration wedge | |
| plate scale: | 51
|
| number of plates: | 162 B (epochs 1963-1997) |
| 18 U (epochs 1966-1997) | |
| 18 V (epochs 1966-1989) | |
| 10 R (epochs 1966-1968) |
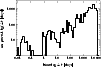 |
Figure 2:
Histogram of the epoch differences |
| Open with DEXTER | |
The limiting magnitudes and epochs of the observations are summarized in Fig. 1. Figure 2 shows the histogram of the epoch differences between all combinations of two individual B plate epochs. The frequency space is almost entirely and quite homogeneously covered for epoch differences larger than one day. The large maximum epoch difference of 34 years, in combination with the huge number of plates, allows the certain detection and subsequent thorough investigation of variable objects with variability timescales of days to decades.
All 208 selected plates have been completely digitised by
means of the Tautenburg Plate Scanner TPS. A detailed description of the
TPS is given by Brunzendorf (2000);
an overview is given by Brunzendorf & Meusinger (1999).
The resulting digital images have a linear resolution of
![]()
![]() per pixel and a resolution
depth of 4 096 grey levels (12 bit) per pixel. The digitised images
are stored on CD-ROMs. Subsequent data reduction is done off-line.
per pixel and a resolution
depth of 4 096 grey levels (12 bit) per pixel. The digitised images
are stored on CD-ROMs. Subsequent data reduction is done off-line.
The object identification on the digitised plates as well as the subsequent determination of the relevant image parameters, like (x,y)-position, internal (i.e., uncalibrated) magnitude and size, are based on the Münster Redshift Project (MRSP) software package (Horstmann et al. 1989). This software requires intensities as input data. Therefore, the measured photometric densities have to be transformed into relative intensities of the incident light. In principle, this transformation should be done via the individual characteristic curve of each plate. The characteristic curve can be measured if a calibration wedge is exposed on, which is not the case for all plates. For the object search, however, it is sufficient to apply a mean characteristic curve which is estimated from least-square fits of a suitable relation (Lehmann & Häupl 1987; Brunzendorf & Meusinger 1999) onto the measured characteristic curves of 94 Tautenburg Schmidt plates. In this way, the measured densities are transformed into approximate relative intensities, which then serve only as input data for the object search and the determination of the image parameters. In its original version, the MRSP software adopts a linear transformation. The use of a non-linear transformation by means of an average characteristic curve ensures that the intensity profiles of star-like images are well-approximated by a Gaussian fit. Measurements on a large number of Tautenburg Schmidt plates have shown that the MRSP Gaussian fitting procedure works well for stars over a wide magnitude range of more than 13 mag (Brunzendorf & Meusinger 1999). The transformation of all plates into a common photometric standard system is done later by means of a sequence of standard stars (Sect. 3.4).
An object is detected if its relative intensity exceeds certain threshold
levels above the background. The threshold levels are measured in units of the
background noise,
![]() ,
which is dominated by the grain noise of
the plate. The peak intensity
,
which is dominated by the grain noise of
the plate. The peak intensity
![]() and the total intensity
and the total intensity
![]() of an object have to meet the constraints
of an object have to meet the constraints
![]() and
and
![]() .
On the
deepest B plates, these conditions are satisfied by stars with magnitudes
.
On the
deepest B plates, these conditions are satisfied by stars with magnitudes
![]() .
.
After the determination of the object positions and magnitudes on all selected plates, one has to decide which objects are to be investigated further. In order to avoid strong contamination of the object list by spurious detections (grain noise, plate faults etc.) it is not efficient to consider all detected objects. A common approach is to declare the deepest plate as a "master plate'', and to identify all objects measured on this plate with the basic object sample. The disadvantage of such a procedure is, however, that all objects not detected on the master plate would be excluded.
In the present project, the basic object sample is defined in the
following way: an object is included if it is detected both on at least
two out of five selected deep first epoch plates (epoch
![]() )
and on at least two out of five selected deep second epoch plates
(epoch
)
and on at least two out of five selected deep second epoch plates
(epoch
![]() ). It is easy to show by means of statistical
considerations, that the completeness limit (here defined as the faintest
magnitude at which 99% of all objects at this brightness are still detected)
of this sample is deeper than for any single plate. In addition, this object
sample contains virtually no spurious detections. On the other hand,
the limiting magnitude is lower than for the deepest single plates.
The reason is, that on single plates the faintest stars are detected
with a low probability; the faintest objects are therefore suppressed in
the final sample whereas some of them may be measured on a single plate.
For the present study, however, a deep completeness limit is by far more
important than a deep limiting magnitude caused by only a few faint
objects detected by chance.
). It is easy to show by means of statistical
considerations, that the completeness limit (here defined as the faintest
magnitude at which 99% of all objects at this brightness are still detected)
of this sample is deeper than for any single plate. In addition, this object
sample contains virtually no spurious detections. On the other hand,
the limiting magnitude is lower than for the deepest single plates.
The reason is, that on single plates the faintest stars are detected
with a low probability; the faintest objects are therefore suppressed in
the final sample whereas some of them may be measured on a single plate.
For the present study, however, a deep completeness limit is by far more
important than a deep limiting magnitude caused by only a few faint
objects detected by chance.
The final sample contains about 35000 objects in the magnitude range
![]() with a completeness limit
with a completeness limit
![]() .
The frequency distribution of the B magnitudes for the objects in the
final sample is shown in Fig. 3.
.
The frequency distribution of the B magnitudes for the objects in the
final sample is shown in Fig. 3.
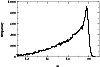 |
Figure 3: Frequency distribution (number of objects per 0.05 mag interval) of the mean B magnitudes for the objects in the final basic sample. |
| Open with DEXTER | |
Each object is to be classified as a star-like object, a galaxy, or a merged object. Only star-like objects are to be considered as QSO candidates, whereas the galaxies in the field define the extragalactic astrometric reference frame, i.e. the zero point of the absolute proper motions. Objects classified as "merged'' are rejected from further considerations as QSO candidates since they do not allow accurate measurements of both variability and proper motion. The overwhelming fraction of them will consist of two stars with images projected by chance in nearly the same direction with a projected distance of typically less than 8''. Of course, star-like images in merged objects can also include QSO images. Such QSOs, as well as those completely hidden by images of other objects in the field, will not be detected. This effect has to be taken into account when the surface density of the resulting QSO sample will be discussed (Paper II). Moreover, the subsample of merged objects can also include QSO pairs and gravitationally lensed QSOs. In spite of their great importance, the chance is exceptionally low to detect such pairs in the present survey if their positional separation is less than about 8''. However, it can be concluded from the statistics of QSO pairs in the 2dF survey (Shanks et al. 2001) that the probability is negligible of having one or more pairs within the magnitude range and field of the present study.
We also stress the importance of an accurate discrimination between galaxies and merged objects, since any stellar contamination of the galaxy sample leads to a systematic non-zero absolute proper motion of the astrometric reference frame.
The morphological classification is performed on the deepest R plate (plate 2787) which contains about 60% more objects than the deepest Bplates and which allows in particular a better identification of faint galaxies. The classification is done in two steps: 1) manual identification of the galaxies by visual inspection, and 2) automatic identification of all objects which have a nonstellar image profile, i.e. galaxies and merged objects. The visual inspection yields 1366 galaxies. Image profile parameters are determined for the overwhelming majority of these galaxies from the automatic classification. Hence, these galaxies can be used to check the results from the automatic classification and to define the morphological selection criteria. Moreover, 534 of these galaxies are identified with objects in the final basic object sample (Sect. 3.2) and are used to define the astrometric reference system (Sect. 3.5). All remaining galaxies are, on the B plates, either too faint and/or too extended and/or too fuzzy to serve as astrometric reference points.
| ref. | type | magnitude range | number of stars | ||
| B | U | B | V | ||
| (1) | photoelectric |
|
44 | 45 | 45 |
| (1) | photographic |
|
- | 14 | 15 |
| (2) | photoelectric |
|
- | 11 | 11 |
| (3) | photoelectric |
|
30 | 40 | 40 |
| (3) | photographic |
|
- | 3 | 3 |
| (4) | photoelectric |
|
- | 9 | 9 |
| (5) | CCD |
|
- | 286 | 286 |
| total |
|
74 | 408 | 409 | |
For the automatic classification, two different methods are applied.
The first one is based on the separation between resolved and
unresolved objects on the radius-magnitude diagram.
We define a nonstellar index
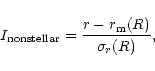 |
(1) |
 |
Figure 4:
Photometric calibration of the plate No. 8629:
internal magnitudes
|
| Open with DEXTER | |
An accurate photometric calibration of each plate is crucial for the
present study. The MRSP software provides internal magnitudes
![]() for all objects in the uncalibrated photometric system of the
individual plates. A photometric
calibration by standard stars has to be applied in order to transform
for all objects in the uncalibrated photometric system of the
individual plates. A photometric
calibration by standard stars has to be applied in order to transform
![]() into the photometric standard system m (e.g.,
Johnson UBV system). In the vicinity of M 92, several
sequences of photometric standard stars have been published
(Table 2). The combination of these sequences covers
the entire magnitude range of the present study, and was used as photometric
reference system in this work. Only those standard stars whose data
obviously did not fit into the general sequence (due to whatever reason)
on several different plates have been excluded from the reference
sample. The number of stars in the final sample of photometric standards
is listed in Table 2.
into the photometric standard system m (e.g.,
Johnson UBV system). In the vicinity of M 92, several
sequences of photometric standard stars have been published
(Table 2). The combination of these sequences covers
the entire magnitude range of the present study, and was used as photometric
reference system in this work. Only those standard stars whose data
obviously did not fit into the general sequence (due to whatever reason)
on several different plates have been excluded from the reference
sample. The number of stars in the final sample of photometric standards
is listed in Table 2.
The Tautenburg photographic UBV system is known to match very closely the Johnson UBV system (van den Bergh 1964; Börngen & Chatchikjan 1967; Andruk & Kharchenko 1994). The deviations are generally smaller than the measurement uncertainties. This result is confirmed by the measurements of standard stars in the present study. Hence, a colour correction of the photometric data is not essential. This is a major advantage, since colour equations are calibrated onto stars and are, therefore, not simply transferable to QSOs with their fundamentally different spectral energy distribution (see also Hewett et al. 1995).
On the other hand, geometrical terms have to be included in the photometric calibration (Andruk & Kharchenko 1994). Since there are no published standard stars in the outer parts of our field, i.e. outside M 92, the calibration is done in three steps:
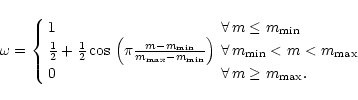 |
(3) |
After the individual calibration of all plates, the mean magnitude of
each object is calculated. These magnitudes then serve as the reference
system for the second photometric calibration which is done in the same
way as the first one, except for the additional inclusion of geometrical
terms
The accuracy of the photometric calibration, which is limited by the
grain noise of the emulsion, can be expressed by the standard deviation
![]() of the calibrated magnitudes of non-variable objects measured
on all plates. The dependence of
of the calibrated magnitudes of non-variable objects measured
on all plates. The dependence of ![]() on the mean
B magnitudes is shown in Fig. 5. The photometric accuracy
on the mean
B magnitudes is shown in Fig. 5. The photometric accuracy ![]() is
better than 0.1 mag for
is
better than 0.1 mag for
![]() and better than 0.07 mag for
and better than 0.07 mag for
![]() .
.
![\begin{figure}
\includegraphics[width=8.4cm,clip]{fig5.eps}
\end{figure}](/articles/aa/full/2001/25/aa1126/Timg102.gif) |
Figure 5:
Standard deviation |
| Open with DEXTER | |
The U and V plates were calibrated in exactly the same way as the
B plates. The resulting photometric accuracies are similar, yet the
limiting magnitudes are lower than for the B plates (
![]() and
and
![]() ;
Fig. 1). Thus, U magnitudes were available for
only 2/3 of all objects. For this reason, 11 deep U plates were
digitally co-added to produce a deeper U band image. A detailed
description of the digital stacking technique is given by Froebrich &
Meusinger (2000). The object search, the
determination of the object parameters, and the photometric calibration
were performed on the stacked plate in the same way as on ordinary
single plates. Figure 6 illustrates the good accuracy of the resulting
calibrated U magnitudes derived from the co-added plate. Within the
measuring accuracies, the U magnitudes derived from single plates
agree with the photometric data derived from the stacked plate.
;
Fig. 1). Thus, U magnitudes were available for
only 2/3 of all objects. For this reason, 11 deep U plates were
digitally co-added to produce a deeper U band image. A detailed
description of the digital stacking technique is given by Froebrich &
Meusinger (2000). The object search, the
determination of the object parameters, and the photometric calibration
were performed on the stacked plate in the same way as on ordinary
single plates. Figure 6 illustrates the good accuracy of the resulting
calibrated U magnitudes derived from the co-added plate. Within the
measuring accuracies, the U magnitudes derived from single plates
agree with the photometric data derived from the stacked plate.
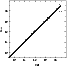 |
Figure 6:
Photometric calibration of the co-added U plates: derived magnitudes
|
| Open with DEXTER | |
For the determination of proper motions, only deep B plates
were used (
![]() )
taken at zenith distances
less than
)
taken at zenith distances
less than
![]() ,
and having no large plate faults.
Among the 162 selected B plates, there are
135 plates found to match these constraints.
The plate-to-plate transformation between the measured coordinate
mapping on a given plate and the reference system, defined by a master plate,
is modelled by two-dimensional second-order polynomials. Higher order
polynomials and/or the introduction of magnitude- and/or colour-dependent
terms do not significantly improve the fit. The advantage of low-order
polynomials is that the fit is rigid and is not sensitive to
small-scale systematic proper motions in the field. Eventually remaining
small-scale systematic residuals are averaged out due to the large
number of plates.
,
and having no large plate faults.
Among the 162 selected B plates, there are
135 plates found to match these constraints.
The plate-to-plate transformation between the measured coordinate
mapping on a given plate and the reference system, defined by a master plate,
is modelled by two-dimensional second-order polynomials. Higher order
polynomials and/or the introduction of magnitude- and/or colour-dependent
terms do not significantly improve the fit. The advantage of low-order
polynomials is that the fit is rigid and is not sensitive to
small-scale systematic proper motions in the field. Eventually remaining
small-scale systematic residuals are averaged out due to the large
number of plates.
The relative proper motion vector
![]() of a given
object is calculated from the linear least-square fit of the positions
of a given
object is calculated from the linear least-square fit of the positions
![]() ,
measured on the plate i, as a function of the
epoch ti. The residuals
,
measured on the plate i, as a function of the
epoch ti. The residuals ![]() between the positions of
a given object measured on the individual plates and the mean positions as
calculated from the linear regression are used as a measure of the
positional accuracy. Figure 7 displays
between the positions of
a given object measured on the individual plates and the mean positions as
calculated from the linear regression are used as a measure of the
positional accuracy. Figure 7 displays ![]() as a
function of the mean B magnitude. The residuals are smaller than
as a
function of the mean B magnitude. The residuals are smaller than
![]() for the majority of stars with
for the majority of stars with ![]() and smaller than
and smaller than
![]() for most stars with
for most stars with
![]() .
The median accuracy
.
The median accuracy
![]() of the derived relative proper motions is
0.5 masyr-1 for objects with
of the derived relative proper motions is
0.5 masyr-1 for objects with
![]() and
1.0 masyr-1 for objects with
and
1.0 masyr-1 for objects with ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{fig7.eps}
\end{figure}](/articles/aa/full/2001/25/aa1126/Timg115.gif) |
Figure 7:
Distribution of the total astrometric least-square errors |
| Open with DEXTER | |
The vector point diagram of the derived relative proper motions
![]() is shown in Fig. 8.
Due to their peculiar velocities, a considerable fraction of the
star-like objects have large proper motions of more than e.g.
is shown in Fig. 8.
Due to their peculiar velocities, a considerable fraction of the
star-like objects have large proper motions of more than e.g.
![]() 10 masyr-1 and are, therefore, easily recognised as
galactic foreground stars. Stars are clearly much more scattered in this
diagram than galaxies. Moreover, a systematic offset
of the relative proper motions of the galaxies relative to the
bulk of the field stars is clearly indicated. (For the stars
in the M 92 cluster area, i.e. within a given distance from the
cluster centre, we find a strong concentration on the vector point
diagram, as well. The proper motion of M 92, however, will be the
subject of a separate paper.)
10 masyr-1 and are, therefore, easily recognised as
galactic foreground stars. Stars are clearly much more scattered in this
diagram than galaxies. Moreover, a systematic offset
of the relative proper motions of the galaxies relative to the
bulk of the field stars is clearly indicated. (For the stars
in the M 92 cluster area, i.e. within a given distance from the
cluster centre, we find a strong concentration on the vector point
diagram, as well. The proper motion of M 92, however, will be the
subject of a separate paper.)
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{fig8.eps}
\end{figure}](/articles/aa/full/2001/25/aa1126/Timg117.gif) |
Figure 8:
Components of the
relative proper motions vectors
|
| Open with DEXTER | |
The absolute proper motion of a given object with respect to the
reference frame calculates as
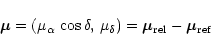 |
(5) |
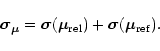 |
(6) |
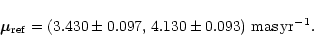 |
(7) |
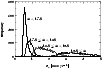 |
Figure 9:
Frequency distribution of the accuracy
|
| Open with DEXTER | |
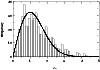 |
Figure 10:
Frequency distribution of the proper motion indices |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{fig11.eps}
\end{figure}](/articles/aa/full/2001/25/aa1126/Timg126.gif) |
Figure 11:
Proper motion index |
| Open with DEXTER | |
The probability p for an object to have a non-zero proper
motion is measured by the proper motion index
The proper motion indices of all objects as a function of B are shown
in Fig. 11. According to Eq. (9), the
probability p for an object with measured ![]() to have a non-zero
proper motion is
to have a non-zero
proper motion is ![]() ;
for an object with
;
for an object with
![]() the
probability for non-zero proper motion is
the
probability for non-zero proper motion is
![]() .
Both limits are
indicated in Fig. 11. The vast majority of the objects
with
.
Both limits are
indicated in Fig. 11. The vast majority of the objects
with
![]() have measured
have measured ![]() well above these limits. At
fainter magnitudes, the mean
well above these limits. At
fainter magnitudes, the mean ![]() decreases due to the increase of
decreases due to the increase of
![]() (Eq. (8)). Nevertheless, significant
proper motions
(Eq. (8)). Nevertheless, significant
proper motions
![]() are measured for 86% (76%) of the
star-like objects with
are measured for 86% (76%) of the
star-like objects with ![]() .
These objects are to be excluded from
the QSO candidate list.
.
These objects are to be excluded from
the QSO candidate list.
The procedure of separating optically variable objects from the non-variable
ones is different from the separation of stationary objects as described
in the previous subsection. Since the variability of a given object is not
a priori known (in contrast to the proper motion, which must be zero
for QSOs), the approach cannot be to exclude all objects which do not
satisfy a given variability criterion. Instead, we have to accept
those objects for the candidate list which exhibit a significant
variability. This different approach is unavoidable, yet causes a
significant selection bias (Sect. 5).
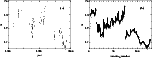 |
Figure 12: Light-curve of the most variable object in our basic object sample, the Seyfert galaxy RXS J17220+4315. The measured B magnitude are shown as a function of the epoch a) and of the running number of the photometric data sorted by the epoch b), respectively. In panel b), the data within the epochs 1966-1968, 1973-1976, 1980-1983, 1989.4-1989.5, and 1992-1997 are interconnected for the sake of clarity. |
| Open with DEXTER | |
Generally speaking, there are two different ways to identify variable
objects. The external method compares the measured brightness
fluctuations ![]() of different yet comparable objects and
identifies those objects with significantly enhanced
of different yet comparable objects and
identifies those objects with significantly enhanced ![]() .
The
internal method, on the other hand, is based on the analysis of the
light-curve of each object to search for systematic structures which
can not be explained by random noise and which are, therefore, taken as indications for
variability. In the present study, both appoaches are
followed up.
.
The
internal method, on the other hand, is based on the analysis of the
light-curve of each object to search for systematic structures which
can not be explained by random noise and which are, therefore, taken as indications for
variability. In the present study, both appoaches are
followed up.
A useful measure of the variability is given by the weighted standard
deviation
![]() of the measured magnitudes Bi on the
plates i in units of the photometric random errors
of the measured magnitudes Bi on the
plates i in units of the photometric random errors
![]() of plate i at magnitude Bi:
of plate i at magnitude Bi:
For the thorough evaluation of light-curves, a number of different techniques have been proposed, including the correlation function analysis (e.g., Edelson & Krolik 1988) and the structure function analysis (e.g., Simonetti et al. 1985, 1985), up to complex nonlinear methods, like multi-fractal or chaos analysis (e.g., Vio et al. 1992). Here, we present a different approach since we primarily aim at a measure which expresses the probability that a given light-curve shows indications for any variability at all.
From the statistical point
of view, the hypothesis of a random distribution of the data
points can be disregarded by means of significance tests. A simple yet
powerful trend test is provided by the evaluation of the mean square
successive differences ![]() of the data points
(Neumann et al. 1941; Moore 1955):
if a light-curve exhibits brightness fluctuations on timescales longer
than the typical epoch difference of successive data points, then the square
of the differences between successive data points
of the data points
(Neumann et al. 1941; Moore 1955):
if a light-curve exhibits brightness fluctuations on timescales longer
than the typical epoch difference of successive data points, then the square
of the differences between successive data points
![\begin{figure}
\par\includegraphics[width=18cm,clip]{1126f13.eps}\end{figure}](/articles/aa/full/2001/25/aa1126/Timg170.gif) |
Figure 13:
Long-term variability index
|
| Open with DEXTER | |
From the original list of about 35000 objects in the field (Sect. 3.2), all objects are excluded from further investigations which do not match one or several of the following constraints:
| criterion | high-priority | medium-priority | low-priority |
| QSO candidates | QSO candidates | QSO candidates | |
| proper motion |
|
|
|
| overall variability |
|
|
- |
| long-term variability |
|
|
- |
| B magnitude |
|
|
|
| number of objects in list | 62 | 57 (+62) | 5709 (+62+57) |
The QSO candidate sample is sub-divided into three subsamples of
different priority. The low-priority sample comprises all
stationary star-like objects with
![]() .
It is reasonable to expect that all of the QSOs
in the specified magnitude range are included in this sample.
Those objects from this sample with
variability indices indicating significant variability (
.
It is reasonable to expect that all of the QSOs
in the specified magnitude range are included in this sample.
Those objects from this sample with
variability indices indicating significant variability (
![]() )
are regarded as QSO candidates of medium priority, objects with
highly significant (
)
are regarded as QSO candidates of medium priority, objects with
highly significant (
![]() )
variability and highly significant
zero-proper motion (
)
variability and highly significant
zero-proper motion (
![]() )
are QSO candidates
of high priority. The selection criteria for these three subsamples
are summarized in Table 3 along with the corresponding
numbers of candidates. The variability properties of the QSO candidates are
shown in Fig. 13.
)
are QSO candidates
of high priority. The selection criteria for these three subsamples
are summarized in Table 3 along with the corresponding
numbers of candidates. The variability properties of the QSO candidates are
shown in Fig. 13.
| magnitude | proper motion | overall variability | long-term variability | variability | all |
|
|
|
|
combined | combined | |
|
|
35% / 20% | 12% / 9% | 10% / 6% | 1.9% / 1.0% | 0.8% / 0.4% |
|
|
24% / 13% | 11% / 7% | 10% / 6% | 2.0% / 1.1% | 0.6% / 0.3% |
|
|
14% / 7% | 10% / 6% | 10% / 6% | 2.4% / 1.4% | 0.4% / 0.2% |
|
|
8% / 4% | 20% / 17% | 15% / 11% | 7.9% / 5.8% | 0.8% / 0.2% |
The efficiency of the various selection criteria as well as combinations of them are summarised in Table 4. As already noticed in Sect. 1, the proper motion selection is less efficient than the combined variability selection criteria. The efficiency of the proper motion selection depends strongly on the measuring uncertainties and is higher at brighter magnitudes. Nevertheless, the combination of the variability search with the zero-proper motion constraint reduces the sample by a further factor of about three. In addition, the proper motion criterion is essentially bias-free.
In addition to the constraints listed in Table 3,
both the medium- and the high-priority candidate samples have been confined
to objects fainter than B=16.5. This is motivated by the low surface
density of QSOs with ![]() (Kembhavi & Narlikar 1999).
Moreover, bright QSOs tend to have low redshifts
(Wisotzki 2000),
and should be, therefore, easily detectable by their typical UV excess.
However, there is no UV excess object (
(Kembhavi & Narlikar 1999).
Moreover, bright QSOs tend to have low redshifts
(Wisotzki 2000),
and should be, therefore, easily detectable by their typical UV excess.
However, there is no UV excess object (
![]() )
among the
low-priority candidates with
)
among the
low-priority candidates with ![]() .
.
For our search field, the catalogue of Quasars and Active Galactic Nuclei by
Véron-Cetty & Véron (2000) lists four QSOs
(brighter than MB=-23). One of them
(Q1715+4316) is located in the immediate
cluster region and is therefore excluded from our object list. The
high-redshift QSO FIRSTJ1709+4201 (z=4.23) is too faint in B for
the present survey. The remaining two QSOs, B31707+420 (z=0.307, MB=-23)
and RXSJ17150+4429 (z=0.154, MB=-23), are both detected in the
present study as high-probability candidates with the following properties
![]() and
(2.0,26.9,8.6).
The catalogue by Véron-Cetty & Véron comprises two
Seyfert galaxies in our field, FIRST J1718+4249 and RXS J17220+4315.
Both galaxies have also been identified as stationary and
highly-variable objects with
and
(2.0,26.9,8.6).
The catalogue by Véron-Cetty & Véron comprises two
Seyfert galaxies in our field, FIRST J1718+4249 and RXS J17220+4315.
Both galaxies have also been identified as stationary and
highly-variable objects with
![]() and
(2.1,118,10.8) and are therefore high-priority QSO
candidates in the sense of the present survey.
With
and
(2.1,118,10.8) and are therefore high-priority QSO
candidates in the sense of the present survey.
With
![]() and
and
![]() ,
the optical counterpart of the radio source
FIRST J1718+4249 is, however, slightly above the demarcation
between stellar and nonstellar objects.
,
the optical counterpart of the radio source
FIRST J1718+4249 is, however, slightly above the demarcation
between stellar and nonstellar objects.
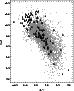 |
Figure 14: Colour-colour diagram of the QSO candidates (symbols as in Fig. 13). |
| Open with DEXTER | |
We have also cross-correlated the QSO candidate list from the Asiago-RASS/ESO
survey (Grazian et al. 2000) against our basic object
sample. Only one object from the former catalogue, 1RXSJ171935.9+424518, is
located within our survey field. This source is clearly identified with a non-variable
(
![]() ,
,
![]() )
foreground star (
)
foreground star (
![]() )
with highly significant proper motion (
)
with highly significant proper motion (![]() ).
).
The colour-colour diagram of all QSO candidates is shown in Fig. 14.
The time-averaged colour indices were derived from the U,B,V magnitudes
measured on the plates from the epoch
![]() .
The colour distribution of both the
high- and medium-priority candidates is similar to that
for the QSO candidates from the VPM search in the M 3 field
(Scholz et al. 1997; their Fig. 16).
It should be emphasized that we do not use colours for candidate
selection but merely as a way of checking on how the VPM search
compares with more traditional methods. The colours suggest that a
large fraction of the VPM-selected candidates are typical QSOs such
as those which would be selected in more traditional surveys.
A UV excess of
.
The colour distribution of both the
high- and medium-priority candidates is similar to that
for the QSO candidates from the VPM search in the M 3 field
(Scholz et al. 1997; their Fig. 16).
It should be emphasized that we do not use colours for candidate
selection but merely as a way of checking on how the VPM search
compares with more traditional methods. The colours suggest that a
large fraction of the VPM-selected candidates are typical QSOs such
as those which would be selected in more traditional surveys.
A UV excess of
![]() is found for more than 70% of the high-priority
candidates and for more than 20% of the
medium-priority candidates. The two-colour QSO selection criterion
is found for more than 70% of the high-priority
candidates and for more than 20% of the
medium-priority candidates. The two-colour QSO selection criterion
![]() (see Scholz et al. 1997)
is matched as well by more than 70% of the high-priority QSO candidates.
On the other hand, we find a substantial fraction of red QSO candidates,
among them a few objects with very red colours. To clarify the nature of
these objects is obviously of particular interest in the context of the
present project. As shall be described in detail in Paper II,
follow-up spectroscopy revealed 65 QSOs/Seyfert1s, but none of them
is found to be unusually red.
(see Scholz et al. 1997)
is matched as well by more than 70% of the high-priority QSO candidates.
On the other hand, we find a substantial fraction of red QSO candidates,
among them a few objects with very red colours. To clarify the nature of
these objects is obviously of particular interest in the context of the
present project. As shall be described in detail in Paper II,
follow-up spectroscopy revealed 65 QSOs/Seyfert1s, but none of them
is found to be unusually red.
The selection criteria of the present survey are based on the following properties: B magnitude, image structure, proper motion, and B band variability. In this section, we will discuss the influence of each criterion on the resulting QSO sample.
For objects with redshifts ![]() ,
the present QSO survey is complete
with regard to magnitude limitations. This results simply from the
definition of QSOs (i.e.,
,
the present QSO survey is complete
with regard to magnitude limitations. This results simply from the
definition of QSOs (i.e.,
![]() )
in combination with
the completeness limit
)
in combination with
the completeness limit
![]() for the candidate samples
(Table 3). For larger z, the survey is consequently
magnitude-limited, where the limiting absolute magnitude is
given by
for the candidate samples
(Table 3). For larger z, the survey is consequently
magnitude-limited, where the limiting absolute magnitude is
given by
![\begin{displaymath}\Delta\,m_{z} = -5\,\log_{10}\,\left[\frac{c\,z}{H_0}\,\left(1+\frac{z(1-q_0)}{\sqrt{1+2\,q_0\,z}+1+q_0\,z}\right)\right],
\end{displaymath}](/articles/aa/full/2001/25/aa1126/img206.gif)
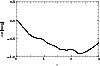 |
Figure 15: K-correction for the Johnson B system as a function of redshift z. |
| Open with DEXTER | |
Due to the low fraction of high-luminosity QSOs
with
MB < -28, the redshift limit of the survey is estimated
to
![]() .
In addition, the detection of QSOs with
z>3 suffers from the strong decrease of the B magnitudes when
the Lyman-break is shifted into the B band.
.
In addition, the detection of QSOs with
z>3 suffers from the strong decrease of the B magnitudes when
the Lyman-break is shifted into the B band.
As in most optical QSO surveys, we exclude objects with significant nonstellar morphology from the candidate list. In order to estimate whether this criterion leads to a significant incompleteness or not, we have to consider the possibility that low-redshift QSOs appear nonstellar on Tautenburg Schmidt plates.
According to Eq. (22), QSOs with B>16.5 must have redshifts z>0.12.
The morphological classification parameters as defined in
Sect. 3.3 correspond to a nonstellar classification for objects
with intrinsic full-width at half-maximum (FWHM) diametres
dFWHM
> 3'', corresponding to a linear FWHM diametre of more than 10 kpc at
![]() .
Therefore, it can not be completely ruled out that a low luminosity
QSO in a giant galaxy at low redshift may be excluded due to the morphology
criterion. From the local QSO density (e.g., Kembhavi & Narlikar
1999) we expect less than two QSOs with z < 0.2 in our
survey field. Therefore, a possible selection effect introduced by the
morhological classification is statistically insignificant for the resulting
QSO sample, yet may be important for lower-luminosity AGNs. On the other hand,
low-redshift QSOs are expected to have a strong UV excess
.
Therefore, it can not be completely ruled out that a low luminosity
QSO in a giant galaxy at low redshift may be excluded due to the morphology
criterion. From the local QSO density (e.g., Kembhavi & Narlikar
1999) we expect less than two QSOs with z < 0.2 in our
survey field. Therefore, a possible selection effect introduced by the
morhological classification is statistically insignificant for the resulting
QSO sample, yet may be important for lower-luminosity AGNs. On the other hand,
low-redshift QSOs are expected to have a strong UV excess
![]() .
Among
the nonstellar objects in the M 92 field with
.
Among
the nonstellar objects in the M 92 field with ![]() ,
only two have such a
UV excess. These two objects are catalogued low-redshift galaxies (NGC 6323
and PGC 060118) with absolute magnitudes MB>-21 (Marzke et al.
1996).
,
only two have such a
UV excess. These two objects are catalogued low-redshift galaxies (NGC 6323
and PGC 060118) with absolute magnitudes MB>-21 (Marzke et al.
1996).
The fraction of QSOs erroneously excluded from the candidate list due
to their proper motion index is 1% or less for the high-priority
sample (![]() ), and 0.01% or less for the medium- and low-priority sample
(
), and 0.01% or less for the medium- and low-priority sample
(
![]() )
(Sect. 4.1).
Compared to the selection effects due to the variability criterion
(Sect. 5.4), the incompleteness introduced by the proper motion
criterion is negligible. In addition, such an effect does obviously
not depend on the apparent magnitudes, redshifts, or
intrinsic properties of the QSOs. It is expected, therefore, that the
proper motion selection does not produce a significant selection bias.
)
(Sect. 4.1).
Compared to the selection effects due to the variability criterion
(Sect. 5.4), the incompleteness introduced by the proper motion
criterion is negligible. In addition, such an effect does obviously
not depend on the apparent magnitudes, redshifts, or
intrinsic properties of the QSOs. It is expected, therefore, that the
proper motion selection does not produce a significant selection bias.
The selection of variable objects introduces a significant bias. The most important factors are the photometric accuracy, the number of observational epochs, and the timescales and amplitudes of the QSO variability. These items will be discussed separately below.
The dependence of the variability indizes ![]() and
and ![]() on the number n of epochs can be expressed easily by the
Taylor series of the corresponding definition relations
(Eqs. (14), (21)):
on the number n of epochs can be expressed easily by the
Taylor series of the corresponding definition relations
(Eqs. (14), (21)):
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{fig16.eps}
\end{figure}](/articles/aa/full/2001/25/aa1126/Timg222.gif) |
Figure 16:
Number of observations n for each object as a function of its mean apparent
magnitude B. The tight correlation is illustrated by the median curve (solid).
The dashed vertical line indicates the survey limit
|
| Open with DEXTER | |
According to Eq. (23), the minimum intrinisic variability
![]() a QSO needs to reach the detection limit
a QSO needs to reach the detection limit
![]() scales with
scales with
![]() .
Hence, QSOs at the limiting magnitude
.
Hence, QSOs at the limiting magnitude
![]() must exhibit a 20% higher intrinsic variability than bright QSOs (
must exhibit a 20% higher intrinsic variability than bright QSOs (![]() )
to
exceed the variability detection limit.
)
to
exceed the variability detection limit.
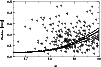 |
Figure 17:
Standard deviation of the intrinsic magnitude fluctuation,
|
| Open with DEXTER | |
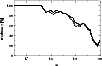 |
Figure 18:
Fraction |
| Open with DEXTER | |
For a given detection limit
![]() and number n of epochs, the
minimum intrinsic variability
and number n of epochs, the
minimum intrinsic variability
![]() ,
above which
QSOs are regarded to be significantly variable, is directly proportional to the
photometric accuracy
,
above which
QSOs are regarded to be significantly variable, is directly proportional to the
photometric accuracy
![]() (Eq. (23)). The latter one is a
function of the apparent magnitude B.
In the magnitude range of the present survey, the mean photometric accuracy
changes by a factor of five (Fig. 5, solid line). Hence, the detection
limit for intrinsic variability is changed by 500% due to the variation
of
(Eq. (23)). The latter one is a
function of the apparent magnitude B.
In the magnitude range of the present survey, the mean photometric accuracy
changes by a factor of five (Fig. 5, solid line). Hence, the detection
limit for intrinsic variability is changed by 500% due to the variation
of
![]() ,
compared to 20% due to the variation of n (see
previous subsection).
,
compared to 20% due to the variation of n (see
previous subsection).
In order to discuss the influence of
![]() on the
completeness of the present survey, we use Eq.(23) to
calculate the detection limit
on the
completeness of the present survey, we use Eq.(23) to
calculate the detection limit
![]() for variability index
limits
for variability index
limits
![]() and
and
![]() ,
respectively, assuming a mean number n(B) of observations according to
Fig. 16 (solid line) as well as n=153. The results (Fig. 17)
show that, for
,
respectively, assuming a mean number n(B) of observations according to
Fig. 16 (solid line) as well as n=153. The results (Fig. 17)
show that, for
![]() ,
objects with an intrinsic variability
,
objects with an intrinsic variability
![]() mag can still be detected as variables.
The limit increases to 0.05 mag at B=17.8, 0.1 mag at B=18.8,
and 0.2 mag at
mag can still be detected as variables.
The limit increases to 0.05 mag at B=17.8, 0.1 mag at B=18.8,
and 0.2 mag at
![]() .
.
Now, let us confront the detection limits with the measured intrinsic
variabilities
![]() of a real sample of QSOs. For this aim, the
variability data provided by Hook et al.(1994) for a large
sample of 332 QSOs in a field near the South Galactic Pole are well suited.
This sample (which is called hereafter the "Hook-sample'') was taken from
several optical surveys which did not use variability as a selection criterion.
For the sake of a simple estimation, we assume that the observed
of a real sample of QSOs. For this aim, the
variability data provided by Hook et al.(1994) for a large
sample of 332 QSOs in a field near the South Galactic Pole are well suited.
This sample (which is called hereafter the "Hook-sample'') was taken from
several optical surveys which did not use variability as a selection criterion.
For the sake of a simple estimation, we assume that the observed
![]() of the Hook-QSOs are comparable to those of the QSOs in the present
survey despite the shorter time-baseline (16 years vs. 34 years) and
the smaller number of epochs in the former study. Hence, the ratio of the
number of Hook-QSOs above the variability
detection limit to the total number of Hook-QSOs at a given B illustrates the
local completeness rate
of the Hook-QSOs are comparable to those of the QSOs in the present
survey despite the shorter time-baseline (16 years vs. 34 years) and
the smaller number of epochs in the former study. Hence, the ratio of the
number of Hook-QSOs above the variability
detection limit to the total number of Hook-QSOs at a given B illustrates the
local completeness rate ![]() as a function of B expected for the present
survey. As can be seen from Fig. 18, the incompleteness due to the
limited photometric accuracy is insignificant for
as a function of B expected for the present
survey. As can be seen from Fig. 18, the incompleteness due to the
limited photometric accuracy is insignificant for ![]() ,
yet increases
strongly for fainter B. At the limiting magnitude
,
yet increases
strongly for fainter B. At the limiting magnitude
![]() of the
present survey, the local completeness rate amounts to
of the
present survey, the local completeness rate amounts to
![]() %.
%.
The number of QSOs with
![]() which will be detected up
to the limiting magnitude
which will be detected up
to the limiting magnitude
![]() is given by
is given by
A significant difference between our VPM survey and most conventional QSO
surveys is that we consider mean QSO magnitudes time-averaged over more
than three decades instead of time-dependent magnitudes at a single
epoch. The surface densities ![]() out of single-epoch magnitudes
would lead to an over-completeness due to the QSO variability.
We estimate the corresponding correction factors according to
Kembhavi & Narlikar (1999)
out of single-epoch magnitudes
would lead to an over-completeness due to the QSO variability.
We estimate the corresponding correction factors according to
Kembhavi & Narlikar (1999)
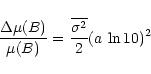 |
(26) |
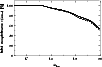 |
Figure 19:
Expected total completeness
|
| Open with DEXTER | |
Adopting ![]() from Fig. 18, we estimate N=62 for the
present survey with
from Fig. 18, we estimate N=62 for the
present survey with
![]() ,
,
![]() and
and
![]() .
This
number is to be compared with the total number of 93 QSOs expected from
Eq. (25) for
.
This
number is to be compared with the total number of 93 QSOs expected from
Eq. (25) for
![]() .
Hence, the selection criterion
.
Hence, the selection criterion
![]() yields a total survey completeness of 67%
(cf.Fig. 19). The completeness is only marginally influenced
by the choice of
yields a total survey completeness of 67%
(cf.Fig. 19). The completeness is only marginally influenced
by the choice of
![]() (Figs. 18 and 19);
a decrease of the detection limit below 1.645 does not
significantly increase the completeness rate yet leads to a rapid increase in
the contamination rate of the candidate sample. The total survey completeness
(Figs. 18 and 19);
a decrease of the detection limit below 1.645 does not
significantly increase the completeness rate yet leads to a rapid increase in
the contamination rate of the candidate sample. The total survey completeness
![]() as a function of the limiting magnitude
as a function of the limiting magnitude
![]()
With regard to further variability-based QSO surveys,
it is of general interest to derive an estimator for the expected
completeness rate as a function of both the photometric accuracy
![]() and the given number of epochs n.
We take for granted that such a survey has a sufficiently long time-baseline,
i.e. two decades or more.
We construct the distribution
and the given number of epochs n.
We take for granted that such a survey has a sufficiently long time-baseline,
i.e. two decades or more.
We construct the distribution
![]() of the intrinsic variabilities of the Hook-QSOs,
assuming that
of the intrinsic variabilities of the Hook-QSOs,
assuming that
![]() is not correlated with B(cf. Fig. 17).
Now, the completeness
is not correlated with B(cf. Fig. 17).
Now, the completeness
![]() is
given by the fraction
is
given by the fraction
![]() and is derived again from the Hook-sample
where
and is derived again from the Hook-sample
where
![]() is the total number of all Hook-QSOs.
The results (Fig. 20)
can be used, in combination with Eq. (23), to derive the
fraction of QSOs with a variability probability
is the total number of all Hook-QSOs.
The results (Fig. 20)
can be used, in combination with Eq. (23), to derive the
fraction of QSOs with a variability probability
![]() ,
i.e.
,
i.e.
![]() (Fig. 21).
(Fig. 21).
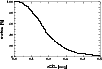 |
Figure 20:
Fraction of Hook-QSOs with an intrinsic
variability
|
| Open with DEXTER | |
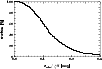 |
Figure 21:
Fraction of Hook-QSOs with significant
variability
|
| Open with DEXTER | |
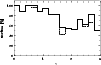 |
Figure 22:
Fraction of Hook-QSOs with significant variability
|
| Open with DEXTER | |
The interpretation of Fig. 21 is straightforward: let us
assume that a photometric accuracy of e.g.
![]() mag is
reached (at a given magnitude, or for the whole survey). With n=16, we have
mag is
reached (at a given magnitude, or for the whole survey). With n=16, we have
![]() mag, which corresponds to a completeness
of
mag, which corresponds to a completeness
of ![]() % (Fig. 21). With n=64, however, the
completeness rate is raised to
% (Fig. 21). With n=64, however, the
completeness rate is raised to ![]() %. The same high completeness rate is
reached for n=16 if the photometric accuracy is
%. The same high completeness rate is
reached for n=16 if the photometric accuracy is
![]() mag.
In general, if a variability-based QSO survey aims at a completeness rate
mag.
In general, if a variability-based QSO survey aims at a completeness rate
![]() or more, it has to meet the requirement
or more, it has to meet the requirement
It was noticed by Hook et al. (1994) that surveys using a
variability selection criterion will be biased. This can be demonstrated by
the comparison of the z distribution of all Hook-QSOs with
the distribution of the variable Hook-QSOs with
![]() .
If
the sample of Hook-QSOs can be taken as representative, the result
(Fig. 22) illustrates the selection function of the present
variability search in the redshift space. A bias against high-luminosity, and
therefore high-redshift QSOs is expected as a consequence of the
anticorrelation between variability and luminosity. However, we have also to
consider the fact that the two subsamples have different completeness functions
.
If
the sample of Hook-QSOs can be taken as representative, the result
(Fig. 22) illustrates the selection function of the present
variability search in the redshift space. A bias against high-luminosity, and
therefore high-redshift QSOs is expected as a consequence of the
anticorrelation between variability and luminosity. However, we have also to
consider the fact that the two subsamples have different completeness functions
![]() and therefore different distributions of apparent magnitudes B.
Hence, let us compare the redshift distribution of the subsample of variable
Hook-QSOs (
and therefore different distributions of apparent magnitudes B.
Hence, let us compare the redshift distribution of the subsample of variable
Hook-QSOs (
![]() )
with randomly-drawn subsamples of Hook-QSOs
which have the same local completeness rate
)
with randomly-drawn subsamples of Hook-QSOs
which have the same local completeness rate ![]() and hence the same Bdistribution as the former one, yet are not selected by a variability
criterion. The comparison was done by means of the parameter-free Wilcoxon
paired signed rank test (Sachs1992) which provides a sensitive
statistical test to evaluate whether two subsamples are drawn from the same
distribution or not. We do not detect significantly different redshift
distributions at the 90% significance level. This obviously means
that the resulting QSO sample is primarily determined by the completeness
function
and hence the same Bdistribution as the former one, yet are not selected by a variability
criterion. The comparison was done by means of the parameter-free Wilcoxon
paired signed rank test (Sachs1992) which provides a sensitive
statistical test to evaluate whether two subsamples are drawn from the same
distribution or not. We do not detect significantly different redshift
distributions at the 90% significance level. This obviously means
that the resulting QSO sample is primarily determined by the completeness
function ![]() ,
i.e. by the photometric accuracy of the survey, rather
than by the intrinsic relationship between variability and luminosity.
,
i.e. by the photometric accuracy of the survey, rather
than by the intrinsic relationship between variability and luminosity.
 |
Figure 23:
Variability indices |
| Open with DEXTER | |
We discuss the dependence of
![]() on the variability timescales by
means of a simple model assuming a sinusoidal light-curve superimposed on
Gaussian noise representing the photometric errors. It is, of course,
well-known that the light-curves of real QSOs are irregular and non-periodic.
However, we argue that any QSO light-curve can be approximated by a Fourier
series of sinusoidal curves, and that the present simple model can be regarded
as such a series truncated after the first term. In this sense,
on the variability timescales by
means of a simple model assuming a sinusoidal light-curve superimposed on
Gaussian noise representing the photometric errors. It is, of course,
well-known that the light-curves of real QSOs are irregular and non-periodic.
However, we argue that any QSO light-curve can be approximated by a Fourier
series of sinusoidal curves, and that the present simple model can be regarded
as such a series truncated after the first term. In this sense, ![]() and
and
![]() were derived from the numerically simulated light-curves as
functions of the period T (observer frame) and the amplitude
were derived from the numerically simulated light-curves as
functions of the period T (observer frame) and the amplitude
![]() of the variability for n=153 epochs. The results
(Fig. 23) confirm that
of the variability for n=153 epochs. The results
(Fig. 23) confirm that
![]() is indeed independent of
T, while
is indeed independent of
T, while
![]() increases with T, as was expected (Sect. 4.2).
increases with T, as was expected (Sect. 4.2).
An intrinsic variability amplitude a=0.44 corresponds to the
![]() detection threshold of the present survey. As can be seen
from Fig. 23, the corresponding
detection threshold of the present survey. As can be seen
from Fig. 23, the corresponding
![]() exceeds the
long-term veriability threshold
exceeds the
long-term veriability threshold
![]() only for
only for ![]() yr.
Thus, the present survey is constrained by the long-term variability index
yr.
Thus, the present survey is constrained by the long-term variability index
![]() for variability timescales
for variability timescales ![]() yr and by the overall
variability index
yr and by the overall
variability index ![]() for objects with
for objects with ![]() yr. The characteristic
variability timescales of typical optically selected QSOs samples were found to
be of the order of 1 yr (Hook et al. 1994, and references
therein). A sample-averaged timescale of more than 1 yr in the quasar-frame,
corresponding to about 4 yr in the observer frame, have been derived by
Meusinger et al. (1994) for a small sample of QSOs with a
time-baseline comparable to that one of the present study. A similar result was
found by Sirola et al. (1998) for a larger sample with a
shorter baseline.
yr. The characteristic
variability timescales of typical optically selected QSOs samples were found to
be of the order of 1 yr (Hook et al. 1994, and references
therein). A sample-averaged timescale of more than 1 yr in the quasar-frame,
corresponding to about 4 yr in the observer frame, have been derived by
Meusinger et al. (1994) for a small sample of QSOs with a
time-baseline comparable to that one of the present study. A similar result was
found by Sirola et al. (1998) for a larger sample with a
shorter baseline.
The fraction of QSOs which match the
![]() criterion
was estimated to about
criterion
was estimated to about
![]() of all QSOs in the field
with
of all QSOs in the field
with
![]() (Sect. 5.4.2).
The simulations discussed above suggest that
the present QSO selection is constrained by
(Sect. 5.4.2).
The simulations discussed above suggest that
the present QSO selection is constrained by ![]() and
and ![]() on approximately the same level. Hence, the total fraction of QSOs in
the field with
on approximately the same level. Hence, the total fraction of QSOs in
the field with ![]() ,
which meet both the
,
which meet both the
![]() and the
and the
![]() criterion, is estimated
to be
criterion, is estimated
to be
![]() .
This
corresponds to a total number of 42 QSOs expected
among the QSO candidates in the high-priority and medium-priority
candidates, whereas about 50 further QSOs obviously failed to match
both variability criteria. These latter QSOs are expected to be comprised
completely in the low-priority sample having magnitudes close
to the survey limit.
.
This
corresponds to a total number of 42 QSOs expected
among the QSO candidates in the high-priority and medium-priority
candidates, whereas about 50 further QSOs obviously failed to match
both variability criteria. These latter QSOs are expected to be comprised
completely in the low-priority sample having magnitudes close
to the survey limit.
In this paper, we have presented the basic observational data, the data reduction, and the selection of QSO candidates by means of a variability and proper motion search. The survey uses a large number of 208 digitised Schmidt plates covering a time-baseline of more than three decades. This long baseline is important for the detection of QSO long-term variability, but also for the accurate measurement of proper motions. Due to proper motion data with Hipparcos-like accuracy, the combination of the variability search with the zero-proper motion constraint yields a substantial enhancement of the efficiency.
The selection criteria of a VPM survey are fundamentally
different from those of conventional optical surveys. The main observational
selection effect is due to the magnitude-dependent accuracy of the
photometric measurements. As a rule of thumb, a completeness
of 90% (80%) is reached,
when for a given number of observations n the ratio
![]() does not exceed 0.05 mag (0.07 mag). For the present
survey, the a priori estimation suggests a number of 42 QSOs (
does not exceed 0.05 mag (0.07 mag). For the present
survey, the a priori estimation suggests a number of 42 QSOs (
![]() )
to be contained in the high- and medium-priority candidate samples. The
low-priority sample is expected to comprise the remaining QSOs. The
resulting QSO sample from the high- and medium-priority candidates
is expected to be biased against higher redshifts
(
)
to be contained in the high- and medium-priority candidate samples. The
low-priority sample is expected to comprise the remaining QSOs. The
resulting QSO sample from the high- and medium-priority candidates
is expected to be biased against higher redshifts
(
![]() ), mainly due to the strong magnitude-dependence of the
completeness function
), mainly due to the strong magnitude-dependence of the
completeness function ![]() .
.
The follow-up spectroscopy of the candidates from the high-priority and the medium-priority subsamples has been completed. The properties of the discovered VPM QSOs will be discussed in Paper II of this series.
Acknowledgements
This paper formed part of J.B.'s Ph.D. Thesis. J.B. acknowledges financial support from the Deutsche Forschungsgemeinschaft under grants Me1350/3 and Me1350/8. This project would not have been possible without the help from several colleagues, above all C. Högner and U. Laux, in the process of scanning the large number of plates. We are also grateful to A. Bruch and R. Ungruhe for providing the MRSP software and to H.-J. Tucholke and R.-D. Scholz for supporting the installation of this software. Finally, the referee, Prof. P.Véron, is grately acknoweledged for his constructive criticism that has helped to improve the paper.This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. The research has also made use of the SIMBAD database, operated at CDS, Strasbourg, France.