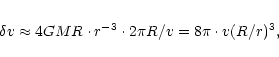
Enhanced SF activity in large gas-rich galaxies is stimulated by various types of galaxy interactions, including: a) mergers of close mass galaxies (e.g., Larson & Tinsley 1978; Joseph et al. 1984); b) sinking dwarf companions (e.g., Mihos & Hernquist 1994; Rudnick et al. 2000); c) strong tidals (e.g., Bernloehr 1993; Keel 1993); d) weak tidals (e.g., Icke 1985; Reshetnikov & Combes 1997; Rudnick et al. 2000). In principle, all these mechanisms could also work for gas-rich low-mass galaxies. The relative importance of these external triggers, as well as their role in comparison to some internal triggers, seemingly should depend on the type of environment.

While a detailed understanding of trigger mechanisms of enhanced SF due to the tidal action of a nearby galaxy on gas-rich dwarfs is still lacking, several schemes were suggested to model the effect of galaxy interaction, which can be applied to low-mass galaxies. The method of Noguchi (1988) is based on the generation of a central bar which in turn disturbs gas clouds and causes them to sink towards the center of galaxy, inducing a central SF burst. Another mechanism, suggested by Olson & Kwan (1990), works via a large tidal increase in the inelastic collision rate of individual gas clouds, and their merging and collapse. It is basically a stochastic process. Both these mechanisms require strong enough tidal disturbance, possible when the fly-by of equal mass galaxies takes place at the pericenter distance of about 8-10 disk scale-lengths.

The mechanism suggested by Icke (1985) involves the generation of shocks in the outer parts of the HI disk, with the subsequent dissipation of their kinetic energy and the loss of dynamical stability of the gas disk. It takes a moderate tidal force, and under similar conditions effectively acts from a distance 2-3 times larger than the two former models. Also, the cross-section of the Icke mechanism is several times larger.

This circumstance favors the Icke mechanism as the most efficient in the stimulation of abnormal SF activity. Some indirect arguments to support the importance of this trigger mechanism are the traces of recent enhanced SF in spiral galaxies with lopsidedness and bent outer parts. The latter are considered to be evidence of minor tidal effects (e.g. Rudnick et al. 2000; Reshetnikov & Combes 1997). However, lopsidedness can be caused by minor mergers as well (Rudnick et al. 2000). Evidently, the two former, or similar, mechanisms also can work to trigger BCG progenitors. However, their role is probably less important.

To illustrate quantitavely the parameters of the Icke mechanism and the pericenter distance at which tidals become effective at generating shocks, we give below the simple formulae taken from the paper by Icke (1985).

The Icke mechanism is based on tidal acceleration of gas layers to supersonic velocities and the subsequent dissipation of shock waves. A characteristic value for the speed gained by gas due to the tidal acceleration by an "intruder'' (the object which exerts the tidal force; the name does not necessarily imply a close approach) over a time span corresponding to one revolution (a characteristic time in the galaxy-"victim'' system) is given by the formula:

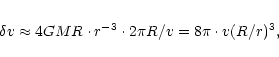
$\begin{eqnarray*}\delta v\approx 4GMR\cdot r^{\rm -3} \cdot 2\pi R/v = 8\pi\cdot v(R/r)^{\rm 3}, \end{eqnarray*}$

For the general case of colliding galaxies of unequal masses, with the mass ratio $\mu =M$ (intruder)/M(victim) the latter relation changes to: $p_{\rm0} \approx R\cdot(8\pi\cdot\mu v/s_{\rm0})^{\rm 1/3}$ .

To illustrate the range of the expected values of $p_{\rm0}$ for several representative cases of the mass ratio, we calculate this according to the formulae above for two low-mass "disk" galaxies with typical of BCG parameters. We accept here $s_{\rm0}=10$ km s $^{\rm -1}$ as the characteristic velocity dispersion in the interstellar gas. One case corresponds to a galaxy with M(victim) $_{\rm tot} = 10^{\rm 10}~M_{\odot}$ ; $v/s_{\rm0}=7$ ; R(victim) $\,=10$ kpc and another - to a galaxy with M(victim) $_{\rm tot} = 10^{\rm 9}~M_{\odot}$ ; $v/s_{\rm0}=3$ ; R(victim) $\,=5$ kpc. R(victim) is taken here as the size of the outer HI-disk, corresponding to the characteristic mass density of ${\sim}0.5~M_{\odot}$ /kpc $^{\rm 2}$ . We notice that according to observations, BCGs, as well as other dwarfs, are dominated dynamically by Dark Matter halos, and their baryonic mass is several times lower than their total mass. So a DM halo plays the same role as a spherical stellar halo in the original Icke model. The respective values of $p_{\rm0}$ for $\mu=200$ , 10, 1 and 0.1 are shown in Table 1. The parameters above correspond to the typical ones of BCGs, as described, e.g., by Taylor et al. (1995). According to the same authors, BCGs with such total masses can have a wide range of blue luminosities, corresponding to M_B = -12.7 to -17.0.

Table 1: Characteristic threshold pericenter distance
M(vict) $_{\rm tot}$ $10^{10}~M_{\odot}$ $10^{9}~M_{\odot}$

M(intrud)
$\mu$ p₀ M(intrud) $\mu$ p₀

(M $_{\odot}$ ) (kpc) ( $M_{\odot}$ ) (kpc)

$2\times 10^{12}$ 200.0 327 $2\times 10^{11}$ 200.0 123

10¹¹ 10.0 121 10¹⁰ 10.0 45

10¹⁰ 1.0 56 10⁹ 1.0 21

10⁹ 0.1 26 10⁸ 0.1 10

**Table 1:** Characteristic threshold pericenter distance
M(vict) $_{\rm tot}$	$10^{10}~M_{\odot}$		$10^{9}~M_{\odot}$
M(intrud)	$\mu$	p₀	M(intrud)	$\mu$	p₀
(M $_{\odot}$ )		(kpc)	( $M_{\odot}$ )		(kpc)
$2\times 10^{12}$	200.0	327	$2\times 10^{11}$	200.0	123
10¹¹	10.0	121	10¹⁰	10.0	45
10¹⁰	1.0	56	10⁹	1.0	21
10⁹	0.1	26	10⁸	0.1	10

One important note related to the problem of the observational search for potential "intruders'' around the target BCGs is connected to the expected time delay between the passage of the pericenter and the beginning of SF burst. For example, for $V_{\rm rot}= 70$ km s $^{\rm -1}$ and R=10 kpc, the characteristic time of development of shocks is comparable (Icke 1985) to $T=2\pi~R/V_{\rm rot} = 8\times10^{\rm 8}$ yr. In general, checking any nearby galaxy as a potential "intruder'' of the target BCG, we need to account for the relative tangential velocities of the two considered galaxies $\delta V$ , in our case up to 300-400 km s $^{\rm -1}$ . Thus, e.g., for $\delta {t} = T/2$ for the disk above, and $\delta V = 200$ km s $^{\rm -1}$ , by the time of a well-developed SF episode, the two galaxies can increase their projected separation from their pericenter position by 90 kpc. Hence, due to the time delay between the maximum tidal action and its consequence as a SF burst, one can expect that even relatively low-mass neighbours can be the real disturbing galaxies if they are found at distances of less than ${\sim}100$ -150 kpc. The delays in the beginning of a SF burst in the more massive component in pairs of interacting spirals with highly different masses were noticed by Bernloehr (1993). These delays range up to several hundred Myr, which in general is compatible with the numbers given above.

Sufficiently detailed observational data for BCG companions to be used to test the role of relatively weak tidals are not abundant. The most suitable are seemingly the results of the search for low-mass HI companions near H II-galaxies by Taylor et al. (1993,1995). The projected distances in the systems with detected HI companions are consistent with the estimates of the threshold pericenter distances with input observational parameters, if again, some reasonable delay in the ignition of SF bursts is taken into account.

We also note that to directly detect shocks in HI gas of BCGs triggered by an interaction is not simple. According to the model, they dissipate to initiate gas instability. Therefore, by the time of the developed SF burst, the signs of shocks can be completely erased. Therefore the search for such disturbed velocity fields should be directed to the systems in the earlier stages of collision, in which an SF burst has not yet occured. Probably gas-rich galaxy pairs with a large mass difference, such as those studied by Bernloehr (1993), can be suitable for this task.

2 Tidal trigger