A&A 373, 329-335 (2001)
DOI: 10.1051/0004-6361:20010583

Search for meteor showers associated with Near-Earth Asteroids

I. Taurid Complex

P. B. Babadzhanov[*]

Institute of Astrophysics, Tajik Academy of Sciences, Dushanbe 734042, Tajikistan and Isaac Newton Institute of Chile, Tajikistan Branch

Received 26 December 2000 / Accepted 20 March 2001

Abstract
Observed meteor showers associated with some Near-Earth asteroids (NEAs) is one of the few criteria that such asteroids may be considered to be candidate extinct cometary nuclei. In order to reveal new NEA-meteor shower associations, we calculated the secular variations of the orbital elements of 17 Taurid Complex asteroids with allowance for perturbations from six planets (Mercury-Saturn) over one cycle of variation of perihelia arguments. The Earth-crossing class of these NEAs and theoretical geocentric radiants and velocities of their meteor showers were determined and compared with available observational data. It turns out that each Taurid Complex asteroid is associated with four meteor showers. This is evidence for the cometary origin of these asteroids.

Key words: comets - meteoroids; meteors - minor planets, asteroids


1 Introduction

It is generally accepted that meteoroid streams are formed as a result of the disintegration of cometary nuclei. The presence of meteor showers associated with some near-Earth asteroids (NEAs) is evidence that such asteroids have a cometary origin, i.e. they are extinct cometary nuclei (Olsson-Steel 1988; Steel 1994; Babadzhanov 1996; Lupishko 1998). The existence of asteroids identifiable with extinct or dormant comets (2060 Chiron, 4015 Willson-Harrington, 1986 TF Parker-Hartley) confirm the cometary origin for some NEAs.

Investigation of NEA-meteor shower associations is important not only for confirmation or denial of the NEA cometary origins, but also to obtain important information about NEA sources - comets from outer regions of the Solar system, and real asteroids from the main belt.

The calculation of theoretical meteor radiants is the first step in revealing the generic relationship between a given near-Earth object (comet or asteroid) and its possible meteor showers. However, methods for the determination of the theoretical radiants of comets and asteroids approaching the Earth's orbit close than 0.1-0.3 AU, which were used by different authors (e.g., Kramer 1973; Drummond 1982, 2000; Artoos 1994) until recently, did not take into account the meteoroid stream evolution and could only roughly predict one or two radiants of the given comet or asteroid. The method of the calculation of theoretical radiants suggested by Hasegawa (1990) and known as the $\omega $-method is more appropriate and takes into account the fact that a meteoroid stream can give rise to a meteor shower only when the orbits of the stream meteoroids cross the Earth's orbit. However, this method also does not predict the radiants of all possible meteor showers of the given near-Earth object and is used only for comets and minor planets with an orbital node currently situated at no more than 0.2-0.3 AU from the Earth's orbit.

As follows from basic principles of meteoroid stream formation and evolution (Babadzhanov & Obrubov 1987, 1992; Babadzhanov 1996; Steel 1994), related meteor showers can be produced also by those comets whose orbits are presently located at distances more than 0.3 AU from the Earth's orbit but which crossed it in the past. The orbit of the parent body when crossing the Earth's orbit can be determined by studying its evolution under the gravitational perturbing action of the major planets.

2 Formation of meteoroid streams

Ejection velocities of meteoroids from their parent bodies and radiation pressure (for small particles) cause an initial dispersion in orbital elements of ejected meteoroids. Because of differences in the semi-major axes (and orbital periods) between the meteoroids and their parent body, some meteoroids lag behind the parent body, while others, overtaking it, spread along the entire orbit and form a complete loop in a comparatively short time (Hughes 1986; Williams 1995).

After the meteoroids are distributed along the orbit of the parent body, due to differences in the planetary perturbing action on stream meteoroids of different semi-major axes and eccentricities, the rates and cycles of variations in the angular orbital elements (the argument of perihelia $\omega $, the longitude of the ascending node $\Omega$,

  \begin{figure} \par\includegraphics[width=5.3cm,clip]{10520f1.eps}\end{figure} Figure 1: a) The projection of Poseidon's orbits onto the plane perpendicular to the ecliptic; b) three dimensional image of the Poseidon's orbits for the period of one cycle of variation of $\omega $; c) mean orbits of Poseidon's stream meteoroids producing 4 meteor showers.
Open with DEXTER

and the inclination to the ecliptic i) will be different for different meteoroids. As a result, the orbits of different meteoroids will be at different evolutionary stages, as distinguished by their arguments of perihelia, i.e. the stream meteoroids occupy all evolutionary tracks of their parent body. This process increases considerably both the size of the meteoroid stream and its thickness (the breadth of a stream is determined by the value of the meteoroids' orbital semi-major axes).

In order to imagine the form of the meteoroid stream let us assume that the stream consists of particles of approximately the same semi-major axis but in all possible evolutionary positions distinguished by their arguments of perihelia $\omega $. For example, to simulate the form of Poseidon's meteoroid stream we consider its osculating orbits for the period of one cycle of variation of $\omega $. The projection of Poseidon's orbit onto the plane perpendicular to the ecliptic is presented in Fig. 1a, and the three-dimensional image of these orbits is given in Fig. 1b. A characteristic feature of the form obtained is its large thickness in the aphelion region and the symmetry with respect to the ecliptic plane near which the disturbing planets are moving.

If the Earth's orbit is assumed to be circular, then it may be intersected by those stream meteoroids which have the orbital node at the heliocentric distance $r\approx 1$ AU, i.e. satisfying the expression:

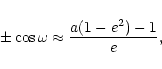\begin{displaymath}\pm\cos\omega\approx\frac{a(1-e^2)-1}{e}, \end{displaymath} (1)

where a is the semi-major axis and e is the eccentricity.

As shown earlier (Babadzhanov & Obrubov 1987, 1992; Babadzhanov 1996) the number of meteor showers produced by a meteoroid stream is determined by the Earth-crossing class of the parent-body orbit. For example, if it is a quadruple-crosser of the Earth's orbit (i.e. during one cycle of variation of the perihelion argument of its orbit under the perturbing action of the major planets, a parent body crosses the Earth's orbit four times) the meteoroids of the stream that separated from its parent might produce four meteor showers: two at the pre-perihelion intersections and two at the post-perihelion intersections with the Earth (Fig. 1c). Crossing before perihelion gives rise to two night-time showers, and after the perihelion, two daytime showers. These two pairs of showers are formed by the same meteoroid stream, each pair consisting of a northern and a southern branch. For example, the meteoroid stream of comet Encke produces night-time Northern and Southern Taurids and daytime $\zeta$-Perseids and $\beta$-Taurids showers.

 

 
Table 1: Near-Earth Asteroids of the Taurid Complex.
Asteroid q a e $i^{\circ}$ $\Omega^{\circ}$ $\omega^{\circ}$ $\pi^{\circ}$ D H d $R_{\rm a}$ $R_{\rm d}$
  AU AU     2000.0         km AU AU
1991 TB2 0.394 2.397 0.836 8.6 297.2 195.6 132.8 0.13 17.0 1.9 3.7 0.4
5143 Heracles 0.420 1.834 0.771 9.2 310.8 226.4 177.2 0.13 13.9 7.7 1.6 0.5
1996 SK 0.494 2.428 0.796 2.0 198.3 283.4 121.7 0.12 17.0 1.9 0.7 1.1
1993 KA2 0.502 2.227 0.775 3.2 239.6 261.3 140.9 0.06 29.0 0.01 1.0 0.8
4197 1982 TA 0.522 2.297 0.773 12.2 10.2 119.2 129.4 0.14 14.5 5.9 1.5 0.7
6063 Jason 0.522 2.216 0.764 4.8 170.0 336.5 146.5 0.07 15.1 4.5 0.5 3.1
4341 Poseidon 0.588 1.835 0.679 11.9 108.2 15.5 123.7 0.20 15.6 3.5 0.6 2.9
2201 Oljato 0.630 2.176 0.711 2.5 76.9 96.0 172.9 0.12 15.3 4.1 1.2 1.0
5025 P-L 0.647 2.140 0.697 3.1 341.6 153.8 135.5 0.12 15.9 3.1 2.9 0.7
1991 GO 0.663 1.956 0.661 9.7 25.0 88.6 113.6 0.19 19.0 0.7 1.1 0.9
1995 FF 0.674 2.321 0.710 0.6 175.6 293.1 108.7 0.14 26.5 0.02 0.9 1.6
1991 BA 0.713 2.242 0.682 2.0 118.9 70.7 189.6 0.15 28.5 0.01 1.0 1.6
4183 Cuno 0.718 1.980 0.637 6.8 295.9 235.2 171.1 0.19 14.5 5.9 1.8 0.9
8201 1994 AH2 0.730 2.527 0.711 9.6 164.4 24.8 189.2 0.20 16.3 2.6 0.8 3.5
1990 HA 0.782 2.571 0.696 3.9 184.8 308.3 133.1 0.20 16.0 3.0 0.9 2.3
5731 Zeus 0.785 2.262 0.653 11.6 282.8 215.6 138.4 0.19 15.5 3.7 2.8 0.8
1996 RG3 0.790 2.000 0.605 3.6 158.5 299.9 98.4 0.20 18.5 0.9 1.0 1.8
2P/Encke 0.331 2.209 0.850 11.9 334.7 186.3 161.0     2.4 4.0 0.3


$\zeta$-Perseids are the northern branch of the shower at daytime and are twins of the Northern Taurids, but $\beta$-Taurids are the southern branch at the daytime intersections of the stream and are twins of the Southern Taurids.

According to the foregoing notion of meteoroid-stream evolution, we use a new method for the determination of theoretical radiants of the near-Earth objects. It consists of the following operations:

(1)
The calculation of secular variations of the cometary (or asteroidal) orbital elements for a time interval covering one cycle of variation of the argument of perihelia;
(2)
The determination of the orbits crossing the Earth's orbit, and of the Earth-crossing class of the parent body, i.e. the number of crossings during one cycle of the perihelion argument. The number of crossing may be from one to eight;
(3)
The calculation of the theoretical geocentric radiants and velocities for the Earth-crossing orbits;
(4)
Search for theoretically predicted radiants in catalogues of observed meteor showers and of individual meteors.

3 Meteor showers associated with the Taurid Complex asteroids

The object of the present paper is to reveal the meteor showers associated with the Taurid Complex asteroids, which has Encke's comet as a member and according to Clube $\&$ Napier (1984) and Asher et al. (1993) have a common cometary origin. Moreover, Asher & Steel (1998) came to the conclusion that a common origin of 2P/Encke and the Tunguska bolide suggested by Kresak (1978) appears likely. A possible association of daytime fireballs and some Taurid Complex asteroids (4486 Mithra, 1990 SM and 1991 BA) was suggested by Hasegawa (1996).

In their earlier paper, Asher & Steel (1995) calculated the theoretical radiants of 15 asteroids and 1 comet of the Taurid Complex and 5 asteroids and 1 comet (P/Helfenzrieder) of Hephaistos group asteroids, and among observed data found 657 individual meteors with radiants similar to theoretical ones. However, the existence of observable associated meteor showers is the only substantial index that a given NEA is a candidate for the cometary origin.

Asher et al. (1993) assumed that near-Earth objects (NEOs) belong to the Taurid Complex asteroids if their longitudes of perihelion $\pi= \Omega+\omega$ lie within the limits of $100^{\circ} < \pi < 190^{\circ}$ and their orbital parameters (a, e, i)satisfy the criterion D < 0.2, where

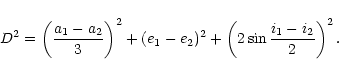\begin{displaymath}D^2=\left(\frac{a_1-a_2}{3}\right)^2+(e_1-e_2)^2+ \left(2\sin\frac{i_1-i_2}{2}\right)^2. \end{displaymath} (2)

Here a1=2.1 AU, $e_1=0.82, \, \, i_1=4^{\circ}$ and the subscript 2 denotes a near-Earth object's orbit. The criterion (2) is a modified Southworth & Hawkins' (1963) criterion of orbital similarity as applied to the membership for the Taurid complex.

Among the 536 near-Earth asteroids known on August 8, 1998 we find 37 whose orbits satisfy the criterion D<0.2, and 17 of these 37 could be associated with the Taurid Complex because their longitudes of perihelion lie within the range $100^{\rm o}<\pi<190^{\rm o}$ like those of Taurid meteors (Babadzhanov et al. 1990; Stohl & Porubcan 1990). Another 5 of the 37 NEAs form a group whose orbital longitudes of perihelion lie within the range $220^{\rm o}<\pi<260^{\rm o}$, and are named after the largest asteroid of this group, Hephaistos (2212). The third group consists of 15 NEAs, whose orbits satisfy the criterion D<0.2, but their longitudes of perihelion differ from those of the Taurid Complex and Hephaistos group. Among the NEAs of the third group is Adonis (2101), associated with four meteor showers. Anomalous radar echoes from Adonis have been regarded as suggestive that this NEA may be an extinct comet (Ostro et al. 1990). Results of the search of meteor showers associated with the NEAs of Hephaistos and Adonis groups will be presented in other papers.

In this paper we present the results of a search for meteor showers associated only with the Taurid Complex asteroids. Data for these NEAs are given in Table 1, where q=a(1-e) is the perihelion distance, H is the absolute magnitude and d the equivalent diameter, calculated using the expression (Bowell & Lumme 1982; Rowe 1993):

\begin{displaymath}\log d=3.12-0.2H-0.5\log p. \end{displaymath} (3)

The candidates for cometary origin should be dark asteroids of C, P and D-types of low albedos in the range of 0.02 to 0.08. The values of d in Table 1 are given for an assumed albedo p=0.08. $R_{\rm a}$and $R_{\rm d}$ are the radius-vector of the ascending and descending nodes respectively.

Using the Halphen-Goryachev method (Goryachev 1937) we calculated the secular variations of the orbital elements of each asteroid mentioned in Table 1,

  \begin{figure} \par\includegraphics[width=12.6cm,clip]{10520f2.eps}\end{figure} Figure 2: The predicted (dots) and observed (crosses) radiants of the meteor showers associated with the Taurid Complex asteroids. The predicted and corresponding observed showers are linked in pairs. The curve delineates the ecliptic.
Open with DEXTER

allowing for perturbations from six planets (Mercury-Saturn) over one cycle of the variation in the arguments of perihelia (4000-10000 yrs). The results of calculations are that all these asteroids are quadruple-crossers of the Earth's orbit, and, therefore, their hypothetical meteoroid streams might produce four meteor showers each.

We calculated the theoretical orbital elements and geocentric radiants and velocities of all meteor showers associated with 17 Taurid Complex asteroids. The theoretical geocentric radiants (the right ascention $\alpha$ and declination $\delta$), the geocentric velocities $V_{\rm g}$ (km s-1), solar longitudes $L_{\odot}$ and corresponding dates of activity of all showers are given in Table 2.

 

 
Table 2: Theoretical and observed geocentric radiants and velocities of the meteor showers associated with the Taurid Complex asteroids (Equinox 2000.0). Type N is for night shower, type D for day shower. $V_{\rm g}$ in km s-1.
Asteroid and Predicted radiants Observed radiants T $D_{{\rm S}-{\rm H}}$ Cat.
associated   y    
meteor showers $L_{\odot}$ Date $\alpha^{\circ}$ $\delta^{\circ}$ $V_{\rm g}$ $L_{\odot}$ Date $\alpha^{\circ}$ $\delta^{\circ}$ $V_{\rm g}$ p    
                      e    
1993 KA2                          
North. Taurids 223.2 Nov. 05 43.7 20.6 23.9 211.2 Oct. 24 43.0 18.6 29.7 N 0.08 L
South. Taurids 218.6 Nov. 01 43.8 11.7 25.0 220.6 Nov. 03 51.2 13.8 27.5 N 0.02 C
$\sigma$ Arietids 59.0 May 20 53.3 15.4 24.0 59.0 May 20 47.9 15.0 27.1 D 0.04 L
$\zeta$ Perseids 63.4 May 24 53.8 24.1 25.2 78.2 Jun. 08 61.0 24.5 28.6 D 0.04 S2
6063 Jason                          
$\zeta$ Perseids 67.2 May 29 58.8 24.4 27.7 71 Jun. 02 52 23 27.8 D 0.01 K
$\beta$ Taurids 63.3 May 25 58.3 17.6 23.6 78 Jun. 09 64.0 15.0 26.6 D 0.08 K
North. Taurids 229.6 Nov. 12 49.8 21.1 23.5 234.0 Nov. 17 52.0 20.8 20.4 N 0.18 L
South. Taurids 226.0 Nov. 09 50.0 14.2 24.6 220.0 Nov. 03 50.5 13.6 27.0 N 0.02 C
1996 SK                          
S.May. Arietids 40.2 May 01 34.4 11.8 24.6 52.8 May 13 33.7 9.2 29.0 D 0.04 K
N.May. Arietids 45.0 May 06 35.5 16.6 25.9 54.9 May 15 37.5 18.2 25.2 D 0.01 L
South. Piscids 198.8 Oct. 01 24.2 7.5 25.8 188.4 Oct. 02 24.9 9.2 29.2 N 0.02 K
North. Piscids 203.6 Oct. 01 24.8 12.6 24.5 199.8 Oct. 13 26.7 14.2 29.0 N 0.00 C
2201 Oljato                          
$\zeta$ Perseids 75.9 Jun. 07 77.7 26.8 20.1 77.6 Jun. 09 79.2 28.1 19.5 D 0.05 L
$\beta$ Taurids 79.5 Jun. 11 80.2 22.9 21.0 76.0 Jun. 08 73.0 19.0 21.3 D 0.19 K
N.$\chi$-Orionids 264.9 Dec. 17 82.8 23.5 21.0 260.3 Dec. 14 83.3 24.2 22.4 N 0.23 L
S.$\chi$-Orionids 268.1 Dec. 21 84.8 19.4 20.3 259.4 Dec. 12 78.7 9.5 18.4 N 0.09 L
5025 P-L                          
  35.3 Apr. 25 38.7 13.6 18.6 Non observed       D    
$\epsilon$ Arietids 39.3 Apr. 29 39.0 19.6 19.7 48.0 May 08 44.3 21.1 20.9 D 0.04 S2
N.$\delta$ Arietids 236.5 Nov. 18 47.8 19.3 18.7 242.7 Nov. 24 47.6 23.5 18.6 N 0.06 L
S.$\delta$ Arietids 231.4 Nov. 13 47.1 13.5 19.8 241.9 Nov. 23 51.8 13.3 16.3 N 0.08 L
1991 TB2                          
North. Piscids 202.7 Oct. 15 29.1 14.5 27.8 199.8 Oct. 12 26.7 14.2 29.0 N 0.04 C
South. Piscids 198.3 Oct. 11 29.0 7.9 28.8 195.6 Oct. 09 27.7 9.2 28.9 N 0.01 K
$\sigma$ Arietids 61.7 May 22 50.2 15.8 27.8 59.0 May 20 47.2 14.9 27.1 D 0.02 L
$\zeta$ Perseids 65.5 May 26 50.7 22.1 29.0 57.6 May 18 52.7 23.2 27.8 D 0.05 K
5143 Heracles                          
$\kappa$ Aurigids 108.3 Jul. 11 98.7 32.8 26.4 101.9 Jun. l4 94.4 27.4 24.0 D 0.13 S2
$\beta$ Taurids 107.3 Jul. 10 97.6 15.9 25.8 96 Jun. 29 86 19 30 D 0.08 C
North. Orionids 247.2 Nov. 30 75.2 30.3 25.6 258 Dec. 10 84 26 25.2 N 0.11 C
South. Orionids 246.3 Nov. 29 77.1 12.9 26.1 241.3 Nov. 24 72.4 13.0 23.1 N 0.10 L
4197 1982 TA                          
N. Arietids 46.7 May 07 35.4 27.4 24.4 54.0 May 14 41.0 23.0 24.6 D 0.11 K
$\alpha$ Cetids 43.4 May 04 42.0 4.3 23.2 58.2 May 18 47.2 14.9 27.1 D 0.18 L
$\alpha$ Arietids 216.5 Oct. 30 32.6 25.4 23.3 210.7 Oct. 24 28.6 18.1 22.2 N 0.11 L
Omicron Cetids 212.8 Oct. 26 39.1 1.8 24.3 208.4 Oct. 22 36.0 -3.3 26.0 N 0.14 L
1995 FF                          
  6.6 Mar. 27 12.3 4.4 18.9 Non observed            
  9.8 Mar. 30 13.1 6.6 19.7 Non observed            
N. Octob. Piscids 210.9 Oct. 24 22.0 10.2 19.0 211.8 Oct. 25 16.2 14.6 17.5 N 0.00 L
S.Octob.Piscids 206.9 Oct. 20 21.4 8.1 19.8 210.8 Oct. 24 23.6 7.2 19.2 N 0.01 L
1991 BA                          
$\rho$ Geminids 281.8 Jan. 02 101.2 26.2 21.7 287.8 Jan. 08 109.8 31.3 21.8 N 0.00 S2
Canids 296.6 Jan. 16 108.8 18.7 18.1 295.3 Jan. 15 106.8 20.2 19.8 N 0.09 S2
$\beta$ Taurids 82.5 Jun. 13 92.1 27.0 17.9 78.2 Jun. 09 80.0 28.2 19.4 D 0.00 L
  98.0 Jun. 29 99.4 20.0 21.7 Non observed            
1991 GO                          
$\phi$ Piscids 217.6 Oct. 30 23.1 26.8 17.6 211.2 Oct. 24 21.8 23.8 19.2 N 0.03 L
$\mu$ Piscids 212.4 Oct. 25 32.9 -4.1 18.9 210.8 Oct. 24 23.2 7.2 19.2 N 0.07 L
$\xi$ Piscids 14.6 Apr. 04 10.0 22.1 18.8 19.1 Apr. 8 19.6 21.0 18.0 D 0.01 S1
  19.9 Apr. 09 24.5 -5.8 19.9 Non observed            



 
Table 2: continued.
Asteroid and Predicted radiants Observed radiants T $D_{{\rm S}-{\rm H}}$ Cat.
associated   y    
meteor showers $L_{\odot}$ Date $\alpha^{\circ}$ $\delta^{\circ}$ $V_{\rm g}$ $L_{\odot}$ Date $\alpha^{\circ}$ $\delta^{\circ}$ $V_{\rm g}$ p    
                      e    
4183 Cuno                          
Day Linxids 110.2 Jul. 13 121.6 35.0 18.2 109.5 Jul. 12 123.5 37.0 17.4 D 0.07  
Day Monocerotids 108.1 Jul. 11 115.9 9.9 17.4 106.2 Jul. 09 116.3 12.1 16.5 D 0.05  
$\rho$ Cancrids 320.3 Feb. 09 138.7 27.9 17.6 331.4 Feb. 020 148.4 32.4 16.9 N 0.09 L
Hydrids 317.5 Feb. 06 130.4 3.1 18.6 332.3 Feb. 21 131.2 3.7 15.9 N 0.18 L
5731 Zeus                          
$\xi$ Piscids 28.6 Apr. 19 28.8 31.3 17.8 18.4 Apr. 08 18.9 20.7 18.0 D 0.01 S2
$\delta$ Cetids 23.8 Apr. 14 40.1 -3.2 16.5 28.2 Apr. 18 37.0 1.6 18.1 D 0.26  
N.Eps.Perseids 252.6 Dec. 05 53.4 37.5 16.7 259.9 Dec. 12 51.4 38.5 17.3 N 0.12 L
S.Eps.Perseids 246.7 Nov. 29 59.9 2.4 18.2 241.0 Nov. 24 56.0 5.0 20.0 N 0.06 L
4341 Poseidon                          
N.May. Arietids 34.7 Apr. 25 27.5 22.2 20.3 54 May 14 41.0 23.0 24.6 D 0.11 K
S.May. Arietids 38.6 Apr. 29 36.0 5.8 21.2 52 May 12 33 9 28.9 D 0.13 K
$\alpha$ Arietids/? 208.7 Oct. 22 26.5 19.8 21.2 210.7 Oct. 24 28.6 18.1 22.3 N 0.05 L
O Cetids 212.8 Oct. 26 35.2 3.2 20.3 208.4 Oct. 22 36.0 -3.3 26.0 N 0.21 L
8201 1994 AH2                          
$\beta$ Taurids 80.6 Jun. 11 90.6 32.7 18.6 78.2 Jun. 09 80.0 28.2 19.4 D 0.04 L
  82.5 Jun. 13 91.5 18.9 18.9 Non observed       D    
$\zeta$ Geminids 297.9 Jan. 18 108.9 12.6 18.9 295.3 Jan. 15 106.4 20.2 19.8 N 0.05 S2
$\rho$ Geminids 296.1 Jan. 16 109.8 26.7 19.1 287.8 Jan. 07 109.8 31.3 21.8 N 0.01 S1
1990 HA                          
  14.6 Apr. 03 31.2 4.8 16.2 Non observed       D    
$\xi$ Piscids 22.6 Apr. 11 29.0 19.1 18.0 19.1 Apr. 08 19.6 21.0 18.0 D 0.05 S2
$\epsilon$ Arietids 249.0 Dec. 01 50.2 25.2 16.6 242.7 Nov. 25 47.6 23.5 23.3 N 0.05 L
$\sigma$ Arietids 242.3 Nov. 24 51.5 12.0 18.3 241.9 Nov. 24 51.8 13.3 16.3 N 0.00 L
1996 RG3                          
  342.0 Mar. 02 0.3 -8.7 14.5 Non observed       D    
  347.1 Mar. 07 357.0 4.2 15.5 Non observed       D    
N.Oct.Piscids 213.8 Oct. 27 15.0 14.4 14.7 211.8 Oct. 25 16.2 14.6 17.5 N 0.10 L
S.Oct.Piscids 209.4 Oct. 23 18.1 2.1 15.6 210.8 Oct. 24 23.2 7.2 19.2 N 0.11 L


A computerized search for the predicted showers was carried out in the catalogues published by: (C) Cook (1973), (K) Kashcheev et al. (1967), (L) Lebedinets et al. (1972), and (S1, S2) Sekanina (1973, 1976) - their parenthesized notation is used in Table 2. This search took into account the closeness in the positions of the theoretical and the observed radiants (the requirement used was $\Delta\alpha=\Delta\delta=\pm 10^{\circ}$), in velocity values ( $\Delta V_{\rm g}\leq 5$ km s-1) and period of activity ( $\Delta t \leq \pm 15$ days) for $D_{{\rm S}-{\rm H}}\leq 0.2$, where $D_{{\rm S}-{\rm H}}$ is the criterion of Southworth & Hawkins (1963), which, in the case under consideration, serves as a measure of the similarity between the theoretical and the observed orbits. With the use of these catalogues, 59 out of the 68 theoretically predicted showers were identified with observed showers. Probably, the other 9 showers also are active, but they are not yet distinguished above the sporadic background. Table 2 lists the observed geocentric radiants, velocities, solar longitudes and corresponding dates of maximum activity for all identified showers. The values of the $D_{{\rm S}-{\rm H}}$ - criterion given in the thirteenth column of Table 2 show good agreement between the parameters of theoretically predicted and observed showers.

Figure 2 represents the theoretical (dots) and observed (crosses) radiants of the meteor showers associated with Taurid Complex asteroids. The theoretical and observed radiants are linked in pairs. The curve delineates the ecliptic. Figure 2 shows that in most cases theoretical and observed radiants coincide or are close to each other, but in some cases their differences reach $10^{\circ}$-12$^{\circ}$ due to daily motion of the radiant which was not taken into account because the published catalogues often lack the corresponding data.

At present about 2000 minor meteor showers and associations are detected from optical and radar observations of meteors, but in the overwhelming majority of cases the parent comets of these showers have not been recognized. Hughes (1986) assumes that if a meteoroid stream has no associated comet, the most likely explanation is that the stream or the comet has moved, and that the two have been identified but not their relationship. As shown in the present paper, the lack of parent comets of many meteoroid streams may be explained not only by different changes in the stream and parent comet's orbits, but by extinction and transformation of parent comets into asteroid-like bodies. Moreover, it turns out that each comet, depending on its Earth-crossing class, might produce up to 8 meteor showers (Babadzhanov & Obrubov 1992).

4 Conclusion

The present investigation shows that each Taurid Complex asteroid is associated with at least two, but in most cases with four detected meteor showers. This is evidence for the cometary origin of these asteroids.

For many meteor showers and associations the parent bodies were identified. This reduces the number of meteor showers whose parent bodies are not known yet.

The northern and southern branches of meteor showers and their corresponding daytime (or night-time) twins were determined.

It turns out that a number of meteor showers are common to several members of the Taurid Complex asteroids. So, for example, Northern and Southern Taurids, $\zeta$-Perseids and $\beta$-Taurids, Northern and Southern May Aquarids, Northern and Southern $\chi$-Orionids, Northern and Southern Piscids and others associated with 2P/Encke (Babadzhanov et al. 1990), are also associated with the NEAs 2101 Oljato, 4341 Poseidon, 5143 Heracles, 6063 Jason, 1993 KA2, 1997 GL3, 1996 SK, 1991 TB2 and others. These results confirm the assumption (Clube & Napier 1984, 1986; Steel 1995) that the Taurid Complex consist of members of all possible sizes, including large asteroid-like bodies (extinct cometary nuclei or their fragments), which have produced meteoroid substreams and contribute to the formation of the enormous Taurid meteoroid stream which, in the Earth's atmosphere, produces more than sixty meteor showers during almost the entire year.

Acknowledgements

The author would like to express his gratitude to the referee Dr. G. B. Valsecchi for useful comments which improved the paper. The annotations of the English copy editor of the A&A is also appreciated.

References

 

Copyright ESO 2001