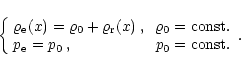A&A 373, 301-306 (2001)
DOI: 10.1051/0004-6361:20010513

Solar acoustic oscillations in a random density field

L. Nocera¹ - M. Medrek² - K. Murawski²

1 - Institute of Atomic and Molecular Physics, National Research Council, Via Moruzzi 1, 56124 Pisa, Italy
2 - Department of Environmental Physics, Technical University of Lublin, ul. Nadbystrzycka 40, 20-618 Lublin, Poland

Received 9 November 2000 / Accepted 2 April 2001

Abstract
The influence of a space-dependent random mass density field on the development of solar p-modes is investigated using analytical and numerical means. Using a perturbative approach, which is valid for a weak random field and small amplitude waves, we derive a linear dispersion relation whose solutions correspond to attenuated oscillations. The real part of the frequency of these oscillations exceeds the one of waves propagating in a medium without random density. We give an interpretation of the "unphysical'' nature of the frequency shift and of the amplitude attenuation which is similar to Landau damping. The analytical findings are compared with the results of the numerical solution of a model wave equation. We find that, for weak random fields and for wavelengths which are a few times the correlation length of the random density fluctuations, numerical results agree with the analytical theory. Two practical formulas for deriving the correlation spectrum of the random density field from observations are also given.

Key words: Sun: oscillations - turbulence - waves

   
1 Introduction

The propagation of sound waves in random media is a topic of intensive investigations (e.g. Youakim & Liu 1970; Liu 1973; Wadati 1990; Gurevich et al. 1993; Razin 1995; Ostashev 1994; Pelinovsky et al. 1998; Lazzaro et al. 2000; Murawski & Diethelm 2000; Murawski & Pelinovsky 2000). The general conclusion drawn from these investigations is that even weak random fluctuations in a medium are able to change the character of coherent waves propagating in that medium.

In particular, coupling among different modes due to a random field was considered by e.g. Youakim & Liu (1970) and Razin (1995) who found a strong coupling for small spatial scales of the random field. Additionally, Razin (1995) showed that random inhomogeneities can cause conversion of different elastic modes which propagate in a solid medium. It is interesting that such waves propagate on average faster than in a homogeneous solid medium, a conclusion which is also supported by the results by Roth et al. (1993), Shapiro et al. (1996) and by Müller & Shapiro (2000).

Nonlinear electromagnetic waves which propagate through a plasma containing random fluctuations of mass density were discussed by Liu (1973) who found that the amplitude of a coherent wave was attenuated and that the attenuation was affected by nonlinearity. The Korteweg-de Vries equation with a random forcing term was proposed by Wadati (1990) to show that Gaussian white-noise leads to damping of the soliton solution of that equation.

A method to derive a model random wave equation was presented by Gurevich et al. (1993). Pelinovsky et al. (1998) considered surface water waves which propagate along a channel with a rough bottom. They found that such waves experience attenuation and "deceleration'' due to the random field. Fast magnetosonic waves which are impulsively generated in a plasma with a random mass density were discussed by Murawski et al. (2001) who showed that, due to the random field, the localized pulses experience spatial delay and attenuation. Murawski & Pelinovsky (2000) performed analytical and numerical studies and showed that a space-dependent random flow is able to "speed up'' and enhance sound waves. Murawski & Diethelm (2000) and Lazzaro et al. (2000) indicated that a random field can generate additional modes.

Many of the above mentioned papers are based on asymptotic methods such as the mean field method of Howe (1971b). This approach is valid for weak random fields and it allows a reduction of a set of random differential equations to a dispersion relation. For a thorough discussion of the method, the reader is referred to Frisch (1968) and Konotop & Vásquez (1994).

The motivation to reconsider the classical problem of acoustic oscillations in a random medium (Howe 1971a) stems from the fact that our computer simulations suggest that oscillations with a phase speed larger than the sound speed may be observed even in the linear approximation. This fact, denoted generically as "wave acceleration'', was also reported by other authors (e.g. Collin 1969). It disagrees with Howe's (1971a) asymptotic formulas and it was generally dismissed as "unphysical'', basically on the grounds that it was counter-intuitive.

This issue assumes a particularly important relevance to Solar Physics due to the well known discrepancies between the observed frequencies of p-mode oscillations and the ones predicted by standard models (e.g. Duvall et al. 1998) and due to the turbulent state of the outer layers of the Sun where the p-modes penetrate. Besides the obvious practical implications of an investigation of the shift of p-mode frequencies, a few related questions arise: a) why does the conservative system of equations governing p-modes develop oscillations which appear to be damped in time? b) when and why does the effect of randomness result in an increase or decrease of the frequency? c) are there analogies between these and similar effects in other areas of Plasma Physics? d) what are the limitations of a purely analytical treatment?

To answer these more fundamental questions it is convenient to adopt a simple model for the propagation of p-modes (Swisdak & Zweibel 1999) in which they are basically reduced to one-dimensional acoustic waves. Furthermore, in tackling problem d) above, numerical techniques attain their significance, as already shown by Murawski (2000), Murawski & Pelinovsky (2000) and Murawski et al. (2001).

In Sect. 2 we give the governing equations of our problem and their physical justification. A linear dispersion relation is derived from these equations by means of perturbative methods which is then solved in Sect. 3. Comparison of this solution with results of numerical simulation is presented in Sect. 4. The paper is concluded by a discussion of the main results in Sect. 5.

   
2 Basic equations

The solar convection zone, in which the p-modes penetrate, is in a turbulent state which drives random mass density oscillations as shown by brightness fluctuations. Let us model this situation by a gravity-free medium with equilibrium pressure $p_{\rm e}$ and density $\varrho_{\rm e}$: let this latter have a homogeneous background component $\varrho_{0}={\rm const.}$ and a component $\varrho_{\rm r}(x)$ which is a random function of the coordinate x:

$$\left\{ \begin{array}{lr} \varrho_{\rm e} (x)=\varrho_{0}... ...m e}=p_{0}\:,&\:p_{0}={\rm const.} \\ \end{array} \right. .$$ (1)

Now consider one-dimensional motions the medium described by the hydrodynamic equations:

   

$$\varrho_{,t}+(\varrho v)_{,x}=0,$$ (2)

$$\varrho(v_{,t}+vv_{,x})=-p_{,x},$$ (3)

$$p_{,t}+(p v)_{,x}=-(\gamma-1)pv_{,x}.$$ (4)

Here time is denoted by t, $\varrho$ is the mass density, v is the x-component of the velocity, and p is the pressure. Indices with a comma denote partial derivatives, e.g. $\varrho_{,t}\equiv\partial \varrho/\partial t$.

In the absence of the random density field ( $\varrho_{\rm r}\equiv0$), sound waves would propagate in the medium whose frequency $\omega$ and wavevector k satisfy the known dispersion relation:

$$\omega^2=c_{0}^2k^2,\;c_{0}^{2}=\gamma p_{0}/\varrho_{0},$$ (5)

where $\gamma$ is the adiabatic index.

The effects of the random density field $\varrho_{\rm r}$ are now analyzed by statistical means. By a random medium we understand a family of media, each with a well-defined value of $\varrho_{\rm r}(x)$, and each with a well-defined probability of being realized in an experiment. We denote by $\langle\hskip1pt\rangle$ the ensemble average (e.g. Ishimaru 1978) over such a family.

Assuming that the density perturbations are small, we expand the fluid variables around the equilibrium of Eq. (1). Neglecting nonlinear terms leads to the linear wave equation

$$L_{\rm e}v\equiv \varrho_{\rm e}v_{,tt}-\gamma p_{0}v_{,xx}=0.$$ (6)

Now we decompose the velocity field into the coherent, or mean field (its ensemble average), and a fluctuating, or random, component, viz.

$$v(x,t)=\langle\hskip1pt v(x,t)\hskip1pt\rangle+v^{\prime}(x,t), \langle\hskip1pt v^{\prime}\hskip1pt\rangle\equiv 0.$$ (7)

The quantity $v^{\prime}$ represents the fluctuation of the actual velocity field about the coherent field in any particular experimental realization of the random density field $\varrho_{\rm r}$. The random field $v^{\prime}$ is assumed to be initially zero and it is generated solely by scattering of energy out of the coherent field by the random density inhomogeneities $\varrho_{\rm r}$.

Substituting Eq. (7) into Eq. (6), we get

 

$$L_{\rm e}(\langle\hskip1pt v\hskip1pt\rangle+{v^{\prime}}) = 0.$$ (8)

Direct ensemble averaging of Eq. (8) yields the equation which governs the evolution of the coherent field

$$L_{0}\langle\hskip1pt v\hskip1pt\rangle = -\langle\hskip1pt\varrho_{\rm r}v^{\prime}\hskip1pt\rangle_{,tt}\;,$$ (9)

where the wave operator L₀ is defined as follows:

$$L_{0}v\equiv\varrho_{0}v_{,tt}-\gamma p_{0}v_{,xx}=0 \;.$$ (10)

The equation for the fluctuating field is obtained after subtracting Eq. (9) from Eq. (8). The assumption of a weak random field approximation in the perturbative analysis (Howe 1971b) leads us to the following equation:

$$L_{0}{v}^{\prime }=-\varrho_{\rm r}\langle\hskip1pt v\hskip1pt\rangle_{,tt}.$$ (11)

Now define the space and time Fourier transforms:

$$\bar v(k,\omega)=\int_{-\infty}^{\infty} {\rm e}^{-{\rm i}kx... ...}\omega t} \langle\hskip1pt v(x,t)\hskip1pt\rangle {\rm d}t.$$ (12)

The time transform given in Eq. (12) is calculated as a causal transform (Roos 1969):

$$\bar{v}(k,\omega)=\lim_{\delta=0^{+}}\bar{v}(k,\omega+{\rm i}\delta).$$ (13)

Likewise the space Fourier transform is calculated as

$$\bar{v}(k,\omega)=\lim_{\delta=0^{+}}\bar{v}(k+{\rm i}\delta,\omega).$$ (14)

The prescriptions in Eqs. (13) and (14) ensure that, in the deterministic case ( $v^{\prime}=0$), the improper eigenfunction of the operator L₀ in Eq. (10) which is bounded as $x\rightarrow\infty$, behaves as an "outgoing wave'' as $x\rightarrow\infty$ (Friedman 1956).

Substituting Eq. (12) into Eqs. (9) and (11), we arrive at the dispersion relation

$$\omega^2-c_{0}^2k^2=\omega^4 \int_{-\infty}^{\infty} \frac{E(k-\bar k)}{\omega^2-c_{0}^2\bar k^2} {\rm d}\bar k,$$ (15)

where E(k) is the space Fourier transform of the correlation function of the normalized random density fluctuation:

$$R(\vert x_1-x_2\vert)=\langle\hskip1pt \varrho_{\rm r}(x_{1})\varrho_{\rm r}(x_{2})/\varrho_{0}^{2}\hskip1pt\rangle,$$ (16)

$$E(k)=\int_{-\infty}^{\infty}R(\vert x\vert){\rm e}^{-{\rm i}kx}{\rm d}x.$$ (17)

We assume that the function R is statistically homogeneous i.e. that its statistical properties are invariant with respect to a spatial transformation. This fact ensures that R depends on the modulus of the difference between the arguments x₁ and x₂, rather than on the arguments themselves. As a consequence its Fourier transform (the correlation spectrum E(k)) is a real and even function of its argument.

Equation (15) shows that, as a consequence of stochastic perturbations, the dispersion relation for the coherent field differs essentially from that for the unperturbed linear problem (see Eq. (5)). The consequences of this difference will be analyzed in Sect. 3.

   
3 Solution of the dispersion relation

It is convenient to introduce the following normalizations:

$$X=\frac{x}{l_{x}},\;K=kl_{x},\;\Omega=\frac{l_{x}}{c_{0}}\omega,$$ (18)

where l_x is the size of the average random density fluctuation.

Using Eq. (18) the dispersion relation in Eq. (15) takes the form

$$\Omega^{2}-K^{2}=-\Omega^{3} \int_{-\infty}^{\infty}\frac{f(K^{\prime})}{K^{\prime}-\Omega}{\rm d}K^{\prime},$$ (19)

where f is related to the correlation spectrum E as

$$f(K^{\prime})=\frac{1}{2l_{x}}[E(K-K^{\prime})+E(K+K^{\prime})].$$ (20)

Note that, like the correlation spectrum E, the function f is a real and even function of its argument. We denote Eq. (19) the Cauchy form of the dispersion relation.

The Cauchy integral is obviously a multivalued function of the complex frequency $\Omega$. However, if we assume that the function f is the restriction to the real axis of an entire function of $\Omega$, analytical continuation of the Cauchy integral is possible into a secondary or "unphysical'' sheet of the complex plane by the definition (Roos 1969)

 

$${\cal F}^{\rm L}(\zeta)= \int_{-\infty}^{\infty}\frac{f(t)}{t-\ze... ...infty}^{\infty}\frac{f(t)}{t-\zeta}{\rm d}t+2{\rm i}\pi f(\zeta), \Im{\zeta}<0.$$ (21)

Likewise, we can analytically continue the Cauchy integral from the lower half of its physical sheet into the upper half of the unphysical sheet. The upper half of the physical sheet and the lower half of the unphysical sheet are now joined; likewise we join the lower half of the physical sheet to the upper half of the unphysical sheet. In such way we form the Riemann surface on which ${\cal F}^{\rm L}$ is analytical. According to the causality principle expressed in Eq. (13) we will be interested in the Cauchy integral as calculated in the upper half of the physical sheet and in its analytical continuation: we refer to this evaluation of the dispersion relation as its principal branch.

Using Eq. (21), we write the principal branch of the dispersion equation in Eq. (19) as

$$\Omega^{2}-K^{2}=-\Omega^{3}{\cal F}^{\rm L}(\Omega).$$ (22)

In solving Eq. (22), we first consider the case in which $K\ne0$. There are no roots of the dispersion relation in Eq. (22) in the upper physical sheet of the dispersion function ${\cal F}^{\rm L}$. However such roots do exist in the unphysical Riemann sheet of ${\cal F}^{\rm L}$. To find them, it suffices to solve the dispersion relation approximately for the complex quantity $\Omega$. Indeed the difference $\Omega^{2}-K^{2}$ on the left hand side of Eq. (19) depends on the correlation spectrum E of the random density fluctuations which, in the derivation of the random dispersion relation, were assumed to be small.

Thus we introduce the following ordering:

$$\Omega=\Omega^{(0)}+\Omega^{(1)}+\dots,\; \vert\Omega^{(1)}\vert\ll\vert\Omega^{(0)}\vert.$$ (23)

Clearly, to lowest order, Eq. (22) gives the frequency of pure sound waves

$$[\Omega^{(0)}]^{2}=K^{2}\Rightarrow\Omega^{(0)}=+K>0,$$ (24)

where the positive sign for $\Omega^{(0)}$ comes from the choice of the principal branch of the analytical continuation of (K²)^1/2 (cf. Eq. (14)).

To first order, we set $\Omega=\Omega^{(0)}$ in the right hand side of Eq. (22) (already a small quantity). We remind that ${\cal F}^{\rm L}$, as defined in Eq. (21), is analytical on the real axis. Furthermore if, for any real number u, f(u) is Hölder continuous, we have the Plemelj formula (Roos 1969)

$${\cal F}^{\rm L}(u)=+{\rm i}\pi f(u)+ P\int_{-\infty}^{\infty}\frac{f(u^{\prime})} {u^{\prime}-u}{\rm d}u^{\prime},$$ (25)

where P denotes Cauchy's principal value.

Substituting Eqs. (23) and (25) into Eq. (22), we have, to ${\cal O}(\sigma^{2})$,

$$\Omega^{(1)}= -\frac{1}{2}[\Omega^{(0)}]^{2} \left[ {\rm i}\p... ...{\prime})}{u^{\prime}-\Omega^{(0)}} {\rm d}u^{\prime}\right].$$ (26)

Since $\Omega^{(0)}$ is the argument of a causal Fourier transform, as prescribed in Eq. (13), the real and imaginary parts of Eq. (26) may be rewritten as (Roos 1969)

 

$$\Re{\Omega^{(1)}}= \frac{1}{2}K^{2}\int_{0}^{\infty}F(X^{\prime})\sin(KX^{\prime}){\rm d}X^{\prime}$$ (27)

and

$$\Im{\Omega^{(1)}}= -\frac{1}{4}[\Omega^{(0)}]^{2}f(\Omega^{(0)})=-\frac{1}{4}K^{2}f(K)<0,$$ (28)

where F(X) denotes the inverse Fourier transform of f. Using Eqs. (16) and (20) and the prescription in Eq. (14), we have

 

$$F(X)=\frac{1}{2\pi}\int_{-\infty}^{\infty}f(k^{\prime}) \exp({\rm i}k^{\prime}x) {\rm d}k^{\prime} = R(X)\cos(KX),$$ (29)

a result which casts Eq. (27) in the form

$$\Re{\Omega^{(1)}}=\frac{1}{2}K^{2}\int_{0}^{\infty}R(X^{\prime}) \sin(2KX^{\prime}){\rm d}X^{\prime}.$$ (30)

On the other hand, substituting Eq. (20) into Eq. (28) we find

$$\Im{\Omega^{(1)}}=-\frac{1}{4}K^{2}[E(0)+E(2K)]<0.$$ (31)

When K=0, in Eq. (19) we find $\Omega=0$, which is the natural limit of the solutions in Eqs. (30) and (31) as $K\rightarrow0$.

Clearly, since, as pointed out in Sect. 2, the correlation spectrum is real, if $\Omega$ solves Eq. (19) then $-\Omega$ and $\pm\Omega^{\ast}$ also do. However $-\Omega$ and $\Omega^{\ast}$ lie in the upper half of the unphysical Riemann sheet, whereas $-\Omega^{\ast}$ lies in the lower half of the physical sheet. None of these roots contribute to the inversion of the causal Fourier transform.

Now we specialize to the case of a Gaussian correlation spectrum of the random fluctuations:

 

$$R(X)= \frac{\sigma^{2}}{2\pi^{1/2}}\exp(-X^{2}/4),\quad E(K)=\sigma^{2}l_{x}\exp(-K^{2}),$$ (32)

where $\sigma\ll1$ takes into account the supposed smallness of the random fluctuations.

Substituting Eqs. (32) and (20) into Eq. (19), we find for the principal branch of the dispersion relation

$$\Omega^{2}-K^{2}=-\frac{\sigma^{2}\Omega^{3}}{2\pi^{1/2}} [Z(\Omega-K)+Z(\Omega+K)],\;\Im{\Omega}>0,$$ (33)

where

$$Z(\zeta)=\frac{1}{\pi^{1/2}} \int_{-\infty}^{\infty}\frac{\exp(-t^{2})}{t-\zeta}{\rm d}t,\; \Im{\zeta}>0$$ (34)

is the plasma dispersion function (Fried & Conte 1961).

Substituting Eq. (32) into Eqs. (30) and (31) and using the well known relation between the sine integral of a Gaussian distribution and Dawson's integral (Gautschi 1972) we find

$$\Re{\Omega^{(1)}}= \frac{\sigma^{2}}{2\pi^{1/2}}K^{2} \exp(-4K^{2}) \int_{0}^{2K}\exp(t^{2}){\rm d}t$$ (35)

and

$$\Im{\Omega^{(1)}}=-\frac{\sigma^{2}}{4}K^{2}[1+\exp(-4K^{2})]<0,$$ (36)

a result which we also retrieved by a direct approximate solution of Eq. (33) for $\sigma\ll1$.

The real and imaginary parts of $\Omega^{(1)}$ for a weakly ( $\sigma =0.1$) random medium with Gaussian random fluctuations are plotted in Fig. 1 as functions of the normalized wavenumber.

	Figure 1: The correction to the frequency of sound waves: $\Re \Omega ^{(1)}$ (solid curve) and $-\Im \Omega ^{(1)}$ (dashed curve). Superimposed are the values of the correction coming from numerical simulations at $\sigma =0.1$ ($\diamond$).
Open with DEXTER

   
4 Numerical solutions of the wave equation

The numerical simulations of the linear wave equation in Eq. (6) were performed by the clawpack code (LeVeque 1997), which is a packet of Fortran routines for solving hyperbolic equations. The code utilizes the Godunov-type method (e.g. Murawski & Tanaka 1997, and references therein). This method is specially designed to adequately represent shocks and complex flows which are associated with random fluctuations.

The random mass density field is represented as follows (Karweit & Blanc-Benon 1991; Karweit et al. 1995; Chevret et al. 1996):

 

$$\varrho_{\rm r}(x)=\rho_{0}\frac{2^{1/2}}{(\pi l_{x})^{1/2}} \sum... ...n})]^{1/2}\cos(k_{n}x +\phi_{n}),\quad k_{n}=\frac{2n\pi}{l_{x}},\;n=1,\dots,N.$$ (37)

Here the phases $\phi_{n}$ are assumed to be random and they are chosen by the random number generator ran1 (Press et al. 1992). We note that, as $N\rightarrow\infty$, substitution of Eq. (37) into the right hand side of Eq. (16) indeed gives a homogeneous correlation R(|x₁-x₂|) and its spectrum of Eq. (17). According to Eq. (37) the random density field changes over spatial sections of length l_x (the size of an average random density fluctuation) and its spatial average is zero. Such random field mimics solar granulation (Sánchez Cuberes et al. 2000).

In our simulations periodic boundary conditions are imposed. At t=0pressure and density are set to their static equilibrium values in Eq. (1); velocity is a Gaussian packet centered at x=Nl_x/2and, since the problem being simulated is linear, its amplitude is arbitrarily set to c₀.

In this framework Eq. (6) is solved over the interval $0\le x\le82 l_{x}$ and for times $0\le t\le131l_{x}/c_{0}$. The wave distributions v(x,t) output by the simulation are first ensemble-averaged over 120 realization of the random density field $\varrho_{\rm r}$; then the averaged distribution is spectrally analyzed in space and time by means of a Fast Fourier Transform. We made sure that averaging over a larger number of realizations gave no improvement in the results.

In Fig. 1 the frequency of maximum spectral concentration is compared, for each wavenumber, with the real part of the frequency given by the approximate analytical approach of Sect. 3: the span of the error bars equals the variance of the frequency shift over the random density statistical ensemble. The results of this comparison are presented in Sect. 5.

   
5 Conclusions

In this work we studied the effect of random density on the oscillations of solar p-modes approximated as purely acoustic oscillations.

First we attempt a perturbative solution of the linear dispersion relation in the assumption that the random density fluctuations are weak. The solution can be written by combining Eqs. (23), (35) and (36) in the following approximate formula, which holds for a Gaussian profile of the correlation function of the random density fluctuations

 

$$\Omega K+\frac{\sigma^{2}}{4\pi^{1/2}}K^{2} \left\{2\exp(-4K^{2})\int_{0}^{2K}\exp(t^{2}){\rm d}t -{\rm i}\pi^{1/2}[1+\exp(-4K^{2})] \right\}\cdot$$ (38)

The oscillation having the frequency given in Eq. (38) is always attenuated in time ( $\Im\Omega<0$) and its phase speed always exceeds the sound speed (K in normalized units). While the former fact is in agreement with Howe's (1971a) general stability criterion established for the oscillations of a string with random density distribution, the latter is at variance with his results, because Howe (1971a) finds a decrease of the phase speed. The reason is that Howe (1971a) adopts a statistical model for the random part of the wave operator which is different from ours. When this is taken into account, Howe's (1971a) results agree with ours, but for terms which are ${\cal O}(\sigma^{4})$. In fact, our dispersion relation is in accordance with Howe's second paper (1971b).

It is thus important to note how two different and yet both plausible models of the random component of the wave operator lead to conflicting results. In this perspective, direct numerical simulations acquire an important role as indeed shown by Murawski (2000), Murawski et al. (2001) and Murawski & Pelinovsky (2000).

Since the oscillation occurring at the frequency reported in Eq. (38) is not a genuine eigenfunction of the wave operator (see below), its numerical reproduction is not an easy task. Nevertheless we were able to observe frequencies which agree with the theoretical prediction, within statistical error (Fig. 1). We surmise that, amongst the several sources of discrepancy between the numerical results and analytical predictions, a most important one is the breakdown of the statistical properties of the random wave operator which are necessary for the derivation of the random dispersion relation in Eq. (15) (see the review by Mysak 1978).

One further result of our investigation can be summarized as an answer to the question: "How can a solution to the conservative system of Eqs. (9) and (11) be attenuated in time?'' Our interpretation of this apparent paradox is that the root of the dispersion function which lies in the lower half of its unphysical Riemann sheet has no associated eigenfunction; the damped oscillation related to this root is rather similar to the "virtual modes'' found in Landau damping (Sedlácek & Nocera 1992), in inhomogeneous plasmas (Sedlácek 1971, 1994) and in the inhomogeneous vibrating string (Sedlácek et al. 1986): they can be aptly named "random virtual modes''.

In conclusion we reach the following results:

1.

The dispersion function of a sound wave propagating in a weakly random medium has a root with a negative imaginary part: the oscillation associated to this root is attenuated in time;

2.

 The real part of this root exceeds the sound frequency;

3.

  There is no eigenfunction associated with this root, since it lies in the unphysical Riemann sheet of the dispersion function;

4.

The spectral density of the fluctuations of a random medium is either given directly by the observed imaginary part of the root (i.e. by the observed attenuation of the associated oscillation), according to Eq. (31) or by the inverse sine transform of the observed real part of the root (i.e. by the observed phase speed of the oscillation), according to Eq. (30). Calculating this transform we have:

$$R(X)=\frac{8}{\pi}\int_{0}^{\infty}\frac{\Re\Omega^{(1)}(K^{\... ...e})} {K^{\prime 2}}\sin\frac{K^{\prime}X}{2}{\rm d}K^{\prime}.$$ (39)

Since high quality data are nowadays available on the frequency shift of solar p-modes, and since they are more reliable than data on the attenuation rate, Eq. (39) rather than Eq. (31) may be used to infer the correlation spectrum of the density fluctuations of the solar convection zone.

Conclusion ii is of great relevance to Solar global oscillations: it suggests that the random state of the Solar atmosphere may increase the frequency of p-modes. We mention that, in the area of Earth's seismology, positive frequency shifts of elastic waves were found by Roth et al. (1993), Shapiro et al. (1996) and by Müller & Shapiro (2000).

One last important consequence of conclusion iii) is that terms like "wave acceleration'' or "deceleration'' can be misleading: indeed the oscillation associated with the virtual frequency is not an eigenmode of the system of Eqs. (9) and (11). Rather it is a superposition of these eigenmodes. The nature, distribution and possible completeness of these eigenfunctions will be dealt with elsewhere.

Acknowledgements

We thank Prof. E. N. Pelinovsky and Dr. V. M. Nakariakov for their useful comments. We acknowledge financial support by the Polish State Committee for Scientific Research under grant No. PO3D 017 17 and by the Italian National Research Council. The numerical simulations were performed at the Department of Complex Systems, Institute of Physics, UMCS Lublin and at the Poznan Supercomputing Centre.

References

 
• Chevret, P., Blanc-Benon, Ph., & Juvé, D. 1996, J. Acoust. Soc. Am., 100, 3587 In the text NASA ADS  
• Collin, R. E. 1969, Radio Sci., 4, 279 In the text  
• Duvall Jr., T. L., Kosovichev, A. G., & Murawski, K. 1998, ApJ, 505, L55 In the text NASA ADS  
• Fried, B. D., & Conte, S. D. 1961, The plasma dispersion function (New York: Academic Press) In the text  
• Friedman, B. 1956, Principles and techniques of applied Mathematics (New York: Wiley) In the text  
• Frisch, U. 1968, Wave propagation in random media, in Probabilistic methods in applied Mathematics, ed. A. T. Bharucha-Reid (New York: Academic Press), vol. 1, 75 In the text  
• Gautschi, W. 1972, Error functions and Fresnel integrals, in Handbook of mathematical functions, ed. M. Abramowitz, & I. A. Stegun (London: Dover), 295 In the text  
• Gurevich, B., Jeffrey, A., & Pelinovsky, E. 1993, Wave Motion, 17, 287 In the text  
• Howe, M. S. 1971a, J. Fluid Mech., 45, 769 In the text  
• Howe, M. S. 1971b, J. Fluid Mech., 45, 785 In the text  
• Ishimaru, A. 1978, Wave propagation and scattering in random media (New York: Academic Press) In the text  
• Karweit, M., & Blanc-Benon, Ph. 1995, J. Comp. Acoust., 3, 203 In the text  
• Karweit, M., Blanc-Benon, Ph., Juvé, D., & Comte-Bellot, G. 1991, J. Acoust. Soc. Am., 89, 52 In the text NASA ADS  
• Konotop, V. V., & Vásquez, L. 1994, Nonlinear random waves (London: World Scientific) In the text  
• Lazzaro, E., Lontano, M., & Ryutov, D. D. 2000, Phys. Rev. E, 61, 3069 In the text NASA ADS  
• LeVeque, R. J. 1997, J. Comp. Phys., 131, 327 In the text  
• Liu, C. H. 1973, J. Plasma Phys., 9, 443 In the text  
• Müller, T., & Shapiro, S. A. 2000, Geophys. J. Int., 144, 83. In the text  
• Murawski, K. 2000, Acta Astron., 50, 269 In the text NASA ADS  
• Murawski, K., & Diethelm, K. 2000, A&A, 358, 753 In the text NASA ADS  
• Murawski, K., Nakariakov, V. M., & Pelinovsky, E. N. 2001, A&A, 366, 306 In the text NASA ADS  
• Murawski, K., & Pelinovsky, E. N. 2000, A&A, 359, 759 In the text NASA ADS  
• Murawski, K., & Tanaka, T. 1997, Astrophys. Space Sci., 254, 187 In the text  
• Mysak, L. A. 1978, Rev. Geophys. Space Phys., 16, 233 In the text  
• Ostashev, V. E. 1994, Waves in Random Media, 4, 403 In the text NASA ADS  
• Pelinovsky, E., Razin, A. V., & Sasarova, E. V. 1998, Waves in Random Media, 8, 255 In the text NASA ADS  
• Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in Fortran. The art of scientific computing (Cambridge: Cambridge University Press) In the text  
• Razin, A. V. 1995, Waves in Random Media, 5, 137 In the text NASA ADS  
• Roos, B. W. 1969, Analytic functions and distributions in Physics and Engineering (New York: Wiley) In the text  
• Roth, M., Müller, G., & Sneider, R. 1993, Geophys. J. Int., 115, 552 In the text  
• Sánchez Cuberes, M., Bonet, J. A., Vázquez, M., & Wittmann, A. D. 2000, ApJ, 538, 940 In the text NASA ADS  
• Sedlácek, Z. 1971, J. Plasma Phys., 5, 239 In the text  
• Sedlácek, Z., & Nocera, L. 1992, J. Plasma Phys., 48, 367 In the text  
• Sedlácek, Z., Adam, J., & Roberts, B. 1986, Initial-Value Problem for the 1-D Wave equation in a Inhomogeneous Medium, Tech. Rep. IPPCZ-268, Institute of Plasma Physics, Prague (CZ) In the text  
• Sedlácek, Z. 1995, in AIP Conf. Proc. 345, Proceedings of the 1994 ICPP, ed. P. Sakanaka, & M. Tendler (Woodbury, New York: AIP Press), 119  
• Shapiro, S. A., Schwarz, R., & Gold, N. 1996, Geoph. J. Int., 127, 783 In the text  
• Swisdak, M., & Zweibel, E. 1999, ApJ, 512, 442 In the text NASA ADS  
• Wadati, M. 1990, J. Phys. Soc. Jpn., 59, 4201 In the text NASA ADS  
• Youakim, M., & Liu, C. H. 1970, Radio Sci., 5, 757 In the text