The last section discussed the flux variations of Crab pulsar over time scales of hours and days. The current section discusses flux variations from period to period.
Figure 3 shows the so
called X-ray fluctuation spectrum of Crab pulsar. At each of the 33 samples
(phases) of the integrated profile of Fig. 1, a time series was formed
comprising of the X-ray flux as a function of the period number in the data file.
This was Fourier transformed in arrays of length 128 ![]() 1024 periods. The
data were centered in the array and zero padded, and then a Hamming window was
applied. To remove long term variations, the data in blocks of 32768 periods were
normalized with the mean value of this block (see Ritchings 1976 and
Vivekanand & Joshi 1997 for details). Fourteen data files were chosen that
had at least 75000 periods each, totalling to 1347028 periods.
Figure 3 shows the power spectrum averaged over the 33 spectra,
after normalizing each spectrum with the variance of its time series.
A polynomial of the form
1024 periods. The
data were centered in the array and zero padded, and then a Hamming window was
applied. To remove long term variations, the data in blocks of 32768 periods were
normalized with the mean value of this block (see Ritchings 1976 and
Vivekanand & Joshi 1997 for details). Fourteen data files were chosen that
had at least 75000 periods each, totalling to 1347028 periods.
Figure 3 shows the power spectrum averaged over the 33 spectra,
after normalizing each spectrum with the variance of its time series.
A polynomial of the form
| y = a0 + a1 x + a2 x2 + a3 x3 | (1) |
The upper limit to any possible weak and broad spectral feature that might be
hidden in the data can be computed to be ![]() 0.06% of the total power in
the spectrum. Therefore Fig. 3 is consistent with the Crab pulsar having
no spectral feature in its pulse to pulse X-ray flux variations.
0.06% of the total power in
the spectrum. Therefore Fig. 3 is consistent with the Crab pulsar having
no spectral feature in its pulse to pulse X-ray flux variations.
The radio flux of rotation powered pulsars varies significantly from pulse to
pulse; this could be due to intrinsic flux variation of the sub pulse, as
well as random position of the sub pulse within the on-pulse window (here one
is ignoring the flux variations due to propagation in the interstellar medium).
This is characterized by the so called modulation index ![]() ,
defined as
,
defined as
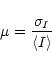 |
(2) |
Figure 4 shows the square of ![]() ,
which is the natural quantity
to average, for all 1868112 periods. First, the mean
,
which is the natural quantity
to average, for all 1868112 periods. First, the mean
![]() and the
variance
and the
variance ![]() are computed at each sample in the integrated profile (
are computed at each sample in the integrated profile (
![]() is plotted in Fig. 1 and the top panel of Fig. 4). Now
is plotted in Fig. 1 and the top panel of Fig. 4). Now ![]() has contribution from two sources:
has contribution from two sources:
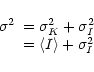 |
(3) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms10443.fg4}\end{figure}](/articles/aa/full/2001/25/aa10443/Timg27.gif) |
Figure 4:
Square of the estimated modulation index ( |
The average value of ![]() in Fig. 4 is
in Fig. 4 is
![]() ,
which
is is consistent with zero as expected. The
,
which
is is consistent with zero as expected. The ![]() of
of ![]() of Fig. 4 with respect to the expected value of 0.0 is 76.3 for 33 degrees of
freedom. Removing sample number 10 reduces the
of Fig. 4 with respect to the expected value of 0.0 is 76.3 for 33 degrees of
freedom. Removing sample number 10 reduces the ![]() to 57.0, and further
removing sample number 11 reduces it to 48.7, which is just 2.25 standard
deviations away from the expected value of 31.0. Therefore to the zeroth order
of accuracy it is reasonable to assume that
to 57.0, and further
removing sample number 11 reduces it to 48.7, which is just 2.25 standard
deviations away from the expected value of 31.0. Therefore to the zeroth order
of accuracy it is reasonable to assume that ![]() is the same (i.e., 0.0) for
all samples in the integrated profile. Its standard deviation is 0.0024 in the
on-pulse window; then the standard deviation of
is the same (i.e., 0.0) for
all samples in the integrated profile. Its standard deviation is 0.0024 in the
on-pulse window; then the standard deviation of ![]() can be estimated as
can be estimated as
![]() % (by simple algebra). Thus the rms X-ray flux
variation at any phase in the on-pulse window of the integrated profile of Crab
pulsar is
% (by simple algebra). Thus the rms X-ray flux
variation at any phase in the on-pulse window of the integrated profile of Crab
pulsar is ![]() 3.5% of its mean value. Then the rms variation of the total
on-pulse X-ray flux of the Crab pulsar will be
3.5% of its mean value. Then the rms variation of the total
on-pulse X-ray flux of the Crab pulsar will be ![]() 3.5/
3.5/
![]() %. A similar calculation for the entire integrated profile gives
%. A similar calculation for the entire integrated profile gives
![]() %, which is essentially the same
result. This is a much tighter limit than the
%, which is essentially the same
result. This is a much tighter limit than the ![]() 7% quoted by Patt et al.
(1999). These authors used totally 105000 periods and a different
method of analysis, on account of which their result might be dominated by
photon noise. The result of this section should ideally reflect the actual
X-ray intensity variations of Crab pulsar (wave noise), that contain
information about the physics of the X-ray emission mechanism.
7% quoted by Patt et al.
(1999). These authors used totally 105000 periods and a different
method of analysis, on account of which their result might be dominated by
photon noise. The result of this section should ideally reflect the actual
X-ray intensity variations of Crab pulsar (wave noise), that contain
information about the physics of the X-ray emission mechanism.
To the next order of accuracy ![]() appears to be correlated with the shape
of the integrated profile; both the lower panel of Fig. 4 as
well as the
appears to be correlated with the shape
of the integrated profile; both the lower panel of Fig. 4 as
well as the ![]() discussed above point to this. The
discussed above point to this. The ![]() at the phase
of the second peak of the integrated profile also appears to be enhanced. The
on-pulse and off-pulse
at the phase
of the second peak of the integrated profile also appears to be enhanced. The
on-pulse and off-pulse ![]() are 69.0 and 7.3, for 26 and 7 degrees of
freedom respectively; the former is 6 standard deviations away from the
expected value, which is quite high. However more data, or better analysis, is
needed to confirm this with good statistical significance.
are 69.0 and 7.3, for 26 and 7 degrees of
freedom respectively; the former is 6 standard deviations away from the
expected value, which is quite high. However more data, or better analysis, is
needed to confirm this with good statistical significance.
Copyright ESO 2001