Integrating the light of the galaxy from the
center to the outskirts the growth curve approches an asymptotic value. This
total intensity, ![]() ,
is related to the total apparent magnitude,
,
is related to the total apparent magnitude, ![]() ,
through:
,
through:
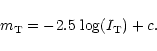 |
(1) |
The model-free effective radius can be read at half of the total growth curve
intensity. As the integration has been done with elliptical apertures, this
radius refers to an equivalent radius,
![]() ,
where a and b are the
major and minor axis of the galaxy, respectively. Together with the total
apparent magnitude this yields the effective surface brightness by:
,
where a and b are the
major and minor axis of the galaxy, respectively. Together with the total
apparent magnitude this yields the effective surface brightness by:
![\begin{displaymath}\langle\mu\rangle_{\rm eff}\,[{\rm mag}/\ifmmode\hbox{\rlap{$...
...$ }]=M+5\,\log(r_{\rm eff}[\hbox{$^{\prime\prime}$ }])
+1.995.
\end{displaymath}](/articles/aa/full/2001/25/aa10318/img41.gif) |
(2) |
Column (2): name of the galaxy;
Column (3): total apparent magnitude in the B band;
Column (4): galactic absorption in B using the extinction maps of Schlegel et al. (1998);
Columns (5) and (6): total apparent magnitude in the V and R band, respectively;
Columns (7), (8) and (9): effective radius in B, V and R, respectively, in arcseconds;
Columns (10), (11) and (12): effective surface brightnesses in B, Vand R, respectively, in mag/
![]() ;
;
Column (13): total B-V colour index;
Column (14): total B-R colour index.
Doubtful values due to low-quality observations (frames hampered with
reflected light or with a bright background due to moon light)
are flagged with a colon. For the error assessment (see Sect. 4.4) these cases
have not been taken into account.
Surface brightness profiles were obtained by differentiating the growth curves
with respect to equivalent radius. The resulting profiles, with a resolution,
or bin size of 2
![]() ,
are shown in Fig. 2. The profiles are traced down to the level where the uncertainties owing to
the fluctuations in the sky level on the profile become dominant, which is at
,
are shown in Fig. 2. The profiles are traced down to the level where the uncertainties owing to
the fluctuations in the sky level on the profile become dominant, which is at
![]()
![]() in B,
in B, ![]()
![]() in
V, and
in
V, and ![]()
![]() in R.
in R.
Radial intensity profiles can be fitted by different models. The exponential
model (De Vaucouleurs 1959; Binggeli & Cameron 1993) works very well for
dwarf elliptical galaxies, because of their steady decrease of brightness from
the center to the outer parts. Owing to their shape and, if present, bright
star forming regions, the brightness of irregular galaxies is not so uniform,
but parts of almost all intensity profiles of the irregulars considered here
exhibit an exponential behaviour. The exponential intensity profile can be
written as
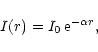 |
(3) |
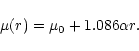 |
(4) |
Using a standard least squares fitting procedure, we determined a best-fitting exponential within that part of the galaxy profile, usually in a medium radius range, that is looking reasonably straight (exponential). This fitting range was defined for each galaxy individually (but is the same for each colour band). However, some noisy profiles (e.g. PGC 17716, A0554+07, DDO 64) were hard to fit and the definition of the fitting region was not obvious. In these cases we used rather large radius ranges for the fits to compensate for the fluctuations. The best-fitting exponential parameters are listed in Table 3. The best-fitting exponential profiles are plotted as dashed lines along with the observed profiles in Fig. 2, where also the fitting range is marked by ticks along the upper axis.
The deviation of the observed profile from a pure exponential law is expressed
by the difference ![]() between the total magnitude of an exponential
intensity law given by
between the total magnitude of an exponential
intensity law given by
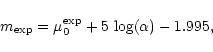 |
(5) |
The columns of Table 3 are as follows (again all values being corrected for galactic extinction based on Schlegel et al. 1998):
Column (2): name of the galaxy;
Columns (3), (4) and (5): extrapolated central surface brightness
according to equation (4) in
![]() ,
,
![]() ,
and
,
and
![]() ,
respectively;
,
respectively;
Columns (6), (7) and (8): exponential scale length in
arcsecs
![]() ,
in B, V, and R, respectively;
,
in B, V, and R, respectively;
Columns (9), (10) and (11): difference between the total magnitude as derived from the exponential model and the true total magnitude in B, Vand R, respectively.
As expected from a sample of late-type galaxies, the median integrated
colour, with
(B-V) = 0.52, is rather blue.
However, the scattering is considerable (see Table 2).
Four galaxies (UGC 685, UGC 2905, PGC
17716 and A0554+07) appear extremly blue (
![]() ).
While UGC685 might indeed be a blue dwarf compact (BCD, see Fig. 1),
the blue colour of the others is probably not real:
all three galaxies lie close to the zone of avoidance and have therefore
high corrections
for galactic extinction (
).
While UGC685 might indeed be a blue dwarf compact (BCD, see Fig. 1),
the blue colour of the others is probably not real:
all three galaxies lie close to the zone of avoidance and have therefore
high corrections
for galactic extinction (
![]() ,
see Table 2).
Any slight uncertainty in the correction with respect to colour will produce
a large error in the "true'' colour index.
On the other hand, there are two very red galaxies: UGC 1281 with
(B-V) = 1.10, and UGC 2689 with
(B-V) = 1.02. UGC 1281 is seen perfectly
edge-on, and so its red colour is clearly caused by internal dust
absorption, while UGC 2689 is a probable background S0 (see notes on
individual galaxies) and therefore quite plausibly red.
,
see Table 2).
Any slight uncertainty in the correction with respect to colour will produce
a large error in the "true'' colour index.
On the other hand, there are two very red galaxies: UGC 1281 with
(B-V) = 1.10, and UGC 2689 with
(B-V) = 1.02. UGC 1281 is seen perfectly
edge-on, and so its red colour is clearly caused by internal dust
absorption, while UGC 2689 is a probable background S0 (see notes on
individual galaxies) and therefore quite plausibly red.
B-R colour profiles, along with the differences of the B and R exponential fits, are shown in Fig. 3. Most colour profiles, where the noise is small enough to allow any significant gradient to be seen, follow the trend of an increasing B-R with increasing galactocentric radius, i.e. a blueing inwards. This is the stellar population gradient known and expected for dwarf irregulars: regions of active or recent star formation, and therefore of blue colour, are concentrated to the inner part of the galaxies. There are two notable, and plausible, exceptions showing the inverse trend, i.e. a reddening inwards (see Fig. 3): UGC 2689, the suspected background S0, and UGC 3303, a large spiral in the zone of avoidance.
![\begin{figure}
{
\includegraphics[width=5.2cm,clip]{10318f5.ps}\hspace*{4mm}
\includegraphics[width=5.2cm,clip]{10318f6.ps} }
\end{figure}](/articles/aa/full/2001/25/aa10318/Timg58.gif) |
Figure 4: Comparison of our data with data from the RC3: our published data vs. RC3 (left panel); data from our "uncleaned'' frames vs. RC3 (right panel). |
The photometric zero point determination represents the greatest source of
error on the global parameters in this work. Other uncertainties, stemming
from the flat-fielding and background subtraction etc., were mentioned
in Sect. 3.
Instead of trying to assess the overall error from all these single error
sources, which seems impossible anyway, it is easier and more reliable to
compare our results with data from the literature.
Ten galaxies of our sample can be compared to RC3 data (Third reference
catalogue of bright galaxies, deVaucouleurs et al. 1991). Figure 4 shows the result of this comparison for total magnitudes (where this time
no correction for galactic extinction was applied). A first plain
comparison of our magnitudes with RC3 magnitudes is disappointing:
deVaucouleurs et al.'s magnitudes are systematically brighter by up to one
magnitude (as evidenced in the left panel of Fig. 4). However, if we take
the magnitudes derived from our uncleaned images and compare them
with RC3, the agreement is quite satisfactory, with a standard deviation in
magnitude of only
![]() mag (shown in the right panel
of Fig. 4). This likely means that the RC3 magnitudes, at least for these
galaxies, are based on images that were not cleaned from disturbing foreground
stars. In fact, they are based on aperture photometry where
the contamination by stars is unavoidable and inherently large for faint
and diffuse dwarf galaxies.
mag (shown in the right panel
of Fig. 4). This likely means that the RC3 magnitudes, at least for these
galaxies, are based on images that were not cleaned from disturbing foreground
stars. In fact, they are based on aperture photometry where
the contamination by stars is unavoidable and inherently large for faint
and diffuse dwarf galaxies.
If we distribute the contribution to the above-mentioned ![]() evenly between our photometry and deVaucouleurs et al.'s, had they
properly accounted for foreground contamination, we arrive at a global
(one sigma) uncertainty of
evenly between our photometry and deVaucouleurs et al.'s, had they
properly accounted for foreground contamination, we arrive at a global
(one sigma) uncertainty of
![]() (for us and them), applying also
to surface brightness. This is indeed the typical photometric accuracy achieved
in our previous papers.
(for us and them), applying also
to surface brightness. This is indeed the typical photometric accuracy achieved
in our previous papers.
Previous photometry for a number of our dwarfs is provided also by some
other studies based on CCD imaging, notably by Makarova et al. (1998).
A comparison
with our ![]() and B-V values often shows large differences. However, since
no details on how the photometry was done is given in that and other papers,
we cannot judge the reliability of the comparison. More details
are given in the notes on individual galaxies below.
and B-V values often shows large differences. However, since
no details on how the photometry was done is given in that and other papers,
we cannot judge the reliability of the comparison. More details
are given in the notes on individual galaxies below.
As far as the typical uncertainty of the model parameters is concerned, given the amount of subjective judgement in choosing the fitting range etc., this is impossible to assess without comparison with independent data from the literature.
Copyright ESO 2001