A&A 372, 945-951 (2001)
DOI: 10.1051/0004-6361:20010549
S. Katajainen1 - F. Scaltriti3,![]() - V. Piirola1
- H. J. Lehto1,2
- E. Anderlucci3,
- V. Piirola1
- H. J. Lehto1,2
- E. Anderlucci3,![]()
1 - Tuorla Observatory, Väisäläntie 20, 21500 Piikkiö,
Finland
2 - Department of Physics, 21400, Turku University, Finland
3 - Osservatorio Astronomico di Torino, 10025 Pino Torinese, Italy
Received 15 December 1999 / Accepted 9 April 2001
Abstract
We present results of the first simultaneous UBVRI-photopolarimetric
observations of the long period (4.6 hrs) AM Herculis system RX
J0203.8+2959. The observed circular polarization shows both negative
and positive polarization, from ![]() to
to ![]() in the B-band.
A rise of the positive
circular polarization is observed near the same orbital phase as
a change in HR1 hardness ratio from soft to hard in the earlier ROSAT X-ray
observations.
The negative circular polarization is observed
near orbital phases where a soft X-ray
component was seen in ROSAT observations. Linear polarization
pulses coincide with the sign reversal of the circular polarization,
and coincide also with
changes in the X-ray hardness ratio in earlier ROSAT data.
The observed polarization variations favour two-pole
accretion. Least square fits to the position angle curves during
linear pulses suggest high orbital inclination,
estimates from
in the B-band.
A rise of the positive
circular polarization is observed near the same orbital phase as
a change in HR1 hardness ratio from soft to hard in the earlier ROSAT X-ray
observations.
The negative circular polarization is observed
near orbital phases where a soft X-ray
component was seen in ROSAT observations. Linear polarization
pulses coincide with the sign reversal of the circular polarization,
and coincide also with
changes in the X-ray hardness ratio in earlier ROSAT data.
The observed polarization variations favour two-pole
accretion. Least square fits to the position angle curves during
linear pulses suggest high orbital inclination,
estimates from
![]() to
to ![]() = 73
= 73
![]() .
The UBVRI-lightcurves show smooth variations with a broad maximum and
minimum. RX J0203.8+2959 was in intermediate accretion state during
observations in November 1998 (
V= 15.7 - 16.7).
The observed flux and circular polarization variations are
reproduced by using constant temperature cyclotron emission models
having two accretion regions and with parameters:
.
The UBVRI-lightcurves show smooth variations with a broad maximum and
minimum. RX J0203.8+2959 was in intermediate accretion state during
observations in November 1998 (
V= 15.7 - 16.7).
The observed flux and circular polarization variations are
reproduced by using constant temperature cyclotron emission models
having two accretion regions and with parameters:
![]() ,
,
![]() and colatitude
and colatitude
![]() for the negative pole, and
for the negative pole, and
![]() ,
,
![]() and
and
![]() for the
main accreting positive pole, and assuming orbital inclination
for the
main accreting positive pole, and assuming orbital inclination
![]() .
.
Key words: stars: magnetic fields - novae, cataclysmic variables - stars: individual: RX J0203.8+2959 - accretion, accretion disks - polarization
The object RX J0203.8+2959 belongs to a sample of very soft X-ray
sources in the ROSAT All-Sky Survey (RASS). It
was preliminarily identified as an AM Herculis star by Beuermann &
Thomas (1993). Schwarz et al. (1998)
confirmed that RX J0203.8+2959 has properties typical for an
AM Herculis star (a subclass of cataclysmic variables, CVs), with an orbital
period of 4.6 hrs and brightness variations between
V=18-15.5.
Schwarz et al. (1998)
detected cyclotron emission harmonics
and estimated the magnetic field strength
![]() MG.
The orbital period of RX J0203.8+2959 is one of the longest
among all the AM Herculis stars; only two systems, V1309 Ori
(7.98 hrs) and V895 Cen (4.76 hrs) have
longer orbital periods. Most of the AM Herculis stars have periods
below the "period gap'', which occurs
between 2 and 3 hours.
Being one of the longest period AM Herculis systems,
RX J0203.8+2959 is an important object to study the
synchronization process between the primary and the secondary
and the accretion mechanism in the long period (
MG.
The orbital period of RX J0203.8+2959 is one of the longest
among all the AM Herculis stars; only two systems, V1309 Ori
(7.98 hrs) and V895 Cen (4.76 hrs) have
longer orbital periods. Most of the AM Herculis stars have periods
below the "period gap'', which occurs
between 2 and 3 hours.
Being one of the longest period AM Herculis systems,
RX J0203.8+2959 is an important object to study the
synchronization process between the primary and the secondary
and the accretion mechanism in the long period (
![]() hrs)
AM Herculis stars.
hrs)
AM Herculis stars.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2666f1.ps}\end{figure}](/articles/aa/full/2001/24/aah2666/Timg23.gif) |
Figure 1: Simultaneous (UBVRI) light curves of RX J0203.8+2959 between nights 13/14 and 19/20 November, 1998. Each point presents a single photometric measurement. |
| Open with DEXTER | |
Our observations were carried out during 7 nights from 13/14 to
19/20 November, 1998, (JD 2451131 - 2451137) with the
Turin-photopolarimeter at the 2.15 metre telescope of
Complejo Astronomico El Leoncito, CASLEO in Argentina
(latitude
![]() ).
The multichannel double image
chopping instrument, with dichroic filters to split the light
into five spectral regions for photomultipliers, follows the design
principles of Piirola
(1973, 1988).
It provides in the U-, B-, V-, R- and I-bands simultaneous circular
and linear polarimetry as well as photometry
in
).
The multichannel double image
chopping instrument, with dichroic filters to split the light
into five spectral regions for photomultipliers, follows the design
principles of Piirola
(1973, 1988).
It provides in the U-, B-, V-, R- and I-bands simultaneous circular
and linear polarimetry as well as photometry
in ![]() /4-mode. The efficiency
for the circular polarimetry is
/4-mode. The efficiency
for the circular polarimetry is ![]() 70% and
70% and ![]() 50% for
the linear polarimetry with the
50% for
the linear polarimetry with the
![]() /4-retarder, and
/4-retarder, and ![]() 100% for linear polarimetry with
the
100% for linear polarimetry with
the ![]() /2-retarder. During the nights of
15/16, 16/17 and 18/19 November, 1998, the instrument was used in
/2-retarder. During the nights of
15/16, 16/17 and 18/19 November, 1998, the instrument was used in
![]() /2-mode
for maximum efficiency for linear polarization data, and on the other nights
(13/14, 14/15, 17/18 and 19/20 November, 1998)
/2-mode
for maximum efficiency for linear polarization data, and on the other nights
(13/14, 14/15, 17/18 and 19/20 November, 1998)
![]() /4-mode was used.
The sky background polarization is directly eliminated by using a
calcite plate as polarizing beam splitter. The instrumental polarization
and the
zero-point of the position angle are determined through observations
of high and low polarization standard stars.
The data have been folded in Figs. 1-3 by using the ephemeris
determined from V-band minima by
Schwarz et al. (1998):
/4-mode was used.
The sky background polarization is directly eliminated by using a
calcite plate as polarizing beam splitter. The instrumental polarization
and the
zero-point of the position angle are determined through observations
of high and low polarization standard stars.
The data have been folded in Figs. 1-3 by using the ephemeris
determined from V-band minima by
Schwarz et al. (1998):
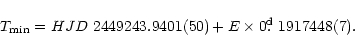 |
(1) |
Photometric UBVRI-data were obtained during 7 nights (from 13/14 to
19/20, November, 1998) with
time resolution of 26 s. Figure 1 presents simultaneous light curves (UBVRI)folded over the 4.6 hr orbital period.
Light curves in Fig. 1 have been plotted twice (from phase ![]() to
to
![]() )
to illustrate the
variations over the orbital period.
Brightness varies between magnitudes 16 and 17 in the B- and
V-bands. The range of variations is about one magnitude in all
bands. The brightness level
in the medium accretion state is V=17-16 and in the high
state V=16-15, according to Schwarz et al. (1998).
The broad maxima in the U- and the
B-bands occur between the orbital phases
)
to illustrate the
variations over the orbital period.
Brightness varies between magnitudes 16 and 17 in the B- and
V-bands. The range of variations is about one magnitude in all
bands. The brightness level
in the medium accretion state is V=17-16 and in the high
state V=16-15, according to Schwarz et al. (1998).
The broad maxima in the U- and the
B-bands occur between the orbital phases
![]() ,
whereas the
V-, R-, and the I-bands have their maximum
0.3 phase later (
,
whereas the
V-, R-, and the I-bands have their maximum
0.3 phase later (
![]() ).
Minima in the light curves occur between the phases
).
Minima in the light curves occur between the phases
![]() in the U- and the B-bands, whereas the V-, R-,
and I-bands have their mimima centered at the phase
in the U- and the B-bands, whereas the V-, R-,
and I-bands have their mimima centered at the phase ![]() .
Schwarz et al. (1998) also reported phase dependent minima:
during their
observations the I-band light curve mimimum
lagged the minimum in the B-band by
.
Schwarz et al. (1998) also reported phase dependent minima:
during their
observations the I-band light curve mimimum
lagged the minimum in the B-band by ![]() 0.12 phase
units.
Small variability in the shape of the light curves from night to night,
accompanied with some flickering, complicate accurate determination of
times of minima. Predicted timing errors in ephemeris given by Schwarz et al.
(1998) in November 1998 are
0.12 phase
units.
Small variability in the shape of the light curves from night to night,
accompanied with some flickering, complicate accurate determination of
times of minima. Predicted timing errors in ephemeris given by Schwarz et al.
(1998) in November 1998 are
![]() 10 min (
10 min (![]() 0.04 phase units).
0.04 phase units).
Due to the Northern declination, the maximum duration of the nightly runs was slightly greater than 4 hours (almost one complete cycle) and the values of air masses were between 2.1 and 2.7. We estimate that the accuracy of our photometry is 0.04 mag for the UBVR bands and 0.08 mag for the I-band. The full average spread of the observations in light curves are: 0.45 mag (U), 0.30 (B), 0.30 (V), 0.27 (R), 0.55 (I). Even though we consider some uncertainty arising from an estimate of the extinction coefficients (due to the low altitude of the object), we believe that the observed spread in the curves reflects real changes in the physical phenomenona in the source.
Figure 3 shows the phase binned linear polarization data,
computed by vectorially averaging individual observations from the B-,V-, R-,
and I-bands in order to increase the S/N ratio. U-band data is
not combined with the data from the other wavelengths due to higher
noise level in this band.
The degree of the linear polarization is low: 3% at maximum and
during most part of the orbital cycle polarization is
less than 1%.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2666f2.ps}\end{figure}](/articles/aa/full/2001/24/aah2666/Timg42.gif) |
Figure 2:
Simultaneous circular polarization curves (UBVRI) of RX J0203.8+2959. Data obtained during 7 nights between 13/14 and 19/20
November 1998, has been averaged to 40 phase bins.
Error bars correspond to the standard error of the mean
(
|
| Open with DEXTER | |
The linear polarization shows pulses with defined position angle
between the orbital phases
![]() and
and
![]() .
Both of these peaks coincide with the change of the sign in the circular
polarization.
A pulse-like feature is seen also near the phase
.
Both of these peaks coincide with the change of the sign in the circular
polarization.
A pulse-like feature is seen also near the phase ![]() ,
but there are no
zero crossings in the circular polarization near the same orbital phase.
The linear polarization drops to low level at the phase
,
but there are no
zero crossings in the circular polarization near the same orbital phase.
The linear polarization drops to low level at the phase ![]() .
A similar drop in polarization is also seen in the circular data
in the U-, B-, and V-bands, almost near the same phase. This may be
due to some unpolarized material (an accretion stream?) crossing our line
of sight to the cyclotron
emission area between orbital phases
.
A similar drop in polarization is also seen in the circular data
in the U-, B-, and V-bands, almost near the same phase. This may be
due to some unpolarized material (an accretion stream?) crossing our line
of sight to the cyclotron
emission area between orbital phases
![]() .
Earlier ROSAT X-ray observations by Schwarz et al. (1998) showed
that
during the short interval near photometric phase
.
Earlier ROSAT X-ray observations by Schwarz et al. (1998) showed
that
during the short interval near photometric phase ![]() HRI-detectors had
almost zero counts. Optical light curves (Fig. 1) do not reveal any
drop in the flux level during the same orbital phase, however.
HRI-detectors had
almost zero counts. Optical light curves (Fig. 1) do not reveal any
drop in the flux level during the same orbital phase, however.
Comparing our polarization data to earlier ROSAT PSPC and HRI
detectors data and HR1 hardness ratio, by Schwarz et al. (1998)
(Fig. 16 in
their paper; HR1 hardness ratio is defined as (H-S)/(H+S),
where H and S are counts above and below 0.4 keV),
it can be noticed that the soft X-ray component (
![]() )
is observed between the
photometrical phases
)
is observed between the
photometrical phases ![]() and
and ![]() .
The
HR1 ratio changes rapidly after the phase
.
The
HR1 ratio changes rapidly after the phase ![]() from
-0.8 to
from
-0.8 to ![]() 0.0 and reaches at the phases
0.0 and reaches at the phases
![]() its maximum,
its maximum,
![]() 0.5, at the same time when also the positive circular
polarization has its maximum peak value. The soft X-ray component thus
either disappears, or strongly reduces,
when a linear pulse is seen and circular
polarization
changes its sign. After photometric phase
0.5, at the same time when also the positive circular
polarization has its maximum peak value. The soft X-ray component thus
either disappears, or strongly reduces,
when a linear pulse is seen and circular
polarization
changes its sign. After photometric phase ![]() ,
HR1 hardnes ratio
drops from hard to soft. This coincides with
linear polarization pulse observed
between the phases
,
HR1 hardnes ratio
drops from hard to soft. This coincides with
linear polarization pulse observed
between the phases
![]() ,
and may be connected to
disappearing of the main emission region (positive pole).
The two X-ray components, soft and hard, seen at different orbital
phases, coinciding with a change from negative to positive circular
polarization, suggest two pole accretion.
,
and may be connected to
disappearing of the main emission region (positive pole).
The two X-ray components, soft and hard, seen at different orbital
phases, coinciding with a change from negative to positive circular
polarization, suggest two pole accretion.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2666f3.ps}\end{figure}](/articles/aa/full/2001/24/aah2666/Timg51.gif) |
Figure 3:
Simultaneous linear polarization (top) and position angle (bottom)
curves of RX J0203.8+2959 calculated by vectorially averaging the
individual observations of B-, V-, R-, and I-bands. Data have been averaged
to 28 phase bins.
Error bars correspond to the standard error of the mean
(
|
| Open with DEXTER | |
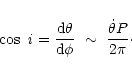 |
(2) |
During the other linear polarization pulse the
least square fit (weighted according errors) to position
angle data
between orbital phases
![]() gives
gives
![]() .
The
observed variations in position angle are noisy, but not
randomly scattered. They suggest (within given error estimates) high
orbital inclination
more probable solution than low inclination. Evidences
of two accreting poles (see Sect. 2.2) also supports
high inclination according Schwarz et al. (1998). Assuming orbital
inclination
.
The
observed variations in position angle are noisy, but not
randomly scattered. They suggest (within given error estimates) high
orbital inclination
more probable solution than low inclination. Evidences
of two accreting poles (see Sect. 2.2) also supports
high inclination according Schwarz et al. (1998). Assuming orbital
inclination
![]() ,
the lack of self-eclipses in the light curves
would require a colatitude
,
the lack of self-eclipses in the light curves
would require a colatitude
![]() for main accreting region.
However,
for main accreting region.
However, ![]() there are more than one
region accreting,
the main accreting region may have self-eclipses if another emission region
is seen during that time interval. By studying circular
polarization curves (Fig. 2) it is obvious that possible self-eclipse of the
main accretion region has quite short duration, because
positive circular
polarization is observed during most of the the orbital cycle.
By using formula
given by Bailey & Axon (1981):
there are more than one
region accreting,
the main accreting region may have self-eclipses if another emission region
is seen during that time interval. By studying circular
polarization curves (Fig. 2) it is obvious that possible self-eclipse of the
main accretion region has quite short duration, because
positive circular
polarization is observed during most of the the orbital cycle.
By using formula
given by Bailey & Axon (1981):
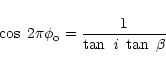 |
(3) |
We have reproduced the observed light curves and polarization variations
by using the numerical modelling codes for cyclotron emission
described in Piirola et al. (1987a,b, 1990, 1993).
For the cyclotron fluxes and
polarization dependence on the viewing angle ![]() ,
the angle between the line of the
sight and the magnetic field, we have used model grids given
by Wickramasinghe & Meggit (1985)
for constant high temperature
,
the angle between the line of the
sight and the magnetic field, we have used model grids given
by Wickramasinghe & Meggit (1985)
for constant high temperature
![]() keV (originally in 10
degrees divisions) which we have
further interpolated over whole range of viewing angle
keV (originally in 10
degrees divisions) which we have
further interpolated over whole range of viewing angle ![]() for one degree divisions.
These models predict the intensity of the cyclotron emission and linear and
circular polarization from a point source for different viewing angles
for each harmonics for a given optical depth parameter
for one degree divisions.
These models predict the intensity of the cyclotron emission and linear and
circular polarization from a point source for different viewing angles
for each harmonics for a given optical depth parameter ![]() and
electron shock temperature
and
electron shock temperature
![]() .
.
The height of the emission region(s) is assumed to be very small
compared to the radius of the white dwarf. The
observations of ST LMi (Cropper 1986), BL Hyi
(Piirola et al. 1987a), VV Pup (Piirola et al.
1990), for example, have
shown that the height of the emitting regions,
![]() ,
is very small in units of white dwarf radius,
,
is very small in units of white dwarf radius, ![]()
![]() 0.01
0.01
![]() .
The orbital inclination is adopted to the value
.
The orbital inclination is adopted to the value
![]() ,
which is
near the estimates from the rate of change of the position angle
during the two pulses (Sect. 3).
The colatitudes and longitudes of the emission regions,
extension of the emission regions in longitude and in colatitude are kept
as free parameters.
,
which is
near the estimates from the rate of change of the position angle
during the two pulses (Sect. 3).
The colatitudes and longitudes of the emission regions,
extension of the emission regions in longitude and in colatitude are kept
as free parameters.
The amount of polarization given by the constant temperature
Wickramasinghe & Meggit (1985) models
is often too high (see Cropper 1985; Piirola et al. 1987a,b, 1990). The
inclusion of an unpolarized background
emission is necessary in order
to bring the polarization values into better agreement with the observations.
We have adopted a colour dependence of the background comparable to
relative flux ratios near ![]() in each band (lowest states during
orbital cycle) to separate unpolarized background effects.
Schwarz et al. (1998) found that the faint
and the bright phase during the orbital cycle in RX J0203.8+2959 was dominated
by blue continuum, where at least three separate components
may contribute: optically thick cyclotron
emission from accretion region, photospheric radiation of the white dwarf
itself, and possible large fraction of reprocessed continuum radiation
from the line emitting regions. Schwarz et al. (1998) also
estimated that only
25% of total visual light observed during the high state originates from
measured cyclotron flux. In our modelling the adopted background fluxes
are in the B-, V-, and R-bands 3-4 times larger than the peak emission from
pure cyclotron flux (depending on wavelength).
in each band (lowest states during
orbital cycle) to separate unpolarized background effects.
Schwarz et al. (1998) found that the faint
and the bright phase during the orbital cycle in RX J0203.8+2959 was dominated
by blue continuum, where at least three separate components
may contribute: optically thick cyclotron
emission from accretion region, photospheric radiation of the white dwarf
itself, and possible large fraction of reprocessed continuum radiation
from the line emitting regions. Schwarz et al. (1998) also
estimated that only
25% of total visual light observed during the high state originates from
measured cyclotron flux. In our modelling the adopted background fluxes
are in the B-, V-, and R-bands 3-4 times larger than the peak emission from
pure cyclotron flux (depending on wavelength).
Calculations are made by dividing extended emission arcs
into three separate strips, each consisting of
20 equidistant points along a line on the surface of the white
dwarf, for which Stokes parameters Q, U, V and I are calculated
independently, as an approximation
for regions where volume elements do not obscure each other,
and their contributions to total polarization and flux are summed together as
a function of orbital phase.
The geometric model which gives acceptable fits to our data for different
temperatures
![]() ,
plasma parameter
,
plasma parameter ![]() values and for
different
harmonics numbers
values and for
different
harmonics numbers
![]() ,
by using
value
,
by using
value
![]() for orbital inclination, contains two extended
emission regions, (separated
for orbital inclination, contains two extended
emission regions, (separated
![]() in longitude):
positive (main) circular polarization region
between colatitudes
in longitude):
positive (main) circular polarization region
between colatitudes
![]() and 30
and 30![]() and the
other region (negative polarization) between
and the
other region (negative polarization) between
![]() and 140
and 140![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2666f4.ps}\end{figure}](/articles/aa/full/2001/24/aah2666/Timg76.gif) |
Figure 4:
Calculated circular polarization curves from orbital phase |
| Open with DEXTER | |
The general pattern of circular polarization variations over the orbital
cycle (Fig. 2) is fairly well reproduced by the model, using cyclotron model
parameters
![]() keV,
keV,
![]() ,
and the harmonics 8, 7, 6, 5, and 4 in
the UBVRI bands, respectively (Fig. 4) for the main accretion region.
These harmonics correspond to magnetic field of about 32-33 MG. The low S/N
ratio in the U and I bands (Fig. 2) does not allow any detailed comparison of
the phase dependent variations in U and I, but the amplitude level in these
bands is roughly in accordance with the predictions from the model. The
relative amount of negative circular polarization is largest in the blue, which
points to the possibility of stronger magnetic field in the second, less
active, pole. Our best fit, with
,
and the harmonics 8, 7, 6, 5, and 4 in
the UBVRI bands, respectively (Fig. 4) for the main accretion region.
These harmonics correspond to magnetic field of about 32-33 MG. The low S/N
ratio in the U and I bands (Fig. 2) does not allow any detailed comparison of
the phase dependent variations in U and I, but the amplitude level in these
bands is roughly in accordance with the predictions from the model. The
relative amount of negative circular polarization is largest in the blue, which
points to the possibility of stronger magnetic field in the second, less
active, pole. Our best fit, with
![]() keV and the
harmonics (7), 6, 5, 4,
and (3), in the (U)BVR(I) bands, respectively for the negative circular
polarization, corresponds to magnetic field of about 40-41 MG. These field
estimates are in reasonable agreement with the value
keV and the
harmonics (7), 6, 5, 4,
and (3), in the (U)BVR(I) bands, respectively for the negative circular
polarization, corresponds to magnetic field of about 40-41 MG. These field
estimates are in reasonable agreement with the value ![]() MG obtained by
Schwarz et al. (1998).
Tight constraints for the field strength can not
be set based to our cyclotron model fittings,
but varying a large range of
harmonics with different temperatures and plasma parameters, we can say that
harmonic numbers 3 or lower, are not able to predict well variations
observed in the
I-band, as well the harmonics clearly higher than 8 or 10,
do not seem to give enough
high polarization for B-band, setting the field range to be
about 25-43 MG.
Confirmed two-pole accretors, like VV Pup (Wickramasinghe et al. 1989), UZ For (Schwope et al. 1990),
DP Leo (Cropper & Wickramasinghe 1993) and QS Tel
(Schwope et al. 1995), have
shown significantly different fields in two accreting regions.
In some cases, nearly a factor of 2 difference has been
observed between magnetic
field strengths in different poles. The more strongly
accreting pole has usually the weaker magnetic field.
MG obtained by
Schwarz et al. (1998).
Tight constraints for the field strength can not
be set based to our cyclotron model fittings,
but varying a large range of
harmonics with different temperatures and plasma parameters, we can say that
harmonic numbers 3 or lower, are not able to predict well variations
observed in the
I-band, as well the harmonics clearly higher than 8 or 10,
do not seem to give enough
high polarization for B-band, setting the field range to be
about 25-43 MG.
Confirmed two-pole accretors, like VV Pup (Wickramasinghe et al. 1989), UZ For (Schwope et al. 1990),
DP Leo (Cropper & Wickramasinghe 1993) and QS Tel
(Schwope et al. 1995), have
shown significantly different fields in two accreting regions.
In some cases, nearly a factor of 2 difference has been
observed between magnetic
field strengths in different poles. The more strongly
accreting pole has usually the weaker magnetic field.
The models predict brightness variations (Fig. 5) which are about three
times smaller than observed and not that smooth.
If we reduce the amount of unpolarized background, the relative flux
variations increase, but then the polarization predicted by the model
will be too high.
The observed linear polarization pulses at phases 0.5 and 0.95 are well
reproduced by the model (Fig. 6). The negative pole is near the limb
at the phase 0.5. The minimum in the brightness
near the phase ![]() is due to having both emission regions at
self-eclipse by the white dwarf limb.
The length of the extended accretion regions are not
very strongly constrained. The fit to the observed smooth and
asymmetric variations in circular polarization and flux, by using small
and very short accretion regions is worse comparing to fitting by
longitudinally
extended emission regions. The short emission regions
produce also a short-term, sharp linear pulse with too high peak value,
whereas the longer emission regions give flatter and weaker linear
polarization peaks (consistent with observations) when the angle between
magnetic field and our line of the sight,
is due to having both emission regions at
self-eclipse by the white dwarf limb.
The length of the extended accretion regions are not
very strongly constrained. The fit to the observed smooth and
asymmetric variations in circular polarization and flux, by using small
and very short accretion regions is worse comparing to fitting by
longitudinally
extended emission regions. The short emission regions
produce also a short-term, sharp linear pulse with too high peak value,
whereas the longer emission regions give flatter and weaker linear
polarization peaks (consistent with observations) when the angle between
magnetic field and our line of the sight, ![]() ,
is close
,
is close
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2666f5.ps}\end{figure}](/articles/aa/full/2001/24/aah2666/Timg81.gif) |
Figure 5: By using the same parameters as in Fig. 4 (for circular polarization) the calculated light curves are presented. |
| Open with DEXTER | |
The best fit to observed data
is achieved by assuming relatively long emission regions (tens of degrees
in longitude). The length of the main emission region in our model shown
in Figs. 4, 5, and 6 (60![]() in longitude)
corresponds
in longitude)
corresponds ![]()
![]() in units of white dwarf radius.
The asymmetry seen in our light (Fig. 1) and
polarization curves (Fig. 2) of RX J0203.8+2959, suggests also that the
cyclotron emission regions are longitudinally extended.
This is in accordance with earlier modelling
of cyclotron emission in AM Herculis stars.
The assumption that the accretion takes place over a small spot
near the magnetic pole in centered dipole field is showed to be too
simplified. Longitudinally
extended arc-shaped accretion region(s), slightly offset from
the magnetic pole, have been proposed to explain the circular polarization
curves in AM
Herculis stars, see e.g.: Wickramashinge & Ferrario (1988),
and Ferrario & Wickramasinghe
(1990).
in units of white dwarf radius.
The asymmetry seen in our light (Fig. 1) and
polarization curves (Fig. 2) of RX J0203.8+2959, suggests also that the
cyclotron emission regions are longitudinally extended.
This is in accordance with earlier modelling
of cyclotron emission in AM Herculis stars.
The assumption that the accretion takes place over a small spot
near the magnetic pole in centered dipole field is showed to be too
simplified. Longitudinally
extended arc-shaped accretion region(s), slightly offset from
the magnetic pole, have been proposed to explain the circular polarization
curves in AM
Herculis stars, see e.g.: Wickramashinge & Ferrario (1988),
and Ferrario & Wickramasinghe
(1990).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2666f6.ps}\end{figure}](/articles/aa/full/2001/24/aah2666/Timg83.gif) |
Figure 6:
Calculated linear polarization and position angle curves for
harmonic number
|
| Open with DEXTER | |
Observed polarization and brightness variations
have been succesfully modelled by using extended emission regions, for
example, in
ST LMi (Ferrario et al. 1989; Ferrario et al. 1993; Cropper & Horne 1994),
DP Leo (Schmidt 1988; Cropper & Wickramasinghe 1993);
V347 Pav (Bailey et al. 1995; Ramsay et al. 1996;
Potter et al. 2000).
The extension of emission regions have been estimated to be, for example:
![]() (Wickramasinghe 1988),
(Wickramasinghe 1988),
![]() (UZ For in high state, Schwope et al. 1990),
(UZ For in high state, Schwope et al. 1990),
![]() (DP Leo, Schmidt
1988)
or extended from 15
(DP Leo, Schmidt
1988)
or extended from 15![]() to
to ![]() 100
100![]() in longitude (V834 Cen, Cropper 1989; ST LMi,
Cropper & Horne 1994; VV Pup,
Piirola et al. 1990; DP Leo,
Cropper & Wickramasinghe 1993; EV UMa, Hakala et al. 1994).
Recent X-ray observations have also shown that hard X-ray emission regions
in systems BL Hyi (Wolff et al. 1999) and V2301 Oph
(Steinman-Cameron et al. 1999) have extension of
45
in longitude (V834 Cen, Cropper 1989; ST LMi,
Cropper & Horne 1994; VV Pup,
Piirola et al. 1990; DP Leo,
Cropper & Wickramasinghe 1993; EV UMa, Hakala et al. 1994).
Recent X-ray observations have also shown that hard X-ray emission regions
in systems BL Hyi (Wolff et al. 1999) and V2301 Oph
(Steinman-Cameron et al. 1999) have extension of
45![]() -50
-50![]() in longitude.
in longitude.
Although that our model is able to produce the observed
variations in polarization acceptable well (Figs. 4, 5, and 6),
we can not assert that our solution is unique. The model fits are depending on
several parameters, such as orbital inclination,
(data favours high inclination, see Sect. 2.2) and choice of the correct
electron shock temperature
![]() and plasma parameter
and plasma parameter ![]() (values kT = 20 keV are adopted from Schwarz et al. 1998
fits to ROSAT-data).
(values kT = 20 keV are adopted from Schwarz et al. 1998
fits to ROSAT-data).
We have observed RX J0203.8+2959 and collected a large amount of
circular and linear polarimetric and photometric data covering well the
orbital phase.
A rise of positive
circular polarization is observed near the same orbital phases as
the change in X-ray spectrum HR1 hardness ratio in 1994
during ROSAT observations. Negative circular polarization is observed
at the same orbital phase when the soft X-ray
component is seen (Schwarz et al. 1998). Linear polarization
show pulses at the orbital phases when
the sign of the circular polarization
is reversed. Two pulses coincide with
the change in the X-ray spectrum. Observed polarization variations
favour a two-pole accretion instead of one accreting pole model.
The position angle variations suggest
relatively high values for the inclination angle of the white dwarf
spin axis,
![]() ).
).
Acknowledgements
This work was supported by the Finnish Academy of Sciences and Letters (Academia Scientiarum Fennica). We thank the referee for profound comments, which have improved our manuscript. We thank also Dr. C. Flynn for a reading of the manuscript.