A&A 372, 824-832 (2001)
DOI: 10.1051/0004-6361:20010573

Distance to the Active Galaxy NGC 6951 via the type Ia Supernova 2000E[*]

J. Vinkó 1 - B. Csák 1,6 - Sz. Csizmadia 2 - G. Fürész 3,7 - L. L. Kiss 3,7 - K. Sárneczky 4,6,7 - Gy. Szabó 3,6,7 - K. Sziládi 3,7 - I. B. Bíró 5,7


1 - Department of Optics & Quantum Electronics, University of Szeged, POB 406, Szeged 6701, Hungary
2 - Konkoly Observatory of the Hungarian Academy of Sciences, POB 67, Budapest 1525, Hungary
3 - Department of Experimental Physics, University of Szeged, Dóm tér 9, Szeged 6720, Hungary
4 - Department of Physical Geography, ELTE University, Ludovika tér 2, Budapest 1088, Hungary
5 - Baja Observatory, POB 766, Baja 6500, Hungary
6 - Visiting Astronomer, German-Spanish Astronomical Centre, Calar Alto, Spain
7 - Guest Observer, Piszkésteto Station, Konkoly Observatory, Hungary

Received 11 October 2000 / Accepted 9 April 2001

Abstract
CCD-photometry and low-resolution spectroscopy of the bright supernova SN 2000E in NGC 6951 are presented. Both the light curve extending up to 150 days past maximum and the spectra obtained at 1 month past maximum confirm that SN 2000E is of type Ia. The reddening of SN 2000E is determined as $E(B-V) = 0.36 \pm 0.15$, its error is mainly due to uncertainties in the predicted SN (B-V) colour at late epochs. The $V(RI)_{\rm C}$ light curves are analyzed with the Multi-Colour Light Curve Shape (MLCS) method. The shape of the late light curve suggests that SN 2000E was overluminous by about 0.5 mag at maximum comparing with a fiducial SN Ia. This results in an updated distance of $33 \pm 8$ Mpc of NGC 6951 (corrected for interstellar absorption). The SN-based distance modulus is larger by about +0.7 mag than the previous Tully-Fisher estimates. However, possible systematic errors due to ambiguities in the reddening determination and estimates of the maximum luminosity of SN 2000E may plague the present distance measurement.

Key words: stars: supernovae - individual: SN 2000E


1 Introduction

Type Ia supernovae (SNe Ia) are considered to be the most reliable distance indicators on extragalactic, even cosmological distance scales (e.g. Gibson et al. 2000; Parodi et al. 2000; Perlmutter et al. 1995; Riess et al. 1998; Hamuy et al. 1996b and references therein). This is mainly based on their exceptional brightness and homogeneity, despite of the existence of "peculiar'' SNe Ia, such as SN 1991T or SN 1991bg (e.g. Filippenko 1997). Although the frequency of these "standard bombs'' (Jha et al. 1999) is low, regular monitoring of numerous galaxies (e.g. by the Lick Observatory Supernova Search, the Nearby Galaxies Supernova Search, etc.) supplies more than a hundred type Ia SN events per year. The reliability of SN-based distances is increased by the number of bright, well-observed, nearby SNe Ia in host galaxies whose distances can also be determined by other methods, such as Cepheids (Saha et al. 1997; Gibson et al. 2000; Jha et al. 1999), Tully-Fisher relation, or surface brightness fluctuation (e.g. Riess et al. 1996).

In this paper we present an updated distance to the type 2 Seyfert galaxy NGC 6951 via the type Ia SN 2000E. This galaxy has received considerable attention recently, especially its active nucleus and circumnuclear star-forming ring (Boer & Schulz 1993; Barth et al. 1995; Elmegreen et al. 1999; Kohno et al. 1999; Perez et al. 1999). Its distance has been determined via Tully-Fisher relation by several groups. Bottinelli et al. (1984) gives $\mu_{\rm0} = 31.85$ mag for the true distance modulus (corresponding to 23.4 Mpc), while Tully (1988) lists 24.1 Mpc ( $\mu_{\rm0} = 31.91$ mag).

SN 2000E has occurred just outside the origin of the long, northern spiral arm, in a relatively low surface brightness region (Fig. 1). This SN was discovered by G. Valentini and coworkers (Valentini et al. 2000) on Jan. 26, 2000, and immediately announced to be a type Ia event by Turatto et al. (cf. IAUC 7351). They reported the appearance of Si II, Si III, S II, Ca II and Fe III, the usual ions characterizing type Ia SNe, and also the presence of Na D indicating considerable reddening. The occurrence of SN 2000E was particularly interesting, because it appeared just a few months after the maximum of the type II SN 1999el, the first SN observed in NGC 6951. SN 1999el was located closer to the bar-dominated central region, but definitely outside the circumnuclear regime where star-forming processes are most active (Perez et al. 1999).

The expected maximum brightness of SNe Ia at the distance of NGC 6951 (about 13.5 mag) indicates that SN 2000E offers a good chance to increase the sample of bright, well-observed SNe Ia. The comparison of distances determined via SNe Ia and other methods may result in the refinement of the distance measuring techniques and the cosmic distance scale itself. This is especially important in the case of SNe, because they are used to measuring cosmological distances, where other methods often do not work, and its technique relies on a relatively small number of local calibrator SNe.

In the following the new photometric and spectroscopic observations of SN 2000E are described then the results are presented and discussed.

2 Observations


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2491f1r.eps} \end{figure} Figure 1: NGC 6951 showing SN 1999el (left panel) and SN 2000E (right panel).
Open with DEXTER

2.1 Photometry

The CCD-photometric observations were obtained with four telescopes: the 28 cm Schmidt-Cassegrain at the campus site of University of Szeged (#1), the 60/90 cm Schmidt at Piszkésteto Station of Konkoly Observatory (#2), the 1 m Ritchey-Chrétien-Cassegrain at Piszkésteto (#3) and the 1.2 m Cassegrain at Calar Alto Observatory, Spain (#4). The small-aperture instrument was used only around the maximum of the SN. The CCD-frames were exposed through standard Johnson-Cousins filters, most often V and $R_{\rm C}$. $I_{\rm C}$ was used at early epochs, and a few B frames were also obtained at later phases. It would have been better to use the same telescope and setup to obtain a homogeneous dataset. However, this was strongly limited by the weather conditions and the availability of the instruments.

Transformation to the standard system has been performed by applying the following equations:


$\displaystyle V =~ v + C_{\rm V} (V-R) + D_{\rm V}$     (1)
$\displaystyle R =~ r + C_{\rm R} (V-R) + D_{\rm R}$     (2)
$\displaystyle I =~ i + C_{\rm I} (V-I) + D_{\rm I}.$     (3)

The occasional B data have been transformed in a similar way, except that (B-V) was used in the colour term. The instrumental coefficients (the Ci slopes and Di zero points) have been determined by observing Landolt standard fields (Landolt 1992) or the M67 standard sequence (Montgomery et al. 1993) at each site. Actually, the use of the zero points have been eliminated by observing local comparison stars in the field of SN 2000E and computing differential magnitudes. Differential extinction correction between the SN and the local comparison stars was neglected, due to the small field of view. For each telescope the transformation slopes are collected in Table 1. The magnitudes of the standard stars could be recovered within $\pm$0.03 mag.


 

 
Table 1: Transformation slopes. See text for the telescope codes.
Tel. $C_{\rm V}$ $C_{\rm R}$ $C_{\rm I}$
1 -0.11 -0.08 -0.04
2 +0.10 +0.08 -
3 -0.06 +0.06 +0.05
4 +0.06 +0.07 -


Figure 2 shows the field of NGC 6951 and SN 2000E with the local comparison stars labelled. The standard magnitudes of these stars were determined via Landolt standards observed with the Calar Alto telescope, where the photometric conditions were the best during our campaign. The results are listed in Table 2. Note that B1, B2 and B3 were used only for the frames taken with telescope #3.


 

 
Table 2: Standard magnitudes of local comparison stars. Errors are given in parentheses.
Star V (B-V) (V-R) (V-I)
F1 12.53 (0.01) 1.64 (0.02) 0.81 (0.01) 1.74 (0.01)
F2 14.86 (0.01) 0.87 (0.02) 0.52 (0.02) 1.01 (0.02)
F3 13.90 (0.03) 0.72 (0.04) 0.44 (0.01) 0.87 (0.02)
F4 15.55 (0.02) 0.74 (0.04) 0.43 (0.02) 0.92 (0.04)
F5 14.97 (0.02) 0.91 (0.03) 0.54 (0.02) 1.01 (0.02)
F6 15.71 (0.03) 0.88 (0.05) 0.49 (0.03) 1.07 (0.06)
F7 14.53 (0.02) 0.88 (0.02) 0.51 (0.02) 1.06 (0.03)
F8 saturated      
B1 15.88 (0.03) 0.97 (0.05) 0.57 (0.03) 1.16 (0.04)
B2 16.42 (0.05) 1.01 (0.11) 0.54 (0.06) 1.21 (0.07)
B3 16.60 (0.05) 1.18 (0.11) 0.64 (0.06) 1.32 (0.07)


The magnitudes of SN 2000E were inferred with aperture photometry, and transformed to the standard system via the local comparison stars. A small aperture radius of 4 pixels has been used in order to minimize the effect of the host galaxy background. The background light was estimated within a 4 pixel-wide annulus having 5 pixels inner radius. This background was determined on each frame and subtracted from the SN flux. PSF-photometry was not applied, because the frames with telescopes #1 and #2 had undersampled and/or strongly varying PSF. The transformation equations (Eqs. (1-3)) were applied for all observed SN data including those that were obtained more than 1 month past maximum. The colour terms in Eqs. (1-3) resulted in magnitude corrections in the order of 0.05 mag in the nebular phase. It may caused some additional uncertainty, because at late epochs the spectral distribution of the SN light resembles more a nebula than a star. K-correction has been neglected, because at the redshift of NGC 6951 (z = 0.005) it does not exceed 0.01-0.02 mag in V (Hamuy et al. 1993), i.e. it is well below the photometric uncertainty. The effect of the host galaxy background on the SN flux was investigated on frames taken in October, 1999 showing SN 1999el only (see Fig. 1, left panel). An aperture with the same size was placed on the position of SN 2000E and the surrounding background was subtracted, as above. The remaining flux was negligible even in the R filter. Thus, the background subtraction with the small aperture-annulus combination gave acceptable magnitudes for SN 2000E, minimizing the effect of the host galaxy light.


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{h2491f2r.eps} \end{figure} Figure 2: Local secondary standard stars in the field of NGC 6951. North is up and east is to the left. See Table 2 for magnitudes.
Open with DEXTER

The list of standard magnitudes of SN 2000E is given in Table 3. The errors were estimated from the rms deviations of the SN magnitudes from the comparison stars on each frame, and do not contain the possible systematic errors arise from the standard transformation. We believe that this latter error source is smaller than the uncertainites of the instrumental magnitudes measured with smaller telescopes.

The magnitudes in Table 3 were also compared with filtered CCD-magnitudes of Hornoch & Hanzl (2000) that were made between JD 51655 and 51666. Their R-magnitudes differ by about 0.4 mag from our values. This is a 4$\sigma$difference considering the given uncertainty of their data ($\pm$0.1 mag). Because the details of the standard transformation of the data of Hornoch & Hanzl were not published, the cause of this discrepancy cannot be studied in more detail here, except to underline that this may indicate a systematic error in either datasets at late epochs of SN 2000E. More published standardized measurements are needed to resolve this issue.


 

 
Table 3: Photometric data of SN 2000E. Errors are given in parentheses.
JD B V $R_{\rm C}$ $I_{\rm C}$ Tel.
2451572.2 - - 13.77 (0.03) - 2
2451576.2 - 13.88 (0.07) 13.53 (0.04) 13.72 (0.06) 1
2451578.3 - 13.73 (0.04) 13.51 (0.02) 13.57 (0.06) 1
2451579.3 - 13.67 (0.04) 13.51 (0.08) 13.68 (0.05) 1
2451581.3 - 13.78 (0.10) 13.50 (0.16) 13.59 (0.15) 1
2451582.3 - 13.80 (0.11) 13.63 (0.08) 13.60 (0.05) 1
2451585.3 - 14.02 (0.07) 13.76 (0.04) 13.75 (0.05) 1
2451589.5 - 14.21 (0.02) 14.12 (0.02) 14.14 (0.03) 2
2451656.5 - - 16.39 (0.02) - 2
2451657.5 - - 16.43 (0.02) - 2
2451658.5 17.64 (0.02) 16.65 (0.03) 16.48 (0.02) - 2
2451661.5 17.66 (0.02) 16.79 (0.02) 16.52 (0.02) - 2
2451662.5 17.80 (0.03) 16.88 (0.02) - - 2
2451664.5 17.85 (0.02) 16.93 (0.02) - - 2
2451667.5 - 16.82 (0.10) 16.51 (0.15) - 2
2451696.5 - 17.63 (0.02) 17.24 (0.03) - 3
2451705.6 - 17.89 (0.04) 17.87 (0.08) 18.09 (0.08) 3
2451706.6 - 17.89 (0.06) 17.86 (0.10) - 3
2451727.4 - 18.22 (0.02) 18.41 (0.05) 18.24 (0.05) 4


The light curves in V, R and I filters are plotted in Fig. 3. The continuous line is the optimal result of the Multi-Colour Light Curve Shape (MLCS) method (see next section). It can be revealed that the maximum brightness in V occurred around JD 51580, and the peak V-magnitude was about 13.7 mag, being in good agreement with the predicted peak brightness of SNe Ia at the distance of NGC 6951 (see Sect. 1).


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{h2491f3r.eps} \end{figure} Figure 3: Light curves of SN 2000E in B,V,R,I filters. The B,R,I data have been shifted vertically for better visibility. The continuous line is the template calculated with the MLCS method using $\Delta =-0.5$, E(B-V)=0.34 and $\mu _{\rm0}=32.70$ mag (see Table 4).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{h2491f4r.eps} \end{figure} Figure 4: Comparison of $V(RI)_{\rm C}$ light curves of SN 2000E (filled circles) with those of SN 1998bu (open symbols). All SN 1998bu data have been shifted vertically by 1.88 mag in order to bring them into agreement with SN 2000E. The similarity of the light curves is apparent.
Open with DEXTER

In order to test the reliability of our measurements and standard transformation, the light curves of SN 2000E were compared with those of SN 1998bu. For this bright SN, which appeared in the Leo I group galaxy M96, published light curves of very good quality are available, and it received considerable attention recently (Jha et al. 1999; Suntzeff et al. 1999). Figure 4 shows that the V, R, I magnitudes of SN 2000E (filled symbols) at the early part of the light curve agree satisfactorily with the data of SN 1998bu. This agreement was reached by adding 1.88 mag to the light curves of SN 1998bu in all filters. This suggests that the reddening of the two SNe were similar, about $E(B-V) \approx 0.3$ mag (Jha et al. 1999; see also Sect. 3). At present, the accuracy of inhomogeneous SNe light curves is usually not better than $\pm$0.1 (see e.g. Fig. 8 of Jha et al. 1999), so the small deviations in Fig. 4 (especially in the I band) are probably not significant. The light curves will be analysed further in Sect. 3.

2.2 Objective-prism spectroscopy

Spectroscopic observations were gathered with an objective prism attached to the 60/90 cm Schmidt telescope at Piszkésteto Station of Konkoly Observatory, between 26th and 28th February, 2000 (JD 2451601 - 03), when SN 2000E was about 1 month past maximum. The images were exposed onto an electronically cooled Thomson $1536 \times 1024$ CCD-chip (readout noise about 16 e-). The dispersion axis was aligned in the north-south direction, along the shorter side of the CCD-chip.

An objective prism spectrograph is certainly not an ideal tool for SN spectroscopy. However, this was the only spectroscopic instrument available to us at that time.

A considerable number of image processing steps were necessary to extract the SN from the smeared spectrum of the host galaxy. The location of the SN spectrum was determined from an intensity plot along the line perpendicular to the dispersion axis. At first, this was possible only in the blue region where the host galaxy showed negligible contribution. The red side, however, was heavily contaminated by the smeared background spectrum of the host galaxy. Removal of this background was essential to obtain reliable SN spectra.

The easier way to correct for the galaxy background would have been the usage of an objective prism picture of the host galaxy without the SN. Since it was not possible for us, we had to choose another, more approximative approach. First, the central peak of the background galaxy spectrum was identified visually. Then, the galaxy image was cut into two pieces at this central ridge, and the western part (including the SN) was dropped. The eastern side was reflected and added back into the position of the western side, thus, generating a symmetric picture of the galaxy. This picture was then subtracted from the original one, resulting in a much cleaner SN spectrum. While the removal of the galaxy "spectrum'' was far from complete, its contribution at the position of the SN spectrum was considerably suppressed in this way.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{h2491f5r.eps} \end{figure} Figure 5: Objective-prism spectra of SN 2000E. The epochs of the observations are indicated to the right of each spectrum. Some spectral features are marked (see text for reference).
Open with DEXTER

The extraction of the cleaned SN spectrum was performed with the standard subroutines in IRAF/SPECRED[*]. The intensities within a 3-4 pixel-wide aperture were summed and this aperture was slid along the dispersion axis, taking into account the tilt of the spectrum. The remaining background light was subtracted after a low-order polynomial fit. The wavelength calibration was performed using the lines in the spectrum of Vega taken with the same instrument and setup. The Vega spectrum was also used for the flux calibration. First, the telescope response function was determined by matching the measured continuum fluxes of the Vega spectrum with the tabulated ones (given in e.g. Gray 1992). Then, the SN spectrum was multiplied by the response function producing a flux-calibrated spectrum. The resulting spectra of SN 2000E are plotted together in Fig. 5, where an arbitrary vertical shift was applied for better visibility. Information for line identification was collected from Filippenko (1997).

It is apparent from Fig. 5 that SN 2000E shows the standard spectral features of a type Ia SN at one month after maximum light. A closer inspection of the features around 6000 Å with those of SN 1998aq taken at the same phase (Vinkó et al. 1999) showed good agreement, despite of the much lower resolution of the present spectra. This confirms the classification of type Ia, although a slightly confusing description of the presence of the $H\alpha$ line was also reported in IAUC 7353 by Polcaro et al. (2000). This was then revised in IAUC 7359.

There is continuously growing amount of evidence that SNe Ia show considerable diversity in peak brightness, decline rate, spectral features, etc. (see e.g. Filippenko 1997; Phillips et al. 1999; Nugent et al. 1995; Hatano et al. 2000 and references therein). The similarity between the spectra of SN 2000E and SN 1998aq may mean that SN 2000E is close to the "normal'' SNe Ia being neither SN 1991T-like, nor SN 1991bg-like event. It should be noted, however, that the spectroscopic diversity between these subclasses of SNe Ia is usually studied at earlier epochs, between $\pm$10 days around maximum. Therefore, the spectra presented here are too late for such a distinction. This issue will be studied in more detail using the shape of the light curve in the next section.

3 Results and discussion

In this section, first, we estimate the reddening of SN 2000E, then its distance is determined from the analysis of the light curve. Finally, the discussion of the errors of distance measurement is presented.

3.1 Reddening

The presence of Na D was reported in the very first spectrum of SN 2000E (see Sect. 1) indicating significant reddening. This feature might also be visible in the spectra in Fig. 5, although it is quite difficult to identify the heavily blended lines at the end of the photospheric phase. Nevertheless, the determination of reddening is essential if SN 2000E is to be used for distance measurement.

The reddening map of Burnstein & Heiles (1982) indicates E(B-V)=0.20 at the position of SN 2000E, while the more recent map of Schlegel et al. (1998) gives 0.36 mag. This is referred as the galactic component of the reddening, originating mostly from the interstellar medium (ISM) within the Milky Way. The map of Schlegel et al. is thought to be a better representative of the true amount of reddening, but it has been pointed out that this map systematically overestimates the reddening at directions where $E(B-V) \geq 0.15$ mag (Arce & Goodman 1999). Since several galactic cirrus clouds are visible on the long-exposure frames of NGC 6951, substantial reddening due to the Milky Way ISM is expected. Taking into account the possible overestimate in the map of Schlegel et al., the galactic component of E(B-V) may be somewhere between the two values given above (0.2-0.36 mag).

The total reddening of SN 2000E was estimated by comparing the observed (B-V) index with its expected value at the given epoch. This may give reasonable results, because SNe Ia are thought to show some kind of homogeneity in their (B-V) colours at epochs later than 60 days post-maximum (Phillips et al. 1999). Using JD 51578 as the epoch of the B-maximum (see next section), the phase of the B-data in Table 3 is between $\tau = 80$ and 86 days. The empirical formula of Phillips et al. (1999) results in $(B-V)_0 = 0.49 ~\pm~ 0.05$ at $\tau$ = 80 days, while the tabulated (B-V)0 of Riess et al. (1996) gives $0.73 \pm 0.02$ at this epoch. It is apparent, that, although both values are based on empirical data of "standard'' SNe Ia, their difference is large and significant. Certainly, this method of reddening determination has ambiguity, and the result may strongly depend on the adopted fiducial (B-V)0. The referee of this paper, Kevin Krisciunas, mentioned that his own analysis of recent SNe (Krisciunas 2000) gave a $(B-V)_0 ~-~ \tau$ relation with a zero point 0.070 mag redder than in Phillips et al. (1999).

Nevertheless, as a first approximation, we decided to adopt an averaged E(B-V) using the values above. Thus, the reddening was calculated by subtracting the expected (B-V)0s from the observed ones at the epochs when the B-V observations were taken, and then averaging the results. The Phillips et al.-relation resulted in $E(B-V)=0.49 \pm 0.02$ mag, while the Riess et al.-method produced $E(B-V)=0.24 \pm 0.01$ mag. Their average, $E(B-V) = 0.36 \pm 0.15$ was accepted as the best result at present. This is in very good agreement with the value of Schlegel et al. (1998). It suggests that most of the observed reddening of SN 2000E is due to dust in the Milky Way. The rather large uncertainty ($\pm$0.15 mag) reflects the ambiguity of choosing the intrinsic (B-V)0 of SNe Ia at late epochs. Using the standard $R_{\rm V} = 3.1$ coefficient of the galactic reddening law, the resulting uncertainty of the total absorption is $\Delta A_{\rm V} = \pm 0.46$ mag.

3.2 MLCS method

The light curves of type Ia SNe correlate with their peak brightness such that intrinsically brighter SNe Ia are bluer at maximum and decline more slowly than intrinsically dimmer SNe. The Multi-colour Light Curve Shape (MLCS) method parametrizes the light curve family by introducing $\Delta$ that measures approximately the V magnitude difference of a particular SN from a fiducial light curve at the time of B-maximum. The first version of the MLCS-method (MLCS-1, Riess et al. 1996) assumed a linear dependence of the light curve shape on $\Delta$, which was calibrated via a few nearby SNe. The second version (MLCS-2) uses a quadratic dependence on $\Delta$, and it is based on a more extended set of SNe light curves (Riess et al. 1998).

The light curves of SN 2000E (Table 3) were analysed with the second-order MLCS-2 method. The observed magnitude of the SN in filter $k\,(=B,V,R,I)$ at a particular epoch $\tau$ was described as

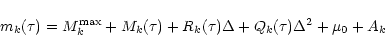\begin{displaymath}m_k(\tau) = M^{\max}_k + M_k(\tau) + R_k(\tau) \Delta + Q_k(\tau) \Delta^2 + \mu_{\rm0} + A_k \end{displaymath} (4)

where $M^{\max}_k$ is the magnitude zero point at the time of B-maximum ($\tau = 0$), $\mu_{\rm0}$ is the true distance modulus, Ak is the total extinction in the given filter, and $M_k(\tau)$, $R_k(\tau)$, $Q_k(\tau)$ are the template vectors of MLCS-2. The template vectors were kindly supplied to us by the referee with the permission of Adam Riess. The $M^{\max}$fiducial zero points were chosen as -19.46, -19.46, -19.41 and -19.81 mag for B,V,R,I filters, respectively. The interstellar extinction was calculated by assuming the galactic reddening law with coefficients given by Schlegel et al. 1998: $A_{\rm V} = 3.1 E(B-V)$, $A_{\rm B} = 4.1 E(B-V)$, $A_{\rm R} = 2.46 E(B-V)$, $A_{\rm I} = 1.72 E(B-V)$. Thus, the observed light curve is modelled via four free parameters: the time of B-maximum $T_{\max}(B)$, the true distance modulus $\mu_{\rm0}$, the reddening E(B-V) and the luminosity parameter $\Delta$.

The template vectors were fitted to the light curves of SN 2000E simultaneously, i.e. the difference between the observed and calculated light curves were combined into a single chi-squared function. The weighting factors were chosen as $1/\sigma_i^2$where $\sigma_i$ is the photometric uncertainty of the given data point (listed in Table 3). In order to avoid giving too strong weight to any specific data point, the minimal photometric uncertainty was increased to 0.05 mag. Because the template vectors are better determined at early epochs than at the nebular phase, more weight was assigned to the data around maximum (Riess, personal communication). For this purpose, the error bars at late epochs ($\tau >70$ days) were multiplied by $\sqrt 2$ thus producing a factor of 2 less weight for these data.

Three kinds of solution have been determined with the MLCS-2 vectors. First, E(B-V) = 0.36, estimated in Sect. 3.1, was treated fixed and only $\mu_{\rm0}$ and $\Delta$ were optimized. The solution converged to $\mu_{\rm0} = 32.62 \,\pm\, 0.1$ and $\Delta = -0.5\, \pm\, 0.1$. Second, relaxing this constraint and optimizing all three parameters we have got $E(B-V) = 0.34 \pm 0.05$, $\mu_{\rm0} = 32.70 \pm 0.1$ and $\Delta = -0.5 \pm 0.05$. These two solutions agree quite well and suggest that this SN belongs to the overluminous subclass of SNe Ia. Finally, forcing the solution only to the data around maximum (dropping the points at late epochs) resulted in $E(B-V) = 0.32 \pm 0.08$, $\mu_{\rm0} = 32.12 \pm 0.2$ and $\Delta = +0.14 \pm 0.1$. Thus, the data around maximum favour slightly positive $\Delta$ and a shorter distance, while late-time photometry, which gives tighter constraint on $\Delta$, indicates strongly negative $\Delta$ and a higher distance. The two solutions are significantly different from each other, the distance moduli of solution #2 and #3 differs by $3 \sigma$. Of course, $\mu_{\rm0}$ and $\Delta$ are strongly correlated parameters, a negative $\Delta$ (brighter SN) results in a larger distance modulus for the same E(B-V). Note that the application of MLCS-1 (the previous, linear version of the method), to the whole light curve resulted in $E(B-V) = 0.30 \pm 0.1$, $\mu_{\rm0} = 32.16 \pm 0.1$ and $\Delta = +0.15 \pm 0.1$, which is closer to the MLCS-2 solution #3. This is due to the fact that the MLCS-1 fiducials produce brighter light curves at late phases than the MLCS-2 vectors, so a smaller $\Delta$ is needed to fit the late data of SN 2000E. The parameters of these solutions are collected in Table 4.


 

 
Table 4: Parameters of SN 2000E optimized with MLCS. $T_{\max}(B)=51578.0$ was used in all solutions. Uncertainties are given in parentheses. #1-3 were computed with MLCS-2, while #4 was obtained with MLCS-1.
No. E(B-V) $\mu_{\rm0}$ $\Delta$ $\chi^2$
#1 0.36 (fixed) 32.62 (0.1) -0.50 (0.10) 2.32
#2 0.34 (0.05) 32.70 (0.1) -0.50 (0.05) 2.27
#3 0.32 (0.08) 32.12 (0.2) +0.14 (0.10) 6.58
#4 0.30 (0.10) 32.16 (0.1) +0.15 (0.05) 2.52


Is it possible that SN 2000E had $\Delta =-0.5$? Such overluminous SNe Ia often belong to the "SN 1991T'' subgroup, which show peculiar premaximum spectra: almost featureless continuum with no sign of Si or S, but a few ionized Fe lines (Filippenko 1997). According to the description given in Sect. 1, Si II, S II and Ca II could be identified in the premaximum spectra of SN 2000E, which argues against an SN 1991T-like object. The postmaximum spectra of such SNe are more-or-less normal, so the spectra of SN 2000E presented in Sect. 2.2 cannot be used for identifying this subclass. On the other hand, there is an example of a strongly overluminous SN ( $\Delta \approx -0.5$), SN 1992bc, that otherwise had normal premaximum spectrum (Hamuy et al. 1992; Riess et al. 1998). If the $\Delta =-0.5$ solution of MLCS-2 is true then SN 2000E might be similar to SN 1992bc. How can we get closer to the "true'' value of $\Delta$? $\Delta$ is constrained by both the shape of the light curve and the colour at maximum. SNe with $\Delta < -0.1$ show the bump in their I light curve at later epochs than SNe with $\Delta \approx 0$ do. Unfortunately, the observed I curve of SN 2000E does not extend into the bump phase, so this constraint could not be applied. Alternative methods, such as the $\Delta m_{\rm 15}(B)$ decline rate of the early B light curve (Phillips 1993; Hamuy et al. 1996a), or infrared JHKphotometric templates (Krisciunas et al. 2000) could not be used for the same reason, i.e. the lack of the necessary data. The colour around maximum, in principle, may be indicative of a negative $\Delta$, because overluminous SNe are bluer at maximum. However, this is distorted by reddening which must be determined separately to use this constraint. Uncertainty in the reddening would directly influence the inferred $\Delta$, especially in the $\Delta < 0$ domain, because a negative $\Delta$ corresponds to less colour change than a positive $\Delta$ in MLCS-2.

The fact that the early light curve of SN 2000E was very similar to that of a normal SN Ia makes the determination of $\Delta$ very difficult from the present dataset. The result of $\Delta =-0.5$ greatly relies on our late-epoch photometry. Because at late epochs the light of the SN is more affected by the background of its host galaxy, an incorrect background subtraction could easily lead to brighter SN magnitudes, thus, suggesting a slower decline and a negative $\Delta$. We have checked the efficiency of the background subtraction (Sect. 2.1), still, such systematic error cannot be ruled out completely. Also, the standard transformation is more uncertain in the nebular phase, as mentioned in Sect. 2. It is not possible to reach an unambiguous result at present. Thus, we conclude that the available data suggest that SN 2000E was overluminous at maximum, but otherwise showed normal spectral features, similarly to SN 1992bc.

3.3 The distance of NGC 6951

The MLCS analysis described above resulted in essentially two sets of distances to the host galaxy of SN 2000E. The "long'' distance, corresponding to $\Delta =-0.5$, is $d = 34 \pm 2$ Mpc (this uncertainty reflects simply the difference between the two solutions in Table 4), while the "short'' distance is about $d = 26 \pm 3$ Mpc. The d = 34 Mpc distance is more likely, but the "short'' distance (meaning that SN 2000E was close to the fiducial SN Ia) cannot be ruled out.

The MLCS distances are tied to a Cepheid distance scale (Riess et al. 1996; Jha et al. 1999, and references therein). This can be checked by comparing the light curves and distance moduli of SN 2000E and SN 1998bu. As presented in Sect. 2.1, the light curves of these two SNe differs by 1.88 mag uniformly in all VRI bands. Rearranging the basic equation of the MLCS method, around maximum in V filter one can get

$\displaystyle \mu_{\rm0}(E)=\mu_{\rm0}(bu)+(m(E)-m(bu))-(A_{\rm V}(E) -A_{\rm V}(bu))- R_{\rm v} (\Delta(E) - \Delta(bu))$     (5)

where E denotes SN 2000E and bu is for SN 1998bu and all symbols have their usual meaning (the $Q \Delta^2$ term is negligible around maximum). The terms on the right-hand side are $\mu_{\rm0}(bu) = 30.37$ mag (Jha et al. 1999), m(E) - m(bu) = 1.88 mag (Sect. 2.1), $A_{\rm V}(E) - A_{\rm V}(bu) = 0.15$ mag (adopting E(B-V) = 0.31for SN 1998bu, Jha et al. 1999), $R_{\rm v} \approx 1$ and $\Delta(E) - \Delta(bu) = -0.52$. These values give $\mu_{\rm0}(E) = 32.62$ mag, in good agreement with the MLCS result (Table 4). Similarly, the solutions #3 and #4 in Table 4 would give $\mu_{\rm0}(E) = 32.08$ mag which agrees with the MLCS distance modulus within the error. The small difference is attributed to the ambiguity of the Cepheid distance scale. For example, Gibson et al. (2000) derived $\mu_{\rm0} = 30.20 \pm 0.1$ mag for the Cepheid distance modulus of M96, which differs by 0.17 mag from the value used by Jha et al. (1999). Using this for $\mu_{\rm0}(bu)$ one could get systematically less distance modulus for SN 2000E. Accordingly, the SN-distances are uncertain by about 0.2 mag due to the uncertainties of the adopted distance scale. The discussion of the distance scale calibrations is beyond the scope of this paper.

The distance to NGC 6951 was finally calculated by adopting the average of the "long'' distance moduli (32.70 by MLCS, 32.62 by the Jha et al.-distance to M96 and 32.45 by the Gibson et al.-distance to M96). The result is $\mu_{\rm0} = 32.59 \pm 0.1$ mag, or $33 \pm 2$ Mpc. Note that the similar average of the "short'' distances results in 32.28 $\pm$ 0.2 mag, or 29 $\pm$ 3 Mpc. The new distance of NGC 6951 is significantly larger (by about 0.7 mag, or 9 Mpc) than the previous Tully-Fisher distance estimates (see Sect. 1). This is close to the "usual'' systematic difference between the two distance scales (e.g. Riess et al. 1996). Recently Shanks 1997 proposed a modification of Tully-Fisher distances by adding 0.46 mag to T-F distance moduli to bring them into agreement with SNe Ia distances. This correction is less than the difference above, but it is known that the T-F distance moduli of individual galaxies can be uncertain by at least 0.3-0.4 mag. Naturally, the "short'' distance given above would agree better with the T-F distances than the "long'' distance. Note that a recent revision of the Cepheid distance scale by Gibson et al. (2000), suggests a better agreement with the Cepheid and T-F distance scales. Indeed, the distance of SN 2000E would agree with the previous T-F distance of NGC 6951 by Tully (1988), if the SN were normal (i.e. not overluminous) and the distance scale of Gibson et al. (2000) was used.

The referee suggested a check of the inferred distance of NGC 6951 based on the measured redshift and the expected Hubble-flow at that distance. The SIMBAD catalogue gives $v_{\rm rad}\rm (NGC~6951) = 1424$ kms-1. The galactic coordinates of this galaxy are $l = 100\hbox{$.\!\!^\circ$ }89$ and $b = 14\hbox{$.\!\!^\circ$ }85$, thus, the radial velocity in the galactic system is represented by a vector of (+365; +1352; -260) kms-1. The additive correction for the Milky Way motion within the Local Group can be computed as (-30; +297; -27) (Riess et al. 1996). The drift of the Local Group with respect to the CMB can be approximated by adding (+10; -542; +300) (Smoot et al. 1992) or (+57; -540; 313) (Kogut et al. 1993). Both corrections results in $v_{\rm rad}\rm (NGC~6951) = 1307$ kms-1 in the CMB rest frame. The expected Hubble-flow velocity at the inferred distance of NGC 6951 (d = 33 Mpc) is 2145 kms-1 using $H_{\rm0} = 65$ kms-1 Mpc-1. This is significantly larger than the corrected radial velocity of NGC 6951. However, it is not an unexpected result, because at this distance the observed radial velocities usually deviate from the smooth Hubble-flow. Note that using a recent estimate of the short-distance scale Hubble-constant $H_{\rm0} = 76$ (Jensen et al. 2000) one would get $v_{\rm rad} = 2508$ kms-1, increasing further the discrepancy. The shorter SN-distance (29 Mpc) with $H_{\rm0} = 65$ would lead to $v_{\rm rad} = 1885$ kms-1, which is still higher than the observed rest-frame radial velocity. So, the conclusion is that NGC 6951 is probably too close to predict a reliable radial velocity from the smooth Hubble-flow.

3.4 Error budget

The overall error of the distance moduli determined above contains contribution from measurement errors (random and systematic) and the systematic uncertainties of several assumptions.

The standard deviation of the MLCS distance can be expressed as

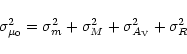
\begin{displaymath}\sigma^2_{\mu_{\rm0}} = \sigma^2_m + \sigma^2_M + \sigma^2_{A_{\rm V}} + \sigma^2_R \end{displaymath}

where $\sigma_m$ and $\sigma_M$ are the uncertainties of the measured and the template V light curve, $\sigma^2_{A_{\rm V}} = 3.1^2 \sigma^2_{E(B-V)}$ and $\sigma_R$ is the uncertainty of the $R_{\rm v} \Delta$ product (see Riess et al. 1996). Assigning $\sigma_m = 0.05$ mag (random), $\sigma_M = 0.15$ mag (systematic zero-point error and random scattering of the template light curves), $\sigma_{E(B-V)} = 0.15$ mag (random measurement error and systematic uncertainty of the fiducial (B-V)0) and $\sigma_R = 0.1$ (systematic) the result is $\sigma_{\mu_{\rm0}} = 0.50 ~{\rm mag}.$ Note that this uncertainty does not contain the possible systematic error of the standard transformation of the SN-photometry.

The Cepheid-based distance via SN 1998bu has lower uncertainty, because in this case the errors of the parameter differences are considered. From Eq. (4) the error can be expressed as

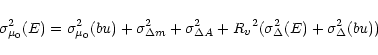
\begin{displaymath}\sigma^2_{\mu_{\rm0}}(E) = \sigma^2_{\mu_{\rm0}}(bu) + \sigma... ...ta A} + {R_v}^2 (\sigma^2_{\Delta}(E) + \sigma^2_{\Delta}(bu)) \end{displaymath}

where $\sigma_{\Delta m}$ is the error of the magnitude shift between the two sets of light curves, $\sigma_{\Delta A}$ is the uncertainty of the $A_{\rm V}(E) - A_{\rm V}(bu)$ difference. These uncertainties are estimated as $\sigma_{\Delta m} = 0.03$, $\sigma_{\Delta A} = 0.1$, $\sigma_{\Delta}(bu) = 0.02$(Sect. 3.3), $\sigma_{\Delta}(E) = 0.1$ (as above), and $R_{\rm v} \approx 1$ around maximum. The error of the distance modulus of SN 1998bu was considered to be $\sigma_{\mu_{\rm0}}(bu) = 0.2$ mag taking into account both random and systematic uncertainties (see Sect. 3.3). Substituting these into the above expression, the result is $\sigma_{\mu_{\rm0}} = 0.25 ~{\rm mag}.$

The uncertainties above do not contain the possible large systematic error of the luminosity parameter $\Delta$(i.e. the problem of the "long'' vs. "short'' distances of SN 2000E). Clearly, $\Delta$ has a crucial role in the distance determination, therefore, any systematic error in $\Delta$ directly distorts the photometric distance. If we adopt a rather pessimistic viewpoint, and assign 0.5 mag to the systematic error of $\Delta$ (which would mean that the slower decline of SN 2000E is due to systematic errors in our photometry) the error of the MLCS distance modulus grows up to $\sigma_{\mu_{\rm0}} = 0.71$ mag, while the distance modulus via SN 1998bu has uncertainty of $\sigma_{\mu_{\rm0}} = 0.56$ mag.

The other factor that contributes significantly to the total uncertainty is the reddening E(B-V). It is multiplied by 3.1 to take into account the total absorption, which, unfortunately, greatly amplifies the overall uncertainty. Generally, SNe Ia are better distance indicators than the case presented here, because most of them have much lower reddening. However, it cannot be expected that all SNe Ia have negligible reddening, thus, the uncertainties in E(B-V) can seriously disturb even the distances of relatively nearby SNe. Because the better understanding of SNe Ia greatly relies on the nearby, well-observed events, it is essential to work out reliable methods for the reddening determination. The increasing number of such objects would certainly help to solve this problem.

4 Summary

1.
$V(RI)_{\rm C}$ photometry of SN 2000E in NGC 6951 was obtained starting from 1 week before maximum light and extending up to 150 days past maximum. The shape of the light curves and the objective-prism spectra collected at 1 month past maximum confirm the type Ia nature of SN 2000E;

2.
The reddening of the supernova is estimated from the comparison of the measured and expected (B-V) colour at late epochs (around 80 days past maximum). Two different template (B-V) curves were used resulting in $E(B-V) = 0.36 \pm 0.15$ as an averaged final result. It is consistent with the prediction of the galactic reddening map of Schlegel et al. (1998). The error reflects the systematic uncertainties of the template colour curves at late epochs;

3.
The distance of SN 2000E has been inferred from the second-order MLCS-method. The fitting to $BV(RI)_{\rm C}$light curves resulted in $\mu_{\rm0} = 32.70 \pm 0.50$ and $\Delta = -0.5 \pm 0.1$ mag as true distance modulus and light curve parameter, respectively. The negative $\Delta$ suggests that SN 2000E was overluminous relative to the fiducial type Ia supernova, but this is based on inhomogeneous, low signal-to-noise photometric data, thus, it may be systematically in error;

4.
The similarity of the light curve of SN 2000E with that of SN 1998bu in M96 allowed us to tie the distance of SN 2000E to the HST Cepheid distance scale. $\mu_{\rm0} = 32.62$- $32.45 ~\pm 0.26$ mag was obtained depending on the adopted Cepheid-distance modulus of M96, which agrees with the MLCS-distance given above. Averaging the distance moduli of SN 2000E supplied by various methods, the estimated distance modulus becomes

\begin{displaymath}\mu_{\rm0} = 32.59 \pm 0.5 ~{\rm mag}\end{displaymath}

corresponding to $33 \pm 8$ Mpc geometric distance. The largest error sources in the distance estimates are the systematic errors in $\Delta$ and E(B-V). If the $\Delta$ parameter of SN 2000E were determined incorrectly, the distance would be systematically lower and its uncertainty would grow up to $\pm$10 Mpc.

Acknowledgements

This work was supported by Hungarian OTKA Grants No. T032258, T034615, the Magyary Postdoctoral Fellowship to JV from Foundation for Hungarian Education and Science (AMFK), the ``Bolyai János'' Research Scholarship to LLK from Hungarian Academy of Sciences and Pro Renovanda Cultura Hungariae Foundation (travel grants to BCs, KS and GySz). We are grateful to the referee, Dr. Kevin Krisciunas, who made several contributions that helped us to improve the paper. We acknowledge the permission by Prof. Adam Riess to use the updated MLCS template vectors for light curve fitting. Thanks are due to Konkoly Observatory and Calar Alto Observatory for generously allocating the necessary telescope time. The NASA Astrophysics Data System, the SIMBAD database and the Canadian Astronomy Data Centre were used to access data and references. The availability of these services are gratefully acknowledged.

References

 
Copyright ESO 2001