4 The global mass function

In Fig. 6, we compare the local MF obtained in annuli A1-A3 using FORS1 with that measured by De Marchi et al. (1999) with the TC at $r = 135^{\prime\prime}$. Rather than converting the three individual LFs of annuli A1-A3 into MFs, we have first combined them into one single function by averaging their values in each magnitude bin, and have taken the standard deviation as a measure of the associated uncertainty (error bars). We have done that for compatibility with the approach used by De Marchi et al. (1999) for the LF obtained with the TC, and because the LFs of the three annuli are very similar to one another. In all cases (FORS1 and TC), we have obtained the MF by dividing the corresponding average LF by the derivative of the mass-luminosity (ML) relation appropriate for the metallicity of NGC 6712 ([Fe/H]=-1.01; Harris 1897).

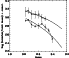Figure 6: Comparison between the average MF in annuli A1-A3 (boxes) and that derived by (De Marchi et al. 1999) with the VLT-TC (diamonds) farther out in the cluster (see text). Thick solid lines mark the best fitting power-law, with index respectively $\alpha = 0.9$ and $\alpha =1.5$.

We plot here the results obtained using the ML relation of Baraffe et al. (1997), but using the models of Cassisi et al. (2000) would have yielded an almost identical result. The MFs derived in this way are shown in Fig. 6, where boxes connected by dashed lines represent the average of the MF in annuli A1-A3 (upper curve) and in the TC field (lower curve), whereas the thick solid lines show the best fitting power-law MF, with index $\alpha = 0.9$ and $\alpha =1.5$, respectively for the FORS1 data (upper curve) and TC data (lower curve). We should note here, however, that ignoring the data-point at $\sim$0.4 $M_{\odot }$ in the lower curve would result in two MFs that agree perfectly well with one another, within the errors, and the best fitting power-law to the TC data would also have $\alpha \simeq 0.9$(this agreement is hardly surprising as it was already implied by the remarkable similarity of the LF). Regardless of the last data-point, however, the net result in both cases is that the number of stars decreases steadily with mass.

This result gives strong support to the claim of De Marchi et al. that there is a relative deficiency of low mass stars with respect to the stars at the TO ( $M \simeq 0.75$ $M_{\odot }$), although our data do not reach deep enough to see whether this observed drop continues all the way to $\sim$0.3 $M_{\odot }$ where all known GC feature a peak in their MF (Paresce & De Marchi 2000) before plunging to the H-burning limit.

The dynamical evolution of a cluster depends on both the interaction among the stars in the cluster, which locally modifies the distribution of masses (internal dynamics, i.e. mass segregation), and on the interaction with the Galaxy. In our particular case, even though NGC 6712 is likely to have experienced strong tidal shocks during its life-time (De Marchi et al. 1999; Takahashi & Portegies Zwart 2000), one wonders whether the almost identical LFs (and ensuing MFs) that we observe at the various radial distances as shown in Fig. 5 can be ascribed to the internal two-body relaxation mechanism.

Figure 7: Theoretical LF as a function of distance as predicted by the multi-mass Michie-King model described in the text. Diamonds represent the observed LFs in annuli A1-A3, and in the TC field.

To address this issue more specifically, we have simulated the dynamical structure of the cluster using a multi-mass Michie-King model constructed with an approach close to that of Gunn & Griffin (1979), as extensively described in Meylan (1987, 1988), and following the technique developed more recently by Pulone et al. (1999) and De Marchi et al. (2000), to whom we refer the reader for further details.

Each model is characterized by three structural parameters describing, respectively, the scale radius ($r_{\rm c}$), the scale velocity ($v_{\rm s}$), the central value of the gravitational potential ($W_{\rm o}$), and a global MF of the form d $N \propto m^{\alpha}$, where the exponent $\alpha$ would equal -2.35 in the case of Salpeter's IMF. Stellar masses have been distributed into nineteen different mass classes, covering MS stars, white dwarfs (WDs) and other heavy remnants. All stars lighter than $0.8 ~M_{\odot}$ have been considered still on their MS, while heavier stars with initial masses in the range 8.5 - 100 $M_{\odot }$ have been assigned a final mass of 1.4 $M_{\odot }$. WD have been subdivided into three mass classes, following the prescriptions of Meylan (1987, 1988) and assigned to the corresponding MS mass using the relations presented by Weidemann (1988) and Bragaglia et al. (1995). The lower mass limit is assumed to be 0.085 $M_{\odot }$. As already shown by Meylan (1987), the exact value of different mass cutoffs does not significantly influence the result of the dynamical modelling.

In order to fit the structural parameters of NGC 6712, two different mass function exponents have been adopted: $\alpha_{\rm up}$ for stellar masses in the range 0.8 - 100 $M_{\odot }$, and $\alpha_{\rm ms}$ for MS stars below 0.8 $M_{\odot }$. We have furthermore assumed complete isotropy in the velocity distribution. From the parameter space, we have considered only those models characterised by a surface brightness profile (SBP), a velocity dispersion profile (VDP) and a mass-to-light (M/L) ratio which would simultaneously agree well with their corresponding observed values. We have further constrained the choice among the best fitting dynamical models with the smallest reduced chi-squares, by imposing the condition that the four observed LFs (A1-A3 and TC) had to be simultaneously fitted by their theoretical counterparts as predicted by the mass stratification of the dynamical structure of the cluster (see Pulone et al. 1999 and De Marchi et al. 2000 for an extensive description of this technique). As regards the SBP of NGC 6712, in our simulations we have followed the approach of Trager et al. (1985) and have used its Chebyshev polynomial fit as evaluated on our own data (see Fig. 8), while for the VDP we have used the mean values obtained by Grindlay et al. (1988) within about three core radii. The value of M/L=0.7 has also been taken from Grindlay et al. (1988).

Thanks to the many observational constraints that we force our model to satisfy, we are able to considerably reduce the space in which parameters can range. The best fitting set of parameters requires the indices of a power-law global MF $\alpha_{\rm up}$ and $\alpha_{\rm ms}$ to take on values respectively around -2.3 (the Salpeter slope) and 0.9, as shown in Fig. 7. The line of sight velocity dispersion at the centre is in this case $\sigma_{\rm v} = 4.3$kms^-1 and the derived mass-luminosity ratio turns out to be M/L=0.74, in perfect agreement with Grindlay et al. (1988) values $\sigma_{\rm v} = 4$kms^-1 and M/L = 0.7. The key result here, then, is that the global MF of NGC 6712 is indeed an inverted function, i.e. one that decreases with decreasing mass below $\sim 0.8$ $M_{\odot }$. The other parameter values of the best fitting model are: core radius $r_{\rm c} = 1^\prime$, half-light radius $r_{\rm hl} = 1\hbox{$.\mkern-4mu^\prime$ }8$, tidal radius $r_{\rm t}=5\hbox {$.\mkern -4mu^\prime $ }2$, concentration ratio c=0.7, total mass of the cluster $M_{\rm cl} = 7 \times 10^4$ $M_{\odot }$, mass fraction in heavy remnants f=0.6. A large fraction of mass in the form of white dwarfs, neutron stars and black holes such as the one that we find here might be surprising. Heavy remnants are usually thought to account for up to 20-30% of the mass of a cluster (Meylan & Heggie 1997), whereas our result suggests at least twice as many. The amount of heavy remnants depends here exclusively on the shape of the IMF for stars more massive than 0.8 $M_{\odot }$. Because the latter have already evolved off the MS and are no longer observable, the value of $\alpha_{\rm up}$ is not as strongly constrained in our model as is that that of $\alpha_{\rm ms}$for less massive stars. If, for instance, a value of $\alpha_{\rm up}= -6$ were used, the fraction of heavy remnants could be brought down to $\sim$25%. Besides being highly suspicious in a mass range where all known stellar populations display a Salpeter-like IMF (see e.g. Kroupa 2001), such a steep MF exponent would also strongly affect the M/L ratio, forcing it to take on the value of $\sim$0.2, which is very discordant with the M/L=0.7 measured by Grindlay et al. (1988). We, therefore, leave the value of $\alpha_{\rm up}$ unchanged and consider in the next section the observational consequences that the ensuing large fraction of heavy remnants implies. The key result here, nevertheless, is that the current global MF of NGC 6712 is indeed an inverted function, i.e. one that decreases with decreasing mass, starting at least from 0.8 $M_{\odot }$. Although all clusters whose LF has been studied in the core show an inverted local MF there (as a result of mass segregation: see e.g. Paresce et al. 1995; King et al. 1995; De Marchi & Paresce 1996), NGC 6712 is the only known cluster so far to feature an inverted MF on a global scale. McClure et al. (1985) and Smith et al. (1986) have observed a LF that drops with decreasing luminosity in the halo clusters E3 (see also Veronesi et al. 1996) and Palomar5, respectively. The actual shape of the corresponding global MF, however, is not known, as only a single field is available in each cluster. These objects are, nonetheless, very interesting and should be studied using deeper, higher resolution photometry at several locations in the clusters to properly address the effects of mass segregation.