2 Observations and data reduction

Our data consist of images of 5 fields in the V and R bands, four of which are located as shown in Fig. 1. The fifth field, used as a control field (field F0), is located $42^\prime$N of the cluster centre and was imaged using FORS1 in its standard resolution mode of $0\hbox{$.\!\!^{\prime\prime}$ }2$/pixel.

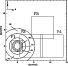Figure 1: Locations of the four FORS1 fields on NGC 6712. The centre of the cluster is located at the origin of the coordinate system. Dashed circles represent the annuli A1-A5 described in the text.

Because the level of crowding varies considerably from the core of the cluster out to its periphery, our observations were carried out according to the following strategy: the fields covering the external regions of the cluster were imaged at low resolution (plate-scale $0\hbox{$.\!\!^{\prime\prime}$ }2$/pixel) and cover an area of 46.2 arcmin square each ( $6\hbox{$.\mkern-4mu^\prime$ }8 \times 6\hbox{$.\mkern-4mu^\prime$ }8$); they are located respectively $5^{\prime}$W (field F2), $8^{\prime}$NW (field F3) and $11^{\prime}$W (field F4) of the centre of the cluster; to improve the photometry in the central regions, where the level of crowding is particularly high, we have covered it with images taken in the high resolution mode of FORS1 (plate-scale $0\hbox{$.\!\!^{\prime\prime}$ }1$/pixel), with a field $3\hbox {$.\mkern -4mu^\prime $ }4 \times 3\hbox {$.\mkern -4mu^\prime $ }4$ in size (field F1, shown in Fig. 2). To ensure a homogeneous calibration and to transform the coordinates into a common local system from the centre of the cluster out to the more external regions, each field has been selected so as to overlap with at least a neighbouring one.

Since NGC 6712 is situated in the midst of a rich star field at the centre of the Scutum cloud (Sandage 1965), which is one of the highest surface-brightness regions with high space-density gradients of the Milky Way (Karaali 1978), we were anticipating that we would have had to deal with significant foreground contamination and, therefore, took the control field F0 in a region situated well away from the cluster but representing a typical field in that area.

The journal of the observations is reported in Table1, where the columns represent respectively: the fields covered, the date of each observation, the distance of the fields from the centre of the cluster and their coordinates, and the exposure time for the single images and for each filter. Also listed in Table1 is the number of stars detected simultaneously in both filters for each observed field (see below).

 

Table 1: Journal of the observations.

Except for a small subset of the R-band images, we have adopted the reduced and calibrated (i.e. bias-subtracted and flat-fielded) data as provided by the standard ESO-VLT pipeline. Some of the raw R-band data, however, had not been processed through the automated pipeline, and for them we had to run standard IRAF routines following the same recipe employed in the ESO-VLT pipeline. Subsequent data reduction and analysis was done using standard IRAF photometry routines (digiphot.daophot).

Since our goal was to reliably detect the faintest object in these images, for each field and filter we first created a mean frame using all the applicable frames available and then ran the standard digiphot.daofind routine on the average images so obtained to locate the stars. Typical values of the PSF-FWHM are $0\hbox{$.\!\!^{\prime\prime}$ }3$ and $0\hbox{$.\!\!^{\prime\prime}$ }7$, respectively at high and low resolution. Although, in principle, we could have also averaged images in different filters, the presence of bad columns in the R-band frames (usually due to heavily saturated pixels and spikes of the bright stars) suggested that we not follow this approach. With a detection threshold set in the V and R band typically at $3{-}5\,\sigma$ above the local average background level, we obtained two independent coordinate lists for each field (one per filter), which we then fed to the PSF-fitting routine allstar to measure the instrumental magnitude of each object in each filter. We found that a Moffat function gave the best representation of the shape of the PSF, both at high and low resolution.

The positions of the identified objects in each mean R- and V-band image were matched to one another, so as to obtain a final catalogue containing only the positions and magnitudes of the stars common to both filters.

Figure 2: VLT-FORS1 high resolution image (180s exposure) of the core of NGC 6712 in the R band (field F1). The size of the image is $3\hbox {$.\mkern -4mu^\prime $ }4 \times 3\hbox {$.\mkern -4mu^\prime $ }4$. North is up and East to the left.

Objects lying in overlapping regions between two adjacent fields were used to determine the transformations between instrumental magnitudes and to translate local frame coordinates to a common coordinate system, with origin at the cluster centre. Typically, about one hundred stars in each overlapping region were used to derive such transformations. Only linear transformations were used to match star measurements, with all magnitudes being referred to those of the high resolution field (F1). For stars in the overlapping region, multiple magnitude measurements were averaged using appropriate weights (which take into account the photometric quality of each field). At the end of this procedure, a homogeneous set of instrumental magnitudes, colours and positions (referred to field F1) were obtained for a total of 106092 stars, in F1, F2, F3 and F4.

Instrumental (F1) magnitudes were finally transformed to the standard Johnson system, using the stars in common with the bright portion of the CMD which has been properly calibrated using 10 standard stars (see Paltrinieri et al. 2001).

Figure 3 shows the total CMD of the central region of NGC 6712 (field F1). The figure is obtained by merging the deep (180 s long exposure) and the bright (10 s exposure) data covering the core of the cluster. In the following, we deal exclusively with the properties of the cluster MS (from the TO at $R \simeq 19$ to $R \simeq 23$; see Table1) while the bright portion of the CMD and the properties of the evolved stellar population are discussed elsewhere (Ferraro et al. 2000; Paltrinieri et al. 2001).

Figure 3: Color-magnitude diagramme of the stars in field F1 (core) of NGC 6712.

2.1 Incompleteness corrections

A reliable assessment of the correction for incompleteness is a crucial step because the main goal of this work is to compare with one another the R-band LFs obtained at different radial distances from the centre of the cluster and to extract in this way information on the underlying global MF. Clearly, the completeness depends on the level of crowding in the observed fields and, therefore, on their location with respect to the cluster centre. In particular, an insufficient or inappropriate correction for crowding will result in the distortion of the stellar LF with a preferential loss of fainter stars and a relative increase of bright and spurious objects. In our case, crowding is not the only source of incompleteness: the distribution in luminosity of the stars is also modified by the large number of hot pixels and bad columns affecting the original images.

To correct our photometry for incompleteness, we ran artificial star tests on both sets of frames (V and R) independently, so as to be able to estimate the overall completeness of our final CMD. First, we applied the artificial star test to the mean R-band images: artificial stars in each given 0.5 mag bin were added randomly to the frames, making sure not to exceed a few percent ($\leq$10%) of the total number of stars actually present in that bin so as to avoid a significant enhancement of image crowding. We then added an equal number of stars at the same positions in the V-band frames and with a magnitude such that they would fall on the cluster MS. It should be noted that we made the assumption that all artificial stars were to lie on the MS since our intent was to verify the photometric completeness of MS stars. This procedure was repeated for all the bins of each field's CMD in both filters. To obtain a robust result, we simulated more than 200000 stars in 250 artificial images for each field. All pairs of V and R frames obtained in this way were then subjected to the same analysis used for the original frames, with the result being a catalogue of matching objects, each characterised by a position and a pair of V and R-band magnitudes. Each of these 250 catalogues (one per artificial pair of images) was compared with the catalogue of input artificial stars: an artificial star was considered detected only when its final position and magnitudes were found to coincide with the input catalogue to within $\Delta x$, $\Delta y \leq 1.5$pixel, $\Delta$mag $\leq 0.3$. This approach allowed us to build a map showing how photometric completeness varies with position in our frames.

If $N_{\rm rec}$ is the number of recovered stars in a given magnitude bin, and $N_{\rm sim}$ the number of the simulated stars in the same bin, the ratio $N_{\rm rec}/N_{\rm sim} = \Phi$ gives the completeness in that bin for the location considered.

2.2 Field subtraction

In addition to correcting for photometric incompleteness, a reliable determination of the LF of NGC 6712 requires that we account for the contamination caused by field stars. We have dealt with this correction in a statistical way by using the comparison field F0, for which we have produced a CMD and assessed photometric incompleteness precisely as we did for all other fields. When it comes to measuring the LF - our final goal - we subtract from the stars found in a given magnitude bin on the cluster CMD the objects detected in the same magnitude bin in an area of equal size on the F0 field. Clearly, both numbers are corrected for their respective photometric incompleteness before doing the subtraction.

By applying the statistical field star subtraction described above, we discovered that stars located in fields F3 and F4 can be considered as belonging to the field because all the objects in the CMD of these fields are statistically compatible with being field stars. We show this in Fig. 4, where we plot the R-band LF, corrected for incompleteness, as measured in fields F3 and F0 (the solid and dashed lines, respectively). The absence of any significant trend or systematic departures of one function with respect to the other (to within $2\sigma$) confirms that there are no residual cluster stars at distances greater than $\sim$$5^{\prime}$ from the cluster centre. As a result of this finding, we decided to consider all stars lying in F3 and F4 as field stars, thus improving the statistical sample of the field, and re-defined the decontamination procedure above using as a comparison field the whole catalogue for F3, F4 and F0 ( $r \geq 5^\prime$). This result also shows that the field around NGC 6712 is relatively uniform at our required level of accuracy and further confirms that the statistical decontamination correction that we apply is reliable.

Figure 4: Luminosity functions measured in fields F0 (dashed line) and F3 (solid line).

We, therefore, regarded only the F1 and F2 fields as containing cluster stars. Because of the richness of our sample of stars, we decided to investigate the variation of the LF as a function of distance on a scale smaller than the typical size of a frame. We have, thus, divided our combined photometric catalogue into a number of annuli which are centered on the cluster centre and whose size increases with distance so as to guarantee a similar number of objects in each of them. Table2 lists the five annuli A1-A5 that we have used, whose positions are also marked in Fig. 1. The columns in Table2 represent, respectively, the position and size of these annuli and the number of objects measured before (N) and after ($N_{\rm S}$) the statistical decontamination. N is the number of objects in the range 19 < R < 22 in each annulus before subtraction for field stars, while $N_{\rm S}$ is the number of objects after that subtraction in the same range (selected so as to have photometric completeness always >50% in each annulus). Correction for photometric incompleteness is always applied before performing the subtraction. We note here that annulus A3 is not properly annular in shape, in that it extends from a radius of $96^{\prime\prime}$ all the way to the edge of field F1. The outer radius given in Table 2 ( $105^{\prime\prime}$) is that which an annulus of equivalent area would have.

 

Table 2: Location of the annuli A1-A5 in arcsec and in units of $r_{\rm h}$ ( $1\hbox {$.\mkern -4mu^\prime $ }3$; Djorgovski 1993); see text for the definition of N and $N_{\rm S}$.

Annulus	$r/1\hbox{$^{\prime\prime}$ }$	$r/r_{\rm h}$	N	$N_{\rm S}$
A1	60-78	0.77-1.00	4335	3573
A2	78-96	1.00-1.23	3742	2794
A3	96-116	1.23-1.34	3433	2169
A4	150-230	1.92-2.94	4434	744
A5	230-320	2.94-4.1	4053	72

We did not use the innermost regions of the cluster ( $r \leq 60^{\prime\prime}$), as the high level of crowding and the large ensuing incompleteness would have resulted in a poor determination of the LF. Moreover, we did not include a region between annuli A3 and A4 because the level of crowding there is too high for the low resolution of the FORS1 camera at $0\hbox{$.\!\!^{\prime\prime}$ }2$/pixel and a standard seeing quality of FWHM $~\simeq 0\hbox{$.\!\!^{\prime\prime}$ }6$.