A&A 372, 1064-1070 (2001)
DOI: 10.1051/0004-6361:20010542
The Si(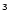 PJ) + O
PJ) + O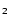 reaction: A fast source of SiO at very low
temperature; CRESU measurements
reaction: A fast source of SiO at very low
temperature; CRESU measurements
and interstellar consequences
S. D. Le Picard1 - A. Canosa1 - G. Pineau des Forêts2 -
C. Rebrion-Rowe1 - B. R. Rowe1
1 - UMR 6627: Physique des Atomes, Lasers, Molécules et Surfaces,
Équipe Astrochimie Expérimentale,
Université de Rennes I, Campus de
Beaulieu, 35042 Rennes Cedex, France
2 -
Observatoire de Paris, 92195 Meudon Principal Cedex, France
Received 8 March 2001 / Accepted 23 March 2001
Abstract
The rate coefficient of the reaction Si(3PJ) + O2
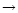 SiO + O
has been measured at temperatures down to 15 K using a CRESU (Cinétique de Réaction en
Écoulement Supersonique Uniforme) apparatus coupled with the PLP-LIF (Pulsed Laser Photolysis
- Laser Induced Fluorescence) technique. The temperature dependence of the rate coefficient
is well fitted using the expression:
SiO + O
has been measured at temperatures down to 15 K using a CRESU (Cinétique de Réaction en
Écoulement Supersonique Uniforme) apparatus coupled with the PLP-LIF (Pulsed Laser Photolysis
- Laser Induced Fluorescence) technique. The temperature dependence of the rate coefficient
is well fitted using the expression:
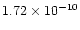 (T/300 K)-0.53
(T/300 K)-0.53
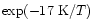 cm3 molecule-1s-1 in the temperature range
15-300 K. The silicon chemistry in interstellar clouds is reviewed and possible
consequences of our study are stressed.
cm3 molecule-1s-1 in the temperature range
15-300 K. The silicon chemistry in interstellar clouds is reviewed and possible
consequences of our study are stressed.
Key words: molecular processes - methods: laboratory - ISM: molecules
The silicon monoxide molecule SiO is the most widespread silicon-bearing
molecule in the interstellar medium. Its abundance, however, shows large
variations under the differing physical conditions of interstellar objects.
The largest fractional abundance (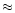
 )
has
been observed in star-forming regions (Martin-Pintado et al. 1992)
whereas it is found to be extremely low in cold dense clouds such as TMC1
and L183 (<
)
has
been observed in star-forming regions (Martin-Pintado et al. 1992)
whereas it is found to be extremely low in cold dense clouds such as TMC1
and L183 (<
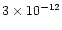 ,
Ziurys et al. 1989). Intermediate
values of about 10-10 were also measured in several translucent
molecular
clouds (Turner 1998), in "spiral arm'' clouds (Greaves et al.
1996), and in photodissociation regions (Schilke et al.
2001). Although several models have been elaborated to explain
the large variations of the SiO abundance, this is still a matter of debate.
Briefly, two main ideas can be found in the literature. It is first argued
that silicon bearing molecules are strongly depleted onto grains in cold
quiescent regions whereas in photodominated regions or in dynamical active
regions their abundance increases due to photodesorption (Turner
1998; Walmsley et al. 1999) from grains or to local
shocks inside which grains are partially destroyed, releasing silicon back
to the gas phase (Gueth et al. 1998; Schilke et al.
1997).
Alternatively, observations by Ziurys et al. (1989) led these
authors
to propose that SiO production is dependent on the kinetic temperature of
the
gas. Their major guess was to suggest that the chemistry has an activation
energy barrier of
,
Ziurys et al. 1989). Intermediate
values of about 10-10 were also measured in several translucent
molecular
clouds (Turner 1998), in "spiral arm'' clouds (Greaves et al.
1996), and in photodissociation regions (Schilke et al.
2001). Although several models have been elaborated to explain
the large variations of the SiO abundance, this is still a matter of debate.
Briefly, two main ideas can be found in the literature. It is first argued
that silicon bearing molecules are strongly depleted onto grains in cold
quiescent regions whereas in photodominated regions or in dynamical active
regions their abundance increases due to photodesorption (Turner
1998; Walmsley et al. 1999) from grains or to local
shocks inside which grains are partially destroyed, releasing silicon back
to the gas phase (Gueth et al. 1998; Schilke et al.
1997).
Alternatively, observations by Ziurys et al. (1989) led these
authors
to propose that SiO production is dependent on the kinetic temperature of
the
gas. Their major guess was to suggest that the chemistry has an activation
energy barrier of 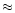 90 K.
Gas phase SiO production in available models occurs via a series of ion-molecule reactions (see for example Herbst et al. 1989) or/and neutral-neutral reactions amongst which
90 K.
Gas phase SiO production in available models occurs via a series of ion-molecule reactions (see for example Herbst et al. 1989) or/and neutral-neutral reactions amongst which
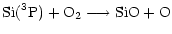 |
|
|
(1) |
and
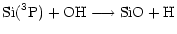 |
|
|
(2) |
are used by almost all models and are the most straightforward.
For instance, Langer & Glassgold (1990) proposed a simple model where SiO is formed mainly via these two reactions. Going deeply into the Ziurys et al. assumptions, Langer & Glassgold extended a theoretical study by Graff (1989) and used rate coefficients proportional to  K/ T where 111 K corresponds to the difference in energy between the first two spin-orbit levels of the silicon ground state: 3P0 and 3P1. This inferred temperature dependence was also used by Schilke et al. (1997) and Turner (1998). Other authors, however, preferred a T0.5 dependence based on the collision theory (Herbst et al. 1989; MacKay 1995, 1996; Turner 1998; Walmsley et al. 1999). In every case, therefore, authors were expecting a lower rate coefficient as the temperature decreased but obviously some clarification was required, as for example stressed by Pineau des Forêts & Flower (1997) who claimed: "It should be noted that Si + O2
K/ T where 111 K corresponds to the difference in energy between the first two spin-orbit levels of the silicon ground state: 3P0 and 3P1. This inferred temperature dependence was also used by Schilke et al. (1997) and Turner (1998). Other authors, however, preferred a T0.5 dependence based on the collision theory (Herbst et al. 1989; MacKay 1995, 1996; Turner 1998; Walmsley et al. 1999). In every case, therefore, authors were expecting a lower rate coefficient as the temperature decreased but obviously some clarification was required, as for example stressed by Pineau des Forêts & Flower (1997) who claimed: "It should be noted that Si + O2
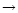 SiO + O is a key reaction for the production of SiO in dense clouds, and it would be interesting to measure the rate coefficient for this neutral-neutral reaction below 300 K''.
From an experimental point of view, indeed, the reaction Si(3P) + O2
SiO + O is a key reaction for the production of SiO in dense clouds, and it would be interesting to measure the rate coefficient for this neutral-neutral reaction below 300 K''.
From an experimental point of view, indeed, the reaction Si(3P) + O2
 SiO + O has only been studied by two groups (Husain & Norris 1978; Swearengen et al. 1978) and only close to room temperature. Husain & Norris (1978) used a slow He flow tube apparatus working at room temperature in which silicon atoms were produced by pulsed irradiation of SiCl4 and detected in absorption in the ultraviolet using resonance radiation derived from a microwave-powered flow lamp. They obtained a fast rate of
SiO + O has only been studied by two groups (Husain & Norris 1978; Swearengen et al. 1978) and only close to room temperature. Husain & Norris (1978) used a slow He flow tube apparatus working at room temperature in which silicon atoms were produced by pulsed irradiation of SiCl4 and detected in absorption in the ultraviolet using resonance radiation derived from a microwave-powered flow lamp. They obtained a fast rate of
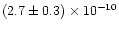 cm3molecule-1s-1 at 300 K. In the fast flow tube experiment by Swearengen et al. (1978), silicon atoms were produced by flowing a mixture of argon and SiH4 through a hollow cathode discharge and their detection was achieved using resonance absorption at 251.6 nm (3p2 3P2
cm3molecule-1s-1 at 300 K. In the fast flow tube experiment by Swearengen et al. (1978), silicon atoms were produced by flowing a mixture of argon and SiH4 through a hollow cathode discharge and their detection was achieved using resonance absorption at 251.6 nm (3p2 3P2
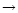 4s 3P1). Although this study was carried out at a slightly higher temperature (350 K) than that of Husain & Norris, Swearengen et al. measured a rate constant which was 30 times lower:
4s 3P1). Although this study was carried out at a slightly higher temperature (350 K) than that of Husain & Norris, Swearengen et al. measured a rate constant which was 30 times lower:
 cm3molecule-1s-1 than the value of Husain & Norris.
In interstellar cloud models, most of the authors interested in the silicon chemistry used the value of Husain & Norris (with the exception of Langer & Glassgold 1990) in their simulations.
cm3molecule-1s-1 than the value of Husain & Norris.
In interstellar cloud models, most of the authors interested in the silicon chemistry used the value of Husain & Norris (with the exception of Langer & Glassgold 1990) in their simulations.
The aim of the present work was therefore to answer the request of Pineau des Forêts & Flower (1997) by studying the kinetics of the Si(3P) + O2
 SiO + O reaction in the temperature range 15-300 K. This work was carried out at the University of Rennes I using the CRESU facility associated to the PLP-LIF technique (Pulsed Laser Photolysis - Laser Induced Fluorescence). In recent years, experiments using this technique, in close collaboration between our laboratory at Rennes and Prof. Ian Smith's laboratory at Birmingham, allowed us to measure the rate coefficients for many rapid neutral reactions at extremely low temperature involving radicals CN, OH, CH, C2H (Smith & Rowe and references therein 2000), and atoms, Al(2P) (Le Picard et al. 1997) and C(3P) (Chastaing et al. 2000, 2001).
SiO + O reaction in the temperature range 15-300 K. This work was carried out at the University of Rennes I using the CRESU facility associated to the PLP-LIF technique (Pulsed Laser Photolysis - Laser Induced Fluorescence). In recent years, experiments using this technique, in close collaboration between our laboratory at Rennes and Prof. Ian Smith's laboratory at Birmingham, allowed us to measure the rate coefficients for many rapid neutral reactions at extremely low temperature involving radicals CN, OH, CH, C2H (Smith & Rowe and references therein 2000), and atoms, Al(2P) (Le Picard et al. 1997) and C(3P) (Chastaing et al. 2000, 2001).
The apparatus will be briefly described in the next section followed by a presentation of the experimental results and their relevance to interstellar environments.
The CRESU apparatus and the PLP-LIF technique have been extensively described elsewhere (Sims et al. 1994) so that only specific features will be reported here.
Low temperatures were achieved via the isentropic expansion of a
buffer gas (argon or helium) through a suitably designed Laval nozzle.
The resulting supersonic flow was found to be axially and radially
uniform in temperature, density and velocity (Sims et al. 1994).
Due to the relatively high density (1016-1018 cm-3) of the expansion, thermal equilibrium is maintained along the flow.
The Laval nozzle was mounted on a moveable reservoir into which the buffer gas
as well as reagent gases were injected. Each nozzle is designed for a given set of temperature and pressure in the supersonic flow so that changes in temperature were achieved by using different nozzles. Our collection of nozzles (about 30) allowed us to work in the temperature range 15-300 K at a typical pressure of 0.2 mbar, although some of the nozzles work at a few mbar (1-6 mbar).
Rate constants were measured using the Pulsed Laser Photolysis (PLP),
Laser Induced Fluorescence (LIF) technique.
The silicon atoms were produced in the supersonic flow by multiphoton photolysis of
tetramethylsilane, Si(CH3)4. Photolysis was achieved using a 266 nm YAG pulsed (10 Hz)
laser beam, propagated along the flow axis through the throat of the Laval Nozzle and focused at
the nozzle exit using a UV lens (37 cm focal length) located inside the moveable reservoir. A
burst of silicon atoms was therefore produced in a small volume around the focal point. It then
took several tens of microseconds to flow and reach the detection zone where a tuneable pulsed
laser beam (MOPO 730, 10Hz), propagating perpendicularly to the flow, excited the 3p2 3P0
 4s 3P1 transition of Si at 251.43 nm. After passing through a narrowband
interference filter centred at 250 nm, the resonant fluorescence was then collected on the
photocathode of a UV-sensitive photomultiplier tube set perpendicular both to the flow axis
and the excitation laser beam.
4s 3P1 transition of Si at 251.43 nm. After passing through a narrowband
interference filter centred at 250 nm, the resonant fluorescence was then collected on the
photocathode of a UV-sensitive photomultiplier tube set perpendicular both to the flow axis
and the excitation laser beam.
The time delay between the two laser pulses was set equal to the time necessary for the silicon atoms formed at the focal point to reach the detection zone. The LIF signal from Si(3P0) atoms was then measured and averaged over 200 laser shots for different oxygen flow rates. Figure 1 presents a typical decrease of the LIF signal as a function of the oxygen density for a given time delay (i.e. a given distance between the focal point and the detection zone).
This decrease was well fitted using an exponential function
![$\exp ^{-k_{\rm 1st}[{\rm O}_2]}$](/articles/aa/full/2001/24/aa1228/img23.gif) where
where
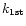 is a first order rate coefficient expressed in cm3 molecule-1 units. Such a set of measurements was then repeated for different focal point positions by moving the Laval nozzle so that several
is a first order rate coefficient expressed in cm3 molecule-1 units. Such a set of measurements was then repeated for different focal point positions by moving the Laval nozzle so that several
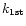 were obtained and plotted as a function of the time delay. This is illustrated in Fig. 2 where data are very well fitted using a straight line, crossing both axes at the origin. The slope of this line gave the second order rate coefficient k (expressed in cm3molecule-1s-1 units) for the conditions of temperature and pressure for the particular Laval nozzle used.
were obtained and plotted as a function of the time delay. This is illustrated in Fig. 2 where data are very well fitted using a straight line, crossing both axes at the origin. The slope of this line gave the second order rate coefficient k (expressed in cm3molecule-1s-1 units) for the conditions of temperature and pressure for the particular Laval nozzle used.
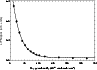 |
Figure 1:
Silicon atoms fluorescence signal as a function of oxygen density at 15 K
for a time delay set to 130 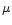 s. s. |
| Open with DEXTER |
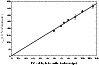 |
Figure 2:
First order rate coefficients
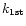 plotted as a function of the time
delay for the Laval nozzle working at 23 K.
plotted as a function of the time
delay for the Laval nozzle working at 23 K. |
| Open with DEXTER |
Due to laser focusing, a large amount of energy was focused into the small volume where the silicon atoms were formed.
The initial spin-orbit population of the Si(3PJ) ground state was therefore found to be strongly off-Boltzmann equilibrium. Furthermore, the first electronic excited state of silicon, Si (1D2), lying 0.78 eV (i.e. 9065 K) above the ground state was also detected resonantly by exciting the transition 3p2 1D2
 4s 1P1 at 288.16 nm. Collisional relaxation of the Si(1D2) state to the Si(3PJ) ground state presented different behaviour according to the nature of the buffer gas. Using argon, we observed a rapid decrease of the 1D2 LIF signal along the supersonic flow, indicating that collisional relaxation occurred rapidly as no 1D2 was ever detected after about 30
4s 1P1 at 288.16 nm. Collisional relaxation of the Si(1D2) state to the Si(3PJ) ground state presented different behaviour according to the nature of the buffer gas. Using argon, we observed a rapid decrease of the 1D2 LIF signal along the supersonic flow, indicating that collisional relaxation occurred rapidly as no 1D2 was ever detected after about 30 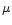 s. On the other hand, using helium as a buffer gas, the Si(1D2) state turned out to relax slowly on the time scale of the experiment. Therefore, for all Laval nozzles working in helium, we introduced a small amount of N2 (
s. On the other hand, using helium as a buffer gas, the Si(1D2) state turned out to relax slowly on the time scale of the experiment. Therefore, for all Laval nozzles working in helium, we introduced a small amount of N2 (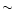 1%) which was found to be a very efficient quencher of Si(1D2).
To ensure the complete spin-orbit relaxation of the Si(3P) states, the three different levels
(J=0, 1, 2) were also individually probed as a function of time, exciting the
transitions 3p2 3P0
1%) which was found to be a very efficient quencher of Si(1D2).
To ensure the complete spin-orbit relaxation of the Si(3P) states, the three different levels
(J=0, 1, 2) were also individually probed as a function of time, exciting the
transitions 3p2 3P0
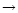 4s 3P1 (251.43 nm), 3p2 3P1
4s 3P1 (251.43 nm), 3p2 3P1
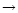 4s 3P2 (250.69 nm), 3p2 3P2
4s 3P2 (250.69 nm), 3p2 3P2
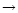 4s 3P2 (251.61 nm) respectively. In every condition, relative intensities of these transitions were found to be constant after about 40
4s 3P2 (251.61 nm) respectively. In every condition, relative intensities of these transitions were found to be constant after about 40 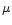 s.
Kinetic measurements, therefore, were only started after relaxation of Si(1D2) and Si(3PJ) had taken place. Consequently, the rate coefficients derived from our experiments concern Si(3PJ) atoms fully thermalised to the temperature of the supersonic flow.
It is worth noting, however, that at 15 K, only the J=0 state was present, whereas at 23 K the signal arising from the J=1 state was hardly detectable. This is consistent with the energy spacing between the fine structure levels of Si(3PJ) since Si(3P1) and Si(3P2) lie at energies equivalent to 111 K and 321 K above Si(3P0) respectively. The lowest temperature measurement presented here can then be considered as a state-selected (J=0) experiment. This is very specific as, usually, state-to-state studies are not possible using the CRESU apparatus since collisional relaxation time scales are much shorter than the reaction time scale. This is essentially due to the high density (1016-1018 cm-3 according to the nozzle used) prevailing in the CRESU supersonic flow.
s.
Kinetic measurements, therefore, were only started after relaxation of Si(1D2) and Si(3PJ) had taken place. Consequently, the rate coefficients derived from our experiments concern Si(3PJ) atoms fully thermalised to the temperature of the supersonic flow.
It is worth noting, however, that at 15 K, only the J=0 state was present, whereas at 23 K the signal arising from the J=1 state was hardly detectable. This is consistent with the energy spacing between the fine structure levels of Si(3PJ) since Si(3P1) and Si(3P2) lie at energies equivalent to 111 K and 321 K above Si(3P0) respectively. The lowest temperature measurement presented here can then be considered as a state-selected (J=0) experiment. This is very specific as, usually, state-to-state studies are not possible using the CRESU apparatus since collisional relaxation time scales are much shorter than the reaction time scale. This is essentially due to the high density (1016-1018 cm-3 according to the nozzle used) prevailing in the CRESU supersonic flow.
Our results for the rate coefficient measurements are summarised in Table 1, which also reports the main flow conditions for each experiment. Only statistical errors are quoted. Some systematic errors due to flow control inaccuracies
or inaccuracies in the determination of the total buffer gas
density should, however, also be taken into account. Every effort was made to minimize these, and we estimate that the additional error does not exceed 10%. A plot of the temperature dependence of the rate constant is presented in Fig. 3, indicating a slight increase of the rate coefficient when the temperature is lowered. Furthermore, a plateau seems to be reached at about 20-40 K followed by a slight decrease. Such a behaviour may result from a possible spin-orbit dependence of the reaction, as at 15 K, only the J=0 was present (see Experimental section). Our results can be well fitted by the following expression in cm3molecule-1s-1 units
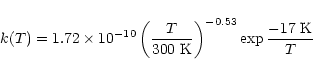 |
(3) |
that we advise the reader to use only in the experimental temperature range (15-300 K).
 |
Figure 3:
Rate constant for the reaction of silicon atoms with O2 as a function of temperature,
displayed in a log-log scale. Experimental results are fitted using the following expression:
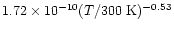
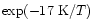 cm3molecule-1s-1,
only valid in the temperature range 15-300 K. cm3molecule-1s-1,
only valid in the temperature range 15-300 K. |
| Open with DEXTER |
Our measurement at room temperature was found to fall in between those of Husain & Norris and Swearengen et al., much closer, however, to the result obtained by the former. Nevertheless Husain & Noris were criticized by Swearengen et al. who claimed that in experiments using the flash lamp photolysis method, the temperature is not precisely known and hot atoms could be produced as well as some oxygen photolysis. In our experiment, the possibility of partial photolysis of the reactant gas O2 due to laser focusing was examined. We returned to a previous study involving reactions of aluminum atoms with molecular oxygen (Le Picard et al. 1997). In this experiment, no focusing of the photolysis laser was required to produce aluminum atoms from the precursor Al(CH3)3. We then repeated that experiment for a given temperature (141 K) using the present protocol and found no significant differences between the measured rate coefficients. We can therefore conclude that the oxygen density was not affected by the focusing of the photolysis laser.
The fraction of elemental silicon which is deduced from observations
of the gas phase varies greatly amongst the different components
of the interstellar medium. In the hot gas, from a few per cent
to 70 per cent of the Si is observed to be in the gas phase in
its ionized form (Si+, Si++)
(Sofia et al. 1994; Fitzpatrick 1996).
In dark clouds, on the other hand, where atomic silicon
reacts with O2 and is rapidly transformed into SiO, as is
now confirmed by the present study, most
of the gas-phase silicon is expected to be in the form of SiO.
This is essentially a result of the high dissociation energy
of SiO (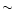 8 eV) and consequent stability (Herbst et al.
1989).
Thus, in steady state as well as in time dependent situations,
it is difficult to construct realistic chemical models where SiO
represents less than ten percent of gas phase silicon.
However, very low upper limits (<
8 eV) and consequent stability (Herbst et al.
1989).
Thus, in steady state as well as in time dependent situations,
it is difficult to construct realistic chemical models where SiO
represents less than ten percent of gas phase silicon.
However, very low upper limits (<
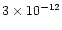 )
have been
established for the SiO/H2 abundance ratio from observations
in several well studied dark clouds (Ziurys et al. 1989;
Martin-Pintado et al. 1992). This suggests a degree of depletion
of silicon relative to the solar value by as much as six orders
of magnitude. In quiescent clouds, silicon must then be present
in the solid phase, most probably in the form of refractory silicate
grains or, possibly, in the ice mantles of dust grains. An
alternative to this assumption was proposed by Langer & Glassgold
(1990) who suggested that reaction (1) would not
proceed if the silicon atoms were in the ground fine-structure state
but would have a dominant effect if the silicon atoms were in the first
excited spin state, J=1. Consequently, they used a rate coefficient
for reaction (1) proportional to
)
have been
established for the SiO/H2 abundance ratio from observations
in several well studied dark clouds (Ziurys et al. 1989;
Martin-Pintado et al. 1992). This suggests a degree of depletion
of silicon relative to the solar value by as much as six orders
of magnitude. In quiescent clouds, silicon must then be present
in the solid phase, most probably in the form of refractory silicate
grains or, possibly, in the ice mantles of dust grains. An
alternative to this assumption was proposed by Langer & Glassgold
(1990) who suggested that reaction (1) would not
proceed if the silicon atoms were in the ground fine-structure state
but would have a dominant effect if the silicon atoms were in the first
excited spin state, J=1. Consequently, they used a rate coefficient
for reaction (1) proportional to 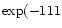 K/T). The main
interest of this model, at that time, was to explain both the
non-detection of SiO in cold dense clouds and the much higher
abundances found in star-forming regions. The present study, however,
definitely rules out the assumption of a possible activation barrier
for the reaction between Si and O2. For a cloud of density
105 cm-3 we have calculated the rate coefficient for the
reaction Si(3P) + O2 at 100 K using Eqs. (1) and (2) from the Langer &
Glassgold paper and the experimental result from Swearengen et al.
which was chosen by these authors. This is three orders of magnitude
lower than our experimental work and the disagreement would be even
larger at lower temperatures. The present study confirms that the
reaction of Si(3P) with O2 is still fast at low temperature and therefore cannot
explain the low upper limit detection of SiO in dense clouds.
Indeed, SiO emission is mostly observed only from dynamically
active regions: molecular outflows, supernovae remnants, the Galactic
centre and more recently, in photodissociation regions, as we will
see below.
K/T). The main
interest of this model, at that time, was to explain both the
non-detection of SiO in cold dense clouds and the much higher
abundances found in star-forming regions. The present study, however,
definitely rules out the assumption of a possible activation barrier
for the reaction between Si and O2. For a cloud of density
105 cm-3 we have calculated the rate coefficient for the
reaction Si(3P) + O2 at 100 K using Eqs. (1) and (2) from the Langer &
Glassgold paper and the experimental result from Swearengen et al.
which was chosen by these authors. This is three orders of magnitude
lower than our experimental work and the disagreement would be even
larger at lower temperatures. The present study confirms that the
reaction of Si(3P) with O2 is still fast at low temperature and therefore cannot
explain the low upper limit detection of SiO in dense clouds.
Indeed, SiO emission is mostly observed only from dynamically
active regions: molecular outflows, supernovae remnants, the Galactic
centre and more recently, in photodissociation regions, as we will
see below.
Large enhancements of the gas-phase silicon abundance are observed
in high velocity components, not only of diffuse clouds (Sofia et al.
1993; Gry et al. 1997), but also of dense
clouds associated with supernova remnants (van Dishoeck et al.
1993).
In molecular outflows, up to 10% of the silicon can be in the gas
phase, in the form of SiO (see, for example, Gueth et al. 1998).
The spatial and velocity distributions of the SiO emission suggest
that SiO is formed in shocked layers, in which grains have been
partially destroyed, releasing silicon into the gas phase. Another piece of
evidence is the fine structure line emission at 68.5 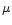 m from
atomic silicon associated with the Orion KL flow observed by Gry
et al. (1999) using the LWS spectrometer on the satellite ISO.
The most likely explanation is that the silicon is sputtered from
the grains by the action of shocks, which are associated with bipolar
outflows, in which case SiO emission is a good tracer of shock activity.
Schilke et al. (1997) have considered the formation of Si
and SiO through non-thermal sputtering of interstellar grain driven by
two-fluid C-type shocks. The silicon is released from the grain cores,
predominantly through impact by particles heavier than He, and then
oxidised in the gas phase.
More recently, Gry et al. (1999) have shown that the observed fine
structure line of Si, together with the observed lines of SiO, is
consistent with C-shock models.
To illustrate the silicon chemistry in a C-shock, we adopted a value
for the density of the preshock gas,
m from
atomic silicon associated with the Orion KL flow observed by Gry
et al. (1999) using the LWS spectrometer on the satellite ISO.
The most likely explanation is that the silicon is sputtered from
the grains by the action of shocks, which are associated with bipolar
outflows, in which case SiO emission is a good tracer of shock activity.
Schilke et al. (1997) have considered the formation of Si
and SiO through non-thermal sputtering of interstellar grain driven by
two-fluid C-type shocks. The silicon is released from the grain cores,
predominantly through impact by particles heavier than He, and then
oxidised in the gas phase.
More recently, Gry et al. (1999) have shown that the observed fine
structure line of Si, together with the observed lines of SiO, is
consistent with C-shock models.
To illustrate the silicon chemistry in a C-shock, we adopted a value
for the density of the preshock gas,
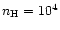 cm-3, which
is within the range of the estimates of densities in molecular outflows.
The initial value of the magnetic induction, B = 100
cm-3, which
is within the range of the estimates of densities in molecular outflows.
The initial value of the magnetic induction, B = 100 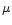 G, was
obtained from the frequently-used scaling relation
B(
G, was
obtained from the frequently-used scaling relation
B(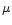 G) = [
G) = [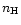 (cm-3)]0.5.
A shock speed of 30 km s-1 was adopted; this value is within
the range of velocities derived from radio emission line profiles,
particularly of SiO, and is sufficient to cause sputtering of
refractory grain materials, such as silicates (Field et al. 1997).
Other information on initial conditions is to be found in Schilke
et al. (1997).
The mantles of the grains are rapidly removed in the shock wave,
exposing the grain core. In the model presented here, about ten per
cent of the elemental silicon is then released from the grain nucleus,
by sputtering. Latest low energy sputtering yields on olivine
(MgFeSiO4), using the TRIM code and computed by May et al.
(2000), have been used in this model.
Once in the gas phase, the atomic silicon is oxidised, first to
SiO via reaction (1) and (2) and subsequently to SiO2,
through the reaction
(cm-3)]0.5.
A shock speed of 30 km s-1 was adopted; this value is within
the range of velocities derived from radio emission line profiles,
particularly of SiO, and is sufficient to cause sputtering of
refractory grain materials, such as silicates (Field et al. 1997).
Other information on initial conditions is to be found in Schilke
et al. (1997).
The mantles of the grains are rapidly removed in the shock wave,
exposing the grain core. In the model presented here, about ten per
cent of the elemental silicon is then released from the grain nucleus,
by sputtering. Latest low energy sputtering yields on olivine
(MgFeSiO4), using the TRIM code and computed by May et al.
(2000), have been used in this model.
Once in the gas phase, the atomic silicon is oxidised, first to
SiO via reaction (1) and (2) and subsequently to SiO2,
through the reaction
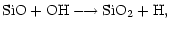 |
|
|
(4) |
owing to the enhanced abundance of OH in the postshock gas.
However, discrepancies exist in the rate constant of this latter reaction.
Figures 4 and 5 compares fractional abundances, expressed
as functions of the flow time (i.e. the time required by a fluid particle
to flow through the shock), and illustrates the crucial role played by
this second oxidation on the silicon chemistry.
In Fig. 4 a rate constant of
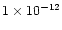 (T/300 K)-0.70 cm3molecule-1s-1 for reaction (4) has been used (Schilke et al. 1997). In this model,
SiO2 is the most abundant Si-bearing species for times comparable
with the estimated lifetimes of molecular clouds (few 105 yr),
when the fractional abundance of SiO is only of the order of 10-9.
SiO2 is ultimately destroyed in reactions with ions, yielding SiO in
the far postshock gas. However, in molecular outflows associated with
low-mass star formation, the dynamical timescales (
103-104 yr)
are too short for the oxidation of SiO to SiO2 to be completed,
and so Si and SiO are likely to be the most abundant silicon-bearing
species in the hot gas. If adsorption processes are neglected, SiO2
(which is a stable molecule) is practically the only Si-bearing species
in the postshock gas for a time as long as
(T/300 K)-0.70 cm3molecule-1s-1 for reaction (4) has been used (Schilke et al. 1997). In this model,
SiO2 is the most abundant Si-bearing species for times comparable
with the estimated lifetimes of molecular clouds (few 105 yr),
when the fractional abundance of SiO is only of the order of 10-9.
SiO2 is ultimately destroyed in reactions with ions, yielding SiO in
the far postshock gas. However, in molecular outflows associated with
low-mass star formation, the dynamical timescales (
103-104 yr)
are too short for the oxidation of SiO to SiO2 to be completed,
and so Si and SiO are likely to be the most abundant silicon-bearing
species in the hot gas. If adsorption processes are neglected, SiO2
(which is a stable molecule) is practically the only Si-bearing species
in the postshock gas for a time as long as
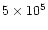 yr, but
is invisible as it does not possess a permanent dipole moment.
It is eventually destroyed in reactions with atomic ions, and SiO
becomes the main silicon bearing species, as predicted by steady-state
models of the gas-phase chemistry in dark clouds (Herbst et al.
1989). SiO may then have a very low abundance in the postshock
gas during its lifetime. This could explain why it appears to be absent
from the gas phase of dark clouds (Ziurys et al. 1989).
yr, but
is invisible as it does not possess a permanent dipole moment.
It is eventually destroyed in reactions with atomic ions, and SiO
becomes the main silicon bearing species, as predicted by steady-state
models of the gas-phase chemistry in dark clouds (Herbst et al.
1989). SiO may then have a very low abundance in the postshock
gas during its lifetime. This could explain why it appears to be absent
from the gas phase of dark clouds (Ziurys et al. 1989).
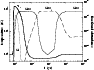 |
Figure 4:
Abundances of Si (dotted line), SiO (full line) and SiO2
(dashed line) computed in the C-shock model, plotted as a function of the
flow time along the direction of shock propagation. The temperature of
neutral species (bold line) is shown for comparison (left-hand axis).
The preshock gas is to the left. Calculations are for a model with
preshock density 104 cm-3, shock velocity 30 km s-1,
and preshock magnetic field 100 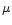 G. A rate constant of G. A rate constant of
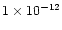 (T/300 K)-0.70 cm3molecule-1s-1 for reaction
(4) have been used.
(T/300 K)-0.70 cm3molecule-1s-1 for reaction
(4) have been used. |
| Open with DEXTER |
Theoretical calculations have been made however by Zachariah & Tsang
(1995) on chemical reactions involving silicon bearing
molecules, leading to a rate constant for reaction (4) of
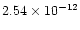 (T/300 K)0.78
(T/300 K)0.78
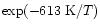 cm3molecule-1s-1
(see their Table 7). As these calculations were made for a high temperature
range (1000-2500 K), this rate constant, and more specifically the activation
barrier, remains highly speculative for temperatures as low as 10 K that we are
interested in. Figure 5 shows the same shock model as in Fig. 4, but using this rate constant. Owing to the activation
barrier of reaction SiO + OH, no SiO2 formation occurs and SiO
remains the main silicon bearing molecule in the cold postshock gas.
If such an activation barrier exists, an explanation of the absence
of SiO in dark clouds is still to be found. This is the reason why
it would be extremely interesting to measure the rate coefficient
of this second oxidation at low temperature.
cm3molecule-1s-1
(see their Table 7). As these calculations were made for a high temperature
range (1000-2500 K), this rate constant, and more specifically the activation
barrier, remains highly speculative for temperatures as low as 10 K that we are
interested in. Figure 5 shows the same shock model as in Fig. 4, but using this rate constant. Owing to the activation
barrier of reaction SiO + OH, no SiO2 formation occurs and SiO
remains the main silicon bearing molecule in the cold postshock gas.
If such an activation barrier exists, an explanation of the absence
of SiO in dark clouds is still to be found. This is the reason why
it would be extremely interesting to measure the rate coefficient
of this second oxidation at low temperature.
 |
Figure 5:
Same model as in Fig. 4 where a rate constant of
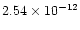 (T/300 K)0.78
(T/300 K)0.78
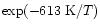 cm3molecule-1s-1
for reaction (4) have been used (Zachariah & Tsang 1995).
cm3molecule-1s-1
for reaction (4) have been used (Zachariah & Tsang 1995). |
| Open with DEXTER |
There is also evidence that photodesorption, through UV radiation
from nearby stars, brings silicon back into the gas phase.
The observations of the Orion Bar represent
an interesting test case. Jansen et al. (1995) deduced from
their observations in Orion Bar an upper limit on the SiO
abundance of [SiO]/[H] less than 10-10, which corresponds
to less than
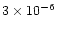 of the solar abundance of silicon.
However, in recent observations of the Orion Bar (Schilke et al.
2001), SiO has been detected with the IRAM 30-m telescope
at levels consistent with the previous upper limits.
The Si+ fine structure line at 35
of the solar abundance of silicon.
However, in recent observations of the Orion Bar (Schilke et al.
2001), SiO has been detected with the IRAM 30-m telescope
at levels consistent with the previous upper limits.
The Si+ fine structure line at 35 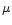 m wavelength has also
been detected in several PDRs, including Orion Bar (Haas et al. 1986).
It appears to be fairly certain that this line is emitted from a
partially ionized (neutral) layer and not from the adjacent ionized
gas. Schilke et al. (2001) estimate that the observed
column density of SiO is roughly five orders of magnitude less than
Si+; which makes it difficult to reconcile the SiO measurements
with the column density inferred from the fine structure line.
Walmsley et al. (1999) computed a PDR model and concluded that
the data could be consistent with silicon being photodesorbed
(with a small photodesorption yield) for FUV photons incident
on silicate dust grains.
To illustrate the chemistry of Si-bearing species in a PDR,
we present in Fig. 6 a model, for the conditions of the Orion Bar,
showing the fractional abundances of Si+, Si and SiO as
a function of depth (parameterized in terms of the visual
extinction
m wavelength has also
been detected in several PDRs, including Orion Bar (Haas et al. 1986).
It appears to be fairly certain that this line is emitted from a
partially ionized (neutral) layer and not from the adjacent ionized
gas. Schilke et al. (2001) estimate that the observed
column density of SiO is roughly five orders of magnitude less than
Si+; which makes it difficult to reconcile the SiO measurements
with the column density inferred from the fine structure line.
Walmsley et al. (1999) computed a PDR model and concluded that
the data could be consistent with silicon being photodesorbed
(with a small photodesorption yield) for FUV photons incident
on silicate dust grains.
To illustrate the chemistry of Si-bearing species in a PDR,
we present in Fig. 6 a model, for the conditions of the Orion Bar,
showing the fractional abundances of Si+, Si and SiO as
a function of depth (parameterized in terms of the visual
extinction 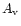 ). We assume the incident radiation field to
be a factor of
). We assume the incident radiation field to
be a factor of
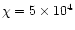 times the standard
interstellar UV field, and the hydrogen density
times the standard
interstellar UV field, and the hydrogen density 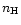 to be
to be
 cm-3 (see Walmsley et al. 1999,
for more details on the parameters of the model).
In contrast to the case of shocks, sputtering is expected
to play no role in a PDR. Instead, we consider the case that
silicon is ejected into the gas phase in atomic form, due to
photodesorption from a refractory grain surface component,
and using a photodesorption yield which has been deduced
from the observations of Turner (1998).
The importance of the reaction of Si with OH has the consequence
that the silicon chemistry in a PDR is also sensitive to the OH
abundance, formed at high temperature through the reaction O + H2,
and consequently to the kinetic temperature variation
with depth. In this case, the region where OH is abundant
(
cm-3 (see Walmsley et al. 1999,
for more details on the parameters of the model).
In contrast to the case of shocks, sputtering is expected
to play no role in a PDR. Instead, we consider the case that
silicon is ejected into the gas phase in atomic form, due to
photodesorption from a refractory grain surface component,
and using a photodesorption yield which has been deduced
from the observations of Turner (1998).
The importance of the reaction of Si with OH has the consequence
that the silicon chemistry in a PDR is also sensitive to the OH
abundance, formed at high temperature through the reaction O + H2,
and consequently to the kinetic temperature variation
with depth. In this case, the region where OH is abundant
(
 )
is sufficiently close to the ionization front
(
)
is sufficiently close to the ionization front
(
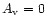 )
that Si photoionization is a competitive process.
It should be noted that the SiO + OH reaction discussed
in Sect. 4.2 plays no role in PDRs models as the destruction
of SiO is dominated by photodissociation.
The SiO abundance is of the order of 10-10 and is thus
similar to the limit of Jansen et al. (1995) and a few times larger
than the recent measured value of Schilke et al.
(2001).
The main conclusion is that the Si+ fine structure
emission observed in many PDRs is likely to be a consequence of
photo-erosion of grain mantles at depths corresponding to a few
magnitudes of visual extinction. A small photodesorption yield,
together with the assumption that silicon comes off in atomic
form, suffice to explain the weakness of the emission from SiO
in the Orion Bar and to account for the observed Si+.
Modest amounts of atomic Si (typically 0.001 of the ionized Si)
are predicted by such models.
In cold gas phase chemistry, SiO appears to be the main
form of silicon and is formed through the reaction
Si(3P) + O2
)
that Si photoionization is a competitive process.
It should be noted that the SiO + OH reaction discussed
in Sect. 4.2 plays no role in PDRs models as the destruction
of SiO is dominated by photodissociation.
The SiO abundance is of the order of 10-10 and is thus
similar to the limit of Jansen et al. (1995) and a few times larger
than the recent measured value of Schilke et al.
(2001).
The main conclusion is that the Si+ fine structure
emission observed in many PDRs is likely to be a consequence of
photo-erosion of grain mantles at depths corresponding to a few
magnitudes of visual extinction. A small photodesorption yield,
together with the assumption that silicon comes off in atomic
form, suffice to explain the weakness of the emission from SiO
in the Orion Bar and to account for the observed Si+.
Modest amounts of atomic Si (typically 0.001 of the ionized Si)
are predicted by such models.
In cold gas phase chemistry, SiO appears to be the main
form of silicon and is formed through the reaction
Si(3P) + O2
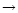 SiO + O, but SiO remains undetected
in dark clouds.
In addition to this reaction, the key reactions are
Si(3P) + OH
SiO + O, but SiO remains undetected
in dark clouds.
In addition to this reaction, the key reactions are
Si(3P) + OH
 SiO + H which can dominate the formation
of SiO in the hot gas, and SiO + OH forming SiO2 which is "invisible''
and could be, partly, the reservoir of silicon-bearing species
in the cold gas. It would then be interesting to measure the rate
coefficients of these two reactions at low temperature in the
laboratory. This is presently, however, a difficult task, as when studying radical-radical reactions, one of the reactants has to be produced in large, well-known, and variable amounts. Furthermore, not only is the silicon sputtered from the silicate grains in the shock regions, but also Fe and Mg,
which have not been detected in a molecular form. The study
of oxidation of these two species by laboratory work and
theoretical studies would also be very valuable.
Another crucial parameter for oxidation to occur in molecular
clouds is the O2 fractional abundance. We note that recent
results from the SWAS satellite (Goldsmith et al. 2000)
suggest upper limits to the [O2]/[H] abundance ratio
of 10-6.
SiO + H which can dominate the formation
of SiO in the hot gas, and SiO + OH forming SiO2 which is "invisible''
and could be, partly, the reservoir of silicon-bearing species
in the cold gas. It would then be interesting to measure the rate
coefficients of these two reactions at low temperature in the
laboratory. This is presently, however, a difficult task, as when studying radical-radical reactions, one of the reactants has to be produced in large, well-known, and variable amounts. Furthermore, not only is the silicon sputtered from the silicate grains in the shock regions, but also Fe and Mg,
which have not been detected in a molecular form. The study
of oxidation of these two species by laboratory work and
theoretical studies would also be very valuable.
Another crucial parameter for oxidation to occur in molecular
clouds is the O2 fractional abundance. We note that recent
results from the SWAS satellite (Goldsmith et al. 2000)
suggest upper limits to the [O2]/[H] abundance ratio
of 10-6.
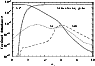 |
Figure 6:
Abundances of Si-containing species as functions of
depth for the temperature profile (
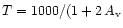 )
K).
Calculations were carried out for a constant photodesorption
yield of )
K).
Calculations were carried out for a constant photodesorption
yield of
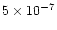 .
Bold dots show the variation of the
abundance of Si in "refractory form'', whereas the dashed lines
and the full curve show the variation of gaseous SiO and Si+,
respectively; the light dots indicate atomic silicon. .
Bold dots show the variation of the
abundance of Si in "refractory form'', whereas the dashed lines
and the full curve show the variation of gaseous SiO and Si+,
respectively; the light dots indicate atomic silicon. |
| Open with DEXTER |
A key role in understanding the balance between solid
and gaseous phases in the interstellar medium is played by
interstellar silicon, which is known to be depleted both in
diffuse and dense interstellar clouds. The computed sputtering
yields using the TRIM code (May et al. 2000) are a first
step but laboratory studies of low energy sputtering yields
for ions incident upon different silicate materials containing
Fe, Mg and Si are also needed.
Finally, another key problem which remains to be studied is
how Si (and other refractory species) gets onto grains in
molecular clouds and, more specifically, how Si reaches
sites of high binding energy.
Acknowledgements
We wish to thank the Programme National "Physique Chimie du Milieu Interstellaire'' and the European community under the Training and Mobility of Researchers programme (Astrophysical Chemistry network) for funding this work and also our colleagues from the University of Birmingham for having
kindly lent us their 15 K nozzle. We are also grateful to Prof. Brian Mitchell for his comments on this manuscript.
-
Chastaing, D., Le Picard, S. D., & Sims, I. R. 2000, J. Chem. Phys., 112, 8466
In the text
NASA ADS
-
Chastaing, D., Le Picard, S. D., Sims, I. R., & Smith, I. W. M. 2001, A&A, 365, 241
In the text
NASA ADS
-
Field, D., May, P. W., Pineau des Forêts, G., & Flower, D. R. 1997, MNRAS, 285, 839
In the text
NASA ADS
-
Fitzpatrick, E. L. 1996, ApJ 473, L55
In the text
NASA ADS
-
Goldsmith, P. F., Melnick, G. J., Bergin, E. A., et al. 2000, ApJS, 539, L123
In the text
-
Graff, M. M. 1989, ApJ, 339, 239
In the text
NASA ADS
-
Greaves, J. S., Ohishi, M., & Nyman, L. A. 1996, A&A, 307, 898
In the text
NASA ADS
-
Gry, C., Boulanger, F., Falgarone, E., Pineau des Forêts, G., & Lequeux J. 1997, A&A, 331, 1070
In the text
NASA ADS
-
Gry, C., Pineau des Forêts, G., & Walmsley, C. M. 1999, A&A, 348, 227
In the text
NASA ADS
-
Gueth, F., Guilloteau, S., & Bachiller, R. 1998, A&A, 333, 287
In the text
NASA ADS
-
Haas, M. R, Hollenbach, D. J., & Erickson, E. F. 1986, ApJ, 301, L57
In the text
NASA ADS
-
Herbst, E., Millar, T. J., Wlodek, S., & Bohme, D. K. 1989,
A&A, 222, 205
In the text
NASA ADS
- Husain, D., & Norris, P. E. 1978,
J. Chem. Soc. Faraday Trans. II, 74, 93
In the text
-
Jansen, D. J., Spaans, M., Hogerheijde, M. R., & van Dishoeck, E. F. 1995, A&A, 303, 541
In the text
NASA ADS
-
Jones, A. P., Tielens, A. G. G. M., Hollenbach, D. J., & McKee, C. F.
1994, ApJ, 433, 797
NASA ADS
-
Langer, W. D., & Glassgold, A. E. 1990,
ApJ, 352, 123
In the text
NASA ADS
-
Le Picard, S. D., Canosa, A., Travers, D., et al. 1997,
J. Phys. Chem., 131, 529
In the text
-
MacKay, D. D. S. 1995,
MNRAS, 274, 694
In the text
NASA ADS
-
MacKay, D. D. S. 1996,
MNRAS, 278, 62
In the text
NASA ADS
-
Martin-Pintado, J., Bachiller, R., & Fuente, A. 1992, A&A, 254, 315
In the text
NASA ADS
-
May, P. W., Pineau des Forêts, G., Flower, et al. 2000, MNRAS, 318, 809
In the text
NASA ADS
-
Pineau des Forêts, G., & Flower, D. R. 1997,
Molecules in Astrophys.: Probes and Proce.; Int. Astr.
Union, Symposium No. 178, 113 (Kluwer Academic.)
In the text
-
Schilke, P., Walmsley, C. M., Pineau des Forêts, G., & Flower, D. R. 1997,
A&A, 321, 293
In the text
NASA ADS
-
Schilke, P., Pineau des Forêts, G., Walmsley, C. M., & Martin-Pintado,
J. 2000, A&A, in press
In the text
-
Sims, I. R., Queffelec, J. L., Defrance, A., et al. 1994, J. Chem. Phys., 100, 4229
In the text
NASA ADS
-
Smith, I. W. M., & Rowe, B. R. 2000, Acc. Chem. Res., 33, 261
In the text
-
Sofia, U. J., Savage, B. D., & Cardelli, J. A. 1993, ApJ, 423, 251
In the text
-
Sofia, U. J., Cardelli, J. A., & Savage, B. D. 1994, ApJ, 430, 650
In the text
NASA ADS
- Swearengen, P. M., Davis, S. J., & Niemczyk T. M. 1978, Chem. Phys. Lett., 55, 274
In the text
-
Turner, B. E. 1998, ApJ, 495, 804
In the text
NASA ADS
-
van Dishoeck, E. F., Jansen, D. J., & Phillips, T. G. 1993, A&A, 279, 541
In the text
NASA ADS
-
Walmsley, C. M., Pineau des Forêts, G., & Flower, D. R. 1999, A&A, 342, 542
In the text
NASA ADS
-
Zachariah, M. R., & Tsang W. 1995, J. Phys. Chem., 99, 5308
In the text
-
Ziurys, L. M., Friberg, P., & Irvine, W. M. 1989, ApJ, 343, 201
In the text
NASA ADS
Copyright ESO 2001
![]() SiO + O
has been measured at temperatures down to 15 K using a CRESU (Cinétique de Réaction en
Écoulement Supersonique Uniforme) apparatus coupled with the PLP-LIF (Pulsed Laser Photolysis
- Laser Induced Fluorescence) technique. The temperature dependence of the rate coefficient
is well fitted using the expression:
SiO + O
has been measured at temperatures down to 15 K using a CRESU (Cinétique de Réaction en
Écoulement Supersonique Uniforme) apparatus coupled with the PLP-LIF (Pulsed Laser Photolysis
- Laser Induced Fluorescence) technique. The temperature dependence of the rate coefficient
is well fitted using the expression:
![]() (T/300 K)-0.53
(T/300 K)-0.53
![]() cm3 molecule-1s-1 in the temperature range
15-300 K. The silicon chemistry in interstellar clouds is reviewed and possible
consequences of our study are stressed.
cm3 molecule-1s-1 in the temperature range
15-300 K. The silicon chemistry in interstellar clouds is reviewed and possible
consequences of our study are stressed.
![]() SiO + O reaction in the temperature range 15-300 K. This work was carried out at the University of Rennes I using the CRESU facility associated to the PLP-LIF technique (Pulsed Laser Photolysis - Laser Induced Fluorescence). In recent years, experiments using this technique, in close collaboration between our laboratory at Rennes and Prof. Ian Smith's laboratory at Birmingham, allowed us to measure the rate coefficients for many rapid neutral reactions at extremely low temperature involving radicals CN, OH, CH, C2H (Smith & Rowe and references therein 2000), and atoms, Al(2P) (Le Picard et al. 1997) and C(3P) (Chastaing et al. 2000, 2001).
SiO + O reaction in the temperature range 15-300 K. This work was carried out at the University of Rennes I using the CRESU facility associated to the PLP-LIF technique (Pulsed Laser Photolysis - Laser Induced Fluorescence). In recent years, experiments using this technique, in close collaboration between our laboratory at Rennes and Prof. Ian Smith's laboratory at Birmingham, allowed us to measure the rate coefficients for many rapid neutral reactions at extremely low temperature involving radicals CN, OH, CH, C2H (Smith & Rowe and references therein 2000), and atoms, Al(2P) (Le Picard et al. 1997) and C(3P) (Chastaing et al. 2000, 2001).
![]() 4s 3P1 transition of Si at 251.43 nm. After passing through a narrowband
interference filter centred at 250 nm, the resonant fluorescence was then collected on the
photocathode of a UV-sensitive photomultiplier tube set perpendicular both to the flow axis
and the excitation laser beam.
4s 3P1 transition of Si at 251.43 nm. After passing through a narrowband
interference filter centred at 250 nm, the resonant fluorescence was then collected on the
photocathode of a UV-sensitive photomultiplier tube set perpendicular both to the flow axis
and the excitation laser beam.
![]() where
where
![]() is a first order rate coefficient expressed in cm3 molecule-1 units. Such a set of measurements was then repeated for different focal point positions by moving the Laval nozzle so that several
is a first order rate coefficient expressed in cm3 molecule-1 units. Such a set of measurements was then repeated for different focal point positions by moving the Laval nozzle so that several
![]() were obtained and plotted as a function of the time delay. This is illustrated in Fig. 2 where data are very well fitted using a straight line, crossing both axes at the origin. The slope of this line gave the second order rate coefficient k (expressed in cm3molecule-1s-1 units) for the conditions of temperature and pressure for the particular Laval nozzle used.
were obtained and plotted as a function of the time delay. This is illustrated in Fig. 2 where data are very well fitted using a straight line, crossing both axes at the origin. The slope of this line gave the second order rate coefficient k (expressed in cm3molecule-1s-1 units) for the conditions of temperature and pressure for the particular Laval nozzle used.


![]() 4s 1P1 at 288.16 nm. Collisional relaxation of the Si(1D2) state to the Si(3PJ) ground state presented different behaviour according to the nature of the buffer gas. Using argon, we observed a rapid decrease of the 1D2 LIF signal along the supersonic flow, indicating that collisional relaxation occurred rapidly as no 1D2 was ever detected after about 30
4s 1P1 at 288.16 nm. Collisional relaxation of the Si(1D2) state to the Si(3PJ) ground state presented different behaviour according to the nature of the buffer gas. Using argon, we observed a rapid decrease of the 1D2 LIF signal along the supersonic flow, indicating that collisional relaxation occurred rapidly as no 1D2 was ever detected after about 30 ![]() s. On the other hand, using helium as a buffer gas, the Si(1D2) state turned out to relax slowly on the time scale of the experiment. Therefore, for all Laval nozzles working in helium, we introduced a small amount of N2 (
s. On the other hand, using helium as a buffer gas, the Si(1D2) state turned out to relax slowly on the time scale of the experiment. Therefore, for all Laval nozzles working in helium, we introduced a small amount of N2 (![]() 1%) which was found to be a very efficient quencher of Si(1D2).
To ensure the complete spin-orbit relaxation of the Si(3P) states, the three different levels
(J=0, 1, 2) were also individually probed as a function of time, exciting the
transitions 3p2 3P0
1%) which was found to be a very efficient quencher of Si(1D2).
To ensure the complete spin-orbit relaxation of the Si(3P) states, the three different levels
(J=0, 1, 2) were also individually probed as a function of time, exciting the
transitions 3p2 3P0
![]() 4s 3P1 (251.43 nm), 3p2 3P1
4s 3P1 (251.43 nm), 3p2 3P1
![]() 4s 3P2 (250.69 nm), 3p2 3P2
4s 3P2 (250.69 nm), 3p2 3P2
![]() 4s 3P2 (251.61 nm) respectively. In every condition, relative intensities of these transitions were found to be constant after about 40
4s 3P2 (251.61 nm) respectively. In every condition, relative intensities of these transitions were found to be constant after about 40 ![]() s.
Kinetic measurements, therefore, were only started after relaxation of Si(1D2) and Si(3PJ) had taken place. Consequently, the rate coefficients derived from our experiments concern Si(3PJ) atoms fully thermalised to the temperature of the supersonic flow.
It is worth noting, however, that at 15 K, only the J=0 state was present, whereas at 23 K the signal arising from the J=1 state was hardly detectable. This is consistent with the energy spacing between the fine structure levels of Si(3PJ) since Si(3P1) and Si(3P2) lie at energies equivalent to 111 K and 321 K above Si(3P0) respectively. The lowest temperature measurement presented here can then be considered as a state-selected (J=0) experiment. This is very specific as, usually, state-to-state studies are not possible using the CRESU apparatus since collisional relaxation time scales are much shorter than the reaction time scale. This is essentially due to the high density (1016-1018 cm-3 according to the nozzle used) prevailing in the CRESU supersonic flow.
s.
Kinetic measurements, therefore, were only started after relaxation of Si(1D2) and Si(3PJ) had taken place. Consequently, the rate coefficients derived from our experiments concern Si(3PJ) atoms fully thermalised to the temperature of the supersonic flow.
It is worth noting, however, that at 15 K, only the J=0 state was present, whereas at 23 K the signal arising from the J=1 state was hardly detectable. This is consistent with the energy spacing between the fine structure levels of Si(3PJ) since Si(3P1) and Si(3P2) lie at energies equivalent to 111 K and 321 K above Si(3P0) respectively. The lowest temperature measurement presented here can then be considered as a state-selected (J=0) experiment. This is very specific as, usually, state-to-state studies are not possible using the CRESU apparatus since collisional relaxation time scales are much shorter than the reaction time scale. This is essentially due to the high density (1016-1018 cm-3 according to the nozzle used) prevailing in the CRESU supersonic flow.
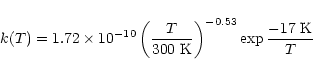

![]() m from
atomic silicon associated with the Orion KL flow observed by Gry
et al. (1999) using the LWS spectrometer on the satellite ISO.
The most likely explanation is that the silicon is sputtered from
the grains by the action of shocks, which are associated with bipolar
outflows, in which case SiO emission is a good tracer of shock activity.
Schilke et al. (1997) have considered the formation of Si
and SiO through non-thermal sputtering of interstellar grain driven by
two-fluid C-type shocks. The silicon is released from the grain cores,
predominantly through impact by particles heavier than He, and then
oxidised in the gas phase.
More recently, Gry et al. (1999) have shown that the observed fine
structure line of Si, together with the observed lines of SiO, is
consistent with C-shock models.
To illustrate the silicon chemistry in a C-shock, we adopted a value
for the density of the preshock gas,
m from
atomic silicon associated with the Orion KL flow observed by Gry
et al. (1999) using the LWS spectrometer on the satellite ISO.
The most likely explanation is that the silicon is sputtered from
the grains by the action of shocks, which are associated with bipolar
outflows, in which case SiO emission is a good tracer of shock activity.
Schilke et al. (1997) have considered the formation of Si
and SiO through non-thermal sputtering of interstellar grain driven by
two-fluid C-type shocks. The silicon is released from the grain cores,
predominantly through impact by particles heavier than He, and then
oxidised in the gas phase.
More recently, Gry et al. (1999) have shown that the observed fine
structure line of Si, together with the observed lines of SiO, is
consistent with C-shock models.
To illustrate the silicon chemistry in a C-shock, we adopted a value
for the density of the preshock gas,
![]() cm-3, which
is within the range of the estimates of densities in molecular outflows.
The initial value of the magnetic induction, B = 100
cm-3, which
is within the range of the estimates of densities in molecular outflows.
The initial value of the magnetic induction, B = 100 ![]() G, was
obtained from the frequently-used scaling relation
B(
G, was
obtained from the frequently-used scaling relation
B(![]() G) = [
G) = [![]() (cm-3)]0.5.
A shock speed of 30 km s-1 was adopted; this value is within
the range of velocities derived from radio emission line profiles,
particularly of SiO, and is sufficient to cause sputtering of
refractory grain materials, such as silicates (Field et al. 1997).
Other information on initial conditions is to be found in Schilke
et al. (1997).
The mantles of the grains are rapidly removed in the shock wave,
exposing the grain core. In the model presented here, about ten per
cent of the elemental silicon is then released from the grain nucleus,
by sputtering. Latest low energy sputtering yields on olivine
(MgFeSiO4), using the TRIM code and computed by May et al.
(2000), have been used in this model.
Once in the gas phase, the atomic silicon is oxidised, first to
SiO via reaction (1) and (2) and subsequently to SiO2,
through the reaction
(cm-3)]0.5.
A shock speed of 30 km s-1 was adopted; this value is within
the range of velocities derived from radio emission line profiles,
particularly of SiO, and is sufficient to cause sputtering of
refractory grain materials, such as silicates (Field et al. 1997).
Other information on initial conditions is to be found in Schilke
et al. (1997).
The mantles of the grains are rapidly removed in the shock wave,
exposing the grain core. In the model presented here, about ten per
cent of the elemental silicon is then released from the grain nucleus,
by sputtering. Latest low energy sputtering yields on olivine
(MgFeSiO4), using the TRIM code and computed by May et al.
(2000), have been used in this model.
Once in the gas phase, the atomic silicon is oxidised, first to
SiO via reaction (1) and (2) and subsequently to SiO2,
through the reaction

![]() (T/300 K)0.78
(T/300 K)0.78
![]() cm3molecule-1s-1
(see their Table 7). As these calculations were made for a high temperature
range (1000-2500 K), this rate constant, and more specifically the activation
barrier, remains highly speculative for temperatures as low as 10 K that we are
interested in. Figure 5 shows the same shock model as in Fig. 4, but using this rate constant. Owing to the activation
barrier of reaction SiO + OH, no SiO2 formation occurs and SiO
remains the main silicon bearing molecule in the cold postshock gas.
If such an activation barrier exists, an explanation of the absence
of SiO in dark clouds is still to be found. This is the reason why
it would be extremely interesting to measure the rate coefficient
of this second oxidation at low temperature.
cm3molecule-1s-1
(see their Table 7). As these calculations were made for a high temperature
range (1000-2500 K), this rate constant, and more specifically the activation
barrier, remains highly speculative for temperatures as low as 10 K that we are
interested in. Figure 5 shows the same shock model as in Fig. 4, but using this rate constant. Owing to the activation
barrier of reaction SiO + OH, no SiO2 formation occurs and SiO
remains the main silicon bearing molecule in the cold postshock gas.
If such an activation barrier exists, an explanation of the absence
of SiO in dark clouds is still to be found. This is the reason why
it would be extremely interesting to measure the rate coefficient
of this second oxidation at low temperature.

