A&A 372, 730-754 (2001)
DOI: 10.1051/0004-6361:20010489
A spectrophotometric atlas of Narrow-Line Seyfert 1 galaxies
M.-P. Véron-Cetty 1 - P. Véron 1
- A. C. Gonçalves 2
1 - Observatoire de Haute Provence, CNRS, 04870 Saint-Michel l'Observatoire,
France
2 -
European Southern Observatory (ESO), Karl Schwarzschild Strasse 2, 85748
Garching bei München, Germany
Received 8 February 2001 / Accepted 20 March 2001
Abstract
We have compiled a list of 83 objects classified as Narrow-Line Seyfert 1
galaxies (NLS1s) or known to have a broad Balmer component narrower than 2000 km s-1. Of these, 19 turned out to have been spectroscopically
misidentified in previous studies; only 64 of the selected objects are genuine
NLS1s. We have spectroscopically observed 59 of them and tried to characterize
their Narrow and Broad-Line Regions (NLR and BLR) by fitting the emission-lines
with Gaussian and/or Lorentzian profiles.
In most cases, the broad Balmer components are well fitted by a single
Lorentzian profile, confirming previous claims that Lorentzian rather than
Gaussian profiles are better suited to reproduce the shape of the NLS1s broad
emission lines. This has consequences concerning their FWHMs and line ratios:
when the broad Balmer components are fitted with a Lorentzian, most narrow line
regions have line ratios typical of Seyfert 2s while, when a Gaussian profile is
used for fitting the broad Balmer components, the line ratios are widely
scattered in the usual diagnostic diagrams (Veilleux & Osterbrock 1987);
moreover, the FWHM of the best fitting Lorentzian is systematically smaller than
the FWHM of the Gaussian.
We find that, in general, the [O III] lines have a relatively narrow Gaussian
profile ( 200-500 km s-1 FWHM) with often, in addition, a second
broad (
200-500 km s-1 FWHM) with often, in addition, a second
broad ( 500-1800 km s-1 FWHM), blueshifted Gaussian component.
We do not confirm that the [O III] lines are weak in NLS1s.
500-1800 km s-1 FWHM), blueshifted Gaussian component.
We do not confirm that the [O III] lines are weak in NLS1s.
As previously suggested, there is a continuous transition of all properties
between NLS1s and classical Broad-Line Seyfert 1 Galaxies (BLS1s) and the limit
of 2000 km s-1 used to separate the two species is arbitrary; R4570,
the ratio of the Fe II to the H fluxes, could be a physically more
meaningful parameter to distinguish them.
fluxes, could be a physically more
meaningful parameter to distinguish them.
Key words: galaxies: Seyfert
Osterbrock & Pogge (1985) have identified a class of AGNs having all
properties of the Seyfert 1s with, however, very narrow Balmer lines and strong
optical Fe II lines; they are called NLS1s. Quantitatively, a Seyfert 1 is
called an NLS1 if the "broad" component of the Balmer lines is narrower than
2000 km s-1 FWHM (Osterbrock 1987). NLS1s often have strong Fe II
emission; many of them have a strong soft X-ray excess and display
high-amplitude X-ray variability.
The 2-10 keV spectrum of classical BLS1s can be fitted with a power-law with
a photon index
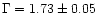 (Nandra & Pounds 1994; Reynolds 1997;
George et al. 1998a); in NLS1s,
(Nandra & Pounds 1994; Reynolds 1997;
George et al. 1998a); in NLS1s, 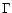 is significantly steeper (
is significantly steeper (
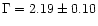 )
(Leighly 1999b); in fact, it is anticorrelated with the H
)
(Leighly 1999b); in fact, it is anticorrelated with the H FWHM
(Brandt et al. 1997; Reeves & Turner 2000).
FWHM
(Brandt et al. 1997; Reeves & Turner 2000).
Some Seyfert 1s show evidence for an excess of soft X-rays above the hard X-ray
power-law extrapolation, dominant below  1 keV (Saxton et al. 1993; George
et al. 2000). This excess is more important and more frequent in NLS1s than in
BLS1s (Vaughan et al. 1999a; Leighly 1999b; Reeves & Turner 2000). The soft
photon spectral index
1 keV (Saxton et al. 1993; George
et al. 2000). This excess is more important and more frequent in NLS1s than in
BLS1s (Vaughan et al. 1999a; Leighly 1999b; Reeves & Turner 2000). The soft
photon spectral index 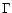 (0.1-2.4 keV), which measures the relative
strength of the soft component, is correlated with the Balmer line width in the
sense that steep soft X-ray spectra corresponds to narrow Balmer lines
(Puchnarewicz et al. 1992; Boller et al. 1996; Wang et al. 1996; Laor et al. 1997a). In fact NLS1s may show both steep as well as flat X-ray spectra, while
BLS1s always have flat spectra (Grupe et al. 1999). However, several NLS1s show
a significant intrinsic neutral hydrogen column density in excess of the
Galactic value; the unability to detect a soft excess in the X-ray spectrum of
some NLS1s could be due to the presence of such a high column density. Therefore
the soft excess may be more prevalent in NLS1s than observed (Leighly 1999b).
(0.1-2.4 keV), which measures the relative
strength of the soft component, is correlated with the Balmer line width in the
sense that steep soft X-ray spectra corresponds to narrow Balmer lines
(Puchnarewicz et al. 1992; Boller et al. 1996; Wang et al. 1996; Laor et al. 1997a). In fact NLS1s may show both steep as well as flat X-ray spectra, while
BLS1s always have flat spectra (Grupe et al. 1999). However, several NLS1s show
a significant intrinsic neutral hydrogen column density in excess of the
Galactic value; the unability to detect a soft excess in the X-ray spectrum of
some NLS1s could be due to the presence of such a high column density. Therefore
the soft excess may be more prevalent in NLS1s than observed (Leighly 1999b).
Most AGN spectra show the presence of a "Big Blue Bump" (BBB) extending from
optical frequencies upwards (Elvis et al. 1986; Sanders et al. 1989). The BBB
has been interpreted as the thermal emission of a physically thin, optically
thick accretion disk (Sun & Malkan 1989; Siemiginowska et al. 1995).
The soft X-ray spectral index is correlated to the strength of the ultraviolet
bump in unabsorbed Seyfert 1s, indicating that the BBB is in fact an ultraviolet
to soft X-ray bump (Walter & Fink 1993; Puchnarewicz et al. 1995; Page et al.
1999). NLS1s have significantly bluer spectra than BLS1s which is consistent
with the presence of a more pronounced BBB in NLS1s (Grupe et al. 1998).
However, when sufficient data are available, it seems that a single standard
accretion disk model cannot fit the optical/UV/X-ray bump (Kolman et al. 1993;
Wisotzki et al. 1995).
NLS1s very frequently exhibit rapid and/or high-amplitude X-ray variability
(Boller et al. 1996; Forster & Halpern 1996; Molthagen et al. 1998). The
X-ray-steep, narrow-H AGNs systematically show larger amplitude
variations than the X-ray-flat, broad-H
AGNs systematically show larger amplitude
variations than the X-ray-flat, broad-H AGNs on time scales from 2 to 20 days (Fiore et al. 1998; Leighly 1999a; Turner et al. 1999b).
Observed variability by a factor 2 in a few hours or less shows that a
substantial fraction of the soft component comes from a compact region, smaller
than a light-day.
Giant-amplitude X-ray variability (from one up to more than two orders of
magnitude on a time scale of one to a few years) has been observed in several
NLS1s (see for instance Brandt et al. 1999 and Uttley et al. 1999). In the cases
of NGC 4051 and IRAS 13224-3809, changes by a factor of 10 or more have
occured within a few hours (Leighly 1999a).
It is quite remarkable that all these objects, except NGC 4051, have a very
high soft photon index (
AGNs on time scales from 2 to 20 days (Fiore et al. 1998; Leighly 1999a; Turner et al. 1999b).
Observed variability by a factor 2 in a few hours or less shows that a
substantial fraction of the soft component comes from a compact region, smaller
than a light-day.
Giant-amplitude X-ray variability (from one up to more than two orders of
magnitude on a time scale of one to a few years) has been observed in several
NLS1s (see for instance Brandt et al. 1999 and Uttley et al. 1999). In the cases
of NGC 4051 and IRAS 13224-3809, changes by a factor of 10 or more have
occured within a few hours (Leighly 1999a).
It is quite remarkable that all these objects, except NGC 4051, have a very
high soft photon index (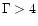 ), at least when they are bright.
), at least when they are bright.
A few BLS1s have also displayed X-ray flux variability by a factor of 10 or
more such as NGC 3227 (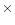 15) (Komossa & Fink 1997a; George et al. 1998b)
and NGC 3786 (
15) (Komossa & Fink 1997a; George et al. 1998b)
and NGC 3786 (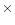 10) (Komossa & Fink 1997b); in both cases, however, the
variability has been attributed to a change in the column density of a warm
absorber.
10) (Komossa & Fink 1997b); in both cases, however, the
variability has been attributed to a change in the column density of a warm
absorber.
A number of observations suggests that NLS1s are Seyfert 1s with a near- or
super-Eddington accretion rate.
If the broad-line emitting region is gravitationally linked to the central
black hole (BH), one can show that the FWHM of the lines depends on the mass of
the BH, the ratio of the luminosity to the Eddington luminosity and the angle
between the rotation axis of the gas disk and the line of sight. The NLS1s could
be either normal Seyfert 1s seen perpendicularly to the disk, or objects with a
low mass BH radiating near the Eddington limit (Wang et al. 1996).
The combination of strong soft X-ray excess and steep power law prompted Pounds
et al. (1995) to postulate that NLS1s represent the supermassive BH analogue of
Galactic BH candidates (GBHC) in their high states. The high states of GBHCs are
thought to be triggered by increases in the accretion rate resulting in strong
thermal emission from a disk accreting at the Eddington limit.
Standard accretion disks are not able to account for the soft X-ray excess
unless the Eddington ratio is close to unity; a large accretion rate results in
a more pronounced BBB which is shifted toward higher energies, resulting in
stronger soft X-ray emission and hence steeper soft X-ray slope (Pounds et al.
1987; Ross et al. 1992; Kuraszkiewicz et al. 2000).
At a fixed luminosity, BHs radiating at higher fractions of the Eddington rate
will have lower masses; lower mass BHs are thought to be associated with
physically smaller emission regions that vary more rapidly. This may explain
why higher amplitude short term X-ray variability is observed in NLS1s (Fiore
et al. 1998; Leighly 1999a; Turner et al. 1999b).
Nicastro (2000) proposed a model in which, for accretion rates
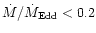 (sub-Eddington regime), the predicted FWHMs are quite broad
(>4000 km s-1), while for
(sub-Eddington regime), the predicted FWHMs are quite broad
(>4000 km s-1), while for
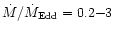 (Eddington to
moderately super-Eddington), the corresponding FWHMs span the interval
(Eddington to
moderately super-Eddington), the corresponding FWHMs span the interval
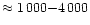 km s-1.
km s-1.
The amount of published data on NLS1s increased dramatically over the last few
years, specially since the launch of the ROSAT and ASCA satellites,
and important progress has been made in the X-ray domain. NLS1s,
however, are still subject to much debate; our knowledge of the basic properties
concerning their emission-line regions (line profiles, line ratios, etc.), and
of their relation to the X-ray properties, is still rather limited, as is the
relationship between NLS1s and classical BLS1s. This is largely due to the fact
that little effort has been put into providing a set of high-quality optical
spectroscopic data. Published data are very heterogeneous; spectra often have a
resolution insufficient to separate unambiguously the broad and narrow
components of the Balmer lines; in addition, the presence of strong Fe II lines
makes it difficult to measure H .
.
Aware of the fact that a detailed and consistent study of NLS1 emission-line
properties was missing and that the knowledge of these properties is of crucial
importance for understanding the basic physical differences between BLS1s and
NLS1s and, ultimately, for fitting them into the standard unifying picture, we
have obtained a homogeneous set of moderate resolution (3.4 Å FWHM or 200 km s-1 at H )
spectra around H
)
spectra around H and/or H
and/or H of a large
number of NLS1s; this setting turned out to be adequate as narrow line
individual components are, in most cases, resolved with this resolution;
however, in the few objects where a H II region is present near the galaxy
nucleus, a better resolution would of course allow us to separate more easily the
Seyfert 2 emission lines from the much narrower H II lines.
of a large
number of NLS1s; this setting turned out to be adequate as narrow line
individual components are, in most cases, resolved with this resolution;
however, in the few objects where a H II region is present near the galaxy
nucleus, a better resolution would of course allow us to separate more easily the
Seyfert 2 emission lines from the much narrower H II lines.
We have compiled all 83 objects known to us before January 1998 to either to be
NLS1s or to have a "broad" Balmer component narrower than 2000 km s-1,
north of
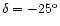 ,
brighter than B=17.0 and with z<0.100. We
have spectroscopically observed 76 of them.
,
brighter than B=17.0 and with z<0.100. We
have spectroscopically observed 76 of them.
Table 1:
Observations dates and standard stars.
| Date |
 range (Å)
range (Å) |
Standard stars |
| 21.03.95 |
6500-7400 |
BD 26 2606 2606 |
| 31.08.95 |
4855-5755 |
Feige 15, BD 25 3941 3941 |
| 01.09.95 |
4855-5755 |
and BD 28 4211 4211 |
| 10.05.96 |
6700-7600 |
GD 140, BD 26 2606 2606 |
| 11.05.96 |
4860-5760 |
Feige 98, Kopff 27 |
| 15 - 16.07.96 |
4675-5575 |
BD 28 4211 4211 |
| 24.07.96 |
6335-7235 |
BD 28 4211 4211 |
| 07.01.97 |
4720-5620 |
EG 247 |
| 09 - 10.01.97 |
6175-7075 |
EG 247 |
| 04 - 07.03.97 |
4825-5725 |
Feige 66 |
| 08 - 12.03.97 |
6310-7210 |
Feige 66 |
| 13.03.97 |
4825-5725 |
Feige 66 |
| 29.10.97 |
6500-6950 |
Feige 24, EG 247 |
| 30.10.97 |
4825-5280 |
Feige 24, EG 247 |
| 31.10.97 |
6455-7355 |
Feige 24 |
| 01 - 02.11.97 |
4655-5555 |
Feige 24 |
| 27 - 29.05.98 |
4645-5545 |
Feige 66, Kopff 27 |
| 31.05.98 |
6430-7330 |
Feige 66 |
| 15.06.98 |
4420-6265 |
GD 190 |
| 16.06.98 |
6020-7870 |
GD 190 |
| 23.09.00 |
4255-6090 |
Feige 15, EG 247 |
- On October 29 and 30, 1997, we have used a dispersion of 33 Å mm-1
instead of 66 Å mm-1.
- In June 1998 and September 2000, we have used an EEV 42-20 instead of a
TK 512 CCD.
The observations were carried out during several observing runs with
the spectrograph CARELEC (Lemaître et al. 1989) attached to the Cassegrain
focus of the Observatoire de Haute-Provence (OHP) 1.93 m telescope. Table 1 gives the list of observing runs with the observed wavelength
ranges and the standard stars used.
The detector was a
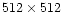 pixels,
pixels,
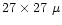 m Tektronic CCD, except in June 1998 and September 2000 when
we used a
m Tektronic CCD, except in June 1998 and September 2000 when
we used a
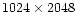 pixels,
pixels,
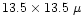 m EEV 42-20 CCD. We
generally used a 600 lmm-1 grating resulting in a dispersion of 66 Å mm-1. On October 29 and 30, 1997, we used a dispersion of 33 Å mm-1. In each case, the galaxy nucleus was centered on the slit. Three to
five columns of the CCD (3 to 5
m EEV 42-20 CCD. We
generally used a 600 lmm-1 grating resulting in a dispersion of 66 Å mm-1. On October 29 and 30, 1997, we used a dispersion of 33 Å mm-1. In each case, the galaxy nucleus was centered on the slit. Three to
five columns of the CCD (3 to 5
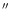 )
were extracted on the Tektronic CCD and
7 column (
)
were extracted on the Tektronic CCD and
7 column ( 3
3
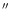 )
on the EEV. The slit width was 2
)
on the EEV. The slit width was 2
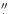 1, corresponding
to a projected slit width on the detector of 52
1, corresponding
to a projected slit width on the detector of 52 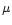 m i.e. 1.9 and 3.8 pixels with the Tektronic and the EEV CCD respectively. The resolution, as
measured on the night sky lines, was
m i.e. 1.9 and 3.8 pixels with the Tektronic and the EEV CCD respectively. The resolution, as
measured on the night sky lines, was  3.4 Å FWHM.
3.4 Å FWHM.
The spectra were flux calibrated using the standard
stars given in Table 1, taken from Oke (1974); Stone (1977);
Oke & Gunn (1983) and Massey et al. (1988).
The spectra were analysed as described in Véron et al. (1980; 1981a,b) and
Gonçalves et al. (1999a). Briefly, the three emission lines, H and
[N II]
and
[N II]
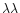 6548, 6583 (or H
6548, 6583 (or H and [O III]
and [O III]
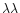 4959, 5007) were fitted by one or several sets of three Gaussian components; the width
and redshift of each component in a set were forced to be the same and the
intensity ratios of the [N II] and [O III] lines were taken to be equal to their
theoretical values. The broad Balmer components were fitted by one or several
Gaussian or Lorentzian profiles.
4959, 5007) were fitted by one or several sets of three Gaussian components; the width
and redshift of each component in a set were forced to be the same and the
intensity ratios of the [N II] and [O III] lines were taken to be equal to their
theoretical values. The broad Balmer components were fitted by one or several
Gaussian or Lorentzian profiles.
Nineteen galaxies turned out to have been misidentified as NLS1s; their spectra
will be published in Véron-Cetty et al. (2001). The 64 others are listed in
Table 2.
Table 2:
List of NLS1s with z<0.100, B<17.0 and
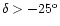 .
Column 1: name, Col. 2: short position, Col. 3: the Galactic hydrogen column
density in units of 1020 cm-2 Col. 4: redshift, Col. 5: B magnitude,
Cols. 6 and 7: FWHM (in km s-1) of the broad component of the Balmer lines,
and reference, Cols. 8 and 9: ROSAT (0.1-2.4 keV) photon index
.
Column 1: name, Col. 2: short position, Col. 3: the Galactic hydrogen column
density in units of 1020 cm-2 Col. 4: redshift, Col. 5: B magnitude,
Cols. 6 and 7: FWHM (in km s-1) of the broad component of the Balmer lines,
and reference, Cols. 8 and 9: ROSAT (0.1-2.4 keV) photon index  resulting from a power-law fit with Galactic absorption, and reference, Col. 10:
ROSAT X-ray flux in cts s-1 in the energy band 0.1-2.4 keV either from the
RASS catalogue or from the 1WGA catalogue (*), Col. 11:
"A" if we have obtained a red spectrum, "B" for a blue spectrum.
References:
(1) Appenzeller & Wagner (1991);
(2) Bade et al. (1995);
(3) Bassani et al. (1989);
(4) Boller et al. (1992);
(5) Boller et al. (1996);
(6) Boroson & Green (1992);
(7) Boroson & Meyers (1992);
(8) Brandt et al. (1995);
(9) Ciliegi & Maccacaro (1996);
(10) Goodrich (1989);
(11) Green et al. (1989);
(12) Grupe et al. (1998);
(13) Grupe et al. (1999);
(14) Leighly (1999b);
(15) Maza & Ruiz (1989);
(16) Moran et al. (1996);
(17) Netzer et al. (1987);
(18) Osterbrock (1977a);
(19) Osterbrock & de Robertis (1985);
(20) Osterbrock & Pogge (1985);
(21) Osterbrock & Pogge (1987);
(22) Osterbrock & Shuder (1982);
(23) Puchnarewicz et al. (1994);
(24) Puchnarewicz et al. (1995);
(25) Rush et al. (1996);
(26) Stephens (1989);
(27) Stirpe (1990);
(28) Walter & Fink (1993);
(29) Wang et al. (1996);
(30) Winkler (1992);
(31) Yuan et al. (1998);
(32) Zamorano et al. (1992);
(33) Pfefferkorn et al. (2001).
resulting from a power-law fit with Galactic absorption, and reference, Col. 10:
ROSAT X-ray flux in cts s-1 in the energy band 0.1-2.4 keV either from the
RASS catalogue or from the 1WGA catalogue (*), Col. 11:
"A" if we have obtained a red spectrum, "B" for a blue spectrum.
References:
(1) Appenzeller & Wagner (1991);
(2) Bade et al. (1995);
(3) Bassani et al. (1989);
(4) Boller et al. (1992);
(5) Boller et al. (1996);
(6) Boroson & Green (1992);
(7) Boroson & Meyers (1992);
(8) Brandt et al. (1995);
(9) Ciliegi & Maccacaro (1996);
(10) Goodrich (1989);
(11) Green et al. (1989);
(12) Grupe et al. (1998);
(13) Grupe et al. (1999);
(14) Leighly (1999b);
(15) Maza & Ruiz (1989);
(16) Moran et al. (1996);
(17) Netzer et al. (1987);
(18) Osterbrock (1977a);
(19) Osterbrock & de Robertis (1985);
(20) Osterbrock & Pogge (1985);
(21) Osterbrock & Pogge (1987);
(22) Osterbrock & Shuder (1982);
(23) Puchnarewicz et al. (1994);
(24) Puchnarewicz et al. (1995);
(25) Rush et al. (1996);
(26) Stephens (1989);
(27) Stirpe (1990);
(28) Walter & Fink (1993);
(29) Wang et al. (1996);
(30) Winkler (1992);
(31) Yuan et al. (1998);
(32) Zamorano et al. (1992);
(33) Pfefferkorn et al. (2001).
![\begin{table}\par
\par\includegraphics[width=20cm,clip]{tab2.eps}\end{table}](/articles/aa/full/2001/24/aa1123/img26.gif) |
Table 2:
Continued.
![\begin{table}
\par\includegraphics[width=20cm,clip]{tab2c.eps}\par\end{table}](/articles/aa/full/2001/24/aa1123/img27.gif) |
Before analysing our blue spectra, the Fe II multiplets were removed
following the method described in Boroson & Green (1992). This consists of
subtracting a suitable fraction of a Fe II template from the NLS1 spectrum so
that the flux and width of the H and [O III] lines are no longer affected
by the underlying multiplet emission. Such a template is usually obtained by
taking a high signal-to-noise spectrum of I Zw 1, an NLS1 showing strong narrow
Fe II emission, from which the H
and [O III] lines are no longer affected
by the underlying multiplet emission. Such a template is usually obtained by
taking a high signal-to-noise spectrum of I Zw 1, an NLS1 showing strong narrow
Fe II emission, from which the H and [O III] lines are carefully removed.
We have observed I Zw 1 with the same instrumental setting as the rest of the
galaxies in our sample and used it to build an Fe II template, following this
method.
and [O III] lines are carefully removed.
We have observed I Zw 1 with the same instrumental setting as the rest of the
galaxies in our sample and used it to build an Fe II template, following this
method.
Our spectra are shown in Figs. 1 to 5.
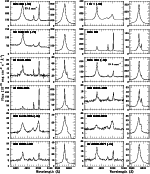 |
Figure 1:
Deredshifted blue and red spectra of the observed NLS1s. |
| Open with DEXTER |
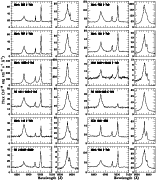 |
Figure 2:
Deredshifted blue and red spectra of the observed NLS1s (continued). |
| Open with DEXTER |
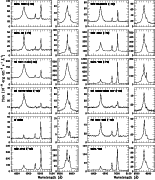 |
Figure 3:
Deredshifted blue and red spectra of the observed NLS1s (continued). |
| Open with DEXTER |
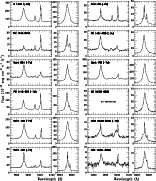 |
Figure 4:
Deredshifted blue and red spectra of the observed NLS1s (continued). |
| Open with DEXTER |
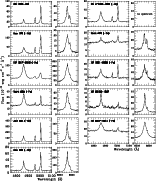 |
Figure 5:
Deredshifted blue and red spectra of the observed NLS1s (continued). |
| Open with DEXTER |
The Fe II strength is usually quantified by
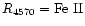
 4570/H
4570/H ,
i.e. the ratio of the fluxes of the
,
i.e. the ratio of the fluxes of the  4570 Å blend measured between
4570 Å blend measured between  4434 and
4434 and  4684 and of H
4684 and of H ,
including the narrow component (Boroson & Green 1992).
,
including the narrow component (Boroson & Green 1992).
We have measured the H equivalent width (EW) and the ratio R4570
for all objects in our sample. Figure 6 shows plots of our measurements
vs. published ones for the H
equivalent width (EW) and the ratio R4570
for all objects in our sample. Figure 6 shows plots of our measurements
vs. published ones for the H EW (a) and R4570 (b).
Our values of the H
EW (a) and R4570 (b).
Our values of the H EW are in good agreement with those of Boroson &
Green (1992); the ratios for the 13 objects in common have a mean value of 1.0
with a dispersion of 12%. Our values are also in good agreement with those of
Goodrich (1989) with however a larger dispersion (40%); this could be due
partly to variability. Our measurements of R4570 are 25% lower than the
values published by Boroson & Green (1992) (13 objects in common) and 30%
lower than those of Goodrich (1989) (10 objects); in both cases the dispersion
is
EW are in good agreement with those of Boroson &
Green (1992); the ratios for the 13 objects in common have a mean value of 1.0
with a dispersion of 12%. Our values are also in good agreement with those of
Goodrich (1989) with however a larger dispersion (40%); this could be due
partly to variability. Our measurements of R4570 are 25% lower than the
values published by Boroson & Green (1992) (13 objects in common) and 30%
lower than those of Goodrich (1989) (10 objects); in both cases the dispersion
is  25%. A significant difference exists for NGC 4051.
25%. A significant difference exists for NGC 4051.
In Seyfert 1s, the broad emission lines can be separated into two distinct
systems: the "high-ionization lines" (HILs): C IV  1550, He II
1550, He II
 4686, He II
4686, He II  1640, etc, and the "low-ionization lines" (LILs):
Fe II, Mg II
1640, etc, and the "low-ionization lines" (LILs):
Fe II, Mg II  2800, etc. (Collin-Souffrin & Lasota 1988; Gaskell 2000).
2800, etc. (Collin-Souffrin & Lasota 1988; Gaskell 2000).
The HILs and LILs show strong kinematic differences (Sulentic et al. 1995).
C IV is systematically broader than Mg II (Mathews & Wampler 1985) or H (Wang et al. 1998) and shows a strongly blueshifted and blue asymmetric profile
(Marziani et al. 1996), and He II
(Wang et al. 1998) and shows a strongly blueshifted and blue asymmetric profile
(Marziani et al. 1996), and He II  4686 systematically broader than
H
4686 systematically broader than
H (Boroson & Green 1992; Peterson et al. 2000). The widths of
H
(Boroson & Green 1992; Peterson et al. 2000). The widths of
H and Fe II (Boroson & Green 1992) and of H
and Fe II (Boroson & Green 1992) and of H and
C III]
and
C III] 1909 (Wills et al. 2000) are strongly correlated; in two NLS1s,
Leighly (2001) found that Si III]
1909 (Wills et al. 2000) are strongly correlated; in two NLS1s,
Leighly (2001) found that Si III] 1892 and C III] have the same width
as the LILs;
but, if Puchnarewicz et al. (1997) found that the FWHM of H
1892 and C III] have the same width
as the LILs;
but, if Puchnarewicz et al. (1997) found that the FWHM of H and Mg II are
also correlated, they concluded that that of C III] and Mg II are not. These
observations support the idea of separate HIL and LIL emitting regions although
it is not quite clear if C III] belongs to the HIL or to the LIL region.
and Mg II are
also correlated, they concluded that that of C III] and Mg II are not. These
observations support the idea of separate HIL and LIL emitting regions although
it is not quite clear if C III] belongs to the HIL or to the LIL region.
The Fe II emission in most AGNs is too strong to be explained by
photoionization (Phillips 1978b; Kwan et al. 1995); Fe II lines, and the other
LILs as well, are more likely to
be explained in the framework of collisional models where both the excitation of
the lines and the ionization of the elements are due to collisions in a high
density optically-thick medium illuminated mainly by hard X-rays; the Fe II
emission region has a high density (
 or
1012 cm-3), a high column density (
or
1012 cm-3), a high column density (
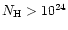 cm-2)
and a low temperature (
cm-2)
and a low temperature (
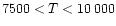 K) (Collin-Souffrin et al. 1980;
1988b; Joly 1981; Clavel et al. 1983; Collin-Souffrin & Lasota 1988; Kwan et al. 1995). There is a significant correlation between
Si III]/C III] and R4570; Si III and C III have
similar ionization potentials, but Si III] has a critical density more than
one order of magnitude larger than C III] (
K) (Collin-Souffrin et al. 1980;
1988b; Joly 1981; Clavel et al. 1983; Collin-Souffrin & Lasota 1988; Kwan et al. 1995). There is a significant correlation between
Si III]/C III] and R4570; Si III and C III have
similar ionization potentials, but Si III] has a critical density more than
one order of magnitude larger than C III] (
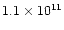 and
and
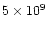 cm-3 respectively); Si III]/C III] is thus a density indicator and becomes
larger when density is higher; Si III]/C III] increases with increasing
cm-3 respectively); Si III]/C III] is thus a density indicator and becomes
larger when density is higher; Si III]/C III] increases with increasing
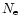 up to
up to
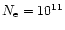 cm-3 (Aoki & Yoshida 1999;
Wills et al. 1999;
Kuraszkiewicz et al. 2000). It seems therefore likely that the C III] line comes
from the same high density region as H
cm-3 (Aoki & Yoshida 1999;
Wills et al. 1999;
Kuraszkiewicz et al. 2000). It seems therefore likely that the C III] line comes
from the same high density region as H and Fe II where it is at least
partially suppressed by collisions.
and Fe II where it is at least
partially suppressed by collisions.
HILs are emitted by low-pressure optically thin clouds (density of at most a
few 109 cm-3) illuminated by a rather soft continuum radiation (UV and
soft X-rays) (Collin-Souffrin & Lasota 1988). Collin-Souffrin et al. (1988a)
suggested that these lines are produced in clouds undergoing predominantly
outward motions along the system axis, the clouds receding from us being hidden
by an opaque structure such as the accretion disk.
The bipolar outflow could be a hydromagnetically driven wind accelerated
radiatively and centrifugally away from the surface of the accretion disk
(Emmering et al. 1992; Königl & Kartje 1994; Bottorf et al. 1997; Murray & Chiang 1998).
The broad Balmer lines exhibit a wide variety of profile shapes and a large
range in width (Osterbrock & Shuder 1982; de Robertis 1985; Crenshaw 1986;
Stirpe 1991; Miller et al. 1992); they are often strongly asymmetric (Corbin
1995). The BLR consists of two
components: one Intermediate Line Region (ILR) with line width  2000 km s-1 FWHM, with the peak within a few hundred kilometers per second of the
systemic redshift, and a Very Broad Line Region (VBLR) with lines of width
>7000 km s-1 and blueshifted by more than 1000 km s-1;
differences in the relative strengths of these components account for much of
the diversity of broad line profiles
(Wills et al. 1993; Brotherton et al. 1994;
Corbin 1995, 1997; Francis et al. 1992). The spectra of the VBLR and ILR are very different (Brotherton et al. 1994); the VBLR and the ILR can probably be
identified with the HIL and LIL regions respectively (Puchnarewicz et al. 1997).
This is confirmed by variability studies: the profile of the broad emission
lines are variable; many of them can be
described by two Gaussian components that are nearly stationary in wavelength,
and which vary independently of one another in relative flux (Peterson et al.
1999). This is the case for NGC 5548 (Dumont et al. 1998) and NGC 3516 (Goad
et al. 1999) in which the emission lines are best explained by the superposition
of an emission line cloud with variable lines and another which shows no
variability; the emission spectrum of the non variable cloud is dominated by
Balmer lines and Fe II emission. In the case of PG 1416-129, the broad
H
2000 km s-1 FWHM, with the peak within a few hundred kilometers per second of the
systemic redshift, and a Very Broad Line Region (VBLR) with lines of width
>7000 km s-1 and blueshifted by more than 1000 km s-1;
differences in the relative strengths of these components account for much of
the diversity of broad line profiles
(Wills et al. 1993; Brotherton et al. 1994;
Corbin 1995, 1997; Francis et al. 1992). The spectra of the VBLR and ILR are very different (Brotherton et al. 1994); the VBLR and the ILR can probably be
identified with the HIL and LIL regions respectively (Puchnarewicz et al. 1997).
This is confirmed by variability studies: the profile of the broad emission
lines are variable; many of them can be
described by two Gaussian components that are nearly stationary in wavelength,
and which vary independently of one another in relative flux (Peterson et al.
1999). This is the case for NGC 5548 (Dumont et al. 1998) and NGC 3516 (Goad
et al. 1999) in which the emission lines are best explained by the superposition
of an emission line cloud with variable lines and another which shows no
variability; the emission spectrum of the non variable cloud is dominated by
Balmer lines and Fe II emission. In the case of PG 1416-129, the broad
H component (4000 km s-1 FWHM) is strongly variable while the very
broad component (13000 km s-1 FWHM) has a much smaller amplitude
(Sulentic et al. 2000b).
component (4000 km s-1 FWHM) is strongly variable while the very
broad component (13000 km s-1 FWHM) has a much smaller amplitude
(Sulentic et al. 2000b).
LILs could be produced in the outer part of the disk itself as a result of
energy reflected from the flow above the disk (Collin-Souffrin et al. 1988a).
The profile of the lines produced in a disk are generally not double peaked,
except if the radius of the disk is small (
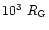 where
where
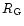 is the gravitational radius of the central BH), in which case the
line intensities are small, the line profiles are U-shaped and very broad; if
the disk radius is large (>10
is the gravitational radius of the central BH), in which case the
line intensities are small, the line profiles are U-shaped and very broad; if
the disk radius is large (>10
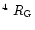 ), the line intensities are
large and their profile generally single peaked; the spectrum consists mainly of
LILs and can be a major part of the broad line emission (Dumont &
Collin-Souffrin 1990); these lines are, under certain conditions, more similar
to a Lorentzian than to a Gaussian (see their Fig. 4b).
), the line intensities are
large and their profile generally single peaked; the spectrum consists mainly of
LILs and can be a major part of the broad line emission (Dumont &
Collin-Souffrin 1990); these lines are, under certain conditions, more similar
to a Lorentzian than to a Gaussian (see their Fig. 4b).
According to Moran et al. (1996) and Leighly (1999b), many NLS1s have
symmetric emission lines with more nearly Lorentzian than Gaussian profiles.
However Rodríguez-Ardila et al. (2000b) claimed that Lorentzian profiles
are not suited to represent the NLS1 broad emission-lines; this conclusion
is based on the fact that these authors were unable to get a good fit when using
a single Lorentzian for each of the emission lines; however, there is a major
inconsistency in their procedure: they assumed that the Balmer lines (either
H or H
or H )
had a pure Lorentzian profile, not allowing for the
presence of a narrow component.
It so happens that one of the objects they present as an example of the poor
results obtained when fitting the emission lines with Lorentzians (Mark 1239)
is one of those for which we obtain a very good fit using a Lorentzian profile
for the broad Balmer line components in addition to a narrow component having
the same Gaussian profile as the forbidden lines.
)
had a pure Lorentzian profile, not allowing for the
presence of a narrow component.
It so happens that one of the objects they present as an example of the poor
results obtained when fitting the emission lines with Lorentzians (Mark 1239)
is one of those for which we obtain a very good fit using a Lorentzian profile
for the broad Balmer line components in addition to a narrow component having
the same Gaussian profile as the forbidden lines.
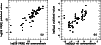 |
Figure 6:
a) Comparison between our measurements of the H EW and the published
ones. b) Comparison between our measurements of R4570 and the published
ones.
EW and the published
ones. b) Comparison between our measurements of R4570 and the published
ones. |
| Open with DEXTER |
Although not all broad Balmer components in our sample are well fitted by a
single Lorentzian, this is true in most cases (Table 3 lists, for all
observed objects, the FWHM of the H and H
and H broad components
obtained by using a single Lorentzian). As an illustration, we show in Fig. 7 the blue and red spectra of four objects fitted by a single
broad Gaussian and by a single broad Lorentzian; the narrow lines have been
fitted either by a single Gaussian or by two Gaussians.
In three cases, the fit of the red spectra is significantly better with a
Lorentzian than with a Gaussian, as judged from the residuals. The improvement
of the fit of the blue spectra with a Lorentzian is significant only for
PG 1244+026. But, in all cases, the Lorentzian fit leads to
broad components
obtained by using a single Lorentzian). As an illustration, we show in Fig. 7 the blue and red spectra of four objects fitted by a single
broad Gaussian and by a single broad Lorentzian; the narrow lines have been
fitted either by a single Gaussian or by two Gaussians.
In three cases, the fit of the red spectra is significantly better with a
Lorentzian than with a Gaussian, as judged from the residuals. The improvement
of the fit of the blue spectra with a Lorentzian is significant only for
PG 1244+026. But, in all cases, the Lorentzian fit leads to
 6583/H
6583/H and
and  5007/H
5007/H ratios which are more similar
to the values expected for Seyfert 2 nebulosities (see below).
ratios which are more similar
to the values expected for Seyfert 2 nebulosities (see below).
The use of a Lorentzian rather than a Gaussian leads, for the
NLR of most NLS1s, to line ratios typical of classical Seyfert 2s which strongly
confirms that these broad Balmer components have a profile which is genuinely
more similar to a Lorentzian.
We give in Table 4 the FWHM of the broad Gaussian and Lorentzian
profiles for these four objects; we first note that the FWHM of the H and H
and H Lorentzians are equal within
Lorentzians are equal within  10%, while the H
10%, while the H FWHM
of the Gaussians are on average 50% larger than the H
FWHM
of the Gaussians are on average 50% larger than the H FWHM; this
probably reflects the better quality of the fits obtained with Lorentzians. The
FWHM of the Gaussians are systematically larger than the FWHM of the
Lorentzians; in particular, HS 2247+1044 would not be classified as an NLS1
from a Gaussian fit.
FWHM; this
probably reflects the better quality of the fits obtained with Lorentzians. The
FWHM of the Gaussians are systematically larger than the FWHM of the
Lorentzians; in particular, HS 2247+1044 would not be classified as an NLS1
from a Gaussian fit.
The fact that the broad Balmer lines in NLS1s have a nearly Lorentzian profile
seems to suggest that they are produced in a large disk without the contribution
from an outflowing component. However, the high ionization UV emission lines in
the spectrum of NLS1s appear to be significantly broader than H (Rodríguez-Pascual et al. 1997; Kuraszkiewicz et al. 2000; Wills et al.
2000). In addition, Leighly (2001) showed that the high-ionization UV emission
lines in two NLS1s (IRAS 13224-3809 and 1H 0707-495) are much broader and
strongly blueshifted than the low-ionization lines. These observations suggest
that, in NLS1s, the outflowing component exists but is relatively weak, its
contribution being negligible in the optical range.
(Rodríguez-Pascual et al. 1997; Kuraszkiewicz et al. 2000; Wills et al.
2000). In addition, Leighly (2001) showed that the high-ionization UV emission
lines in two NLS1s (IRAS 13224-3809 and 1H 0707-495) are much broader and
strongly blueshifted than the low-ionization lines. These observations suggest
that, in NLS1s, the outflowing component exists but is relatively weak, its
contribution being negligible in the optical range.
As we have seen above, for all objects for which a single Lorentzian gave a
good fit to the broad Balmer component, we also made a fit with a single
Gaussian. In this way, we obtained two sets of line ratios
( 5007/H
5007/H and
and  6583/H
6583/H )
which are plotted in Fig. 8
(when the signal to noise ratio is low, the fit with a single broad
H
)
which are plotted in Fig. 8
(when the signal to noise ratio is low, the fit with a single broad
H Lorentzian sometimes gives a low value for the
Lorentzian sometimes gives a low value for the  5007/H
5007/H ratio; in these cases, when forcing this ratio to be equal to 10, the fit is
not worse as illustrated for IRAS 05262+4432 in Fig. 9). The left
panel shows the ratios obtained by fitting the broad Balmer component with a
Gaussian; the right panel, the ratios obtained with a Lorentzian. While, in the
left panel, many points are located in the H II region or composite domain
(Gonçalves et al. 1999a), in the right panel, most of the points are in the
Seyfert 2 region; one object (HS 0328+0528) belongs to the rare class of
weak-[N II] Seyfert galaxies (Gonçalves et al. 1999a) while six (Mark 42,
MS 12170+0700, Mark 69, Mark 684, IRAS 15462-0450 and Mark 507) have an
emission line component which falls in or near the H II region domain and is a
genuine H II region; they are shown as open circles; these objects are most
probably composite type objects similar to those described by Véron et al.
(1981b) and Gonçalves et al. (1999a).
The fit of the broad component of I Zw 1 with a single component is clearly
unsatisfactory; we got a better fit with two Lorentzians which puts the
representative point of the narrow line region in the Seyfert 2 area.
ratio; in these cases, when forcing this ratio to be equal to 10, the fit is
not worse as illustrated for IRAS 05262+4432 in Fig. 9). The left
panel shows the ratios obtained by fitting the broad Balmer component with a
Gaussian; the right panel, the ratios obtained with a Lorentzian. While, in the
left panel, many points are located in the H II region or composite domain
(Gonçalves et al. 1999a), in the right panel, most of the points are in the
Seyfert 2 region; one object (HS 0328+0528) belongs to the rare class of
weak-[N II] Seyfert galaxies (Gonçalves et al. 1999a) while six (Mark 42,
MS 12170+0700, Mark 69, Mark 684, IRAS 15462-0450 and Mark 507) have an
emission line component which falls in or near the H II region domain and is a
genuine H II region; they are shown as open circles; these objects are most
probably composite type objects similar to those described by Véron et al.
(1981b) and Gonçalves et al. (1999a).
The fit of the broad component of I Zw 1 with a single component is clearly
unsatisfactory; we got a better fit with two Lorentzians which puts the
representative point of the narrow line region in the Seyfert 2 area.
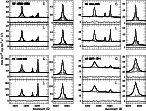 |
Figure 7:
Deredshifted blue and red spectra of four NLS1 galaxies in our sample. The data
points were
fitted by a set of narrow Gaussian profiles, reproducing the narrow emission
lines, plus a Gaussian (G) or Lorentzian (L) profile, to fit the broad Balmer
component. The individual profiles are represented by a thin solid line, the
total fit by a thick solid line and the differences between the data and the
fit (the residuals) by the lower dotted line. |
| Open with DEXTER |
Table 3:
Line properties of the 59
observed NLS1s (H II components have been systematically removed). Column 1:
name, Col. 2: R4570, ratio of the Fe II to the total H fluxes,
Cols. 3 and 4: FWHM (in km s-1) of the broad
H
fluxes,
Cols. 3 and 4: FWHM (in km s-1) of the broad
H and H
and H lines fitted with a Lorentzian profile, Col. 5:
EW (Å) of the broad H
lines fitted with a Lorentzian profile, Col. 5:
EW (Å) of the broad H component, Col. 6:
R5007, ratio of the
component, Col. 6:
R5007, ratio of the  5007 to the total H
5007 to the total H fluxes, Col. 7:
FWHM (corrected for instrumental broadening) of the [O III] line, Cols. 8 and 9: FWHM of the individual components (F1 and F2) of the [O III] lines, Col. 10: velocity difference between the two [O III] components (broad-narrow),
Col. 11: intensity ratio of the two [O III] components (broad/narrow).
a: a good fit can only be obtained with two broad components, a Lorentzian
and a Gaussian or two Lorentzians.
b: the broad H
fluxes, Col. 7:
FWHM (corrected for instrumental broadening) of the [O III] line, Cols. 8 and 9: FWHM of the individual components (F1 and F2) of the [O III] lines, Col. 10: velocity difference between the two [O III] components (broad-narrow),
Col. 11: intensity ratio of the two [O III] components (broad/narrow).
a: a good fit can only be obtained with two broad components, a Lorentzian
and a Gaussian or two Lorentzians.
b: the broad H component is weak.
component is weak.
| Name |
R4570 |
FWHM (L) |
EW |
R5007 |
FWHM |
FW1 |
FW2 |
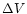 |
F2/F1 |
| |
|
H |
H |
H
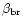 |
|
 5007 5007 |
|
|
|
|
Mark335 |
0.38 |
a |
a |
86 |
0.25 |
280 |
245 |
910 |
-190 |
1.23 |
| IZw1 |
1.14 |
a |
a |
48 |
0.44 |
1660 |
1040 |
1070 |
-1180 |
0.43 |
| TonS180 |
1.03 |
1250 |
1085 |
46 |
0.18 |
675 |
435 |
1060 |
-465 |
1.00 |
| Mark359 |
<0.5 |
830 |
900 |
18 |
1.32 |
180 |
|
|
|
|
| MS01442-0055 |
<0.6 |
1260 |
1100 |
35 |
0.35 |
240 |
|
|
|
|
| Mark1044 |
0.61 |
905 |
1010 |
63 |
0.15 |
420 |
335 |
720 |
-340 |
0.69 |
| HS0328+0528 |
<0.6 |
1455 |
1590 |
79 |
1.67 |
220 |
|
|
|
|
| IRAS04312+4008 |
<1.4 |
1060 |
860 |
16 |
0.35 |
380 |
|
|
|
|
| IRAS04416+1215 |
1.14 |
1500 |
1470 |
55 |
0.67 |
1320 |
650 |
1790 |
-480 |
1.95 |
| IRAS04576+0912 |
<1.0 |
1100 |
1210 |
13 |
1.40 |
1290 |
380 |
1260 |
-500 |
6.40 |
| IRAS05262+4432 |
1.09 |
695 |
740 |
23 |
0.35 |
365 |
|
|
|
|
| RXJ07527+2617 |
0.71 |
1080 |
1185 |
50 |
0.21 |
400 |
|
|
|
|
| Mark382 |
<0.8 |
1270 |
1280 |
20 |
0.56 |
155 |
|
|
|
|
| Mark705 |
0.36 |
1745 |
1790 |
85 |
0.41 |
365 |
365 |
1630 |
-290 |
0.62 |
| Mark707 |
0.47 |
1180 |
1295 |
102 |
0.53 |
315 |
|
|
|
|
| Mark124 |
0.60 |
1645 |
1840 |
43 |
0.72 |
540 |
380 |
935 |
-335 |
0.75 |
| Mark1239 |
0.63 |
905 |
1075 |
78 |
1.29 |
630 |
400 |
1395 |
-475 |
1.16 |
| IRAS09571+8435 |
1.05 |
1270 |
1185 |
26 |
0.53 |
430 |
240 |
845 |
-370 |
1.07 |
| PG1011-040 |
0.46 |
1370 |
1455 |
41 |
0.33 |
400 |
|
|
|
|
| PG1016+336 |
0.60 |
1205 |
1590 |
65 |
0.06 |
315 |
|
|
|
|
| Mark142 |
0.92 |
1335 |
1370 |
60 |
0.14 |
260 |
|
|
|
|
| KUG1031+398 |
<1.5 |
1225 |
935 |
17 |
0.93 |
1000 |
315 |
1115 |
-280 |
1.27 |
| RXJ10407+3300 |
<0.6 |
1425 |
1985 |
32 |
0.75 |
460 |
|
|
|
|
| Mark734 |
0.67 |
1345 |
1825 |
45 |
0.49 |
450 |
180 |
525 |
-230 |
1.41 |
| Mark739E |
0.61 |
1415 |
1615 |
63 |
0.23 |
380 |
|
|
|
|
| MCG06.26.012 |
0.52 |
1070 |
1145 |
83 |
0.14 |
220 |
|
|
|
|
| Mark42 |
0.90 |
805 |
865 |
36 |
|
220 |
|
|
|
|
| NGC4051 |
0.25 |
970 |
1120 |
50 |
0.55 |
300 |
200 |
665 |
-175 |
0.65 |
In contrast, Rodríguez-Ardila et al. (2000b) found that the
 5007/H
5007/H
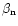 ratio emitted in the NLR of NLS1s varies from 1
to 5, instead of
ratio emitted in the NLR of NLS1s varies from 1
to 5, instead of  10 for BLS1s. This is most probably due to the fact
that they modelled the broad Balmer component with a Gaussian rather than a
Lorentzian. On the other hand, Nagao et al. (2001) showed that the line ratios
[O I]
10 for BLS1s. This is most probably due to the fact
that they modelled the broad Balmer component with a Gaussian rather than a
Lorentzian. On the other hand, Nagao et al. (2001) showed that the line ratios
[O I] 6300/[O III]
6300/[O III] 5007 and
[O III]
5007 and
[O III] 4363/[O III]
4363/[O III] 5007 are statistically indistinguishable in
NLS1s and BLS1s.
5007 are statistically indistinguishable in
NLS1s and BLS1s.
The majority of the profiles of the [O III] lines in Seyfert 1s are markedly
asymmetric, exhibiting a sharper falloff to the red than to the blue (Heckman et al. 1981;
Vrtilek & Carleton 1985; Whittle 1985a; Veilleux 1991b); these
profiles often have a two component structure with a narrow core superposed on
a broader, blueshifted base (Heckman et al. 1981; Leighly 1999b); it seems that
the velocity of the core is equal to the systemic velocity of the galaxy
(Heckman et al. 1981, 1984; Whittle 1985a).
Many Seyferts have an "ionization cone" appearing as either one- or two-sided
structures emanating from the active nucleus; when single (one-sided) cones are
seen, they generally project against the far side of the galaxy disk, suggesting
that the counter cone is present but obscured by dust in the disk (Pogge 1989;
Wilson et al. 1993; Wilson 1994).
Colbert et al. (1996) suggested that more than 25% of Seyfert galaxies have
good evidence (from the kinematics of the H and [N II] lines) for minor
axis galactic outflows.
Crenshaw et al. (1999) showed, from the observation of UV absorption lines
(mainly C IV and N V), that large scale outflows with a velocity of a few
hundreds km s-1 are common in Seyfert galaxies. High spatial resolution
spectroscopic observations of the nuclear emission lines of NGC 1068 (Crenshaw
& Kraemer 2000) and NGC 4151 (Crenshaw et al. 2000; Kaiser et al. 2000) give strong support for biconical radial outflows in these objects.
and [N II] lines) for minor
axis galactic outflows.
Crenshaw et al. (1999) showed, from the observation of UV absorption lines
(mainly C IV and N V), that large scale outflows with a velocity of a few
hundreds km s-1 are common in Seyfert galaxies. High spatial resolution
spectroscopic observations of the nuclear emission lines of NGC 1068 (Crenshaw
& Kraemer 2000) and NGC 4151 (Crenshaw et al. 2000; Kaiser et al. 2000) give strong support for biconical radial outflows in these objects.
Whittle et al. (1988), Storchi-Bergmann et al. (1992), Arribas & Mediavilla
(1993) and Kaiser et al. (2000) showed that the AGN NLRs have two line-emitting
constituents: the
"[O III] components" (the broad blueshifted bases of the [O III] lines; Heckman
et al. 1981; Vrtilek 1985; Whittle 1992; Christopoulou et al. 1997), to be
identified with the biconical structure and which are outflowing from the
nucleus with a speed of a few hundreds km s-1, and the "ambient [O III]
emission" which is more widely distributed and shows normal galactic rotation.
A detailed kinematic study of the emission line gas in the Seyfert galaxy
NGC 2992 shows the presence of both a disk component which is well modeled
by pure circular rotation and an outflowing component distributed into two wide
cones (Veilleux et al. 2001).
Smith (1993) suggested that the "[O III] component" could be accelerated
outwards by a supersonic wind generated by the active nucleus. The relative
intensity of the two components varies widely from object to object.
High-ionization lines ([Fe VII], [Fe X] and [Fe XI]) are often present in
emission in NLS1s; these coronal lines tend to be blueshifted relative to, and
broader than, the low-ionization lines; the systematic blueshift indicates an
outflow of the gas emitting these features (Grandi 1978; Erkens et al. 1997).
There is a strong correlation between the [O III] 5007 line width and
luminosity (Whittle 1985b).
The [O III] FWHM is correlated with the absolute magnitude of the galaxy bulge
(Véron & Véron-Cetty 1986) and the observed galaxy rotation (Véron
1981; Whittle 1992) showing that gravity plays a dominant role in the NLR of
most objects, at least in the "ambient [O III] emission" region which dominates
in most AGNs.
For a number of objects in our sample (30), the fit of the [O III] lines with
a single Gaussian was poor, either because of the simultaneous presence on the
slit of a H II region (6), or because the lines are asymmetrical with a blue
wing (24); in these last cases, we fitted them with two Gaussians following the
procedure described in Sect. 2; as a result, we found a red component with a
FWHM in the range 180-650 km s-1 and a blue component with a FWHM in the
range 525-1790 km s-1, blueshifted by 90 to 570 km s-1 with respect
to the red component (Table 3; in this table, the [O III] FWHM have
been corrected for the instrumental profile); there is one exception, I Zw 1,
for which the red component is exceptionally broad (1040 km s-1 FWHM) and
the blue component is blueshifted by 1180 km s-1. This is in agreement
with previous findings.
For the objects requiring an additional [O III] component, the associated
H
5007 line width and
luminosity (Whittle 1985b).
The [O III] FWHM is correlated with the absolute magnitude of the galaxy bulge
(Véron & Véron-Cetty 1986) and the observed galaxy rotation (Véron
1981; Whittle 1992) showing that gravity plays a dominant role in the NLR of
most objects, at least in the "ambient [O III] emission" region which dominates
in most AGNs.
For a number of objects in our sample (30), the fit of the [O III] lines with
a single Gaussian was poor, either because of the simultaneous presence on the
slit of a H II region (6), or because the lines are asymmetrical with a blue
wing (24); in these last cases, we fitted them with two Gaussians following the
procedure described in Sect. 2; as a result, we found a red component with a
FWHM in the range 180-650 km s-1 and a blue component with a FWHM in the
range 525-1790 km s-1, blueshifted by 90 to 570 km s-1 with respect
to the red component (Table 3; in this table, the [O III] FWHM have
been corrected for the instrumental profile); there is one exception, I Zw 1,
for which the red component is exceptionally broad (1040 km s-1 FWHM) and
the blue component is blueshifted by 1180 km s-1. This is in agreement
with previous findings.
For the objects requiring an additional [O III] component, the associated
H line was often very weak; as a result, the fitting routine sometimes
gave a negative flux; in such cases, we set the ratio
line was often very weak; as a result, the fitting routine sometimes
gave a negative flux; in such cases, we set the ratio  5007/H
5007/H to 10, the mean value for Seyfert galaxies. This is a common procedure used to
prevent the fitting routine from yielding non-physical values whenever the line
intensities are too small to be disentangled from the noise.
to 10, the mean value for Seyfert galaxies. This is a common procedure used to
prevent the fitting routine from yielding non-physical values whenever the line
intensities are too small to be disentangled from the noise.
The soft X-ray photon index is available for 41 of the objects for which we
have a
blue spectrum. Twenty of them have
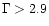 ,
21 have a smaller value;
among the 20 objects with a steep soft X-ray spectrum, 12 have a blueshifted
[O III] component, while only eight of the other set have such a component;
moreover, two of the eight steep X-ray spectrum objects without a blueshifted
component (PG 1404+226 and RXS J07527+2617) have an optical spectrum with a
poor signal to noise ratio and relatively broad [O III] lines (950 and 400 km s-1 respectively) so that the presence of a blueshifted component could
have been overlooked. So there is a weak, statistically unsignificant, trend
for the objects with a soft X-ray excess to have an outflowing [O III]
component. It is interesting to note that Erkens et al. (1997) have found that
strong coronal lines occur predominantly in objects with the steepest soft X-ray
spectra and that these lines are relatively broad and blueshifted. The FWHM and
velocity shifts are comparable for the blueshifted [O III] lines and the coronal
lines. Could these lines all come from the same emitting clouds?
,
21 have a smaller value;
among the 20 objects with a steep soft X-ray spectrum, 12 have a blueshifted
[O III] component, while only eight of the other set have such a component;
moreover, two of the eight steep X-ray spectrum objects without a blueshifted
component (PG 1404+226 and RXS J07527+2617) have an optical spectrum with a
poor signal to noise ratio and relatively broad [O III] lines (950 and 400 km s-1 respectively) so that the presence of a blueshifted component could
have been overlooked. So there is a weak, statistically unsignificant, trend
for the objects with a soft X-ray excess to have an outflowing [O III]
component. It is interesting to note that Erkens et al. (1997) have found that
strong coronal lines occur predominantly in objects with the steepest soft X-ray
spectra and that these lines are relatively broad and blueshifted. The FWHM and
velocity shifts are comparable for the blueshifted [O III] lines and the coronal
lines. Could these lines all come from the same emitting clouds?
 |
Figure 8:
Diagnostic diagrams for the narrow line region of the objects in our sample. In
the left panel, the line ratios have been derived by fitting the broad Balmer
components with a single Gaussian, while in the right panel we have used a
single Lorentzian. In the right panel, Seyfert 2s are shown by black squares and
H II regions by open circles. |
| Open with DEXTER |
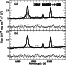 |
Figure 9:
In a), we have fitted the blue spectrum of
IRAS 05262+4432
with a set of Gaussian profiles for the narrow lines plus a single Lorentzian
profile for the broad component of H ;
in b), we forced the ;
in b), we forced the
 5007/H 5007/H ratio to be equal to 10. Examination of the residuals
shows that the two solutions have equal merits.
ratio to be equal to 10. Examination of the residuals
shows that the two solutions have equal merits. |
| Open with DEXTER |
Typical AGNs have
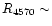 0.4 with
0.4 with  90% of objects in the range 0.1
to 1 (Osterbrock 1977a; Bergeron & Kunth 1984). Moderately strong Fe II
emission (R4570 > 1) occurs in perhaps 5% of all
objects (Lawrence et al. 1988). A few
superstrong Fe II emitters (R4570 > 2) have been found
(Lawrence et al. 1988; Lipari et al. 1993; Lipari 1994; Moran et al. 1996; Xia
et al. 1999); they are listed in Table 5. They are roughly an order
of magnitude rarer.
90% of objects in the range 0.1
to 1 (Osterbrock 1977a; Bergeron & Kunth 1984). Moderately strong Fe II
emission (R4570 > 1) occurs in perhaps 5% of all
objects (Lawrence et al. 1988). A few
superstrong Fe II emitters (R4570 > 2) have been found
(Lawrence et al. 1988; Lipari et al. 1993; Lipari 1994; Moran et al. 1996; Xia
et al. 1999); they are listed in Table 5. They are roughly an order
of magnitude rarer.
Table 5:
Known superstrong Fe II emitters (
R4570 > 2).
| Name |
Position |
R4570 |
H
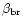 FWHM
FWHM |
| |
|
|
km s-1 |
| IRAS 04312+4008 |
0431+40 |
2.4 |
1230 |
| IRAS 07598+6508 |
0759+65 |
2.6 |
3200 |
| IRAS 10026+4347 |
1002+43 |
2.0 |
2500 |
| IRAS 11598-0112 |
1159-01 |
3.3 |
780 |
| Mark 231 |
1254+57 |
2.1 |
3000 |
| IRAS 13224-3809 |
1322-38 |
2.4 |
650 |
| Mark 507 |
1748+68 |
2.9 |
965 |
| IRAS 18508-7815 |
1850-78 |
2.4 |
3100 |
| IRAS 23410+0228 |
2341+02 |
4.0 |
970 |
Wills (1982) was the first to suggest that R4570 is roughly inversely
proportional to line width (FWHM of the broad H component). Gaskell
(1985) showed that R4570 increases dramatically for
FWHM <1600 km s-1, but is relatively
constant for
FWHM > 1600 km s-1. Zheng
& Keel (1991) found that for AGNs with
FWHM>6000 km s-1, the mean
value of R4570 is 0.21, less than half of that of the other objects,
confirming that strong Fe II emission is not found in objects showing very broad
emission lines; they showed that this is not an artifact resulting from blending
of the Fe II lines when they are broad. Boroson & Green (1992), followed by
Wang et al. (1996) and Rodríguez-Ardila et al. (2000a), confirmed the
existence of a strong anticorrelation between R4570 and H
component). Gaskell
(1985) showed that R4570 increases dramatically for
FWHM <1600 km s-1, but is relatively
constant for
FWHM > 1600 km s-1. Zheng
& Keel (1991) found that for AGNs with
FWHM>6000 km s-1, the mean
value of R4570 is 0.21, less than half of that of the other objects,
confirming that strong Fe II emission is not found in objects showing very broad
emission lines; they showed that this is not an artifact resulting from blending
of the Fe II lines when they are broad. Boroson & Green (1992), followed by
Wang et al. (1996) and Rodríguez-Ardila et al. (2000a), confirmed the
existence of a strong anticorrelation between R4570 and H FWHM. This
anticorrelation could be due either to the existence of an anticorrelation
between Fe II EW and H
FWHM. This
anticorrelation could be due either to the existence of an anticorrelation
between Fe II EW and H FWHM (Zheng & O'Brien 1990; Boroson & Green
1992) or of a correlation
between H
FWHM (Zheng & O'Brien 1990; Boroson & Green
1992) or of a correlation
between H EW and FWHM (Osterbrock 1977a;
Gaskell 1985; Goodrich 1989).
EW and FWHM (Osterbrock 1977a;
Gaskell 1985; Goodrich 1989).
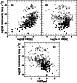 |
Figure 10:
Plots of the broad H luminosity: in a) vs.
the EW of the broad H
luminosity: in a) vs.
the EW of the broad H component; the two parameters are highly correlated
(r=0.43) for low luminosity objects (L(H
component; the two parameters are highly correlated
(r=0.43) for low luminosity objects (L(H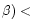 1042.5 erg s-1); but
the H 1042.5 erg s-1); but
the H EWs saturate at
EWs saturate at  100 Å for larger luminosity objects; in
b), vs. the Fe II EW; it is a scatter diagram (r=0.20); in c)
vs. R4570. The anticorrelation observed (r=0.42) is
clearly due to the weakness of H 100 Å for larger luminosity objects; in
b), vs. the Fe II EW; it is a scatter diagram (r=0.20); in c)
vs. R4570. The anticorrelation observed (r=0.42) is
clearly due to the weakness of H in the low luminosity objects rather
than to the strength of
R4570. Several samples of Seyfert 1s have been used; our own is shown as
filled circles; others (see text) are shown as open squares.
in the low luminosity objects rather
than to the strength of
R4570. Several samples of Seyfert 1s have been used; our own is shown as
filled circles; others (see text) are shown as open squares. |
| Open with DEXTER |
We have plotted in Fig. 10 the broad H luminosity vs. the
H
luminosity vs. the
H
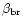 EW, the Fe II EW and R4570 for all objects in our sample
and in those of Boroson & Green (1992);
Brotherton (1996); Moran et al. (1996);
Marziani et al. (1996); Corbin & Boroson
(1996); Corbin (1997); Grupe et al.
(1999) and McIntosh et al. (1999); Grupe et al. reported the EW of the
whole Fe II complex from 4250 to 5880 Å; Leighly (1999b) used 30% of this
value; we used 20%. This figure clearly shows that the anticorrelation between
H
EW, the Fe II EW and R4570 for all objects in our sample
and in those of Boroson & Green (1992);
Brotherton (1996); Moran et al. (1996);
Marziani et al. (1996); Corbin & Boroson
(1996); Corbin (1997); Grupe et al.
(1999) and McIntosh et al. (1999); Grupe et al. reported the EW of the
whole Fe II complex from 4250 to 5880 Å; Leighly (1999b) used 30% of this
value; we used 20%. This figure clearly shows that the anticorrelation between
H luminosity and R4570 (r=0.42) is the result of the correlation
between H
luminosity and R4570 (r=0.42) is the result of the correlation
between H luminosity and EW (r=0.43) as there is no correlation between
H
luminosity and EW (r=0.43) as there is no correlation between
H luminosity and Fe II EW (r=0.20) (here and in what follows, r is the
linear correlation coefficient; the number of degrees of freedom is in each case
luminosity and Fe II EW (r=0.20) (here and in what follows, r is the
linear correlation coefficient; the number of degrees of freedom is in each case
 290). This confirms Gaskell (1985) result that NLS1s have weak H
290). This confirms Gaskell (1985) result that NLS1s have weak H rather than strong Fe II.
At very high densities (
rather than strong Fe II.
At very high densities (
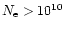 cm-3), the hydrogen lines become
thermalized and their intensity drops considerably (Rees et al. 1989) which is a
possible explanation of the decrease of the H
cm-3), the hydrogen lines become
thermalized and their intensity drops considerably (Rees et al. 1989) which is a
possible explanation of the decrease of the H EW in NLS1s (Gaskell 1985).
EW in NLS1s (Gaskell 1985).
Goodrich (1989) noted that a defining characteristic of NLS1s is that the ratio
R5007 of the [O III] 5007 flux to the total H
5007 flux to the total H flux is <3.
In fact, when the first NLS1s were observed spectroscopically,
the spectra were of relatively low resolution and the permitted and forbidden
lines were believed to have the same width; these objects could therefore be
mistaken for Seyfert 2s except for the presence in their spectra of strong Fe II
emission, a strong blue continuum and a small
flux is <3.
In fact, when the first NLS1s were observed spectroscopically,
the spectra were of relatively low resolution and the permitted and forbidden
lines were believed to have the same width; these objects could therefore be
mistaken for Seyfert 2s except for the presence in their spectra of strong Fe II
emission, a strong blue continuum and a small  5007/H
5007/H ratio due
to the unrecognized presence of a broad H
ratio due
to the unrecognized presence of a broad H component; as, in Seyfert 2s,
this ratio is larger than 3, a smaller value was an indication of the presence
of a broad H
component; as, in Seyfert 2s,
this ratio is larger than 3, a smaller value was an indication of the presence
of a broad H component.
But Osterbrock (1981) has divided the Seyfert 1s into five subgroups: S1.0,
1.2, 1.5, 1.8 and 1.9 on the basis of the appearance of the Balmer lines; a
quantitative definition of these subgroups has been given by Winkler (1992)
using the value of R5007: for S1.0s,
R5007<0.2, for S1.2,
0.2<R5007<0.5, for S1.5,
0.5<R5007<3.
The higher values of R5007 observed in S1.8 and S1.9 are believed to be
due to partial extinction of the broad H
component.
But Osterbrock (1981) has divided the Seyfert 1s into five subgroups: S1.0,
1.2, 1.5, 1.8 and 1.9 on the basis of the appearance of the Balmer lines; a
quantitative definition of these subgroups has been given by Winkler (1992)
using the value of R5007: for S1.0s,
R5007<0.2, for S1.2,
0.2<R5007<0.5, for S1.5,
0.5<R5007<3.
The higher values of R5007 observed in S1.8 and S1.9 are believed to be
due to partial extinction of the broad H component.
It follows that, for
all S1s which do not suffer extinction, the condition
R5007<3 is fulfilled.
We have measured on our spectra the parameter R5007 (given in Table
3); we have excluded for the computation of R5007 the contribution
of the H II regions mentioned above. All objects have R5007 values lower
than 0.8 except IC 3599 for which it exceeds 3.
component.
It follows that, for
all S1s which do not suffer extinction, the condition
R5007<3 is fulfilled.
We have measured on our spectra the parameter R5007 (given in Table
3); we have excluded for the computation of R5007 the contribution
of the H II regions mentioned above. All objects have R5007 values lower
than 0.8 except IC 3599 for which it exceeds 3.
Boroson & Green (1992); Grupe et al. (1999) and McIntosh et al. (1999) found
that Fe II is strong in objects with weak [O III] lines and vice versa. Let us
note however that while Grupe et al. and McIntosh et al. found an
anticorrelation between R5007 and Fe II EW, Boroson & Green found a strong
anticorrelation, not between the Fe II and [O III] EWs, but rather between the
Fe II EW and the ratio of the peak height of the [O III] 5007 line to
that of H
5007 line to
that of H which depends both on the value of R5007 and the width
of H
which depends both on the value of R5007 and the width
of H ;
this correlation results from the anticorrelation between
R4570 and the H
;
this correlation results from the anticorrelation between
R4570 and the H FWHM.
FWHM.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{o5007.eps}
\end{figure}](/articles/aa/full/2001/24/aa1123/Timg55.gif) |
Figure 11:
Plot of R5007 vs. R4570 (left panel) and
Fe II EW (right panel) for several samples of Seyfert 1s. There is no
correlation between R5007 and R4570 (r=0.05), while there is a trend
for objects with a large Fe II EW to have a weak R5007 (r=0.29). The
symbols are as in Fig. 10. |
| Open with DEXTER |
In Fig. 11, we have plotted R5007 vs. R4570 and Fe II
EW. There is a weak anticorrelation between Fe II EW and R5007, but not
between R4570 and R5007. Therefore we do not confirm that Fe II is
strong when the [O III] lines are weak.
Figure 12 shows the broad H luminosity vs. the broad
H
luminosity vs. the broad
H and
and  5007 EWs, and R5007; the H
5007 EWs, and R5007; the H luminosities and
luminosities and
 5007 EWs are not correlated; the weak anticorrelation between H
5007 EWs are not correlated; the weak anticorrelation between H luminosity and R5007 is due to the weakness of the H
luminosity and R5007 is due to the weakness of the H EW in low
luminosity objects, rather than to the strength of the
EW in low
luminosity objects, rather than to the strength of the  5007 EW.
5007 EW.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{hbetalum.eps}
\end{figure}](/articles/aa/full/2001/24/aa1123/Timg56.gif) |
Figure 12:
Plots of the broad
H luminosity: in a) vs. the EW of the broad
H
luminosity: in a) vs. the EW of the broad
H component (as in Fig. 10); in b), vs. the
component (as in Fig. 10); in b), vs. the
 5007 EW. It is a scatter diagram (r=0.16). As
a result, the H 5007 EW. It is a scatter diagram (r=0.16). As
a result, the H luminosity is anticorrelated with R5007
(r=0.43) c).
The symbols are as in Fig. 10.
luminosity is anticorrelated with R5007
(r=0.43) c).
The symbols are as in Fig. 10. |
| Open with DEXTER |
Initially, as we have seen, NLS1s were defined as having narrow "broad" Balmer
components (<2000 km s-1 FWHM). However, there is a continuous
distribution of optical line widths in Seyfert 1s and the separation between
BLS1s and NLS1s is arbitrary (Turner et al. 1999b; Sulentic et al. 2000a).
Sulentic et al. (2000a) suggested that Seyfert 1s with H FWHM <4000 km s-1 constitute a homogeneous class of objects having strikingly
different line profiles compared to Seyfert 1s with broader lines. Grupe
et al. (1999) have found objects displaying NLS1 properties
(strong Fe II
emission, a soft X-ray excess and variability) in spite of their H
FWHM <4000 km s-1 constitute a homogeneous class of objects having strikingly
different line profiles compared to Seyfert 1s with broader lines. Grupe
et al. (1999) have found objects displaying NLS1 properties
(strong Fe II
emission, a soft X-ray excess and variability) in spite of their H FWHM
exceeding 2000 km s-1. IRAS 10026+4347 has a large soft X-ray excess
(
FWHM
exceeding 2000 km s-1. IRAS 10026+4347 has a large soft X-ray excess
(
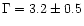 or
or 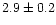 ), strong Fe II emission (
R4570=2.0),
and a high amplitude X-ray variability (
), strong Fe II emission (
R4570=2.0),
and a high amplitude X-ray variability (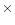 8); but the H
8); but the H FWHM is
FWHM is
 2500 or 2990 km s-1 (Grupe et al. 1998; Xia et al. 1999).
Similarly, PDS 456 has a H
2500 or 2990 km s-1 (Grupe et al. 1998; Xia et al. 1999).
Similarly, PDS 456 has a H FWHM equal to 3500 km s-1 although
the Fe II lines are relatively strong (
R4570=0.46) (Simpson et al. 1999)
and the X-ray spectrum shows a soft excess (
FWHM equal to 3500 km s-1 although
the Fe II lines are relatively strong (
R4570=0.46) (Simpson et al. 1999)
and the X-ray spectrum shows a soft excess (
 )
(Reeves et al.
2000; Vignali et al. 2000). A few objects are known which have strong Fe II
emission and relatively broad H
)
(Reeves et al.
2000; Vignali et al. 2000). A few objects are known which have strong Fe II
emission and relatively broad H lines, but no soft X-ray excess; Mark 231
and IRAS 07598+6508 are two such examples.
Mark 231 has a strong Fe II emission (
R4570=2.03 or 1.60), its H
lines, but no soft X-ray excess; Mark 231
and IRAS 07598+6508 are two such examples.
Mark 231 has a strong Fe II emission (
R4570=2.03 or 1.60), its H FWHM is
FWHM is  3000 km s-1 (Boroson & Meyers 1992; Lipari et al.
1993); the hard X-ray spectrum is heavily attenuated making it difficult to
detect the eventual presence of a soft X-ray component (Turner 1999).
IRAS 07598+6508 also has strong Fe II emission (
R4570=2.60) and a
relatively broad H
3000 km s-1 (Boroson & Meyers 1992; Lipari et al.
1993); the hard X-ray spectrum is heavily attenuated making it difficult to
detect the eventual presence of a soft X-ray component (Turner 1999).
IRAS 07598+6508 also has strong Fe II emission (
R4570=2.60) and a
relatively broad H line (2550-3200 km s-1 FWHM) (Lawrence et al. 1997; Lipari et al. 1993; Boroson & Meyers 1992); it is probably a highly
obscured X-ray source (Gallagher et al. 1999).
line (2550-3200 km s-1 FWHM) (Lawrence et al. 1997; Lipari et al. 1993; Boroson & Meyers 1992); it is probably a highly
obscured X-ray source (Gallagher et al. 1999).
We have plotted in Fig. 13, H
 FWHM vs.
R4570 for all objects in our sample as well as in the other samples
listed above; this plot shows a trend for the objects with the strongest Fe II
emission to have narrower Balmer lines, with FWHM up to 3500 km s-1. We have drawn a line such that, for most objects below this line,
R4570>0.50 while, for many objects above it,
R4570< 0.50. This could
be a better definition of NLS1s.
FWHM vs.
R4570 for all objects in our sample as well as in the other samples
listed above; this plot shows a trend for the objects with the strongest Fe II
emission to have narrower Balmer lines, with FWHM up to 3500 km s-1. We have drawn a line such that, for most objects below this line,
R4570>0.50 while, for many objects above it,
R4570< 0.50. This could
be a better definition of NLS1s.
Figure 14 is a plot of the ROSAT photon index  vs. R4570; open
circles represent the objects above the line in Fig. 13 and filled
circles the objects below this line. This figure shows a definite correlation
between
vs. R4570; open
circles represent the objects above the line in Fig. 13 and filled
circles the objects below this line. This figure shows a definite correlation
between  and R4570. Although the objects with strong Fe II emission
(black dots) show a large dispersion in
and R4570. Although the objects with strong Fe II emission
(black dots) show a large dispersion in  ,
most objects with small Fe II
have
,
most objects with small Fe II
have
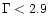 .
.
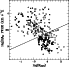 |
Figure 13:
Plot of the broad H component FWHM
vs. R4570. Filled circles represent the objects in our
sample, open circles other radio quiet objects and stars radio loud objects; the
correlation between the two parameters is strong
(r=0.54). The
straight line divides the plane into BLS1s (above the line) and what could be
the newly defined class of NLS1s (below the line).
component FWHM
vs. R4570. Filled circles represent the objects in our
sample, open circles other radio quiet objects and stars radio loud objects; the
correlation between the two parameters is strong
(r=0.54). The
straight line divides the plane into BLS1s (above the line) and what could be
the newly defined class of NLS1s (below the line). |
| Open with DEXTER |
Among the objects classified as NLS1s, having both narrow "broad" Balmer
components and a strong Fe II emission, two have a very small photon
index: IRAS 09571+8435 (
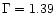 )
and Mark 507 (
)
and Mark 507 (
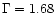 ). Mark 507
has an intrinsic neutral hydrogen column density
). Mark 507
has an intrinsic neutral hydrogen column density
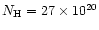 cm-2 (see notes), this value being derived
assuming that the intrinsic X-ray spectrum is a single power-law; it is quite
possible that the column density is even higher and hides a soft X-ray
component; this could also be true for IRAS 09571+8435.
cm-2 (see notes), this value being derived
assuming that the intrinsic X-ray spectrum is a single power-law; it is quite
possible that the column density is even higher and hides a soft X-ray
component; this could also be true for IRAS 09571+8435.
 |
Figure 14:
Plot of the ROSAT photon index  vs. R4570. Filled circles represent the points below the line in the
previous figure and open circles the points above the line. This diagram
clearly shows that the soft X-ray excess tends to be large when the Fe II
emission is large (r=0.40).
vs. R4570. Filled circles represent the points below the line in the
previous figure and open circles the points above the line. This diagram
clearly shows that the soft X-ray excess tends to be large when the Fe II
emission is large (r=0.40). |
| Open with DEXTER |
The FWHM of the broad H component has been found to increase with the
H
component has been found to increase with the
H luminosity (Miller et al. 1992). Figure 15 is a plot of the
H
luminosity (Miller et al. 1992). Figure 15 is a plot of the
H luminosity vs. the H
luminosity vs. the H FWHM; the correlation between these
two parameters is indeed quite strong; the linear correlation coefficient is
r=0.76 for 294 data points, corresponding to a probability
FWHM; the correlation between these
two parameters is indeed quite strong; the linear correlation coefficient is
r=0.76 for 294 data points, corresponding to a probability 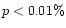 for no
correlation between the two parameters; luminous BLS1s tend to have
broader Balmer lines (but we should keep in mind that the published H
for no
correlation between the two parameters; luminous BLS1s tend to have
broader Balmer lines (but we should keep in mind that the published H FWHM have not been measured in a uniform way and that the presence of the narrow
component of the line has not always been taken properly into account). This
leads to question whether the defining criterion for NLS1s should be a function
of luminosity (Wills et al. 2000).
FWHM have not been measured in a uniform way and that the presence of the narrow
component of the line has not always been taken properly into account). This
leads to question whether the defining criterion for NLS1s should be a function
of luminosity (Wills et al. 2000).
 |
Figure 15:
Plot of the broad H luminosity vs. the
FWHM of the broad H
luminosity vs. the
FWHM of the broad H component. The symbols are as in Fig. 14. There is
clearly a strong correlation between the two plotted parameters (r=0.76).
component. The symbols are as in Fig. 14. There is
clearly a strong correlation between the two plotted parameters (r=0.76). |
| Open with DEXTER |
In most cases, the broad Balmer components of NLS1s are well fitted by a
single Lorentzian profile, confirming previous claims that Lorentzian rather
than Gaussian profiles are better suited to reproduce the shape of the broad
lines in NLS1s. This has consequences concerning their FWHMs and line ratios:
when the broad Balmer components are fitted with a Lorentzian, most narrow line
regions have line ratios typical of Seyfert 2s, while when they are fitted with
a Gaussian they are widely scattered in the usual diagnostic diagrams; moreover,
the FWHM of the best fitting Lorentzian is systematically smaller than the FWHM
of the Gaussian. The Lorentzian shape of the broad emission lines could be the
result of these lines being produced in a large disk.
We find that the [O III] lines usually have a relatively narrow Gaussian
profile ( 200-500 km s-1 FWHM) with often, in addition, a second
broad (
200-500 km s-1 FWHM) with often, in addition, a second
broad ( 500-1800 km s-1 FWHM), blueshifted Gaussian component.
500-1800 km s-1 FWHM), blueshifted Gaussian component.
We do not confirm that the [O III] lines are weak in NLS1s.
As previously suggested, there is a continuous transition of all properties
between NLS1s and BLS1s. The strength of Fe II relative to H (R4570)
could be the best parameter to recognize an NLS1 defined as a Seyfert 1 with a
high accretion rate. The maximum FWHM of the broad Balmer component of NLS1s
could be an increasing function of the H
(R4570)
could be the best parameter to recognize an NLS1 defined as a Seyfert 1 with a
high accretion rate. The maximum FWHM of the broad Balmer component of NLS1s
could be an increasing function of the H luminosity.
luminosity.
As all objects with H FWHM smaller than 2000 km s-1 seem to be
genuine NLS1s, we plan to make similar spectroscopic observations of a sizeable
sample of Seyfert 1s with 2000 < H
FWHM smaller than 2000 km s-1 seem to be
genuine NLS1s, we plan to make similar spectroscopic observations of a sizeable
sample of Seyfert 1s with 2000 < H FWHM <4000 km s-1 in the
hope of better define the properties of those galaxies intermediate between
NLS1s and BLS1s.
FWHM <4000 km s-1 in the
hope of better define the properties of those galaxies intermediate between
NLS1s and BLS1s.
Mark 335 (0003+19) is an NLS1 with strong Fe II emission and narrow
"broad" Balmer lines (
R4570=0.62 and H
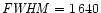 km s-1)
(Boroson & Green 1992) and relatively strong coronal lines (Grandi 1978).
km s-1)
(Boroson & Green 1992) and relatively strong coronal lines (Grandi 1978).
The broad Balmer components clearly have a complex and asymmetrical profile
(van Groningen 1987; Arav et al. 1997); to get a satisfactory fit of our
spectra, two broad components were necessary, a Gaussian and a Lorentzian.
I Zw 1 (0050+12) is the prototype NLS1; its optical spectrum reveals
narrow emission lines and strong Fe II emission (Phillips 1976). The H FWHM is in the range 1050-1500 km s-1 (Osterbrock 1977a; Phillips
1978a; Peterson et al. 1982; de Robertis 1985) although
Wilkes et al. (1999)
measured 2590 km s-1.
The broad Balmer components clearly have a complex and asymmetrical profile; to
get a satisfactory fit of our spectra, two Lorentzians were needed.
FWHM is in the range 1050-1500 km s-1 (Osterbrock 1977a; Phillips
1978a; Peterson et al. 1982; de Robertis 1985) although
Wilkes et al. (1999)
measured 2590 km s-1.
The broad Balmer components clearly have a complex and asymmetrical profile; to
get a satisfactory fit of our spectra, two Lorentzians were needed.
An UV spectrum shows that ions of increasing ionization level show increasing
excess blue-wing flux and an increasing line peak velocity shift (Laor et al.
1997b).
UV absorption lines have been observed, indicating the likely presence of a
warm absorber (Crenshaw et al. 1999).
Ton S180 (0054-22) is an NLS1 (Comastri et al. 1998) with strong
Fe II emission (
R4570=0.84; Comastri et al. 1998, or 1.02, Winkler 1992)
and narrow Balmer lines (
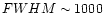 km s-1) (Winkler 1992; Comastri
et al. 1998; Grupe et al. 1999).
Mark 359 (0124+18) is an NLS1 (Osterbrock & Pogge 1985). The FWHM of
the broad H
km s-1) (Winkler 1992; Comastri
et al. 1998; Grupe et al. 1999).
Mark 359 (0124+18) is an NLS1 (Osterbrock & Pogge 1985). The FWHM of
the broad H component is 780 km s-1; the forbidden lines are
exceptionally narrow (
component is 780 km s-1; the forbidden lines are
exceptionally narrow (
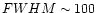 km s-1) (Veilleux 1991a). Discrepent
values have been published for R4570: 0.62 (Goodrich 1989) and <0.08
(Osterbrock & Pogge 1985).
The coronal lines are very strong (Veilleux 1988; Erkens et al. 1997).
km s-1) (Veilleux 1991a). Discrepent
values have been published for R4570: 0.62 (Goodrich 1989) and <0.08
(Osterbrock & Pogge 1985).
The coronal lines are very strong (Veilleux 1988; Erkens et al. 1997).
MS 01442-0055 (0144-00) is an NLS1 with H FWHM= 1940 km s-1 and
R4570=0.78 (Stephens 1989).
FWHM= 1940 km s-1 and
R4570=0.78 (Stephens 1989).
Mark 1044 (0227-09) is an NLS1 with strong narrow Fe II emission
(Osterbrock & Dahari 1983). The H FWHM is 1280 (Goodrich 1989) or
1400 km s-1 (Rafanelli 1985).
FWHM is 1280 (Goodrich 1989) or
1400 km s-1 (Rafanelli 1985).
HS 0328+0528 (0328+05). The spectra published by Perlman et al. (1996)
and Engels et al. (1998) suggest that it is an NLS1, although they do not show
the presence of Fe II emission. Our spectra show that the broad Balmer
components are narrow ( 1500 km s-1) which confirms the
classification as an NLS1.
1500 km s-1) which confirms the
classification as an NLS1.
The [N II] lines are extremely weak; we measured  6583/H
6583/H
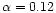 .
.
IRAS 03450+0055 (0345+00). Boroson & Meyers (1992) measured an
H FWHM of 1310 km s-1 and
R4570=0.96. Giannuzzo & Stirpe
(1996) included it in their sample of NLS1s.
FWHM of 1310 km s-1 and
R4570=0.96. Giannuzzo & Stirpe
(1996) included it in their sample of NLS1s.
We have not observed this object.
IRAS 04312+4008 (0431+40) is an NLS1 with very strong Fe II emission:
R4570=2.36 (Moran et al. 1996).
It is located at low galactic latitude: b=-5.0 with
with
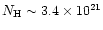 cm-2.
cm-2.
Mark 618 (0434-10). The Balmer line FWHM lies in the range
1760-2300 km s-1 (Osterbrock 1977a; Feldman & MacAlpine 1978;
Phillips 1978a; Peterson et al. 1982; Boroson & Meyers 1992); it is a
relatively strong Fe II emitter with
R4570=0.50 (Boroson & Meyers 1992).
It has however been classified as a Seyfert 1 rather than an NLS1 by Moran et al. (1996).
It is a X-ray source, variable on a time scale of 1000 s (Rao et al. 1992).
We have not observed this object.
IRAS 04416+1215 (0441+12) is an NLS1 with an H FWHM =1670 km s-1 (Moran et al.
1996).
The [O III] lines are very broad (FWHM=1150 km s-1 according to Moran et al. 1996);
we find 1320 km s-1.
FWHM =1670 km s-1 (Moran et al.
1996).
The [O III] lines are very broad (FWHM=1150 km s-1 according to Moran et al. 1996);
we find 1320 km s-1.
IRAS 04576+0912 (0457+09) is an NLS1 according to Moran et al. (1996)
with H FWHM=1220 km s-1 and
R4570=1.51. It is a ROSAT
X-ray source with a poorly determined photon index
FWHM=1220 km s-1 and
R4570=1.51. It is a ROSAT
X-ray source with a poorly determined photon index
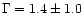 (Boller
et al. 1992).
(Boller
et al. 1992).
The [O III] lines are very broad (FWHM=1310 km s-1 according to Moran et al. 1996; we find 1290 km s-1).
IRAS 04596-2257 (0459-22) is an NLS1 with H FWHM < 1500 km s-1 (Green et al. 1989).
FWHM < 1500 km s-1 (Green et al. 1989).
We have not observed this object.
IRAS 05262+4432 (0526+44) is an NLS1 with H FWHM =700 km s-1
(Moran et al. 1996).
FWHM =700 km s-1
(Moran et al. 1996).
The narrow lines are clearly extended on our spectra, with
 6583/H
6583/H
 0.4 outside the nucleus; the 33 Å mm-1red nuclear spectrum is well fitted by a Lorentzian (695 km s-1 FWHM) and
two sets of narrow components with the same
0.4 outside the nucleus; the 33 Å mm-1red nuclear spectrum is well fitted by a Lorentzian (695 km s-1 FWHM) and
two sets of narrow components with the same  6583/H
6583/H ratio
ratio
 0.4 clearly coming from a H II region. The blue narrow line spectrum is
composite: a H II region with weak [O III] emission and a Seyfert 2 nebulosity
with weak H
0.4 clearly coming from a H II region. The blue narrow line spectrum is
composite: a H II region with weak [O III] emission and a Seyfert 2 nebulosity
with weak H which is too weak to be detected in either H
which is too weak to be detected in either H nor
[N II].
nor
[N II].
It is a ROSAT X-ray source with
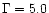 ,
but the uncertainty in this
value is large because of the high column density (Boller et al. 1992). It is
located at a low galactic latitude: b=5.7
,
but the uncertainty in this
value is large because of the high column density (Boller et al. 1992). It is
located at a low galactic latitude: b=5.7 with
with
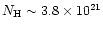 cm-2.
cm-2.
RX J07527+2617 (0749+26) is an NLS1; the Balmer line FWHM is  1000 km s-1 (Bade et al. 1995).
1000 km s-1 (Bade et al. 1995).
Mark 382 (0752+39) is an NLS1; the H FWHM is 1500 (Osterbrock
1977a) or 1400 km s-1 (Peterson et al. 1982). We measured 1280 km s-1.
FWHM is 1500 (Osterbrock
1977a) or 1400 km s-1 (Peterson et al. 1982). We measured 1280 km s-1.
Mark 110 (0921+52) is a Seyfert 1 (Hutchings & Craven 1988). The
H FWHM is in the range 1670-2500 km s-1 (Osterbrock 1977a;
Crenshaw 1986; Boroson & Green 1992; Bischoff & Kollatschny 1999).
The Fe II emission is weak (
R4570=0.09-0.16) (Osterbrock 1977a; Meyers &
Peterson 1985; Boroson & Green 1992); the Fe II line flux remains constant
while the Balmer line fluxes vary (Bischoff & Kollatschny 1999).
FWHM is in the range 1670-2500 km s-1 (Osterbrock 1977a;
Crenshaw 1986; Boroson & Green 1992; Bischoff & Kollatschny 1999).
The Fe II emission is weak (
R4570=0.09-0.16) (Osterbrock 1977a; Meyers &
Peterson 1985; Boroson & Green 1992); the Fe II line flux remains constant
while the Balmer line fluxes vary (Bischoff & Kollatschny 1999).
We have not observed this object.
Mark 705 (0923+12). The H FWHM is in the range 1670-2400 km s-1 (Zheng & O'Brien 1990; Miller et al. 1992; Boroson & Green 1992).
We found that the broad Balmer components have a FWHM of
FWHM is in the range 1670-2400 km s-1 (Zheng & O'Brien 1990; Miller et al. 1992; Boroson & Green 1992).
We found that the broad Balmer components have a FWHM of  1770 km s-1. Coronal lines have been observed by Erkens et al. (1997).
1770 km s-1. Coronal lines have been observed by Erkens et al. (1997).
Mark 707 (0934+01) is an NLS1; the H FWHM is 1320 (Boroson &
Green 1992) or 2000 km s-1 (Miller et al. 1992).
FWHM is 1320 (Boroson &
Green 1992) or 2000 km s-1 (Miller et al. 1992).
Mark 124 (0945+50) is an NLS1 (De Grijp et al. 1992); the FWHM of the
broad H component is in the range 1050-1400 km s-1 (Osterbrock
1977a; Phillips 1978a). Grandi (1978) did not find high excitation lines.
component is in the range 1050-1400 km s-1 (Osterbrock
1977a; Phillips 1978a). Grandi (1978) did not find high excitation lines.
Mark 1239 (0949-01) is an NLS1 (Osterbrock & Pogge 1985); the FWHM of
the broad Balmer components is  1000 km s-1 (Osterbrock & Pogge
1985; de Robertis & Osterbrock 1984). In contrast, Rodríguez-Ardila et al.
(2000b) gave 2968 and 2278 km s-1 FWHM for the broad H
1000 km s-1 (Osterbrock & Pogge
1985; de Robertis & Osterbrock 1984). In contrast, Rodríguez-Ardila et al.
(2000b) gave 2968 and 2278 km s-1 FWHM for the broad H and
H
and
H component respectively but called it however an NLS1, while Rafanelli
& Bonoli (1984) measured 5000 and 4800 km s-1 respectively. We have
measured 1075 and 905 km s-1 respectively, confirming that the object is
an NLS1.
Coronal lines have been observed by Rafanelli & Bonoli (1984) and Erkens et al. (1997).
component respectively but called it however an NLS1, while Rafanelli
& Bonoli (1984) measured 5000 and 4800 km s-1 respectively. We have
measured 1075 and 905 km s-1 respectively, confirming that the object is
an NLS1.
Coronal lines have been observed by Rafanelli & Bonoli (1984) and Erkens et al. (1997).
IRAS 09571+8435 (0957+84) is an NLS1 with H FWHM= 1120 km s-1 and
R4570=1.46 (Moran et al. 1996).
FWHM= 1120 km s-1 and
R4570=1.46 (Moran et al. 1996).
Boller et al. (1992) found that the ROSAT photon index is
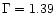 ,
a very small value for an NLS1, but the uncertainty is large.
,
a very small value for an NLS1, but the uncertainty is large.
PG 1011-040 (1011-04). The H FWHM is 1440 (Boroson & Green
1992) or 1980 km s-1 (Miller et al. 1992). The spectrum published by
Simpson et al. (1996) suggests that it is indeed an NLS1.
PG 1011-040 has been detected by ASCA as an X-ray source with a photon
index
FWHM is 1440 (Boroson & Green
1992) or 1980 km s-1 (Miller et al. 1992). The spectrum published by
Simpson et al. (1996) suggests that it is indeed an NLS1.
PG 1011-040 has been detected by ASCA as an X-ray source with a photon
index
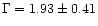 ;
its 2-10 keV luminosity is
;
its 2-10 keV luminosity is
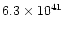 erg s-1; it is a weak X-ray source for its optical luminosity (Gallagher et al. 2001).
erg s-1; it is a weak X-ray source for its optical luminosity (Gallagher et al. 2001).
PG 1016+336 (1016+33) is an NLS1 (Osterbrock & Pogge 1987). The
H FWHM is 1310 km s-1 and
R4570=0.87 (Goodrich 1989).
FWHM is 1310 km s-1 and
R4570=0.87 (Goodrich 1989).
Mark 142 (1022+51) is an NLS1; the H FWHM is in the range
1350-1790 km s-1 (Osterbrock 1977a; Phillips 1978a; Boroson & Green
1992; Grupe et al. 1999).
FWHM is in the range
1350-1790 km s-1 (Osterbrock 1977a; Phillips 1978a; Boroson & Green
1992; Grupe et al. 1999).
KUG 1031+398 (1031+39). The broad component of the Balmer lines is
relatively narrow and, consequently, this object has been classified as an NLS1
by Puchnarewicz et al. (1995).
The profile of the emission lines in KUG 1031+398 is complex; four emission
components are present: an extended H II region, two distinct Seyfert-type
clouds identified with the NLR (one of which has quite broad lines:
 1115 km s-1 FWHM), and a relatively narrow "broad line" component
(1060 km s-1 FWHM) (Gonçalves et al. 1999b).
1115 km s-1 FWHM), and a relatively narrow "broad line" component
(1060 km s-1 FWHM) (Gonçalves et al. 1999b).
According to Pounds et al. (1995), this object is unlike some other
steep-spectrum (soft X-ray) AGNs in showing a marked absence of rapid X-ray
variability and of strong Fe II line emission.
RX J10407+3300 (1037+33). The FWHM of the Balmer lines is 1700 km s-1 and
R4570=0.56 (Bade et al. 1995) suggesting that it is an NLS1.
Mark 734 (1119+12). The spectrum published by Simpson et al. (1996)
suggests that it is an NLS1; the H FWHM is 1820 (Boroson & Green 1992)
or 1940 km s-1 (Miller et al. 1992).
FWHM is 1820 (Boroson & Green 1992)
or 1940 km s-1 (Miller et al. 1992).
Mark 739E (1133+21). The double nucleus nature of Mark 739 was first
described by Petrosian et al. (1979). The eastern component is an NLS1 with
H FWHM=900 km s-1 and very strong Fe II emission (Netzer et al.
1987; Mazzarella & Boroson 1993). Our Lorentzian fit to the Balmer lines has a
FWHM of
FWHM=900 km s-1 and very strong Fe II emission (Netzer et al.
1987; Mazzarella & Boroson 1993). Our Lorentzian fit to the Balmer lines has a
FWHM of  1500 km s-1, substantially larger than the published value.
1500 km s-1, substantially larger than the published value.
MCG 06.26.012 (1136+34) is an NLS1; the H FWHM is equal to
1685 km s-1 (Grupe et al. 1999). Our observations confirm this
classification.
FWHM is equal to
1685 km s-1 (Grupe et al. 1999). Our observations confirm this
classification.
Mark 42 (1151+46) is an NLS1 with relatively strong Fe II emission
(Osterbrock & Pogge 1985). The H emission line is very narrow, in the
range 550-670 km s-1 FWHM (Osterbrock & Pogge 1985; Phillips 1978a).
Grandi (1978) detected [Fe VII]
emission line is very narrow, in the
range 550-670 km s-1 FWHM (Osterbrock & Pogge 1985; Phillips 1978a).
Grandi (1978) detected [Fe VII] 6087.
6087.
On our spectra, the narrow lines are very narrow (<200 km s-1 FWHM
corrected for the instrumental broadening) and the line ratios are those of a
H II region.
NGC 4051 (1200+44) is an NLS1 (Leighly 1999a). The H FWHM is 990
(De Robertis & Osterbrock 1984) or 1150 km s-1 (Leighly 1999b). The
coronal lines are strong (Grandi 1978; Veilleux 1988; Erkens et al. 1997).
Peterson et al. (2000) found that the Balmer lines could arise in a disk-like
configuration and the high-ionization lines in an outflowing wind, of which we
observe preferentially the near side. The structure and the kinematics of the
[O III] lines also suggest an outflow (Christopoulou et al. 1997).
FWHM is 990
(De Robertis & Osterbrock 1984) or 1150 km s-1 (Leighly 1999b). The
coronal lines are strong (Grandi 1978; Veilleux 1988; Erkens et al. 1997).
Peterson et al. (2000) found that the Balmer lines could arise in a disk-like
configuration and the high-ionization lines in an outflowing wind, of which we
observe preferentially the near side. The structure and the kinematics of the
[O III] lines also suggest an outflow (Christopoulou et al. 1997).
Our observations show the presence of two components in the [O III] lines, a
narrow one (200 km s-1 FWHM) and a broader one (665 km s-1 FWHM)
blueshifted by 175 km s-1 with respect to the first.
The X-ray source is variable by at least a factor 30 (Papadakis & Lawrence
1995; Leighly 1999a; Uttley et al. 1999; Komossa & Meerschweinchen 2000); long
term variations in the average X-ray flux might in principle be caused by
absorption by a varying column of material along the line of sight; but this is
ruled out by the spectral data; it is the 2-10 keV luminosity which shows large
amplitude long-term variations (Uttley et al. 1999).
PG 1211+143 (1211+14). The broad Balmer component FWHM has been
measured to be in the range
1500-1860 (Zheng & O'Brien 1990; Stirpe 1990, 1991; Appenzeller &
Wagner 1991; Miller et al. 1992; Boroson & Green 1992;
Wilkes et al. 1999),
except for Miller et al. (1992) who found 2280 km s-1 for the FWHM of
H .
The [Fe VII] line was detected by Appenzeller & Wagner (1991).
.
The [Fe VII] line was detected by Appenzeller & Wagner (1991).
The soft (0.1-2 keV) X-ray flux varied by at least a factor of 16 (Yaqoob et al. 1994).
Mark 766 (1215+30) is an NLS1 (Osterbrock & Pogge 1985). The H FWHM is 1600 (González Delgado & Pérez 1996) or 2400 km s-1
(Osterbrock & Pogge 1985). Our own measurements give 1150 and 1630 km s-1 for the broad H
FWHM is 1600 (González Delgado & Pérez 1996) or 2400 km s-1
(Osterbrock & Pogge 1985). Our own measurements give 1150 and 1630 km s-1 for the broad H and H
and H components respectively. The
spectrum shows relatively strong Fe II emission (Meyers & Peterson 1985;
González Delgado & Pérez 1996) and coronal lines (Veilleux 1988; González
Delgado & Pérez 1996).
The nucleus shows circumnuclear emission, the spectrum of which is well fitted
by H II region models (González Delgado & Pérez 1996).
components respectively. The
spectrum shows relatively strong Fe II emission (Meyers & Peterson 1985;
González Delgado & Pérez 1996) and coronal lines (Veilleux 1988; González
Delgado & Pérez 1996).
The nucleus shows circumnuclear emission, the spectrum of which is well fitted
by H II region models (González Delgado & Pérez 1996).
MS 12170+0700 (1216+07) has been identified with an AGN (Maccacaro et al. 1994). Our spectra show strong broad Balmer components with FWHM equal to
1405 and 1765 km s-1 for H and H
and H respectively; the
narrow line system is most probably a H II region as shown by the line ratios
(
respectively; the
narrow line system is most probably a H II region as shown by the line ratios
( 5007/H
5007/H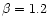 and
and  6583/H
6583/H
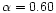 ).
).
MS 12235+2522 (1223+25) is an NLS1 with H FWHM=1730 km s-1 and
FWHM=1730 km s-1 and  5007 FWHM=1700 km s-1 according to Stephens (1989).
The broad Balmer components in our spectra were both fitted by a single
Lorentzian (
5007 FWHM=1700 km s-1 according to Stephens (1989).
The broad Balmer components in our spectra were both fitted by a single
Lorentzian (
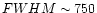 km s-1).
km s-1).
IC 3599 (1235+26). An optical spectrum, taken in May 1991, shows
permitted lines with widths  1200-1500 km s-1 showing that this
object is an NLS1; the forbidden lines are narrow and weak (
R5007< 0.1)
(Brandt et al. 1995; Mason et al. 1995). Low dispersion spectra taken by Grupe
et al. (1995, 1999) from 1992 to 1995 show narrow Balmer and forbidden lines
placing this object close to the borderline between Seyfert 2 and H II galaxies
in the diagnostic diagrams of Veilleux & Osterbrock (1987); the resolution used
was unsufficient to clearly show the composite nature of the spectrum; during
this period, the line ratio R5007 was constant (
1200-1500 km s-1 showing that this
object is an NLS1; the forbidden lines are narrow and weak (
R5007< 0.1)
(Brandt et al. 1995; Mason et al. 1995). Low dispersion spectra taken by Grupe
et al. (1995, 1999) from 1992 to 1995 show narrow Balmer and forbidden lines
placing this object close to the borderline between Seyfert 2 and H II galaxies
in the diagnostic diagrams of Veilleux & Osterbrock (1987); the resolution used
was unsufficient to clearly show the composite nature of the spectrum; during
this period, the line ratio R5007 was constant (
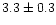 ). Assuming that
the [O III]
). Assuming that
the [O III] 5007 line flux is not variable, it follows that, between May 1991 and February 1992, the flux of the Balmer lines has decreased by a factor
5007 line flux is not variable, it follows that, between May 1991 and February 1992, the flux of the Balmer lines has decreased by a factor
 27 (Grupe et al. 1995). [Fe VII]
27 (Grupe et al. 1995). [Fe VII]  6087 have been detected (Komossa
& Bade 1999).
6087 have been detected (Komossa
& Bade 1999).
Our spectra were taken in March 1997; the line ratio R5007 was then
 3.3. The H
3.3. The H line was too weak for a significant fit to be made, but
the broad H
line was too weak for a significant fit to be made, but
the broad H component could be fitted with a Lorentzian profile with a
FWHM of
component could be fitted with a Lorentzian profile with a
FWHM of  500 km s-1.
500 km s-1.
IC 3599 has been detected as a ROSAT X-ray source (Bade et al. 1995).
The 0.1-2.5 keV X-ray spectrum is extremely steep and is variable by an
extremely large amount; the count-rate decreased by a factor of  80 from
December 1990 to June 1992 and then by an additional factor of
80 from
December 1990 to June 1992 and then by an additional factor of  2 to June 1993 (Grupe et al. 1995; Brandt et al. 1995; Mason et al. 1995).
2 to June 1993 (Grupe et al. 1995; Brandt et al. 1995; Mason et al. 1995).
PG 1244+026 (1244+02) is an NLS1; the FWHM of the H line is
830 (Boroson & Green 1992) or 1350 km s-1 (Miller et al. 1992).
line is
830 (Boroson & Green 1992) or 1350 km s-1 (Miller et al. 1992).
NGC 4748 (1249-13) is an NLS1 with strong Fe II emission (Osterbrock
& de Robertis 1985; Moran et al. 1996). The H FWHM is in the range
1100-1500 km s-1 (Osterbrock & de Robertis 1985;
Maza & Ruiz 1989;
Winkler 1992). Rodríguez-Ardila et al. (2000b)
measured
FWHM is in the range
1100-1500 km s-1 (Osterbrock & de Robertis 1985;
Maza & Ruiz 1989;
Winkler 1992). Rodríguez-Ardila et al. (2000b)
measured  2350 km s-1 for the FWHM of the broad Balmer components. Our own measurements show
that they have a FWHM of
2350 km s-1 for the FWHM of the broad Balmer components. Our own measurements show
that they have a FWHM of  1500 km s-1.
1500 km s-1.
Mark 783 (1300+16) is an NLS1, however the Fe II emission is very weak:
R4570<0.11 (Osterbrock & Pogge 1985).
R 14.01 (1338-14) is an NLS1 with H FWHM=1790 km s-1
(Maza & Ruiz 1989).
FWHM=1790 km s-1
(Maza & Ruiz 1989).
Mark 69 (1343+29). Osterbrock (1977a) noted that it is a Seyfert 1 with
relatively narrow "broad" Balmer lines ( 1500 km s-1 FWHM). The
emission lines on our spectra are well fitted with a single Lorentzian for the
broad Balmer component and one set of Gaussians for the narrow lines, with line
ratios indicating a H II region (
1500 km s-1 FWHM). The
emission lines on our spectra are well fitted with a single Lorentzian for the
broad Balmer component and one set of Gaussians for the narrow lines, with line
ratios indicating a H II region ( 5007/H
5007/H
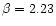 and
and
 6583/H
6583/H
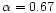 ).
).
2E 1346+2646 (1346+26) is a Seyfert 1 with a relatively narrow "broad"
H component (Hill & Oegerle 1993). Our red spectrum is equally well
fitted with either a broad Gaussian (FWHM=1680 km s-1) or a broad
Lorentzian (FWHM=1235 km s-1). On the blue spectrum, the broad H
component (Hill & Oegerle 1993). Our red spectrum is equally well
fitted with either a broad Gaussian (FWHM=1680 km s-1) or a broad
Lorentzian (FWHM=1235 km s-1). On the blue spectrum, the broad H component is weak and the measurement quite uncertain.
PG 1404+226 (1404+22) is an NLS1 with a narrow H
component is weak and the measurement quite uncertain.
PG 1404+226 (1404+22) is an NLS1 with a narrow H line:
880 (Boroson & Green 1992) or 1290 km s-1 FWHM (Miller et al. 1992).
line:
880 (Boroson & Green 1992) or 1290 km s-1 FWHM (Miller et al. 1992).
The X-ray flux has changed by a factor 13.1 in 10 years (Forster & Halpern
1996) and by a factor 4 in 
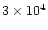 s (Ulrich et al. 1999).
s (Ulrich et al. 1999).
Mark 684 (1428+28) is an NLS1 (Osterbrock & Pogge 1987) with prominent
Fe II emission (Persson 1988).
On the red spectrum, the broad line component is poorly fitted by a single
Lorentzian; a second, Gaussian component is needed. The broad H line
is too weak for a meaningful fit to be made. The spectrum is composite in the
sense that the narrow line region has two components, one with relatively broad
lines, the other with very narrow lines and line ratios typical of a H II
region.
line
is too weak for a meaningful fit to be made. The spectrum is composite in the
sense that the narrow line region has two components, one with relatively broad
lines, the other with very narrow lines and line ratios typical of a H II
region.
Mark 478 (1440+35) is an NLS1 (Gondhalekar et al. 1994; Moran et al.
1996). The H FWHM is in the range 1300-1915 km s-1 (Phillips
1978a; Peterson et al. 1982; Boroson & Green 1992; Gondhalekar et al. 1994;
Grupe et al. 1999). The Fe II emission is strong (Phillips 1977). Grandi (1978)
could not detect high excitation lines.
FWHM is in the range 1300-1915 km s-1 (Phillips
1978a; Peterson et al. 1982; Boroson & Green 1992; Gondhalekar et al. 1994;
Grupe et al. 1999). The Fe II emission is strong (Phillips 1977). Grandi (1978)
could not detect high excitation lines.
PG 1448+273 (1448+27) is an NLS1; the H FWHM is in the range
910-1200 km s-1 (Stirpe 1991; Boroson & Green 1992).
FWHM is in the range
910-1200 km s-1 (Stirpe 1991; Boroson & Green 1992).
IRAS 15091-2107 (1509-21) is an NLS1 (Osterbrock & de Robertis
1985), although Moran et al. (1996) rather classified it as a Seyfert 1.
Goodrich (1989) measured H FWHM= 1480 km s-1 and
R4570= 0.54.
Winkler (1992) and Maza & Ruiz (1989) measured 2000 and 1600 km s-1
respectively for the H
FWHM= 1480 km s-1 and
R4570= 0.54.
Winkler (1992) and Maza & Ruiz (1989) measured 2000 and 1600 km s-1
respectively for the H FWHM.
FWHM.
We have not observed this object.
MS 15198-0633 (1519-06) is an AGN (Margon et al. 1985). The H FWHM is equal to 1304 km s-1; the [Fe VII]
FWHM is equal to 1304 km s-1; the [Fe VII] 6087 line was not
detected (Appenzeller & Wagner 1991).
We have only a red spectrum with a relatively poor signal-to-noise ratio.
6087 line was not
detected (Appenzeller & Wagner 1991).
We have only a red spectrum with a relatively poor signal-to-noise ratio.
Mark 486 (1535+54). The H FWHM is in the range 1410-1650 km s-1 (Boroson & Green 1992; de Robertis 1985; Osterbrock & Shuder 1982;
Boroson et al. 1985). The Fe II emission is relatively strong (Phillips 1978a).
Erkens et al. (1997) have observed coronal lines.
FWHM is in the range 1410-1650 km s-1 (Boroson & Green 1992; de Robertis 1985; Osterbrock & Shuder 1982;
Boroson et al. 1985). The Fe II emission is relatively strong (Phillips 1978a).
Erkens et al. (1997) have observed coronal lines.
The X-ray source has an ASCA photon index
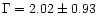 and a
high neutral absorption column density (
and a
high neutral absorption column density (
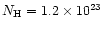 cm-2 plus an unabsorbed component scattered by electrons towards the
observer; its 2-10 keV luminosity is
cm-2 plus an unabsorbed component scattered by electrons towards the
observer; its 2-10 keV luminosity is
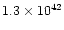 erg s-1; if the
optical nucleus was also absorbed by such a large column density, it would not
be observable and the galaxy would appear as a Seyfert 2 (Gallagher et al.
2001).
erg s-1; if the
optical nucleus was also absorbed by such a large column density, it would not
be observable and the galaxy would appear as a Seyfert 2 (Gallagher et al.
2001).
IRAS 15462-0450 (1546-04) has been identified with the northern 16.6 mag spiral member of a loose interacting pair (Strauss et al. 1992; Duc et al.
1997). It is an ultraluminous IR galaxy with a Seyfert 1 spectrum and strong
Fe II lines (Duc et al. 1997); the [O III] lines are broad with FWHM=1560 km s-1 (Kim et al. 1998).
On our spectra, the broad Balmer components have a FWHM of  1700 km s-1; the narrow lines have a complex profile and can be fitted with two
Gaussian systems: one has very narrow lines (<180 km s-1 FWHM corrected
for instrumental broadening), with line ratios indicating that it is a H II
region; the second system has very broad lines (
1700 km s-1; the narrow lines have a complex profile and can be fitted with two
Gaussian systems: one has very narrow lines (<180 km s-1 FWHM corrected
for instrumental broadening), with line ratios indicating that it is a H II
region; the second system has very broad lines ( 1600 km s-1 FWHM)
and correspond to a Seyfert 2 nebulosity.
1600 km s-1 FWHM)
and correspond to a Seyfert 2 nebulosity.
Mark 493 (1557+35) is an NLS1 with H FWHM = 410 km s-1
(Osterbrock & Pogge 1985).
FWHM = 410 km s-1
(Osterbrock & Pogge 1985).
EXO 16524+3930 (1652+39) is an NLS1 with Balmer line FWHMs equal to
1000 km s-1 (Bassani et al. 1989), which is confirmed by our own
observations.
B3 1702+457 (1702+45) is an NLS1 according to Moran et al. (1996)
and Wisotzki & Bade (1997) who give 490 and 800 km s-1 respectively for
the H FWHM. Leighly (1999b) measured
R4570=1.86.
FWHM. Leighly (1999b) measured
R4570=1.86.
Komossa & Bade (1998) have shown the presence of a warm absorber. The
ASCA spectrum is well fitted by a single power law
(
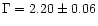 )
plus Galactic absorption, a warm absorber and no soft
excess (Leighly 1999b; Vaughan et al. 1999a).
)
plus Galactic absorption, a warm absorber and no soft
excess (Leighly 1999b; Vaughan et al. 1999a).
RX J17450+4802 (1743+48) is a Seyfert 1 (Perlman et al. 1996). The
Balmer line FWHM is 1600 km s-1 (Bade et al. 1995). Our blue spectrum
shows that the H broad component FWHM is 1355 km s -1 and
R4570=0.78, so this object is an NLS1.
broad component FWHM is 1355 km s -1 and
R4570=0.78, so this object is an NLS1.
Kaz 163 (1747+68) is the southern member of an interacting pair. It is an
NLS1 (Stephens 1989). The H FWHM is in the range 1040-2110 km s-1 (Kriss & Canizares 1982; Stephens 1989; Goodrich 1989; Leighly
1999b).
FWHM is in the range 1040-2110 km s-1 (Kriss & Canizares 1982; Stephens 1989; Goodrich 1989; Leighly
1999b).
Mark 507 (1748+68) has been variously classified as a H II region
(Terlevich et al. 1991), a Seyfert 2 (Koski 1978) or a Liner with a
"transition" type nucleus (Heckman 1980). It is however an NLS1 according to
Halpern & Oke (1987); Goodrich (1989); Moran et al. (1996) and Leighly (1999b).
The H FWHM is 965 (Goodrich 1989) or 1150 km s-1 (Leighly 1999b).
The Fe II emission is strong with
R4570=2.71 (Goodrich 1989) or 1.45
(Leighly 1999b).
FWHM is 965 (Goodrich 1989) or 1150 km s-1 (Leighly 1999b).
The Fe II emission is strong with
R4570=2.71 (Goodrich 1989) or 1.45
(Leighly 1999b).
Our spectra show narrow "broad" Balmer components ( 1335 km s-1
FWHM). The [O III] lines and the narrow component of H
1335 km s-1
FWHM). The [O III] lines and the narrow component of H are best fitted by
two sets of Gaussians, one with narrow components and weak [O III] lines,
typical of a H II region, the other with much broader lines and a large
are best fitted by
two sets of Gaussians, one with narrow components and weak [O III] lines,
typical of a H II region, the other with much broader lines and a large
 5007/H
5007/H ratio. The presence of the H II region component is not
very surprising as Halpern & Oke (1987) have found that the emission lines away
from the nucleus are similar to those of a H II region.
ratio. The presence of the H II region component is not
very surprising as Halpern & Oke (1987) have found that the emission lines away
from the nucleus are similar to those of a H II region.
The ROSAT photon index is
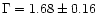 (Leighly 1999b), with an
intrinsic neutral hydrogen column density:
(Leighly 1999b), with an
intrinsic neutral hydrogen column density:
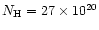 cm-2 in excess of the Galactic value (Iwasawa et al. 1998; Leighly 1999b).
The photon index of this object is very small for an NLS1; this could be due to
the presence of a high column density.
cm-2 in excess of the Galactic value (Iwasawa et al. 1998; Leighly 1999b).
The photon index of this object is very small for an NLS1; this could be due to
the presence of a high column density.
HS 1817+5342 (1817+53). A spectrum published by Engels et al. (1998)
suggests that this object could be an NLS1. Our spectra show that the broad
Balmer line component FWHM are  1620 km s-1 and
R4570=0.59,
so there is no doubt that this is an NLS1.
1620 km s-1 and
R4570=0.59,
so there is no doubt that this is an NLS1.
HS 1831+5338 (1831+53). A spectrum published by Engels et al. (1998)
suggests that this object could be an NLS1. Our spectra show that the FWHMs of
the broad Balmer components are  1510 km s-1 and
R4570=0.74,
so there is no doubt that this is an NLS1.
1510 km s-1 and
R4570=0.74,
so there is no doubt that this is an NLS1.
Mark 896 (2043-02) is a Seyfert 1 with relatively narrow Balmer lines
and strong Fe II emission (Osterbrock & Dahari 1983; Morris & Ward 1988). The
H FWHM is 1390 (Stirpe 1991) or 1330 km s-1 (Stirpe 1990).
However Moran et al. (1996) classified it as a Seyfert 1 rather than an NLS1.
Our spectra show quite narrow "broad" Balmer components (
FWHM is 1390 (Stirpe 1991) or 1330 km s-1 (Stirpe 1990).
However Moran et al. (1996) classified it as a Seyfert 1 rather than an NLS1.
Our spectra show quite narrow "broad" Balmer components ( 1100 km s-1) and
R4570=0.50, so it is an NLS1.
1100 km s-1) and
R4570=0.50, so it is an NLS1.
MS 22102+1827 (2210+18) has been identified with an AGN (Stocke et al.
1991; Maccacaro et al. 1994). Our spectra show quite narrow "broad" Balmer
components ( 750 km s-1), so this is most probably an NLS1.
750 km s-1), so this is most probably an NLS1.
Akn 564 (2240+29) is an NLS1 (Goodrich 1989). The H and H
and H FWHM lie in the ranges 600-730 and 720-1030 km s-1 respectively
(Osterbrock & Shuder 1982; de Robertis & Osterbrock 1984; Stirpe 1990, 1991;
Moran et al. 1996; Comastri et al. 2001). The coronal lines are strong
(Veilleux 1988; Erkens et al. 1997; Comastri et al. 2001).
FWHM lie in the ranges 600-730 and 720-1030 km s-1 respectively
(Osterbrock & Shuder 1982; de Robertis & Osterbrock 1984; Stirpe 1990, 1991;
Moran et al. 1996; Comastri et al. 2001). The coronal lines are strong
(Veilleux 1988; Erkens et al. 1997; Comastri et al. 2001).
The X-ray flux varies by  50% in 1.6 h; the X-ray light-curve shows no
evidence for energy dependence of the variability within the 0.6-10 keV
bandpass (Turner et al. 1999a; Vaughan et al. 1999b).
50% in 1.6 h; the X-ray light-curve shows no
evidence for energy dependence of the variability within the 0.6-10 keV
bandpass (Turner et al. 1999a; Vaughan et al. 1999b).
UV absorption lines have been detected, indicating the presence of a warm
absorber (Crenshaw et al. 1999).
HS 2247+1044 (2247+10). A spectrum published by Engels et al. (1998)
suggested that this object could be an NLS1. This classification is confirmed
by our spectra.
Kaz 320 (2257+24) is an NLS1 according to Zamorano et al. (1992) who
measured 1700 and 1800 km s-1 for the FWHM of the broad component of
H and H
and H respectively. Our spectra confirm this classification.
respectively. Our spectra confirm this classification.
Acknowledgements
We thank C. Boisson for a careful reading of the manuscript.
-
Aoki, K., & Yoshida, M. 1999, ASP Conf. Ser., 162, 385
In the text
-
Appenzeller, I., & Wagner, S. J. 1991, A&A, 250, 57
In the text
NASA ADS
-
Arav, N., Barlow, T. A., Laor, A., & Blandford, R. D. 1997, MNRAS, 288, 1015
In the text
NASA ADS
-
Arribas, S., & Mediavilla, E. 1993, ApJ, 410, 552
In the text
NASA ADS
-
Bade, N., Fink, H. H., Engels, D., et al. 1995, A&AS, 110, 469
In the text
NASA ADS
-
Bassani, L., Coe, M. J., Malkan, M. A., et al. 1989, ApJ, 344, 726
In the text
NASA ADS
-
Bergeron, J., & Kunth, D. 1984, MNRAS, 207, 263
In the text
NASA ADS
-
Bischoff, K., & Kollatschny, W. 1999, A&A, 345, 49
In the text
NASA ADS
-
Boller, T., Meurs, E. J. A., Brinkmann, W., et al. 1992, A&A, 261, 57
In the text
NASA ADS
-
Boller, T., Brandt, W. N., & Fink, H. 1996, A&A, 305, 53
In the text
NASA ADS
-
Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109
In the text
NASA ADS
-
Boroson, T. A., & Meyers, K. A. 1992, ApJ, 397, 442
NASA ADS
-
Boroson, T. A., Persson, S. E., & Oke, J. B. 1985, ApJ, 293, 120
In the text
NASA ADS
-
Bottorff, M., Korista, K. T., Schlosman, I., & Blandford, R. D. 1997, ApJ, 479, 200
In the text
NASA ADS
-
Brandt, W. N., Pounds, K. A., & Fink, H. 1995, MNRAS, 273, L47
In the text
NASA ADS
-
Brandt, W. N., Mathur, S., & Elvis, M. 1997, MNRAS, 285, L25
In the text
NASA ADS
-
Brandt, W. N., Boller, T., Fabian, A. C., & Ruszkowski, M. 1999, MNRAS, 303, L53
In the text
NASA ADS
-
Brotherton, M. S. 1996, ApJS, 102, 1
In the text
NASA ADS
-
Brotherton, M. S., Wills, B. J., Francis, P. J., & Steidel, C. C. 1994, ApJ, 430, 495
NASA ADS
-
Christopoulou, P. E., Holloway, A. J., Steffen, W., et al. 1997, MNRAS, 284, 385
In the text
NASA ADS
-
Ciliegi, P., & Maccacaro, T. 1996, MNRAS, 282, 477
In the text
NASA ADS
-
Clavel, J., Joly, M., Collin-Souffrin, S., Bergeron, J., & Penston, M. V. 1983,
MNRAS, 202, 85
In the text
NASA ADS
-
Colbert, E. J. M., Baum, S. A., Gallimore, J. F., et al. 1996, ApJS, 105, 75
In the text
NASA ADS
-
Collin-Souffrin, S., & Lasota, J.-P. 1988, PASP, 100, 1041
In the text
NASA ADS
-
Collin-Souffrin, S., Dumont, S., Heidmann, N., & Joly, M. 1980, A&A, 83, 190
In the text
NASA ADS
-
Collin-Souffrin, S., Dyson, J. E., McDowell, J. C., & Perry, J. J. 1988a, MNRAS, 232, 539
In the text
NASA ADS
-
Collin-Souffrin, S., Hameury, J.-M., & Joly, M. 1988b, A&A, 205, 19
In the text
NASA ADS
-
Comastri, A., Fiore, F., Guainazzi, M., et al. 1998, A&A, 333, 31
In the text
NASA ADS
-
Comastri, A., Stirpe, G. M., Vignali, C., et al. 2001, A&A, 365, 400
In the text
NASA ADS
-
Corbin, M. R. 1995, ApJ, 447, 496
In the text
NASA ADS
-
Corbin, M. R. 1997, ApJS, 113, 245
In the text
NASA ADS
-
Corbin, M. R., & Boroson, T. A. 1996, ApJS, 107, 69
In the text
NASA ADS
-
Crenshaw, D. M. 1986, ApJS, 62, 821
In the text
NASA ADS
-
Crenshaw, D. M., & Kraemer, S. B. 2000, ApJ, 532, L101
In the text
NASA ADS
-
Crenshaw, D. M., Kraemer, S. B., Boggess, A., et al. 1999, ApJ, 516, 750
In the text
NASA ADS
-
Crenshaw, D. M., Kraemer, S. B., Hutchings, J. B., et al. 2000, AJ, 120, 1731
In the text
NASA ADS
-
de Grijp, M. H. K., Keel, W. C., Miley, G. K., Goudfrooij, P., & Lub, J. 1992, A&AS, 96, 389
In the text
NASA ADS
-
de Robertis, M. M. 1985, ApJ, 289, 67
In the text
NASA ADS
-
de Robertis, M. M., & Osterbrock, D. E. 1984, ApJ, 286, 171
In the text
NASA ADS
-
Duc, P. A., Mirabel, I. F., & Maza, J. 1997, A&AS, 124, 533
In the text
NASA ADS
-
Dumont, A.-M., & Collin-Souffrin, S. 1990, A&A, 229, 313
In the text
NASA ADS
-
Dumont, A.-M., Collin-Souffrin, S., & Nazarova, L. 1998, A&A, 331, 11
In the text
NASA ADS
-
Elvis, M., Green, R. F., Bectold, J., & Fabbiano, G. 1986, ApJ, 310, 291
In the text
NASA ADS
-
Emmering, R. T., Blandford, R. D., & Shlosman, I. 1992, ApJ, 385, 460
In the text
NASA ADS
-
Engels, D., Hagen, H.-J., Cordis, L., et al. 1998, A&AS, 128, 507
In the text
NASA ADS
-
Erkens, U., Appenzeller, J., & Wagner, S. 1997, A&A, 323, 707
In the text
NASA ADS
-
Feldman, F. R., & MacAlpine, G. M. 1978, ApJ, 221, 486
In the text
NASA ADS
-
Fiore, F., Laor, A., Elvis, M., Nicastro, F., & Giallongo, E. 1998, ApJ, 503, 607
In the text
NASA ADS
-
Forster, K., & Halpern, J. P. 1996, ApJ, 468, 565
In the text
NASA ADS
-
Francis, P. J., Hewett, P. C., Foltz, C. B., & Chaffee, F. H. 1992, ApJ, 398, 476
In the text
NASA ADS
-
Gallagher, S. C., Brandt, W. N., Sambruna, R. M., et al. 1999, ApJ, 519, 549
In the text
NASA ADS
-
Gallagher, S. C., Brandt, W. N., Laor, A., et al. 2001, ApJ, 546, 795
In the text
NASA ADS
-
Gaskell, C. M. 1985, ApJ, 291, 112
In the text
NASA ADS
-
Gaskell, C. M. 2000, New Astron. Rev., 44, 563
In the text
NASA ADS
-
George, I. M., Turner, T. J., Netzer, H., et al. 1998a, ApJS, 114, 73
In the text
NASA ADS
-
George, I. M., Mushotzky, R., Turner, T. J., et al. 1998b, ApJ, 509, 146
In the text
NASA ADS
-
George, I. M., Turner, T. J., Yaqoob, T., et al. 2000, ApJ, 531, 52
In the text
NASA ADS
-
Giannuzzo, M. E., & Stirpe, G. M. 1996, A&A, 314, 419
In the text
NASA ADS
-
Gliozzi, M., Boller, T., Brinkmann, W., & Brandt, W. N. 2000, A&A, 356, L17
NASA ADS
-
Goad, M. R., Koratkar, A. P., Kim-Quijano, J., et al. 1999, ApJ, 524, 707
In the text
NASA ADS
-
Gonçalves, A. C., Véron, P., & Véron-Cetty, M.-P. 1999a, A&AS, 135, 437
In the text
NASA ADS
-
Gonçalves, A. C., Véron, P., & Véron-Cetty, M.-P. 1999b, A&A, 341, 662
In the text
NASA ADS
-
Gondhalekar, P. M., Kellett, B. J., Pounds, K. A., Matthews, L., & Quenby, J. J. 1994,
MNRAS, 268, 973
In the text
NASA ADS
-
González Delgado, R. M., & Pérez, E. 1996, MNRAS, 278, 737
In the text
NASA ADS
-
Goodrich, R. W. 1989, ApJ, 342, 224
In the text
NASA ADS
-
Grandi, S. A. 1978, ApJ, 221, 501
In the text
NASA ADS
-
Green, P. J., Ward, M. J., Anderson, S. F., et al. 1989, ApJ, 339, 93
In the text
NASA ADS
-
Grupe, D., Beuerman, K., Mannheim, K., et al. 1995, A&A, 299, L5
In the text
NASA ADS
-
Grupe, D., Beuerman, K., Thomas, H. C., et al. 1998, A&A, 330, 25
In the text
NASA ADS
-
Grupe, D., Beuerman, K., Mannheim, K., & Thomas, H. C. 1999, A&A, 350, 805
In the text
NASA ADS
-
Halpern, J. P., & Oke, J. B. 1987, ApJ, 312, 91
of IPC X-ray sources, Smithsonian astrophysical observatory, Cambridge
In the text
NASA ADS
-
Heckman, T. M. 1980, A&A, 87, 152
In the text
NASA ADS
-
Heckman, T. M., Miley ,G. K., van Breugel, W. J. M., & Butcher, H. R. 1981, ApJ, 247, 403
In the text
NASA ADS
-
Heckman, T. M., Miley, G. K., & Green, R. F. 1984, ApJ, 281, 525
In the text
NASA ADS
-
Hill, J. M., & Oegerle, W. R. 1993, AJ, 106, 831
In the text
NASA ADS
-
Hutchings, J. B., & Craven, S. E. 1988, AJ, 95, 677
In the text
NASA ADS
-
Iwasawa, K., Brandt, W. N., & Fabian, A. C. 1998, MNRAS, 293, 251
In the text
NASA ADS
-
Joly, M. 1981, A&A, 102, 321
In the text
NASA ADS
-
Kaiser, M. E., Bradley, L. D., Hutchings, J. B., et al. 2000, ApJ, 528, 260
In the text
NASA ADS
-
Kim, D.-C., Veilleux, S., & Sanders, D. B. 1998, ApJ, 508, 627
In the text
NASA ADS
-
Kolman, M., Halpern, J. P., Shrader, C. R., et al. 1993, ApJ, 402, 514
In the text
NASA ADS
-
Komossa, S., & Fink, H. 1997a, A&A, 327, 483
In the text
NASA ADS
-
Komossa, S., & Fink, H. 1997b, A&A, 327, 555
NASA ADS
-
Komossa, S., & Bade, N. 1998, A&A, 331, L49
In the text
NASA ADS
-
Komossa, S., & Bade, N. 1999, A&A, 343, 775
In the text
NASA ADS
-
Komossa, S., & Meerschweinchen, J. 2000, A&A, 354, 411
In the text
NASA ADS
-
Königl, A., & Kartje, J. F. 1994, ApJ, 434, 446
In the text
NASA ADS
-
Koski, A. T. 1978, ApJ, 223, 56
In the text
NASA ADS
-
Kriss, G. A., & Canizares, C. R. 1982, ApJ, 261, 51
In the text
NASA ADS
-
Kuraszkiewicz, J. K., Wilkes, B. J., Czerny, B., & Mathur, S. 2000, ApJ, 542, 692
In the text
NASA ADS
-
Kwan, J., Cheng, F.-Z., Fang, L.-Z., Zheng, W., & Ge, J. 1995, ApJ, 440, 628
In the text
NASA ADS
-
Laor, A., Fiore, F., Elvis, M., Wilkes, B. J., & McDonnel, J. C. 1997a, ApJ, 477, 93
In the text
NASA ADS
-
Laor, A., Jannuzi, B. T., Green, R. F., & Boroson, T. A. 1997b, ApJ, 489, 656
In the text
NASA ADS
-
Lawrence, A., Saunders, W., Rowan-Robinson, M., et al. 1988, MNRAS, 235, 261
In the text
NASA ADS
-
Lawrence, A., Elvis, M., Wilkes, B. J., McHardy, I., & Brandt, N. 1997, MNRAS, 285, 879
In the text
NASA ADS
-
Leighly, K. M. 1999a, ApJS, 125, 297
In the text
NASA ADS
-
Leighly, K. M. 1999b, ApJS, 125, 317
In the text
NASA ADS
-
Leighly, K. M. 2001, HST SIS ultraviolet spectral evidence for
outflows in extreme narrow-line Seyfert 1 galaxies, ed. B. M. Peterson, R. S.
Polidan, & R. W. Pogge, ASP Conf. Ser., 224, in press
In the text
-
Lemaître, G., Kohler, D., Lacroix, D., Meunier, J.-P., & Vin, A. 1989, A&A,
228, 546
In the text
NASA ADS
-
Lipari, S. 1994, ApJ, 436, 102
In the text
NASA ADS
-
Lipari, S., Terlevich, R., & Macchetto, F. 1993, ApJ, 406, 451
In the text
NASA ADS
-
Maccacaro, T., Wolter, A., McLean, B., et al. 1994, Astrophys. Lett. & Comm., 29, 267
In the text
-
Margon, B., Downes, R. A., & Chanan, G. A. 1985, ApJS, 59, 23
In the text
NASA ADS
-
Marziani, P., Sulentic, J. W., Dultzin-Hacyan, D., Calvani, M., & Moles, M. 1996, ApJS,
104, 37
In the text
NASA ADS
-
Mason, K. O., Hassall, B. J. M., Bromage, G. E., et al. 1995, MNRAS, 274, 1194
In the text
NASA ADS
-
Massey, P., Strobel, K., Barnes, J. V., & Anderson, E. 1988, ApJ, 328, 315
In the text
NASA ADS
-
Mathews, W. G., & Wampler, E. J. 1985, PASP, 97, 966
In the text
NASA ADS
-
Maza, J., & Ruiz, M. T. 1989, ApJS, 69, 353
In the text
NASA ADS
-
Mazzarella, J. M., & Boroson, T. A. 1993, ApJS, 85, 27
In the text
NASA ADS
-
McIntosh, D. H., Rieke, M. J., Rix, H.-W., Foltz, C. B., & Weyman, R. J. 1999, ApJ, 514, 40
In the text
NASA ADS
-
Meyers, K. A., & Peterson, B. M. 1985, PASP, 97, 734
In the text
NASA ADS
-
Miller, P., Rawlings, S., Saunders, R., & Eales, S. 1992, MNRAS, 254, 93
In the text
NASA ADS
-
Molthagen, K., Bade, N., & Wendker, H. J. 1998, A&A, 331, 925
In the text
NASA ADS
-
Moran, E. C., Halpern, J. P., & Helfand, D. J. 1996, ApJS, 106, 341
In the text
NASA ADS
-
Morris, S. L., & Ward, M. J. 1988, MNRAS, 230, 639
In the text
NASA ADS
-
Murray, N., & Chiang, J. 1998, ApJ, 494, 125
In the text
NASA ADS
-
Nagao, T., Murayama, T., & Taniguchi, Y. 2001, ApJ, 546, 744
In the text
NASA ADS
-
Nandra, K., & Pounds, K. A. 1994, MNRAS, 268, 405
In the text
NASA ADS
-
Netzer, H., Kollatschny, W., & Fricke, K. J. 1987, A&A, 171, 41
In the text
NASA ADS
-
Nicastro, F. 2000, ApJ, 530, L65
In the text
NASA ADS
-
Oke, J. B. 1974, ApJS, 27, 21
In the text
NASA ADS
-
Oke, J. B., & Gunn, J. E. 1983, ApJ, 206, 713
In the text
NASA ADS
-
Osterbrock, D. E. 1977a, ApJ, 215, 733
In the text
NASA ADS
-
Osterbrock, D. E. 1977b, PASP, 89, 620
NASA ADS
-
Osterbrock, D. E. 1981, ApJ, 249, 462
In the text
NASA ADS
-
Osterbrock, D. E. 1987, Lecture Notes in Physics, 307, 1
In the text
-
Osterbrock, D. E., & Dahari, O. 1983, ApJ, 273, 478
In the text
NASA ADS
-
Osterbrock, D. E., & Shuder, J. M. 1982, ApJS, 49, 149
In the text
NASA ADS
-
Osterbrock, D. E., & de Robertis, M. M. 1985, PASP, 97, 1129
In the text
NASA ADS
-
Osterbrock, D. E., & Pogge, R. W. 1985, ApJ, 297, 166
In the text
NASA ADS
-
Osterbrock, D. E., & Pogge, R. W. 1987, ApJ, 323, 108
In the text
NASA ADS
-
Page, M. J., Carrera, F. J., Mittaz, J. P. D., & Mason, K. O. 1999, MNRAS, 305, 775
In the text
NASA ADS
-
Papadakis, I. E., & Lawrence, A. 1995, MNRAS, 272, 161
In the text
NASA ADS
-
Perlman, E. S., Stocke, J. T., Schachter, J. F., et al. 1996, ApJS, 104, 251
In the text
NASA ADS
-
Persson, S. E. 1988, ApJ, 330, 751
In the text
NASA ADS
-
Peterson, B. M., Foltz, C. G., Byard, P. L., & Wagner, R. M. 1982, ApJS, 49, 469
In the text
NASA ADS
-
Peterson, B. M., Pogge, R. W., & Wanders, I. 1999, ASP Conf. Ser., 175, 41
In the text
-
Peterson, B. M., McHardy, I. M., Wilkes, B. J., et al. 2000, ApJ, 542, 161
In the text
NASA ADS
-
Petrosian, A. R., Saakian, K. A., & Khachikian, E. E. 1979, Astrophys., 15, 250
In the text
NASA ADS
-
Pfefferkorn, F., Boller, T., & Rafanelli, P. 2001, A&A, 368, 797
In the text
NASA ADS
-
Phillips, M. M. 1976, ApJ, 208, 37
In the text
NASA ADS
-
Phillips, M. M. 1977, ApJ, 215, 746
In the text
NASA ADS
-
Phillips, M. M. 1978a, ApJS, 38, 187
In the text
NASA ADS
-
Phillips, M. M. 1978b, ApJ, 226, 736
In the text
NASA ADS
-
Pogge, R. W. 1989, ApJ, 345, 730
In the text
NASA ADS
-
Pounds, K. A., Stanger, V. J., Turner, T. J., King, A. R., & Czerny, B. 1987, MNRAS, 224, 443
In the text
NASA ADS
-
Pounds, K. A., Done, C., & Osborne, J. P. 1995, MNRAS, 277, L5
In the text
NASA ADS
-
Puchnarewicz, E. M., Mason, K. O., Córdova, F. A., et al. 1992, MNRAS, 256, 589
In the text
NASA ADS
-
Puchnarewicz, E. M., Mason, K. O., Córdova, F. A., et al. 1994, MNRAS, 270, 663
In the text
NASA ADS
-
Puchnarewicz, E. M., Mason, K. O., Siemiginowska, A., & Pounds, K. 1995, MNRAS, 276, 20
In the text
NASA ADS
-
Puchnarewicz, E. M., Mason, K. O., Carrera, F. J., et al. 1997, MNRAS, 291, 177
In the text
NASA ADS
-
Rafanelli, P. 1985, A&A, 146, 17
In the text
NASA ADS
-
Rafanelli, P., & Bonoli, C. 1984, A&A, 131, 186
In the text
NASA ADS
-
Rao, A. R., Singh, K. P., & Vahia, M. N. 1992, MNRAS, 255, 197
In the text
NASA ADS
-
Rees, M. J., Netzer, H., & Ferland, G. J. 1989, ApJ, 347, 640
In the text
NASA ADS
-
Reeves, J., & Turner, M. J. L. 2000, MNRAS, 316, 234
In the text
NASA ADS
-
Reeves, J., O'Brien, P. T., Vaughan, S., et al. 2000, MNRAS, 312, L17
In the text
NASA ADS
-
Reynolds, C. S. 1997, MNRAS, 286, 513
In the text
NASA ADS
-
Rodríguez-Ardila, A., Pastoriza, M. G., & Donzelli, C. J. 2000a, ApJS, 126, 63
In the text
NASA ADS
-
Rodríguez-Ardila, A., Binette, L., Pastoriza, M. G., & Donzelli, C. J. 2000b, ApJ,
538, 581
In the text
NASA ADS
-
Rodríguez-Pascual, P. M., Mas-Hesse, J. M., & Santos-Lléo, M. 1997, A&A, 327, 72
In the text
NASA ADS
-
Ross, R. R., Fabian, A. C., & Mineshige, S. 1992, MNRAS, 258, 189
In the text
NASA ADS
-
Rush, B., Malkan, M. A., Fink, H. H., & Voges, W. 1996, ApJ, 471, 190
In the text
NASA ADS
-
Sanders, D. B., Phinney, E. S., Neugebauer, G., Soifer, B. T., & Matthews, K. 1989, ApJ,
347, 29
In the text
NASA ADS
-
Saxton, R. D., Turner, M. J. L., Williams, O. R., et al. 1993, MNRAS, 262, 63
In the text
NASA ADS
-
Siemiginowska, A., Kuhn, O., Elvis, M., et al. 1995, ApJ, 454, 77
In the text
NASA ADS
-
Simpson, C., Ward, M., Clements, D. L., & Rawlings, S. 1996, MNRAS, 281, 509
In the text
NASA ADS
-
Simpson, C., Ward, M., O'Brien, P., & Reeves, J. 1999, MNRAS, 303, L23
In the text
NASA ADS
-
Smith, S. J. 1993, ApJ, 411, 570
In the text
NASA ADS
-
Stephens, S. A. 1989, AJ, 97, 10
In the text
NASA ADS
-
Stirpe, G. M. 1990, A&AS, 85, 1049
In the text
NASA ADS
-
Stirpe, G. M. 1991, A&A, 247, 3
In the text
NASA ADS
-
Stocke, J. T., Morris, S. L., Gioia, I. M., et al. 1991, ApJS, 76, 813
In the text
NASA ADS
-
Stone, R. P. S. 1977, ApJ, 218, 767
In the text
NASA ADS
-
Storchi-Bergmann, T., Wilson, A. S., & Baldwin, J. A. 1992, ApJ, 396, 45
In the text
NASA ADS
-
Strauss, M. A., Huchra, J. P., Davis, M., et al. 1992, ApJS, 83, 29
In the text
NASA ADS
-
Sulentic, J. W., Marziani, P., Dultzin-Hacyan, D., Calvani, M., & Moles, M. 1995,
ApJ, 445, L85
In the text
NASA ADS
-
Sulentic, J. W., Zwitter, T., Marziani, P., & Dultzin-Hacyan, D. 2000a, ApJ, 536, L5
In the text
NASA ADS
-
Sulentic, J. W., Marziani, P., Zwitter, T., Dultzin-Hacyan, D., & Calvani, M. 2000b,
ApJ, 545, L15
In the text
NASA ADS
-
Sun, W.-H., & Malkan, M. A. 1989, ApJ, 346, 68
In the text
NASA ADS
-
Terlevich, R., Melnick, J., Masegosa, J., Moles, M., & Copetti, M. V. F. 1991, A&AS, 91, 285
In the text
NASA ADS
-
Turner, T. J. 1999, ApJ, 511, 142
In the text
NASA ADS
-
Turner, T. J., George, I. M., & Netzer, H. 1999a, ApJ, 526, 52
In the text
NASA ADS
-
Turner, T. J., George, I. M., Nandra, K., & Turcan, D. 1999b, ApJ, 524, 667
In the text
NASA ADS
-
Ulrich-Demoulin, M.-H., & Molendi, S. 1996, ApJ, 457, 77
NASA ADS
-
Uttley, P., M
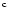 Hardy, I. M., Papadakis, I. E., Guainazzi, M., & Fruscione, A.
1999, MNRAS, 307, L6
In the text
NASA ADS
Hardy, I. M., Papadakis, I. E., Guainazzi, M., & Fruscione, A.
1999, MNRAS, 307, L6
In the text
NASA ADS
-
van Groningen, E. 1987, A&A, 186, 103
In the text
NASA ADS
-
Vaughan, S., Reeves, J., Warwick, R., & Edelson, R. 1999a, MNRAS, 309, 113
In the text
NASA ADS
-
Vaughan, S., Pounds, K. A., Reeves, J., Warwick, R., & Edelson, R. 1999b, MNRAS, 308, L34
In the text
NASA ADS
-
Veilleux, S. 1988, AJ, 95, 1695
In the text
NASA ADS
-
Veilleux, S. 1991a, ApJ, 368, 158
In the text
NASA ADS
-
Veilleux, S. 1991b, ApJS, 75, 383
In the text
NASA ADS
-
Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295
In the text
NASA ADS
-
Veilleux, S., Shopbell, P. L., & Miller, S. T. 2001, AJ, 121, 198
In the text
NASA ADS
-
Véron, P., & Véron-Cetty, M. P. 1986, A&A, 161, 145
In the text
NASA ADS
-
Véron, P., Lindblad, P. O., Zuiderwijk, E. J., Véron-Cetty, M. P., & Adam, G. 1980,
A&A, 87, 245
In the text
NASA ADS
-
Véron, P., Véron-Cetty, M. P., & Zuiderwijk, E. J. 1981a, A&A, 102, 116
In the text
NASA ADS
-
Véron, P., Véron-Cetty, M. P., Bergeron, J., & Zuiderwijk, E. J. 1981b,
A&A, 97, 71
In the text
NASA ADS
-
Véron, M.-P. 1981, A&A, 100, 12
In the text
NASA ADS
-
Véron-Cetty, M.-P., Véron, P., & Gonçalves, A. C. 2001, in preparation
In the text
-
Vignali, C., Comastri, A., Nicastro, F., et al. 2000, A&A, 362, 69
In the text
NASA ADS
-
Vrtilek, J. M. 1985, ApJ, 294, 121
In the text
NASA ADS
-
Vrtilek, J. M., & Carleton, N. P. 1985, ApJ, 294, 106
In the text
NASA ADS
-
Walter, R., & Fink, H. H. 1993, A&A, 274, 105
In the text
NASA ADS
-
Wang, T., Brinkmann, W., & Bergeron, J. 1996, A&A, 309, 81
In the text
NASA ADS
-
Wang, T.-G., Lu, Y.-J., & Zhou, Y.-Y. 1998, ApJ, 493, 1
In the text
NASA ADS
-
Whittle, M. 1985a, MNRAS, 213, 1
In the text
NASA ADS
-
Whittle, M. 1985b, MNRAS, 213, 33
In the text
NASA ADS
-
Whittle, M. 1992, ApJ, 387, 109
In the text
NASA ADS
-
Whittle, M., Pedlar, A., Meurs, E. J. A., et al. 1988, ApJ, 326, 125
In the text
NASA ADS
-
Wilkes, B. J., Kuraszkiewicz, J., Green, P. J., Mathur, S., & McDonnel, J. C. 1999, ApJ,
513, 76
In the text
NASA ADS
-
Wills, B. J. 1982, IAU Symp. 97, 373
In the text
NASA ADS
-
Wills, B. J., Brotherton, M. S., Fang, D., Steidel, C. C., & Sargent, W. L. W. 1993, ApJ, 415, 563
In the text
NASA ADS
-
Wills, B. J., Laor, A., Brotherton, M. S., et al. 1999, ApJ, 515, L53
In the text
NASA ADS
-
Wills, B. J., Shang, Z., & Yuan, J. M. 2000, New Astron. Rev., 44, 511
In the text
NASA ADS
-
Wilson, A. S. 1994, in Oxford astrophysics workshop on Evidence for the torus,
ed. M. J. Ward, 55
In the text
-
Wilson, A. S., Braatz, J. A., Heckman, T. M., Krolik, J. H., & Miley, G. K. 1993, ApJ,
419, L61
In the text
NASA ADS
-
Winkler, H. 1992, MNRAS, 257, 677
In the text
NASA ADS
-
Wisotzki, L., & Bade, N. 1997, A&A, 320, 395
In the text
NASA ADS
-
Wisotzki, L., Dreizler, S., Engels, D., Fink, H.-H., & Heber, U. 1995, A&A, 297, L55
In the text
NASA ADS
-
Xia, X.-Y., Mao, S., Wu, H., et al. 1999, A&A, 341, L13
In the text
NASA ADS
-
Yaqoob, T., Serlemitsos, P., Mushotzky, R., et al. 1994, PASJ, 46, L173
In the text
NASA ADS
-
Yuan, W., Brinkmann, W., Siebert, J., & Voges, W. 1998, A&A, 330, 108
In the text
NASA ADS
-
Zamorano, J., Gallego, J., Rego, M., Vitores, A. G., & Gonzalez-Riesta, R. 1992, AJ,
104, 1000
In the text
NASA ADS
-
Zheng, W., & O'Brien, P. T. 1990, ApJ, 353, 433
In the text
NASA ADS
-
Zheng, W., & Keel, W. C. 1991, ApJ, 382, 121
In the text
NASA ADS
Copyright ESO 2001
![\begin{table}\par
\par\includegraphics[width=20cm,clip]{tab2.eps}\end{table}](/articles/aa/full/2001/24/aa1123/img26.gif)
![\begin{table}
\par\includegraphics[width=20cm,clip]{tab2c.eps}\par\end{table}](/articles/aa/full/2001/24/aa1123/img27.gif)









![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{o5007.eps}
\end{figure}](/articles/aa/full/2001/24/aa1123/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{hbetalum.eps}
\end{figure}](/articles/aa/full/2001/24/aa1123/Timg56.gif)


