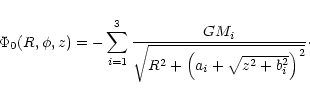A&A 372, 784-792 (2001)
DOI: 10.1051/0004-6361:20010571

Periodic orbits in warped disks

Y. Revaz - D. Pfenniger

Geneva Observatory, University of Geneva, 1290 Sauverny, Switzerland

Received 22 November 2000 / Accepted 9 April 2001

Abstract
It is often assumed that a warped galaxy can be modeled by a set of rings. This paper verifies numerically the validity of this assumption by the study of periodic orbits populating a heavy self-gravitating warped disk. The phase space structure of a warped model reveals that the circular periodic orbits of a flat disk are transformed in quasi annular periodic orbits which conserve their stability. This lets us also explore the problem of the persistence of a large outer warp. In particular, the consistency of its orbits with the density distribution is checked as a function of the pattern speed.

Key words: galaxies: kinematics and dynamics of galaxies - galaxies: spiral

1 Introduction

In the conventional understanding of galaxies embedded in a kinematically hot spheroidal or triaxial halos of dark matter, the frequently observed pronounced outer warps of neutral hydrogen, interstellar dust and, to a lesser noticeable extent, optical disks set a challenge for explaining their presumably long-lived existence, and particularly, their frequent quasi-straight line of nodes (LON), or pair of quasi-straight LON (Briggs 1990). At least half the spirals possess a detectable warped HI and stellar disk(e.g., Briggs 1990, and more should remain undetected due to projection confusion.

Hypotheses like cosmic infall (Jiang & Binney 1999), gravitational interactions (Hernquist 1991; Weinberg 1995, 1998), normal modes (Sparke 1984; Sparke & Casertano 1988), misaligned dark halos (Kuijken 1991; Dubinski & Kuijken 1995; Debattista & Sellwood 1999) or magnetic fields (Battaner et al. 1990) have been proposed, without clearly satisfying all the constraints provided by the observations. See Binney (1992) or Kuijken (2000) for reviews.

But, as argued by Arnaboldi et al. (1997), Becquaert & Combes (1998) and Reshetnikov & Combes (1998), also in the context of polar rings, the evidence for non-self-gravitating HI disks is actually weak. Instead, the opposite assumption of coexistence of warps containing most of the dynamical mass is not in contradiction with the available observations. Such an assumption of thick and flaring disks of visible and dark matter in the form of cold gas approximately proportional to neutral hydrogen has been proposed by Pfenniger et al. (1994) to account for many more known facts about spirals. For the warp problem, the self-gravitating disk assumption is attractive for several reasons. HI observations reveal that most of the galaxies possess an inner flat disk, while the warp develops beyond a specific radius (Briggs 1990; Burton 1992). Such a comportment, which is the signature of a radical change of the dynamic along the radius, can hardly be explained by a hot halo which would impose a uniform dynamic over a larger scale. In contrast, a strong rotational support in the dark matter component offers a natural explanation for the straight lines of nodes. They would result as a natural consequence of the weak diffusive properties of angular momentum in a self-gravitating disk: if, following for example an accretion event, angular momentum is deposited in a self-gravitating disk, bending its outer parts, the angular momentum will slowly diffuse across the whole disk in a monotonous way, because angular momentum is a quasi conserved quantity. As its diffusion is slow, the line of nodes must be quasi-straight and persist for many rotational periods. Finally, self-gravitating optical disks are in agreement with the often stated maximum disk interpretation of observations of the Milky Way and other spirals (see for example Gerhard 2000). In numerous models of warped galaxies, and also polar ring models, stars are assumed to move along circular rings which are tilted as a function of radius. Because stars are driven by periodic orbits, which are the backbone of galaxies, such models implicitly presuppose the existence of stable circular tilted periodic orbits. Yet, to our knowledge they have never been verified, and do not appear obvious in non-spherical geometries. It is far from obvious that a perturbation in the form of a warp will conserve the well known circular orbits of a flat disk. In order to verify the latter assumptions, it is useful to find the exact periodic orbits existing in a warped disk. Moreover, understanding the stable periodic orbits allows us to grasp the basic properties of the other quasi-periodic orbits in an efficient way, particularly when no analytical tools exist. Such an approach has been very useful in the context of barred galaxies for which the complexity of motion is substantial (e.g., Contopoulos & Papayannopoulos 1980; Pfenniger 1984). For studying the principal periodic orbits in a galactic potential, even rough representations of the potential are sufficient to yield the basic properties of the main periodic orbits, as that shown in numerous situations. In this work, the disk autogravitation will play a dominant role. Therefore, the following results will be applicable as long as the local density is dominated by the disk.

The alternative case would be the existence of a hot dark matter halo. In this case, one must admit a center dominated by the halo density, because the density of a warm gravitating system increases at the center. The following implications should be explored:

1)

A hot halo is aligned with the central stellar disk. The outer gaseous disk acts as a tracer of the main periodic orbits in the halo. The only reason for the disk to warp is then to follow the orbits generated by a vertical 1:1 resonance. But in spheroidal halos, stable warped orbits do not exist due to the invariance in azimuth of the potential. To avoid this problem, one has to take in account both the mass of the halo and the self-gravity of the disk (Sparke 1984; Sparke & Casertano 1988). In triaxial halos more periodic 1:1 orbit families exist. 1:1 resonances are strong only in rapidly rotating triaxial potentials (e.g. Mulder 1983), and associated orbits would be compatible with warps only outside the corotation radius: the dynamics would resemble the one of a rescaled triaxial bar (Pfenniger 1984). But such triaxial halos appear difficult to reconcile with the axisymmetrization that follows the inclusion of even a weak fraction of dissipative matter (Dubinski 1994);

2)

The gaseous disk is aligned with the outer part of a hot halo, and the optical disk is tilted. This case appears dynamically highly unstable because the optical disks appear maximum (cf. Gerhard 2000), i.e., self-gravitating to a large extent;

3)

The halo follows the warp of the disk. Such a halo can survive if it possesses enough angular momentum and therefore should be flattened. This case becomes very similar to the case of the massive disk, and the comportment of the periodic orbits is not changed dramatically.

In this paper we present succinctly a study of periodic orbits in a simple model of warped disk galaxies, in which the stability and consistency with the density distribution is also determined. The influence of a global rotation of the warp pattern is examined too. A subsequent study will investigate the orbits in self-consistent N-body models of warps.

2 Model

2.1 Warped disk model

In order to compute periodic orbits, we have based our model on a superposition of three simple Miyamoto-Nagai potentials (Nagai & Miyamoto 1975). The three components can be viewed as representing respectively a bulge, a visible disk and a gas disk containing a large amount of dark matter. In cylindrical coordinates, the total potential can be written as:

$$\Phi_0(R,\phi,z) = -\sum_{i=1}^{3} \frac{GM_i} {\sqrt{R^2+\left(a_i+\sqrt{z^2 + b_i^2}\right)^2}}\cdot$$ (1)

Observations suggest that warps seen on edge take the shape of an integral sign, i.e., the disk deformation is proportional to the cosine azimuthal angle $\phi$ and increases with radius. Analytically, the warp is well represented by a term $\Delta z$ where:

$$\Delta z = w R^2 \cos\phi,$$ (2)

and w is an adjustable parameter characterizing the warp's amplitude.

Replacing z by $z-\Delta z$ in the potential (1) we get an analytical warped disk potential model:

$$\Phi_{w}(R,\phi,z) = -\sum_{i=1}^{3} \frac{GM_i} {\sqrt{R^2+(a_i+d_i)^2}},$$ (3)

with

$$d_i=\sqrt{\left(z-w R^2 \cos\phi\right)^2 + b_i^2}\ .$$ (4)

Note that the potential is bi-symmetric with respect to the y=0 plane, $\Phi(x,y,z) = \Phi(-x,y,-z)$.

2.2 Parameters

The parameters a_i, b_i and GM_i have been chosen to provide a typical rotation curve, increasing linearly below $3~ \rm kpc$ and staying flat up to $40~ \rm kpc$, beyond which it decreases smoothly. For the bulge, $a_{\rm b}=0$, $b_{\rm b}=1.5$ and $GM_{\rm b}=0.066$, which is equivalent to a Plummer sphere. The parameters for the visible and gas disks are respectively: $a_{\rm d}=6.5$, $b_{\rm d}=0.5$, $GM_{\rm d}=0.171$, $a_{\rm g}=25$, $b_{\rm g}=0.5$, $GM_{\rm g}=0.763$. For convenience the length unit is chosen to be the kpc and time unit the Myr. Fixing the gravitational constant G to a value of 1, the mass unit corresponds to $2.2 \times 10^{11}~M_\odot$. With this set, the velocity unit is about $1000~ \textrm{km}\,\textrm{s}^{-1}$. Figure 1 shows the isodensity curves corresponding to the model. Well above the galaxy disk, negative density regions do exist, however our results are not spoiled by negative densities as long as orbits do not cross such regions.

	Figure 1: 3D isodensity surface of the warped model at $5\times 10^{-4}$ and $5\times10^{-5}~M_{\odot}~\textrm{kpc}^{-3}$ (w=0.005 kpc-1). The surface is sliced with respect to the y=0 plane.
Open with DEXTER

The amplitude of the deformation w is chosen to be equal to 0.005 kpc^-1, developing a warp of the same order as the one of the Galaxy. For example, see the values indicated by Burton (1992) or Smart et al. (1998). Hence, the results obtained are applicable in typical cases of observed warped galaxies.

2.3 Hamiltonian

In the present model, we allow the possibility for a global rotation of the warped potential about the z-axis. This rotation is parametrised by the angular pattern speed $\Omega_{\rm p}$ or, equivalently, by the corotating radius $R_{\rm c}$, taking a negative value for retrograde rotation. Thus, the Hamiltonian in the rotating frame of reference with angular speed $\Omega_{\rm p}$ is:

$$H=\frac{1}{2}\left( p_x^2 + p_y^2 + p_z^2 \right) +\Phi(x,y,z)-\Omega_{\rm p}\left( x\,p_y-y\,p_x \right),$$ (5)

where the variables p_x, p_y, and p_z are the respective canonical momenta of x, y, and z. The equations of motion to integrate are:

$$\begin{array}{l c l c l c l} \dot x&=&p_x + \Omega_{\rm p}... ...p_z, & & \dot p_z &=& -\partial_z\Phi_w,\nonumber \end{array}$$ (6)

with $\Phi_w$ given by Eq. (3).

2.4 Numerical method

The periodic orbits are found by numerically determining the fixed points of the 4D Poincaré map (T) at y=0, $\dot x <0$ generated by the equations of motion (see, e.g., Pfenniger & Friedli 1993). The algorithm uses in particular the method proposed by Hénon (1982) giving the intersection between an orbit and a surface, and a least squares stabilized Newton-Raphson root-finding procedure.

The stability of the orbits are determined by the eigenvalues of the Jacobian of the Poincaré map ($\nabla T$). Since the system is Hamiltonian and the motion is described by real numbers, the four eigenvalues of $\nabla T$ occur by conjugate and inverse pairs and it is possible to condense the information with two stability indexes b₁, b₂:

$$b_i = -(\lambda_i + \lambda_i^{-1}), \quad i=1,2, \\$$ (7)

where $\lambda_1$ and $\lambda_2$ represent a pair of reciprocal eigenvalues. A periodic orbit is stable only when b₁ and b₂ are real and |b₁|, |b₂|<2. It is unstable in all other cases. If |b₁|=2 or |b₂|=2, or if |b₁|=|b₂|, at least two eigenvalues are equal, $\nabla T$ is degenerate and eventually allows a bifurcation. For a more complete description of the instability cases, see Pfenniger & Friedli (1993).

In this work, we will focus our investigations on orbits following the potential disk. Hence, we choose initial conditions with a starting position on the line of nodes, here equivalent to the y-axis. We concentrate on the main orbit families keeping the symmetry of the potential, thus the initial velocity is perpendicular to it (p_y(0)=0) and points to arbitrary negative values of x (p_x(0)<0). In this way, the free parameters in the initial conditions are the Jacobi constant ($\approx$energy, H), the position y(0) along the y axis, and the velocity component p_z(0) along the z direction. This latter parameter will be small compared to p_x(0), which avoids a situation where orbits stray too far from the disk and penetrate negative density regions. This point has been systematically checked because, a priori, orbits may explore regions far from the expected ones.

3 Families of periodic orbits

3.1 Families without perturbation

In order to understand the influence of the warp, we first look at the model without deformation (w=0) which is completely axisymmetric. The rotation of the potential is set to zero ( $\Omega_{\rm p} =0$).

Below the orbit, families are shown with their initial starting point in the H-p_z(0) diagram. In Fig. 2, bottom, we recognize the circular orbit family (horizontal line at p_z(0)=0). The stability indices for this family are traced at the top of Fig. 2. In this particular case, b₁ indicates the stability in the galaxy plane while b₂ corresponds to the stability transverse to it. Both indices remain in the interval [-2,+2], insuring the stability for this family.

At H=-0.0701, b₁=+2, $\nabla T$ is also degenerate with two eigenvalues equal to -1. A bifurcation occurs through period doubling. This bifurcation coincides with the resonance between the radial frequency $\kappa$ and the circular frequency $\Omega$ ( $2\kappa=3\,\Omega$).

At H=-0.0748, -0.0566, -0.0451, -0.0345, and -0.0236, b₂=+2 generating transverse bifurcations through period doubling. These bifurcations coincide with the resonances between the transverse frequency $\nu$ and the circular frequency $\Omega$ ( $2\nu=(2k+1)\,\Omega$, $k=1,\ldots 5$). Orbit families from period doubling bifurcations will not be discussed further in this paper.

Transverse bifurcations keeping the same period occur at H=-0.0632, -0.0508, -0.0396, -0.0294, and -0.0158. In this case b₂=-2 and $\nu = k\, \Omega$, $k=2,\ldots 6$. The two latter families have a non zero p_z(0)initial velocity and also oscillate round the z=0 plane crossing it respectively 2k and 2(k+1) times per period. All these sub-families are marginally stable with b₂=-2 due to the axisymmetry of the potential.

	Figure 2: H-pz(0) phase space for w=0.
Open with DEXTER

3.2 Influence of the warp

The break in the z symmetry transforms the family of circular orbits in the unperturbed model into a set of families pk (main families) with $p_z(0)\neq 0$. The significance of the indice k will be explained further. Except at bifurcations, the pk families are stable.

The shape of the corresponding orbits can be approximated with the following parametric function:

 

$$R_0(H) + A_R(H) \cos(2\phi - \pi),$$ R(H) = (8)

$$z_0(H) + A_z(H) \cos\phi,$$ z(H) = (9)

parametrised by the azimuthal angle $\phi$. For increasing H, A_R increases from 0 to 1 kpc, while A_z increases from 0 to 8 kpc. This latter variation corresponds almost exactly to the amplitude of the warp as a function of radius ( $A_z \cong wR^2$). In other words, the main orbit family follows the density maximum at any radius.

Another influence of the warp is to move the bifurcations toward slightly lower energies. The corresponding transverse bifurcations arise at H=-0.0633, -0.0509, -0.0398, -0.0298, and -0.0176. Moreover, a new bifurcation takes place within the limits of the diagram at H=-0.0108, where the subfamily starting at H=-0.0176 rejoins the main family. The other families would also rejoin the main family at higher energies, yet they would reach radii larger than $y(0)=50~\rm kpc$, which was chosen as a limit for our study of a warped disk.

	Figure 3: H-pz(0) phase space (w=0.005).
Open with DEXTER

The subfamilies coming from the corresponding transverse bifurcations are given the symbol "$sk\pm$'' where k gives the frequency ratio $\nu / \Omega$ at the corresponding bifurcation and the sign is the one of the difference of p_z(0) between the subfamily and the main family. These families evolve in the same way as family pk, i.e. they follow the warped disk, so may be significantly populated in a real disk. Note that the families with an odd k conserve the bi-symmetry of the potential, which is not the case when k is even. Figure 4 displays a set of three orbits extracted from different subfamilies, s4+, s5+ and s6-. The right panels show the elevation z of the orbits as a function of the azimuth $\phi$ in comparison to the elevation of the corresponding main family (dashed lines). The more the energy grows, the more the subfamilies follow well the main orbit.

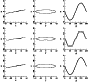	Figure 4: Projections over the y=0, z=0 planes and the evolution of z as a function of azimuthal angle $\phi$ of orbits of the families s4+ (H=-0.03), s5+ (H=-0.02) and s6- (H=-0.015). The dashed line represents the potential minimum of the warped disk at a fixed radius which is similar to the main family.
Open with DEXTER

Although in the absence of the warp all subfamilies are stable, this is no longer the case with a weak warp. This point will be discussed further below.

3.3 Surfaces of section around bifurcations

If the warp has only a slight influence on the shape of the orbits, it is important to look carefully at the behavior of the bifurcations in presence of the perturbation. Figures 5 and 8 present a magnification of the H-p_z(0) phase space around the first (r1) and second (r2) bifurcations. Here the periodic orbits are computed with w=0.01 in order to increase the effect of the warp. The physical correspondent would be a galaxy with a warp twice as high as that observed in the Milky Way at a radius of 30 kpc.

Except for the weak decreasing of p_z(0) with respect to H, the type of the first bifurcation (around H=-0.0633) remains similar to the one without perturbation (pitchfork). The two new generated families (s2+ and s2-) are both stable. They appear at the same energy as two other unstable families, namely z2+ and z2-. These are not seen in Fig. 5 because their projection merges with the p2 family. They are distinguished from it by a non zero z(0) and p_y(0). Projections of families s2+ and s2- are plotted in Fig. 7.

In order to estimate the importance of orbits associated with a stable periodic orbit, we have computed the surface of the section (z,p_z) near the bifurcation (H=-0.06). Moreover, it allows us to know the number of effective integrals of motion in this specific region of phase space. In Fig. 6 the stable p2 family is represented by the cross near the center (z=0, p_z=-0.0058) and is surrounded by quasi periodic families. The thinness of these curves indicates that the motion is well decoupled in z and a third integral exists. At p_z=0.031,z=0 and p_z=-0.043,z=0 we find respectively the s2+ and s2- families. The upper and lower panels show details of the section around these two families. Very thin stability islands exist. For comparison, the width in p_z of the separatrix (squares points) is about 1/100 times smaller than the width between families s2+ and s2-. This gives an indication of the phase space occupied by orbits associated with these families. The unstable z2+ and z2- families appear on the separatrix, at p_z=-0.0054,z=0.427 and p_z=-0.0054,z=-0.427. Outside the separatrix, the invariant curves are regular until p_z= 0.06 where the motion in z begins to be strongly coupled to the motion in x and y.

	Figure 5: H-pz(0) and H-y(0) phase space around the firstbifurcation (w=0.01).
Open with DEXTER

Figure 6: Section (z,pz) at H=-0.06, near the bifurcation r1. The crosses represent the three stable periodic families s2+ (top), p2 (middle) and s2- (bottom) and the two unstable sz+ (right) and sz- (left). The upper and lower panels show a zoom of the section around s2+ and s2-. In this panels the separatrix is marked with squares while in the middle it is marked with a bold line. The crosses indicate the position of the periodic families.

Open with DEXTER

	Figure 7: Shape of three orbits linked to the r1 bifurcation (H=-0.06). The dot indicates the starting point of the computation and the arrow shows the direction of the corresponding initial velocity.
Open with DEXTER

The behavior of the second bifurcation r2 around H=-0.0509 is quite different. Figure 8 reveals that the family s3+ is in fact the extension of the main family p2. This arises because the perturbation favors a higher p_z. The s3+ family is also stable. At H=-0.0508 the families p3 and s3- are created simultaneously. They are respectively stable and unstable. The whole bifurcation forms a pitchfork with a symmetry breaking. The shapes of three of the four families involved in this bifurcation are presented in Fig. 10. The section after the bifurcations is shown in Fig. 9 (H=-0.05). The stable p3 family appears at p_z=-0.009 and is surrounded by a set of quasi periodic orbits embedded in the separatrix. The unstable s3- family belongs to the separatrix at p_z=-0.023. The s3+ family is located at p_z=0.006 and its associated orbits occupy the crescent-shaped region between the separatrix. Outside, the invariant curves are regular until p_z=-0.03 where the motion in z is not longer decoupled.

	Figure 8: H-pz(0) and H-y(0) phase space around the second bifurcation (w=0.01).
Open with DEXTER

	Figure 9: Section (z,pz) at H=-0.05, after the bifurcation r2. The separatrix is marked with a bold line. The crosses indicate the position of the three periodic families s3+ stable (top), p3 stable (middle) and s3- unstable (bottom).
Open with DEXTER

Looking at Figs. 6 and 9, one can expect a chaotic region around the separatrix. Due to the thinness of the region around the unstable points, it is very difficult to find it numerically.

Our study of the bifurcation is limited to the two first bifurcations, r1 and r2. The behavior of the following bifurcations are similar to the first two. The rk bifurcation with an odd (resp. even) k is of the same type as r1 (resp. r2). This difference is related to the symmetry of the families which depends on the parity of k.

In summary, the warp does not destroy the strength of the main family, which at any H possesses a comfortable surrounding stable region. For an odd k, the effect of the warp is: (i) to change the stability of sk- subfamilies and (ii) to increase the phase space allowed to the associated sk+families. For an even k, the subfamilies are quasi unchanged, preserving a very thin phase space around the stable subfamilies $sk\pm$.

3.4 Influence of rotation

To study the influence of the rotation, we first look for Lagrangian points. The latter are found by setting the right terms of Eq. (6) to zero. Substituting p_x, p_y and p_z, the Lagrangian points are solutions of the following equations:

 

$$\partial_x\Phi_w \Omega_{\rm p}^2 x,$$ =

$$\partial_y\Phi_w \Omega_{\rm p}^2 y,$$ = (10)

$$\partial_z\Phi_w$$ = 0.

With the form (3) of the warped potential, one can easily see that the z coordinate must satisfy:

$$z = \Delta z,$$ (11)

with $\Delta z$ defined in Eq. (2). This causes the two first equations of (10) to become:

 

$$\partial_x\Phi_0 \Omega_{\rm p}^2 x,$$ = (12)

$$\partial_y\Phi_0 \Omega_{\rm p}^2 y,$$ =

which corresponds to the definition of the corotation, where $\Phi_0$ is the potential without perturbation (Eq. (1)). Thus the Lagrangian points are degenerated, forming an annulus following the density maximum with a projection on the z=0 plane corresponding to the corotation without perturbation (w=0).

	Figure 10: Shape of three among the four orbits linked to the r2 bifurcation (H=-0.0509). The dot indicates the starting point of the computation and the arrow shows the direction of the corresponding initial velocity.
Open with DEXTER

Despite the fact that a direct and retrograde rotations respectively add and remove resonances, the type of bifurcations as well as the stability and the shape of orbits are not affected by a global pattern speed. This has been tested in the range $-30 > R_{\rm c}$ and $R_{\rm c} > 30~\textrm{kpc}$, where $R_{\rm c}$ is the corotation radius and a negative value corresponds to a retrograde rotation.

For a radius less than 40 kpc, both prograde and retrograde 1:1 resonances are not observable in this range of pattern speed. For a corotation of 7 kpc they appear only beyond 40 kpc (resp. 30 kpc). Thus they have not been studied.

The main influence appears when we look at the consistency of orbits with the mass density. If the warp is mostly self-gravitating and made of thin and distinct tube orbits, one can check the self-consistency constraint by noting that the spatial occupation of a periodic orbit is locally inversely proportional to its local speed ( $t_{\rm so} \sim 1/\vert v\vert$). The reason is explained by the fact that at a given point of the orbit, the local speed remains constant in time. This argument is not available at exceptional points, for example the points where an orbit crosses itself. Since the density is proportional to the spatial occupation time, it must also be proportional to the inverse speed along the orbit ( $\rho \sim t_{\rm so}\sim 1/\vert v\vert$). Strictly this condition is only fulfilled by a structure entirely made of distinct exactly periodic orbits, such as a disk made of circular orbits. Nevertheless the check is useful in this problem because few hot orbits far from periodic round orbits are expected to exist.

In practice, the consistency has been calculated using the indice I defined by the norm:

$$I(\Omega_{\rm p},H)=\frac{1}{2\pi}\left[\int_0^{2\pi}\left[\D... ...\rho(\phi)- \Delta u(\phi)\right]^2{\rm d}\phi\right]^{1/2},$$ (13)

with

$$\Delta\rho(\phi)=\frac{\rho(\phi)-\rho_{\min}}{\rho_{\max}-\rho_{\min}},$$ (14)

$$\Delta u(\phi)=\frac{u(\phi)-u_{\min}}{u_{\max}-u_{\min}},$$ (15)

and $u(\phi)=1/\vert v(\phi)\vert$. The values $\rho_{\min}$, $\rho_{\max}$, $u_{\min}$ and $u_{\max}$ are calculated over a period of the azimuthal angle $\phi$. When $\Delta\rho$ and $\Delta u$ vary in the same direction, I=0 and the orbit is consistent. If they vary inversely, as two cosines with a phase difference of $\pi$, $I=\sqrt{\pi}/{2\pi}$.

We have tested the consistency of families pk with respect to the energy (Fig. 11) and radius (Fig. 12), which is more convenient in galactic dynamics. This has been calculated for different (direct and retrograde) pattern speeds between $-30 > R_{\rm c}$ and $R_{\rm c} > 30~\textrm{kpc}$ corresponding to $-4.5\times 10^{-3} < \Omega_{\rm p} < 4.5\times 10^{-3}~\textrm{Myr}^{-1}$. The white regions correspond to I=0 (consistency) while the darker gray correspond to a value of $\sqrt{\pi}/{2\pi}$ (inconsistency). The shaded parts give the limit of the computation, either because of the corotation or because of the positive energy regions. The black pattern points out the missing data due to computational difficulty arising because of the proximity of the forbidden regions.

	Figure 11: Consistency of orbit occupation with the mass density as a function of the energy and the global rotation. The dark gray corresponds to inconsistent regions while the white are consistent regions. The black parts are missing data. The shading part represents the limit of the corotation.
Open with DEXTER

	Figure 12: Same graph than in Fig. 11 but as a function of radius R. The upper shading part represents the limit of the corotation. While the lower is the region where H>0. The vertical resonances ( $\nu = k\, \Omega$, $k=2,\ldots 10$) are drawn in solid lines.
Open with DEXTER

For a direct rotation, except in small regions near the corotation, the inverse local speed along an orbit varies exactly in opposition to the density ( $I=\sqrt{\pi}/{2\pi}$). This causes it to depopulate the higher density regions to the advantage of the lower. The density distribution is also slowly modified. However, for a slowly retrograde rotation a zone appears around 3 kpc, where the inverse local speed varies exactly as the density. This latter is also reinforced and the potential is self-consistent. This zone grows with increasing rotation and a second zone appears for larger radii. For a corotation smaller than $R_{\rm c}=-50~\textrm{kpc}$ the zones of consistency cover the whole disk under the curve of zero energy.

The same work applied to the subfamilies $sk\pm$ reveals that they are clearly inconsistent with the density distribution, but these families are also less relevant with the assumption of almost circular rotation.

4 Conclusions

The previous description of periodic orbits in a warped analytical potential allows us to draw the following conclusions.

1)

The circular orbit family with an axisymmetric potential survives the warp and becomes quasi-annular with a tilt corresponding to the warped galactic disk. Thus, this work confirms the intuitive idea that the orbits follow the warp. Without this confirmation, the ring model of warps would have remained baseless. Note that the ring model has been used in the past in different contexts, but if the underlying circular orbits do not exist, the ring model is nonphysical;

2)

The existing transverse resonances in the axisymmetric case are also preserved in the warped case but occur at slightly lower energies. Subfamilies with the same period as the quasi-annular family are generated and most of them keep their stability. In our model, the perturbation induced by the warp is not strong enough to generate observable chaotic regions;

3)

Since no bifurcation with $\nu=\Omega\pm\Omega_{\rm p}$ is generated by the warp, it is not possible in our model to excite a 1:1 normal mode, which is often invoked to explain the galactic warps. Other modes are not favored either because the stable regions around their corresponding subfamilies remain very thin;

4)

The study of the consistency of the density distribution underlines the importance of the global rotation. A direct rotation of the warp pattern generates orbits destroying the density distribution, but on the contrary, orbits can locally reinforce the density in the presence of a retrograde rotation. This could help maintaining external warped regions.

The behavior of the discussed periodic orbits will be examined in N-body models and the results will be the object of a future paper.

Acknowledgements

This work as been supported by the Swiss National Science Foundation.

References

 
• Arnaboldi, M., Oosterloo, T., Combes, F., Freeman, K. C., & Koribalski, B. 1997, AJ, 113, 585A In the text NASA ADS  
• Briggs, F. H. 1990, ApJ, 352, 15 In the text NASA ADS  
• Battaner, E., Florido, E., & Sanchez-Saavedra, M. L. 1990, A&A, 236, 1 In the text NASA ADS  
• Becquaert, J.-F., & Combes, F. 1998, A&A, 325, 41 In the text NASA ADS  
• Binney, J. 1992, ARA&A, 30, 51 In the text NASA ADS  
• Burton, W. B. 1992, in SAAS-Fee Advanced Course 21, The Galactic Interstellar Medium, ed. D. Pfenniger, & P. Bartholdi (Springer, Berlin) In the text  
• Casertano, S., Sackett, P., & Briggs, F. H. 1991, Warped disks and inclined rings around galaxies (Cambridge University Press) In the text  
• Contopoulos, G., & Papayannopoulos, T. 1980, A&A, 92, 33 In the text NASA ADS  
• Debattista, V. P., & Sellwood, J. A. 1999, ApJ, 513, L107 In the text NASA ADS  
• Dubinski, J. 1995, ApJ, 431, 617 In the text  
• Dubinski, J., & Kuijken, K. 1995, ApJ, 442, 492 In the text NASA ADS  
• Gerhard, O. 2000, preprint [astro-ph/0010539] In the text  
• Hénon, M. 1982, Physica D, 5, 412 In the text  
• Jiang, I.-G., & Binney, J. 1999, MNRAS, 303, L7 In the text NASA ADS  
• Kuijken, K. 1991, ApJ, 376, 467 In the text NASA ADS  
• Kuijken, K. 2000, preprint [astro-ph/0011345] In the text  
• Nagai, R., & Miyamoto, M. 1975, PASJ, 27, 533 In the text  
• Mulder, W. A. 1983, A&A, 121, 91 In the text NASA ADS  
• Pfenniger, D. 1984, A&A, 134, 171 In the text  
• Pfenniger, D., & Friedli, D. 1993, A&A, 270, 561 In the text NASA ADS  
• Pfenniger, D., Combes, F., & Martinet, L. 1994, A&A, 285, 79 In the text NASA ADS  
• Reshetnikov, V., & Combes, F. 1998, A&A, 337, 9 In the text NASA ADS  
• Smart, R., Drimmel, R., Lattanzi, M., & Binney, J. 1998, Nature, 392, 471 In the text NASA ADS  
• Sparke, L. 1984, MNRAS, 211, 911 In the text NASA ADS  
• Sparke, L., & Casertano, S. 1988, MNRAS, 234, 87 In the text NASA ADS  
• Weinberg, M.-D. 1995, ApJ, 455, 31 In the text  
• Weinberg, M.-D. 1998, MNRAS, 299, 499 In the text NASA ADS