A&A 372, 981-997 (2001)
DOI: 10.1051/0004-6361:20010515
L. Verstraete1 - C. Pech2 - C. Moutou3 - K. Sellgren4 - C. M. Wright5 - M. Giard2 - A. Léger1 - R. Timmermann6 - S. Drapatz6
1 - Institut d'Astrophysique Spatiale, Bât. 121,
Université de Paris XI, 91405 Orsay Cedex, France
2 - CESR, 9 avenue du Colonel Roche, 31028 Toulouse Cedex, France
3 - Alonso de Cordoba 3107, Santiago 19, Chile
4 - Astron. Dept., Ohio State University, 140 West 18th avenue,
Colombus OH 43210, USA
5 - Univ. College, ADFA, UNSW Canberra, Australia
6 - Max-Planck Inst. für extraterr. Physik, Postfach 1603, 85740
Garching, Germany
Received 2 October 2000 / Accepted 29 March 2001
Abstract
We discuss the Aromatic Infrared Band (AIB) profiles observed by ISO-SWS towards
a number of bright interstellar regions where dense molecular gas is
illuminated by stellar radiation. Our sample spans a broad range of excitation
conditions (exciting radiation fields with effective temperature,
![]() ,
ranging from 23000 to
45000 K). The SWS spectra are decomposed coherently in our sample
into Lorentz profiles and a broadband continuum. We find that the individual
profiles of the main AIBs at 3.3, 6.2, 8.6 and 11.3
,
ranging from 23000 to
45000 K). The SWS spectra are decomposed coherently in our sample
into Lorentz profiles and a broadband continuum. We find that the individual
profiles of the main AIBs at 3.3, 6.2, 8.6 and 11.3 ![]() m are well represented with at most two
Lorentzians.
The 7.7
m are well represented with at most two
Lorentzians.
The 7.7 ![]() m-AIB has a more complex shape and requires at least three Lorentz profiles.
Furthermore, we show that the positions and widths of these AIBs are remarkably stable (within a few cm_1)
confirming, at higher spectral resolution, the results from ISOCAM-CVF and ISOPHOT-S. This spectral
decomposition with a small number of Lorentz profiles implicitly assumes that most of the observed bandwidth arises from a
few, large carriers. Boulanger et al. (1998b) recently proposed that the AIBs are the intrinsic profiles of resonances
in small carbon clusters. This interpretation can be tested by comparing the AIB profile parameters
(band position and width) given in this work to laboratory data on relevant species when it becomes available.
m-AIB has a more complex shape and requires at least three Lorentz profiles.
Furthermore, we show that the positions and widths of these AIBs are remarkably stable (within a few cm_1)
confirming, at higher spectral resolution, the results from ISOCAM-CVF and ISOPHOT-S. This spectral
decomposition with a small number of Lorentz profiles implicitly assumes that most of the observed bandwidth arises from a
few, large carriers. Boulanger et al. (1998b) recently proposed that the AIBs are the intrinsic profiles of resonances
in small carbon clusters. This interpretation can be tested by comparing the AIB profile parameters
(band position and width) given in this work to laboratory data on relevant species when it becomes available.
Taking advantage of our decomposition, we extract the profiles of individual AIBs from the data and compare
them to a state-of-the-art model of Polycyclic Aromatic Hydrocarbon (PAH) cation emission. In this model, the
position and width of the AIBs are rather explained by a redshift and a broadening of the PAH vibrational bands
as the temperature of the molecule increases (Joblin et al. 1995).
In this context, the present similarity of the AIB profiles
requires that the PAH temperature distribution remains roughly the same whatever the radiation field hardness.
Deriving the temperature distribution of interstellar PAHs, we show that
its hot tail, which controls the AIB spectrum, sensitively depends on
![]() (the number of C-atoms in the smallest PAH) and
(the number of C-atoms in the smallest PAH) and
![]() .
Comparing the observed profiles
of the individual AIBs to our model results, we can match all the AIB profiles (except the
8.6
.
Comparing the observed profiles
of the individual AIBs to our model results, we can match all the AIB profiles (except the
8.6 ![]() m-AIB profile) if
m-AIB profile) if ![]() is increased with
is increased with
![]() .
This increase is naturally explained
in a picture where small PAHs are more efficiently photodissociated in harsher radiation fields.
The observed 8.6
.
This increase is naturally explained
in a picture where small PAHs are more efficiently photodissociated in harsher radiation fields.
The observed 8.6 ![]() m-profile, both intensity and width, is not explained by our model.
m-profile, both intensity and width, is not explained by our model.
We then discuss our results in the broader context of ISO observations
of fainter interstellar regions where PAHs are expected to be in neutral form.
Key words: infrared: ISM: lines and bands - ISM: dust, extinction - ISM: molecules
The family of infrared features at 3.3, 6.2, 7.7, 8.6, 11.3 and 12.7 ![]() m has been
observed towards a large number of sightlines in the Galaxy and in other
galaxies since the nineteen seventies. Early on, it was recognized that these bands
correspond to vibrational modes in carbonaceous aromatic systems (Duley & Williams 1981;
Léger & Puget 1984; Allamandola et al. 1985). These dust bands are therefore dubbed
the Aromatic Infrared Bands (hereafter AIBs). The bands at 3.3, 8.6, 11.3 and
12.7
m has been
observed towards a large number of sightlines in the Galaxy and in other
galaxies since the nineteen seventies. Early on, it was recognized that these bands
correspond to vibrational modes in carbonaceous aromatic systems (Duley & Williams 1981;
Léger & Puget 1984; Allamandola et al. 1985). These dust bands are therefore dubbed
the Aromatic Infrared Bands (hereafter AIBs). The bands at 3.3, 8.6, 11.3 and
12.7 ![]() m
stem from vibrational modes of the aromatic C-H bond; the remaining bands are ascribed to
vibrations of the aromatic C-C bonds. The Infrared Space Observatory
(ISO, Kessler et al. 1996) mission has provided us with an unprecedented wealth of
data in this context.
m
stem from vibrational modes of the aromatic C-H bond; the remaining bands are ascribed to
vibrations of the aromatic C-C bonds. The Infrared Space Observatory
(ISO, Kessler et al. 1996) mission has provided us with an unprecedented wealth of
data in this context.
Comparative studies of the AIBs in a wide variety of environments have been made possible
by the high sensitivity of the ISO camera (ISOCAM, Cesarsky C. et al. 1996) with its circular
variable filter and of the ISOPHOT-S spectrophotometer (Lemke et al. 1996), which both have low
spectral resolutions (
![]() and 90 respectively:
Boulanger et al. 1996, 1998a, 1998b;
Cesarsky et al. 1996a, 1996b, 2000a, 2000b;
Crété et al. 1999; Klein et al. 1999;
Laureijs et al. 1996; Mattila et al. 1996; Persi et al. 1999;
Uchida et al. 1998, 2000).
The AIB profiles as seen in these data are very similar (in position and width) over
a range of objects where the stellar radiation field and effective temperature vary
greatly (1 to 104 times the standard interstellar radiation field,
and 90 respectively:
Boulanger et al. 1996, 1998a, 1998b;
Cesarsky et al. 1996a, 1996b, 2000a, 2000b;
Crété et al. 1999; Klein et al. 1999;
Laureijs et al. 1996; Mattila et al. 1996; Persi et al. 1999;
Uchida et al. 1998, 2000).
The AIB profiles as seen in these data are very similar (in position and width) over
a range of objects where the stellar radiation field and effective temperature vary
greatly (1 to 104 times the standard interstellar radiation field,
![]() 000
to 50000 K). The profile invariance as well as the large width of the AIBs lead Boulanger
et al. (1998b) to conclude that the carriers of these bands are large aromatic systems
containing more than 50 C-atoms.
000
to 50000 K). The profile invariance as well as the large width of the AIBs lead Boulanger
et al. (1998b) to conclude that the carriers of these bands are large aromatic systems
containing more than 50 C-atoms.
The Short Wavelength Spectrometer (SWS, de Graauw et al. 1996) onboard ISO, less sensitive
than ISOCAM but with higher spectral resolution (
![]() )
and broader
wavelength coverage (2.4-45
)
and broader
wavelength coverage (2.4-45 ![]() m), brings a better view of the interstellar AIBs in the
brightest regions. Such detailed data have the ability to constrain the nature and
physical state of the band carriers (Beintema et al. 1996; Molster et al. 1996; Roelfsema et al. 1996;
Verstraete et al. 1996; Moutou et al. 2000; van Kerckhoven et al. 2000; Hony et al. 2000). In the first part
of this paper, we decompose the AIB spectrum into Lorentz profiles and a broadband continuum in order
to characterize (band position and width) each individual AIB and to compare them between objects.
In the second part of the paper, we compare these
new observations with a model considering free-flying aromatic molecules (Polycyclic Aromatic Hydrocarbons
or PAHs) as the origin of the AIBs. Indeed, the presence of AIBs in the low-excitation
diffuse interstellar medium (Boulanger et al. 1996; Mattila et al. 1996; Onaka et al. 1996) requires the
existence of free-flying PAHs or small grains excited by starlight; furthermore, these PAHs or grains
must be small enough to undergo strong temperature fluctuations leading to emission of the AIBs in the
near-infrared (Sellgren 1984). In this emission mechanism, the shape of the emergent AIB spectrum only depends
on the radiation field hardness (or
m), brings a better view of the interstellar AIBs in the
brightest regions. Such detailed data have the ability to constrain the nature and
physical state of the band carriers (Beintema et al. 1996; Molster et al. 1996; Roelfsema et al. 1996;
Verstraete et al. 1996; Moutou et al. 2000; van Kerckhoven et al. 2000; Hony et al. 2000). In the first part
of this paper, we decompose the AIB spectrum into Lorentz profiles and a broadband continuum in order
to characterize (band position and width) each individual AIB and to compare them between objects.
In the second part of the paper, we compare these
new observations with a model considering free-flying aromatic molecules (Polycyclic Aromatic Hydrocarbons
or PAHs) as the origin of the AIBs. Indeed, the presence of AIBs in the low-excitation
diffuse interstellar medium (Boulanger et al. 1996; Mattila et al. 1996; Onaka et al. 1996) requires the
existence of free-flying PAHs or small grains excited by starlight; furthermore, these PAHs or grains
must be small enough to undergo strong temperature fluctuations leading to emission of the AIBs in the
near-infrared (Sellgren 1984). In this emission mechanism, the shape of the emergent AIB spectrum only depends
on the radiation field hardness (or
![]() ,
see Sect. 2) and not on the flux of stellar photons (parameterized
as
,
see Sect. 2) and not on the flux of stellar photons (parameterized
as ![]() in Sect. 2).
in Sect. 2).
In Sect. 2, we present the SWS spectra. The observed AIB profiles are characterized in Sect. 3. These results are compared to the predictions of the PAH model in Sect. 4. We summarize and discuss the significance of our results in Sect. 5.
SWS has observed the AIB spectrum along a number of interstellar sightlines covering a wide range of excitation conditions. We discuss here three spectra which sample well the radiation field sequence covered by the SWS observations. The lines of sight selected all correspond to interface conditions, i.e., regions where fresh molecular material is directly exposed to the stellar light. At interfaces, the AIB emission is usually strong (probably because of an enhanced PAH abundance, Bernard et al. 1993): this is why we selected such regions to carry out the present study.
At the low excitation end, we have the reflection
nebula NGC 2023 (
![]() ,
SWS01 speed 3). This spectrum has already been presented in Moutou et al. (1999).
SWS looked at a filament, 60'' south of the central star (central star:
,
SWS01 speed 3). This spectrum has already been presented in Moutou et al. (1999).
SWS looked at a filament, 60'' south of the central star (central star:
![]() 41
41![]() 38.3
38.3![]() ,
,
![]()
![]() 16'32.6''), which is bright in fluorescent H2 emission (Field et al. 1998).
At the high excitation end, we present here a spectrum of the M17-SW photodissociation interface
(
16'32.6''), which is bright in fluorescent H2 emission (Field et al. 1998).
At the high excitation end, we present here a spectrum of the M17-SW photodissociation interface
(
![]() 20
20![]() 22.1
22.1![]() ,
,
![]()
![]() 12'41.3'';
12'41.3'';
![]() ,
SWS01 speed 4): this is position
number 6 of the data presented in Verstraete et al. (1996). Finally, we also have the Orion Bar
(
,
SWS01 speed 4): this is position
number 6 of the data presented in Verstraete et al. (1996). Finally, we also have the Orion Bar
(
![]() 35
35![]() 20.3
20.3![]() ,
,
![]()
![]() 25'20'';
25'20'';
![]() ,
SWS01 speed 4) at the position of the
peak of fluorescent H2 emission (van der Werf et al. 1996). All positions given above are in J2000.
,
SWS01 speed 4) at the position of the
peak of fluorescent H2 emission (van der Werf et al. 1996). All positions given above are in J2000.
The data reduction was undertaken with the SWS-IA3 environment running at the Institut
d'Astrophysique Spatiale, Orsay. The spectrum of NGC 2023 lacks a small range around 4 ![]() m because
of bad dark current measurements.
The flux calibration files CAL-G version 030 have been used.
For the beam sizes, we took the values recently determined by Salama (2000).
This assumes that the source completely fills the beam. To check this assumption, we compared
our SWS spectra of M17-SW and of the Orion Bar to CAM-CVF data
(Cesarsky et al. 1996a,b;
Cesarsky et al. 2000b): the continuum fluxes (per solid angle) of the two instruments were found to agree
within 20%. In the case of NGC 2023, the emission seen in the ISOCAM-map of Abergel et al. (2000,
in preparation) looks homogeneous at the position of our SWS spectrum.
The 6 arcsecond pixels of ISOCAM are much smaller than the SWS field of view, and since the ISOCAM
image of each of our sources is smooth in the region observed by SWS, we can safely say
that our sources uniformly fill the SWS beam. This statement only holds over
the 5-16
m because
of bad dark current measurements.
The flux calibration files CAL-G version 030 have been used.
For the beam sizes, we took the values recently determined by Salama (2000).
This assumes that the source completely fills the beam. To check this assumption, we compared
our SWS spectra of M17-SW and of the Orion Bar to CAM-CVF data
(Cesarsky et al. 1996a,b;
Cesarsky et al. 2000b): the continuum fluxes (per solid angle) of the two instruments were found to agree
within 20%. In the case of NGC 2023, the emission seen in the ISOCAM-map of Abergel et al. (2000,
in preparation) looks homogeneous at the position of our SWS spectrum.
The 6 arcsecond pixels of ISOCAM are much smaller than the SWS field of view, and since the ISOCAM
image of each of our sources is smooth in the region observed by SWS, we can safely say
that our sources uniformly fill the SWS beam. This statement only holds over
the 5-16 ![]() m wavelength range. In fact, to assure continuity in our spectra, we had to deviate from the
Salama SWS beam sizes above 27
m wavelength range. In fact, to assure continuity in our spectra, we had to deviate from the
Salama SWS beam sizes above 27 ![]() m (the spectral bands 3E and 4 of the SWS, see de Graauw et al. 1996).
m (the spectral bands 3E and 4 of the SWS, see de Graauw et al. 1996).
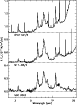 |
Figure 1:
The SWS 2.4-25 |
| Open with DEXTER | |
| Line of sight | NGC 2023 | Orion Bar | M17-SW |
|
|
2.3a | 3.7c | 4.5e |
| 3.2a,b | 8.5b | 12 | |
| 0.14 | 0.24 | 1.10 | |
|
|
2.66 | 6.38 | 0.96 |
| 1.2 | 42 | 12.5 |
References: (a) Buss et al. (1994), (b) Lang (1991), (c) Rubin et al. (1991), (d) van der Werf et al. (1996), (e) Felli et al. (1984)
The continuum below the AIBs shows a clear evolution from NGC 2023 to the Orion Bar (see Fig. 1):
continuous emission of hot, small (radii of a few 10 to 100 Å, Désert et al. 1990) grains between
10 and 20 ![]() m is prominent in M17-SW and the Orion Bar whereas this is completely absent in NGC 2023.
This is a consequence of the stronger flux and harder radiation field in the Orion Bar which heats up these
small grains.
m is prominent in M17-SW and the Orion Bar whereas this is completely absent in NGC 2023.
This is a consequence of the stronger flux and harder radiation field in the Orion Bar which heats up these
small grains.
The 6.2 and 7.7 ![]() m bands do not vary much with respect to each other whereas they do
relative to the 3.3, 8.6 and 11.3
m bands do not vary much with respect to each other whereas they do
relative to the 3.3, 8.6 and 11.3 ![]() m AIBs. Such variations cannot be interpreted
as the result of different emission temperature distributions of PAHs (obtained
with different size distributions and/or radiation field effective temperature).
In fact, the 3.3
m AIBs. Such variations cannot be interpreted
as the result of different emission temperature distributions of PAHs (obtained
with different size distributions and/or radiation field effective temperature).
In fact, the 3.3 ![]() m-band is dominated by the emission of small (hot) PAHs while
the 11.3
m-band is dominated by the emission of small (hot) PAHs while
the 11.3 ![]() m-band is contributed to by larger (cold) PAHs (Schutte et al. 1993): thus, changing
the PAH temperature distribution
cannot explain why the 11.3
m-band is contributed to by larger (cold) PAHs (Schutte et al. 1993): thus, changing
the PAH temperature distribution
cannot explain why the 11.3 ![]() m-band varies along with the 3.3
m-band varies along with the 3.3 ![]() m-band. Instead, modifications of the
physical state of PAHs have to be invoked. Theoretical (de Frees et al. 1993; Pauzat et al. 1995, 1997;
Langhoff 1996) and laboratory (Szczepanski & Vala 1993; Hudgins et al. 1994; Hudgins &
Allamandola 1995; Hudgins & Sandford 1998) studies
showed that ionized species have stronger C-C bands.
On the other hand, dehydrogenated PAHs have weaker C-H bands (Pauzat et al. 1995, 1997).
As we show in Sect. 4.4.1, the weaker C-H band emission in M17-SW can be explained if the hydrogenation
fraction is significantly reduced.
m-band. Instead, modifications of the
physical state of PAHs have to be invoked. Theoretical (de Frees et al. 1993; Pauzat et al. 1995, 1997;
Langhoff 1996) and laboratory (Szczepanski & Vala 1993; Hudgins et al. 1994; Hudgins &
Allamandola 1995; Hudgins & Sandford 1998) studies
showed that ionized species have stronger C-C bands.
On the other hand, dehydrogenated PAHs have weaker C-H bands (Pauzat et al. 1995, 1997).
As we show in Sect. 4.4.1, the weaker C-H band emission in M17-SW can be explained if the hydrogenation
fraction is significantly reduced.
Moreover, the AIB profiles show little spectral substructure even though most AIBs are fully resolved
in our SWS data (the resolving power is
![]() 200 to 500).
A direct comparison of the spectra displayed in Fig. 1 shows that the position and width of the major,
simple AIBs (at 3.3, 6.2, 8.6 and 11.3
200 to 500).
A direct comparison of the spectra displayed in Fig. 1 shows that the position and width of the major,
simple AIBs (at 3.3, 6.2, 8.6 and 11.3 ![]() m) are roughly the same. The decomposition of the spectra we discuss
below primarily aims at quantifying this comparison and also at disentangling in a systematic way the profile of
a given AIB from the other bands, as well as from the underlying continuum due to hot small grains.
m) are roughly the same. The decomposition of the spectra we discuss
below primarily aims at quantifying this comparison and also at disentangling in a systematic way the profile of
a given AIB from the other bands, as well as from the underlying continuum due to hot small grains.
Boulanger et al. (1998b) showed that the AIBs in CAM-CVF data can be decomposed
into Lorentz profiles and a linear underlying continuum. It must be emphasized,
however, that the AIBs are barely resolved in the CAM-CVF data (in particular
the 6.2, 8.6 and 11.3 ![]() m bands, see Table 2 in Boulanger et al. 1998b and Fig. 3 of Cesarsky et al.
2000). The
SWS data at high spectral resolution presented here do not suffer from this limitation.
The use of a Lorentzian band shape implicitly assumes that the AIB profiles arise from the intrinsic
width of molecular transitions and/or resonances in small solid particles (e.g. , Bohren & Huffman 1983).
m bands, see Table 2 in Boulanger et al. 1998b and Fig. 3 of Cesarsky et al.
2000). The
SWS data at high spectral resolution presented here do not suffer from this limitation.
The use of a Lorentzian band shape implicitly assumes that the AIB profiles arise from the intrinsic
width of molecular transitions and/or resonances in small solid particles (e.g. , Bohren & Huffman 1983).
In the current paradigm, the AIBs result from the superposition of many vibrational bands produced by a population of interstellar PAHs with a wide range of sizes (molecules containing a few tens to a few hundred carbon atoms, Désert et al. 1990; Schutte et al. 1993). In this respect, laboratory and theoretical studies on small PAH species teach us that the band shapes (position and width) of vibrational transitions (i) depend on the temperature of the molecule (Joblin et al. 1995) and, (ii) vary from one species to another (in particular, the position of the vibrational bands depends on the size and symmetry of the molecule: Szczepanski & Vala 1993; Hudgins & Allamandola 1995 and 1998; Joblin et al. 1995; Langhoff 1996). The observed AIBs may actually result from a combination of these two effects. Elaborating on these studies, variability in the AIBs (changing band ratios, presence of substructure in the band profiles) from different interstellar sightlines is predicted as a consequence of a changing PAH population and/or different exciting radiation fields. Specifically, the position and width of individual bands are expected to vary by a few to several tens of cm_1 from one species to another and/or as a result of different emission temperatures. Some changes in the AIB profiles have been observed towards H II regions and reflection nebulae (Roelfsema et al. 1996; Verstraete et al. 1996; Cesarsky et al. 2000a; Uchida et al. 2000; Peeters et al. 2000 in preparation). The case of the general (bright) interstellar medium is covered below with a quantitative comparison of the AIB profiles.
In this work, rather than establish the "final'' AIB profile parameters, we aim at comparing on the same footing the individual AIB profiles under different excitation conditions. We have therefore decomposed the present spectra into Lorentz profiles and a modified blackbody as underlying continuum. We restricted ourselves to the minimum number of Lorentz profiles required in order to produce a reasonable overall fit and a good representation of every individual AIB.
We used a classical gradient-expansion algorithm
with analytical partial derivatives and performed the fit in the wavenumber space (
![]() in cm_1)
over the 2.4-25
in cm_1)
over the 2.4-25 ![]() m wavelength range. In addition to the Lorentz profiles,
the underlying continuum is fitted simultaneously. For the latter, we took a modified blackbody with an
emissivity law proportional to x, the temperature and peak brightness of which were the free parameters.
The same set of fit parameters was used for all objects. Such a set was first fixed on the M17-SW
spectrum which has a high signal-to-noise ratio and a good feature-to-continuum contrast.
To fit the 2.4-25
m wavelength range. In addition to the Lorentz profiles,
the underlying continuum is fitted simultaneously. For the latter, we took a modified blackbody with an
emissivity law proportional to x, the temperature and peak brightness of which were the free parameters.
The same set of fit parameters was used for all objects. Such a set was first fixed on the M17-SW
spectrum which has a high signal-to-noise ratio and a good feature-to-continuum contrast.
To fit the 2.4-25 ![]() m spectrum, twenty Lorentz profiles were necessary.
Then, the parameter values of the Lorentz profiles and of the continuum in M17-SW were used as input to
fit the other AIB spectra: very good fits were obtained by first relaxing the Lorentz amplitudes and
blackbody continuum parameters, suggesting a complete and robust decomposition of the AIB spectrum.
After adjusting the amplitudes, the profile (position and width) and continuum parameters
were fine-tuned, simultaneously, over restricted spectral ranges.
The centroids, widths and amplitudes of the Lorentzian fits to the main AIBs are given in Table 2.
Our fit to the 5-25
m spectrum, twenty Lorentz profiles were necessary.
Then, the parameter values of the Lorentz profiles and of the continuum in M17-SW were used as input to
fit the other AIB spectra: very good fits were obtained by first relaxing the Lorentz amplitudes and
blackbody continuum parameters, suggesting a complete and robust decomposition of the AIB spectrum.
After adjusting the amplitudes, the profile (position and width) and continuum parameters
were fine-tuned, simultaneously, over restricted spectral ranges.
The centroids, widths and amplitudes of the Lorentzian fits to the main AIBs are given in Table 2.
Our fit to the 5-25 ![]() m-AIB spectrum is shown in Fig. 2. The blackbody component of this decomposition
is consistent with the emission of warm dust in the mid-infrared and in particular its
exponential decay (the Wien tail of the blackbody). The observed strong
variability of the 20
m-AIB spectrum is shown in Fig. 2. The blackbody component of this decomposition
is consistent with the emission of warm dust in the mid-infrared and in particular its
exponential decay (the Wien tail of the blackbody). The observed strong
variability of the 20 ![]() m-continuum flux (very weak in NGC 2023 whereas strong in M17-SW and the Orion Bar)
then reflects the varying temperature of the warm dust component.
As can be seen in Fig. 2, the underlying continuum contributes little below the AIBs.
On the other hand,
additional, colder blackbody, type continua are required to fit the full SWS spectra out to 45
m-continuum flux (very weak in NGC 2023 whereas strong in M17-SW and the Orion Bar)
then reflects the varying temperature of the warm dust component.
As can be seen in Fig. 2, the underlying continuum contributes little below the AIBs.
On the other hand,
additional, colder blackbody, type continua are required to fit the full SWS spectra out to 45 ![]() m.
m.
We note that broad bands are required at about 1000 and 1450 cm_1 in order to explain the continuum
between the AIBs. These bands may not be associated with the AIBs but, for simplicity,
we assumed their profiles to be Lorentzian. Their parameters are not well
constrained in our decomposition: the sole requirement is that
the corresponding profiles are broad enough to reproduce the smooth continuum observed
in these spectral regions.
The fitted profiles of the neighbouring AIBs are somewhat sensitive to the widths
adopted for the 1000 and 1450 cm_1 bands: for instance, if the full width at half maximum (FWHM) of the
1450 cm_1 band is increased from 200 to 300 cm_1, the 6.2 ![]() m-band has its FWHM reduced by 2.5 cm_1 and
its position redshifted by 0.8 cm_1. In order to coherently compare the AIB profiles, we have fixed the
width of these broad bands: namely,
m-band has its FWHM reduced by 2.5 cm_1 and
its position redshifted by 0.8 cm_1. In order to coherently compare the AIB profiles, we have fixed the
width of these broad bands: namely,
![]() cm_1 for the 1000 cm_1-band and
cm_1 for the 1000 cm_1-band and
![]() cm_1 for the
1450 cm_1-band. At this stage, we can point out that combinations of PAH vibrational modes
have been predicted to accumulate between 1000 and 2000 cm_1 in a broad structure (Bernard et al. 1989).
cm_1 for the
1450 cm_1-band. At this stage, we can point out that combinations of PAH vibrational modes
have been predicted to accumulate between 1000 and 2000 cm_1 in a broad structure (Bernard et al. 1989).
| AIB | NGC 2023 | M17-SW | Orion Bar |
| 11.3 |
888.6 1 | 889.9 | 889.7 |
| 20.8 2 | 17.8 | 14.2 | |
| 877 3 | 2292 | 7241 | |
| Core | 889.3 | 890.2 | 889.9 |
| 13.1 | 10.1 | 10.9 | |
| 564 | 1644 | 5928 | |
| Red wing | 881.9 | 880.3 | 880.5 |
| 29.6 | 30.4 | 30.0 | |
| 384 | 915 | 1820 | |
| 8.6 |
1164.0 | 1163.8 | 1161.5 |
| 49.3 | 44.6 | 48.0 | |
| 355 | 780 | 1957 | |
| 7.8 |
1274.2 | 1273.5 | 1275.1 |
| 70.2 | 67.6 | 54.2 | |
| 392 | 1494 | 2417 | |
| 7.6 |
1309.9 | 1312.6 | 1311.3 |
| 22.9 | 28.6 | 25.6 | |
| 130 | 912 | 1760 | |
| 7.5 |
1328.1 | 1327.8 | 1329.7 |
| 68.2 | 74.5 | 55.9 | |
| 466 | 1074 | 2022 | |
| 6.2 |
1608.1 | 1607.7 | 1609.7 |
| 48.6 | 42.6 | 38.9 | |
| 550 | 1748 | 3428 | |
| Core | 1608.5 | 1608.6 | 1610.5 |
| 17.1 | 30.0 | 25.5 | |
| 224 | 1376 | 2369 | |
| Red wing | 1600.5 | 1586.2 | 1594.9 |
| 80.0 | 64.4 | 64.8 | |
| 338 | 546 | 1291 | |
| 3.3 |
3041.8 | 3039.1 | 3040.0 |
| 43.0 | 38.8 | 40.4 | |
| 98 | 171 | 834 |
|
1 center in cm_1 ( |
|
2 width in cm_1 ( |
| 3 amplitude in MJy/sr. |
Also noteworthy is that two Lorentzians are required to correctly reproduce the red
wing asymmetry of the 1609 cm_1 (6.2 ![]() m) and 890 cm_1 (11.3
m) and 890 cm_1 (11.3 ![]() m) bands: these components are labelled
"core'' and "red wing'' in Table 2. The feature centered around 1300 cm_1 (the classical "7.7
m) bands: these components are labelled
"core'' and "red wing'' in Table 2. The feature centered around 1300 cm_1 (the classical "7.7 ![]() m-band'')
shows 3 sub-peaks at about 1273, 1310 and 1328 cm_1. In the following, we will call the narrow
1310 cm_1 peak the "7.6
m-band'')
shows 3 sub-peaks at about 1273, 1310 and 1328 cm_1. In the following, we will call the narrow
1310 cm_1 peak the "7.6 ![]() m-band'' while the broader 1273 and 1328 cm_1 components will be dubbed
the "7.8'' and "7.5
m-band'' while the broader 1273 and 1328 cm_1 components will be dubbed
the "7.8'' and "7.5 ![]() m-bands'' respectively.
The observed 1310 cm_1-feature
has a narrow core and a broad blue wing which demands another component at 1328 cm_1.
A Lorentzian is also required around 1204 cm_1 (
m-bands'' respectively.
The observed 1310 cm_1-feature
has a narrow core and a broad blue wing which demands another component at 1328 cm_1.
A Lorentzian is also required around 1204 cm_1 (
![]() cm_1) to fill the gap between the 7.8 and
the 8.6
cm_1) to fill the gap between the 7.8 and
the 8.6 ![]() m-features. In the case of Orion this band shifts to 1209 cm_1 in order to reproduce the
pronounced and extended blue wing of the 8.6
m-features. In the case of Orion this band shifts to 1209 cm_1 in order to reproduce the
pronounced and extended blue wing of the 8.6 ![]() m-band.
m-band.
In Fig. 3 we show the profile and fit of the 3.3 ![]() m band. The band shape is also
Lorentzian and the continuum has the same functional form as in the 5-25
m band. The band shape is also
Lorentzian and the continuum has the same functional form as in the 5-25 ![]() m region.
In other words, we fitted the 2.4-25
m region.
In other words, we fitted the 2.4-25 ![]() m continuum with a single blackbody component.
m continuum with a single blackbody component.
The decomposition presented above is not unique: we also tried to use a multicomponent power-law
continuum (A/x3 + B/x2 + C/x + D with
![]() and where
A,B,C and D are constant parameters) below the AIBs
from 2.4 to 16
and where
A,B,C and D are constant parameters) below the AIBs
from 2.4 to 16 ![]() m. Such a continuum gives a notable contribution below the AIBs, in particular, it replaces completely
the 1000 cm_1 broad band. However, a multicomponent power-law continuum has no
straightforward physical
interpretation and it cannot describe the
strong rise of the spectrum beyond 16
m. Such a continuum gives a notable contribution below the AIBs, in particular, it replaces completely
the 1000 cm_1 broad band. However, a multicomponent power-law continuum has no
straightforward physical
interpretation and it cannot describe the
strong rise of the spectrum beyond 16 ![]() m observed in M17-SW and the Orion Bar. Nor can it accommodate the
weak 20
m observed in M17-SW and the Orion Bar. Nor can it accommodate the
weak 20 ![]() m-flux in NGC 2023. In any case,
comparing the fits obtained with the two types of continua (power-law and blackbody), we found the positions
and widths of the main AIBs characterized in Table 2 to vary by less than 1.6 and 4 cm_1 respectively in a
given object.
Finally, using gaussian band shapes for the AIBs, we got as good a
decomposition (see also Boulanger et al. 1998b): yet the continuum under the
AIBs was stronger and more structured because of the weaker profile wings. We believe that the fit
quality does not preclude any band profile: in fact, the SWS AIB spectrum is so rich that there are always
enough parameters in the fit to accomodate any choice of band profile.
m-flux in NGC 2023. In any case,
comparing the fits obtained with the two types of continua (power-law and blackbody), we found the positions
and widths of the main AIBs characterized in Table 2 to vary by less than 1.6 and 4 cm_1 respectively in a
given object.
Finally, using gaussian band shapes for the AIBs, we got as good a
decomposition (see also Boulanger et al. 1998b): yet the continuum under the
AIBs was stronger and more structured because of the weaker profile wings. We believe that the fit
quality does not preclude any band profile: in fact, the SWS AIB spectrum is so rich that there are always
enough parameters in the fit to accomodate any choice of band profile.
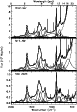 |
Figure 2:
The decomposition of the AIB spectra between 5 and 25 |
| Open with DEXTER | |
We have thus determined in a coherent way the position and width of the strong,
well-delineated AIBs at 3.3, 6.2, 7.6, 8.6 and 11.3 ![]() m with an accuracy of 0.8 and 2 cm_1
respectively.
Inspection of Table 2 shows that there are significant variations in the width of the 6.2 and
11.3
m with an accuracy of 0.8 and 2 cm_1
respectively.
Inspection of Table 2 shows that there are significant variations in the width of the 6.2 and
11.3 ![]() m-bands (9.7 and 6.6 cm_1 respectively) as well as in the position of the 3.3 and
7.6
m-bands (9.7 and 6.6 cm_1 respectively) as well as in the position of the 3.3 and
7.6 ![]() m-bands (2.7 cm_1 in both cases). However, all these variations come within the accuracy
range given above when the values of NGC 2023 are excluded. In this latter object, the poorer
signal-to-noise ratio and resolving power (see Fig. 1 and Figs. 8 to 11) has degraded the band
profiles: this is probably why some AIB parameters are singular in NGC 2023.
On the other hand,
we find that the position of the 8.6
m-bands (2.7 cm_1 in both cases). However, all these variations come within the accuracy
range given above when the values of NGC 2023 are excluded. In this latter object, the poorer
signal-to-noise ratio and resolving power (see Fig. 1 and Figs. 8 to 11) has degraded the band
profiles: this is probably why some AIB parameters are singular in NGC 2023.
On the other hand,
we find that the position of the 8.6 ![]() m-band varies by 2.5 cm_1 (Table 2) and that most of this
variation is due to a redshift in the Orion Bar spectrum. As noted above, the 8.6
m-band varies by 2.5 cm_1 (Table 2) and that most of this
variation is due to a redshift in the Orion Bar spectrum. As noted above, the 8.6 ![]() m-band in this object
has an extended blue wing: this spectral change is related to the redshift of the band itself.
This result may point to the more profound modifications seen in this
spectral range by Roelfsema et al. (1996)
and Verstraete et al. (1996) towards more excited regions.
m-band in this object
has an extended blue wing: this spectral change is related to the redshift of the band itself.
This result may point to the more profound modifications seen in this
spectral range by Roelfsema et al. (1996)
and Verstraete et al. (1996) towards more excited regions.
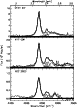 |
Figure 3:
Same as Fig. 2 in the region of the 3.3 |
| Open with DEXTER | |
From the above discussion, we conclude that most AIB profiles (except the 8.6 ![]() m-AIB in the Orion Bar)
do not vary within the accuracy of our spectral decomposition.
At 3.3
m-AIB in the Orion Bar)
do not vary within the accuracy of our spectral decomposition.
At 3.3 ![]() m, a similar result was already obtained by Tokunaga et al. (1991) who compared the band profile of planetary
nebulae and H II regions (their Type 1 profile)
with excitation conditions (
m, a similar result was already obtained by Tokunaga et al. (1991) who compared the band profile of planetary
nebulae and H II regions (their Type 1 profile)
with excitation conditions (
![]() and
and ![]() )
similar to that of our sample (see Table 1).
Roche et al. (1996) confirmed this result on a larger, lower-excitation sample of planetary nebulae.
Similarly, Witteborn et al. (1989) showed that the 11.3
)
similar to that of our sample (see Table 1).
Roche et al. (1996) confirmed this result on a larger, lower-excitation sample of planetary nebulae.
Similarly, Witteborn et al. (1989) showed that the 11.3 ![]() m-band profile is rather stable.
Furthermore, the observed smoothness and invariance of the AIBs across a wide range of excitation conditions appears
difficult to reconcile with the variability expected from laboratory results.
m-band profile is rather stable.
Furthermore, the observed smoothness and invariance of the AIBs across a wide range of excitation conditions appears
difficult to reconcile with the variability expected from laboratory results.
Having performed this mathematical parameterization of the SWS spectra, we are now able to extract the individual
AIB profiles and to compare them in different objects and to model predictions.
Yet, what is the physical meaning of this spectral decomposition? We have chosen Lorentzian band shapes and we
represented most AIBs (except the 7.7 ![]() m) with one or two Lorentz profiles: this implicitly assumes that the
AIBs arise from a few vibrational bands common to many PAHs and that most of the bandwidth arises from a single
carrier. The invariance and smoothness of the AIBs is then naturally explained (Boulanger et al. 1998b).
To verify this interpretation of the AIBs, the band parameters of Table 2 can
be compared directly to laboratory or theoretical studies on relevant PAHs (large molecules
containing more than 50 C-atoms as argued by Boulanger et al. 1998b). But there are other ways to look at the
interstellar AIB spectrum which do not result in Lorentzian bandshapes.
For instance, simulations of astronomical spectra based on recent laboratory studies
of small PAHs (Allamandola et al. 1999) have shown that the AIB spectrum may be decomposed by assigning a
multiplicity of (species dependent) vibrational bands to each AIB. Another possibility to interpret the AIB spectrum
is based on the laboratory work of Joblin et al. (1995) which shows that the vibrational bands of PAHs
are broadened and redshifted as the temperature of the molecule is raised. In this picture, the profile
of a vibrational band from a single molecule with a given internal energy has a Lorentz shape (the intrinsic profile)
which only depends on the
temperature of the molecule (and not on the species). The observed AIBs are then interpreted as the superposition of
many Lorentz profiles corresponding to all the possible temperatures reached by a population of PAHs.
m) with one or two Lorentz profiles: this implicitly assumes that the
AIBs arise from a few vibrational bands common to many PAHs and that most of the bandwidth arises from a single
carrier. The invariance and smoothness of the AIBs is then naturally explained (Boulanger et al. 1998b).
To verify this interpretation of the AIBs, the band parameters of Table 2 can
be compared directly to laboratory or theoretical studies on relevant PAHs (large molecules
containing more than 50 C-atoms as argued by Boulanger et al. 1998b). But there are other ways to look at the
interstellar AIB spectrum which do not result in Lorentzian bandshapes.
For instance, simulations of astronomical spectra based on recent laboratory studies
of small PAHs (Allamandola et al. 1999) have shown that the AIB spectrum may be decomposed by assigning a
multiplicity of (species dependent) vibrational bands to each AIB. Another possibility to interpret the AIB spectrum
is based on the laboratory work of Joblin et al. (1995) which shows that the vibrational bands of PAHs
are broadened and redshifted as the temperature of the molecule is raised. In this picture, the profile
of a vibrational band from a single molecule with a given internal energy has a Lorentz shape (the intrinsic profile)
which only depends on the
temperature of the molecule (and not on the species). The observed AIBs are then interpreted as the superposition of
many Lorentz profiles corresponding to all the possible temperatures reached by a population of PAHs.
In the next section, devoted to modelling, we adopt and detail this latter view of the AIB spectrum.
In this context, using the relationship between bandwidth and temperature established by Joblin et al. (1995),
we note that the width of the observed 3.3 ![]() m-band (40 cm_1) is well explained if the emitting
PAH has a temperature of about 1000 K. Such emission temperatures are in good
agreement with what is expected for interstellar PAHs emitting during temperature fluctuations
(see Sect. 4).
Using the present spectral decomposition of the SWS data, we can now extract the individual AIB profiles
and compare them to the predictions of a PAH emission model that uses the best available laboratory
data on PAHs.
m-band (40 cm_1) is well explained if the emitting
PAH has a temperature of about 1000 K. Such emission temperatures are in good
agreement with what is expected for interstellar PAHs emitting during temperature fluctuations
(see Sect. 4).
Using the present spectral decomposition of the SWS data, we can now extract the individual AIB profiles
and compare them to the predictions of a PAH emission model that uses the best available laboratory
data on PAHs.
To first order, the AIB profiles essentially remain identical
while the exciting radiation hardens considerably:
![]() 000 K in NGC 2023 to
45000 K in M17-SW corresponding to the mean energy of the photons absorbed by a PAH
of 6 and 9 eV respectively. Such contrasted internal energies
imply differences in the emission temperature of a few 100 K for a given molecular size.
With this temperature change, band position shifts and band broadening of at least 10 cm_1 are expected
(Joblin et al. 1995). How can then the interstellar AIB profiles be so stable? One possibility
is that some process keeps the temperature distribution of interstellar PAHs essentially
the same.
000 K in NGC 2023 to
45000 K in M17-SW corresponding to the mean energy of the photons absorbed by a PAH
of 6 and 9 eV respectively. Such contrasted internal energies
imply differences in the emission temperature of a few 100 K for a given molecular size.
With this temperature change, band position shifts and band broadening of at least 10 cm_1 are expected
(Joblin et al. 1995). How can then the interstellar AIB profiles be so stable? One possibility
is that some process keeps the temperature distribution of interstellar PAHs essentially
the same.
To investigate this issue, we have computed the temperature distribution and
associated infrared (IR) emission of an interstellar PAH population using a modified version of the model
described in Pech et al. (2000 hereafter PJB) where we study in detail the temperature fluctuations and the
temperature distribution of PAHs. Improving on former work (Léger et al. 1989b; Schutte et al. 1993;
Cook & Saykally 1998), this model takes
into account the full spectral distribution of the exciting radiation and implements the recent results of Joblin
et al. (1995) on the temperature dependence of the band profiles of neutral PAHs.
In addition, it must be emphasized that the PAH IR emission cross-section of the PJB model was derived from
studies on PAH cations: indeed, we show in Sect. 4.4.1 that singly ionized PAHs
reproduce better the astronomical AIB spectra confirming previous work (Langhoff 1996; Cook & Saykally 1998;
Allamandola et al. 1999; Hudgins & Allamandola 1999). This observational requirement is supported by theoretical
studies on the charge state of interstellar PAHs for physical conditions comparable to those of our sample
of objects (Bakes & Tielens 1994; Dartois & d'Hendecourt 1997).
We first briefly describe the equations giving
the PAH cooling curve and emission, compute the temperature distribution of interstellar PAHs and then
compare our model PAH emission spectrum to the data. For the sake of clarity, we limit the model-to-data
comparison to NGC 2023 and M17-SW which are the extreme cases of our data sample and we focus on the well-defined
3.3, 6.2, 8.6 and 11.3 ![]() m-bands.
In order to emphasize the temperature fluctuations of PAHs
and the resulting temperature distribution, we have written the model equations in terms of cross-sections rather
than Einstein A-coefficients: this formulation is however strictly equivalent to that of PJB (see, e.g. ,
Schutte et al. 1993, Eq. (15)).
m-bands.
In order to emphasize the temperature fluctuations of PAHs
and the resulting temperature distribution, we have written the model equations in terms of cross-sections rather
than Einstein A-coefficients: this formulation is however strictly equivalent to that of PJB (see, e.g. ,
Schutte et al. 1993, Eq. (15)).
In the interstellar medium, a PAH containing ![]() carbon atoms absorbs radiation from the surrounding
stars at a rate:
carbon atoms absorbs radiation from the surrounding
stars at a rate:
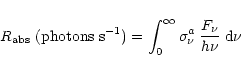 |
(1) |
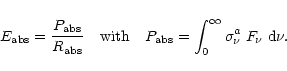 |
(2) |
As shown by Léger et al. (1989a) and Schutte et al. (1993), the IR emission of a
PAH is well treated within the thermal approximation and using
Kirchhoff's law. In the following, we will discuss the complete spectrum emitted by PAHs in terms of
the spectral energy distribution (SED) noted ![]() which is equal to
which is equal to
![]() .
The SED (in Watt) emitted by a single
molecule containing
.
The SED (in Watt) emitted by a single
molecule containing ![]() carbon atoms is thus:
carbon atoms is thus:
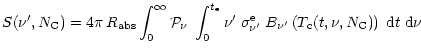 |
(3) |
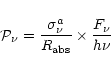 |
(4) |
The PAH IR emission cross-section is defined as in PJB. The band profiles have a Lorentzian shape
and at 3.3, 6.2, 8.6 and 11.3 ![]() m, the band position and width follow temperature dependent laws.
Each Lorentz profile is normalized to the peak value of the band cross-section,
m, the band position and width follow temperature dependent laws.
Each Lorentz profile is normalized to the peak value of the band cross-section,
![]() and
we assume that the integrated cross-section (or Einstein A-coefficient, see Schutte et al. 1993) of each band profile
is conserved with temperature. As already noted above, the resulting IR cross-section describes the properties of singly-ionized PAHs.
To match the observed AIB, the 8.6
and
we assume that the integrated cross-section (or Einstein A-coefficient, see Schutte et al. 1993) of each band profile
is conserved with temperature. As already noted above, the resulting IR cross-section describes the properties of singly-ionized PAHs.
To match the observed AIB, the 8.6 ![]() m-band had to be multiplied by 3. Because the available laboratory results do not account for the
complex shape of the observed 7.7
m-band had to be multiplied by 3. Because the available laboratory results do not account for the
complex shape of the observed 7.7 ![]() m-band (see Sect. 3), we define an empirical 7.7
m-band (see Sect. 3), we define an empirical 7.7 ![]() m-band with a shape derived from the
observations (profile centre at 1300 cm_1 and
m-band with a shape derived from the
observations (profile centre at 1300 cm_1 and
![]() cm_1 from the present data) and
with the (laboratory determined) Einstein A-coefficient of PJB. This profile of the 7.7
cm_1 from the present data) and
with the (laboratory determined) Einstein A-coefficient of PJB. This profile of the 7.7 ![]() m-band is furthermore assumed temperature
independent. We also added the 16.4
m-band is furthermore assumed temperature
independent. We also added the 16.4 ![]() m-AIB detected by ISO towards many sightlines (Moutou et al. 2000;
van Kerckhoven et al. 2000). This band is often
associated with the "classical'' 3 to 13
m-AIB detected by ISO towards many sightlines (Moutou et al. 2000;
van Kerckhoven et al. 2000). This band is often
associated with the "classical'' 3 to 13 ![]() m-AIBs and its intensity is not related to the hot dust
continuum appearing in more excited objects (see Fig. 1), i.e. , as for the other AIBs.
We represent the 16.4
m-AIBs and its intensity is not related to the hot dust
continuum appearing in more excited objects (see Fig. 1), i.e. , as for the other AIBs.
We represent the 16.4 ![]() m-band with a Lorentz profile centered at 609 cm_1, with
m-band with a Lorentz profile centered at 609 cm_1, with
![]() cm_1
(both being observational values, see Moutou et al. 2000) and an Einstein A-coefficient of
cm_1
(both being observational values, see Moutou et al. 2000) and an Einstein A-coefficient of
![]() s-1 per carbon atom
which corresponds to the average value of the laboratory measurements given in Moutou et al. (1996, Table 3).
As we will see below, the intensity of the 16.4
s-1 per carbon atom
which corresponds to the average value of the laboratory measurements given in Moutou et al. (1996, Table 3).
As we will see below, the intensity of the 16.4 ![]() m-band can constrain the power-law index of the PAH
size distribution. At longer wavelengths, we adopted the far-IR (
m-band can constrain the power-law index of the PAH
size distribution. At longer wavelengths, we adopted the far-IR (
![]()
![]() m) cross-section
of Schutte et al. (1993).
m) cross-section
of Schutte et al. (1993).
The size distribution of PAHs is defined by d
![]() ,
i.e., the number of PAHs with a
number of C-atoms between
,
i.e., the number of PAHs with a
number of C-atoms between ![]() and
and
![]() .
Writing the size distribution with respect to
.
Writing the size distribution with respect to ![]() frees us of
any assumptions on the PAH geometrical shape
frees us of
any assumptions on the PAH geometrical shape![]() . The number of H-atoms per
molecule is assumed to be
. The number of H-atoms per
molecule is assumed to be
![]() (Omont 1986, in the case of symmetric PAHs) with
(Omont 1986, in the case of symmetric PAHs) with ![]() the
hydrogenation fraction of a molecule: if
the
hydrogenation fraction of a molecule: if
![]() the molecule is completely dehydrogenated, if
the molecule is completely dehydrogenated, if
![]() the
molecule is fully hydrogenated. Unless otherwise stated, we will assume
the
molecule is fully hydrogenated. Unless otherwise stated, we will assume
![]() .
The mass distribution is then straightforwardly found as d
.
The mass distribution is then straightforwardly found as d
![]() where
where ![]() is the carbon atomic mass and
is the carbon atomic mass and ![]() the atomic mass of hydrogen. The
normalization factor, B, is determined from the PAH abundance in terms of the
fraction of interstellar carbon ([C/H]
the atomic mass of hydrogen. The
normalization factor, B, is determined from the PAH abundance in terms of the
fraction of interstellar carbon ([C/H]
![]() ,
Snow & Witt 1996) locked up
in PAHs. Finally, the emergent SED emitted by PAHs is
,
Snow & Witt 1996) locked up
in PAHs. Finally, the emergent SED emitted by PAHs is
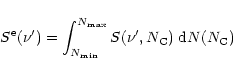 |
(5) |
Upon absorption of a UV-photon, the PAH temperature is raised to a peak value,
![]() .
The molecule then cools rapidly by the emission of IR vibrational mode photons.
The peak temperature
.
The molecule then cools rapidly by the emission of IR vibrational mode photons.
The peak temperature ![]() is found from first principles:
is found from first principles:
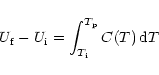 |
(6) |
The cooling curve
![]() is obtained by numerical integration (vs. temperature)
of the energy conservation relationship during cooling,
is obtained by numerical integration (vs. temperature)
of the energy conservation relationship during cooling,
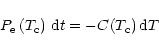 |
(7) |
The power emitted by a PAH at temperature T is:
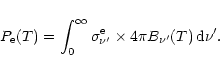 |
(8) |
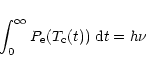 |
(9) |
Each molecule sees its cooling interrupted by the absorption of the next photon which
is a stochastic process (Désert et al. 1986). Moreover,
gas-grain exchanges must be taken into account (Rouan et al. 1992; Draine & Lazarian 1998)
to reliably estimate the temperature of a PAH in the low temperature part of the cooling curve.
In fact, the emission from
the cool (but long-lasting) tail of the cooling curves will peak in the far-IR/submillimeter, far away
from the 3 to 20 ![]() m-range on which we focus here. The
detailed treatment of this problem is outside the scope of this paper and we adopt the
following simple criterion to truncate our cooling curves.
The mean time elapsed between two photon absorptions is
m-range on which we focus here. The
detailed treatment of this problem is outside the scope of this paper and we adopt the
following simple criterion to truncate our cooling curves.
The mean time elapsed between two photon absorptions is
![]() :
it is for instance 6.9 and 2.6 hours
in the radiation field of NGC 2023 and M17-SW respectively and for a molecule with
:
it is for instance 6.9 and 2.6 hours
in the radiation field of NGC 2023 and M17-SW respectively and for a molecule with
![]() .
Consequently, all cooling curves have been truncated at
.
Consequently, all cooling curves have been truncated at
![]() to
account for the repeated absorptions of UV photons by a molecule;
to
account for the repeated absorptions of UV photons by a molecule; ![]() decreases as
decreases as
![]() because
because
![]() .
We thus define the lowest
temperature of a PAH heated by a photon of energy
.
We thus define the lowest
temperature of a PAH heated by a photon of energy ![]() as
as
![]() ,
i.e. , equal
to the temperature at the end of the cooling.
For instance, in the radiation field of NGC 2023 small PAHs
(
,
i.e. , equal
to the temperature at the end of the cooling.
For instance, in the radiation field of NGC 2023 small PAHs
(
![]() )
eventually reach temperature as low as 15 K at time
)
eventually reach temperature as low as 15 K at time ![]() whereas bigger PAHs
(
whereas bigger PAHs
(
![]() )
remain at around 35 K.
)
remain at around 35 K.
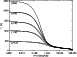 |
Figure 4:
Cooling curves for various energy per carbon atom (the zero time point has
been excluded).
The numbers in parenthesis give the value of
|
| Open with DEXTER | |
In Fig. 4, we show
the cooling curves obtained for various energies per C-atom
![]() .
As expected, the
peak temperatures are identical for a given
.
As expected, the
peak temperatures are identical for a given ![]() .
We note that
the
.
We note that
the ![]() -curves do not change much for different
-curves do not change much for different ![]() -values while
-values while ![]() remains fixed: in fact if the emission cross-section were only proportional to
remains fixed: in fact if the emission cross-section were only proportional to ![]() all the cooling curves with (
all the cooling curves with (![]() ,
,
![]() )
combinations yielding the same
)
combinations yielding the same
![]() would merge. Cooling curves with larger
would merge. Cooling curves with larger ![]() have higher temperatures
because emission in the C-H modes is less important (in a fully
hydrogenated PAH we have
have higher temperatures
because emission in the C-H modes is less important (in a fully
hydrogenated PAH we have
![]() ). The small variation in the
). The small variation in the ![]() -curves at fixed
-curves at fixed ![]() then reflects the decrease of the emission cross-section per carbon atom with increasing size.
then reflects the decrease of the emission cross-section per carbon atom with increasing size.
As noted above, the observed similarity of the AIB profiles in our sample means that the range of PAH emission temperatures does not vary much: to test this idea, we determine here the temperature distribution of PAHs. Moreover, as we show below, the effect of the size distribution and exciting radiation field parameters are illustrated in a synthetic fashion in the temperature distribution.
The observed AIB spectrum results principally from the superposition of many blackbodies
at different temperatures (Eqs. (3) and (5)). Following Eq. (3) it is clear that
a given blackbody will have a significant contribution to the emergent
spectrum if its temperature T is high and/or if it remains a long time
at that temperature: a PAH with a temperature between T and
![]() (corresponding to the time interval
(corresponding to the time interval
![]() )
will thus contribute to the
total emitted luminosity
)
will thus contribute to the
total emitted luminosity ![]() (see the end of Sect. 4.1) with a weight proportional to
(see the end of Sect. 4.1) with a weight proportional to
![]() or the fraction of the total available energy,
or the fraction of the total available energy, ![]() (the energy of the absorbed photon), that is dissipated
between t and
(the energy of the absorbed photon), that is dissipated
between t and
![]() .
This definition of the temperature weight is different from previous work
(Draine & Anderson 1985; Désert et al. 1986) which only considered the time that
a given grain spends in the temperature interval
.
This definition of the temperature weight is different from previous work
(Draine & Anderson 1985; Désert et al. 1986) which only considered the time that
a given grain spends in the temperature interval
![]() ,
namely dt/dT:
the present definition which takes into account the emitted power actually reflects
the contribution of a given temperature to the final spectrum.
,
namely dt/dT:
the present definition which takes into account the emitted power actually reflects
the contribution of a given temperature to the final spectrum.
From Eq. (7), we see that the temperature weight in the total luminosity is simply
![]() .
Taking into account the probability distribution of the exciting photons and the fraction
of PAHs containing
.
Taking into account the probability distribution of the exciting photons and the fraction
of PAHs containing ![]() carbon atoms, we define the temperature weight
carbon atoms, we define the temperature weight ![]() as:
as:
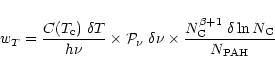 |
(10) |
To obtain the PAH temperature distribution in a given exciting radiation field, we build the
histogram of all cooling curves for all molecular sizes in temperature bins of constant size
(
![]() K), each temperature T being given the weight wT.
K), each temperature T being given the weight wT.
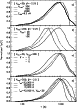 |
Figure 5:
The distribution of PAH temperatures
|
| Open with DEXTER | |
 |
Figure 6:
The spectral energy densities corresponding to the temperature distributions shown in Fig. 5.
All the curves have been normalized to 1 at the peak value of the 7.7 |
| Open with DEXTER | |
From our weight definition, p(T)dT is the fractional contribution of all PAHs with temperatures
in the range
![]() to the total emitted luminosity
to the total emitted luminosity ![]() .
.
The PAH temperature distributions, normalized to 1 at their peak values to facilitate the comparison, are shown in Fig. 5:
they all present a maximum between 300 and 800 K.
The shape of these distributions can be understood as follows. Assuming that all molecules absorb a photon of energy
![]() ,
the temperature weights are proportional to
,
the temperature weights are proportional to
![]() .
At low T, all the C(T)-curves corresponding
to the different
.
At low T, all the C(T)-curves corresponding
to the different ![]() 's sum up to give wT. As the temperature increases, the largest molecules do not contribute anymore to wT
because they are too cold: this fade out more than compensates for the rise of C(T) with the temperature and produces a maximum in the
temperature distribution.
's sum up to give wT. As the temperature increases, the largest molecules do not contribute anymore to wT
because they are too cold: this fade out more than compensates for the rise of C(T) with the temperature and produces a maximum in the
temperature distribution.
Figure 5 illustrates the sensitivity of the PAH temperature distribution to the size distribution parameters,
![]() ,
,
![]() and
and ![]() (Figs. 5a to 5c) and to the hardness of the exciting radiation
field, parameterized as
(Figs. 5a to 5c) and to the hardness of the exciting radiation
field, parameterized as
![]() (Fig. 5d). The associated changes in the AIB spectrum are shown in Fig. 6.
In all these figures (except the M17-SW case in Fig. 5d), we used the same dilution factor for the radiation field
(
(Fig. 5d). The associated changes in the AIB spectrum are shown in Fig. 6.
In all these figures (except the M17-SW case in Fig. 5d), we used the same dilution factor for the radiation field
(
![]() ,
corresponding to NGC 2023): indeed, as long as one is in the regime of temperature fluctuations,
the spectral distribution of the PAH emission spectrum does not depend on the radiation field intensity (Sellgren 1984) while its
absolute level scales with it (see Eq. (3)). Moreover, for the purpose of comparison, all the spectra of Fig. 6 have been normalized
to 1 at the peak value of the 7.7
,
corresponding to NGC 2023): indeed, as long as one is in the regime of temperature fluctuations,
the spectral distribution of the PAH emission spectrum does not depend on the radiation field intensity (Sellgren 1984) while its
absolute level scales with it (see Eq. (3)). Moreover, for the purpose of comparison, all the spectra of Fig. 6 have been normalized
to 1 at the peak value of the 7.7 ![]() m-band because its profile is independent of the PAH temperature (see Sect. 4.1).
m-band because its profile is independent of the PAH temperature (see Sect. 4.1).
In Fig. 5a, we consider the effect of taking the full spectral distribution of exciting photons
instead of the same mean absorbed photon energy,
![]() (i.e. ,
(i.e. ,
![]() ).
In the following, we will refer to the
).
In the following, we will refer to the
![]() -approximation whenever it is assumed that each molecule absorbs the
same photon of energy
-approximation whenever it is assumed that each molecule absorbs the
same photon of energy
![]() at the rate
at the rate
![]() in the given radiation field. The
in the given radiation field. The
![]() -approximation
only affects the high temperature tail of the distribution. As we will see in Sect. 4.4.2, this tail matters for
the width of the 3.3
-approximation
only affects the high temperature tail of the distribution. As we will see in Sect. 4.4.2, this tail matters for
the width of the 3.3 ![]() m-band. Nevertheless, the rest of the AIB spectrum is little affected by the
m-band. Nevertheless, the rest of the AIB spectrum is little affected by the
![]() -approximation.
-approximation.
![]() has a weak influence on the temperature distribution (Fig. 5b) and its impact, which is most noticeable at long
wavelengths (
has a weak influence on the temperature distribution (Fig. 5b) and its impact, which is most noticeable at long
wavelengths (
![]() 10
10 ![]() m, see Fig. 6a), is easily drowned by small changes of
m, see Fig. 6a), is easily drowned by small changes of ![]() ,
the index of the
power-law size distribution of PAHs (see Figs. 5c and 6c). When
,
the index of the
power-law size distribution of PAHs (see Figs. 5c and 6c). When ![]() decreases, the contribution of the smallest PAHs
becomes more important and the cold tail of the temperature distribution is somewhat reduced (Fig. 5c): this leads to an enhanced
3.3/11.3
decreases, the contribution of the smallest PAHs
becomes more important and the cold tail of the temperature distribution is somewhat reduced (Fig. 5c): this leads to an enhanced
3.3/11.3 ![]() m-band ratio and to somewhat broader bandwidths (Fig. 6c and Figs. 8 to 11).
Note that, due to this broadening, the band peak value diminishes
(see the 6.2
m-band ratio and to somewhat broader bandwidths (Fig. 6c and Figs. 8 to 11).
Note that, due to this broadening, the band peak value diminishes
(see the 6.2 ![]() m-band in Fig. 6c) because the band integrated cross-section is conserved with temperature.
Both
m-band in Fig. 6c) because the band integrated cross-section is conserved with temperature.
Both ![]() and
and
![]() (which determines
(which determines
![]() ,
here
,
here
![]() to 45000 K corresponds to
to 45000 K corresponds to
![]() to 9 eV)
affect the hot tail of p(T) (Figs. 5b and 5d) which merely reflects the hottest part of the cooling curve
(Fig. 4).
This behaviour of p(T) follows from the fact that the PAH peak temperature only depends on the energy content per carbon atom in a molecule,
to 9 eV)
affect the hot tail of p(T) (Figs. 5b and 5d) which merely reflects the hottest part of the cooling curve
(Fig. 4).
This behaviour of p(T) follows from the fact that the PAH peak temperature only depends on the energy content per carbon atom in a molecule,
![]() (see Sect. 4.2) and that a typical value for
(see Sect. 4.2) and that a typical value for ![]() is
is
![]() (
(![]() is close to the mean value of
is close to the mean value of ![]() because of the
steep power-law size distribution). In fact, the temperature distribution and the shape of the emission spectrum are similar for different
because of the
steep power-law size distribution). In fact, the temperature distribution and the shape of the emission spectrum are similar for different
![]() -couples yielding the same energy per carbon atom. As expected, an increase of
-couples yielding the same energy per carbon atom. As expected, an increase of ![]() leads to colder PAHs (Fig. 5b)
which contribute more to the long-wavelength bands (Fig. 6b) while an increase of
leads to colder PAHs (Fig. 5b)
which contribute more to the long-wavelength bands (Fig. 6b) while an increase of
![]() has the reverse effect (see Figs. 5d and 6d).
We pointed out earlier that the PAH temperature distribution must remain unchanged in order to explain the similarity of the observed AIB profiles:
we show in Fig. 5d that this condition is fulfilled if
has the reverse effect (see Figs. 5d and 6d).
We pointed out earlier that the PAH temperature distribution must remain unchanged in order to explain the similarity of the observed AIB profiles:
we show in Fig. 5d that this condition is fulfilled if ![]() is raised along with
is raised along with
![]() .
Specifically, an increase of
.
Specifically, an increase of
![]() from
23000 K (the case of NGC 2023) to 45000 K (the case of M17-SW) requires
from
23000 K (the case of NGC 2023) to 45000 K (the case of M17-SW) requires
![]() to 30, respectively.
In the next sections, we show that this requirement allows to consistently reproduce the overall AIB spectrum as well as the individual band
profiles.
to 30, respectively.
In the next sections, we show that this requirement allows to consistently reproduce the overall AIB spectrum as well as the individual band
profiles.
We now present the PAH IR-emission as computed from the formalism described above in the case of NGC 2023 and M17-SW. We selected these two objects because they present the largest contrast in the effective temperature of the exciting radiation field: we therefore expect these spectra to provide the strongest constraints on our model.
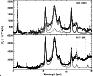 |
Figure 7:
The spectral energy density in Watt per hydrogen for our sample of objects from the SWS data (dotted curve)
and assuming a column density of
|
| Open with DEXTER | |
Having determined the temperature distribution of a population of PAHs, we can
now compute the corresponding IR emission using Eqs. (3) and (5).
The PAH size distribution parameters were constrained as follows.
We note that the overall shape of the 3-13 ![]() m AIB spectrum which is dominated by emission from molecules at
m AIB spectrum which is dominated by emission from molecules at
![]() K is not much affected by changes in
K is not much affected by changes in ![]() or
or ![]() (see Figs. 6a and 6c).
For simplicity, we fix from now on
(see Figs. 6a and 6c).
For simplicity, we fix from now on
![]() .
First,
.
First, ![]() is fixed so as to reproduce
the observed 3.3/11.3
is fixed so as to reproduce
the observed 3.3/11.3 ![]() m-band ratio in a given exciting radiation field (described by
m-band ratio in a given exciting radiation field (described by
![]() ):
we require
):
we require
![]() in NGC 2023 while
in NGC 2023 while
![]() in M17-SW. The hydrogenation fraction,
in M17-SW. The hydrogenation fraction, ![]() ,
is
constrained from the 7.7/11.3
,
is
constrained from the 7.7/11.3 ![]() m-band ratio: a good match to the observed band ratios is obtained with
m-band ratio: a good match to the observed band ratios is obtained with
![]() for NGC 2023 and
for NGC 2023 and
![]() for M17-SW.
The index of the power law size distribution,
for M17-SW.
The index of the power law size distribution, ![]() ,
can be constrained from the requirement that the
predicted 16.4
,
can be constrained from the requirement that the
predicted 16.4 ![]() m-band (on top of the broadband continuum) matches the observed band:
we find that
m-band (on top of the broadband continuum) matches the observed band:
we find that
![]() reproduces the 16.4
reproduces the 16.4 ![]() m-band well in both objects
m-band well in both objects![]() .
Unfortunately, individual PAH species show a large spread in the integrated
cross-section of the 16.4
.
Unfortunately, individual PAH species show a large spread in the integrated
cross-section of the 16.4 ![]() m-band (see Table 3 of Moutou et al. 1996) which does not constrain
m-band (see Table 3 of Moutou et al. 1996) which does not constrain ![]() :
specifically, to match the observed 16.4
:
specifically, to match the observed 16.4 ![]() m-band we require
m-band we require
![]() for the lowest
cross-section value while
for the lowest
cross-section value while
![]() for the largest cross-section value.
More laboratory work on PAHs is warranted in order to understand the trend of the 16.4
for the largest cross-section value.
More laboratory work on PAHs is warranted in order to understand the trend of the 16.4 ![]() m-band
profile with respect to
m-band
profile with respect to ![]() and to the various isomer states.
As discussed by PJB, an additional constraint on
and to the various isomer states.
As discussed by PJB, an additional constraint on ![]() is provided by the intensity and width of the AIB
profiles (see the next section).
The
is provided by the intensity and width of the AIB
profiles (see the next section).
The ![]() -value can then be adjusted in order to
match the peak position and the FWHM of the 3.3
-value can then be adjusted in order to
match the peak position and the FWHM of the 3.3 ![]() m-band (see Sect. 4.4.2): in fact, the value of -3.5 found
from the 16.4
m-band (see Sect. 4.4.2): in fact, the value of -3.5 found
from the 16.4 ![]() m-band gives a good fit in the case of NGC 2023 and M17-SW (see Fig. 8).
m-band gives a good fit in the case of NGC 2023 and M17-SW (see Fig. 8).
At this point, it is interesting to note that that the 6-to-13 ![]() m part of the spectrum is produced by
molecules with emission temperatures between 400 and 1000 K. During temperature fluctuations,
most PAHs go through these temperatures:
this is why the maximum of the temperature distribution (Fig. 5) always falls in this range.
In fact, the emission of any PAH with
m part of the spectrum is produced by
molecules with emission temperatures between 400 and 1000 K. During temperature fluctuations,
most PAHs go through these temperatures:
this is why the maximum of the temperature distribution (Fig. 5) always falls in this range.
In fact, the emission of any PAH with
![]() shows ratios of band
peak values which are quite comparable to the observed 6-13
shows ratios of band
peak values which are quite comparable to the observed 6-13 ![]() m AIB spectrum (see PJB and Draine & Li 2001).
On the other hand,
the match of the observed band position and width in the present data sample and in CAM-CVF spectra of similar
interstellar regions requires small molecules (see next section). However, taking into account the
full size distribution of PAHs will add emission mostly at 3.3
m AIB spectrum (see PJB and Draine & Li 2001).
On the other hand,
the match of the observed band position and width in the present data sample and in CAM-CVF spectra of similar
interstellar regions requires small molecules (see next section). However, taking into account the
full size distribution of PAHs will add emission mostly at 3.3 ![]() m (from the smaller species, see Fig. 6b) and in the far-infrared
(from the larger species, see Fig. 6a) without changing much the 6-13
m (from the smaller species, see Fig. 6b) and in the far-infrared
(from the larger species, see Fig. 6a) without changing much the 6-13 ![]() m region. Thus, in the framework of the present
model, the observed invariance of the AIB spectrum in CAM-CVF data (6-16
m region. Thus, in the framework of the present
model, the observed invariance of the AIB spectrum in CAM-CVF data (6-16 ![]() m) implies that the AIB
carriers are small enough to undergo large temperature fluctuations (at least 400 K) during which
they emit in this wavelength range.
m) implies that the AIB
carriers are small enough to undergo large temperature fluctuations (at least 400 K) during which
they emit in this wavelength range.
Our best fit SED's are displayed in Fig. 7: we assumed a total column density of
![]() cm-2 (i.e. , 1 visible magnitude of extinction) for both NGC 2023 and M17-SW with
10% and 8%, respectively of the interstellar carbon in PAH cations (using [C/H]
cm-2 (i.e. , 1 visible magnitude of extinction) for both NGC 2023 and M17-SW with
10% and 8%, respectively of the interstellar carbon in PAH cations (using [C/H]
![]() ,
Snow & Witt 1996). The hydrogenation fraction of PAHs was taken to be 80% for NGC 2023 and 50% for M17-SW.
To compare in a meaningful fashion the predicted PAH emission to the observed spectrum, the broadband continuum described
in Sect. 3 has been added to our model spectrum. This continuum consists of the modified blackbody along with
the 1000 and 1450 cm_1 broad profiles (in M17-SW an additional broad profile at 600 cm_1 is required,
see Fig. 2). All the main AIBs (at 3.3, 6.2, 7.7, 8.6 and 11.3
,
Snow & Witt 1996). The hydrogenation fraction of PAHs was taken to be 80% for NGC 2023 and 50% for M17-SW.
To compare in a meaningful fashion the predicted PAH emission to the observed spectrum, the broadband continuum described
in Sect. 3 has been added to our model spectrum. This continuum consists of the modified blackbody along with
the 1000 and 1450 cm_1 broad profiles (in M17-SW an additional broad profile at 600 cm_1 is required,
see Fig. 2). All the main AIBs (at 3.3, 6.2, 7.7, 8.6 and 11.3 ![]() m) are matched within 20%.
We note that the model fails to reproduce the 12.7
m) are matched within 20%.
We note that the model fails to reproduce the 12.7 ![]() m-band in M17-SW: this may be due to an ill-definition of the
underlying broadband continuum in this complex spectral region (see Fig. 2).
The AIB spectrum corresponding to the neutral
PAHs (we took the IR cross-sections from Léger et al. 1989b) is shown in the case of NGC 2023 with a PAH
abundance corresponding to 6% of the interstellar carbon, with
m-band in M17-SW: this may be due to an ill-definition of the
underlying broadband continuum in this complex spectral region (see Fig. 2).
The AIB spectrum corresponding to the neutral
PAHs (we took the IR cross-sections from Léger et al. 1989b) is shown in the case of NGC 2023 with a PAH
abundance corresponding to 6% of the interstellar carbon, with
![]() ,
,
![]() and
and
![]() .
The
.
The ![]() -value was fixed so as to reproduce the position and width of the 3.3
-value was fixed so as to reproduce the position and width of the 3.3 ![]() m-band (see next section)
and it is the same as for the cations.
In the case of neutral PAHs, the C-C/C-H band ratio is reduced by about one order
of magnitude with respect to the cations. Matching the observed AIB with neutral PAHs would require a very low
hydrogen coverage (
m-band (see next section)
and it is the same as for the cations.
In the case of neutral PAHs, the C-C/C-H band ratio is reduced by about one order
of magnitude with respect to the cations. Matching the observed AIB with neutral PAHs would require a very low
hydrogen coverage (
![]() )
which would produce a strongly discrepant 8.6
)
which would produce a strongly discrepant 8.6 ![]() m-band and also would be at
odds with theoretical predictions on the hydrogen coverage of PAHs (Allain et al. 1996).
m-band and also would be at
odds with theoretical predictions on the hydrogen coverage of PAHs (Allain et al. 1996).
In the following,
we compare in detail the profiles of the observed 3.3, 6.2, 8.6 and
11.3![]() m-AIBs to our model results: we restrict our comparison to these bands
because they are well defined in the data and involve a small number of Lorentz fit
components.
m-AIBs to our model results: we restrict our comparison to these bands
because they are well defined in the data and involve a small number of Lorentz fit
components.
In order to highlight the match in band width and position,
our model profiles are compared to the observed AIBs in a normalized fashion.
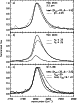 |
Figure 8:
The normalized profile of the 3.3 |
| Open with DEXTER | |
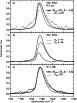 |
Figure 9:
Same as Fig. 8 for the 6.2 |
| Open with DEXTER | |
Figures 8 to 11 show our model representation of the AIB profiles. The contribution of vibrational
hot bands are not included in our model profiles: in the case of the 6.2 and 11.3 ![]() m-bands, hot
bands provide an additional broadening of less than 5 cm_1 (PJB).
In Fig. 8c, we note the effect of making the
m-bands, hot
bands provide an additional broadening of less than 5 cm_1 (PJB).
In Fig. 8c, we note the effect of making the
![]() -approximation
(i.e., all molecules are heated
by photons of the
same energy
-approximation
(i.e., all molecules are heated
by photons of the
same energy
![]() ,
see Sect. 4.3): the lack of the hot tail in the PAH temperature distribution yields a
narrower band profile. Hence, using this approximation would lead to an underestimate of
,
see Sect. 4.3): the lack of the hot tail in the PAH temperature distribution yields a
narrower band profile. Hence, using this approximation would lead to an underestimate of
![]() :
e.g., in the case of NGC 2023,
:
e.g., in the case of NGC 2023,
![]() is required to match the observed 3.3
is required to match the observed 3.3 ![]() m-band if one
makes the
m-band if one
makes the
![]() -approximation.
This approximation has, however, negligible consequences for the other bands.
The effect of a larger
-approximation.
This approximation has, however, negligible consequences for the other bands.
The effect of a larger ![]() ,
-2.25 (corresponding to the classical power-law exponent of -3.5 when the size
distribution is expressed in terms of the grain radius,
Mathis et al. 1977) is shown as the dashed line in Figs. 8a to 11a: a low
,
-2.25 (corresponding to the classical power-law exponent of -3.5 when the size
distribution is expressed in terms of the grain radius,
Mathis et al. 1977) is shown as the dashed line in Figs. 8a to 11a: a low ![]() -value is
clearly required to match the observed band profiles. Decreasing
-value is
clearly required to match the observed band profiles. Decreasing ![]() ,
however, has a moderate impact
on the band profiles because the then enhanced contribution of small molecules
is compensated by a strong increase of the band width leading to a decrease in intensity
(the integrated cross-sections of the IR bands,
,
however, has a moderate impact
on the band profiles because the then enhanced contribution of small molecules
is compensated by a strong increase of the band width leading to a decrease in intensity
(the integrated cross-sections of the IR bands,
![]() ,
are assumed to be conserved
with temperature).
,
are assumed to be conserved
with temperature).
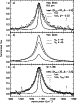 |
Figure 10:
Model results for the 8.6 |
| Open with DEXTER | |
The harder radiation field of M17-SW results in PAHs at higher temperatures
(see Fig. 5d), consequently the model AIB-profiles are clearly too broad and redshifted
(see the dashed line in the bottom panel of Figs. 8 to 11) if we use the same size distribution
as for NGC 2023. For the profile width and position,
![]() is also required in
order to match the observed AIBs of M17-SW. This change of
is also required in
order to match the observed AIBs of M17-SW. This change of ![]() has a physical
interpretation: the photo-dissociation and fragmentation rates rise steeply
with the molecular temperature (Léger et al. 1989a). The
has a physical
interpretation: the photo-dissociation and fragmentation rates rise steeply
with the molecular temperature (Léger et al. 1989a). The ![]() values we find are smaller than the theoretical predictions of Allain et al. (1996).
values we find are smaller than the theoretical predictions of Allain et al. (1996).
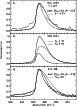 |
Figure 11:
Same as Fig. 9 for the 11.3 |
| Open with DEXTER | |
Except for the 8.6 ![]() m-band, all AIB profiles are well explained by the PAH emission model.
The hot (small) molecules dominate the emission profiles, in particular in the AIB wings;
they also produce the observed red asymmetry (6.2 and 11.3
m-band, all AIB profiles are well explained by the PAH emission model.
The hot (small) molecules dominate the emission profiles, in particular in the AIB wings;
they also produce the observed red asymmetry (6.2 and 11.3![]() m-bands). The cool (large) molecules
contribute the blue wing of the AIB. We want to stress that this match of the AIBs is obtained
by using the cross-sections and profile temperature dependence measured on small molecules: no
additional broadening, reflecting the decrease of the level lifetime with increasing
molecular size (see Sect. 5), has been taken into account here.
m-bands). The cool (large) molecules
contribute the blue wing of the AIB. We want to stress that this match of the AIBs is obtained
by using the cross-sections and profile temperature dependence measured on small molecules: no
additional broadening, reflecting the decrease of the level lifetime with increasing
molecular size (see Sect. 5), has been taken into account here.
The observed width of the 8.6 ![]() m-band is not at all reproduced by the temperature broadening
law derived from laboratory work. In fact, a broadening 5.5 times faster (
m-band is not at all reproduced by the temperature broadening
law derived from laboratory work. In fact, a broadening 5.5 times faster (
![]() cm_1/K) with temperature would match the observations (see Fig. 10). In this latter case,
we note that (i) the symmetrical shape of the 8.6
cm_1/K) with temperature would match the observations (see Fig. 10). In this latter case,
we note that (i) the symmetrical shape of the 8.6 ![]() m-band is well explained by the slow
redshift of the band centroid with temperature (
m-band is well explained by the slow
redshift of the band centroid with temperature (
![]() cm_1/K whereas the other
AIBs have 2 to
cm_1/K whereas the other
AIBs have 2 to
![]() cm_1/K) and (ii) the emission of large molecules dominates the
core of the 8.6
cm_1/K) and (ii) the emission of large molecules dominates the
core of the 8.6 ![]() m-band (conversely to the other AIBs).
m-band (conversely to the other AIBs).
We have not modelled the 7.7 ![]() m-band because it includes several components whose assignment
to features in laboratory spectra of PAHs is not straightforward. However, it is interesting
to note that the observed width (23 to 29 cm_1) of the 7.6
m-band because it includes several components whose assignment
to features in laboratory spectra of PAHs is not straightforward. However, it is interesting
to note that the observed width (23 to 29 cm_1) of the 7.6 ![]() m-band (see Sect. 3) is comparable
to the width predicted by PJB.
m-band (see Sect. 3) is comparable
to the width predicted by PJB.
We emphasize here that the model profile of a PAH emission band is the result of the superposition
of many Lorentz profiles conversely to the implicit assumption behind the decomposition performed in Sect. 3.
Consider for instance a PAH containing ![]() carbon atoms which has been heated
by a photon of energy
carbon atoms which has been heated
by a photon of energy ![]() :
the emerging band profile of this molecule will be the sum
of all the Lorentz profiles corresponding to the temperatures of the cooling curve,
:
the emerging band profile of this molecule will be the sum
of all the Lorentz profiles corresponding to the temperatures of the cooling curve,
![]() (i.e. , the time integral in Eq. (3)). The total band profile of a PAH interstellar population is eventually
obtained from the weighted sum of the emerging band profiles from all molecules, for all energies of the
exciting photon (see Eqs. (3) and (5)).
(i.e. , the time integral in Eq. (3)). The total band profile of a PAH interstellar population is eventually
obtained from the weighted sum of the emerging band profiles from all molecules, for all energies of the
exciting photon (see Eqs. (3) and (5)).
This spectral decomposition, which separates the AIB emission from the underlying continuum, allowed us to do a detailed comparison
of the observed AIB spectrum with the predictions of the PAH model where the AIB carriers are free-flying aromatic molecules
emitting during temperature fluctuations.
This model uses recent laboratory data and assumes that PAHs are predominantly in cationic form as is expected from
theoretical work (Bakes & Tielens 1994; Dartois & d'Hendecourt 1997).
Within this framework, the position and width of the AIBs are rather explained by a redshift and a broadening of the PAH
vibrational bands as the temperature of the molecule increases (Joblin et al. 1995).
The observed similarity in the AIB profiles thus requires that some process
renders the temperature distribution of PAHs rather constant in the interstellar
regions considered here.
We first derived the temperature distribution
for a population of interstellar PAHs. In particular, we show that the hot tail of the temperature distribution
of PAHs (which determines the AIB spectrum) depends sensitively on ![]() and
and
![]() which are respectively the size of the smallest PAH (in terms of the number of C-atoms in the
molecule) and the effective temperature of the exciting radiation field.
The size of the largest PAH,
which are respectively the size of the smallest PAH (in terms of the number of C-atoms in the
molecule) and the effective temperature of the exciting radiation field.
The size of the largest PAH, ![]() (by number of C-atoms), and the index of the power law
size distribution (expressed in terms of the number of C-atoms per molecule),
(by number of C-atoms), and the index of the power law
size distribution (expressed in terms of the number of C-atoms per molecule), ![]() ,
were found to have little
impact on the overall AIB emission.
,
were found to have little
impact on the overall AIB emission.
We compared our model results to the data in the two extreme
cases of our sample: NGC 2023 (
![]() K) and M17-SW (
K) and M17-SW (
![]() K). We are able
to reproduce the spectral distribution of the AIB emission with
K). We are able
to reproduce the spectral distribution of the AIB emission with
![]() in NGC 2023 and
in NGC 2023 and
![]() in M17-SW and a PAH abundance amounting to 10 and 8% of the interstellar carbon (these latter values are in good agreement with
the constraints set by the extinction curve,
Joblin et al. 1992; Verstraete et al. 1992; and the infrared
emission, Désert et al.
1990. An abundance twice as high is required in the case of the cold
interstellar medium, Dwek et al. 1997). The minimum PAH size
in M17-SW and a PAH abundance amounting to 10 and 8% of the interstellar carbon (these latter values are in good agreement with
the constraints set by the extinction curve,
Joblin et al. 1992; Verstraete et al. 1992; and the infrared
emission, Désert et al.
1990. An abundance twice as high is required in the case of the cold
interstellar medium, Dwek et al. 1997). The minimum PAH size ![]() was found from the requirement that the observed 3.3/11.3
was found from the requirement that the observed 3.3/11.3 ![]() m-band
be well matched.
This change in
m-band
be well matched.
This change in ![]() may reflect the enhanced photodestruction rate of small PAHs
in regions with harder radiation fields (small PAHs reach higher temperatures and evaporate efficiently).
Using the same
may reflect the enhanced photodestruction rate of small PAHs
in regions with harder radiation fields (small PAHs reach higher temperatures and evaporate efficiently).
Using the same ![]() -values, we find that all AIB profile shapes,
except for the 8.6
-values, we find that all AIB profile shapes,
except for the 8.6 ![]() m-band, can be explained with the temperature dependence of the
band position and width measured in the laboratory. We also show that the PAH size distribution must be very
steep (
m-band, can be explained with the temperature dependence of the
band position and width measured in the laboratory. We also show that the PAH size distribution must be very
steep (
![]() )
in order to account for the observed bandwidths: in our model representation, the AIB profiles
are thus mostly contributed to by small PAH species.
The case of the 8.6
)
in order to account for the observed bandwidths: in our model representation, the AIB profiles
are thus mostly contributed to by small PAH species.
The case of the 8.6 ![]() m-band is anomalous:
first, the laboratory cross-section is 3 times too weak to explain the observed AIB ratios;
in addition, we find that the broadening of this band with the temperature should be 5.5 times
faster in order to match the profile width seen in the SWS data. More laboratory work is required
to explain this issue.
m-band is anomalous:
first, the laboratory cross-section is 3 times too weak to explain the observed AIB ratios;
in addition, we find that the broadening of this band with the temperature should be 5.5 times
faster in order to match the profile width seen in the SWS data. More laboratory work is required
to explain this issue.
In summary, using the present best knowledge of PAH spectroscopy, it is possible
to account for the AIB spectrum towards bright interstellar objects where the
fraction of singly-ionized PAHs is high. We emphasize that both the spectral shape
of the AIB spectrum as well as the individual AIB shapes are explained
consistently with a single set of parameter (![]() and
and ![]() )
values.
In this context, the remarkable stability of the AIB profiles arises if the
hot tail of the PAH temperature distribution remains essentially the same,
whatever the exciting radiation field (the low-temperature side corresponding
to the larger molecules is practically unaffected by changes in the radiation
field). This requirement is naturally met while considering the photodestruction
of PAHs: when the energy per bond (which is directly proportional to the
molecular temperature) is sufficient the molecule efficiently loses its atoms.
A consequence of this is that interstellar PAHs would predominantly be destroyed
by thermal evaporation (photo-thermo-dissociation, see Léger et al. 1989a) rather
than non-equilibrium processes like direct photodissociation (Buch 1989) or
Coulomb explosion (Leach 1989).
)
values.
In this context, the remarkable stability of the AIB profiles arises if the
hot tail of the PAH temperature distribution remains essentially the same,
whatever the exciting radiation field (the low-temperature side corresponding
to the larger molecules is practically unaffected by changes in the radiation
field). This requirement is naturally met while considering the photodestruction
of PAHs: when the energy per bond (which is directly proportional to the
molecular temperature) is sufficient the molecule efficiently loses its atoms.
A consequence of this is that interstellar PAHs would predominantly be destroyed
by thermal evaporation (photo-thermo-dissociation, see Léger et al. 1989a) rather
than non-equilibrium processes like direct photodissociation (Buch 1989) or
Coulomb explosion (Leach 1989).
These results must however be placed in the broader context of ISO
observations which include less irradiated regions (![]() to 1000).
Indeed, ISOCAM-CVF and ISOPHOT-S spectra of faint AIB emission
highlight the pre-requisites of this work. Namely, two strong assumptions have
been made in the present model:
to 1000).
Indeed, ISOCAM-CVF and ISOPHOT-S spectra of faint AIB emission
highlight the pre-requisites of this work. Namely, two strong assumptions have
been made in the present model:
We have assumed that PAHs are all singly ionized (cations) throughout our
data sample. Such a choice is required to reproduce the observed
band ratios, in particular the C-H/C-C ratio (Langhoff 1996; Allamandola et al. 1999).
Yet, this requirement is not fully consistent with theoretical predictions (Dartois et al.
1997) of the PAH ionized fraction along our lines of sight, namely, 0.5 (50% of PAHs are
cations). Furthermore, this problem becomes even more acute in the context of other
observations spanning a broader range of physical conditions: ISOCAM-CVF and ISOPHOT-S
data (Boulanger et al. 1998a, 1999;
Chan et al. 2000; Miville-Deschênes et al. 1999;
Onaka et al. 1999, 2000, Onaka 2000;
Uchida et al. 1998, 2000) obtained
towards regions with ![]() = 1 to 105 (from the diffuse interstellar medium to
H II region interfaces and reflection nebulae) show that the C-H/C-C ratio of the AIBs is
roughly constant and always corresponds to that of PAH cations. Over such a large range of UV
radiation flux, the state of PAHs is actually
expected to change from fully neutral to fully ionized. The ionized fraction of PAHs
is determined by the value of
= 1 to 105 (from the diffuse interstellar medium to
H II region interfaces and reflection nebulae) show that the C-H/C-C ratio of the AIBs is
roughly constant and always corresponds to that of PAH cations. Over such a large range of UV
radiation flux, the state of PAHs is actually
expected to change from fully neutral to fully ionized. The ionized fraction of PAHs
is determined by the value of
![]() with T the gas temperature and
with T the gas temperature and ![]() the electron density (this parameter is proportional to the
ratio of the ionization rate to the recombination rate of PAHs, Bakes & Tielens 1994).
To keep the AIB band ratios constant, and hence the ionized fraction of PAHs, requires that
the ratio
the electron density (this parameter is proportional to the
ratio of the ionization rate to the recombination rate of PAHs, Bakes & Tielens 1994).
To keep the AIB band ratios constant, and hence the ionized fraction of PAHs, requires that
the ratio
![]() can vary over five orders of magnitude in order to compensate the
variation of
can vary over five orders of magnitude in order to compensate the
variation of ![]() .
In reality, T probably does not change by more than 2 orders of
magnitudes: then
.
In reality, T probably does not change by more than 2 orders of
magnitudes: then ![]() ,
which reflects the density variations mostly, would
have to vary by three orders of magnitude across the regions observed to keep
,
which reflects the density variations mostly, would
have to vary by three orders of magnitude across the regions observed to keep ![]() constant.
Such large density contrasts at large scale are
at odds with what is currently known of the structure of these interstellar regions.
constant.
Such large density contrasts at large scale are
at odds with what is currently known of the structure of these interstellar regions.
More generally, the predicted strong variability of the physico-chemical state (ionization,
dehydrogenation) of PAHs in space is not reflected in the recent ISO spectroscopy database which covers
a variety of astrophysical conditions. This prediction was based on studies of small
PAHs (
![]() ), the only species currently accessible for investigation either in the
laboratory or with quantum chemistry.
As shown by Schutte et al. (1993), the 6 to 16
), the only species currently accessible for investigation either in the
laboratory or with quantum chemistry.
As shown by Schutte et al. (1993), the 6 to 16 ![]() m-AIB spectrum
is also contributed to by large PAHs (
m-AIB spectrum
is also contributed to by large PAHs (
![]() )
while the 3.3
)
while the 3.3 ![]() m-AIB is
dominated by the smallest species (
m-AIB is
dominated by the smallest species (
![]() ,
see Fig. 8): this other solution (large "PAHs''
or carbon clusters) to the 6 to 16
,
see Fig. 8): this other solution (large "PAHs''
or carbon clusters) to the 6 to 16 ![]() m-AIB spectrum may alleviate the present difficulties. However, the
spectroscopical and structural properties of carbon clusters are poorly known at present: the ISO
spectroscopic database is ideally suited to identify plausible candidates and stimulate future work on
the physics and chemistry of carbon clusters.
m-AIB spectrum may alleviate the present difficulties. However, the
spectroscopical and structural properties of carbon clusters are poorly known at present: the ISO
spectroscopic database is ideally suited to identify plausible candidates and stimulate future work on
the physics and chemistry of carbon clusters.
Acknowledgements
We are grateful to François Boulanger, Alain Abergel, Christine Joblin and Anthony Jones for many stimulating discussions and our referee for helpful comments. We also thank the MPE-SDC (Garching) and the DIDAC (Groningen) for their constant support in the data reduction phase and with the use of SWS-IA3. SWS-IA3 is a joint developement of the SWS consortium. Contributing institutes are SRON, MPE, KUL and the ESA Astrophysics division. K. S. gratefully acknowledges support from a NATO collaborative Research Grant nr. 951347.