A&A 372, 1005-1018 (2001)
DOI: 10.1051/0004-6361:20010280

On the relation between total irradiance and radius variations

J. Pap 1,[*] - J. P.  Rozelot 2 - S.  Godier 2 - F.  Varadi 3


1 - Department of Physics and Astronomy, University of California, Los Angeles, 405 Hilgard Ave., Los Angeles, CA 90095, USA
2 - OCA/CERGA, Avenue Copernic, 06130 Grasse, France
3 - UCLA, Department of Physics, 90095-1562, Los Angeles, USA

Received 29 August 2000 / Accepted 18 January 2001

Abstract
We use Singular Spectrum Analysis (SSA) to analyze total solar irradiance variations and CERGA radius measurements. Total solar irradiance has been monitored from space for more than two decades, whilst ground-based radius measurements are available as a coherent time series from 1975. We compare these indicators to try to understand the origin of energy production inside the Sun. One of the main objectives was to assess the reality of the observed variations of the Sun's radius by distinguishing the signal from the noise. Two approaches were used: one using SSA on ground-based data averaged over 90 days, in order to smooth the signal (especially over periods when no data were obtained, mainly in winter time); the second repeats the analysis on individual measurements corrected by reporting data to the zenith. As expected, the level of noise is higher in the first case and the reconstructed noise level, which is large, indicates the difficulty in ascertaining the solar origin in the apparent variability of the solar radius. It is shown from the reconstructed components that the main variation in amplitude (over 930 days) is pronounced during the first part of the measurements and seems to disappear after 1988. There is also a variation with a periodicity of 1380 days, of lower amplitude than that of the shorter component. In both cases, these variations disappear during the rising portion of cycle 23. The first reconstructed component shows that total irradiance varies in parallel with the solar cycle, being higher during maximum activity conditions. The reconstructed radius trend indicates that the solar radius was higher during the minimum of solar cycle 21, but its decrease with the rising activity of cycle 23 is less obvious. The observed value of the solar radius increased by about 0.11 arcsec from the maximum of cycle 21 to the minimum between cycles 21 and 22. Most importantly, we report a long-term radius variation which increased from the maximum of cycle 21 to minimum by about 0.015%, while a smaller decrease (around 0.01%) is seen from the minimum of cycle 21 to the maximum of cycle 22. This study indicates need for measurements of the degree of the radius changes taken from space, together with total irradiance measurements to establish the phase relation between these two quantities.

Key words: Sun: general - Sun: fundamental parameters


1 Introduction

Study of the Sun's variability is of interest for both astrophysics and solar-terrestrial physics. The Sun - a fairly typical star - has the special advantage of proximity, which allows the detailed study of a variety of important phenomena. Furthermore, the total radiative output of the Sun establishes the Earth's radiation environment and influences its temperature and atmospheric composition. Recent studies indicate that small but persistent variations in solar energy flux may play an important role in climate changes (e.g. Hansen et al. 1981; Reid 1991; Sofia 1998; Rozelot 2001), for example, during the Maunder-type minima, the exceptionally low sunspot activity coincided with cold periods of Little Ice Ages in Europe and the Atlantic Region (e.g., Eddy 1997). Although the ultimate source of the solar energy is the nuclear reactions taking place in the center of the Sun, the immediate source of energy is the solar surface. The nuclear reactions are almost certainly constant on time scales shorter than millions of years, but the mechanisms which carry the energy to the solar surface may not be. Indeed, observations of the solar radiation integrated over the entire solar spectrum (total irradiance), obtained by space-based experiments over the last two decades, have demonstrated that total irradiance varies on time scales of minutes to the 11-year solar cycle (Willson & Hudson 1991). If the central energy source remains constant while the rate of energy emission from the surface varies, there must be an intermediate reservoir where the energy can be stored or released depending on the variable rate of energy transport. The gravitational field of the Sun is one such energy reservoir. If the energy is stored in this energy reservoir, it will result in a change in the solar radius (Pap et al. 1998). Thus, a careful determination of the time dependence of the solar radius can provide a constraint on models of total irradiance variations (e.g. Lydon & Sofia 1995). For example, a radius change of 0.06'' would be sufficient to explain the long-term 0.1% variation in total irradiance (Sofia 1998). Therefore, it is particularly important to define the relation between total irradiance and radius variations. Historical observations of the solar radius over the last 300 years may provide an estimate of the past luminosity changes and their possible climate effects (Sofia et al. 1979). In this paper we compare the long-term composite total irradiance, compiled by Fröhlich & Lean (1998), with the radius measurements which have been carried out at the Calern Observatory in South-East France since 1975 (Laclare et al. 1996).

2 Total Irradiance and radius measurements

2.1 Description of the total irradiance measurements

The total rate of the electromagnetic energy crossing a unit area above the Earth's atmosphere at 1 AU distance from the Sun is called the "solar constant", a concept introduced in the last century. The first measurements of direct solar radiation were performed by Pouillet in 1837. Continuous observational programs of total irradiance to detect its variability started at the beginning of this century, first from high altitude mountain stations, and later from balloons and aircraft. The first attempts to measure total irradiance above the Earth's atmosphere were made in the sixties from rockets and the Mariner space probes. However, these early measurements were inconclusive and could not reveal real solar changes in total irradiance because of the lack of radiometric precision and the selective absorption of the terrestrial atmosphere (Fröhlich 1977). Considerable improvement in radiometry took place in the sixties, when a new generation of radiometers, the so-called electrically self-calibrating active cavity radiometers, were developed in various US and European institutes. The absolute accuracy of these radiometers is about $\pm $0.2%; the precision and stability of the instruments, however, is much better, which makes it possible to study the relative variations in total irradiance. In addition to improvements in radiometry, long-term flight opportunities from various satellite platforms have made it possible to monitor total solar irradiance above the Earth's atmosphere since the late seventies. The first and longest high precision total irradiance monitoring program from space was carried out by the "Earth Radiation Budget" (ERB) experiment on the Nimbus-7 satellite (Kyle et al. 1994). The "Active Cavity Radiometer Irradiance Monitor" (ACRIM) experiment was launched in February 1980 on the Solar Maximum Mission (SMM) satellite and was operated until November 1989 (Willson & Hudson 1991). The SMM/ACRIM I experiment was followed by the ACRIM II on the Upper Atmosphere Research Satellite (UARS), which was launched in September 1991 and is still operating as of this time (Willson 1997). The "Earth Radiation Budget Experiment" (ERBE) on the ERBS satellite has been providing an additional total irradiance data set since October 1984 (Lee et al. 1995). The "SOlar VAriability" (SOVA) experiment on board the EUropean REtrievable CArrier (EURECA, July 31, 1992 to June 1993), consisted of two different types of absolute radiometers, the "Differential Dual Absolute Radiometer" (DIARAD) and the PMO-6 type of absolute radiometer (Crommelynck et al. 1994; Romero et al. 1994). The "Variability of solar IRradiance and Gravity Oscillations" (VIRGO) experiment on the SOlar Heliospheric Observatory (SOHO) carried two radiometers (DIARAD and PMO6-V) and provided another important segment of the long-term total irradiance data base since January 1996 (Fröhlich et al. 1997). Based on the Nimbus-7/ERB, SMM/ACRIM I, UARS/ACRIM II, and SOHO/VIRGO measurements, Fröhlich & Lean (1998) compiled a "composite" total irradiance, taking into account all possible corrections for the measurements. The various total irradiance measurements are summarized in Fig. 1. The different scale of these measurements is related to the absolute accuracy ($\pm $0.2%) of the calibration of the individual measurements. These space observations established conclusively that the value of the solar "constant" is not constant, rather, it changes over a wide range of periodicities: from minutes to the 11-year solar cycle. The most important discovery of these satellite-based measurements is that total irradiance varies with about 0.1% over the solar cycle, being higher during maximum activity conditions (Willson & Hudson 1991). A major portion of this long-term variation is attributed to the changing emission of bright faculae and the magnetic network (e.g. Foukal & Lean 1988). Short-term variations on time scales of days to months are directly related to the evolution of active regions via the combined effect of sunspots and faculae (Willson et al. 1981; Chapman 1987; Fröhlich & Pap 1989). On time scales of minutes to hours, the effect of granulation, meso- and super-granulation is seen in the total irradiance, whereas in the 5-minute range the p-modes cause rapid irradiance fluctuations (Fröhlich et al. 1997).
  \begin{figure} \includegraphics[width=12cm,clip]{10232fig1.eps}\end{figure} Figure 1: Summary of total solar irradiance measurements (Fröhlich 1998).
Open with DEXTER

Although considerable information exists on total irradiance variations, the underlying physical mechanisms are not well-understood. It has been shown that empirical models of total irradiance, solely based on the surface manifestations of solar magnetic activity, cannot explain all the aspects of irradiance changes (Fröhlich & Pap 1989; Kuhn 1996; Fröhlich et al. 1997; Wehrli 1992). Identification of the causes of the residual variability in total irradiance, which is not explained by the effect of sunspots, faculae, and the magnetic network, is a difficult problem since global effects may also produce variations in total irradiance. It has been shown that changes in the differential rotation in the interior of the Sun, the solar dynamo magnetic field near the base of the convective zone (Kuhn 1996, 1998), photospheric temperature changes (Kuhn et al. 1988), large scale missing flows or large scale convective cells (Ribes et al. 1985; Fox & Sofia 1994) and/or radius changes (Delache et al. 1985; Ulrich & Bertello 1995; Kuhn et al. 1985, 1988; Godier & Rozelot 2000) may also contribute to irradiance variations. Therefore, simultaneous studies of total irradiance and solar global parameters are essential to better understand the underlying physical mechanism of irradiance changes and to predict solar-induced climate changes.

2.2 Early measurements of the solar diameter

The first measurements of the solar diameter were carried out by Aristarque from Samos, approximately 350 years BC, and at the end of the Renaissance, by J. Kepler in 1609 and by J. Horrocks - an English astronomer - in 1619. In the 17th century, J. Picard, P. La Hire and T. Mayer collected a great number of measurements that allow us to make a posteriori statistical computations and therefore permit one to determine the uncertainty of these measurements. Picard carried out approximately 450 observations: 154 from 1666 to 1681, by the method of the passage to the meridian at the Observatory of Paris and 304 from 1670 to 1673, with the help of a filar micrometer. La Hire carried out some 6800 observations (from 1683 to his death in 1718) and Mayer 137 (105 of which were kept for analysis, from 1756 to 1761). Observations of Picard and La Hire can be consulted at the Record Office of the Paris Observatory (manuscript D1, 14 to 16 and D-2, 1 to 10), while those of Mayer have already been published (Wittman 1990). These sets of observations constitute the bulk of what is known on solar radius variations during that time interval and are today considered as the first astrometric measurements. Additional measurements that cannot be completely disregarded are available from other observers who are not considered as pioneers in precision astronomy. Since we are able to compute with some accuracy the orbital elements of the Sun (such as the declination) for these past observations, it is possible to estimate some of the biaises which may have affected the measurements. For example, refraction effects leading to a systematic diminution of the observed solar diameter. During the 17th century, and then during the 19th, the measurements, although still subject to caution, became more reliable, not only due to technical progress but also to the ability of the observers to characterize their measurements by their necessary uncertainties. From solar eclipse observations, Fiala et al. (1994), were able to determine values of the solar radius from 1715 to the present. Results of these historical observations are shown in Fig. 2.
  \begin{figure} \includegraphics[width=12.5cm,clip]{10232f2.eps}\end{figure} Figure 2: Summary of radius measurements from the time of the Maunder Minimum. These radius measurements, covering a long time interval, suggests that the Sun may have been larger during its exceptionally low magnetic activity during the Maunder Minimum. Triangles represent the Fiala et al. (1994) determinations of the solar radius deduced from eclipse observations.
Open with DEXTER

The analysis of these historical radius measurements shows that the solar diameter was systematically larger during the years 1660-1720, as already pointed out by Ribes et al. (1987, 1993). Obviously, these measurements remain open to criticism (see for instance O'Dell & Van Helden 1987). A very careful analysis of these observations shows that uncertainties do not exceed 3''. From Fig. 2 it can be seen that the average, which is $960.7'' \pm 0.1''$, permits the placing of all the measurements made during that time above this level, whilst the modern measurements are below. This implies that the Sun was bigger during the so-called Maunder Minimum, a fact generally accepted as the "Secchi law", which stipulates that an active Sun has a smaller diameter, and vice versa. However, it is still not possible to say with confidence whether the observed increase in the solar diameter is uniquely due to the suppressed solar magnetic activity at the time of the Maunder Minimum or if it is due to the uncertainty in the past measurements, or to other solar processes. Reconstruction of the solar irradiance during that time and comparison with the evolution of the solar radius also may help us to understand how the outer layers of the Sun react to alterations in flux. Furthermore, Fig. 2 suggests a general decreasing trend in the solar diameter of about 0.3 arcsec per century. This value is different from that found by Eddy & Bornazzian (1979), who claimed that the Sun was contracting at the rate of $0.1\%$, or one arcsec, in angular diameter per century, which is an unlikely, large value. However, this is a fundamentally important question since all observations support a negative secular trend (of about 0''1; Gilligand 1981), in contradiction with theories of stellar evolution, which predict a positive, albeit small, secular trend of the solar radius. Rather, Fig. 2 suggests the presence of a 120-year (or longer) modulation of amplitude of the solar radius (peak to peak max of 0.8 arcsec), suggesting that a few tenths of an arcsec variations of the solar radius on time scales of decades cannot be ignored.

2.3 The Danjon astrolabe radius measurements

The heritage

Visual measurements of the solar radius have been made for more than twenty years at the Calern Observatory (South-East France) using a visual Danjon astrolabe (Laclare et al. 1983). Several technical improvements were made to optimize the observations of the semi-diameter measurements. The number of zenithal angle observations was increased from one possibility per day in 1975 to eleven nowadays; in the near future, quasi-continuous observations will be possible. In 1986 a CCD camera was installed to reduce biaises arising from visual observations (Laclare & Merlin 1991). Both visual and CCD observations have been performed daily since then, and comparison of these measurements shows that they are consistent (Laclare et al. 1996). Other measurements of the semi-diameter of the Sun, based on the same principle of the solar astrolabe, have been performed in other places, such as Brazil and Chile (Jilinski et al. 1999; Noël 1997, 1998). In this paper we rely only on the CERGA measurements, as the observations were made by a single observer over a long period of time. Comparison of the CERGA radius measurements with those obtained in other observatories and with different measuring methods will be the subject of another paper.

The principle of the measurements
The Sun's semi-diameter is obtained by measuring the time of the transit of the edges of the solar limb through a fixed circle of altitude, using a reduction method described by Débarbat & Guinot (1970) and Kovalevsky (1997). The principle of the measurements is given in Fig. 3. Let C be a great circle on the celestial sphere for a given elevation above the horizon (named the almucantar). The Sun crosses C twice a day, before and after the meridian, so that two determinations of the semi-diameter of the Sun per day can be obtained, for the same parallel of altitude, which is defined in the instrument by the angle of the reflector prism used. Considering now only one transit, the Danjon-type astrolabe permits the observer to follow the motion of the Sun when it crosses the almucantar. A direct image of the Sun gives its motion on the celestial sphere, whereas a reflected image on a mercury bath (which visualizes the horizontal plane) gives its opposite movement. The procedure consists of timing the two points at which the upper edge (Sun in C1) and the lower one (Sun in C2) just cross the almucantar. In practise, the observer keeps the two images in contact by means of a micrometric screw, which compensates for the change of the zenith distance. The observed semi-diameter is given by the difference of the two zenith angles z1 and z2, and is then reduced to a constant distance of one astronomical unit. As pointed out by Chollet & Noël (1993) and Noël (1997), the accuracy of the results strongly depends on the stability of the instrumental zenith distance, on the stability of the filters used, and on the stability of the reference clock. These effects are negligible, as the prisms and filters are made in zero-expansion coefficient materials and as the time is given at the observatory with a higher precision than needed (the time is available to approximately one nanosecond; an accuracy of 0.1 millisecond is sufficient to determine the time at which a solar limb crosses the almuncatar). Three other corrections are required: the focal plane position, the curvature of the declination and altitude parallels, and the attitude of the reflector prism edge, which should be in the horizontal plane. These three corrections are discussed by Laclare et al. (1996); the two first terms have no systematic character and are less than 0.05 arcsec; the third one can reach 0.3 arcsec. All parameters which are necessary for the corrections are evaluated during the observations.
  \begin{figure} \includegraphics[width=6.5cm,clip]{10232f3_new.eps}\end{figure} Figure 3: Principle of the measurement of the Sun's radius by means of an astrolabe. The observed radius is the difference between the zenith distances of the upper and lower solar edges.
Open with DEXTER

It is often claimed that observations are not affected by atmospheric refraction, since the components of any model used to take into account refraction will be subtracted when taking the difference z1-z2. In fact, refraction affects the measurement of the radius, but only during the few minutes which separate the two crossings of the Sun's edge. Computations show that this effect is not completely negligeable, and can be taken into account, if necessary, by a curvilar interpolation using Lagrange polynomials (Noël 1997).
Analysis
From 1975 to 1978, only one prism was used ( $30\hbox{$^\circ$ }$); then $60\hbox{$^\circ$ }$ and $45\hbox{$^\circ$ }$ in 1978; $37.5\hbox{$^\circ$ }$ and $52.5\hbox{$^\circ$ }$ in 1983; $70\hbox{$^\circ$ }$ in 1984 followed by a set of 12 prisms today, i.e. $5\hbox{$^\circ$ }$, $30\hbox{$^\circ$ }$, $34\hbox{$^\circ$ }$, $37.5\hbox{$^\circ$ }$, $41.5\hbox{$^\circ$ }$, $45\hbox{$^\circ$ }$, $49\hbox{$^\circ$ }$, $52.50\hbox{$^\circ$ }$, $56.5\hbox{$^\circ$ }$, $60\hbox{$^\circ$ }$, $65\hbox{$^\circ$ }$ and $70\hbox{$^\circ$ }$. In this configuration up to 22 measurements per day can be performed that significantly reduces the dispersion for a given day. In the future, these fixed prisms will be replaced by a prism of variable angle, so that nearly continuous measurements will be possible. It is expected to increase the present scattering by nearly 1$\%$. Presently, scatter on about 50 averaged points is around 0.25'', with all zenithal angles merged, whereas the accuracy on individual points is about 0.04''. To maintain as homogeneous a data set as possible, it is desirable that visual measurements are carried out by the same observer. To avoid personal biases, the instrument has been equipped with a CCD camera since 1989. The process has been already described by Laclare & Merlin (1991), Irbah et al. (1994) and Sinceac (1998). Direct and reflected solar images are alternatively recorded. A sequence of about 100 images are obtained within 20 s (integration time of one image is 20 ms). The solar edge is reconstructed through a least-square fit of a parabola (an ellipse), and the inflection point is determined; the solar diameter is deduced from the time interval between the two solar limb transits. Such a process is more precise because the limb's shift can be accurately defined through a deconvolution of the theoretical limb profile of the Sun with atmospheric Fried functions of increasing parameter (which modelize the state of the atmosphere at the time of the observation, and thus permits determination of the seeing in real time, Rösch et al. 1996). The radius database used in this paper consists of 6.477 visual observations (from April 30, 1975 to December 31, 1998) made by the same observer (F. Laclare), distributed throughout the year, with some observational gaps mainly in winter time. Data for 1977 are missing, due to technical operations, so that our analysis starts on February 14, 1978 (only 114 days of observations are missing). More than 2.000 CCD measurements are also available, but they have not been incorporated into our analysis, as they are currently being used to validate the entire sequence of visual observations. The latitude of the observational site permits measurements of the diameter of the Sun only above 15 $\hbox{$^\circ$ }$ of heliographic latitude (whereas other astrolabes in operation in Brazil and Chile give access to equatorial diameters). Note that the mean value of the semi-diameter data obtained from visual measurements is 959.42 $\pm $ 0.01 arcsec (959.58 $\pm $ 0.05 arcsec after correction for the zenith distance effect), whereas CCD measurements yield an average of 959.40 $\pm $ 0.01 arcsec. Although these values are somewhat lower than the reference radius value (959.63 arcsec $\pm $ 0.10) as published in the "American Ephemeris'' or in "Connaissance des Temps'', our goal is to study the relative variations in the solar diameter instead of determining its absolute value.

3 Comparison of solar radius and total irradiance

In this study, we averaged the measurements made at several zenithal angles, for a given day, when such observations were available. A weighted running mean over 90-day periods was obtained, which smooths the periods of time where no data was obtained. To assign an error bar to a point which is a 90-days average, we can disregard as "noise" the variations present in the data, or we can assign to each point an error bar whose length is the standard deviation of a single observation divided by the square root of the number of added data. We took their inverse squares as weights in the above-mentionned "weighted running average". The general level of noise is slightly increased, as the quality of the results, mainly due to the seeing, is affected by the altitude of the observations (the lowest altitudes give poorest results). It would be better to correct each measurement by the zenithal function which can be determined only when sufficient data are available, which is just becoming the case now. This was done in the second step of this analysis: in that case, all solar data rather than mean values were used, each individual measurement being only corrected by reporting its value to the zenith.


  \begin{figure} \includegraphics[width=12.5cm,clip]{10232fig4.eps}\end{figure} Figure 4: The CERGA radius measurements for November 16, 1978 to December 31, 1998. This plot is compliant in dates with the composite solar irradiance. Data has been corrected for the zenith distance effect, i.e. reset to Zenith.
Open with DEXTER

The radius measurements used in our analysis are plotted in Fig. 4. Total irradiance varies in parallel with the solar activity cycle, being higher during maximum solar activity. Despite the apparent noise in the semi-diameter data, the CERGA solar diameter seems to show a small variation over the solar cycle, being higher during the solar minimum. In addition to long-term variation in the semi-diameter, Delache et al. (1986) reported variations with periodicities of about 1.800, 1.000, 300 and 120 days. Their analysis was carried out from only 1975 to 1984. One major problem in analyzing observed time series is the presence of gaps which make the detection of periodicities very difficult. The choice of a detection threshold is fundamental and frequencies in the power spectrum may appear which are not real. The origin of these variations is not yet understood; the major question is whether these are real variations related to solar effects or to other effects, such as changes in the atmospheric transparency and/or random fluctuations associated with the noise in the data.

To separate the possible intrinsic solar radius variations from other effects, it is necessary to compare the radius changes to other solar parameters, such as total irradiance. Furthermore, to understand the effect and contribution of various solar features to the radius changes, it is necessary to decompose the examined time series to their major oscillatory components and to separate these components from the noise in the signal. We note that for long, statistically stationary time series with relatively small noise, the traditional methods of time series analysis, such as Fourier Transforms, work well. However, measurements rarely satisfy all these requirements; most time series representing solar variability can be regarded as nonstationary signals with variable spectral properties, e.g., change of periods, amplitudes, and phases (Fröhlich & Pap 1989; Vigouroux & Delache 1993; Vigouroux et al. 1997). Therefore, to separate the possible intrinsic solar radius variations from other effects, we have applied a relatively new technique, "Singular Spectrum Analysis" (SSA, Vautard et al. 1992). The advantage of using SSA is that SSA performs as a data adaptive filter instead of using fixed basis functions, as in the case of Fourier transform or wavelet techniques, therefore, it is highly capable of distinguishing between the dominant and possibly nonlinear oscillations of the system and clarifying the noise characteristics of the data.

3.1 Description of time series analysis technique

Singular Spectrum Analysis (SSA) has been developed and applied to study and understand nonlinear and chaotic dynamical systems. SSA has been successfully used in nonlinear dynamics and in analyzing paleoclimatic and geophysical data sets and global temperature changes. Pap & Varadi (1996) applied SSA to study the effect of the evolution of active regions on total solar irradiance, and Pap (1997a,b) used SSA to study variations in total solar and UV irradiances. SSA is based on Principal Component Analysis in the time domain. The examined time series is augmented into a number of lagged time series up to a fixed value M, called the window length. The basis of SSA is the eigenvalue-eigenvector decomposition of the lag-covariance matrix which is composed of the covariances determined between the shifted time series. The eigenvectors of the lag-covariance matrix, the so-called temporal empirical orthogonal functions (T-EOFs), provide moving average filters which extract uncorrelated parts of the signal and whose contributions to the complete signal are given by the corresponding eigenvalues. Projection of the time series onto the T-EOFs yields the so-called principal components (PCs); these are filtered versions of the original time series. The T-EOFs are data adaptive analogs of sine and cosine functions and the PCs are the analogs of coefficients in Fourier analysis. The actual computation proceeds as follows. One takes the time series

\begin{displaymath}x_1, x_2, \ldots, x_N \end{displaymath}

of length N and generates a sequence of lagged time series. For zero lag we have

\begin{displaymath}x_1, x_2, \ldots, x_N, \end{displaymath}

for lag 1 we have

\begin{displaymath}x_2, x_3, \ldots, x_{N-1}, \end{displaymath}

and for lag l

\begin{displaymath}x_{1+l}, x_{2+l}, \ldots, x_{N-l+1}, \end{displaymath}

and so on up to

\begin{displaymath}x_M, x_{M+1}, \ldots, x_{N-M+1}. \end{displaymath}

Thus we have M number of time series. The lagged time series, of course, get shorter as the lag increases. Alternatively, one can assume that the time series is periodic with period N and fill the missing points in the lagged time series accordingly. Both approaches are used in SSA. The lagged-covariance at lag j can be estimated as

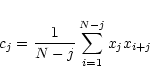
\begin{displaymath}c_j = \frac{1}{N-j} \sum_{i=1}^{N-j} x_j x_{i+j} \end{displaymath}

but there are other ways to do so (e.g., Vautard et al. 1992). The essence of SSA is to consider the matrix T, formed from the lagged covariances as

Tij = c|i-j|.

The matrix T is $M\times M$, symmetric and even Toeplitz. One diagonalizes T to obtain the T-EOFs

Ejk,

which are eigenvectors of T. Here k denotes the index of the eigenvector, j denotes coordinate, i.e., in matrix notation,

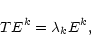
\begin{displaymath}T E^k = \lambda_k E^k, \end{displaymath}

where $\lambda_k$ is the eigenvalue corresponding to Ek. The Eks are orthogonal, i.e., for $k\neq l$,

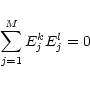
\begin{displaymath}\sum_{j=1}^{M} E^k_j E^l_j = 0 \end{displaymath}

and they are usually normalized to norm 1. The original time series can be projected to the T-EOFs by the formula, for the kth eigenvector Ek, as

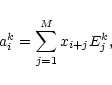
\begin{displaymath}a_i^k = \sum_{j=1}^{M} x_{i+j} E^k_j, \end{displaymath}

which is a filtered version of the original time series. These are the so-called Principal Components. The described process is data adaptive since Eks are not fixed, but they depend on the time series. The reconstructed components (RCs) are moving least squares projections of the time series onto T-EOFs. These are computed by complicated formulae which are, for a chosen subset $\cal A$ of eigenelements,

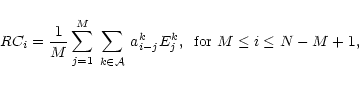
\begin{displaymath}RC_i = \frac{1}{M} \sum_{j=1}^{M} \sum_{\;k \in {\cal A}\;} a^k_{i-j} E^k_j ,\;\; {\rm for} \; M \leq i \leq N-M + 1, \end{displaymath}


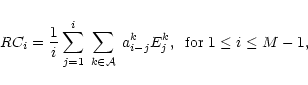
\begin{displaymath}RC_i = \frac{1}{i} \sum_{j=1}^{i} \sum_{\;k \in {\cal A}\;} a^k_{i-j} E^k_j ,\;\; {\rm for} \; 1 \leq i \leq M-1, \end{displaymath}


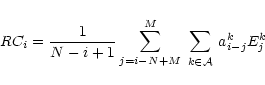
\begin{displaymath}RC_i = \frac{1}{N-i+1} \sum_{j=i-N+M}^{M} \sum_{\;k \in {\cal A}\;} a^k_{i-j} E^k_j \end{displaymath}

for $ \; N-M+2 \leq i \leq N $ (cf. Vautard et al. 1992). In our analyses we mostly used these components since they appear to have the easiest interpretations. The eigenvalue $\lambda_k$ determines what portion of the total variability is associated with the kth T-EOF Ek. These eigenvalues form the Singular Spectrum. They give valuable information about the noise characteristics of the data.
  \begin{figure} \includegraphics[width=8.8cm,clip]{10232fig5.eps}\end{figure} Figure 5: The Singular Spectra of total irradiance and radius are presented. The dots represent the composite total irradiance and the squares the radius.
Open with DEXTER

The original time series above the noise level and/or only parts of interest can be reconstructed as a projection to certain T-EOFs. These reconstructed components are usually associated with trends or with particular, possibly nonsinusoidal, oscillations. The window length M determines which components are resolved and which ones are reconstructed as part of the trend. To reconstruct strange attractors, a larger M is better, but to avoid statistical errors, the window length should be less than one third of the length of the investigated times series (Vautard et al. 1992).

  \begin{figure} \includegraphics[width=8cm,clip]{10232f6a.eps}\par\includegraphics[width=8cm,clip]{10232f6b.eps}\end{figure} Figure 6: The composite total solar irradiance and its first reconstructed component (upper panel) plotted together with the CERGA radius measurements (lower panel) and its first two SSA-reconstructed Components. The solid lines show the SSA reconstructed trend in total irradiance (RC1) and in the radius (RC's 1 and 2). By comparison the 5th degree polynomial fit is also indicated.
Open with DEXTER

3.2 Results

SSA has been applied to the composite total irradiance and for the radius for the time interval of November 16, 1978 to December 31, 1994 (running mean).The analysis was repeated for a longer time interval (1978 to 1998, covering both the maxima and minima of solar cycles 21 and 22), on reprocessed data corrected for the appropriate zenith distance of the particular measurement (as previously explained).

The window length was chosen as 400, considering the yearly gaps in the radius measurements, and was applied with the same window length to the composite total irradiance.

The SSA spectra of the radius and the composite total irradiance are plotted in Fig. 5, where the squares show the composite eigenvalues and the dots show the radius eigenvalues. While there are many oscillatory components above the noise level in the SSA spectrum of total irradiance, in the case of the radius one can identify only 6 significant components; the rest of the eigenvalues fall to the so-called noise floor. This exercise indicates the difficulty of radius measurements from the ground where they are highly affected by the changing atmospheric conditions.

In the case of the solar radius, the solid line in Fig. 6 shows the first two SSA-Reconstructed Components which represent the solar cycle trends in the data. In the case of total irradiance, the solar cycle trend is represented by the first reconstructed components (faint line). As can be seen, total irradiance varies in parallel with the solar cycle, being higher during maximum activity conditions. In contrast, the reconstructed radius trend indicates that the solar radius was higher during the minimum of solar cycle 21, but its decrease with the rising activity of cycle 23 is less obvious. The value of the solar radius increased by about 0.11 ($\pm $0.1) arcsec from the maximum of cycle 21 to the minimum between cycles 21 and 22. The long-term percentage radius variation is given in Fig. 7. As can be seen, the observed increase from the maximum of cycle 21 to minimum is about 0.015%, while a smaller decrease (around 0.01%) is seen from the minimum of cycle 21 to the maximum of cycle 22.

In addition to the first two components in the radius, which represent the solar cycle trends, we have reconstructed the 3rd, 4th, 5th and 6th components, respectively. RCs 3$\&$4 represent the variation of about 1.000 days, which is pronounced during the first part of the measurements but seems to disappear after 1988. RCs 5$\&$6 seem to represent a variation with about a 1.500 day periodicity; however, the amplitude of this variation is much smaller than that of the 1.000 day component. Note that in both cases, these variations disappear during the rising portion of cycle 23. It remains to be seen whether the lack of these periodicities during cycle 23 is related to real solar effects or additional effects (e.g. instrumental effects).

Finally, we have reconstructed the so-called "noise" of the radius data, as shown in Fig. 8. The noise was calculated from the eigenvectors of the eigenvalues in the noise level in the SSA spectrum. As this plot shows, the noise accounts for a considerable portion of the radius signal. This indicates the difficulty in distinguishing between real solar variability and measurement uncertainties in the current ground-based radius measurements. This underscores the necessity of developing more advanced instrumentation to detect small changes in solar diameter and the need for observing these small variations from space (which is free from atmospheric blurring and weather conditions, see also Kuhn et al. 1998). The forthcoming PICARD experiment (a microsatellite mission which is scheduled to be launched in 2005), and other proposed space experiments, such as SPHERIS, will hopefully determine the degree of the radius changes and their phase relation to irradiance variations. Knowledge of these quantities will lead to a better understanding of the physical mechanisms within the convective zone or below, which is essential for an understanding of the role of solar variability in long-term climate changes.


  \begin{figure} \includegraphics[width=8.8cm,clip]{10232f7.eps}\end{figure} Figure 7: The long-term radius variation in percentage from cycle 21 to rise of cycle 23 (2 first components, i.e. noise removed). From this figure, it can be deduced that the peak-to-peak value of the solar radius is less than 0.11 arcsec ($\pm $0.1), indicating a variability, albeit very weak, and less than that often quoted.
Open with DEXTER


  \begin{figure} \includegraphics[width=9.2cm,clip]{10232f8.eps}\end{figure} Figure 8: Reconstruction of the CERGA radius (RC's 1 to 6) and reconstructed noise of the radius data (RC's larger than 6). Even if the picture clearly depicts that the noise is the dominant effect, a weak signal appears, stronger in the data up to 1988. This figure indicates the necessity to measure from space the degree of the radius changes.
Open with DEXTER

4 Discussion

A careful determination of the time-dependence of the solar shape and diameter, as well as distortion effects when they can be taken into account, is of importance. The subadiabatically stratified plasma in the convective zone provides both plasma motions (mainly differential rotation) and mechanical stability (mainly an intensification of the magnetic field). Solar cycles, for which the basic physics is still an enigma, are probably driven by convection in the solar interior. Apparent solar radius variations can provide useful information regarding the processes which may be occuring. Moreover, as pointed out by Ulrich & Bertello (1995), a change in the apparent solar radius could assist in the interpretation of frequency variations (as the most probable interpretation of the diameter variability is a change in the temperature profile of the solar limb). The magnitude of the radius fluctuations, compared to the irradiance change during a solar cycle, contains information that has not been previously completely used. Showing that a change in the irradiance leads to a change in the diameter will indicate a unique relationship between these two parameters (Sofia & Endal 1979). Such a law would be particularly useful to tackle problems relevant to our Earth's climatic system.

4.1 Comparison with other measurements of the solar radius

Several observations of the Sun's diameter exist obtained using different techniques. No convincing results have been obtained, due to the difficulty of detecting a hundred milliarcsecond point swamped by a fuzzy solar limb, worsened by the atmospheric seeing effects. The unavoidable question which arises is whether the results from ground can be considered sufficiently trustworthy to warrant more ground-based efforts. Even from space, the question is not trivial (see Emilio et al. 2001, from the MDI-SOHO limb observations). One of the major goals of this paper is thus to try to determine unambiguously the level of noise in at least one ground data set, in order to separate the contribution of the Sun's intrinsic variability from that originating from the instrument and the atmosphere. Ground-based measurements can be briefly report as follows (see also for instance Ribes et al. 1988)

1.    Ulrich & Bertello (1995) showed that the apparent radius of the Sun, when viewed in the spectral line of neutral iron at 525 nm, varies in phase with solar activity. Observations were made at the Mount Wilson observatory and the method of measuring the Sun's apparent radius has been described by La Bonte & Howard (1991). The error on an annual average measurement (the mean derived from the daily observations for each year) is about 0.03''. It was concluded that the variations in the apparent radii of the Sun's disk (at all wavelengths) should contribute between 0.013 and 0.025 per cent variation in the total irradiance;

2.    Between mid-1981 and 1987, Brown et al. (1982) observed the solar radius at the High Altitude Observatory by means of a horizontal instrument timing the interval required for solar meridian transits. They report no significant variation in the solar radius at all. This was based on a definition of the solar limb that minimizes the effect of the seeing. A reanalysis of the data carried out by means of a model of the solar limb intensity permitted the elimination of several uncertainties affecting earlier determinations, allowing an accurate measurement of the solar photospheric radius (Brown & Christensen-Dalsgaard 1998). The authors concluded that no significant variation could be found during the observation period (1981-1987);

3.    Wittman (1997) studied possible time variations in the solar diameter, using a method combining the advantage of both photoelectric and visual drift techniques; the system was put into operation at Observatorio del Teide in Tenerife. He concluded that, at least for his data between 1990 and 1992, there was no strong indication of a variation in diameter with the 11-yr activity cycle in excess of $\pm $0.05'';

4.    All the above-mentioned measurements were performed using techniques other than the solar astrolabe. In order to render the measurements more homogeneous and to cover a larger set of heliographic latitudes, a network of solar astrolabes has been set up in Brazil and in Chile; two other instruments are under construction in Turkey and Algeria. The measurements, performed from 1974 in Brazil (Leister & Benevides 1990) are from visual observations, which were followed by CCD measurements since 1997 (Jilinski et al. 1999) and since 1990 in Chile (Noël 2000). A recent comparison of these data has been made by Lefebvre (2000). If all these observations lead to a variability in the solar diameter, the peak-to-peak amplitude and the phase disagree from one dataset to another one. In the case of the Santiago observations, the measurements, made at $30^{\circ}$ and $60^{\circ}$ zenith distances, show around a 1 arcsec amplitude variation in the data over a solar cycle, the peak-to-peak variability being taken from a sinusoidal fit of the data. The standard deviation given by second order fits of the data is $\sigma = \pm 0''35$ at $30^{\circ}$ (461 observations) and $\sigma = \pm 0''41$ at $60^{\circ}$ (817 observations) zenith distances. Over the solar cycle, the monthly mean values of solar radius measurements show a clear variation in phase with solar magnetic activity.

In the case of the Brazilian measurements, the results show a variability out of phase with the solar cycle, of peak-to-peak amplitude approximately 1.2 arcsec; the average error bar is $\pm $0''20 (4630 observations). All published results are similar to those of the CERGA observatory. Other results can be found, for example Chapman et al. (1999) and Costa et al. (1999). What could be the possible explanations for such discrepancies?

Brown and Christensen-Dalsgaard argued that the limb-position slope shows fairly substantial variations, variable in magnitude. This suggests that the long-term variation may result from localized activity-dependent features such as faculae.

Observations made by Ulrich and Bertello were not conducted at the same optical depth as observations made with the solar astrolabe. The iron line is strongly dependent on magnetic field, suggesting that the measurements may follow the solar activity cycle.

To explain discrepent values from Laclare and Noel, we note that they measure different heliographic latitudes on the same day (due to the different latitudes of observations). When the measurements are grouped by classes of latitude of at least 5 to 10 degrees, the results are more in accordance (Godier & Rozelot 1999). This can be explained, as part of the radius variation is due to solar deformation, linked on the one hand with the royal zones where the existence of spots diminishes the measured brightness, and as a consequence the measured radius; and on the other hand, with the high-latitude activity zones where the presence of faculae have the inverse effect (Pecker 1996).

Obviously, all these measurements are affected by the atmosphere. The degradations are directly related to the optical turbulence along the line of sight and evolve rapidly in time. Therefore, it is important to evaluate the level of noise in the data due to the combination of the instrument and the atmosphere.

4.2 Examination of the noise level in the irradiance and diameter data

The importance of noise in the two sets of data (irradiance and diameter) is well illustrated in Fig. 5. As the eigenvalues are arranged in a monotonically decreasing order, the cut-off at a certain order forms a "tail'' in the spectrum which is the noise floor of the data. The number of eigenvalues above the floor represents the degrees of freedom of the variability, or, in other words, the statistical dimension of the data, which is associated with the number of oscillatory components in the signal. The highest eigenvalues represent the fundamental oscillations in the data and are related to the trend. The two Singular Spectra are far from being identical as only six components can be recognized in the diameter data, the reminder creating the level of noise. By comparison, as many as 20 degrees of freedom in the irradiance data are established from the eigenvalues above the noise level. The reconstruction of these eigenvalues lead to a fairly good agreement with the observed irradiance data, indicating that these first 20 components represent the observed variability; the noise contributes to only a very small fraction of the observed irradiance signal. However, the reconstruction of the 6 first eigenvalues of the diameter data do not reproduce the observed data (Fig. 8, bottom), which are better described by all the components larger than 6. As one may expect, the noise contributes to a large part of the measured variable signal. Figure 5 shows that the level of noise inside the diameter data is far above that of the irradiance, a result not surprising as the previous data are ground-based measurements and the second from space observations.

Analyzing the long term trend (the 2 first components of the diameter data), the peak-to-peak variation is only about 100 milliarcsecond. Is such a value statiscally significant over the studied time range? The full amplitude of the cosine function adjusting the semi-diameter data is 0''62, greater than five times the root mean square residuals (0''18). The reduced $\chi ^{2}$for such a fit is 2.25. Under normal statistics one expect a good fit to have a reduced $\chi ^{2}$ of about 1. A larger $\chi ^{2}$ can result from systematic errors in the data sets (including seeing effects), random variations, or underestimated $\sigma$i. The trend deduced from the SSA shows a modulation of $0''11 \pm 0''10$ so that $\chi ^{2}$ drops to about unity, indicating a confidence level of more than 95%. This does not demonstrate that the radius variability is 100 milliarcsecond in amplitude, but indicates that if such a variability exist, it must be no more than this value.

4.3 Some astrophysical implications

One of the most important implications concerns the changes in the irradiance due to the changes in the radius. Sofia et al. (1979), calculated the so-called w parameter which measures such changes. According to different authors (Spruit 1982; Gilligand 1980; Deadborn & Blake 1980), the value of w ranges from $2\times10^{-4}$ to 0.075 and is strongly model dependent. Observational measurements are still very poor. Assuming that w is constant in time, Ribes et al. (1991) give w close to unity, while Rozelot (2001) gives a w of about 0.85. This rather high value may certainly comes from the fact that the data used in the study were not filtered. These present results yield a value of w of 0.05, not too far from the first theoretical value given by Sofia et al. i.e. 0.075. However, space measurements lead to a value of w = 0.02, which is claimed to be an upper limit (Emilio et al. 2001). How reliable are these estimates? Our ability to make more precise measurements may be expected to improve in an era of dedicated space missions (mainly PICARD and SPHERIS). A direct application of a precise determination of w would help in understanding how small perturbations in the solar irradiance may induce changes in the terrestrial surface temperature of a fraction of a degree centigrade (see for instance Eddy et al. 1982 or Sofia 1998).

5 Conclusion

It has been demonstrated that Singular Spectrum Analysis provides an excellent tool to decompose various solar activity time series, such as total irradiance and radius, to their various oscillatory components and to distinguish these dominant variations from the noise in the data. Our results can be summarized as follows:

1.    From SSA, an amplitude in the solar diameter signal of no more than 110 milliarcsecond can be detected, the remainder being noise, coming jointly from the atmospheric seeing and from the instrumental effects. A statistical test indicates that this level is significant $(P \approx 0.05)$, but as an upper limit;

2.    The CERGA measurements show that the long-term variation of the radius over the solar cycle anticorrelates with both total irradiance and sunspot number. In contrast, measurements on other sites indicate a positive correlation between the solar radius and the activity cycle. Some explanations have been attempted: in the case of observations made by techniques other than the solar astrolabe, it can be argued that measurements probe different optical depths, or result either from variations in the limb-temperature profiles or from localized activity dependent features. In the case of measurements made by the solar astrolabe, but leading to different results, it can be suggested that the discrepancy comes from observations at different heliographic latitudes due to the different latitudes of the observation sites. Gathered by classes of heliographic latitudes, the discrepancies tend to disappear;

3.    Considering the pure signal-to-noise ratio in the radius data, further measurements above the Earth's atmosphere are required to determine the phase between the radius and irradiance variations and to probe the solar interior. Such space experiments whose main objectives are to measure simultaneously the solar diameter and the solar irradiance would permit us to unambiguously confirm or disaprove the occurence of diameter variations without atmospheric effects. In turn, these space observations will also help to calibrate the ground-based radius measurements if the variations are real. Moreover, these measurements can be compared with theoretical models to identify the physical processes responsible for the observed changes of both diameter and irradiance. Such high-quality measurements and their analyses are absolutely necessary not only for astrophysics, but also for climate research. One of the main goals is to understand the origin of climate changes which occurred prior to the industrial era and to determine the degree of the contribution of solar variability to the current and future climate changes.

Acknowledgements
We gratefully acknowledge the referee for his helpful remarks which have enabled us to improve the paper.

References

 

Copyright ESO 2001