A&A 372, 571-578 (2001)
DOI: 10.1051/0004-6361:20010506

Lithium on the surface of cool magnetic CP stars. II. Spectrum analysis of HD 83368
and HD 60435 with lithium spots

A. V. Shavrina¹ - N. S. Polosukhina² - J. Zverko³ - L. I. Mashonkina⁴ - V. Khalack¹ - J. Ziznovský³ - M. Hack⁵ - V. Tsymbal⁶ - P. North⁷ - V. V. Vygonec⁴

1 - Main Astronomical Observatory, National Academy of Sciences, Kiev 03680, Ukraine,
2 - Crimean Astrophysical Observatory, Nauchnyj, Ukraine,
3 - Astronomical Institute, Slovak Academy of Sciences, 059 60 Tatranská Lomnica, Slovakia,
4 - Kazan State University, Kazan 420008, Russia,
5 - Dept. of Astronomy, Trieste Univ., 34131 Trieste, Italy,
6 - Simpheropol State University, Simpheropol 330000, Ukraine,
7 - Inst. d'Astronomie, Univ. Lausanne, 1290 Chavannes-des-Bois, Switzerland,

Received 31 May 2000 / Accepted 2 April 2001

Abstract
As a further step in our Lithium project we present results of abundance determination of some elements in the roAp star HD 60435. Possible NLTE effects were considered. Equivalent widths of spectral lines vary with rotational phase which suggests nonuniform distribution of chemical elements over the stars' surface. Large abundance differences derived from various ions of some rare earth elements indicate their possible vertical stratification. Two spots of enhanced lithium abundance were distinguished at the magnetic poles on HD 60435 and their parameters derived. The rotational axis inclination $i=133^\circ$ or $47^\circ$ and surface magnetic field $H_{\rm s}=3 \pm 1$ kG were determined for the first time for HD 60435. The results are compared with HD83368, the other star with lines of lithium remarkably variable in intensity and wavelength.

Key words: stars: individual: HD 83368, HD 60435 - stars: abundances - stars: chemically peculiar -
stars: magnetic field

1 Introduction

The behaviour of the Li line at 6708 Å in spectra of several magnetic CP stars was studied in previous papers by Hack et al. (1997), North et al. (1998) and Polosukhina et al. (1999a, henceforth Paper I) in the framework of the project "Lithium in CP stars''. A different behaviour of the 6708 Å line which divided the stars into four different groups, was explained in terms of the oblique rotator model and occurrence of Li spots at the magnetic poles. In general, the line profile variations seen in CP stars are due to abundance inhomogeneities on the surface of a rotating star. In Paper I we described the behaviour of the Li line on HD 83368 with two spots of the same size, near the magnetic poles and at opposite places of the star's surface. On HD 60435 the spots do not lie on the opposite sides and/or are not of the same size. Nothing could be said about its magnetic field.

We intend to derive abundances of lithium and other elements in the CP stars with lithium spots. The best way to do this is to use the Doppler imaging technique, which inverts rotationally modulated line profiles to surface abundance distribution (Khokhlova 1975; Rice 1991; Hatzes 1991). This method, however, needs about 20 observations well distributed in phase. Thus, our observations, 7 and 8 for HD 60435 and HD 83368 respectively, allow only coarse modelling using the method of Doppler variations of selected line profiles. While the seven spectra of HD 60435 are well distributed in phase, its low value of $v\sin{i}$ $(11\;{\rm km~s^{-1}})$ and poor definition of the second lithium spot radial velocities (Fig. 5 in Paper I) result in a less precisely derived parameters of spots. On the other hand, the eight spectra of HD 83368 are grouped in three short phase intervals only, but $v\sin{i} = 34\; {\rm km~s^{-1}}$ is more appropriate for the modelling. Despite these problems, however, we consider it worth the coarse modelling because the possible lithium spot occurrence on CP stars is a new phenomenon.

In this paper the method of spectrum analysis, model parameters and magnetic field determination are described in Sect. 2. In Sect. 3 the resulting abundances are discussed and compared with other determinations. In Sect. 4 the Li spots sizes and locations are determined for HD 60435. Possible NLTE corrections are discussed briefly in Sect. 5.

 

 

Table 1: List of observations. Spectral range: A: 6675-6735 Å, B: 6120-6180 Å, C: 6615-6671 Å.

	Date	UT	Exp.	HJD	Rot.	Range
#	d.m.y	h m	[m]	2450000+	phase
HD 83368
23	10.3.96	4 41	20	152.705	0.331	A
38	11.3.96	5 11	20	153.726	0.689	A
48	12.3.96	6 15	20	154.770	0.055	A
57	13.3.96	0 25	20	155.527	0.320	B
61	13.3.96	4 19	20	155.690	0.378	A
65	13.3.96	4 44	20	155.707	0.384	A
71	13.3.96	7 02	30	155.807	0.419	A
77	14.3.96	0 50	20	156.545	0.678	A
83	14.3.96	6 23	30	156.779	0.760	A
85	14.3.96	6 57	30	156.803	0.768	C
HD 60435
03	8.3.96	1 48	90	150.608	0.741	A
13	9.3.96	2 45	90	151.647	0.877	A
21	10.3.96	0 36	90	152.558	0.995	A
22	10.3.96	2 27	90	152.635	0.005	B
33	11.3.96	0 39	90	153.560	0.128	A
47	12.3.96	4 02	90	154.701	0.274	A
60	13.3.96	2 37	90	155.642	0.397	A
78	14.3.96	1 13	90	156.583	0.519	A

2 Spectrum analysis

The observations were made by PN with the ESO Coudé Auxiliary Telescope. The Coudé Échelle Spectrograph was used with resolving power $R = 100\,000$ and the S/N ratio for an individual spectrogram was better than 100 per pixel at the 1 $\sigma$ level. The detector was ESO CCD 34 with 2048 pixels along the dispersion. A thorium-argon lamp was used for the wavelength calibrations with an accuracy better than 0.3kms^-1. Primary data reduction was done by PN during the observing run, using the old IHAP system of ESO.

In Table 1 the date, exposure time, phase and wavelength coverage are given.

The rotational phases for HD 60435 are computed according to the ephemeris of Kurtz et al. (1990):

${\rm JD~ (mean}~ B_{\rm min}) = 2445385.75 + 7.6793E$

and those for HD 83368 according to the ephemeris of Kurtz et al. (1997):

$${\rm JD}~(t_{\rm0}~{\rm puls}) = 2448312.23606 + 2.851976E.$$

2.1 Method

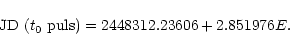
The quantitative analysis without surface spot structure was carried out by means of synthetic spectra using the code STARSP (Tsymbal 1994) and atmospheric models by Kurucz (1993). Line lists with atomic data were those by Kurucz (1995) (CDROM 23) and VALD (Piskunov et al. 1995; Kupka et al. 1999; Ryabchikova et al. 1999), accessible on INTERNET. For doubly ionized rare earth elements (REE) the atomic data were mainly taken from Reader & Corliss (1980). Cowley (private communication), Bord (private communication) and Sugar (private communication) provided us with data for Nd III, Pr III, Ce II and Ce III. For the purposes of line identification we calculated wavelengths of ionized REE using energy levels from Martin et al. (1978), and for Dy III by Spector et al. (1997). Computation of spot parameters (size, location and elemental abundance) were performed with Tsymbal's ROTATE code (see Polosukhina et al. 2000), which allows us to calculate line profiles due to the photosphere with spots for a rotating star. Both STARSP and ROTATE codes take into account the magnetic effects by including a spectral line list with previously calculated components of a split line for each phase.

   
2.2 Model atmosphere parameters.

The values of $T_{\rm eff},~ \log g$ and $v\sin{i}$were taken from Polosukhina et al. (2000) and Zverko et al. (1998) as follow

$$T_{\rm eff}~ = 7750, \log{g} = 4.0~~ \mbox{for HD~83368 and}$$

$$T_{\rm eff}~ = 8250, \log{g} = 4.5~~ \mbox{ for HD~60435.}$$

The adopted $T_{\rm eff}$ of HD 83368 is very close to the value obtained from Geneva photometry using the B2-G index calibrated by Hauck & North (1993) and assuming no reddening (the distance is only 72 pc). The $\log g$ value is also compatible with the Hipparcos parallax and mass interpolated in theoretical evolutionary tracks. For HD 60435, the adopted $T_{\rm eff}$ and $\log g$ values are close to the results of $uvby\beta$photometry calibrated by Moon & Dworetsky (1985). The surface gravity is larger than that inferred from the Hipparcos parallax, but the latter has an uncertainty of 20 percent and, therefore, is not very reliable. There is an additional uncertainty linked with the visual absorption, which is not negligible at the distance of 234 pc.

Models with [M/H] = 0.0 were adopted after testing Fe lines on models with $\rm [M/H] = \pm 0.5$ and $\pm$ 1.0 and finding a normal iron abundance.

Comparing the synthetic spectra with the observed ones at individual rotational phases, we then derived the abundance variations of several elements with rotation. In this procedure we assumed that the abundances in the stellar atmosphere are constant over the entire visible surface seen in a given spectrum. The effects of the magnetic field were not included here.

 

 

Table 2: Elemental abundances for HD 83368 and HD 60435 as compared with data of Zverko et al. (unpublished) for HD 60435, (Grevesse & Sauval 1998) for the Sun and Roby & Lambert (1990) and Ryabchikova et al. (1997) for HD 24712.

	HD 83368		HD 60435		N	error	HD 60435		Sun	HD 24712
El	max	min	max	min	lines	(dex)	model 1b	model 2c
1	2	3	4	5	6	7	8	9	10	11	12
C I	-3.8	-4.5	-3.6	-3.8	6	.3			-3.52	-4.5
N I	-3.0	-4.0	-3.2	-3.4	10	.3			-4.09	-4.4
O I	-3.4	-4.3	-3.9	-4.5	2	.3	-4.0	-4.0	-3.21	-3.8
Na I	-6.1	-6.1	-5.8	-5.8	2	.3		-5.9	-5.72
Al I	-6.0	-6.6	-6.2	-6.2	1	.2		-6.8	-5.57	-5.53
Si I	-3.9	-4.9	-3.6	-4.4	5	.2		-4.9	-4.48	-4.43
S I	-5.2	-5.2			5	.3			-4.84
Ca I	-5.1	-5.6	-4.7	-5.1	2	.1	-5.4	-5.4	-5.69	-5.69
Ca II	-5.3	-5.8	-5.8	-5.8	3	.3				-5.22	-4.88
Ti II	-6.8	-7.3	-7.2	-7.3	2	.2			-7.10	-7.22	-7.29
Cr I	-4.1	-5.0	-4.3	-4.4	4	.2			-6.35	-5.93	-5.80
Cr II	-4.2	-4.6	-4.6	-4.6	4	.3	-4.9	-5.0		-5.58	-5.33
Fe I	-4.6	-4.9	-4.1	-4.2	4	.1	-4.4	-4.5	-4.54	-4.77	-4.88
Fe II	-4.3	-4.7	-4.3a	-4.3a	10	.2	-4.4	-4.5		-4.80	-5.11
Co I	-5.5	-6.3			1	.3		-5.7	-7.13	-5.88	-5.57
Y I	-6.4	-7.0			4	.2		-8.5	-9.81	-7.80	-7.80
Ba II	-9.1	-9.1	-9.1a	-9.1a	1	.2	-9.5	-10.0	-9.82	-9.12	-8.98
La II	-8.4	-9.2			3	.4		-10.3	-10.82	-9.40	-8.75
Ce II	-8.1	-8.7			2	.2		-9.4	-10.41	-9.18	-8.90
Pr II	-9.3	-9.3	-9.3	-9.3	4	.2			-11.24	-10.15	-9.60
Pr III	-8.5	-9.1	-8.4	-8.8	2	.2
Nd II	-8.2	-9.3	-7.9	-8.6	4	.3		-9.2	-10.55	-9.13	-8.64
Nd III	-7.2	-8.0	-7.5	-8.0	2	.2
Sm II	-8.4	-9.1	-8.1	-8.4	3	.2		-9.9	-11.06	-9.75	-9.16
Eu II	-9.8	-9.8			2	.2		-9.5	-11.07	-9.50	-9.00
Gd II	-8.4	-8.9			6	.3	-8.2		-10.95	-9.11	-8.70
Er II	-8.1	-8.6			1	.3			-11.07	-9.79	-9.53
Yb II			-9.3	-9.4	1	.3			-11.08	-8.30	-8.30
Lu II	-9.2	-9.2	-9.4	-9.4	1	.2			-11.91
a) - from spectral range 6120-6180 Å; b) - $T_{\rm eff} = 8250~$K, $\log g = 4.5,~ v\sin{i} = 11\; {\rm km~s^{-1}}$and $\rm [M/H] = 1$;
c) - $T_{\rm eff} = 7750~$K, $\log{g} = 3.0,~ v\sin{i} = 11\; {\rm km~s^{-1}}$and $\rm [M/H] = 1$.

The maximum and minimum values of $\log({\rm N/H})$for the corresponding phases are given in Table 2 for HD 83368 (Cols. 2 and 3) and for HD 60435 (Cols. 4 and 5). The number of lines used and the errors for each element are given in Cols. 6 and 7 respectively. The procedure of fitting the observed and calculated spectra was repeated until the disagreement for all analyzed lines of each element reached its minimum. The errors are estimated as uncertainties of the fitting procedure; they do not include the errors of the physical stellar parameters.

The next two columns of Table 2 give the previously determined abundances for HD 60435 by Zverko et al. (unpublished) for the atmosphere model $T_{\rm eff} = 8250~$K, $\log{g} = 4.5$ (Col. 8, model 1) and $T_{\rm eff} = 7750~$K, $\log{g} = 3.0$ (Col. 9, model 2) with $\rm [M/H] = 1$ and $v\sin{i} = 11\; {\rm km~s^{-1}}$. The last three columns give, for comparison, the solar abundances (Grevesse & Sauval 1998) and the abundances for a similar roAp star, HD 24712, by Roby & Lambert (1990) from C I to Ca I and Ryabchikova et al. (1997) for the other elements. HD 24712 also shows variability of chemical composition versus the rotational phase, but has no measurable Li 6708 Å line.

   
2.3 Magnetic field

Figure 1: Profiles of Fe II 6147.74 and 6149.26 Å. Thick full line: observed spectrum; left: HD 83368, phase 0.320, $v \sin i = 34~ {\rm km~s^{-1}}$; thin solid line: 2 kG plus spots, thin dashed line 2 kG without spots, thin dotted line: spots without magnetic field, thick dashed line: 11 kG (Paschen-Back effect) plus spots. Two spots of Fe II and one of Pr II were taken into account; right: HD 60435, phase 0.005, $v \sin i = 11~ {\rm km~s^{-1}}$; thin solid line: 3 kG (Zeeman splitting) plus spots, dashed line: no field, no spots.

Open with DEXTER

The structure and intensity of the magnetic field for HD 83368 are discussed in details in the papers of Bagnulo et al. (1999) and Polosukhina et al. (1999b).

In the latter paper (Polosukhina et al. 2000, Sect. 3) reasons are given for using 2 kG. The unusually large difference was discussed by Mathys himself as follows: "The rather strong quadratic field of HD 83368, with its average intensity of about 11 kG, is somewhat unexpected, given the very moderate $(\vert \langle H_{z} \rangle \vert < 1~ {\rm kG})$ longitudinal field of this star''.

We attempted to determine the value of the surface magnetic field from the Fe II 6147 Å and 6149 Å line profiles. We computed the synthetic profiles taking into account magnetic splitting for two values of the magnetic field, namely 2 kG (Zeeman splitting), and 11 kG (Paschen-Back effect, see Mathys 1995; Mathys & Hubrig 1997). We calculated the wavelength and gf-values for all the $\sigma$- and $\pi$-components of magnetically split Fe II 6147 Å and 6149 Å lines assuming the L-S coupling and for various values of vector modulus of surface magnetic field and inclinations to the line of sight (corresponding to each rotational phase) without polarization effects in the transfer equation. The list of these components (as unpolarized) was included in the common line list for ROTATE code, which takes the surface spots into account.

In the case of 2 kG the resulting line profiles (with $v \sin i = 34~ {\rm km~s^{-1}}$) are almost symmetrical relative to the line centre, while after including the spots, asymmetrical features fitting better the observed profiles appear (Fig. 1a). In the case of 11 kG the red component of the 6147Å  line and the blue one of the 6149 Åline blend each other.

Beside the influence of the surface magnetic field on line profiles, the field strength remarkably influences the ratio of the central line intensities of these two Fe II lines. The ratio of the central intensities is 6147/6149 > 1 for 11 kGs and Paschen-Back effect while 6147/6149 < 1 for 2 kGs and Zeeman splitting, which also better fits the observed ratio of the central intensities (see Fig. 1a). The best fit with the observed profiles was reached for $H_{\rm s}$ = 2 kG, including two Fe II spots, located at longitudes $l_{1} = 110\hbox{$^\circ$ }$ and $l_{2} = 170\hbox{$^\circ$ }$, and one Pr II spot (visible at this phase) with $l=100\hbox{$^\circ$ }$, where $l = 0\hbox{$^\circ$ }$ corresponds to the subsolar point on the stellar surface at photometric phase zero (Paper I).

In Fig. 1a we show also the calculated spectrum for the other value of the surface magnetic field, 11 kG (Mathys 1995), which fits the observed profile considerably worse. Thus, we consider the value $H_{\rm s} =$ 2 kG to be more satisfactory; moreover, it is also confirmed by the good fit of the computed profiles of the Eu II 6645.46 Å (See Fig. 6 in Polosukhina et al. 2000), Nd III 6145.07 Å and Ba II 6141 Å lines to the observed ones, taking into account the surface spot structure (see Fig. 2a).

Contrary to the case of HD 83368, there are no previous measurements of magnetic field for HD 60435. Considering the similarity of these two stars we followed the same method for HD 60435. Here we assume that two observed lithium spots also reflect the symmetric dipole structure of the magnetic field, as in the case of HD 83368. The analysis of the Li line profiles reveals that the maximum of the intensity of this line occurs at phases 0.519 and 0.995. The latter phase is near to 0.005, the moment when we see the second Li spot near the central meridian of the star, and so it is possible to use the corresponding spectrum taken in the range 6120-6180 Å to determine the magnetic field using lines of Ba II and Fe  II.

We computed the profiles of the lines mentioned for the corresponding orientation of the magnetic field with Zeeman splitting for a set of values of $H_{\rm s}$ in the range 2-8 kG and $v\sin{i} = 11\pm2\; {\rm km\,s^{-1}}$. The best fit of the computed profiles to the observed ones (the profile shape and the intensity ratio for two Fe II lines) was achieved for $H_{\rm s}$ = 2 kG. In the case of the Ba II lines the best fit corresponded to $H_{\rm s}$ = 3.5 kG (see Fig. 2b). We were able to reach a good fit for both elements simultaneously with a single value $H_{\rm s}$ = 3 kG, by convolving the Fe II lines with a $v\sin{i} = 9\; {\rm km~s^{-1}}$ rotational profile (Fig. 1b) and the Ba II line with $v\sin{i} = 13\; {\rm km~s^{-1}}$. Thus our estimate of the surface magnetic field of HD 60435 is $H_{\rm s}=3 \pm 1$ kG with $v\sin{i} = 11\pm2\; {\rm km~s^{-1}}$.

	Figure 2: Profile of the Ba II 6141.71 Å line with Zeeman splitting. Full line: observed spectrum, dashed line: synthetic spectrum. a) HD 83368, two spots at $l = 85\hbox {$^\circ $ }$ and $l = 160\hbox {$^\circ $ }$, 2 kG. b) HD 60435, 3.5 kG, $v \sin i = 11~ {\rm km~s^{-1}}$.
Open with DEXTER

	Figure 3: Calculated abundances relative to the Sun (Grevesse & Sauval 1998); full squares: HD 60435, open squares: HD 83368.
Open with DEXTER

3 Abundances

As it can be seen from Table 2, the abundances of the elements undergo variations of 1 dex or less in both stars, in general, as the stars rotate. The main difference between the stars is in the iron peak group, since in HD 60435 the changes are well below the determination error while in HD 83368 they vary from 0.3 to 0.9 dex (especially Cr I).

As regards abundances, Ti and Fe are normal while Cr is overabundant by 2 dex as compared with the Sun and by 1.5 dex compared with the other roAp star HD 24712 (Ryabchikova et al. 1997) in both stars. Y is overabundant by 3.1 dex in HD 83368 relative the Sun and by 1.1 dex relative the HD 24712.

The abundances given in Table  2 for Ca  I and Ca  II, Nd  II and Nd  III, Pr  II and Pr  III are very discordant which may be the evidence for a strongly contrasted surface distribution (Babel 1993) and/or vertical stratification of these elements.

3.1 Light elements

In HD 83368, all studied elements from C through Ca (excluding Na and S) vary significantly, from 0.5 to 1 dex, while in HD 60435 only Si and O show larger variability, 0.8 and 0.6 dex respectively.

As compared with the Sun, the abundance of Na is normal in both stars (see Fig. 3). O is underabundant, while N is overabundant in both stars. C is underabundant in HD 83368 and normal in HD 60435. Si and Ca are normal in HD 83368 and slightly overabundant in HD 60435.

As compared with HD 24712, N is remarkably overabundant (by 1 dex) in both stars, C and Ca are overabundant by 0.8 dex in HD 60435. The abundances of the other light elements studied are the same within the abundance errors. In HD 83368 O is the same as in HD 24712 and underabundant by 0.4 dex in HD 60435.

   
3.2 Rare earths

Spectra of these roAp stars are rich in REE lines. Especially strong are lines of Nd II, Pr II and Pr III. The problem of line identification of REE lines as well as determination of missing gf values are discussed in detail in Polosukhina et al. (2000). The most significant abundance variations are shown by the La II, Ce II, Nd III, Sm II and Gd II lines in HD 83368, and by Nd II and Nd III lines in HD 60435.

As regards abundances, all elements studied are overabundant by $\sim$2 dex in both stars; only Eu is overabundant by only 1.3 dex in HD 83368. Sm is overabundant by 2.3 dex and 2.8 dex respectively in HD 83368 and HD 60435 as compared with the Sun (see Fig. 3).

As compared with HD 24712, in HD 83368 La, Nd and Gd have the same abundance within the errors, while Ce, Pr, Sm show overabundances of $\sim$0.6 dex and Eu an underabundance of $\sim$0.5 dex. In HD 60435 Pr, Nd and Sm are overabundant by 0.6, 0.6 and 1.2 dex respectively.

As it was shown in Polosukhina et al. (2000), REE create ring-like structures surrounding the Li spots in HD 83368. In the same way we tried to determine the position of REE spots on HD 60435 using the lines of ionized rare earths near the Li line (Pr III, Sm II and Ce II) and Pr III 6160.22 Å and 6161.24 Å (spectral region 6120-6180 Å) for the phase 0.005. However, due to the low value of $v\sin{i}$ ( $11\pm2~{\rm km\,s^{-1}}$) and the insufficient phase coverage, it is not possible to determine the REE spots locations with a higher accuracy.

   
4 The lithium line at 6708 Å

Preliminary analysis of the spectra of HD 83368 in Paper I and of HD 60435 by Zverko et al. (1998) showed that lithium is distributed inhomogeneously on their surfaces.

The reliability of our abundance determinations in a spot is limited by the visible part of the spot, inhomogeneous distribution of elements in the spot and also by line blending. The method used for line profile computation for a rotating star with a spotted surface was elaborated by Tsymbal and is described in details in Polosukhina et al. (2000).

To derive the locations of the two spots we first set their longitudes to the points where the RV curve of the Li line coincides with the mean radial velocity of the star. Assuming the spots' latitudes are zero and based on the known value of $v\sin{i}$ (Sect. 2.2), we changed the angle i and the equatorial velocity v accordingly, to reach the best agreement between the computed (with the ROTATE code) and observed profiles of the Li line. We further improved the fit at different phases by varying the latitudes of the spots. In the end correcting the longitudes and bringing minute corrections to abundances we obtained the final fit. It should be noted, that only one combination of the Li spots' parameters allows us to reach agreement between model and observations at all phases. In general a good fit was reached for phases where the spot is near the centre of the visible disk, while the worst ones were found when the spot was near the limb.

	Figure 4: Observed and computed spectra for 8 rotational phases for HD 83368. For spots' parameters see text. The 2 Å distance between the short wing of the most blue shifted line (phase 0.760) and the long wing of the most redshifted line (phase 0.689) is due to separation of the doublet components 0.15Åand broadening effects: rotational 0.76Å, thermal 0.15Å, magnetic 0.08Å.
Open with DEXTER

	Figure 5: Observed and computed spectra for 7 rotational phases for HD 60435. For spots' parameters see text.
Open with DEXTER

The lithium spots parameters for HD 83368 were determined in Polosukhina et al. (2000) for the atmospheric model with $T_{\rm eff} = 7750~ {\rm K}, \log{g} = 4.0$, $i = 90\hbox{$^\circ$ }, v_{\rm e} = 35\, {\rm km\,s^{-1}}$ and photospheric Li abundance $\varepsilon_{\rm Li} = -10.2$ as follow:

• spot 1: $l_{1} = 173\pm6\hbox{$^\circ$ }, \varphi = 0\pm6\hbox{$^\circ$ }, R = 33\pm6\hbox{$^\circ$ },\\ \log(N_{\rm Li}/N_{\rm H}) = -8.4\pm0.2$
• spot 2: $l_{2} = 337\pm6\hbox{$^\circ$ }, \varphi = 0\pm6\hbox{$^\circ$ }, R = 35\pm6\hbox{$^\circ$ },\\ \log(N_{\rm Li}/N_{\rm H}) = -8.5\pm0.2$.

where l is the longitude, $\varphi$ the latitude and R the radius of the spot ( $R=90\hbox{$^\circ$ }$ would correspond to a whole hemisphere).

In these calculations we included 10 components of the Li line fine structure for a magnetic field value, corresponding to each phase. As a model we adopted a sinusoidal variation of the modulus with phase.

For HD 60435 Matthews et al. (1999), using $T_{\rm eff}=8200\, \rm K$ from $uvby{\rm H}\beta$ photometry (which corresponds to the spectroscopic determination by Zverko et al. 1998) determined asteroseismologically the value $L/L_{\odot}= 21.4$. Then from the Stephan-Boltzmann law we obtained a radius value $R_{\rm\star} = 2.30\pm0.45~ R_{\odot}$. Taking into account the value of the stellar rotational period $P_{\rm rot} = 7.6793\pm0.0006$ d (Kurtz et al. 1990) and an appropriate value $v\sin{i} = 11\pm2\; {\rm km~s^{-1}}$ (see Sect. 2.3), we derived the equatorial velocity $v_{\rm e} = 15\pm3\; {\rm km~s^{-1}}$from the equation

$$v_{\rm e} = \frac{2 \pi R_{\rm\star}}{P_{\rm rot}}$$

and obtained the corresponding inclination angle of rotational axis to the line of sight $i = 47\hbox{$^\circ$ }\pm23\hbox{$^\circ$ }$ or $133\hbox{$^\circ$ }\pm23\hbox{$^\circ$ }$.

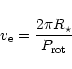
In the next step we used the method of line profile computation for a rotating star with a spotted surface for the atmospheric model $T_{\rm eff} = 8250~{\rm K},~ \log{g} = 4.5,~ {\rm [M/H]} = 0$, $i = 133\hbox{$^\circ$ }$ (or $i = 47\hbox{$^\circ$ }),~ v_{\rm e} = 15\;{\rm km~s^{-1}}$. The best fit of the computed to observed profiles of the lithium line at all phases was reached for the photospheric Li abundance (outside the spots) $\log(N_{\rm Li}/N_{\rm H}) = -10.2$ and for the lithium spots parameters as follow:

• spot 1: $l_{1} = 205\pm10\hbox{$^\circ$ }, \varphi = \pm15\pm5\hbox{$^\circ$ }, R = 40\pm7\hbox{$^\circ$ },\\ \log(N_{\rm Li}/N_{\rm H})~=~-9.3\pm0.2$
• spot 2: $l_{2} = 11\pm6\hbox{$^\circ$ }, \varphi = \mp15\pm5\hbox{$^\circ$ }, R = 44\pm3\hbox{$^\circ$ },\\ \log(N_{\rm Li}/N_{\rm H})=~-8.2\pm0.2$.

Again, the 10 Zeeman components of the Li line at each phase were taken into account.

5 Model of the LiI atom and NLTE effects

All the computations made so far were done under the LTE hypothesis. As the line is observed in some, but not all CP stars and its profile is complicated by magnetic field and inhomogeneous distribution of chemical elements, we tried to estimate possible NLTE corrections. Many authors dealt with the NLTE approach for the 6707.8 Å resonance line (transition 2s ²S - 2p ²P⁰), e.g. Muller et al. (1975), Luck (1977), De la Reza et al. (1981), Steenbock & Holweger (1984), Carlsson et al. (1994), Pavlenko (1996), but none of them considered the case of CP stars.

The model atom of Li I used here is the same as in the paper of Pavlenko (1996) and includes all the levels nl ($n \leq 7$, $l \leq 3$) and the ground state of Li II (20 levels altogether). Levels energy and oscillator strengths $f_{\rm ij}$ were taken from Wiese et al. (1996). For calculation of radiative rates of free-bound transitions, the photoionization cross sections $\sigma_{\rm ph}$ from Hofsaess (1979) were used. These are close to the analogic data for Li I from TOPbase. The NLTE abundance corrections in photoshere which arise from deviations from hydrogenic photoionization cross sections, that are usually applied for Li I (see Pavlenko 1996), decrease the abundance by < 0.01 dex for $T_{\rm eff} = 7000~{\rm K},~ \log{g} = 4.0,~ {\rm [M/H]} = 0,~ \log({N_{\rm Li}/N_{\rm H}}) = -8.5$. It should be noted that the correction increases to -0.05 dex towards lower temperatures and $\log g$ values ( $T_{\rm eff} = 4000$ K, $\log{g} = 3.0$, ${\rm [M/H]} = 0$, $\log(N_{\rm Li}/N_{\rm H}) = -8.5$).

NLTE abundance corrections for barium (Mashonkina et al. 1999) and europium (Mashonkina 2000) are as follow: for HD 83368 ( $T_{\rm eff} = 7750~ {\rm K}, \log{g} = 4.0$, ${\rm [M/H]} = 0$, $v_{\rm turb} = 2$ kms^-1) -0.17 dex and +0.18 dex respectively; for HD 60435 ( $T_{\rm eff} = 8250$ K, $\log{g} = 4.5$, ${\rm [M/H]} = 0$, $v_{\rm turb} = 2$ kms^-1) the correction (for barium only) amounts to -0.08 dex.

6 Conclusions

We find that the abundances of elements in both stars differ from each other and differ considerably from the solar one, which is a common feature of CP stars. As compared with the other roAp star HD 24712, almost all elements studied show overabundances in both stars, while O is deficient in HD 60435.

In HD 83368, the abundances of the elements studied vary with rotation by up to 0.9 dex in general, while in HD 60435 the most prominent variations (up to 0.7 dex) are shown by REE and some of the light elements (O, Si). The main difference between these two stars consists in the fact that in HD 60435 the iron peak elements are non-variable within the abundance errors.

In HD 83368, the abundance maximum of the most variable elements occurs at phases when the Li line is outside of its extrema. From this we deduce that some of the other elements (mainly REE) may form ring-like features surrounding the lithium spots. A similar structure can be expected on HD 60435, though its characteristics were derived with lower accuracy.

In HD 83368 the behaviour of the Li line profile and magnetic field shows that lithium spots approximately coincide with magnetic poles. The positions $l_{\rm 1}$, $l_{\rm 2}$ of the two lithium spots given in Sect. 4 correspond to a lag between magnetic poles and spots of $\sim$23 $\hbox{$^\circ$ }$ which is in good agreement with the lag derived in Paper I. At the same time the values of $l_{\rm 1}$, $l_{\rm 2}$ show that the lithium spots possibly are not exactly $180\hbox{$^\circ$ }$ apart. In HD 60435 we derived from the line profile variations the positions of the lithium spots, which similarly do not lie strictly at opposite sites. Like on the former star, we suppose that magnetic poles may coincide approximately with the lithium spots.

For HD 83368 the determination of inclination i was described in Polosukhina et al. (2000) and it has to be close to $90\hbox{$^\circ$ }$. For HD 60435 using HIPPARCOS data we derived $i = 133\hbox{$^\circ$ }$ (or $i= 47 \hbox{$^\circ$ }) \pm23\hbox{$^\circ$ }$ (see Sect. 4). Under these conditions our analysis of profiles of magnetically sensitive Fe II lines (6147 Å, 6149 Å) lead to surface field value $H_{\rm s} = 3$ kG for HD 60435 and $H_{\rm s} = 2$ kG for HD 83368.

Tsymbal's code of line profile computation for a spotted stellar surface allowed us to derive the spot parameters: location, size, element abundance. As a rule it results in a good agreement between calculated and observed profiles for subsolar position of spots. When the spots lie near the limb, however, it is difficult to achieve a good agreement due to a complicated blending with lines of other elements (mainly REE) and to the weakness of the Li line. A similar problem was mentioned in other papers too with Piskunov's code (Kuschnig et al. 1999).

As we have already noted, the phase coverage of our observations is not sufficiently dense and from this point of view our results should be considered as preliminary.

We showed that NLTE effects are small and do not have to be taken into account for abundance determination in these stars.

Acknowledgements

We are grateful to S. Sergeev for SPE code for spectra analysis, to Ch. Cowley for numerous consultations and for sending us the rare earth element data, to M. Ya. Orlow for discussing our work, to D. Bord and J. Sugar for suggestions and advises to use their data. The data from Kurucz's CDROM 23, NASA ADC, VALD, NIST, were used and we thank the administrators of these databases, accessible through INTERNET. Special thanks are due to J. Landstreet for his valuable comments and suggestions leading to improvement of this paper. A partial support of VEGA grant No. 7107 is acknowledged. V. Tsymbal thanks Mr. Yakushechkin for his support. P. North thanks the Swiss National Science Foundation for its support.

References

 
• Bagnulo, S., Landolfi, M., & Landi Degl'Innoncenti, E. 1999, A&A, 343, 865 In the text NASA ADS  
• Babel, J. 1993, in Peculiar versus normal phenomena in A-type and related stars, ed. M. M. Dworetsky, F. Castelli, & R. Faraggiana, ASP Conf. Ser., 44, 458 In the text  
• Carlsson, M., Rutten, R. J., Bruls, J. H. M. J., & Shchukina, N. G. 1994 A&A, 288, 860 In the text NASA ADS  
• De la Reza, R., Torres, C. A. O., & Busko, I. C. 1981, MNRAS, 194, 829 In the text NASA ADS  
• Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 In the text NASA ADS  
• Hack, M., Polosukhina, N. S., Malanushenko, V., & Castelli, F. 1997, A&A, 319, 637 In the text NASA ADS  
• Hatzes, A. P. 1991, MNRAS, 253, 89 In the text NASA ADS  
• Hauck, B., & North, P. 1993, A&A, 269, 403 In the text NASA ADS  
• Hofsaess, D. 1979, Atomic Data and Nuclear Data Tables, 24, 285 In the text NASA ADS  
• Khokhlova, V. L. 1975, AZh, 55, 1950 In the text  
• Kupka, F., Piskunov, N. E., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 In the text NASA ADS  
• Kurtz, D. W., van Wyk, F., & Maran, F. 1990, MNRAS, 243, 289 In the text NASA ADS  
• Kurtz, D. W., van Wyk, F., Goberts, G., et al. 1997, MNRAS, 287, 69 In the text NASA ADS  
• Kurucz, R. L. 1993, CDROM13, CDROM23 In the text  
• Kurucz, R. L. 1995, Harvard-Smithsonian Center for Astrophysics, Preprint No. 4080 In the text  
• Kuschnig, R., Ryabchikova, T. A., Piskunov, N. E., Weiss, W. W., & Gelbman, M. J. 1999, A&A, 348, 924 In the text NASA ADS  
• Luck, R. E. 1977, ApJ, 218, 752 In the text NASA ADS  
• Martin, W. C., Zalubas, R., & Hagan, L. 1978, Natl. Stand. Ref. Data Ser., Natl. Bur. Stand. (U.S.), 60 In the text  
• Mashonkina, L., Gehren, T., & Bikmaev, I. 1999, A&A, 343, 519 In the text NASA ADS  
• Mashonkina, L. 2000, Astron. Rep., in press In the text  
• Mathys, G. 1995, A&A, 293, 746 In the text NASA ADS  
• Mathys, G., & Hubrig, S. 1997, A&AS, 124, 475 In the text NASA ADS  
• Matthews, J., Kurtz, D., & Martinez, P. 1999, ApJ, 511, 422 In the text NASA ADS  
• Moon, T. T., & Dworetsky, M. M. 1985, MNRAS, 217, 305 In the text NASA ADS  
• Muller, E. A., Peytremann, E., & De la Reza, R. 1975, Solar Phys., 41, 53 In the text NASA ADS  
• North, P., Polosukhina, N., Malanushenko, V., & Hack, M. 1998, A&A, 333, 644 In the text NASA ADS  
• Pavlenko, Ya. V. 1996, The non-LTE formation of lithium lines in the late type stellar atmospheres, Ph.D. Thesis, Kiev In the text  
• Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffrey, C. S. 1995, A&AS, 112, 525 In the text NASA ADS  
• Polosukhina, N. S., Kurtz, D., Hack, M., et al. 1999a, A&A, 351, 283 (Paper I) In the text NASA ADS  
• Polosukhina, N. S., Khalack, V. R., & Shavrina, A. V. 1999b, Astron. Lett., 25, No. 9, 608 In the text  
• Polosukhina, N. S., Shavrina, A. V., Hack, M., et al. 2000, A&A, 357, 920 In the text NASA ADS  
• Reader, J., & Corliss, Ch. H. 1980, Line Spectra of the Elements, NASA ADC, CDROM 3 (1980-1) In the text  
• Rice, J. B. 1991, A&A, 245, 561 In the text NASA ADS  
• Roby, S. N., & Lambert, D. L. 1990, ApJS, 73, 67 In the text NASA ADS  
• Ryabchikova, T. A., Landstreet, J. D., Gelbmann, M. J., et al. 1997, A&A, 327, 1137 In the text NASA ADS  
• Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., Kupka, F., & Weiss, W. W. 1999, Physica Scripta, T83, 162 In the text  
• Spector, N., Sugar, J., & Wyart, J.-F. 1997, J. Opt. Soc. Am. B, 14(3), 511 In the text NASA ADS  
• Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 In the text NASA ADS  
• Tsymbal, V. V. 1994, Odessa Astron. Publ., 7, part 2, 146 In the text  
• Wiese, W. L., Smith, M. W., & Miles, B. M. 1996, Atomic Transition Probabilities. NBS Reference Data - 1 (Washington, D.C.) In the text  
• Zverko, J., Ziznovský, J., & North, P. 1998, Contrib. Astron. Obs. S. Pleso, 28, 109 In the text NASA ADS