A&A 372, L37-L40 (2001)
DOI: 10.1051/0004-6361:20010576

Dust emission from the lensed Lyman break galaxy cB58

A. J. Baker - D. Lutz - R. Genzel - L. J. Tacconi - M. D. Lehnert

Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany

Received 5 October 2000 / Accepted 20 April 2001

Abstract
We detect 1.2mm continuum emission from dust in the gravitationally lensed Lyman break galaxy MS1512+36-cB58. Our detected flux is surprisingly low: relative to local starburst galaxies, cB58 appears to produce somewhat less far-IR emission than its UV reddening predicts. After comparing several different estimates of the source's dust content, we conclude that the apparent discrepancy is most likely related to uncertainty in its UV spectral slope. Alternate scenarios to account for a far-IR "deficit'' which rely on a high dust temperature or differential magnification are less satisfactory. Our result underscores one of the risks inherent in characterizing the cosmic star formation history from rest-UV data alone.

Key words: galaxies: fundamental parameters, high-redshift, photometry, starburst - submillimeter - ultraviolet: galaxies


1 Introduction

Large samples of actively star-forming galaxies at $z \geq 2$ can now be identified through color selection techniques which exploit the Lyman break (e.g., Steidel et al. 1999). In many respects, these sources resemble UV-bright starburst galaxies at z = 0: the two populations have similar bolometric surface brightnesses (Meurer et al. 1997), UV-through-optical spectral energy distributions (SEDs: e.g., Ellingson et al. 1996; Sawicki & Yee 1998), and blueshifted interstellar absorption from outflowing gas (e.g., Pettini et al. 1998). The analogy between Lyman break galaxies (LBGs) and local starbursts is not exact, however: LBGs appear to be forming stars at rates which are "scaled up'' by their larger physical sizes (Meurer et al. 1997). At longer wavelengths, moreover, the analogy can barely be evaluated, since few direct far-IR and submillimeter observations of LBGs exist. Two recent attempts have been made to fill this gap. Chapman et al. (2000) detect only one of sixteen LBGs at $450\,{\rm\mu m}$ and $850\,{\rm\mu m}$ with the Submillimeter Common-User Bolometer Array (SCUBA). Peacock et al. (2000) compare HST and SCUBA observations of the Hubble Deep Field and achieve a statistical detection at $850\,{\rm\mu m}$ of the HST sources with photometric redshifts, but can make no statement about specific objects with spectroscopic redshifts. The limitations of these studies motivated us to observe the gravitationally lensed system MS1512+36-cB58 (hereafter cB58: Yee et al. 1996). Thanks to magnification by the z = 0.37 cluster MS1512+36, this z = 2.7 LBG was already well-studied in the rest UV and optical (e.g., Ellingson et al. 1996; Pettini et al. 2000; Teplitz et al. 2000), and promised to be unusually detectable at longer wavelengths.

2 Observations

From 3-7 March 2000, we observed cB58 in on-off photometric mode with the 37-element Max-Planck Millimeter Bolometer (MAMBO) array (Kreysa et al. 1998) at the IRAM 30 m telescope. We pointed the array's central pixel at the optical position (J2000 coordinates 15:14:22.20 and +36:36:24.4) determined by Abraham et al. (1998). We chopped the secondary mirror by $53^{\prime\prime}$ in azimuth at 0.5Hz and nodded by the same $53^{\prime\prime}$ throw every ten seconds; the HPBW of our beam was $11^{\prime\prime}$ at 1.2mm. We reduced the data with the MOPSI package, using all pixels in the first ring around the central pixel for estimating and removing correlated fluctuations due to the sky background. Our flux scale of $6250\,{\rm counts\,Jy^{-1}}$ was based on observations of planets. If we include all data from our total on+off integration time of 200 min, we achieve a $6.0\sigma$ detection of $1.32 \pm 0.22\,{\rm mJy}$. For the purposes of this paper, however, we will exclude 60 min of data from our last observing night, for which pointing and sky background instabilities coupled with a large opacity correction ( $\tau \sim 0.3$ vs. $\leq 0.16$ over the rest of our run) reduce our confidence in the photometry. Including a 10% uncertainty in our flux scale then yields a final [$4.4\sigma$] detection of $1.06 \pm 0.35\,{\rm mJy}$.

3 A comparison with local starbursts

Heckman et al. (1998) and Meurer et al. (1999) have showed that local starburst and star-forming galaxies obey scaling relations between various global properties and the parameters of their UV spectra. We can therefore test the proposition that cB58 is a "scaled-up'' local starburst by seeing if it fits those relations which are independent of distance (and lensing magnification). A key parameter here is the UV spectral slope $\beta$ ( $f_\lambda \propto \lambda^\beta$), whose observed value indicates the amount of reddening by dust (i.e., from some intrinsically blue $\beta_0$) for an assumed star formation history. Because the same dust which reddens stellar UV continua will re-radiate the energy which it absorbs, it is natural that UV-bright local systems should obey a relationship between $\beta$ and the ratio of far-IR to UV emission. Meurer et al. (1999) determine this relation for a sample which includes only galaxies whose starbursts are small enough to fit entirely within the IUE aperture. They quantify the fraction of reprocessed UV emission as a ratio between

\begin{displaymath}F_{\rm FIR} = 1.26 \times 10^{-11}[2.58\,f_\nu (60) + f_\nu (100)]\,{\rm erg\,cm^{-2}\,s^{-1}} \end{displaymath} (1)

for $60\,{\rm\mu m}$ and $100\,{\rm\mu m}$ IRAS flux densities in Jy, and $F_{1600} = \nu f_\nu$ evaluated at $\nu = c/1600\,{\rm\AA}$. Figure 1 plots this ratio versus $\beta$ for the 43 sources which (a) appear in their Fig. 1, and (b) have flux densities in the Version 2.0 IRAS Faint Source and/or Point Source Catalogs. The local starbursts occupy a predictable locus in the diagram, extending from blue, metal-poor systems at the lower left to reddened, dusty systems at the upper right.


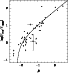  \begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{Ck051_f1.eps}} \end{figure} Figure 1: Far-IR-to-UV flux ratio vs. UV spectral slope. Estimates for local starbursts are triangles (for IRAS PSC flux densities), circles (for IRAS FSC flux densities), or pairs of arrows (for FSC $60\,{\rm\mu m}$ detections and $100\,{\rm\mu m}$ upper limits). The fit and (for NGC2537) representative error bars are taken from Meurer et al. (1999). cB58 is an open square.
Open with DEXTER

To place cB58 on this diagram, we first measure $\beta$ from the rest-UV spectrum of Pettini et al. (2000), according to the prescription of Meurer et al. (1999) for the sake of consistency. A least-squares fit (with iterative $\pm 3\sigma$ rejection) to eight spectral windows between 1100 and $1975\,{\rm\AA}$ gives $\beta = -1.12 \pm 0.10$, slightly bluer than the -0.8 ( $\beta = -2 -\alpha$ for $f_\nu \propto \nu^\alpha$) measured by Pettini et al. (2000) from their fit to continuum flux densities at 1300 and 1800Å. Meurer et al. (1999) also add an offset $\Delta \beta = -0.16 \pm 0.04$ for each source lacking spectral coverage longwards of 1975Å; making the same adjustment for cB58 yields our final value of $\beta = -1.28 \pm 0.14$. Next, we can estimate F1600 from the $V_{\rm AB} = 20.64 \pm 0.12$ observed by Ellingson et al. (1996), corresponding to a rest wavelength of 1474.9Å (for z = 2.7290: Teplitz et al. 2000):

F1474.9 = $\displaystyle \nu f_\nu({\rm observed}\ 5500\,{\rm\AA})$  
  = $\displaystyle 1.10 \pm 0.13 \times 10^{-13}\,{\rm erg\,cm^{-2}\,s^{-1}}.$ (2)

Scaling this flux by a factor $(1600/1474.9)^{1 + \beta} = 0.98 \pm 0.01$ then gives $F_{1600} = 1.07 \pm 0.14 \times 10^{-13}\,{\rm erg\,cm^{-2}\, s^{-1}}$.

Our final step is to derive $F_{\rm FIR}$ from our observed 1.2mm flux density. We must multiply the observed $\nu f_\nu = 2.65\times 10^{-15}\,{\rm erg\,cm^{-2}\,s^{-1}}$ by a rest-frame ratio of the form

\begin{displaymath}{\frac {F_{\rm FIR}}{\nu f_{\nu}}} = {\frac {1.26 \times 10^{... ...f_\nu (321.8)}} + {\frac {f_\nu (100)}{f_\nu (321.8)}}\right] \end{displaymath} (3)

where now $\nu = c\,(1+z)/1.2\,{\rm mm} = c/321.8\,{\rm\mu m}$. We must evaluate the term in brackets by assuming some rest-frame SED for cB58. Since comparably deep SCUBA observations of cB58 at $850\,{\rm\mu m}$ have yielded both a detection of $4.2 \pm 0.9\,{\rm mJy}$ (van der Werf et al. 2001) and a $3\sigma$ upper limit of $3.9\,{\rm mJy}$ (Sawicki 2001), the prospects for an observationally-derived SED are not encouraging. Instead, we simply extend the scaled-up starburst hypothesis for LBGs: we assign to cB58 a dust emissivity index $\epsilon = 2$ and dust temperature $T_{\rm d} = 33.0 \pm 4.5\,{\rm K}$ (the mean and dispersion of the $60/100\,{\rm\mu m}$ color temperatures for the local galaxies in Fig. 1, as determined from $\epsilon = 2$ modified Planck function fits). We then predict an observed flux in the rest-FIR window of $1.28^{+1.63}_{-0.84}\times 10^{-13}\,{\rm erg\,cm^{-2}\,s^{-1}}$, with large and asymmetric error bars dominated by the uncertainty in $T_{\rm d}$. We emphasize that our extrapolated FIR flux is conservatively large: adoption of $\epsilon = 1$ and the corresponding mean $T_{\rm d} = 40.7 \pm 7.1\,{\rm K}$ would have lowered our estimate by a factor of two. We have also ignored the potential impact of optically thick dust emission, or of a dust component colder than 33.0K which could dominate the $321.8\,{\rm\mu m}$ emission but contribute little to $F_{\rm FIR}$.

When plotted in Fig. 1, cB58 falls below and/or to the right of all objects except UGC6456. While the scatter in the local sample is large, it is strictly true that relative to the fit by Meurer et al. (1999), cB58 appears to have too red a UV spectral slope for its $F_{\rm FIR}/F_{1600}$, and too low a far-IR-to-UV ratio (by a factor of $\sim$4.7) for its $\beta$.

4 Four estimates of the dust content in cB58

In physical terms, Fig. 1 suggests that cB58 has somewhat more dust than its far-IR emission predicts or somewhat less dust than its UV reddening predicts. We can explore these two possibilities by making four distinct estimates of the source's dust content on the basis of the local starburst analogy. We rely in particular on the effective attenuation curve $k^\prime(\lambda)$ and other empirical relations presented by Calzetti (2000) and references therein.

I. The far-IR-to-UV ratio

From their local starburst sample, Meurer et al. (1999) derive an empirical relation between $A(1600\,{\rm\AA})$ - the extinction at $1600\,{\rm\AA}$ - and the $F_{\rm FIR}/F_{1600}$ ratio:

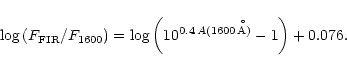\begin{displaymath}{\rm log}\,(F_{\rm FIR}/F_{1600}) = {\rm log}\left(10^{0.4\, A{{(1600\,{\rm {\AA}})}}} - 1\right) + 0.076. \end{displaymath} (4)

From our detection of cB58, we deduce $A(1600\,{\rm\AA}) = 0.75^{+0.63}_{-0.47}$; we then use the Calzetti attenuation curve to evaluate the color excess of the stellar continuum, $E_{\rm s}(B-V) = A(\lambda)/k^\prime(\lambda) = 0.075^{+0.063}_{-0.047}$.

II. The H ${\rm\alpha}$-to-H ${\rm\beta}$ ratio

Because ionizing stars are generally younger and more embedded than those which dominate the UV continuum, the color excess measured from observations of (gas) recombination lines, $E_{\rm g}(B-V)$, tends to exceed $E_{\rm s}(B-V)$ and can be straightforwardly measured using any optical extinction curve $k(\lambda)$. In cB58, Teplitz et al. (2000) report a Balmer decrement of $3.23 \pm 0.4$, which for the LMC extinction curve of Howarth (1986) implies $E_{\rm g}(B-V) = 0.12 \pm 0.12$ (rather than the former authors' $\sim$0.27). Since Calzetti (2000) finds that local starbursts obey the proportionality $E_{\rm s}(B-V) = 0.44\,E_{\rm g}(B-V)$, we conclude $E_{\rm s}(B-V) \simeq 0.053^{+0.051}_{-0.053}$.

III. The UV line spectrum and UV-to-H ${\rm\alpha}$ ratio

The rest-UV spectrum of cB58 obtained by Pettini et al. (2000) is of a quality which permits detailed population synthesis modelling. Pettini et al. (2000) themselves argue that the presence of P Cygni features due to massive stars supports a history of continuous star formation, with an Initial Mass Function (IMF) which is Salpeter up to $M \sim 100\,{M_\odot}$. De Mello et al. (2000) use the strengths of both O and B star features to argue that continuous star formation has proceeded for 25-100Myr, an age range whose lower end agrees with the SED fit of Ellingson et al. (1996). For a metallicity $Z = 0.4\,{Z_\odot}$ (comparable to the $Z \simeq 0.32\,{Z_\odot}$ measured by Teplitz et al. 2000), the appropriate Starburst99 models of Leitherer et al. (1999) predict that the intrinsic ratio $R_0 = F_{1475}/F_{\rm H\alpha}$ will rise from $\sim$98 to $\sim$120 over the course of the 25-100Myr interval. cB58 has an observed R = 90; the fact that R < R0 can be attributed to the fact that extinction is higher in the UV than in the optical. Using the Calzetti $k^\prime(\lambda)$, the LMC $k(\lambda)$, and the relation between color excesses, we can derive a single equation in $E_{\rm s}(B-V)$:

$\displaystyle {\rm log}\,(R/R_0) = 0.4\,E_{\rm s}(B-V) \Big(k(6563\,{\rm\AA})/0.44 - k^\prime(1475\,{\rm\AA})\Big)$     (5)

whose solution is $E_{\rm s}(B-V) = 0.042 \pm 0.021$. Such low values are required to avoid discordant UV and ${\rm H\alpha}$-based estimates of the star formation rate in cB58.

IV. The UV spectral slope

According to the empirical relation derived by Meurer et al. (1999), $A(1600\,{\rm\AA}) = 1.99(\beta - \beta_0)$ for $\beta_0 = -2.23$. Using the Calzetti $k^\prime(\lambda)$, we then derive $E_{\rm s}(B-V) = 0.190 \pm 0.028$. From the analogous relation between $\beta$ and $E_{\rm s}(B-V)$ in Calzetti (2000) and her suggestion of $\beta_0 = -2.3$, we would obtain $E_{\rm s}(B-V) = 0.236 \pm 0.032$.

5 Conclusions

Although our calculations of $E_{\rm s}(B-V)$ in cB58 take uncertain measurements and apply scaling relations about which there is substantial local scatter, it remains striking that three of the four estimates are in excellent agreement with each other. Only the UV spectral slope gives a value which is too high by a factor of 2-3. In principle, use of a steeper (e.g., SMC) extinction curve rather than the Calzetti $k^\prime(\lambda)$ would lower the color excess estimated from the observed $\beta - \beta_0$. However, a steeper extinction curve would also reduce the values of $E_{\rm s}(B-V)$ derived from $F_{\rm FIR}/F_{1600}$ and population synthesis models; the difference is real.

The preponderance of evidence for a low dust content in cB58 argues against analyses which would describe its location in Fig. 1 solely in terms of a far-IR deficit (e.g., Sawicki 2001; van der Werf et al. 2001). We can erase an apparent shortfall in $F_{\rm FIR}/F_{1600}$, for example, if we predict $F_{\rm FIR}$ from $\nu f_\nu(321.8\,{\rm\mu m})$ under the assumption that the dust in cB58 is as hot as the dust in the most extreme of the local starbursts, Tololo1924-416 ( $T_{\rm d} = 50.3\,{\rm K}$ for $\epsilon = 2$). However, since none of the other 42 systems has $T_{\rm d} > 40\,{\rm K}$, we would essentially be discarding the local starburst analogy for LBGs while failing to explain how two independent lines of evidence (the ${\rm H\alpha/H\beta}$ and UV/ ${\rm H\alpha}$ ratios) could still favor a low $E_{\rm s}(B-V)$. Similarly, we might imagine that the observed far-IR-to-UV ratio is depressed from its intrinsic value because UV emission reddened by dust along a favored line of sight is more highly magnified than the bulk of the far-IR emission. This scenario too seems implausible. Since the best lensing model of Seitz et al. (1998) predicts that a large fraction ($\sim$0.54-0.67) of the background source is magnified into the cB58 arc, and since UV continuum and ${\rm H\alpha}$ emission have broadly similar spatial distributions in local starbursts (Conselice et al. 2000), we would require exceptional tuning of the lensing geometry to produce agreement in all estimates of $E_{\rm s}(B-V)$ except that from $\beta$.

The most straightforward conclusion about cB58 is that its offset from the local relation in Fig. 1 has more to do with $\beta$ than with $F_{\rm FIR}/F_{1600}$ - i.e., that the local starburst analogy holds more robustly for all other properties of cB58 than it does for the UV spectral slope. Observational systematics may be partly responsible: a spectroscopic $\beta$ can be artificially reddened by differential refraction, while photometry can mislead due to intergalactic absorption - as in the case, perhaps, of the g band magnitude for cB58 used by Ellingson et al. (1996) to derive $E_{\rm s}(B-V) \sim 0.3$. More seriously, $\beta$ may simply be unreliable as a precise indicator of dust content for individual objects. One obvious concern is that different recipes for measuring $\beta$ yield different results for the same objects. cB58 is a case in point, with estimates ranging from our $-1.28 \pm 0.14$ to -0.8 (Pettini et al. 2000) to $-0.74 \pm 0.1$ (van der Werf et al. 2001). However, inconsistencies also exist at z = 0; measurements of $\beta$ from IUE spectra by Heckman et al. (1998) and Meurer et al. (1999), for example, differ by up to 0.77 for common sources. We have at least minimized the vulnerability of our own analysis to systematic errors by measuring $\beta$ with exactly the same prescription used for the comparison sample in Fig. 1. However, given that our understanding of $\beta$ in cB58 seems no more (if not less) secure than our understanding of the source's far-IR SED, sweeping conclusions about the long-wavelength properties of individual LBGs which depend heavily on their UV spectral slopes appear premature.

Recent measurements of the extragalactic far-IR background (e.g., Hauser et al. 1998; Fixsen et al. 1998; Lagache et al. 1999) have placed upper bounds on the luminosity density due to star formation as a function of redshift. These constraints have stimulated competing claims as to what fractions of the background are due to optically detectable star formation (e.g., Ouchi et al. 1999; Adelberger & Steidel 2000), optically invisible star formation (e.g., Barger et al. 2000), and dust-enshrouded nuclear activity (e.g., Almaini et al. 1999). While most of the global properties of cB58 do appear to obey the same scaling relations as local starbursts - encouraging news for the scaled-up starburst hypothesis for LBGs - the misleading redness of its UV spectral slope offers a cautionary example of how extinction corrections and extrapolations of SEDs to long wavelengths can go awry (see also Adelberger & Steidel 2000). For the moment, the true contribution of UV-selected samples to the far-IR background must therefore remain uncertain until we can detect enough LBGs in the rest far-IR to determine how closely they resemble cB58 and/or local starbursts as a group.

Acknowledgements

We thank Frank Bertoldi, Robert Zylka, and the staff of the IRAM 30m for help with the observations and data reduction. We also acknowledge helpful interactions with Tim Heckman, Claus Leitherer, Gerhardt Meurer, Max Pettini, Stella Seitz, and Christy Tremonti. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.

References

 
Copyright ESO 2001