A&A 372, 702-709 (2001)
DOI: 10.1051/0004-6361:20010433

FIRBACK. II. Data reduction and calibration of the 170  $\mathsf{\mu}$m ISO[*] deep cosmological survey

G. Lagache1 - H. Dole1,2


1 - Institut d'Astrophysique Spatiale, Bât. 121, Université Paris XI, 91405 Orsay Cedex, France
2 - Steward Observatory, University of Arizona, 933 N Cherry Ave, Tucson, AZ, 85721, USA

Received 24 January 2001 / Accepted 5 March 2001

Abstract
We present the final reduction and calibration of the FIRBACK ISOPHOT data. FIRBACK is a deep cosmological survey performed at 170 $\mu $m. This paper deals with the ISOPHOT C200 camera with the C160 filter. We review the whole data reduction process and compare our final calibration with DIRBE (for the extended emission) and IRAS (for point sources). The FIRBACK source extraction and galaxy counts is discussed in a companion paper (Dole et al. 2001).

Key words: instrumentation: miscellaneous - cosmology: observations - methods: miscellaneous


1 Introduction

With more than 150 hours of observations, FIRBACK (Far-InfraRed BACKground) is one of the largest observational programmes made with the ISOPHOT instrument on board the Infrared Space Observatory (ISO) satellite. This cosmological deep survey at 170 $\mu $m covers more than 4 square degrees located in two Northern and one Southern fields (Lagache 1998; Dole 2000a). There are 106 sources detected above the sensitivity limit (180 mJy, 4$\sigma$). The number of sources detected above 135 mJy ($ 3 \sigma $) is 196. The first result of this survey is the high number of sources observed when compared to no, or moderate, evolution models for infrared galaxies (e.g. Dole 2000a). Preliminary results in the so-called Marano1 field were published in Puget et al. (1999), and on the whole survey by Dole et al. (2000b). FIRBACK also allows for the first time the detection of the CFIRB fluctuations (Lagache & Puget 2000; Puget & Lagache 2001).

After a presentation of the observational issues of the FIRBACK survey, we present in this paper the final stage of the data reduction and calibration. We use the Phot Interactive Analysis (PIA, Gabriel et al. 1997) for the standard reduction and calibration (Sect. 3.1) with some extra developments: flat-fielding, transient corrections and reprojection (Sects. 3.2-3.7). In Sect. 4, we review our final map calibration and compare it with absolute photometric calibration from other instruments. We then conclude in Sect. 5.


 

 
Table 1: FIRBACK fields main characteristics.
Field l b surface $t_{\rm int}$ Number of
  deg deg deg2 sec rasters
FSM 270 -52 0.95 256 2$\times$11
FN1 84 +45 1.98 128 2$\times$9
FN2 65 +42 0.96 128 4$\times$4


2 FIRBACK observations

FIRBACK covers about 4 square degrees in 3 high galactic latitude fields (chosen to have very low HI column density, typically $N_{\rm HI} \le 10^{20}$ cm-2), the so-called N1 (FN1), N2 (FN2) and Marano (FSM) fields. The observations were performed at an effective wavelength of 170 $\,{\rm\mu m} $ with the C200 array ($2\times 2$ pixels) of ISOPHOT. The pixel field of view is 1.5 arcmin. We use the AOT (Astronomical Observation Template) PHT22 in the multi-pointing staring raster mode. Each FIRBACK field (Table 1) consists of several rasters of 17$\times$17 pixels[*]:

Each raster is performed in the spacecraft (Y, Z) coordinate system which is parallel to the edges of the detector array, with one pixel overlap in both Y and Z direction. The exposure time is 16 s per pixel and thus 128, 128 and 256 s per sky position in the FN1, FN2 and in the FSM fields respectively.

We also have a PHT25 measurement in the FSM1 field. This AOT is the absolute photometry mode for PHT-C, in which photometric calibration is achieved by chopping against the internal fine calibration source. For low fluxes (i.e. in our case), chopping is also done against the switched-off "Fine Calibration Source'', which has a temperature level of about 4 K. This is the temperature of the optical support on which the instrument is mounted. Such a measurement serves to define a zero point. This mode is especially well suited for observations aiming at accurate determination of the absolute brightness of the background emission.

3 Data reduction

  
3.1 PIA data reduction and calibration

We use PIA, the ISOPHOT Interactive Analysis software version 7.2.2 (Gabriel et al. 1997), to correct for instrumental effects, the glitches induced by cosmic particles and to provide an initial calibration. First we apply the non-linearity correction due to 2 independent effects: the non-linearity of the Cold Readout Electronics and the downward curving ramp due to de-biasing. Deglitching is performed for each individual ramp and then the mean signal per position is derived by averaging the ramp slopes (we do not apply any transient correction at this stage). We then apply a second deglitching (for every chopper position, a "running mean'' method is applied; signals that are far away by a number of sigma, typically 5, are flagged). The dark current, which represents less than 5$\%$ of the signal, is subtracted using the orbit dependent calibration files. We also apply the "reset interval correction'', a correction which represents less than 6$\%$ of the signal.

We do exactly the same data reduction for the two "Fine Calibration Source'' (FCS) measurements. The FCS measurements before and after the observation vary by less than 3$\%$ for most of the rasters. We decide to perform the first calibration (from V/s to MJy/sr) by deriving the mean value of the two FCS measurements. We prefer not to use the interpolation between the two FCSs when they are different since it may induce Long Term Transients (LTT) that are not necessary real. On the contrary, when real, the interpolation bewteen the two FCSs could correct for the LTT, but we prefer to correct the LTT following Sect. 3.3.

At this stage of the data reduction, we have the signal variation (in MJy/sr) as a function of time (or position) for each pixel in each raster. We see from Fig. 1 that the instrumental noise is very low. We have, per sky position, a very high reproductibility of the data.


  \begin{figure} \par\includegraphics[width=7.7cm,clip]{1060_fig1.eps} \end{figure} Figure 1: Signal in MJy/sr of the four pixels as a function of the sky position for one raster. The mean signal level is not the same (no flat-field correction has been applied at this stage) but the signal variations are highly reproductible.
Open with DEXTER

3.2 The PHT25 measurement

The AOT PHT25 absolute measurement in the FSM1 field has the following characteristics (Fig. 2):


  \begin{figure} \par\includegraphics[width=8cm,clip]{1060_fig2.eps} \end{figure} Figure 2: Absolute PHT25 measurement sequence for one pixel (in V/s).
Open with DEXTER

With this measurement we check that:

We obtain for the sky measurement a brightness[*] of $3.10\pm 0.14$ MJy/sr, to be compared to the value measured on the final map (Fig. 6), which is 3.08 MJy/sr. We have a very good agreement between both measurements; we do not observe any significant discrepancy between the "raster'' and the "absolute'' mode calibration.

  
3.3 Long term transients

Long Term Transients (LTT) still have an unknown origin. They are observed on a characteristic time scale of about 60-80 min and are the main sensitivity limitation of the ISOCAM diffuse emission analysis (Miville-Deschênes et al. 2000). LTT are observed in FIRBACK data (Fig. 3) but only for some rasters and pixels. We first tried to correct the LTT using the method developped by Miville-Deschênes et al. (2000) for ISOCAM; however, this method fails since (1) ISOCAM and ISOPHOT detectors are different and (2) the redundancy in our observations is too low. The method developed for ISOCAM clearly detects the long term variation. However, for ISOPHOT, all detectors are not contaminated by the LTT (we see Fig. 3 that the LTT is not seen by the four pixels), which is not the case for ISOCAM, where all detectors have at a first order the same behaviour. Therefore, we correct the LTT by assuming that the pixel, in each raster, that exhibits the smallest long term variation (or smallest slope) is representative of the sky. Figure 3 shows the results before and after the correction.


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{1060_fig3.eps} \end{figure} Figure 3: Illustration of the LTT correction on a $17\times 17$raster. The thick solid line is the pixel signal (median filtered over 9 position) with the smallest slope. The long term variation of the three other pixel signals (thin lines: dot, dot-dash, dash) are corrected in order to follow the same slope as the continuous line pixel signal. The result after correcting the slope is shown in thick lines. Note here that the signal of each pixel is not offseted after the LTT correction (this is the flat-field correction detailed in Sect. 3.4).
Open with DEXTER

  
3.4 Individual raster flat-fielding

The flat-field correction, for each individual raster, is directly estimated using the redundancy of our observations and comparing position by position the brightness of the 4 pixels. First, for each raster, we compute the responsivity of the four pixels with respect to the mean responsivity (Fig. 4) for each sky position. We see from Fig. 4 that each pixel has some high frequency instrumental noise. What we are interested in is the low-frequency difference of responsivity between the four pixels. Therefore, we derive the flat-field correction by computing a 30-points running median (and the mean of the correction is equal to 1 per sky position).

The correction is rather constant for the whole 56 rasters and equal on average to: $1.04 \pm 0.02$, $0.91 \pm 0.02$, $1.09 \pm 0.02$ and $ 0.94 \pm 0.02$for pixel 1, 2, 3 and 4 respectively. This highly reproductable behaviour may be used to correct for the flat-fielding in any other C-160 observation that has no redundancy.


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{1060_fig4.eps} \end{figure} Figure 4: Relative response of the 4 pixels as a function of the sky position. The flat-field correction is obtained by computing a 30-points running median (and the mean correction is equal to 1).
Open with DEXTER

3.5 Transients induced by energetic cosmic rays

The procedure described in Sect. 3.4 also reveals some long term transients induced by energetic cosmic rays, as can been seen in Fig. 4 for the dashed line signal around the sky position number 130. These effects induced by energetic cosmic rays are quite rare: we detect only 13 events for FIRBACK (to be compared to 4 detectors $\times$ 56 rasters = 224 timelines). After such a cosmic ray, the signal may show an exponential-like behaviour (with a variable time constant). We correct for such events manually before computing the flat-field correction.

  
3.6 Short term transients

After a sudden increase of flux, most infrared detector signals shows an instantaneous jump followed by a slow rise to the stabilisation level; this is the short term transient. In most observations, the stabilisation level is never reached, due to the limited integration time per chopper plateau.

For the ISOPHOT C200 camera, we have information on the short term transients using our PHT25 absolute measurements. We see in Fig. 5 the signal behaviour of the PHT25 sky measurements for the 4 pixels. These measurements follow the "FCS dark'' observation, whose signal is 10 times weaker (see Fig. 2). We clearly see in Fig. 5 a short term transient before the stabilisation. The instantaneous signal jump is of the order of 85$\%$; and the stabilisation is reached in several tens of seconds.


  \begin{figure} \par\includegraphics[width=9.5cm,clip]{1060_fig5.eps} \end{figure} Figure 5: Signal variation after a flux step (PHT25 sky measurements that follow the "FCS dark'' measurements). For all pixels, the instantaneous jump is at the $\sim $85$\%$ level and the stabilisation is reached in about 80 s.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{1060_fig6.eps} \end{figure} Figure 6: Map of the FIRBACK South Marano (FSM) field. FSM1 is the square on the left, and the rectangle is composed of FSM2, 3 and 4 from top to bottom.
Open with DEXTER

For FIRBACK field observations, the short term transient effect is limited due to the flatness of the fields. Flux variations are very smooth and weak, except when point sources are observed. Therefore, no correction is applied for the diffuse emission. In return, for point sources, a correction of 10$\%$ is applied (this 10$\%$ is derived using the flux measured after 16 s FIRBACK integration time compared to the stabilised flux).

For the FCS FIRBACK measurements, no correction is applied since (1) the difference between the stabilised signal in the PHT25 FCS measurement and the one measured in 32 s (which is the integration time on the FCS) is less than 4$\%$ and (2) the second FCS observation is at the same level as the FIRBACK sky observation (no flux step) and the two FCS measurements (before and after one observation) differ by less than 3$\%$ for most of the rasters.

  
3.7 General "flat-fielding''

The different rasters in the same field have been done at different time (there can be several months between the rasters). Therefore, the absolute calibration performed using the FCS measurements can be slightly different from one raster to another. This difference is observed in the final FIRBACK maps as discontinuities between individual rasters.

To correct for this small absolute calibration difference, we apply a "general flat-field'' correction. This correction makes consistent the level of each raster with its neighbourhood. It consists of adding or subtracting offsets, the sum of the offsets being 0. This effect is very small, less than 5$\%$, except for one raster in FN1 which shows a discontinuity with its neighbourhood of about 11$\%$.

  
3.8 Reprojection

The flux is finally projected on a $10\hbox{$^{\prime\prime}$ }\times 10\hbox{$^{\prime\prime}$ }$ coordinate grid using our own projection procedure. The procedure is the following:

We have checked the accuracy of our method using simulated sky maps, containing both extended emission and point sources. Our reprojection does not change the background brightness and the sources flux (at the 1$\%$ level). One has, however, to note that this method is particularly well adapted to cosmological observations: weak sources on a rather flat background (for fields with very bright sources, this method may not preserve the point source photometry).


  \begin{figure} \par\includegraphics[width=12cm,clip]{1060_fig7.eps} \end{figure} Figure 7: Map of the FIRBACK North 1 (FN1) field.
Open with DEXTER

The final maps are shown in Figs. 6, 7 and 8 for the three fields respectively.

  
4 Calibration

The extended emission calibration has changed by a factor of about 2 between PIA version 6 and PIA version 7. A large part of this factor comes from the different footprint solid angle values used in the different PIA versions.

  
4.1 Footprint observations around Saturn

During the revolution 409, ISOPHOT made several tens of pointing around Saturn at distances between 4.2 and 45.4 arcmin in order to map the extended wings of the PHOT footprint at 170 $\,{\rm\mu m} $during about 5 hours. Observations were made in the Y and Z satellite axis directions. Figure 9 shows the observed pattern on an IRAS 100 $\mu $m map. All directions were observed twice, back and forth. Observations were performed with the following AOTs: PHT 37-38-39 (sparse maps; PHT37: FCS; PHT38: sky; PHT39: FCS) for distances between 4.2 and 27.6 arcmin, and PHT25 (absolute photometry) at the largest distance. Integration times are around 150 s for PHT38, 200 s for PHT37-39 and 400 s for PHT25.

We use PIA V7.2.2 for the data reduction and calibration. For each detector and each position, we keep only the second half of the data corresponding to the stabilised signal. These observations have no transients induced by cosmic rays and we do not apply any flat-field correction. Sixty seven files were used, the others being either unreadable (3 files) or saturated (3 files). Results are presented in Figs. 10 and 11 for all data in the Y and Z direction respectively. Each pixel is plotted and is used as an independent measurement.

4.2 Comparison of the footprint model with Saturn observations

A model for the ISOPHOT footprint has been developed at Heidelberg (Klaas et al., private communication) based on the ISOCAM footprint routines. This model includes the optical characteristics of the telescope, the primary and secondary mirrors, and the filters and detectors. We have used this program to compute the ISOPHOT footprint up to 20 arcmin with the 170 $\mu $m bandpass filter. Results of the model are shown in Fig. 12 together with the Saturn measurements for the Z axis. To make this comparison, we have assumed for Saturn a flux of 32000 Jy and removed the background using the PHT25 measurement.

We see a very good agreement between the model and the measurements. However, around 4.5 arcmin from Saturn, some data, coming from one Y direction scan (only one position), have a significantly higher flux than the model prediction. Data at similar distances from Saturn in other scans cannot be used due to saturation problems. Therefore, we interpret this discrepancy as due to detector saturation problems (one can note, however, that the contribution of these data points to the solid angle is lower than a few percent).


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{1060_fig8.eps} \end{figure} Figure 8: Map of the FIRBACK/ELAIS North 2 (FN2) field.
Open with DEXTER


  \begin{figure} \includegraphics[width=8.8cm,clip]{1060_fig9.eps} \end{figure} Figure 9: ISOPHOT pointing positions (circles) around Saturn on the IRAS 100 $\mu $m map. Saturn positionnal changes during the observations have been computed using the ephemerids of the Bureau des Longitudes (Berthier 1998) and are represented by a small segment at the middle of the cross.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{1060_fig10.eps} \end{figure} Figure 10: Y direction measurements around Saturn. Squares are forward data, crosses, backward data. Dispersion bewteen the 4 pixels at each position comes mainly from the non correction of the flat-field.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.3cm,clip]{1060_fig11.eps} \end{figure} Figure 11: Z direction measurements around Saturn. Triangles are forward data, diamonds, backward data.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{1060_fig12.eps} \end{figure} Figure 12: ISOPHOT footprint model (continuous line) compared to ISOPHOT measurements around Saturn for the Z axis.
Open with DEXTER

In conclusion, the ISOPHOT footprint measurements and model at 170 $\mu $m are in very good agreement. We therefore use, in the following, the model (from Klaas et al., private communication) as the definitive footprint at 170  $\,{\rm\mu m} $.

4.3 The extended brightness photometric correction factor

In PIA V6.5 the solid angle used to convert the flux in brightness was that of the pixel ( $1.88\times10^{-7}$ sr); in PIA V7.2.2, it is the footprint model's one but truncated at 4.1 arcmin ( $2.67\times 10^{-7}$ sr). The full solid angle of the footprint is equal to $3.0\times 10^{-7}$ sr. Therefore, there is a photometric correction factor to be applied to the extended emission:

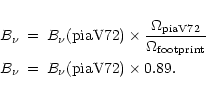
\begin{eqnarray*}B_{\nu} &=& B_{\nu}({\rm piaV72}) \times \frac{\Omega_{\rm piaV... ...rm footprint}}\\ B_{\nu} &=& B_{\nu}({\rm piaV72}) \times 0.89. \end{eqnarray*}


After correction of the absolute calibration of the extended emission, point source fluxes (given in Dole et al. 2001) are computed using the footprint model (Klaas et al., private communication).

4.4 The rejection rate

Unique measurements have been done by the ISOPHOT team during the eclipse of the sun by the earth (Kranz et al. 1998; Klaas et al. 1998a; Lemke et al. 1998) by pointing at a sky region at 60$^\circ$ from the sun before, during, and after the eclipse. These measures reveal no signal variation, leading to an upper limit of 10-13 at 60$^\circ$ for the straylight rejection rate. This exceptional measurement clearly shows that there is no contribution to the flux from the far-side lobes. This demonstrates that ISO is able to make absolute measurements of the extended emission and gives a high degree of confidence to our absolute photometric calibration.

4.5 Comparison with DIRBE extended brightness

We can now compare the extended ISOPHOT FIRBACK brightness with the predicted one using DIRBE and HI measurements. Because of the size of the DIRBE beam, this comparison is only feasible due to the flatness of the FIRBACK fields; this flatness is observed with DIRBE on several degrees around each FIRBACK field.

The sky measurement is the sum of the zodiacal light, Cosmic Infrared Background (CIB) and dust interstellar emission. For each field the zodical light, at the time of the observation, has been computed using the Reach et al. (1995) DIRBE model. The CIB is extrapolated at 170 $\mu $m using the DIRBE measurements of Lagache et al. (2000). For the dust emission, we compute its contribution using (1) the HI column density from the Leiden-Dwingeloo survey, Hartmann & Burton 1997 (we prefer to use the HI column density rather than the DIRBE brightness since DIRBE data are very noisy in FIRBACK fields) and (2) the emissivity from Lagache et al. (2000). The final predicted emission at 170 $\mu $m for the three fields is shown in Table 2. It is in remarkable agreement with the measured ISOPHOT brightness[*].


 

 
Table 2: Cosmic Infrared Background (CIB) from Lagache et al. (2000), zodiacal (from Reach et al. 1995) and dust emission (from Lagache et al. 2000) at 170 $\mu $m for the three FIRBACK fields (in MJy/sr). The total emission is the sum of the three contributions for each field. There is a remarkable agreement between the predicted brightness and the measured ISOPHOT one.
  FN1 FN2 FSM
CIB $1.10\pm0.2$ $1.10\pm0.2$ $1.10\pm0.2$
Zodiacal $0.71\pm0.1$ $0.80\pm0.1$ $0.75\pm0.1$
$N_{\rm HI}$ (cm-2) $8.2\times 10^{19}$ $7.7 \times10^{19}$ $1.0 \times10^{20}$
Dust $1.17\pm0.35$ $1.09\pm0.33$ $1.42\pm0.43$
Total predicted $2.98\pm0.41$ $2.99\pm0.40$ $3.27\pm0.48$
PHOT measured $3.01\pm0.14$ $2.97\pm0.17$ $3.39\pm0.12$



  \begin{figure} \par\includegraphics[width=8.2cm,clip]{1060_fig13.eps} \end{figure} Figure 13: Comparison of the ISOPHOT 170 $\mu $m measured flux with the IRAS extrapolated ones. Data are compatible with a slope of unity.
Open with DEXTER

4.6 Comparison with IRAS point sources measurements

The absolute flux calibration of ISOPHOT is derived using calibration standards such as planets, asteroids or stars (Klaas et al. 1998b; Schulz et al. 1999; ISO Consortium 2000a, 2000b). One can however check, using IRAS detected sources in FIRBACK fields, the consistency between IRAS 60 and 100 $\mu $m flux and the ISOPHOT 170 $\mu $m one. However, we have to keep in mind that it is very difficult to extrapolate the IRAS fluxes at 170 $\mu $m (one can have a factor 2 to 3 in the extrapolation using different models or black-body temperatures).

Twelve FIRBACK sources, well identified as very nearby non interacting galaxies, have IRAS 60 and 100 $\mu $m flux counterparts, measured with SCNAPI[*]. We extrapolate the 60 and 100 $\mu $m IRAS flux using the template spectra of Dale et al. (2000). These spectra are based on the IRAS 60/100 color ratio and are thus well adapted. The comparison is shown in Fig. 13. Uncertainties on the extrapolation, that take into account only the errors on the 100 and 60 $\mu $m fluxes (and not the model uncertainty), are very large. Data are compatible with a slope of unity; but this comparison is only illustrative.

5 Conlusions

We have presented in this paper the final FIRBACK data reduction using: (1) The Phot Interactive Analysis version 7.2.2 and (2) extra developments (corrections of the flat-field, long and short term transients, transients induced by cosmic rays and adapted reprojection). Most of these extra developments have been made possible by the perfect redundancy inside each raster (one pixel overlap in both Y and Z direction). We have then checked the absolute calibration using PHT25 measurements and the footprint measured on Saturn (compared to the footprint model). We have shown that the ISOPHOT 170 $\mu $m extended emission calibration has to be corrected by a factor 0.89, which comes from the difference in solid angle between the PIA v7.2 and the modeled footprint.

Using this data reduction and calibration, we obtain an absolute calibration which is in remarquable agreement (better than 10$\%$) with brightness extrapolation that uses DIRBE data and HI column density measurements. We have in FIRBACK fields a very high signal to noise ratio (greater than 50). The main limitation comes in fact from the extragalactic source confusion itself (Dole et al. 2001).

Acknowledgements
We would like to thank A. Abergel, C. Gabriel, U. Klaas, M.-A. Miville-Deschênes and the ISOPHOT team for many interactions concerning the data reduction and the footprint analysis. We thanks Danny Dale for his help in using the template spectra for IRAS extrapolation. We thank J. L. Puget for his helpful advice all along the data reduction process.

References

 
Copyright ESO 2001