A&A 372, 364-376 (2001)
DOI: 10.1051/0004-6361:20010449

FIRBACK: III. Catalog, source counts, and cosmological implications of the 170 $\mu $m ISO[*] deep survey[*]

H. Dole1,2 - R. Gispert1 - G. Lagache1 - J.-L. Puget1 - F. R. Bouchet3 - C. Cesarsky4 - P. Ciliegi5 -
D. L. Clements6 - M. Dennefeld3 - F.-X. Désert7 - D. Elbaz8,9 - A. Franceschini10 - B. Guiderdoni3 -
M. Harwit11 - D. Lemke12 - A. F. M. Moorwood4 - S. Oliver13,14 - W. T. Reach15 -
M. Rowan-Robinson13 - M. Stickel12


1 - Institut d'Astrophysique Spatiale, bâtiment 121, Université Paris Sud, 91405 Orsay Cedex, France - Present address: Steward Observatory, University of Arizona, 933 N Cherry Ave, Tucson, AZ 85721, USA
2 - Institut d'Astrophysique de Paris, 98bis Bd. Arago, 75014 Paris, France - ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany - Osservatorio Astronomico di Bologna, Via Ranzani 1, 40127 Bologna, Italy - Department of Physics & Astronomy, Cardiff University, PO Box 813, Cardiff CF22 3YB, UK - Laboratoire d'Astrophysique, Obs. de Grenoble, BP 53, 414 Av. de la piscine, 38031 Grenoble Cedex 9, France
3 - Service d'Astrophysique, DAPNIA, DSM, CEA Saclay, 91191, Gif-sur-Yvette, France - Physics and Astronomy Departments, University of California, Santa Cruz, CA 95064, USA - Astronomy Departement, Padova University, Vicolo Osservatorio, 5, 35122 Padova, Italy - 511 H. Street S. W., Washington DC 20024-2725, USA; also Cornell University - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany - Astrophysics Group, Imperial College, Blackett Laboratory, Prince Consort Road, London SW7 2BZ, UK - Astronomy Centre, University of Sussex, Falmer, Brighton BN1 9QJ, UK - IPAC, California Institute of Technology, Pasadena, CA 91125, USA

Received 23 January 2001 / Accepted 5 March 2001

Abstract
The FIRBACK (Far Infrared BACKground) survey is one of the deepest imaging surveys carried out at 170 $\mu $m with ISOPHOT onboard ISO, and is aimed at the study of the structure of the Cosmic Far Infrared Background. This paper provides the analysis of resolved sources. After a validated process of data reduction and calibration, we perform intensive simulations to optimize the source extraction, measure the confusion noise ( $\sigma_{\rm c} = 45$ mJy), and give the photometric and astrometric accuracies. 196 galaxies with flux $S > 3 \sigma_{\rm c}$are detected in the area of 3.89 square degrees. Counts of sources with flux $S > 4 \sigma_{\rm c}$present a steep slope of $3.3 \pm 0.6$on a differential "logN-logS'' plot between 180 and 500 mJy. As a consequence, the confusion level is high and will impact dramatically on future IR deep surveys. This strong evolution, compared with a slope of 2.5 from Euclidian geometry, is in line with models implying a strongly evolving Luminous Infrared Galaxy population. The resolved sources account for less than 10% of the Cosmic Infrared Background at 170 $\mu $m, which is expected to be resolved into sources in the 1 to 10 mJy range.

Key words: cosmology: miscellaneous - galaxies: infrared - galaxies: evolution - galaxies: statistics


1 Introduction

The European Space Agency's Infrared Space Telescope, ISO (Kessler et al. 1996; Kessler 2000) performed about 1000 programs between 1995 and 1998, including the deepest extragalactic observations ever made in the mid- and far-infrared range with an unprecedented sensitivity (for a review see Genzel & Cesarsky 2000). Most of these deep cosmological observations aim at probing galaxy formation and evolution, mainly by resolving the Cosmic Infrared Background (CIB) into discrete sources, but also by studying the CIB fluctuations.

Understanding and observing the sources contributing to the extragalactic background at all wavelengths has become one of the most rapidly evolving fields in observational cosmology since the discovery of the CIB (Désert et al. 1995; Puget et al. 1996). In particular, deep observations from space with ISO, and from the ground with SCUBA on the JCMT and MAMBO on the IRAM 30 m telescope, respectively in the infrared, submillimeter and millimeter range, together with observations at other wavelengths for source identification (in the radio and optical / NIR range), begin to provide a global view of galaxy evolution. The long wavelength observations reveal galaxies through their dust emission, providing a complementary and significantly different view to that of optical and UV observations.

The ISO legacy regarding galaxy evolution includes a number of significant studies. About a dozen deep surveys have been conducted in the mid infrared with ISOCAM (Cesarsky et al. 1996), reaching sensitivity levels of $30 \, \mu$Jy at 15 $\mu $m (Altieri et al. 1999; Elbaz et al. 1999; Aussel et al. 1999; Désert et al. 1999; Flores et al. 1999). The major results of the mid-infrared surveys involve source counts obtained by combining a number of surveys. These exhibit strong evolution with a steep slope up to $2.4 \pm 0.2$ (Elbaz et al. 1999) in the integral $\log N$-$\log S$ diagram. Multiwavelength identifications and redshift distributions constrain the nature of the sources (Flores et al. 1999; Aussel et al. 1999; Chary & Elbaz 2001): most of them are Luminous Infrared Galaxies, LIRG's, at a median redshift of 0.8.

In the far-infrared, the 60-240 $\mu $m spectral domain was explored using the imaging capabilities of ISOPHOT (PHT) (Lemke et al. 1996). As indicated in Fig. 1 of Gispert et al. (2000), this domain corresponds to the maximum emission of the extragalactic background . The main surveys published were carried out in the Lockman Hole on 1.1 sq. deg at 90 and 170 $\mu $m by Kawara et al. (1998), in the FIRBACKMarano field at 170 $\mu $m by Puget et al. (1999) and in the entire FIRBACKsurvey by Dole et al. (1999), in SA57 on 0.4 sq. deg at 60 and 90 $\mu $m by Linden-Vornle et al. (2000), and in 8 small fields covering nearly 1.5 sq. deg at 90, 120, 150 and 180 $\mu $m by Juvela et al. (2000). A shallower survey was performed over an area of 11.6 sq. deg at 90 $\mu $m by Efstathiou et al. (2000) as part of the ELAIS survey. The ISOPHOT Serendipity Survey at 170 $\mu $m (Stickel et al. 1998, 2000) took advantage of ISO slews between targets to detect about 1000 sources between 1 and 1000 Jy.

In the 60 to 120 $\mu $m spectral windows, the C_100 camera, with its $3 \times 3$ array of Ge:Ga detectors, was subject to strong transients and spontaneous spiking, limiting the sensitivity (which is a few times better than IRAS); fortunately, new attemps to overcome these problems with a physical model of the detector seem promising (Coulais et al. 2000; Lari & Rodighiero 2001). At 60 and 90 $\mu $m, no clear evolution in the source counts is observed, since both non-evolution and moderate evolution models can still fit the data (Linden-Vornle et al. 2000; Efstathiou et al. 2000). Furthermore, the K-correction[*] (Fig. 1 from the model of Dole 2000 and Lagache et al. 2001) between 30 and 120 $\mu $m is not favorable for probing galaxy evolution up to redshifts $z\sim 1$. With the ELAIS survey, Serjeant et al. (2001) were able to derive the luminosity function of galaxies up to redshift $z \simeq 0.3$.


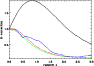  \begin{figure} \par\epsfxsize=8.2cm \epsfbox{1054hdole_fig01.eps} \end{figure} Figure 1: K-corrections at 15 (dot-dashed curve), 60 (dotted curve), 90 (dashed curve) and 170 $\mu $m (solid curve) for a LIRG (Dole 2000; Lagache et al. 2001). The wavelengths of cosmological interest are thus around 15 $\mu $m and above 150 $\mu $m where they benefit from the "negative K-correction effect'', increasing the sensitivity up to redshifts around unity.
Open with DEXTER

At longer wavelengths (120-240 $\mu $m), the C_200 camera, a $2 \times 2$ array of stressed Ge:Ga detectors, is more stable and most of the detectors' behaviour can be characterized and, if needed, properly corrected (Lagache & Dole 2001). The K-correction at 170 $\mu $m (Fig. 1), as well as in the mid-infrared around 15 $\mu $m, is favorable and becomes optimal at redshifts around 0.7. The first analysis of deep surveys at 170 $\mu $m showed a large excess in source counts over predictions of no-evolution models at flux levels below 200 mJy (Kawara et al. 1998; Puget et al. 1999), suggesting strong evolution. Recent work by Juvela et al. (2000) is in agreement with this picture, and includes the far-infrared colors of the sources.

The FIRBACKsurvey (acronym for Far Infrared BACKground) was designed to broaden our understanding of galaxy evolution with its accurate source counts and its catalog allowing multiwavelength follow-up. It also enabled studies of the CIB fluctuations (first detected in the first area surveyed in the FIRBACK program by Lagache & Puget 2000). FIRBACKis one of the deepest surveys made at 170 $\mu $m and the largest at this depth. This survey used about 150 h of observing time, corresponding to the 8th largest ISO program (Kessler 2000).

The aim of this paper is to provide the catalogs and the source counts of the FIRBACKsurvey. Preliminary FIRBACKsource counts were published by Lagache et al. (1998) and Puget et al. (1999) on the 0.25 sq. deg Marano 1 field, and by Dole et al. (2000) on the entire survey. An overview of this paper is as follows. Section 2 presents the observational issues of the FIRBACKsurvey and Sect. 3 summarizes the data processing and the calibration (a complete description can be found in Lagache & Dole 2001). Section 4 explains the extensive simulations and the source extraction technique. Section 5 details the flux measurement by aperture photometry, analyses the photometric and astrometric noise of the sources and provides estimates of accuracies. In Sect. 6 we present the final FIRBACKcatalog ( $S > 4\sigma_{\rm s}$), and the complementary catalog ( $3\sigma_{\rm s} < S < 4\sigma_{\rm s} $) extracted for follow-up purposes. Section 7 describes the corrections that have been applied (completeness, Malmquist-Eddington effect) and presents the final FIRBACKsource counts at 170 $\mu $m. Section 8 compares our results to other observations as well as models, and discusses the cosmological implications of the FIRBACKsource counts: strong evolution and resolution of the CIB.

2 The FIRBACKsurvey: Fields & observations

2.1 Fields

FIRBACKis a survey at 170 $\mu $m covering four square degrees in three high galactic latitude fields, called FIRBACKSouth Marano (FSM), FIRBACKNorth 1 (FN1) and FIRBACK/ ELAIS North 2 (FN2) (see Table 1). They were chosen to have foreground contaminations as low as possible: the typical HI column-density is less than or equal to $N_{\rm H} \simeq 10^{20}$ cm-2, and the 100 $\mu $m brightness is less than 1.7 MJy/sr on DIRBE maps. In addition, FN1 and FN2 were chosen to match some fields from the European Large Area ISO Survey, ELAIS (Oliver et al. 2000), which had been covered at 15 $\mu $m with ISOCAM (Serjeant et al. 2000) and at 90 $\mu $m with ISOPHOT (Efstathiou et al. 2000). FN2 observation time is a collaboration between the ELAIS and FIRBACKconsortia.
 

 
Table 1: Fields of the FIRBACKsurvey at 170 $\mu $m.
field $\alpha _{2000}$ $\delta _{2000}$ l b S100a
FSM 03$^{\rm h}$11$^{\rm m}$ $-54^{\circ}$45$^\prime$ 270$^{\circ}$ $-52^{\circ}$ 1.42
FN1 16$^{\rm h}$11$^{\rm m}$ $+54^{\circ}$25$^\prime$ 84$^{\circ}$ $+45^{\circ}$ 1.17
FN2 16$^{\rm h}$36$^{\rm m}$ + $41^{\circ}$05$^\prime$ 65$^{\circ}$ $+42^{\circ}$ 1.19
a Mean brightness at $100~ \mu$m (MJy/sr) in DIRBE maps
(annual average, zodiacal component subtracted).



 

 
Table 2: Observational characteristics of the FIRBACKfields.
field FSM FN1 FN2
area (sq. deg) 0.95 1.98 0.96
rastersb 4 2 2
redundancyc 16 8 8
$t_{\rm int}$d (sec) 256 128 128
raster stepe (pixels) 1,1 1,1 1,1
offsetf (pixels) 0.5,0.5 <1g <1g
  2,2a    
date Nov.-1997 Dec.-1997 Jan.-1998
  Jul.-1997a    
revolutionh 739 to 744 753 to 774 785 to 798
  593a    
a In the case of the FSM1 field only.
b Number of different rasters mapping the same field.
c Number of different observations per sky pixel on the
center of final coadded map.
d Integration time per sky pixel on the center
of final coadded map.
e Offset in pixel in the Y and Z directions of the spacecraft
between the steps on the raster.
f Offset in pixel between different rasters.
g Offset is irregular due to the rotation of the fields.
h ISO revolution numbers (or number range) of observation.


2.2 Observations

Observations were carried with ISO, using the ISOPHOT spectro-photo-polarimeter. We used the C_200 $2 \times 2$ pixel photometer and C_160 broadband filter centered at $\lambda = 170\, \mu $m. Scanning the sky was done in raster map mode, AOT P22, with one pixel offset between each pointing, to provide the redundancy. Individual rasters were shifted with respect to each other by a fraction of a pixel to provide proper sampling where possible. Table 2 summarizes the observational characteristics of the fields.

The FSM field is composed, for historical reasons, of four individual fields, called FSM1, 2, 3 and 4 (Fig. 6 in Lagache & Dole 2001). FSM1 on the one hand, and FSM2, 3 and 4 on the other, have been observed continuously: transient effects are thus reduced and no rotation of the field occurs between different rasters (same roll angle). FSM1 rasters are offset by two pixels in order to maximise redundancy and establish the ISOPHOT sensitivity for such observations, whereas FSM2, 3 and 4 are offset by a half pixel in both Y and Z directions to increase oversampling.

The FN1 field is composed of eleven individual fields (Fig. 7 in Lagache & Dole 2001), observed twice. Observations were not performed continuously, so that each individual raster has a different roll angle, giving a sampling of the sky that is non uniform.

The FN2 field is composed of nine individual fields (Fig. 8 in Lagache & Dole 2001), observed twice. The other characteristics are the same as for FN1.

   
3 Data reduction, instrumental effects, calibration, maps

The complete process of data reduction and calibration is described in Lagache & Dole (2001). Here, we merely summarize the different steps.

3.1 Interactive analysis

We made use of the PHT Interactive Analysis package (PIA) version 7.2.2 (Gabriel et al. 1997) in the IDL version 5.1 environment, to process the raw data (named ERD: Edited Raw Data) into brightnesses (named AAP: Astronomical and Application Product). After linearizing and deglitching the ramps, we applied the orbit-dependent dark and reset interval corrections. We calibrated the data with the two bracketing FCS lamps (Fine Calibration Source) values, using the mean value in order not to induce baseline effects.

3.2 Glitches, long term transients, flat fielding

Cosmic particles hitting the detector are easy to detect at the time of their impact, but they may cause response variations. On 224 different measurements (that is 56 independent rasters observed by 4 pixels), we report only 13 such cases, which are corrected. Furthermore, thanks to the high redundancy of each raster, a glitch cannot mimic a source because the same piece of the sky is observed independently by the four pixels of the photometer at different times.

Some long term transients (LTT) are seen in the data, and are understood to be the consequence of step fluxes seen by the photometer. During the FIRBACK observations, ISOPHOT was looking at relatively flat fields with low background, but was on more complex fields during the preceding observations. Our best data occur where the observations were made continuously. We correct for the LTT by forcing all the pixels to follow the time variations of the most stable pixel, which is assumed to represent the sky. This correction is found to be linear, and never exceeds 10%.

We then compute a flat field using the redundancy and apply the necessary corrections. The detector behaviour is highly reproducible, leading to constant flat field values: $1.04 \pm 0.02$, $0.91 \pm 0.02$, $1.09 \pm 0.02$and $ 0.94 \pm 0.02$for pixels 1, 2, 3 and 4 respectively.

3.3 Photometric correction

There is a difference of 11% between the solid angle value of the PHT footprint at 170 $\mu $m used by PIA and the value derived by calibration observations around Saturn and the model. We thus apply a multiplicative correcting factor of 0.89 to the brightness values given by PIA to take into account the real profile of the footprint.

3.4 Maps

For a given raster measurement, we project the signal from each pixel on a regular grid defined by the raster. Between each pointing, we make an interpolation and check that the photometry is not changed by more than 1%. Then we sum all these signals on a celestial coordinate grid to get the final map.

3.5 Calibration of extended emission

Using the knowledge of the average interstallar dust emission spectrum, the zodiacal light emission at the time of the observations, and the Cosmic Infrared Background values derived from COBE, together with HI data on our fields, we derive a brightness value at 170 $\mu $m for each of our fields. This extrapolated brightness at 170 $\mu $m for the three fields is in remarkable agreement with the measured ISOPHOT brightness. Furthermore, the rejection level of straylight up to $60^{\circ}$ off-axis observed by ISO during total solar eclipse by the Earth, is better than 10-13, implying that there is no significant contribution to the measured flux coming from the far sidelobes. This confirms that ISO is able to make absolute measurements of the extended emission and gives a high degree of confidence to our photometric calibration.

   
4 Source extraction, simulations

An important part of the present work is the extraction of the sources, the simulation of point source observations and the analyses of noise. After detecting sources on a median-filtered-like map, we measure the fluxes on the final maps with aperture photometry. Our simulation tool validates the flux determination as well as the noise analysis.

4.1 Source extraction

Our original maps are dominated by the fluctuations of the background at 170 $\mu $m, at all spatial scales, mainly due to the cirrus confusion noise and the CIB fluctuations (Lagache & Puget 2000). Because of this, classical extraction algorithms based on thresholding and local background determination mostly fail: it is not easy to use a robust detection algorithm on maps dominated by structures at all scales. On the contrary, flat background maps allow reliable detection with the available processing techniques, like Gaussian fitting methods, e.g. for faint ISOCAM sources by Désert et al. (1999). Because of the undersampling of the PHT Point Spread Function together with a highly fluctuating background, CLEAN-like methods (Hogbom 1974) are difficult to use. Wavelet decomposition, e.g. for ISOCAM by Starck et al. (1999), is not easily implementable because of the poor spatial dynamics of our maps ("big pixels and small maps''). To overcome these difficulties we have developed the following method by combining some well-known techniques for source extraction and flux determination:
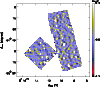  \begin{figure} \par\epsfxsize=8.8cm \epsfbox{1054hdole_fig02.eps} \end{figure} Figure 2: Example of a source map for source detection in the FSM field. Background is subtracted using a median filter in the time space (AAP). Data with only high spatial frequencies are then reprojected on a map with the FIRBACK pipeline.
Open with DEXTER

$\bullet$
background is subtracted in the one dimensional time data (AAP level, brightness as a function of time) using a median filter (size: 5 positions) to create source time data;
$\bullet$
source time data are processed to create 2-dimensional source maps (Fig. 2) through the FIRBACK pipeline as decribed in Sect. 3;
$\bullet$
source detection is performed on the source maps using SExtractor (Bertin & Arnouts 1996);
$\bullet$
flux measurements are performed on the unfiltered maps, using aperture photometry at the positions found by the source detection only if there are at least 4 different observations, and make a temporary version of the source catalog;
$\bullet$
by subtracting iteratively the brightest sources from the temporary catalog using a CLEAN-like method on the final maps, we remeasure with better accuracy the flux of the sources which have bright neighbours. This gives the final catalog after two more corrections: short term transient of 10%, and flux offset of about 15% derived from simultation (see Sect. 5).
Source detection is performed using SExtractor version 2.1.0 on the source maps with the parameters given in Table 3. Note that we do not use the background estimator and set it to a constant value because source maps are flat maps containing fluctuations due to resolved sources, since the background has been filtered. Only the positions in the map of the detected sources will be used in the output catalog computed by SExtractor (e.g. not the flux). We discard the edges by considering only parts of the sky that have been observed at least 4 times. This reduces the total area by about 5%.
 

 
Table 3: Parameters used in SExtractor 2.1.0 applied on the Source Maps.
Parameter Value
DETECT_MINAREA 10
DETECT_THRESH 3.0
BACK_SIZE 10
BACK_FILTERSIZE 1,1
BACK_TYPE MANUAL
BACK_VALUE -0.04,0.0


4.2 Simulations

We have developed a simulation tool of point sources in order to validate the flux determinations and study source completeness of our survey. Kawara et al. (1998) did not make such simulations and Juvela et al. (2000) only tested the significance of their source detection because of a lack of redundancy in their observations. The work of Efstathiou et al. (2000) included large simulations at 90 $\mu $m, but the source detection is performed by eye.

Thanks to the quiet behaviour of the C200 camera at 170 $\mu $m, together with redundancy, the detector noise as well as effects induced by glitches can be neglected to first order with respect to the confusion noise. (This is unlike conditions applying to the C100 camera (Linden-Vornle et al. 2000).)

Here, we present a summary of our simulation process, followed by some details concerning the addition of the sources and the validation:

$\bullet$
select a random sky position for a simulated source inside a FIRBACKfield;
$\bullet$
add the source in each raster in AAP level which has observed the source itself or its wings;
$\bullet$
process maps through the FIRBACKpipeline;
$\bullet$
extract sources with SExtractor;
$\bullet$
identify the extracted sources by comparing the coordinates with the input catalog;
$\bullet$
compute a flux with aperture photometry using the effective footprint (defined in Sect. 5.1);
$\bullet$
validate on different flat backgrounds;
$\bullet$
validate on real data: different input fluxes and positions.

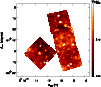  \begin{figure} \par\epsfxsize=8.8cm \epsfbox{1054hdole_fig03.eps} \end{figure} Figure 3: Example of the addition of 500 mJy sources in the FSM field. There are 8 sources spread randomly throughout the field. One example is near the center of the eastern survey square (FSM1).
Open with DEXTER

4.2.1 Adding the sources

We use the best footprint available for PHT at 170 $\mu $m (Lagache & Dole 2001) to simulate a source with a known input flux; its spatial extension is taken to be a five pixel square, that is about $7.7' \times 7.7'$ (note that the PIA footprint profile given in the calibration files extends to only 4.2 arcminutes). This simulated source is added in the one dimensional time data (AAP level). To avoid biases due to specific positions in the fields, we select random positions.

Because we have either 2 or 4 different raster observations of the same parts of the sky, the randomly-selected sky position may fall e.g. on the edge of a pixel in one raster, and at the center of another pixel in another raster. We thus make the following approximation: we cut each PHT pixel in 9 square sub-pixels of about $30.7 \times 30.7$ square arcseconds. We compute the pixelized footprint for the nine configurations corresponding to the cases where the source center falls on one of the sub-pixels.

We make separate realizations for 8 input fluxes (100, 150, 200, 300, 500, 650, 800 and 1000 mJy) and create maps using the FIRBACKpipeline. We add only between 6 and 20 sources per square degree at a time depending on their flux, in order to avoid changing the confusion level when sources are added in the data. We compute the needed number of maps to get 1200 realizations for each flux in each field, or 28800 sources in total, in order to have a statistically significant sample. We finally get about $2 \times 1230$ different simulated maps per field (1 final map + 1 source map for each realization) taking about 14 Gbyte, after about one week of computation under IDL on a MIPS R12000 at 300MHz SGI. Figure 3 shows an example of added sources.

4.2.2 Validation
We extract sources on the final maps and compute fluxes as explained below by aperture photometry. The aperture photometry filter parameters have been optimized to obtain the best signal to noise ratio using the simulations.

The validation is performed on flat background maps with different surface brightness values (0.01, 3 and 10 MJy/sr), to check that the recovered flux does not depend on the background. The difference between the input and recovered flux is less than 1% on an individual raster when the source is centered on a pixel. When using random positions of the sources and 2 or 4 rasters co-added, the recovered fluxes have a dispersion explained by the "edge effect'' (due to the dilution of the flux in other pixels when the source falls on the edge of a pixel) and by the poor sampling of the sky, leading to an overall uncertainty of 10%.

   
5 Photometry, noise analysis, accuracy

   
5.1 Flux measurements by aperture photometry

Once a detection is obtained on source maps, fluxes have to be measured in final maps. Simulations of point sources on a flat background permit derivation of the effective average footprint on the map, which results from the PHT footprint and the final pixeling obtained in a given field, which depends on the exact timing of the observations (roll angle).

We check that strong sources in the data have a profile in agreement with the effective footprint. The growth curve of the effective footprint is plotted in Fig. 4. The determination of the parameters for the aperture photometry filter is performed by measurements of the flux of simulated sources through different sets of apertures. We find that the following values minimize the noise: an internal radius of 90 arcsec for measuring the source and an external radius of 120 arcsec to estimate the background. The determination of the flux takes into account the fact that at these radii we select only a part of the effective footprint, and includes the appropriate correction.


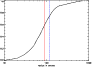  \begin{figure} \par\epsfxsize=8cm \epsfbox{1054hdole_fig04.eps} \end{figure} Figure 4: Growth curve of the effective footprint on a logarithmic scale with the location of the radii of circles used for aperture photometry; dotted vertical line: 90 arcsecond for the inner radius; dashed vertical line: 120 arcsecond for the outer radius.
Open with DEXTER

In order not to be biased by a nearby strong source which could affect the estimate of the local background in a measurement, we used a CLEAN-like procedure. We first compute a temporary catalog that we sort by decreasing flux. Then we measure the brightest source, and remove it, and repeat this process through the whole catalog. Note that this procedure is not used to extract faint sources but only to improve the photometry of sources detected before applying the CLEAN procedure.

At the end of the process, we add 10% to the source flux to account for the transient behaviour of the detector. This value is derived from our absolute measurement in the FSM1 (using AOT P25) in which the instantaneous response and the following transient, as well as the final flux after 256 s, are observed (Lagache & Dole 2001).

5.2 Confusion noise

We made 10000 measurements on each field at random positions, and obtained distributions which are shown in Figs. 5, 6 and 7. These distributions represent the probability of measurements by aperture photometry on a field with sources and dominated by confusion. They are fitted in their central part by a Gaussian, whose dispersion is an estimate of the confusion noise. The distributions are plotted in Figs. 5 to 7. The assymetric part at high flux levels reflects the counts of bright sources. We finally derive $\sigma_{\rm c} \simeq 45$ mJy for the confusion noise in all of the FIRBACKfields (41 mJy for FSM, 44 for FN1 and 46 mJy for FN2). The $3 \sigma_{\rm c}$ level is thus 135 mJy and $4 \sigma_{\rm c}~ 180$ mJy.


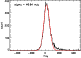  \begin{figure} \par\epsfxsize=7cm \epsfbox{1054hdole_fig05.eps} \end{figure} Figure 5: 10000 random aperture photometry measurements on the FSM map indicating the confusion noise. The small excess at high flux levels is due to real sources in the data.
Open with DEXTER


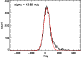  \begin{figure} \par\epsfxsize=7cm \epsfbox{1054hdole_fig06.eps} \end{figure} Figure 6: 10000 random aperture photometry measurements on FN1.
Open with DEXTER


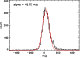  \begin{figure} \par\epsfxsize=7cm \epsfbox{1054hdole_fig07.eps} \end{figure} Figure 7: 10000 random aperture photometry measurements on FN2.
Open with DEXTER


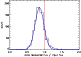  \begin{figure} \par\epsfxsize=7cm \epsfbox{1054hdole_fig08.eps} \end{figure} Figure 8: Histogram of the ratio of measured flux to input flux, when sources of 500 mJy are added to the maps.
Open with DEXTER

This estimate is compatible with the classical definition of the confusion, by computing the number of independent beams in all the FIRBACK fields: with a FWHM of 94 arcsec at 170 $\mu $m in a 3.89 sq. deg surface, we have about 5700 independent beams. At the $3 \sigma$ limit, that is above 135 mJy, we have 196 sources (see Sect. 6), there are about 29 beams per source - in good agreement with the classical definition of the confusion of 30 independent beams per source for sources brighter that $3 \sigma_{\rm c}$. If we have a catalogue cutoff at $4 \sigma _{\rm c}$ (resp. $5 \sigma_{\rm c}$), we obtain 54 (resp 91) independents beams per source. Our analysis is compatible with the simulations of Hogg (2000), who shows that 30 beams per source is a minimum where source counts are steep, and suggests a threshold at about 50 beams per source.

The cirrus fluctuations have a low probability of creating spurious sources at this level of HI column-density, as shown in previous works, such as Gautier et al. (1992), Lagache (1998), Kawara et al. (1998), Puget et al. (1999), and Juvela et al. (2000).

5.3 Detector noise

The first field to be observed in our investigations was FSM1, and the goal was to demonstrate the ability of doing a deep far infrared survey limited by confusion rather than detector noise. With four independent rasters mapping exactly the same sky, that is 16 independent measurements, Lagache (1998) and Puget et al. (1999) show that the detector noise level is about 3 mJy $1 \sigma$, i.e. far below the confusion noise and thus neglected.
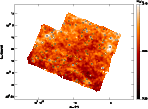  \begin{figure} \par\epsfxsize=13cm \epsfbox{1054hdole_fig09.eps} \end{figure} Figure 9: Detected sources on FN1 field. Circles are sources from the ISO FIRBACK Source Catalog ( $S_{\nu } > 180$ mJy) and squares are sources from the Complementary ISO FIRBACK Source Catalog ( $135 < S_{\nu } < 180$ mJy).
Open with DEXTER

5.4 Photometric accuracy

The histograms of the ratio of recovered flux to input flux of the simulated sources are used to estimate the offset and the error of the fluxes. One of these histograms is shown in Fig. 8 for the FN1 field and 500 mJy sources.

One can see a systematic offset of the distribution's peak with respect to the input flux. This offset is constant for a given field, and equals 16%, 19%, 18% and 16% for the FN1, FN2, FSM1 and FSM234 fields, respectively. The possible explanations for this offset are (1) the variation of the effective footprint inside the field (due to an inhomogeneous sampling of the sky) and (2) the loss of flux at the edges of the pixels. We apply this correction on the source fluxes.

The standard deviation of the fitted Gaussian, $\sigma _{\rm s}$, estimates the dispersion of the source flux measurements. Figure 10 shows the variation of $\sigma _{\rm s}$ in mJy as a function of the source flux in Jy, in the FN1 field; the variation is similar in the other fields. $\sigma _{\rm s}$ can be decomposed in two components:

$\bullet$
a constant component due to confusion noise $\sigma _{\rm c}$;
$\bullet$
a component ( $\sigma _{\rm p}$) proportional to the source flux, due to the difference between the mean effective footprint and the local effective footprint.
The data points are fitted by the quadratic sum of the constant and the proportional component $\sqrt {\sigma _{\rm c}^2 + \sigma _{\rm p}^2}$.

The source flux uncertainties are computed for each field; however, there is little field-to-field variation. The uncertainty in the source flux is about 25% near $3 \sigma_{\rm c}$ at low fluxes, about 20% near $5 \sigma_{\rm c}$ and decreases to about 10% at high flux levels (near 1 Jy).

5.5 Positional accuracy

The identification of the sources in the simulations allows us to derive the positional accuracy. We neglect the telescope absolute pointing error of 1 $^{\prime\prime}$ (Kessler 2000). Figure 11 shows the distribution of the distance offset between the input source and the extracted source positions. All sources brighter than 500 mJy - i.e. where the sample is complete (see Sect. 7.1) - are recovered inside a 65 $^{\prime\prime}$ radius: the mean recovered distance is 15 $^{\prime\prime}$, and 90% of the sample falls inside 28 $^{\prime\prime}$. Taking all the sources with flux levels brighter than 180 mJy, 90% of the sample is recovered inside a radius of 42 $^{\prime\prime}$. We conclude that 99% (respectively 93%) of the sources are found in a circle of radius of 50 $^{\prime\prime}$, and 98% (respectively 90%) in 42 $^{\prime\prime}$ when the sample is complete, above 500 mJy (respectively 180 mJy).

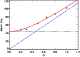  \begin{figure} \par\epsfxsize=7cm \epsfbox{1054hdole_fig10.eps} \end{figure} Figure 10: Evolution of $\sigma _{\rm s}$, standard deviation of measured flux on the histograms, as a function of the source flux (diamonds). $\sigma _{\rm s}$ can be decomposed in two components: (1) a constant component due to confusion noise $\sigma _{\rm c}$ (horizontal dashed line) and (2) a component proportional to the flux $\sigma _{\rm p}$(sloped dashed line). $\sigma _{\rm s}$ is fitted by $\sqrt {\sigma _{\rm c}^2 + \sigma _{\rm p}^2}$(solid line).
Open with DEXTER


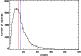  \begin{figure} \par\epsfxsize=7cm \epsfbox{1054hdole_fig11.eps} \end{figure} Figure 11: Histogram of distances of identifications in the simulations. All sources brighter than 500 mJy (where the sample is complete) in the three FIRBACK fields are shown. The solid line corresponds to the median at 13 arcsec and the dashed line at 15 arcsec.
Open with DEXTER

  
6 FIRBACKsource catalogs

6.1 ISO FIRBACKsource catalog

The final catalog, the ISO FIRBACKSource Catalog (IFSC), contains 106 sources with fluxes between 180 mJy ($4 \sigma$) and 2.4 Jy. The catalog is given for each field in Tables 7 to 10. All the sources have been checked for detection in all individual measurements. It is interesting to note that above $5 \sigma_{\rm c}$ the source density is constant in the fields, with 16 sources in FSM, 15 in FN2, and 32 sources in FN1 which is twice the size of the other fields. The source density is thus $16 \pm 4$ sources brighter than 225 mJy per square degree. At the $4 \sigma _{\rm c}$ limit, the source density is $27 \pm 5$sources brighter than 180 mJy per square degree, with a larger field-to-field dispersion. The brightest sources in FSM lie at 497 and 443 mJy, in FN1 at 838, 597 and 545 mJy, and in FN2 at 2377, 1251, 803, 682, 666 and 522 mJy.

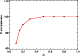  \begin{figure} \par\epsfxsize=7cm \epsfbox{1054hdole_fig12.eps} \end{figure} Figure 12: Completeness of the FIRBACK catalog, computed from the simulations as the ratio of the number of detected sources to the number of added sources.
Open with DEXTER


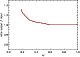  \begin{figure} \par\epsfxsize=7cm \epsfbox{1054hdole_fig13.eps} \end{figure} Figure 13: Malmquist-Eddington bias. Ratio of simulated source counts to simulated observed source counts. Due to flux uncertainties, the number of counts is overestimated at low flux levels.
Open with DEXTER

6.2 Complementary ISO FIRBACKsource catalog

Sources with flux levels above the $3 \sigma_{\rm c}$ limit are higher redshift candidates and they can be used for statistical study of the nature of 170 $\mu $m sources. Nevertheless, the lower signal to confusion-noise ratio leads to lower flux accuracy - reduced to about 25% at 135 mJy - and may include spurious sources: this larger uncertainty suggests avoiding the use of these sources, e.g. in the counts.

Candidates for z > 1 may be selected on the basis of photometric redshift using the FIR-radio correlation (Condon 1992; Helou et al. 1985) and the submillimetre-radio correlation (Carilli & Yun 2000). The success of recent submillimetre detections of FIRBACKsources with SCUBA at the JCMT (Scott et al. 2000, with an rms sensitivity of 2 mJy), and with MAMBO at IRAM-30 m (with an rms sensitivity better than 0.5 mJy, Lagache et al., in prep.) in the millimetre range confirms the relevance of this technique.


   
Table 4: Number of sources per flux bin in $3.89^{\circ \, 2}$ used for the source counts, without any correction.
flux min flux max number per cumulative
(mJy) (mJy) bin number
180.0 190.0 13 106
190.0 210.0 20 93
210.0 240.0 21 73
240.0 300.0 24 52
300.0 500.0 19 28
500.0 $ \infty $ 9 9

In this frame of mind, we compile a Complementary ISO FIRBACKSource Catalog (CIFSC, Tables 11 to 13 for each field) which contains 90 sources whose flux levels lie in the range 135 to 180 mJy (3 to $4 \sigma _{\rm c}$). All the sources have been checked for detection in all individual measurements. There are 15 sources in FSM, 47 in FN1, and 28 in FN2. As an example, Fig. 9 shows of the detected sources in the FN1 field. At this flux level, the source density is not constant between the fields and fluctuates at about $23 \pm 8$ sources per square degree in the range 135-180 mJy.

  
7 Source counts

  
7.1 Completeness

Simulations allow us to derive the completeness, that is the ratio at a given flux between the number of added sources and the number of detected ones. The completeness is plotted in Fig. 12. Our sample is complete above 500 mJy, and is about 90% (respectively about 85%) complete above 225 mJy (respectively 180 mJy). We thus correct the surface source density for this incompleteness.

  
7.2 Malmquist-Eddington bias

Uncertainties in the flux determination introduce an excess in the number of counts, known as the Malquist-Eddington bias. We characterize it with the results of the simulations, by comparing the effect of a flux dispersion on a known input source count model: a simple power law. Figure 13 shows the ratio of an input source count model, to the simulated observations of this model. We apply the appropriate correction to the data: at 225 mJy (respectively 180 mJy) the raw counts have to be decreased by 20% (respectively 30%). We check that these values are not more sensitive than 5% (respectively 10%) at $5 \sigma_{\rm c}$ (respectively $4 \sigma _{\rm c}$) to the power law of the input model in the range 3.0-3.6.

7.3 FIRBACKsource counts

Figure 14 shows the differential source counts at 170 $\mu $m coming from the FIRBACKsurvey (3.89 sq. deg), with 106 sources between 180 ($4 \sigma$) and 2400 mJy. The horizontal error bar gives the flux uncertainty, and the vertical error bar the Poisson noise in $\sqrt{n}$ where n is the number of sources in the bin.

The statistics of sources used for source counts before any correction is given in Table 4. The integral (respectively differential) source count values are given in Table 5 (respectively Table 6). Note that for the differential counts we took only 5 sources in the last flux box, corresponding to highest fluxes (between 500 and 700 mJy).

The two points at high flux levels are compatible with no evolution since we can adjust a horizontal line inside the error bars. The slope of the differential source counts is not constant, but can reasonably be fitted by a linear of slope $3.3 \pm 0.6$ between 180 and 500 mJy.

8 Discussion

8.1 Comparison with other work

Kawara et al. (1998) estimated the confusion level to be 45 mJy, and extracted 45 sources brighter than 150 mJy ( $3 \sigma_{\rm c}$) in the 1.1 sq. deg Lockman Hole field. Juvela et al. (2000) found $\sigma_{\rm c} = 44$ mJy, and detected 55 sources brighter than 150 mJy in 1.5 sq. deg. Both these estimates are consistent with our measurements.

Our raw results are in agreement with the pioneering work on 1/16th of the area of the entire FIRBACKsurvey by Lagache (1998) and Puget et al. (1999). Without completeness or Malmquist-Eddington bias correction, our catalogs are similar. Of the 24 sources of Puget et al. (1999), we detect 18. The six missing sources are: (1) on the edges of the field with fewer observations than required in our procedure of extraction for three of their sources, and (2) in more confused regions for the other three.

For the 18 common sources, the photometry is in excellent agreement (except for one source which is near the edge of the field). Both analyses find 13 sources at fluxes higher than 150 mJy in this field.

In our preliminary work (Dole et al. 1999, 2000), we detected the sources by eye and used the same photometry as Puget et al. (1999) for consistency, but we did not remove bright sources to measure the fainter sources. Statistically, these efforts are compatible with our current source counts.

8.2 Comparison with models

The semi-analytical model from Guiderdoni et al. (1998) was used in the FIRBACKproposal to justify the integration time and surface coverage, and has been improved recently (Devriendt & Guiderdoni 2000). Our phenomenological model (Dole et al. 2000) was developed by taking into account all the observational constraints in the infrared and submillimetre range, and is based on strong evolution of a bright population of galaxies. Both models are presented in Fig. 15. The models of Franceschini et al. (1998), with and without evolution, are shown in Fig. 16 together with the pure luminosity evolution model of Rowan-Robinson (2001).

The data unambiguously reject models without evolution or with low evolution at flux levels fainter than 500 mJy. The no-evolution model of Franceschini et al. (1998) (dots in Fig. 16) and the model without ULIRGs (Sanders & Mirabel 1996) of Guiderdoni et al. (1998) (dotted line in Fig. 15) are incompatible with the data: they predict between 5 and 10 times fewer sources than observed.

Model E of Guiderdoni et al. (1998) with strong evolution and an addition of ULIRGs underestimates the source counts by a factor of 2, and predicts a lower slope than the observations. Nevertheless, the agreement within a factor of 2 between model E and the final observed source counts is quite remarkable: this model was developed to account for the CIB, and was used for predicting the FIRBACKsource counts at the time of submission of this observing program. The phenomenological model of Dole et al. (2000) fits the data at faint fluxes, as well as the model of Rowan-Robinson (2001).

Other semi-analytical models like e.g. Blain et al. (1999), or phenomenological models like e.g. those of Tan et al. (1999), Xu et al. (2000), and Pearson (2000), also try to reproduce the spectrum of the CIB as well as the source counts in the whole spectral domain from the mid infrared (sometimes optical) to the sub-millimeter (sometimes centimeter) range. It is beyond the scope of this paper to compare all these models with our observations, but scenarios without strong evolving populations of LIRGs are uniformly unable to reproduce the data.


   
Table 5: FIRBACK integrated source counts.
$\log_{10}$ of galaxy density flux
(sr -1) (mJy)
$4.919 \pm 0.085 $ $ 180.0 \pm 21.5 $
$4.869 \pm 0.090 $ $ 190.0 \pm 21.8 $
$4.774 \pm 0.102 $ $ 210.0 \pm 22.6 $
$4.638 \pm 0.121 $ $ 240.0 \pm 23.6 $
$4.374 \pm 0.166 $ $ 300.0 \pm 25.8 $
$3.894 \pm 0.301 $ $ 500.0 \pm 33.0 $


   
Table 6: FIRBACK differential source counts.
$\log_{10}$ of $\frac{{\rm d}N}{{\rm d}S} \times S^{2.5}$ flux bin
$ \left ( {\rm sr}^{-1} \times {\rm Jy}^{1.5} \right ) $ (mJy)
$4.179 \pm 0.247 $ 180 - 190
$4.157 \pm 0.198 $ 190 - 210
$4.143 \pm 0.193 $ 210 - 240
$4.107 \pm 0.180 $ 240 - 300
$3.921 \pm 0.203 $ 300 - 500
$3.797 \pm 0.418 $ 500 - 700


  \begin{figure} \par\epsfxsize=7.3cm \epsfbox{1054hdole_fig14.eps} \end{figure} Figure 14: FIRBACKdifferential source counts (normalized to Euclidian counts) at 170 $\mu $m. 106 sources are brighter than 180 mJy ( $4 \sigma _{\rm c}$) on 3.89 sq. deg. The slope of the differential source counts is $3.3 \pm 0.6$ between 180 and 500 mJy.
Open with DEXTER


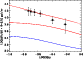  \begin{figure} \par\epsfxsize=7.3cm \epsfbox{1054hdole_fig15.eps} \end{figure} Figure 15: FIRBACKdifferential source counts at 170 $\mu $m with models from Guiderdoni et al. (1998) with evolution and without ULIRG's (A, dotted line) and with evolution with ULIRG's (E, solid line), and from Dole et al. (2000) (strongly evolving LIRGs, dashed line).
Open with DEXTER


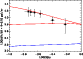  \begin{figure} \par\epsfxsize=7.3cm \epsfbox{1054hdole_fig16.eps} \end{figure} Figure 16: FIRBACKdifferential source counts at 170 $\mu $m with models from Franceschini et al. (1998) without evolution (dotted line) and with evolution (solid line), and from Rowan-Robinson (2001) (pure luminosity evolution, dot-dashed line).
Open with DEXTER

8.3 Resolving the cosmic infrared background at 170 $\mu $m

We now ask what fraction of the CIB is contributed by sources brighter than 135 mJy at 170 $\mu $m? Since the flux integral is dominated by sources at lower flux levels, it is rather simple to compute its value on the assumption that source counts have a constant slope. We estimate that $4 \pm 1$% of the CIB is resolved into sources brighter than 135 mJy.

Using the model of Dole et al. (2000), we show that 7% of the CIB is resolved in sources brighter than 135 mJy.

Thus, the population of individually observed sources in the FIRBACKsurvey does not dominate the CIB at this wavelength.

We can also ask at which flux levels the CIB will be largely resolved at 170 $\mu $m? The observed slope of the source counts may be extrapolated to lower flux levels to predict a convergence. The expected flattening of the source counts close to the convergence is neglected, and thus the derived values give an upper limit. With this proviso, we find that the 170 $\mu $m background should be resolved at flux levels in the range 10 to 20 mJy, an order of magnitude fainter than the ISO sensitivity.

Using our model presented in Fig. 15, we predict that 80 to 90% of the CIB should be resolved in the range 2 to 5 mJy.

The required sensitivity at 170 $\mu $m, about 60 times better than ISO, is not reachable with the 1m-class space infrared observatories such as NASA's SIRTF. SIRTF should be able to break about 15-30% of the background into discrete sources at 160 $\mu $m. 4m-class ESA's Herschel (former FIRST) should be able to break the bulk of the background.

8.4 Survey optimisation and confusion

While the confusion is found to be identical in the 3 FIRBACKfields at about 45 mJy (regardless of sampling), the FSM fields have been observed twice as frequently as the northern fields. This means that the confusion limit was reached faster than expected. Two years after the end of the observations, and five years after the launch of ISO, our analysis shows that the best (ideal) observational strategy would have been to repeat the individual observations (rasters) 4 times to obtain enough redundancy (done in the FSM field) with less integration and proper oversampling. With this optimisation, we could have gained 25% more surface with the earned time, or performed complementary observations at another wavelength.

An early proper determination of the confusion level is thus a key factor for extragalactic infrared surveys from space, since the confusion is high due to the strong evolution, and limits the surveys. It is challenging, given the relatively short time spend in the "Performance Verification'' or "In Orbit Checkout'' phases that normally predece routine astronomical observations in space.

9 Conclusion and summary

The analysis of the FIRBACKISO deep survey sources at 170 $\mu $m is presented. After a process of data reduction and calibration of extended emission (Lagache & Dole 2001), we performed extensive simulations to validate our source extraction process, and studied the sources of noise and accuracy in photometry and astrometry. The confusion $\sigma _{\rm c}$ equals 45 mJy.

We compiled the ISO FIRBACKSource Catalog ( $S_{170} > 4 \sigma_{\rm c}$) and the Complementary ISO FIRBACKSource Catalog ( $3 \sigma_{\rm c} < S_{170} < 4 \sigma_{\rm c}$, for follow-up purposes) containing 196 sources. It is important to note that the extended source calibration is in excellent agreement with DIRBE and the point source calibration is in agreement with IRAS. The differential source counts show a steep slope of $3.3 \pm 0.6$between 180 and 500 mJy, and a significant excess of faint sources with respect to low or moderate evolution expectations.

The steep slope of the source counts has important consequences on the sensitivity limits of the deep surveys conducted in the far infrared: the confusion noise is large, as it will be for future observatories, and will impact dramatically on the future IR deep surveys.

Table 7. FIRBACK Catalog in FSM: coordinates are in hours ( $\alpha _{2000}$) or degrees ( $\delta _{2000}$), minutes, seconds, the flux S and the flux uncertainty $\delta S$ at $170~\mu$m are in mJy.

Table 8. FIRBACK Catalog in FN1: coordinates are in hours ( $\alpha _{2000}$) or degrees ( $\delta _{2000}$), minutes, seconds, the flux S and the flux uncertainty $\delta S$ at $170~\mu$m are in mJy.

Table 9. FIRBACK Catalog in FN1 (continued).

Table 10. FIRBACK Catalog in FN2: coordinates are in hours ( $\alpha _{2000}$) or degrees ( $\delta _{2000}$), minutes, seconds, the flux S and the flux uncertainty $\delta S$ at $170~\mu$m are in mJy.

Table 11. FIRBACK Complementary Catalog in FSM: coordinates are in hours ( $\alpha _{2000}$) or degrees ( $\delta _{2000}$), minutes, seconds, the flux S and the flux uncertainty $\delta S$ at $170~\mu$m are in mJy.

Table 12: FIRBACK Complementary Catalog in FN1: coordinates are in hours ( $\alpha _{2000}$) or degrees ( $\delta _{2000}$), minutes, seconds, the flux S and the flux uncertainty $\delta S$ at $170~\mu$m are in mJy. Table 13: FIRBACK Complementary Catalog in FN2: coordinates are in hours ( $\alpha _{2000}$) or degrees ( $\delta _{2000}$), minutes, seconds, the flux S and the flux uncertainty $\delta S$ at $170~\mu$m are in mJy.
One important intention of the FIRBACKsurvey was to probe the nature of the extragalactic far-infrared sources. According to most of the models, the steep slope of the source counts is due to a strongly evolving population of LIRGs. Our model shows that the effect of the K-correction alone is insufficient to explain the observations. To definitively investigate this question, one has to identify the sources and understand their nature. Discussions of the nature of the FIRBACKsources is beyond of the scope of this paper and will be discussed elsewhere. The multiwavelength follow-up performed at 1.4 GHz, 1.3 mm, 850 and 450 $\mu $m, as well as other ISO and optical / NIR data, seems to show that most of the sources (typically 50%) are local (z < 0.3), and about 10% at high redshift (z > 1). Massive star formation seems also to be dominant. Nevertheless, identifying FIRBACKsources is not easy because of the uncertainty in the positions at 170 $\mu $m.

The summary of the FIRBACKsurvey is as follows:

$\bullet$
observation of about 4 sq. deg in 3 high galactic latitude fields: FSM, FN1 & FN2;
$\bullet$
ISOPHOT AOT P22 raster map mode with the C_200 array and the C_160 filter at 170 $\mu $m;
$\bullet$
128 or 256 seconds of integration per sky pixel;
$\bullet$
extraction of instrumental effects: long and short term transients, photometric correction;
$\bullet$
calibration of extended emission: excellent agreement between PHT and DIRBE;
$\bullet$
calibration of point sources compatible with IRAS;
$\bullet$
instrumental noise: 3 mJy $1 \sigma$;
$\bullet$
confusion noise: 45 mJy $1 \sigma$; $4 \sigma _{\rm c}$ sensitivity: 180 mJy;
$\bullet$
ISO FIRBACKSource Catalog: 106 sources between 180 mJy and 2.4 Jy;
$\bullet$
Complementary ISO FIRBACKSource Catalog: 90 sources between 135 and 180 mJy;
$\bullet$
Flux uncertainty error: 25% at $3 \sigma_{\rm c}$, 20% at $5 \sigma_{\rm c}$, and reduced to 10% at higher flux levels;
$\bullet$
positional error: 100 arcsecond diameter circle (99% of the sources);
$\bullet$
source density for S170 > 225 mJy: $16 \pm 4$ sources per square degree;
$\bullet$
source density for S170 > 180 mJy: $27 \pm 5$ sources per square degree;
$\bullet$
slope of the differential source counts: $3.3 \pm 0.6$ between 180 and 500 mJy;
$\bullet$
4 to 7% of the Cosmic Infrared Background at 170 $\mu $m is resolved into sources brighter than 135 mJy;
$\bullet$
Prediction that the CIB will be resolved at flux levels in the range 1 to 10 mJy at 170 $\mu $m;
$\bullet$
Catalogs, images, and plots available on line at: http://wwwfirback.ias.u-psud.fr.

Acknowledgements
HD, GL & JLP appreciate discussions with Rene Laureijs and Carlos Gabriel at Vilspa and Ulrich Klaas at Heidelberg. We also are greatful to Alain Abergel, Alain Coulais & Marc-Antoine Miville-Deschênes at IAS, for stimulating and helpful discussions through the analysis of the FIRBACKdata. Thanks also go to Martin Kessler and his team who did a great job in planning ISO observations so efficiently. MH acknowledges support of his participation on ISO through NASA grants and contracts. DE acknowledges support from NASA grant NAG5-8218.

References

 
Copyright ESO 2001