3 Modelling the light curve

The observed light curves (Fig. 1) are typical of AMHer in the high state (e.g. Olson 1977; Szkody & Brownlee 1977). The V band shows a broad and round minimum near $\mbox{$\phi_{\rm orb}$ }\approx0.0$ and a secondary minimum near $\mbox{$\phi_{\rm orb}$ }\approx0.5$. The B band is almost unmodulated. Both light curves exhibit a significant amount of flickering on timescales of several minutes, which is probably due to inhomogeneities in the accretion flow (Matt et al. 2000).

We identify four possible emission sites that will contribute to the observed light curves: the (heated) white dwarf, the secondary star, the accretion stream feeding material from the secondary star towards the white dwarf, and the accretion column just above the white dwarf surface near the magnetic pole. In the following, we will discuss the system geometry of AMHer and the four individual emission components.

 

 

Table 1: Optical photometry of AMHer in 1998. Listed are the start time and the the total exposure time.

Date	Time (UT)	Exp. time [s]	Filter	Mean magnitude
Aug. 20	20:45:21	13320	V	13.50
Aug. 22	19:45:20	14040	B	13.64

Figure 1: Calibrated B and V light curves obtained August 20 and 22, respectively, at the Loiano 1.5 m telescope. Indicated are the orbital phase (bottom) and magnetic phase (top). Both observations cover the binary orbit more than once. The two consecutive orbits are shown by black and grey points to highlight the cycle-to-cycle variations.

3.1 The system geometry

The orientation of the accretion column with respect to the observer can be described by a set of three angles: the inclination of the system, i, the co-latitude of the accretion column/spot, $\beta$, measured as the angle between the rotation axis and the field line threading the accretion column and the azimuth of the magnetic axis from the line connecting the centres of the two stars, $\psi$. For our present purpose, the exact knowledge of $\psi$ is not crucial, as it defines only a phase offset between our model light curve and the observed light curve, and we will adjust $\psi$ accordingly below.

The inclination and the co-latitude of AMHer have been subject of dispute. Brainerd & Lamb (1985) derived from the observed polarization properties $i=35^{\circ}\pm5^{\circ}$and $\beta=58^{\circ}\pm5^{\circ}$. Another polarimetric study indicates $i\approx50^{\circ}$ and $\beta\approx50$-60$^{\circ}$(Wickramasinghe et al. 1991). The higher value of the inclination is favoured by spectroscopy of the secondary and of the accretion stream (Davey & Smith 1996; Southwell et al. 1995; Gänsicke et al. 1998). An additional constraint comes from the observed self-eclipse of the X-ray/EUV/ultraviolet emission from the accretion region and from the heated surrounding white dwarf photosphere. Gänsicke et al. (1998) and Sirk & Howell (1998) derive independently $i+\beta=105^{\circ}$.

We will use the combinations ( $i=50^{\circ},\ \beta=55^{\circ}$) and ( $i=35^{\circ},\ \beta=70^{\circ}$) in our models of the B and Vlight curves of AMHer in order to reflect the uncertainties in the exact geometry, while satisfying $i+\beta=105^{\circ}$.

3.2 The heated white dwarf

IUE and HST observations show that the ultraviolet flux of AMHer is dominated by the emission from the accretion-heated white dwarf during both low states and high states (Gänsicke et al. 1995). Gänsicke et al. (1998) could quantitatively model the quasi-sinusoidal flux modulation observed with HST during a high state with a large, moderately hot spot covering a white dwarf of $\mbox{$T_{\rm wd}$ }=20\,000$K. They chose a temperature distribution decreasing linearly in angle from the spot centre merging into $\mbox{$T_{\rm wd}$ }$ at the spot radius. The best-fit spot parameters implied a central temperature of 47000K and a spot size of $f\sim0.09$ of the total white dwarf surface. With a distance of 90pc, the inferred radius of the white dwarf was $\mbox{$R_{\rm wd}$ }=1.12\times10^9$ cm. We use here synthetic phase-resolved spectra computed with the 3D white dwarf model described by Gänsicke et al. (1998), using their best-fit parameters.

We note for completeness that during a low state the U and Blight curves of AMHer can very well be dominated by emission from the heated white dwarf (see e.g. Fig. 1 of Bonnet-Bidaud et al. 2000).

  
3.3 The accretion stream

The near-ultraviolet emission ( Å) of AMHer during the high state is dominated by continuum emission from the accretion stream. Based on phase-resolved IUE spectroscopy, Gänsicke et al. (1995) showed that this near-ultraviolet emission of the accretion stream does not vary noticeably with the orbital phase. In the following, we assume therefore that the accretion stream emission does not vary over the binary orbit, and treat the (constant) stream contributions in B and V as a free parameters. The limitations implied by this assumption will be discussed in Sect. 4.

3.4 The secondary star

The secondary star in AMHer can be detected during low states, and both its spectral type and magnitude are easily measured (Schmidt et al. 1981; Gänsicke et al. 1995). For completeness, we use here B=18.43 and V=16.83, as derived from the low state data, to describe the contribution of the secondary. It is, however, clear that the secondary star contribution to the observed B and V high state light curves is negligible.

3.5 The cyclotron emission

The accreted material releases its kinetic energy in a hydrodynamical shock close to the white dwarf surface. The ions are heated to the shock temperature - a few 10⁷ K - while the electrons retain at first their pre-shock temperature because of their low mass. Coulomb interactions between the particles transfer energy from the ions to the electrons, such that their temperature increases below the shock. The electrons then cool radiatively through emission of cyclotron radiation and thermal bremsstrahlung. This interplay between heating and cooling results in a temperature distribution along the post-shock flow which is characterized by its maximum temperature (Woelk & Beuermann 1996).

Figure 2: Sample cyclotron model spectra from the accretion column in AMHer for several angles $\vartheta$ between the magnetic field line and the line-of-sight and $\dot m=0.06$ $\rm g\;cm^{-2}\,s^{-1}$. Plotted are also the B and V response functions (arbitarily scaled). See Fig. 3 for the variation of  $\vartheta (\phi _{\rm orb})$.

Figure 3: Angle between the magnetic field line and the line-of-sight as function of the orbital phase. Angles $\vartheta$exceeding $90^{\circ }$ are expressed as $180^{\circ }-\vartheta$. The full line corresponds to $i=50^{\circ }$, $\beta =55^{\circ }$, the dashed to $i=35^{\circ }$, $\beta =70^{\circ }$.

Figure 4: Viewing geometry for an inclination $i=50^{\circ }$ and a co-latitude $\beta =55^{\circ }$. $\omega$ denotes the rotation axis, B the magnetic field line in the accretion column. The accretion column with a height of $\sim$0.1  $R_{\rm wd}$ is plotted as bold line segment. Indicated are the lines of sight for inferior conjunction ( $\mbox{$\phi_{\rm orb}$ }\approx0.0$, primary minimum) and superior conjunction ( $\mbox{$\phi_{\rm orb}$ }\approx0.5$, secondary minimum) of the secondary star.

In order to compute the emission from the accretion column we approximated the volume between the shock and the stellar surface with a given cross section and height. The total emission of this column is computed with a ray-tracing algorithm, where we solve the radiative transfer equation for each ray passing through the structured column using an updated version of the code described by van Teeseling et al. (1999). For the computation of the angle-dependent cyclotron emission we assumed that the magnetic field within the accretion column is perpendicular to the stellar surface and does not vary over the considered height of the column. A full description of the code used to solve the radiative and hydrodynamical problem is given elsewhere (Fischer & Beuermann 2001).

High state X-ray observations of AMHer give bolometric hard X-ray fluxes of $\sim$(1-3) $\times10^{-10}$  $\rm erg\;cm^{-2}\,s^{-1}$ (Gänsicke et al. 1995; Ishida et al. 1997; Matt et al. 2000). Assuming that the cyclotron emission can contribute roughly the same amount of flux (Gänsicke et al. 1995), we estimate an accretion rate $\dot M=10^{15}$-10¹⁶ $\rm g\;s^{-1}$ for the stand-off shock region. The magnetic field strength of AMHer is $B=14\,\rm MG$(Bailey et al. 1991). For the accretion rate estimated above and a dipolar field geometry, a cross section of the accretion column of $A_{\rm acc} \approx 5\times10^{16}\,\rm cm^2$ is estimated near the magnetic pole (Lubow & Shu 1975, 1976; Heerlein et al. 1999). From these numbers, a mean local mass flow density $\dot m \approx 0.02$-0.2  $\rm g\;cm^{-2}\,s^{-1}$ is derived. We have computed a grid of spectra for several mass flow densities in the given range and for a number of angles between the line of sight and the magnetic field. A representative sample of spectra for different $\vartheta$ is shown in Fig. 2.

From the computed set of model spectra, we synthesized B and Vlight curves of the cyclotron emission from the accretion column, where the mass flow density $\dot m$ was taken as a free parameter. The fundamental parameter in the computation of the observed cyclotron flux for a given orbital phase is the angle between the line of sight and the magnetic field axis, $\vartheta$. For a given set of inclination i, co-latitutde $\beta$ and orbital phase $\mbox{$\phi_{\rm orb}$ }$

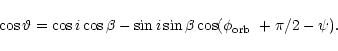$$\cos \vartheta = \cos i \cos\beta - \sin i \sin\beta\cos(\mbox{$\phi_{\rm orb}$ }+\pi/2-\psi).$$ (1)

Figure 3 shows the variation of $\vartheta$ with $\mbox{$\phi_{\rm orb}$ }$for ( $i=50^{\circ},\ \beta=55^{\circ}$) and for ( $i=35^{\circ},\ \beta=70^{\circ}$), the viewing geometry is illustrated in Fig. 4. We chose $\psi=-12^{\circ}$ so that the minimum in $\vartheta$ aligns with the minimum of the observed Vlight curve, i.e. the magnetic pole leads the secondary by $\psi$. This value is in good agreement with the azimuth of the hot accretion region derived from X-ray and ultraviolet light curves, $\psi_{\rm HS}\approx-10^{\circ}{\rm ~to~}0^{\circ}$ (Paerels et al. 1996; Gänsicke et al. 1998). $\vartheta$ reaches a minimum near $\mbox{$\phi_{\rm orb}$ }\approx-0.03$, when the observer looks down along the accretion funnel, passes through $90^{\circ }$ at $\mbox{$\phi_{\rm orb}$ }\approx0.3$ and reaches the maximum of $105^{\circ}$ at $\mbox{$\phi_{\rm orb}$ }\approx0.47$. As the cyclotron beaming is sensitive only to $\vert\cos\vartheta\vert$ we plot $180^{\circ }-\vartheta$when $\vartheta>90^{\circ}$. From Fig. 3 it is clear that a reduction of the cyclotron flux is expected in the range $\mbox{$\phi_{\rm orb}$ }\approx0.3$-0.6 from cyclotron beaming alone, without taking into account a possible occultation of the accretion column by the body of the white dwarf (see also Sect. 4).

A very similar qualitative description of the phase-dependent cyclotron emission has been given by Bailey et al. (1984) in order to explain the polarimetric properties of AMHer: linear polarization pulses and a change of sign of the circular polarization are observed at $\mbox{$\phi_{\rm mag}$ }\approx0.0$ and 0.3, which corresponds to the phases when $\vartheta\simeq90^{\circ}$.

  
3.6 Composite model light curves

We obtain the model light curves by summing the four individual emission components, white dwarf, accretion stream, secondary star, and accretion column. To fit the flux and the shape of the observed B and V light curves, we use two free parameters: the mean local mass flow density $\dot m$ which determines the (phase-dependent) contribution of the cyclotron emission and the (phase-independent) contribution of the accretion stream, $B_{\rm stream}$ and $V_{\rm stream}$. As mentioned above, the contributions of the heated white dwarf and of the secondary star are fixed. The observed light curves are reasonably well reproduced for $\dot m=0.06$  $\rm g\;cm^{-2}\,s^{-1}$, $B_{\rm stream}=15.0$, and $V_{\rm stream}=14.1$ (Figs. 5, 6). Figures 5 and 6 show the model light curves for the two different choices of ($i, \beta$). The contribution of the heated white dwarf to the observed B and V high state light curves is small (Figs. 5, 6), the contribution of the secondary is negligible.

Both fits grossly reproduce the shape of the observed light curves, i.e. a broad and deep minimum at $\mbox{$\phi_{\rm orb}$ }=0.0$ and a shallow secondary minimum at $\mbox{$\phi_{\rm orb}$ }=0.5$ in V and practically no orbital modulation in B. However, for ( $i=50^{\circ},\ \beta=55^{\circ}$) the angle $\vartheta$ drops below $40^{\circ}$ during $\phi=0.8$-1.1, with the result that cyclotron radiation contributes very little to the total V band emission. Consequently, this model light curve has a flat bottom, which contrasts with the observed round shape.

Figure 5: The observed light curves from Fig. 1 have been sampled into $\Delta\mbox{$\phi_{\rm orb}$ }=0.03$ orbital phase bins (grey points). The composite model light curves assuming $i=50^{\circ }$, $\beta =55^{\circ }$ are shown as thick black lines. Contributions to the total fluxes come from the heated white dwarf, from the accretion column, and from the accretion stream (the secondary star contributes too little to show up in the graph). The angles $\vartheta$ indicate the angle between the magnetic field and the line-of-sight (cf. Fig. 3).

Figure 6: As Fig. 5, but assuming $i=35^{\circ }$, $\beta =70^{\circ }$.