A&A 372, 249-259 (2001)
DOI: 10.1051/0004-6361:20010285
U. G. Jørgensen1 - P. Jensen2 - G. O. Sørensen3 - B. Aringer4
1 - Niels Bohr Institute, Astronomical Observatory,
Juliane Maries vej 30, 2100 Copenhagen, Denmark
2 -
Theoretische Chemie, Bergische Universität - Gesamthochschule
Wuppertal, 42097 Wuppertal, Germany
3 -
H. C. Ørsted Institute, Universitetsparken 5, 2100 Copenhagen, Denmark
4 -
Institut für Astronomie der Universität Wien,
Türkenschanzstraße 17, 1180 Wien, Austria
Received 28 December 2000 / Accepted 16 February 2001
Abstract
We have performed a detailed ab initio computation of the dipole moment
surface, the vibrational transition moments, and the spectral lines for the
water molecule. A total of 412 vibrational eigenstates were identified below
30000 cm-1, corresponding to ![]() 85000 vibrational transitions.
In principle there are many billions of allowed vibration-rotation transitions
between these eigenstates. In our most complete test calculations we constructed a
list of 3 billion (
85000 vibrational transitions.
In principle there are many billions of allowed vibration-rotation transitions
between these eigenstates. In our most complete test calculations we constructed a
list of 3 billion (
![]() )
lines.
At room temperature, the computed monochromatic absorption coefficient is in good
overall agreement with the HITRAN data base, while at
higher temperatures its value exceeds the HITRAN-based absorption
coefficient by more than an order of magnitude, due to the lack of high excitation
lines in HITRAN. The agreement with the HITEMP version of HITRAN
is considerably better than with the standard HITRAN.
By comparing stellar model atmospheric structures and synthetic spectra based on our
most extensive
line list with results from calculations excluding the huge number of ultra-weak lines,
we conclude that when the lines are well chosen, a few times 10 million lines are more
than sufficient for all astrophysical purposes. We therefore offer to the community
a line list of 100 million lines, easily accessible by anonymous ftp.
Finally, we have compared results of synthetic
stellar spectra based on this line list with observed ISO spectra and have
found good agreement. In particular in the 2-4
)
lines.
At room temperature, the computed monochromatic absorption coefficient is in good
overall agreement with the HITRAN data base, while at
higher temperatures its value exceeds the HITRAN-based absorption
coefficient by more than an order of magnitude, due to the lack of high excitation
lines in HITRAN. The agreement with the HITEMP version of HITRAN
is considerably better than with the standard HITRAN.
By comparing stellar model atmospheric structures and synthetic spectra based on our
most extensive
line list with results from calculations excluding the huge number of ultra-weak lines,
we conclude that when the lines are well chosen, a few times 10 million lines are more
than sufficient for all astrophysical purposes. We therefore offer to the community
a line list of 100 million lines, easily accessible by anonymous ftp.
Finally, we have compared results of synthetic
stellar spectra based on this line list with observed ISO spectra and have
found good agreement. In particular in the 2-4 ![]() m region around the
strong fundamental bands, the agreement with observations is considerably better
than that obtained with other available water line lists.
m region around the
strong fundamental bands, the agreement with observations is considerably better
than that obtained with other available water line lists.
Key words: molecular data - astronomical data bases: miscellaneous - stars: atmospheres - stars: late-type - infrared: solar system - infrared: stars
Water vapour has been known for a long time to play a very important role in cool stellar atmospheres, but older models were only able to give a rough estimate of the size of the effects (Auman 1967). An important step forward was the laboratory measurement of the integrated intensity at elevated temperatures by Ludwig et al. (1973) and the statistical treatment of these data to generate synthetic line data and opacity samplings from which more realistic model atmospheres were constructed, first by Brown et al. (1989) and later by Plez et al. (1992). The first models based on real line list data for 2o were those of Jørgensen et al. (1994) based on a preliminary version of the present work. Later, several other models were constructed based on various versions of the list we present here, and full line list models were also constructed by Hauschildt et al. (1999); Allard et al. (2000) and others based on the NASA AMES line list by Partridge & Schwenke (1997).
Although several model atmospheres based on various, more or less preliminary versions of the present line list have been used in studies already published, our line list has never been properly finalised in a general, user-friendly form and presented in the literature. In the present work we therefore make up for this omission, and describe the "final'' vibration-rotation line calculation, its organisation, and results of comparison with other line list data and with observed stellar spectra. The resulting line list is easily available to the community by anonymous ftp. It exists in three well documented forms particularly suitable for stellar opacity calculations, for spectroscopic studies, and for planetary analysis, respectively.
The original dipole moment calculations, potential energy surface, and vibrational transitions moment calculations also used for the present version of the line list, were described by Jørgensen & Jensen (1993). With the rapid evolution of computer capacity during recent years, it has now become feasible to test the construction of line lists with several different parameter settings of the rotational parameters, and test these against each other. In the most complete setting we tested a line list containing almost 3 billion lines. This list is, however, not offered to the community other than in the form of an Opacity Sampling for the particularly interested reader, since it was soon realized that astrophysical calculations based on a few times 10 million lines are indistinguishable from the 3-billion-line-list results in all respects (except from the computing time). The three line lists that are made available are therefore a 100-million-lines list for high temperature opacity purposes (i.e. limited to information about gf values, excitation energies, and line strengths), a 1-million-lines list subsample with spectroscopic information for each line (quantum numbers etc.), and a 1-million-lines subsample particularly suitable for planetary atmospheric studies and other medium temperature studies.
In Sect. 2 we summarise the discussion of the vibrational band intensity calculations from the paper by Jørgensen & Jensen (1993) of relevance for the present study, in Sect. 3 we describe the calculation of the rotational transitions, in Sect. 4 we discuss the details of the line list itself, in Sect. 5 we compare the present work with other water line data in the literature, in Sect. 6 we analyse effects on the stellar atmospheric structure of 2o opacities calculated under various assumptions, and finally in Sect. 7 we compare synthetic spectra with observed stellar spectra of cool giant stars rich in gaseous water.
The dipole moment surface was computed at the MC and at the CI level by use of the CASSCF theory (see e.g. Roos et al. 1980 or Langhoff & Bauschlicher 1994 for basic definitions). 8 active electrons in 8 active orbitals were considered. The basis set was a GTO 13s 8p 4d/8s 3p basis on oxygen/hydrogen, contracted to 8s 6p 4d/6s 3p, extended from the work of van Duijneveldt (1971). Experiments with an extra d-function on hydrogen gave no changes in the intensities. At the SCF level this basis set compared well with the results for an un-contracted 15s 8p 4d 1f/10s 3p 1d GTO test basis set, even for very large bend and stretch displacements. The energy in the equilibrium configuration was 0.0014 hartree above the theoretical Hartree-Fock limit.
We describe the dipole moment in terms of its coordinates
![]() and
and
![]() along
axes p and q in the plane defined by the three nuclei.
The q axis bisects the bond angle
along
axes p and q in the plane defined by the three nuclei.
The q axis bisects the bond angle ![]() and points so that the
q coordinates of the two H nuclei (labelled 1 and 2, the
O nucleus is labelled 3) are positive.
The p axis is
perpendicular to the q axis
and points so that the p coordinate of nucleus 2 is positive.
The function
and points so that the
q coordinates of the two H nuclei (labelled 1 and 2, the
O nucleus is labelled 3) are positive.
The p axis is
perpendicular to the q axis
and points so that the p coordinate of nucleus 2 is positive.
The function
![]() is represented by the expansion
is represented by the expansion
The vibrational wavefunctions used for calculating the vibrational transition
moments were generated with the MORBID (Morse Oscillator
Rigid Bender Internal Dynamics) computer program (Jensen 1988).
The potential energy function is expressed as
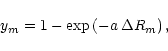 |
(4) |
In the MORBID approach, the rotation-vibration Hamiltonian
is approximated
by the sum of the potential energy function given in
Eq. (3) and an approximate kinetic energy operator obtained
as a fourth order expansion in the ym's and in the
conjugate momenta
![]() =
=
![]() .
The eigenvalues and eigenfunctions of this Hamiltonian are calculated
by diagonalization of a matrix representation for it;
the vibrational basis set used is a product of
.
The eigenvalues and eigenfunctions of this Hamiltonian are calculated
by diagonalization of a matrix representation for it;
the vibrational basis set used is a product of
For vibrational states whose energy has been experimentally measured, our calculated vibrational energy is generally within a few cm-1 of the corresponding experimental value. For a detailed comparison of rotation-vibration energy levels obtained with the potential energy surface used in the present work with experimental results, see Jensen (1989) or Fernley et al. (1991).
We obtain the matrix elements of the dipole moment components in
Eqs. (1) and (2) between the eigenfunctions
of Eq. (5) as
Our results for the intensities of the stronger bands generally
agree with recent laboratory values to within a few percent.
For the strongest fundamental mode (the bending mode at 6![]() m)
our result is 73 km mol-1 compared to 61
m)
our result is 73 km mol-1 compared to 61 ![]() 6 km mol-1for the average of seven recent experimental values.
For the two stretching modes (both close to 2.7
6 km mol-1for the average of seven recent experimental values.
For the two stretching modes (both close to 2.7![]() m) our
results are 45.4km mol-1 and 2.12km mol-1, while the
laboratory values listed in the HITRAN data base are
43.4km mol-1 and 2.98km mol-1, respectively.
These agreements are comparable to or better than the most accurate other
results found in the literature. A detailed description of our derived
integrated band intensities, and a comparison of these with
laboratory measurements, were given by Jørgensen & Jensen (1993).
m) our
results are 45.4km mol-1 and 2.12km mol-1, while the
laboratory values listed in the HITRAN data base are
43.4km mol-1 and 2.98km mol-1, respectively.
These agreements are comparable to or better than the most accurate other
results found in the literature. A detailed description of our derived
integrated band intensities, and a comparison of these with
laboratory measurements, were given by Jørgensen & Jensen (1993).
The average intensity of our computed combination bands follow the experimental values through the 9 orders of magnitude in the intensity reported on in the literature (Rothman et al. 1987, 1998), although, as expected, with a bigger scatter for the weaker bands. Most of the scatter in our data can be explained as pairs of bands which have similar experimental values for their band center frequencies, and therefore suffer from energy level mixing and corresponding intensity borrowing. For such pairs, our calculated intensity is higher than the experimental value for one member and lower for the other member, whereas there is a good agreement with the experiments for the average values of such pairs. In practice, the effect on the total opacity and on the stellar atmospheres will therefore be only marginal, because the effective frequency shift of the combined intensity of a pair, is very small compared to the overall spectral energy distribution.
When disregarding the effective intensity shift between such nearby pairs of bands, our computation of the band strengths are therefore in agreement with laboratory measured intensities to within the accuracy in the laboratory intensities over the complete 9 orders of magnitudes in intensity range covered by existing laboratory measurements.
If the discrepancies within pairs of bands are due to incomplete correction for intensity borrowing in the experimental intensities, use of the experimental intensities as input data for fitting of an empirical dipole moment surface would clearly lead to erroneous values of the resulting "fitted" intensities. This might be the explanation for the less accurate results obtained by fits to observed intensities (e.g., Iachello & Oss 1990), compared to our theoretically based intensities.
Our computations predict many undiscovered bands in the visual and near ultraviolet part of the spectrum with intensities comparable to the experimentally known bands at longer wavelengths, which has strong implications for astrophysics as well as for climate research.
The rotational lines including intensities were computed using conventional
rigid-rotor theory.
The rotational spectrum of water has been extensively studied in the laboratory
at ambient temperatures. For the lower vibrational levels the observed lines
can be fitted quite well using a standard Hamiltonian (see, for example, Sarka
& Demaison 2000), which, however, must
be expanded to include high orders of centrifugal distortion terms. At the
high temperature and low intensity limit required in the present calculations
we reach so high J-values that this type of expansions diverge, and
centrifugal distortion corrections were therefore neglected in producing
the line list. The rotational constants of the higher vibrational levels were
estimated by using a linear expansion in the harmonic quantum numbers.
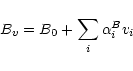 |
(8) |
| Rot. Const. | B0 |
|
|
|
| A | 27.8806 | 0.495 | -3.2488 | 1.234 |
| B | 14.5218 | 0.224 | -0.1655 | 0.112 |
| C | 9.2777 | 0.145 | 0.1488 | 0.169 |
This procedure will of course not automatically ensure a desired accuracy for line identification in high resolution spectroscopy, which is not the primary aim of our list. For such purposes, however, laboratory line lists (for example HITRAN; Rothman et al. 1998) exist, which can be used alone or in combination with the SCAN 2o list.
The list of vibrational-rotational lines for 2o, computed as described above, is available to the community as part of the SCAN line list data base (Jørgensen 1995, 1997). Experience with computation (and use in stellar astronomy) of line list data for other molecules has taught us that it is crucial for the resulting stellar atmosphere, and for the computed synthetic spectra, that the line list be as complete as possible (see for example Jørgensen & Larsson 1990).
For the diatomic molecules in the SCAN data base line list, the completeness has been assured by computing basically all allowed transitions with excitation energy up to the dissociation limit. For CN, for example, this procedure led to a list of 4 million lines (Jørgensen & Larsson 1990).
For 2o this approach is not possible because, in
principle, it would lead to a listing of billions of lines (![]() 85000
vibrational transitions
85000
vibrational transitions ![]() a few hundred rotational levels per band
a few hundred rotational levels per band
![]() the existing branches
the existing branches ![]() a large number of different values
of
a large number of different values
of ![]() for each vib-rot transition).
As will be shown in the following section, for applications of the line list
it is - fortunately enough - sufficient to consider only a few times 10 million lines.
for each vib-rot transition).
As will be shown in the following section, for applications of the line list
it is - fortunately enough - sufficient to consider only a few times 10 million lines.
The procedure of ensuring that sufficiently many vibrational levels are considered has been the same as used for the previous lists. To ensure that sufficiently many rotational transitions are included for each band, we include increasingly weaker lines (at 3500 K) until a convergence in the model atmosphere structure and the synthetic spectrum is reached. This procedure will ensure inclusion of enough lines to exceed the computational (and measurable) accuracy for the integrated opacity, model structures, and low resolution spectroscopy, for high temperature gas conditions (and hence for any conditions).
In order to consider all vibrational transitions up to the dissociation
energy (![]() 40000 cm-1), it would be necessary to consider
energy levels with quantum numbers up to (v1,v2,
40000 cm-1), it would be necessary to consider
energy levels with quantum numbers up to (v1,v2,
![]() (estimated from use of second order molecular
constants fitted to measured energy levels).
In our computation we considered all energy levels up
to (v1,v2,
(estimated from use of second order molecular
constants fitted to measured energy levels).
In our computation we considered all energy levels up
to (v1,v2,
![]() .
This choice
ensures that energy levels corresponding to
.
This choice
ensures that energy levels corresponding to ![]() 98% of the vibrational
partition function for temperatures up to 6000K are included in the
computation. We will say that in this sense the band list is 98% complete.
Our relative choice of maximum quantum numbers is internally slightly
inconsistent, in the sense that the stretching levels are computed to
higher energies than the bending levels, but it still ensures a very high
degree of completeness, and ensures that the considered vibrational
transitions are reduced from
98% of the vibrational
partition function for temperatures up to 6000K are included in the
computation. We will say that in this sense the band list is 98% complete.
Our relative choice of maximum quantum numbers is internally slightly
inconsistent, in the sense that the stretching levels are computed to
higher energies than the bending levels, but it still ensures a very high
degree of completeness, and ensures that the considered vibrational
transitions are reduced from
![]() (1213 being
the number of energy levels with
(1213 being
the number of energy levels with ![]() cm-1),
to
cm-1),
to
![]() .
.
| Temp. |
|
|
|
| 1000. | 1.1239 | 1.1239 | 1.1230 |
| 2000. | 1.7085 | 1.7084 | 1.6925 |
| 3000. | 2.7886 | 2.7853 | 2.7095 |
| 4000. | 4.4637 | 4.4571 | 4.2256 |
| 5000. | 6.8499 | 6.8786 | 6.3191 |
| 6000. | 10.0225 | 10.2293 | 9.0769 |
We show in Table 2 the vibrational partition function as derived
from a summation of the MORBID energy levels,
from a summation of all energy levels with ![]() cm-1 (computed by
use of second order molecular constants), and as the standard analytical
formula derived from the harmonic oscillator approximation,
cm-1 (computed by
use of second order molecular constants), and as the standard analytical
formula derived from the harmonic oscillator approximation,
![]() ).
The fact that the partition function is smaller for T = 2000K to 4000K
when summed over all anharmonic energy levels up to 40000 cm-1
than when summed over the MORBID energy levels up to 30000 cm-1,
reflects that the MORBID energy levels and the anharmonic
molecular constant energy levels are not identical for low
vibrational quantum numbers. The MORBID approximation gives a
better fit to the observed energy levels. For these temperatures we
will therefore say that the partition function is 100% complete within the
uncertainty in the determination of the energy levels.
).
The fact that the partition function is smaller for T = 2000K to 4000K
when summed over all anharmonic energy levels up to 40000 cm-1
than when summed over the MORBID energy levels up to 30000 cm-1,
reflects that the MORBID energy levels and the anharmonic
molecular constant energy levels are not identical for low
vibrational quantum numbers. The MORBID approximation gives a
better fit to the observed energy levels. For these temperatures we
will therefore say that the partition function is 100% complete within the
uncertainty in the determination of the energy levels.
In stellar atmospheres the partial pressures of 2o are negligible above
![]() K,
and our vibrational band calculation is therefore 100% complete for stellar atmosphere
computations in the sense described above.
K,
and our vibrational band calculation is therefore 100% complete for stellar atmosphere
computations in the sense described above.
The latest version of the HITRAN data base (Rothman et al. 1998) includes data for
47716 lines of 1H216O from 86 vibrational transitions. Of these bands, 72 are
from the vibrational ground level (000), while 14 bands are hot bands of some of these, from
vibrational states with
![]() or 020. Typically, the highest rotational quantum number encountered
for each band is around
or 020. Typically, the highest rotational quantum number encountered
for each band is around
![]()
![]() from 3 to 20).
This listing is highly valuable for spectroscopic identification of strong lines
in stellar spectra, and for construction of absorption coefficients at temperatures
close to room temperature. For the higher temperatures often encountered in
astrophysical situations, this listing is insufficient for construction of
the absorption coefficient.
from 3 to 20).
This listing is highly valuable for spectroscopic identification of strong lines
in stellar spectra, and for construction of absorption coefficients at temperatures
close to room temperature. For the higher temperatures often encountered in
astrophysical situations, this listing is insufficient for construction of
the absorption coefficient.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2616f1.ps}\end{figure}](/articles/aa/full/2001/22/aah2616/Timg74.gif) |
Figure 1: Comparison of absorption coefficients calculated from the line list data in HITRAN (thin lines) and in the present work (thick lines), at the three different temperatures given in the panels. |
| Open with DEXTER | |
In Fig.1 we compare the absorption coefficient calculated based on
the HITRAN data base line list and based on our line list. Both absorption coefficients
are calculated by folding each line with a Gausian profile with a half-width of 3 km s-1.
Lower panel is for T = 296K, middle panel for
![]() K, and upper
panel is for
K, and upper
panel is for
![]() K. It is immediately seen that while there is a good
overall agreement between the two lists at room temperature, the integrated absorption
coefficient due to our list divided by the corresponding number for the HITRAN list
increases rapidly with temperature. This is an effect of the lack of hot bands
starting in higher excited states,
weak bands in general, and lines with high rotational quantum number, in the
HITRAN listing. At 3900K the ratio of the two absorption coefficients, integrated over
the spectral interval shown in Fig.1, is approximately 20. This means that
lines accounting for 95% of the integrated absorption coefficient (at this temperature)
are missing in the HITRAN line list.
K. It is immediately seen that while there is a good
overall agreement between the two lists at room temperature, the integrated absorption
coefficient due to our list divided by the corresponding number for the HITRAN list
increases rapidly with temperature. This is an effect of the lack of hot bands
starting in higher excited states,
weak bands in general, and lines with high rotational quantum number, in the
HITRAN listing. At 3900K the ratio of the two absorption coefficients, integrated over
the spectral interval shown in Fig.1, is approximately 20. This means that
lines accounting for 95% of the integrated absorption coefficient (at this temperature)
are missing in the HITRAN line list.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2616f2.ps}\end{figure}](/articles/aa/full/2001/22/aah2616/Timg77.gif) |
Figure 2: Comparison of absorption coefficients calculated from the line list data in HITEMP (thin lines) and in the present work (thick lines), at the three different temperatures given in the panels. |
| Open with DEXTER | |
The data base HITEMP is a high temperature extension of the HITRAN data base for the molecules 2o, CO2, and CO. It includes almost 1.3 million lines for 2o. At 3900K the integrated absorption coefficient is 3 times larger than the one from HITRAN. At 1600K the integrated absorption coefficient of the two compilations differ by only 4%, but the main difference is the many weak lines included in the HITEMP list, which result in a much higher absorption coefficient inbetween the strong absorption bands, with important implications for stellar spectrum synthesis. This list is highly recommendable for identification of individual vibration-rotation lines in stellar spectra. Since it is a direct compilation of laboratory data, it has a much better accuracy in the frequencies of individual lines than our computed line list, and yet it contains probably all lines that will be individually visible in stellar spectra. It is often forgotten in analysis of stellar spectra that also the laboratory measurements of weak lines have quite a large uncertainty in the estimated absolute value of the intensity. For quantitative stellar analysis it is therefore recommendable to consult several estimates of the gf-values, and in this sense our list and the HITEMP list are important complements, because the HITEMP list relies completely on measured values, while our list relies solely on computed values, and this is the basic reason why we offer also a small 1-million-lines list for spectroscopic identification although it will be inferior to the HITEMP list concerning the line positions. Figure 2 compares the low resolution integrated absorption coefficient of the HITEMP data with corresponding results from our full line list compilation.
In a previous paper (Jørgensen & Jensen 1993) we compared the integrated room-temperature absorption coeffcients of all bands listed in the HITRAN data base with the corresponding numbers from our list. For the stronger bands the general agreement is within a few percent, while typical ratios between our band intensity values and those from HITRAN (at room temperature) vary from 0.3 to 3 for the very weakest bands, which are up to 9 orders of magnitude weaker than the fundamental bands. The agreement for pairs of possible intensity mixed bands is considerably better than for individual bands, as described above. The uncertainty is probably within the uncertainty of the laboratory measurements, judged from the results of independent measurements where available. The uncertainty in the ab initio intensities are very hard to judge other than from comparison with laboratory measurements.
While it is therefore not obvious that the derived values from laboratory measurements
are more "correct" than the theoretically derived ones, we experimented with the results of
scaling all bands in our calculation to the values listed in the HITRAN data base.
At least this procedure will give some kind of estimate of the uncertainty of the
computed monochromatic absorption coefficient.
The scaling was done by first determining the ratios of our values for
the temperature independent
band strengths (i.e., the vibrational transition moments) to those of HITRAN
for the 72 bands in the HITRAN list that originate from the vibrational
ground state. It was assumed that this ratio is constant for all hot bands of a
given band. With this assumption, the monochromatic absorption coefficient was
calculated for all the 72 bands and their hot bands at all temperatures. This absorption
coefficient was then complemented with the pure ab initio results for the bands
that have no listing in HITRAN.
In this way the bulk of the absorption coefficient has been scaled.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{h2616f3.ps}\end{figure}](/articles/aa/full/2001/22/aah2616/Timg78.gif) |
Figure 3: Absorption coefficients at 296K calculated with (thin grey line) and without (thick black line) scaling (as described in the text) to the band intensities given in the HITRAN data base. |
| Open with DEXTER | |
The result of the scaling is shown in Fig.3 for the spectral interval
from 0.7 to 3.0 ![]() m. At longer wavelengths (where the integrated absorption
coefficient is dominated by few strong vibrational bands) the two absorption coefficients
are indistinguishable on a plot of the scale of Fig. 3.
The two most pronounced differences in the figure are for the weak bands near 1.6
m. At longer wavelengths (where the integrated absorption
coefficient is dominated by few strong vibrational bands) the two absorption coefficients
are indistinguishable on a plot of the scale of Fig. 3.
The two most pronounced differences in the figure are for the weak bands near 1.6 ![]() m and
near 2.2
m and
near 2.2![]() m. However, being in the weak part of the absorption
coefficient, the final computed spectrum in these two regions are sensitive also to other
molecular absorbers, and to the quality of the continuum drawing.
m. However, being in the weak part of the absorption
coefficient, the final computed spectrum in these two regions are sensitive also to other
molecular absorbers, and to the quality of the continuum drawing.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{h2616f4.ps}\end{figure}](/articles/aa/full/2001/22/aah2616/Timg80.gif) |
Figure 4:
The synthetic spectrum of a
|
| Open with DEXTER | |
The major difference near peaks of the monochromatic absorption coefficient is seen to be
for the three bands near 0.7, 0.8, and 0.9![]() m. In most stellar objects cool enough
to show signatures of water, this region
of the spectrum is, however, dominated by strong bands of TiO, and these water bands are
therefore hardly visible. The most pronounced difference between scaled and non-scaled results
for normal stellar spectra therefore ends up being the strong band centered around 1.9
m. In most stellar objects cool enough
to show signatures of water, this region
of the spectrum is, however, dominated by strong bands of TiO, and these water bands are
therefore hardly visible. The most pronounced difference between scaled and non-scaled results
for normal stellar spectra therefore ends up being the strong band centered around 1.9![]() m.
The two strongest vibrational transitions in this region are the 011 and
the 110 combination bands, with intensities at room temperature of 4.84 km mol-1 and 0.224 km mol-1according to HITRAN and of 6.65 km mol-1 and 0.143 km mol-1 from our calculation.
m.
The two strongest vibrational transitions in this region are the 011 and
the 110 combination bands, with intensities at room temperature of 4.84 km mol-1 and 0.224 km mol-1according to HITRAN and of 6.65 km mol-1 and 0.143 km mol-1 from our calculation.
While Fig.3 shows the effect on the monochromatic absorption coefficient,
Fig.4 shows the corresponding effect on the resulting spectra for a stellar
atmospheric model of
![]() = 3000K,
= 3000K, ![]() = 0.0, and solar metallicity. Obviously, the
intensity of the scaled spectral feature around 1.9
= 0.0, and solar metallicity. Obviously, the
intensity of the scaled spectral feature around 1.9![]() m is slightly weaker than the un-scaled one.
The magnitude of the effect is, however, seen to be relatively small, and it is for the moment not clear
which of the two predicted spectra is in best agreement with stellar observations.
m is slightly weaker than the un-scaled one.
The magnitude of the effect is, however, seen to be relatively small, and it is for the moment not clear
which of the two predicted spectra is in best agreement with stellar observations.
After we had first announced our line list calculation (Jørgensen & Jensen 1993;
Jørgensen et al. 1994), a similar calculation was performed at
NASA AMES (Partridge & Schwenke 1997) based on the same ( CASSCF) ab initio
theory as in our calculation. The main difference between our calculation and
the NASA AMES calculation (hereafter the PS97 list) is that the PS97 list include more
observational data from the HITRAN data base into the list. The main philosophy behind
this inclusion was to first compute the potential purely ab initio and then
adjust it until an optimal fit to the line frequencies in the HITRAN
line list was obtained. The main advantage of this procedure is that the line frequencies
agree with laboratory work, while the main disadvantage is that possibly misidentifications
and other uncertainties in the laboratory work to a large degree are transferred into the
theoretical results.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2616f5.ps}\end{figure}](/articles/aa/full/2001/22/aah2616/Timg81.gif) |
Figure 5: Comparison of the absorption coefficients calculated based on the NASA AMES line list data (thin lines) and in the present work (thick lines). |
| Open with DEXTER | |
In Fig.5 we compare the monochromatic absorption coefficient calculated from
our own list with that obtained from the PS97 list. At room temperature (lowest panel in Fig.5)
we recognize the differences seen also in
Fig.3 (the peaks near 0.7, 0.8, and 0.9![]() m,
and the minima near 1.6 and 2.1
m,
and the minima near 1.6 and 2.1![]() m), while another major difference
is in the 4-5
m), while another major difference
is in the 4-5![]() m region. In particular the 4-5
m region. In particular the 4-5![]() m discrepancy can be traced
to the higher temperatures in the two upper panels (
m discrepancy can be traced
to the higher temperatures in the two upper panels (
![]() K and
K and
![]() K).
At high temperatures also the discrepancies around 10
K).
At high temperatures also the discrepancies around 10![]() m and at wavelengths shorter than
m and at wavelengths shorter than
![]()
![]() m become pronounced. In Sect.7 below, we compare results from
both line lists with observed spectra from the ISO satellite.
m become pronounced. In Sect.7 below, we compare results from
both line lists with observed spectra from the ISO satellite.
The University College London line list (hereafter UCL97; Viti et al. 1997) is based on a method where very accurate frequencies can be achieved, approaching the accuracy commonly obtainable in laboratory measurements. This method has proven very powerful for example for the identification of very high J, high excitation water lines in sun spot spectra (Polyansky et al. 1997). The computing time for this method is very high, and no line list sufficiently complete for stellar opacity calculations is yet available (Viti et al. 1997, and personal communication with J. Tennyson 2000).
Some effects of our computed opacities on the
model structure of a cool red giant are seen in Fig.6, where the
temperature as a function of geometrical depth in the atmosphere is shown.
The models are computed by use of various fractions of our computed
absorption coefficient for H2O, as indicated
in the legend, ranging from no H2O opacity included, over
all lines with intensity greater than 10-3 km mol-1(at 3500K), to all lines with intensity greater than 10-4,
10-5, 10-6, 10-7, and finally 10-20 km mol-1.
| |
Figure 6:
The temperature as function of geometrical depth in
model atmospheres of a red giant star of
|
| Open with DEXTER | |
It is seen that inclusion of the 50000 strongest lines (stronger than
10-2 km mol-1 at 3500 K), which together make up for ![]() 80% of
the integrated absorption coefficient, has almost no effect
on the structure, whereas inclusion of the remaining
80% of
the integrated absorption coefficient, has almost no effect
on the structure, whereas inclusion of the remaining ![]() 20% of the
opacity forces the atmosphere to increase
20% of the
opacity forces the atmosphere to increase ![]() 50% in size
(from 13 to almost 20 million km from atmospheric top to bottom).
Note also the great similarity (almost indistinguishability) of the
models based on 10 million, 30 million, and 3 billion lines, respectively.
50% in size
(from 13 to almost 20 million km from atmospheric top to bottom).
Note also the great similarity (almost indistinguishability) of the
models based on 10 million, 30 million, and 3 billion lines, respectively.
The model atmospheres shown here were computed based on the MARCS code, originally introduced by Gustafsson et al. (1975), and with updates and most of the modifications relevant for the present work being described in Jørgensen et al. (1992) and Jørgensen (1997). In addition to water, the models in Fig. 6 include opacities from TiO, CO, SiO, and OH. If TiO (the other strong absorber in these types of stars) is excluded from the opacity (as in Jørgensen et al. 1994), the effect of inclusion of the weak H2O lines is even more pronounced than shown in Fig.6. Also for dwarf stars, where the role of TiO relative to 2o is smaller, the effect of the weak 2o lines is bigger than illustrated in Fig. 6.
In Fig. 7 we show an observed SWS1 spectrum of the semiregular variable M-type giant star
SVPeg, obtained with the Infrared Space Observatory (ISO).
Details of this spectrum as well as other cool M-type stars from our ISO observation program will
be discussed separately in a second paper (Aringer et al. 2000, in preparation).
Together with the observed spectrum is also shown in Fig. 7 a synthetic spectrum,
computed from a model atmosphere of
![]() = 2900K,
= 2900K, ![]() = 0, Z = Z
= 0, Z = Z![]() ,
and the present line list of 2o (plus the opacity from TiO, CO, SiO, and OH, and with
the model and the spectrum computed mutually consistent).
,
and the present line list of 2o (plus the opacity from TiO, CO, SiO, and OH, and with
the model and the spectrum computed mutually consistent).
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{h2616f7.ps}\end{figure}](/articles/aa/full/2001/22/aah2616/Timg85.gif) |
Figure 7:
Comparison of an observed ISO spectrum of the M-type giant SVPeg (thick black line) and
our computed spectrum (thin grey line) in the region 2 to 5 |
| Open with DEXTER | |
Several vibrational bands of 2o contribute to the observed spectrum in this region.
The two strongest ones are the 001 fundamental (centered at 2.66![]() m) and the 100 fundamental
(centered at 2.73
m) and the 100 fundamental
(centered at 2.73![]() m). As noted above, our computed integrated band intensities
of these (at room temperature) are 45.4 km mol-1 and 2.12 km mol-1, respectively,
while the listed
values in HITRAN are 43.4 km mol-1 and 2.98 km mol-1, respectively. Also several
combination bands contribute in this region, the strongest one being the bending vibration
first overtone 020 at 3.17
m). As noted above, our computed integrated band intensities
of these (at room temperature) are 45.4 km mol-1 and 2.12 km mol-1, respectively,
while the listed
values in HITRAN are 43.4 km mol-1 and 2.98 km mol-1, respectively. Also several
combination bands contribute in this region, the strongest one being the bending vibration
first overtone 020 at 3.17![]() m, with a calculated and listed intensity of 0.61 km mol-1 and
0.456 km mol-1, respectively.
m, with a calculated and listed intensity of 0.61 km mol-1 and
0.456 km mol-1, respectively.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2616f8.ps}\end{figure}](/articles/aa/full/2001/22/aah2616/Timg86.gif) |
Figure 8: The separate contribution to the spectrum in Fig. 7 of the absorption from the molecules OH (top panel), CO (second panel from the top), SiO (third panel), and 2o (bottom panel). |
| Open with DEXTER | |
Other molecules than 2o contribute to the absorption in the SWS1 ISO region in M-type stars, too.
The most pronounced in the region plotted in Fig. 7 are OH, CO, and SiO. The individual
contributions of each of these molecules to the spectrum in Fig. 7 are shown
in panels 1 (OH), 2 (CO), and 3 (SiO) (from the top) in Fig. 8, together with the
contribution of 2o (lowest panel). All spectra in Fig. 8 are computed based
on the same model atmosphere structure, but including only the named species in the
spectrum computation. While 2o is the dominant absorber in all of the spectral region
plotted, also CO and SiO contribute substantially in the long-wavelength part of the region, and
near the short-wavelength edge of the SWS1 spectral capability at 2.3 ![]() m.
m.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h2616f9.ps}\end{figure}](/articles/aa/full/2001/22/aah2616/Timg87.gif) |
Figure 9:
Synthetic spectra in the 2.3 to 4.5 |
| Open with DEXTER | |
In Fig. 9 we show again the ISO spectrum of SVPeg in the 2.3-4.5![]() m
spectral region. From top to bottom in the figure, the panels show in addition to
the observed spectrum, the synthetic spectra computed from (1)
our present Scan 2o line list, (2) a sub-set of this list consisting
only of the lines with an intensity stronger than 10-5km mol-1 at 3500K, (3)
the PS97 list, and (4) the HITRAN data base line list.
All spectra are calculated from a model atmosphere with the same fundamental parameters as in
Figs. 7 and 8, and with the same line data for CO, SiO, OH, and TiO.
Only the line lists for water used in the model computations are different among the
four panels. The same line lists are adopted for the spectrum computation and the
underlying stellar models, such that the
spectra and the model atmospheres are mutually consistent.
m
spectral region. From top to bottom in the figure, the panels show in addition to
the observed spectrum, the synthetic spectra computed from (1)
our present Scan 2o line list, (2) a sub-set of this list consisting
only of the lines with an intensity stronger than 10-5km mol-1 at 3500K, (3)
the PS97 list, and (4) the HITRAN data base line list.
All spectra are calculated from a model atmosphere with the same fundamental parameters as in
Figs. 7 and 8, and with the same line data for CO, SiO, OH, and TiO.
Only the line lists for water used in the model computations are different among the
four panels. The same line lists are adopted for the spectrum computation and the
underlying stellar models, such that the
spectra and the model atmospheres are mutually consistent.
From the two upper most panels it is recognized that almost the same good agreement between the observed and the synthetic spectrum can be obtained from our full 3-billion-lines list and from the 1000 times smaller 3-million-lines list with only lines stronger than 10-5 km mol-1. The obvious conclusion that 3 million lines are sufficient for model and spectrum computations of cool stars, is not valid because most of the shown region is dominated by two of the strongest water bands. Figures 6 and 9 together do, however, illustrate that for most applications a line list of a few times 10 million lines is more than sufficient if the lines are selected wisely with a selection criterion based on the intensities at high temperature.
Panel 3 (from the top) in Fig. 9 shows the corresponding comparison between the observed
spectrum and a spectrum based on the PS97 water line list. The large difference
shown in Fig. 5 between our
line list and the PS97 list in the 3.5-5 ![]() m region manifests its effect
on the spectrum in this panel. The main difference between the two lists
was seen from Fig.5 to be a weaker absorption coefficient in the 4-5
m region manifests its effect
on the spectrum in this panel. The main difference between the two lists
was seen from Fig.5 to be a weaker absorption coefficient in the 4-5![]() m region
in the PS97 work (as in the HITRAN data) than in our data. The reason that the weaker PS97
absorption coefficient does not show up in Fig.9 as a weaker 3.5-5
m region
in the PS97 work (as in the HITRAN data) than in our data. The reason that the weaker PS97
absorption coefficient does not show up in Fig.9 as a weaker 3.5-5![]() m band, but
rather as a too strong absorption in the PS97 synthetic spectrum in the
2.5-3.5
m band, but
rather as a too strong absorption in the PS97 synthetic spectrum in the
2.5-3.5![]() m region, is mainly due
to the wavelength of normalization. We have chosen in all the
spectra shown here to use the same standard normalization at 3.8
m region, is mainly due
to the wavelength of normalization. We have chosen in all the
spectra shown here to use the same standard normalization at 3.8![]() m as in all our previous papers on
ISO observations, as first introduced in our paper on RScl (Hron et al. 1998).
The reason for this choice is the absorption minimum at wavelengths in this region,
which makes the normalization less dependent on the model structure and input data.
If we had chosen to normalize the spectra at shorter wavelengths (e.g. at 3
m as in all our previous papers on
ISO observations, as first introduced in our paper on RScl (Hron et al. 1998).
The reason for this choice is the absorption minimum at wavelengths in this region,
which makes the normalization less dependent on the model structure and input data.
If we had chosen to normalize the spectra at shorter wavelengths (e.g. at 3![]() m)
then the discrepancy between the PS97 synthetic spectrum and the observed spectrum would have
shown up as a flux excess in the PS97 spectrum in the 3.5-5
m)
then the discrepancy between the PS97 synthetic spectrum and the observed spectrum would have
shown up as a flux excess in the PS97 spectrum in the 3.5-5![]() m region instead.
m region instead.
The last panel in Fig. 9 shows the comparison of the observed spectrum with a synthetic
spectrum computed based on the HITRAN line list. At first glance the agreement could
look surprisingly good. However, several details have to be observed. First, the two flux
peaks (at ![]() 2.75
2.75 ![]() m and 3.1
m and 3.1 ![]() m) in the synthetic spectrum,
relative to the observed spectrum, in the middle of the strong water absorption,
bear witnesses to a lack of the veil of weak absorption usually characteristic
for a complete high-temperature monochromatic molecular absorption coefficient. Second, and more
important, is the almost total lack of absorption in between the main bands, seen in Fig. 9
as a coincidence between the spectrum and the theoretical continuum in the 3.5-4.0
m) in the synthetic spectrum,
relative to the observed spectrum, in the middle of the strong water absorption,
bear witnesses to a lack of the veil of weak absorption usually characteristic
for a complete high-temperature monochromatic molecular absorption coefficient. Second, and more
important, is the almost total lack of absorption in between the main bands, seen in Fig. 9
as a coincidence between the spectrum and the theoretical continuum in the 3.5-4.0 ![]() m
spectral region. This lack of continuum-like molecular line absorption has a strong effect on the model structure
and results in stronger bands (and lines) of basically all molecules other than the opacity-dominating species
(which is 2o here).
m
spectral region. This lack of continuum-like molecular line absorption has a strong effect on the model structure
and results in stronger bands (and lines) of basically all molecules other than the opacity-dominating species
(which is 2o here).
Because of this effect, in the bottom panel of
Fig. 9 the agreement with observations for the
SiO fundamental around 4![]() m and the wing of the CO fundamental around 4.5
m and the wing of the CO fundamental around 4.5![]() m
is worse than in the three other panels.
This disagreement will show up even more pronounced elsewhere in the spectrum for
trace elements, but it certainly is noteworthy, and hopefully thought-provoking, to see that the
less complete HITRAN line list appears at a first glance to be showing better agreement
with the observed spectrum than results obtained from the much more complete PS97 list.
It also stresses again the important lesson learned several times before (see e.g. Jørgensen 1989),
that the gross synthetic spectrum can in principle be in excellent agreement with observations
based on a completely wrong model, but that the opacity-weak structures are less likely to look
realistic based on a wrong model structure.
m
is worse than in the three other panels.
This disagreement will show up even more pronounced elsewhere in the spectrum for
trace elements, but it certainly is noteworthy, and hopefully thought-provoking, to see that the
less complete HITRAN line list appears at a first glance to be showing better agreement
with the observed spectrum than results obtained from the much more complete PS97 list.
It also stresses again the important lesson learned several times before (see e.g. Jørgensen 1989),
that the gross synthetic spectrum can in principle be in excellent agreement with observations
based on a completely wrong model, but that the opacity-weak structures are less likely to look
realistic based on a wrong model structure.
We have computed the transition moment of all 85000 vibrational bands due to the water molecule, between vibrational states with energies less than 30000 cm-1. From this complete set of vibrational transitions, line lists based on various settings of the rotational parameters were constructed and tested, the most complete resulting in 3 billion lines.
The resulting 3 billion lines and various sub-sets of these were used to construct opacity sampling functions, by which the effects on stellar atmospheres were analyzed.
It was shown that the interaction between radiation and the high-temperature
gases in a stellar atmosphere is
almost entirely by way of the many relatively weak lines with intensities
between 10-3 and 10-5 km mol-1 although they account for only
about 10% of the integrated opacity. Lines weaker than ![]() 10-6 km mol-1, although
numerous, cause no further change in the computed model atmospheric
structure.
10-6 km mol-1, although
numerous, cause no further change in the computed model atmospheric
structure.
There are about 100 million lines stronger than 10-9 km mol-1(at 3500 K), and these were concluded to be more than sufficient for constructing reliable model atmospheres involving the highest temperature gases up to temperatures where the water molecule dissociates. It was shown with an example that a synthetic spectrum with less than 10% of this number of lines was almost indistinguishable from a spectrum based on the 100-million-lines list (or the full 3-billion-lines list). Thus, it was concluded that the 100 million lines would be more than sufficient for all practical purposes, and the corresponding list was included in the Scan data base and made easily available to the community by anonymous ftp (ftp to stella.nbi.dk, login as anonymous with email address as password, and then cd to pub/scan). Also two, more easily manageable smaller subsets were placed in the Scan data base, particularly suitable for spectroscopic studies and for planetary atmospheric research.
Finally, the results from using the constructed Scan 2o line list were tested by comparison with SWS1 ISO spectra of the late type giant star SVPeg. Very good agreement was found between observed and computed spectra, and it was found that results based on our Scan 2o list were in considerably better agreement with observations than results based on any other available 2o line list data in the literature.
Acknowledgements
We are thankful to F. Kerschbaum for providing us the reduced ISO-SWS spectrum shown in Figs. 7 and 9, and to L. S. Rothman for providing us with the latest version of the HITRAN and the HITEMP line lists. This work was supported by the Danish Natural Science Research Council, the Deutsche Forschungsgemeinschaft, the Fonds der Chemischen Industrie, and the Austrian Science Fund (project S7308). Some of the work was carried out while P. J. was a visiting professor of the Japanese Ministry for Education, Science, and Culture (Monbusho) at the Institute of Astrophysics and Planetary Sciences, Ibaraki University, Mito, Japan. He is grateful for financial support and for hospitality, in particular to Takayoshi Amano.